DATCOM 4.1.1.4 に基づいて、2次元翼型の最大揚力係数を計算する。
はじめに
DATCOM 4.1.1.4 に基づいて、2次元翼型の最大揚力係数を計算する。
PDFのページは481ページ
Method
2次元翼型の最大揚力係数は以下の手順で計算する。
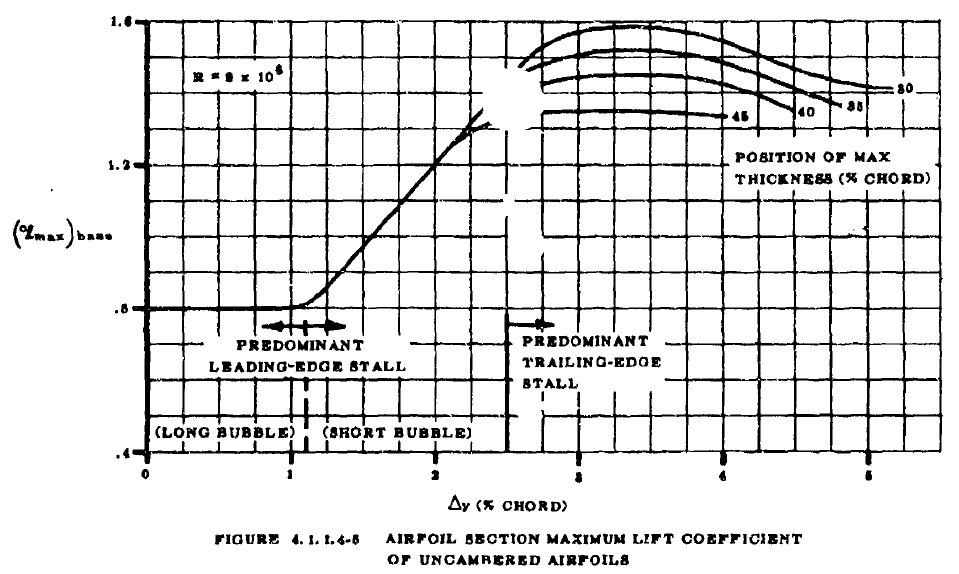
- FIGURE 4.1.1.4-5からsmooth leading-edge、\(Re=9\times 10^6\)における2次元最大揚力係数\(\left(c_{l_{max}}\right)_{base}\)を求める。(キャンバーありの翼型はキャンバーをゼロで固定)
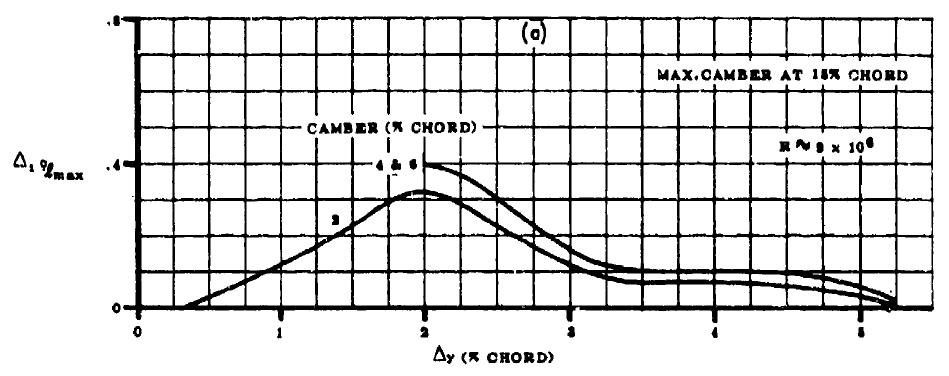
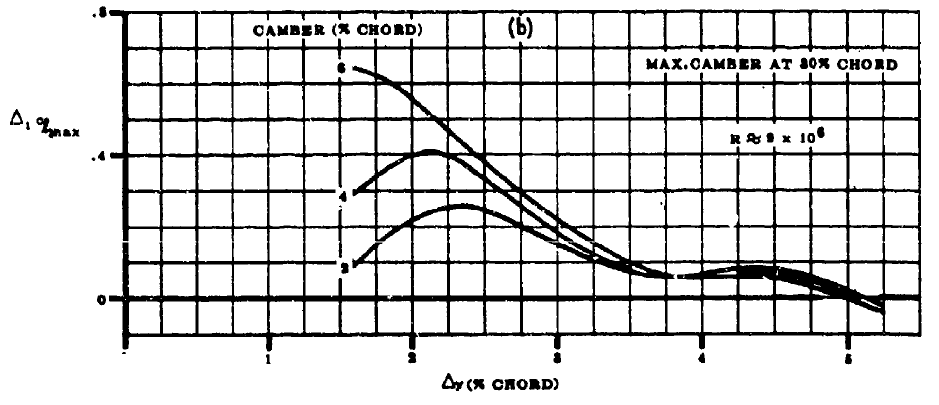
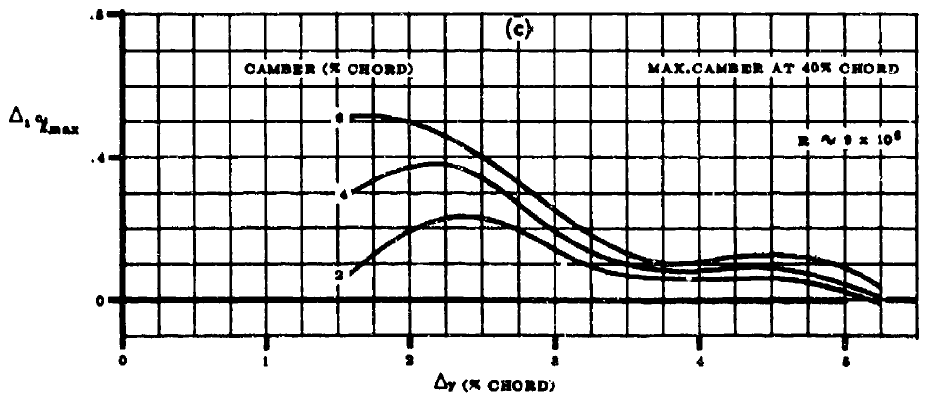
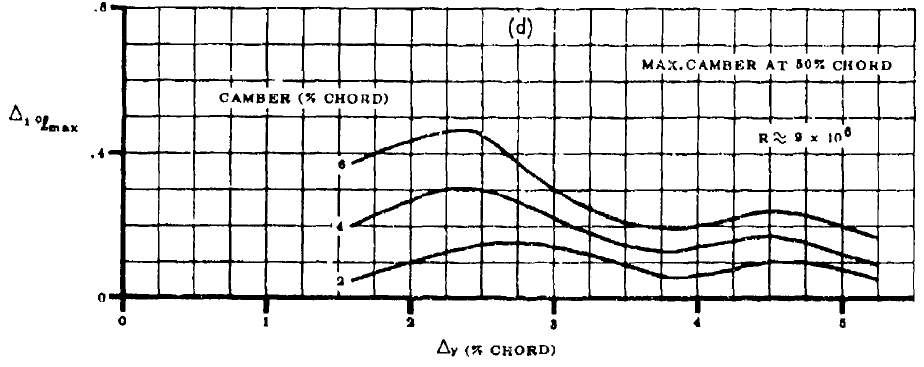
- FIGURE4.1.1.4-6からキャンバーがゼロ以外であるときの2次元最大揚力係数の補正量\(\Delta_{1} c_{l_{max}}\)を求める。(最大翼厚位置は30%で固定)
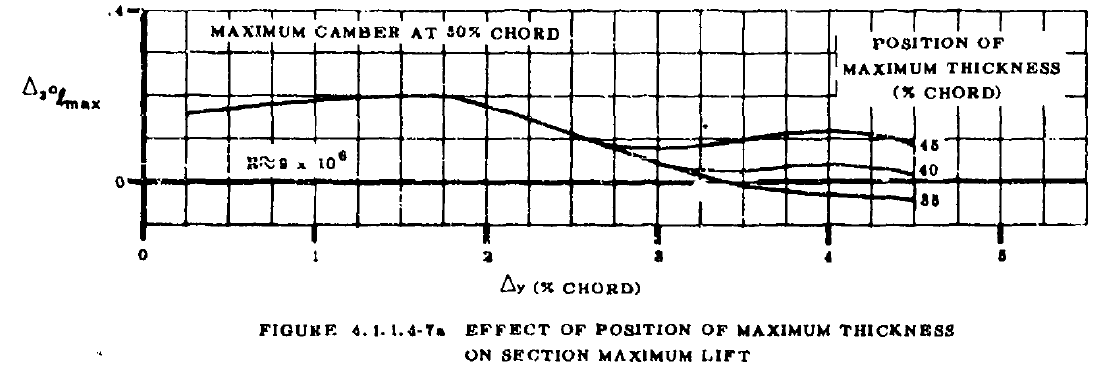
- FIGURE4.1.1.4-7aから最大翼厚位置が30%以外であるときの2次元最大揚力係数の補正量\(\Delta_{2} c_{l_{max}}\)を求める。(\(\Delta_{1} c_{l_{max}}\)に対する追加分)
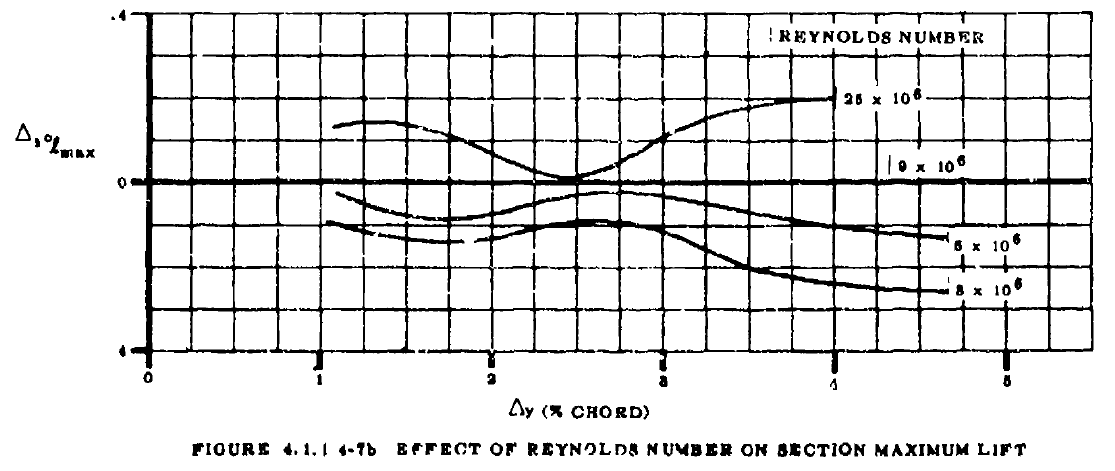
- FIGURE4.1.1.4-7bから\(Re=9\times 10^6\)以外における2次元最大揚力係数の補正量\(\Delta_{3} c_{l_{max}}\)を求める。
- FIGURE4.1.1.4-8aからroughnessに対する2次元最大揚力係数の補正量\(\Delta_{4} c_{l_{max}}\)を求める。
- \(M>0.2\)の場合、マッハ数に対する2次元最大揚力係数の補正量\(\Delta_{5} c_{l_{max}}\)を求める。ただし、\(\Delta_{5} c_{l_{max}}\)の推算に使える一般化された図表はないので、代表的な翼型についてのマッハ数補正量がFIGURE 4.1.1.4-8bから参照できる。
- 1.~6.で求めた値を合計して\(c_{l_{max}}\)を計算する。
\begin{align}
c_{l_{max}}=\left(c_{l_{max}}\right)_{base}+\Delta_{1} c_{l_{max}}+\Delta_{2} c_{l_{max}}+\Delta_{3} c_{l_{max}}+\Delta_{4} c_{l_{max}}+\Delta_{5} c_{l_{max}}
\tag{4.1.1.4-a}
\end{align}
ここで
| 文字 | 単位 | 説明 |
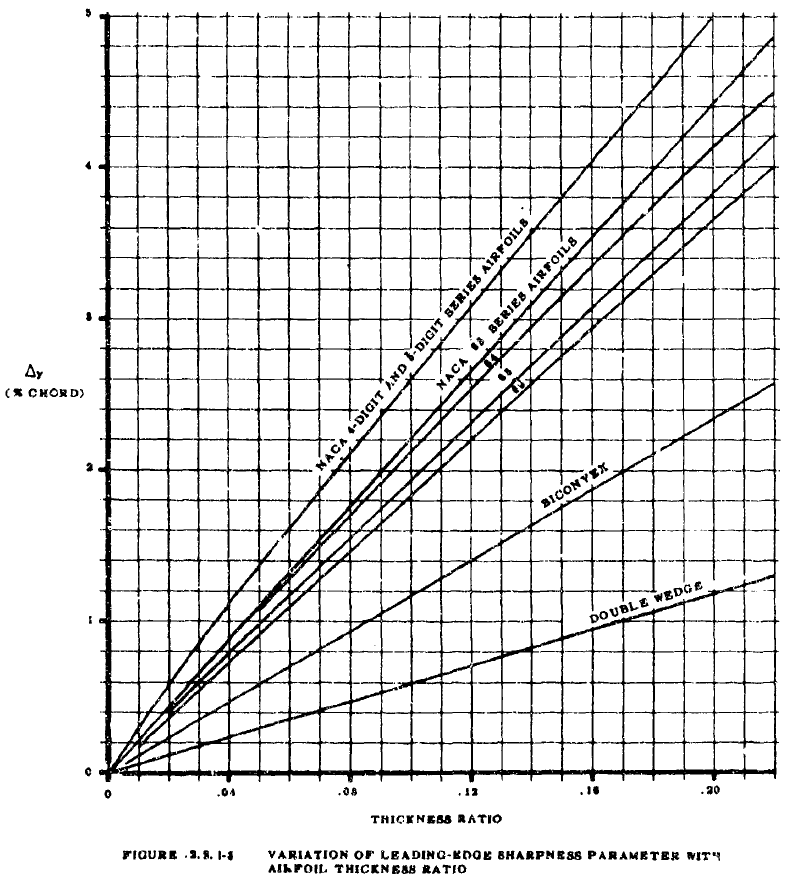
| \(\Delta y\) | %c | 6 [%c]および0.15 [%c]における翼上面のy座標の差。 キャンバーありの翼型はキャンバーをゼロにして計算する。 FIGURE2.2.1-8から求める。 |
reference
-
制限
この手法における注意点は以下の通り
- この計算式は、\(M<0.2\)で使用できる。ただし、試験データが利用可能ならいかなるときでもそちらを使った方がいい
Sample
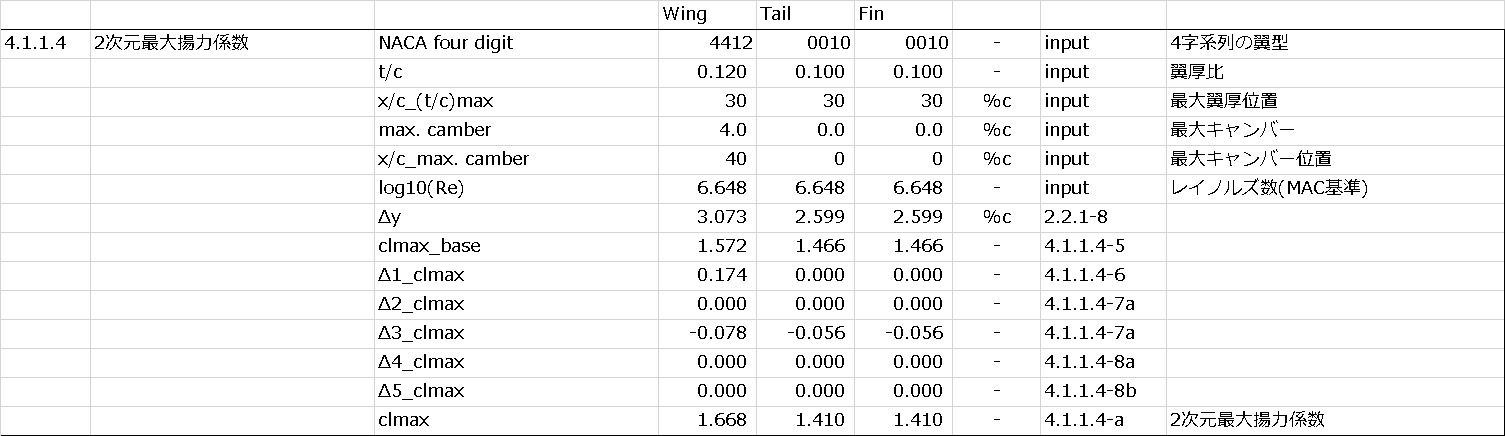
OpenVSPのExample FileにあるPod Planeについて、実際に計算してみる。
↓計算に使用したエクセルファイル(マクロ付き)
↓計算結果
以上
おわりに
DATCOM 4.1.1.4 に基づいて、2次元翼型の最大揚力係数を計算した。
↓次






コメント