DATCOM 4.1.3.1 に基づいて、3次元翼のゼロ揚力角を計算する。
はじめに
DATCOM 4.1.3.1 に基づいて、3次元翼のゼロ揚力角を計算する。
PDFのページは496ページ。
Method
ねじり下げなし、翼型一定の3次元翼では、翼平面形はゼロ揚力角にあまり影響しないため、断面翼型の特性をベースにゼロ揚力角を計算する。
3次元翼のゼロ揚力角\(\alpha_{0}\)は以下の式で計算する。
\begin{align}
& \left(\alpha_{0}\right)_{\theta=0}= \alpha_{i}-\frac{c_{l_{i}}}{c_{l_{\alpha}}}
~\mathrm{[deg]} \tag{4.1.3.1-a} \\\\
& \alpha_{0}= \left(\alpha_{0}\right)_{\theta=0}+\left(\frac{\Delta \alpha_{0}}{\theta}\right)\theta ~\mathrm{[deg]}
\tag{4.1.3.1-c} \\\\
\end{align}
最初にねじり下げなしのゼロ揚力角\(\left(\alpha_{0}\right)_{\theta=0} \)を計算してから、ねじり下げに対する補正を加えたゼロ揚力角\(\alpha_{0}\)を計算している。
ここで、
| 文字 | 単位 | 説明 |
| \(\left(\alpha_{0}\right)_{\theta=0} \) | deg | ねじり下げなしかつ翼型一定の3次元翼のゼロ揚力角 |
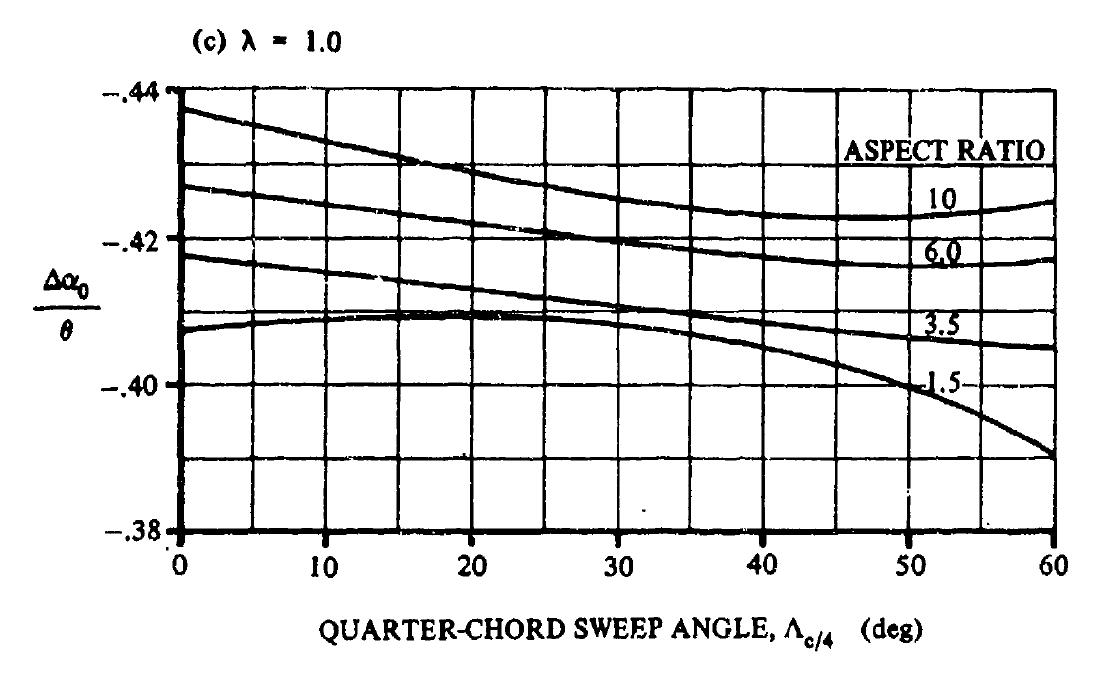
| \(\frac{\Delta \alpha_{0}}{\theta}\) | - | 線形ねじり下げ角に対するゼロ揚力角の変化率 FIGURE 4.1.3.1-4から求める |
| \(\theta \) | deg | ねじり下げ角（ねじり下げる方向が負） |
| \(\alpha_{i} \) | deg | section design lift coefficientとなるときの断面翼の迎角 DATCOM 4.1.1で計算する |
| \(c_{l_{i}} \) | - | section design lift coefficient 翼前縁にあたる流れの向きが翼前縁のキャンバーラインと一致するときの断面揚力係数 =抗力が最小になるときの断面揚力係数 DATCOM 4.1.1で計算する |
| \(c_{l_{\alpha}}\) | 1/deg | 断面揚力傾斜 DATCOM 4.1.1.2で計算する |
| 文字 | 単位 | 説明 |
| \(\Lambda_{c/4}\) | deg | 1/4コードライン後退角。 DATCOM 2.2.2で計算する。 |
| \(A\) | - | アスペクト比。 DATCOM 2.2.2で計算する。 |
| \(\lambda\) | - | テーパー比。 DATCOM 2.2.2で計算する。 |
なお、定義された翼型のコードラインが流れと平行でない場合（後退翼など）は、別途後退角に対する補正も必要になる
reference
-
制限
この手法における注意点は以下の通り。
- 翼型一定の3次元翼であること。
- 遷音速域であること。ただし、キャンバーを持つ翼型のゼロ揚力角はマッハ数によって変化するので、マッハ数が大きい場合は補正が必要である
Sample
OpenVSPのExample FileにあるPod Planeについて、実際に計算してみる。
↓計算に使用したエクセルファイル（マクロ付き）
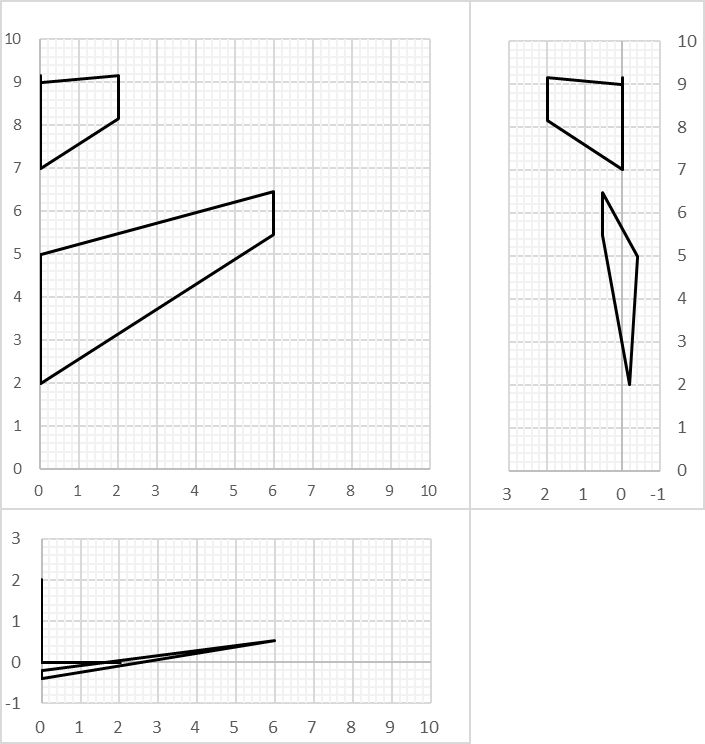
↓計算結果
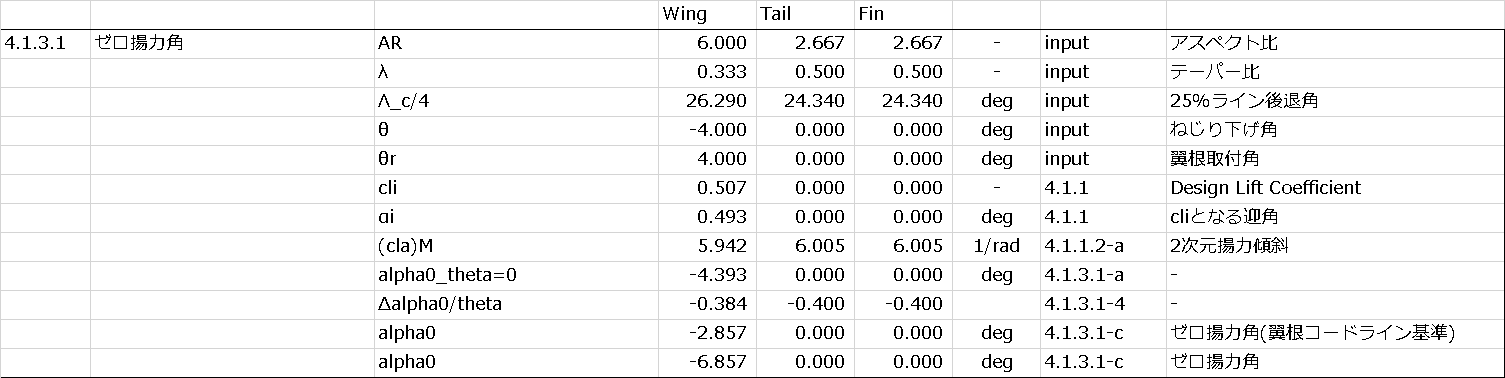
以上
おわりに
DATCOM 4.1.3.1 に基づいて、3次元翼のゼロ揚力角を計算した。
次↓
4.4.1-②
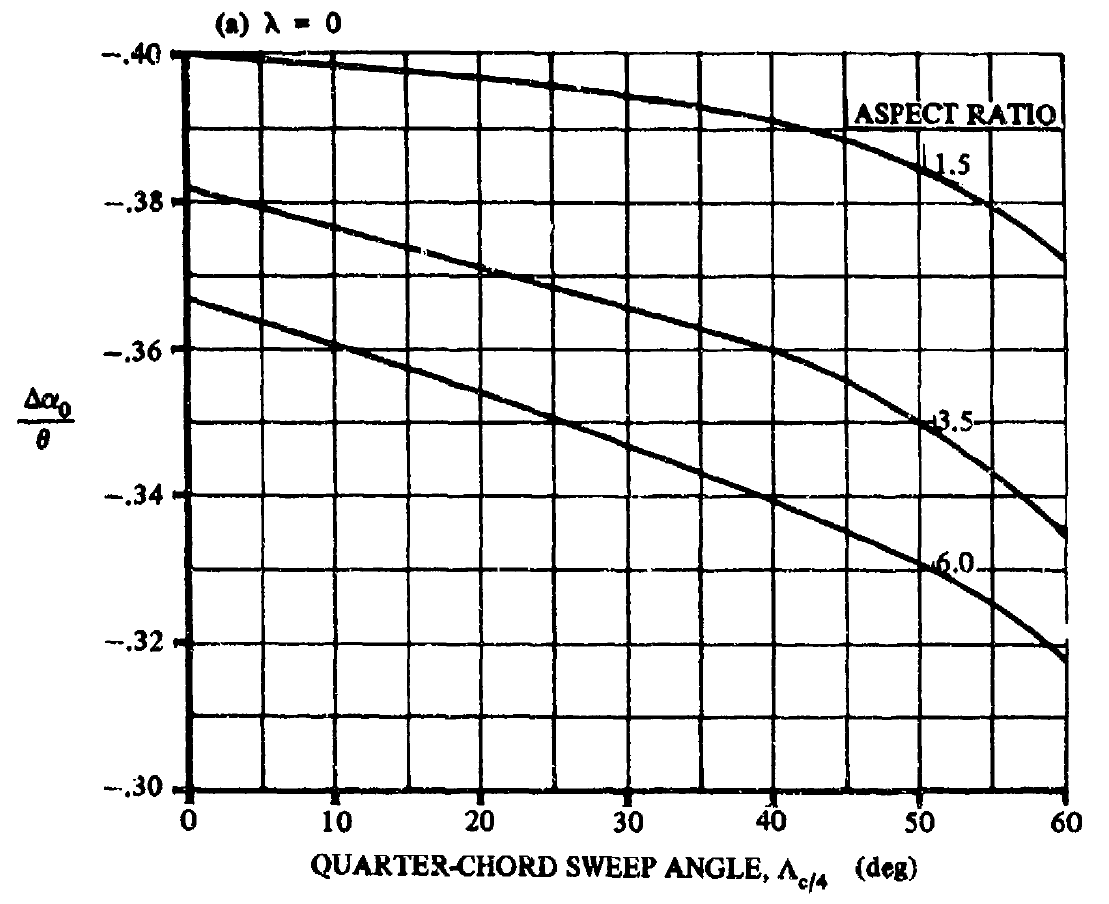
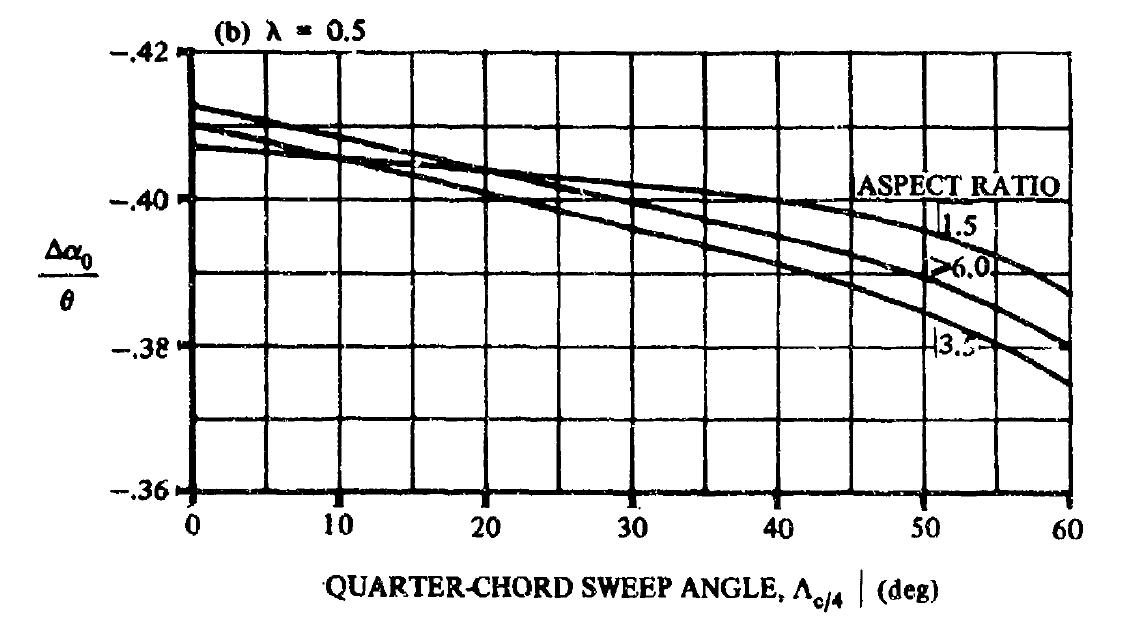
コメント