DATCOM 4.4.1 に基づいて、尾翼における吹き下ろし角の大きさを計算する。
はじめに
DATCOM 4.4.1 に基づいて、尾翼における吹き下ろし角の大きさを計算する。
PDFのページは1203ページ
Method 1
尾翼における吹き下ろし角の大きさは以下の手順で計算する。
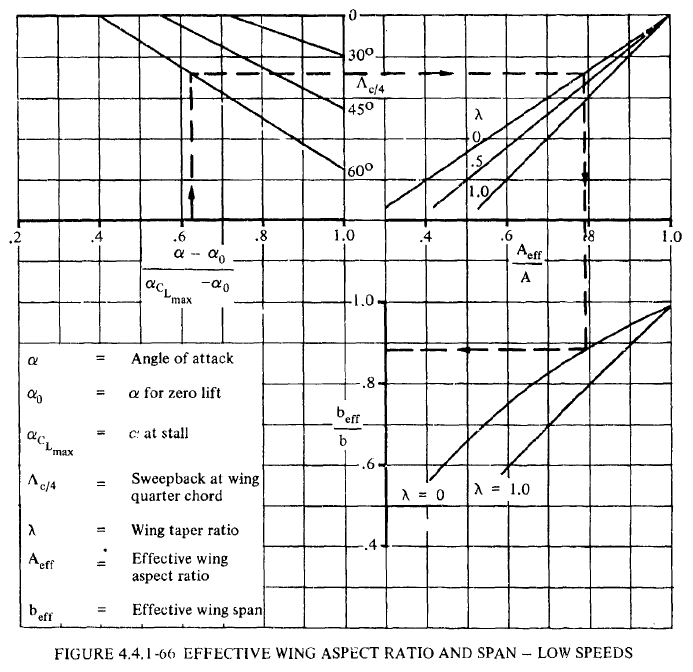
- FIGURE 4.4.1-66から有効アスペクト比\(A_{eff}\)および有効スパン\(b_{reff}\)を求める。
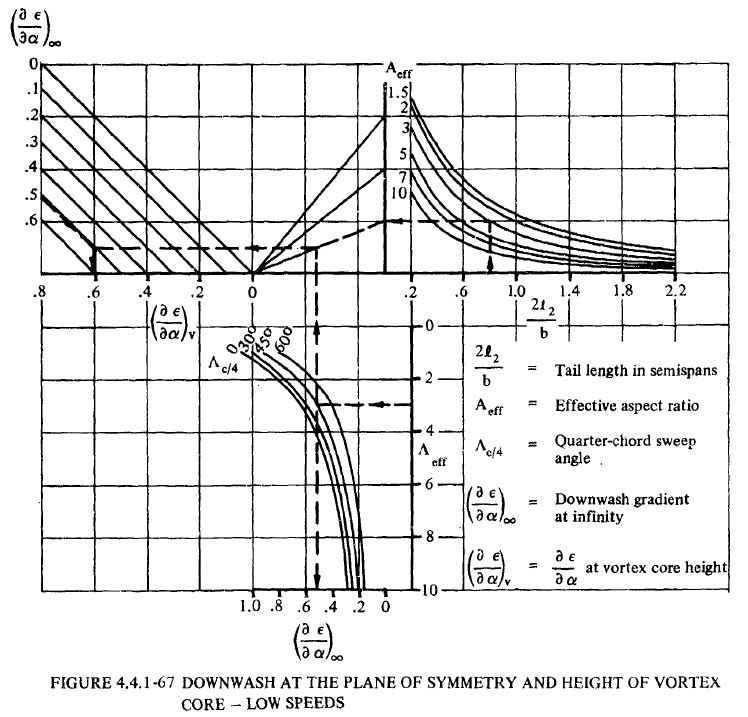
- FIGURE 4.4.1-67から対称面内のvortex coreの高さにおける吹き下ろし角変化\(\left(\partial \epsilon/\partial \alpha\right)_{v}\)を求める。
- 水平尾翼MACの25%コード位置に対するvortex coreの垂直方向距離\(a\)を計算する。
- 水平尾翼MACの25%コード位置におけるvortexのスパン\(b_{v}\)を計算する。
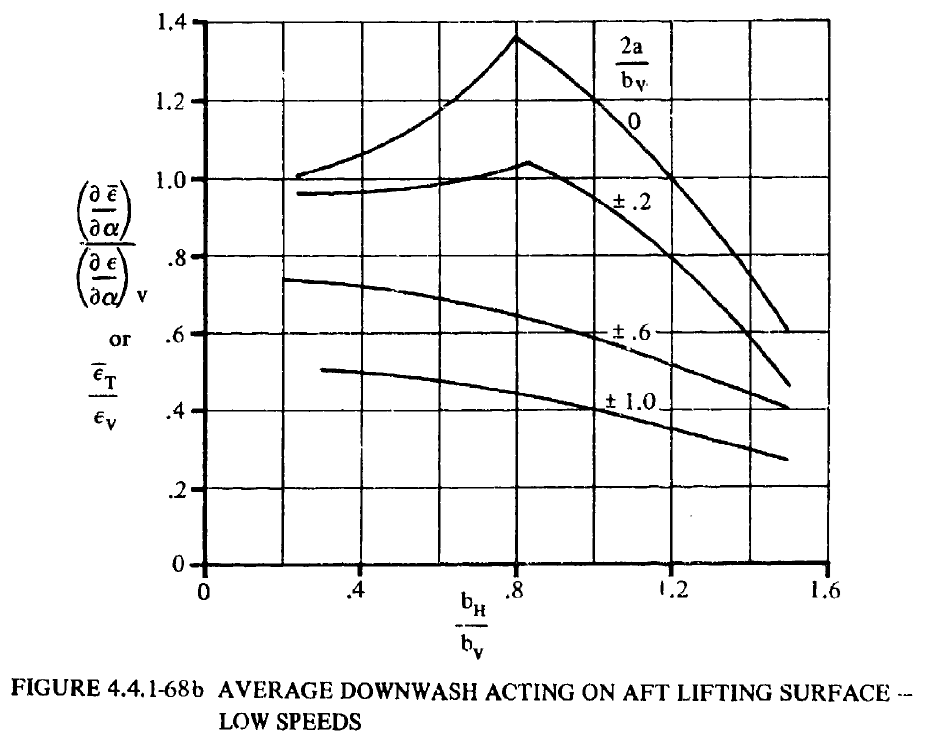
- FIGURE 4.4.1-68bから水平尾翼における平均吹き下ろし角変化\(\partial \overline{\epsilon}/\partial \alpha\)を求める。
- 遷音速域内でマッハ数が大きい場合はマッハ数に対する補正を行う。
- 平均吹き下ろし変化を積分することで、水平尾翼における平均吹き下ろし角\(\overline{\epsilon}\)を計算する。
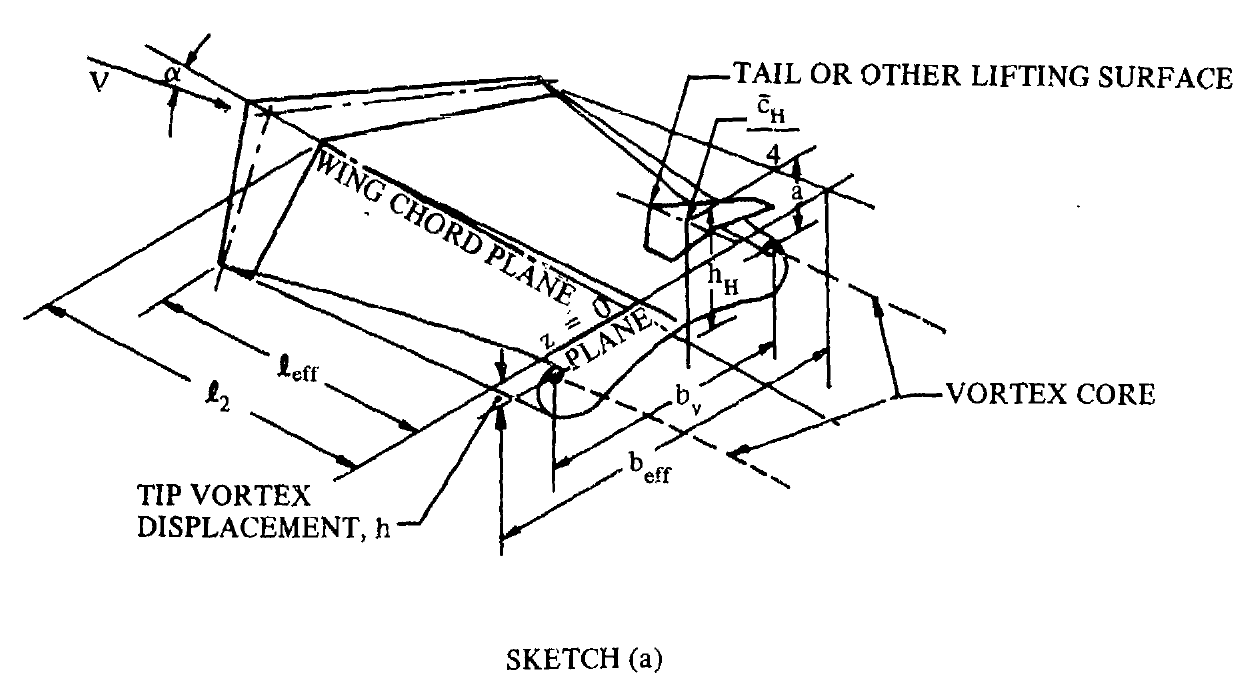
STEP 1
\(\frac{\alpha-\alpha_{0}}{\alpha_{C_{L_{max}}}-\alpha_{0}}\)、\(\Lambda_{c/4}\)、\(\lambda\)をもとに、FIGURE 4.4.1-66から\(\frac{A_{eff}}{A}\)および\(\frac{b_{eff}}{b}\)を読み取る。
ここで
| 文字 | 単位 | 説明 |
| \(\alpha\) | deg | 迎角。 |
| \(\alpha_{0}\) | deg | ゼロ揚力角。 DATCOM 4.1.3.1で求める。 |
| \(\alpha_{C_{L_{max}}}\) | deg | 最大揚力係数における迎角。 DATCOM 4.1.3.4で求める。 |
| \(\Lambda_{c/4}\) | deg | ¼コードライン後退角。 DATCOM 2.2.2で求める。 |
| \(\lambda\) | - | テーパー比。 DATCOM 2.2.2で求める。 |
| \(A_{eff}\) | - | 有効アスペクト比。 |
| \(b_{eff}\) | m | 有効スパン。 |
STEP 2
\(\frac{l_{2}}{(b/2)}\)、\(A_{eff}\)、\(\Lambda_{c/4}\)、をもとに、FIGURE 4.4.1-67から\(\left(\frac{\partial \epsilon}{\partial \alpha}\right)_v\)を読み取る。
ここで
| 文字 | 単位 | 説明 |
| \( l_{2} \) | m | 主翼翼根の後縁から水平尾翼MACの25%位置までの距離。(常に正の値) |
| \(A_{eff}\) | - | 有効アスペクト比。 FIGURE 4.4.1-66から求める。 |
| \(\Lambda_{c/4}\) | deg | ¼コードライン後退角。 DATCOM 2.2.2で求める。 |
| \(\left(\frac{\partial \epsilon}{\partial \alpha}\right)_v\) | - | 対称面内、水平尾翼MACの25%位置、主翼後流渦のコアの高さにおける吹き下ろし角変化率。 FIGURE 4.4.1-67から求める。 |
STEP 3
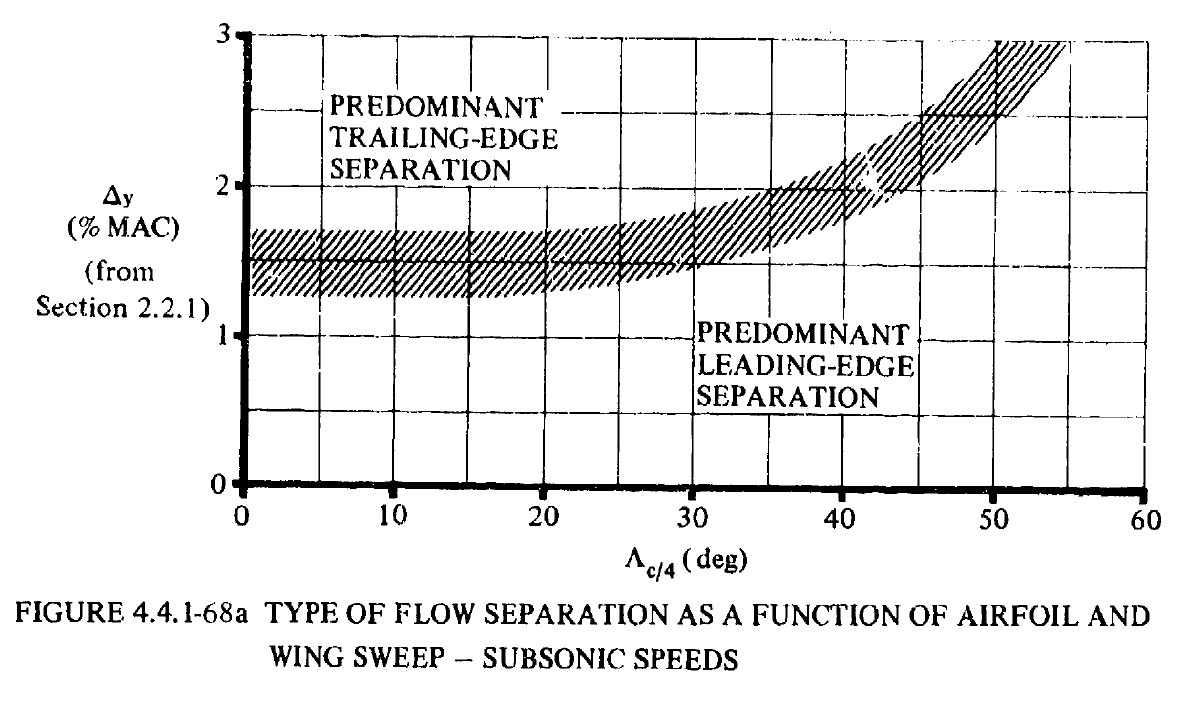
\(\Delta y\)、\(\Lambda_{c/4}\)、をもとに、FIGURE4.4.1-68aから剥離の種類(前縁剥離型/後縁剥離型)を読み取る。
剥離の種類が後縁剥離型なら式(4.4.1-c)、前縁剥離型なら式(4.4.1-d)を用いて\(a\)を計算する。
\begin{align}
a&=h_{_H}-l_{eff}\left(\alpha-\frac{0.41C_{L}}{\pi A_{eff}}\right)-\frac{b_{eff}}{2}\tan{\Gamma} \tag{4.4.1-c} \\\\
a&=h_{_H}-\left(l_{2}+l_{3}\right)\left(\alpha-\frac{0.41C_{L}}{\pi A_{eff}}\right)-\frac{b_{eff}}{2}\tan{\Gamma} \tag{4.4.1-d} \\\\
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(a\) | m | 水平尾翼MACの25%位置から翼端渦のコアまでの高さ方向の距離。 (コアよりも水平尾翼が上にあるとき正) |
| \(h_{_H}\) | m | 主翼翼根から水平尾翼MACの25%位置までの高さ方向の距離。 (主翼翼根よりも水平尾翼が上にあるとき正) |
| \(l_{eff}\) | m | 主翼翼端の25%位置から水平尾翼MACの25%位置までの距離。 (常に正の値) |
| \( l_{2} \) | m | 主翼翼根の後縁から水平尾翼MACの25%位置までの距離。 (常に正の値) |
| \(l_{3}\) | m | 主翼MACの前縁から主翼翼根の後縁までの距離。 (常に正の値) |
| \(\alpha\) | rad | 迎角。単位に注意。 |
| \(C_{L}\) | - | 主翼単体の揚力係数。 \(C_{L}=C_{L_{\alpha}}\left(\alpha-\alpha_{0}\right)\) |
| \(A_{eff}\) | - | 有効アスペクト比。 FIGURE 4.4.1-66から求める。 |
| \(b_{eff}\) | - | 有効スパン。 FIGURE 4.4.1-66から求める。 |
| \(\Gamma\) | deg | 主翼上反角。 |
STEP 4
水平尾翼MACの高さにおける後流渦のスパン\(b_{v}\)を次の式で計算する。
\begin{align}
b_{v}=b_{eff}-\left(b_{eff}-b_{v_{eff}}\right)\left(\frac{2l_{eff}}{b\xi_{ru}}\right)^{\frac{1}{2}} \tag{4.4.1-e}
\end{align}
ここで
\begin{align}
&b_{v_{ru}}=\left[0.78+0.10\left(\lambda-0.4\right)+0.003\Lambda_{c/4}\right)b_{eff} \tag{4.4.1-f} \\\\
&\xi_{ru}=\frac{0.56A}{C_{L}}
\end{align}
ただし、\(\Lambda_{c/4}\)の単位は[deg]
STEP 5
これまでに計算してきた\(\Delta y\)、\(\Lambda_{c/4}\)、をもとに、FIGURE4.4.1-68bから水平尾翼に作用する平均吹き下ろし角変化\(\frac{\partial \overline{\epsilon}}{\partial \alpha}\)を読み取る。
\begin{align}
\frac{\partial \overline{\epsilon}}{\partial \alpha}
=\frac{\frac{\partial \overline{\epsilon}}{\partial \alpha}}{\left(\frac{\partial \epsilon}{\partial \alpha}\right)_{v}}\left(\frac{\partial \epsilon}{\partial \alpha}\right)_{v}
\end{align}
STEP 6
遷音速域の中でも高速側の場合は、マッハ数に対する補正を加える。
STEP 7
平均吹き下ろし角変化を積分することで、平均吹き下ろし角を得る。
\begin{align}
\overline{\epsilon}=\int_{\alpha_{0}}^{\alpha}{\frac{\partial \overline{\epsilon}}{\partial \alpha}d\alpha}
\end{align}
reference
-
制限
この手法における注意点は以下の通り
- 水平尾翼位置で後流渦が完全にrolled upしていることを仮定しているため、テールアームが短く、テールの高さが後流渦のコアに近い場合は注意が必要
Sample(吹き下ろし角)
OpenVSPのExample FileにあるPod Planeについて、実際に計算してみる
↓計算に使用したエクセルファイル(マクロ付き)
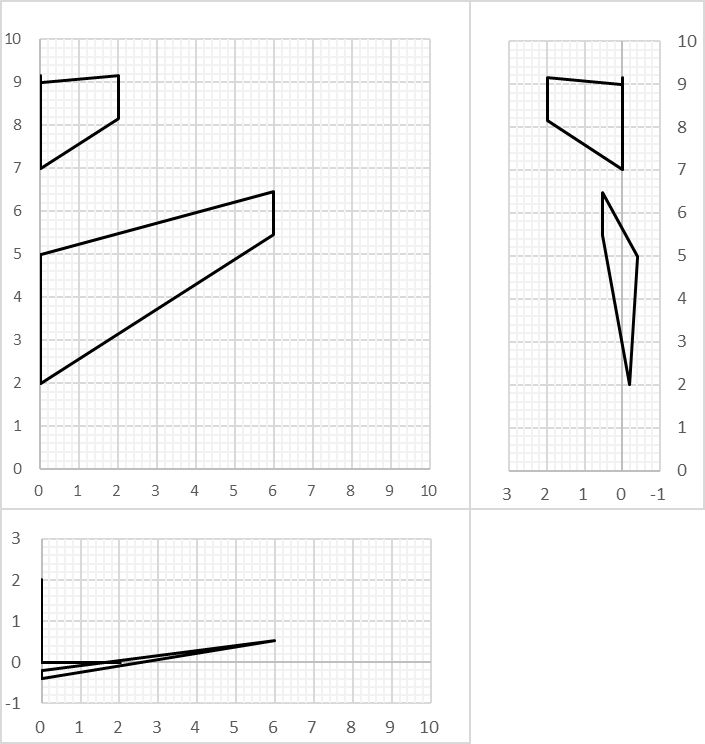
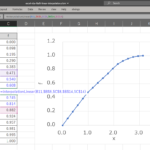
↓計算結果(\(\alpha=0\))
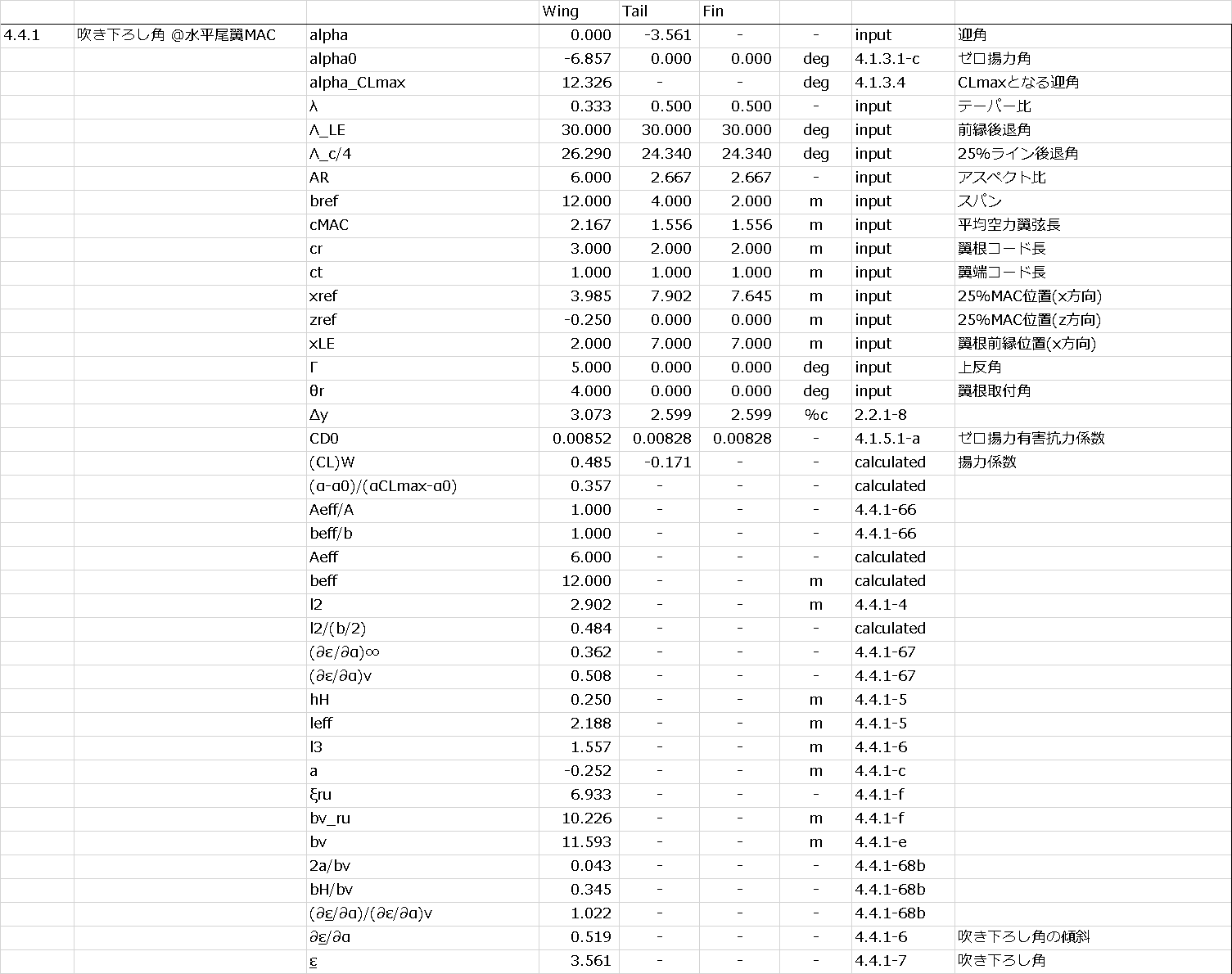
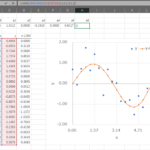
↓いろいろな\(\alpha\)
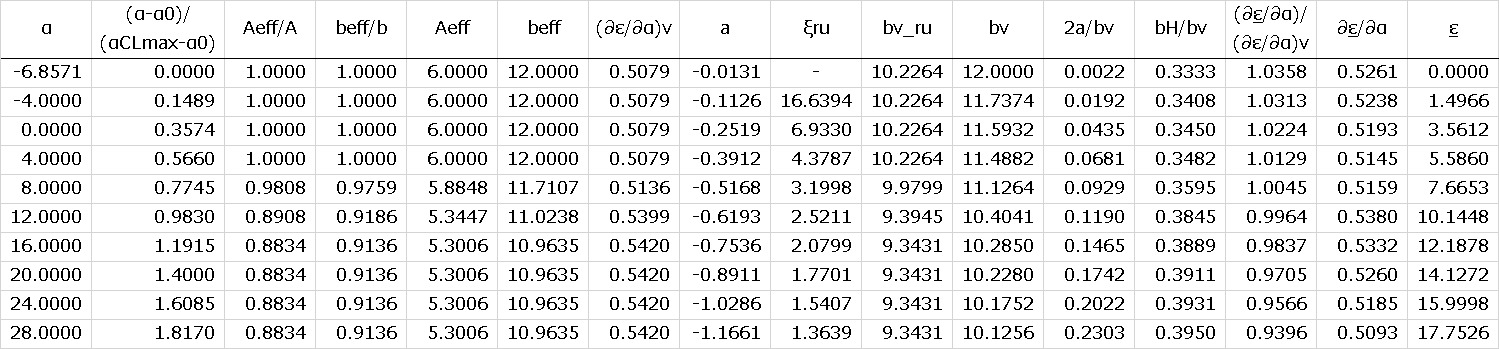
以上
おわりに
DATCOM 4.4.1 に基づいて、尾翼における吹き下ろし角の大きさを計算した。
↓次




コメント