【Excel VBA】最小二乗法で多項式近似したときの回帰係数を求める自作Excel関数（マクロ）

離散化されたデータを最小二乗法で多項式近似したときの回帰係数を求める自作Excel関数（マクロ）について説明する

最小二乗法の定式化 (Least Square Method)
ソースコード
使い方
まとめ

最小二乗法の定式化 (Least Square Method)

最小二乗法を用いた多変数関数の多項式近似とは，離散化されたデータに対して最もいい感じにフィットするような多項式の係数を計算する方法である

最小二乗法の行列表現：
主張1：行列\({\bf A}\)と列ベクトル\({\bf b}\)が与えられたときに
\(||{\bf Ax-b}||\)
を最小にする\({\bf x}\)を求める問題は非常に重要である。
主張2：\({\bf A^t A}\)が正則のとき上記の問題の解は唯一つである：
\({\bf x=(A^T A)^{-1} A^T b}\)
最小二乗法の行列表現（単回帰，多変数，多項式）

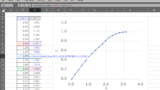
ここでは，適当に生成した乱数波\(y(x)\)の離散データに対して，n次多項式で近似を行う

\begin{align}
y_{_{LSM}}&=\sum_{i=0}^{n}\left(a_{i}x^{i}\right)\\
&=a_{0}x^{0}+a_{1}x^{1}+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5}+\cdots+a_{n}x^{n}
\end{align}

離散データとしては大量の\(x,~y\)の組が与えられる

\(x\)から計算した\(1,~x,~x^{2},~\cdots,~x^{n}\)の組を\({\bf A}\)，\(y\)の組を\({\bf b}\)，これらにベストフィットする係数\(a_{0},~a_{1},\cdots,~a_{n}\)の組を\({\bf x}\)として， \({\bf x=(A^T A)^{-1} A^T b}\)を計算する

ソースコード

ソースコードはこれ

Public Function LSM()

Public Function LSM(ByVal nRef As Long, ByRef xRange As Variant, ByRef yRange As Variant, ParamArray CoeffFlags() As Variant) As Variant
    ' 最小二乗法により回帰係数を計算する関数
    
    ' 入力:
    '   nRef: 返してほしい回帰係数の次数
    '   xRange: 独立変数のデータ範囲
    '   yRange:  従属変数のデータ範囲
    '   CoeffFlags: 回帰係数の計算に使用する項のフラグ (0: 使用しない, 1: 使用する)

    ' 出力:
    '   LSM: 計算された回帰係数

    Dim xParams() As Double
    Dim nData As Long
    Dim nFlag As Long
    Dim nParam As Long

    nData = xRange.Count            ' データ数を取得
    nFlag = UBound(CoeffFlags) + 1  ' フラグ数を取得
    
    ' 使用するパラメータ数をカウント
    nParam = 0
    For i = 0 To nFlag - 1
        If CoeffFlags(i) <> 0 Then nParam = nParam + 1
    Next i

    ' パラメータ配列を初期化
    ReDim xParams(1 To nData, 1 To nParam)

    ' 使用するパラメータの次数ごとにデータをセット
    nParam = 1
    For j = 1 To nFlag
        If CoeffFlags(j - 1) <> 0 Then
            For i = 1 To nData
                'nFlag次多項式で近似する。
                xParams(i, nParam) = xRange(i, 1) ^ (j - 1)
            Next i
            nParam = nParam + 1
        End If
    Next j

    ' 最小二乗法により回帰係数を計算
    With WorksheetFunction
        Coeffs = .MMult(.MMult(.MInverse(.MMult(.Transpose(xParams), xParams)), .Transpose(xParams)), yRange) '(At A)^-1 At b
    End With

    ' 参照された回帰係数を返す
    nParam = 1
    For i = 0 To nRef
        If CoeffFlags(i) <> 0 Then
            If i = nRef And UBound(Coeffs) <> 1 Then LSM = Coeffs(nParam, 1): Exit Function
            If i = nRef And UBound(Coeffs) = 1 Then LSM = Coeffs(nParam): Exit Function
            nParam = nParam + 1
        End If
    Next i
    LSM = 0
    
End Function

Paramarrayを用いて可変長引数に対応している

ParamArray - Visual Basic

詳細情報: ParamArray (Visual Basic)

使い方

使い方は以下の通り

=VLM(知りたい回帰係数の次数,既知のx,既知のy,回帰係数のフラグ)

使用例）\(y=a_{0}+a_{1}x\)　回帰係数のフラグ：1, 1

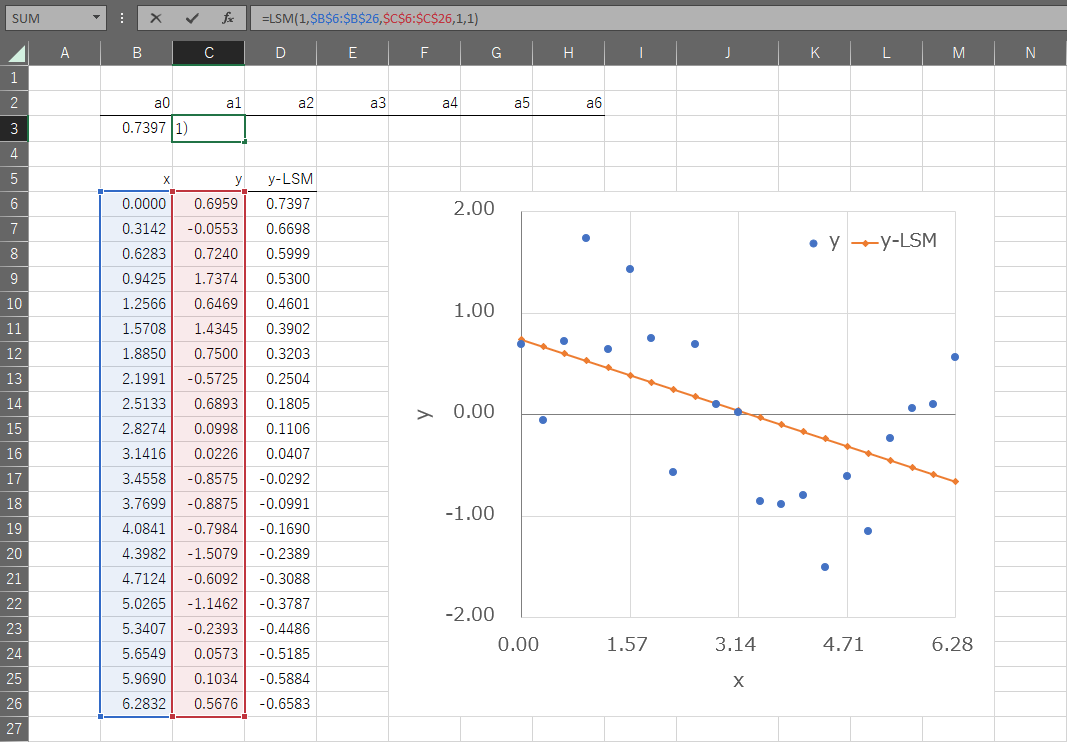
使用例）\(y=a_{1}x\)　回帰係数のフラグ：0, 1

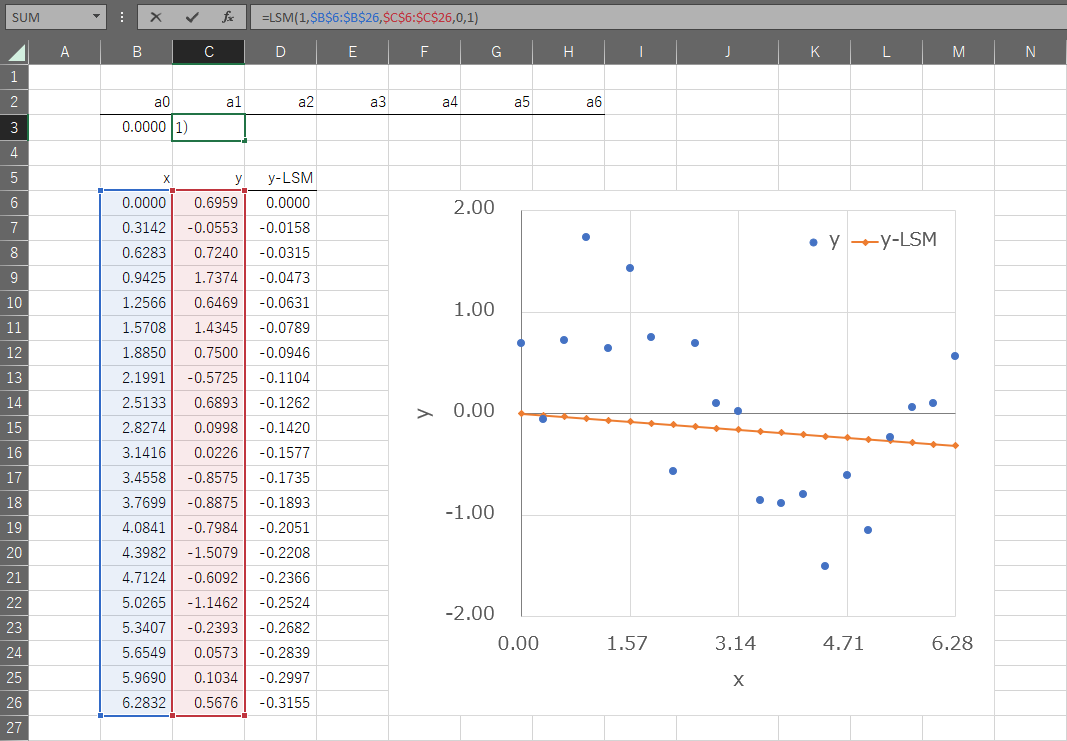
使用例）\(y=a_{0}+a_{2}x^2\)　回帰係数のフラグ：1, 0, 1

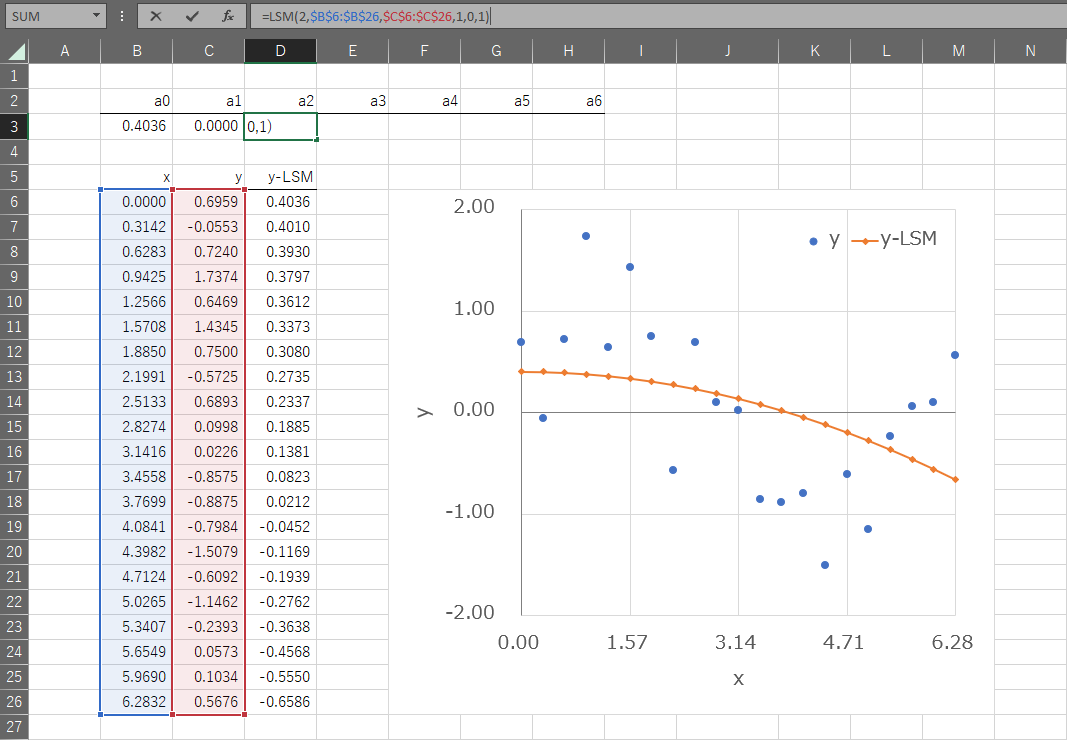
使用例）\(y=a_{1}x+a_{3}x^{3}+a_{5}x^{5}+a_{6}x^{6}\)　回帰係数のフラグ：0, 1, 0, 1, 0, 1, 1

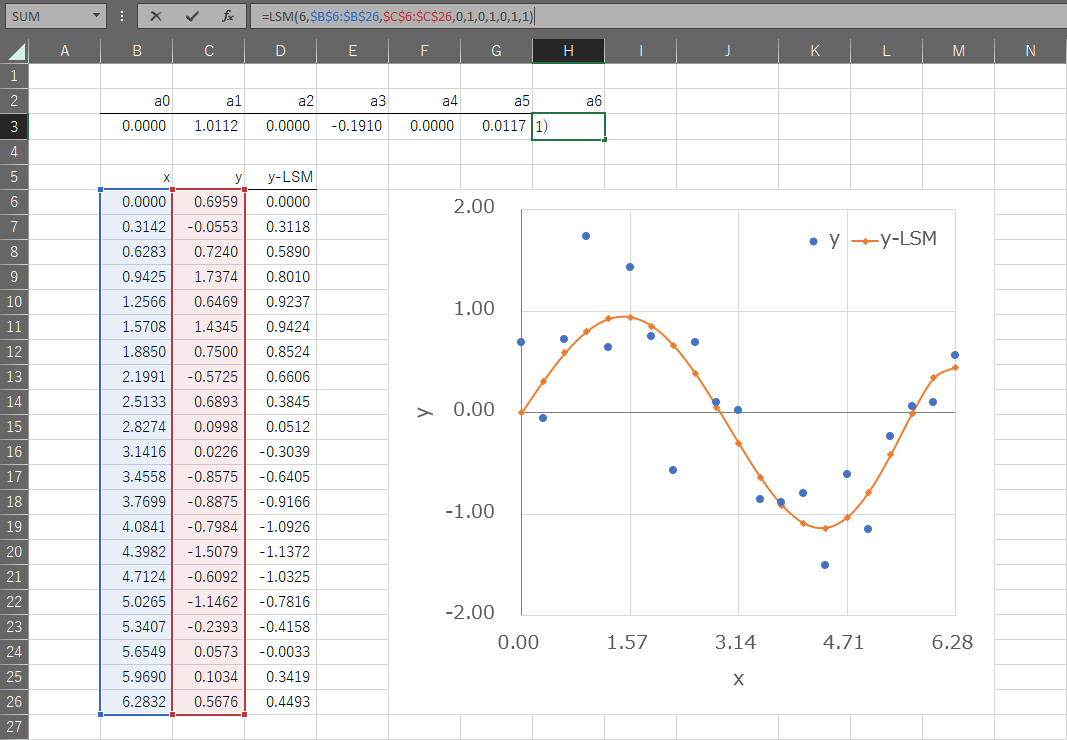
↓参考のマクロ付きブックはこちら

Least-Square-Method-Function.xlsm

1 ファイル 0.06 KB

ダウンロード

まとめ

離散化されたデータを最小二乗法で多項式近似したときの回帰係数を求める自作Excel関数（マクロ）について説明した

↓関連記事