【Unity】フライトシミュレーターを作る：物理演算

Unityを使って鳥人間コンテストの滑空機部門を想定したフライトシミュレーターを作成するための物理演算について説明する

実際に作成したフライトシミュレーターはこれ

BR Simulator for Glider

鳥人間コンテスト滑空機部門を想定したフライトシミュレーター

mtkbirdman.com

2022.11.29

keywords: Unity，物理演算，フライトシミュレーター，人力飛行機，微小擾乱理論

はじめに

Unityを使って鳥人間コンテストの滑空機部門を想定したフライトシミュレーターを作成する

Unityのバージョンは2020.3.8f1

物理演算についての参考書はこちら

(通称：白本)

(通称：青本)

安定微係数の推算については白本の第4章が，運動方程式の立式や微小擾乱方程式については青本の第1章・第2章・第3章がわかりやすい（わかりやすいとは言ってない）

今回はそれっぽい挙動を実現しながらできる限り動作が軽くなるようなモデル化を心掛ける

Unityについては多くの入門サイトがあったが，今回特に参考にしたのはこちら

Unityの全般的な知識は上のサイトで，物理演算の基本については下のサイトを参考にした

≫Unity入門【初心者為の使い方講座】【実際にゲームを作って解説】 _ ゲームの作り方！
≫Unity カテゴリーの記事一覧 - エフアンダーバー

↓鳥人間コンテストのフライトシミュレーターの先駆者様

≫みえ日記
≫人力飛行機　シミュレータ　HPASim　のはなし - きかいや。

↓今回作成したプログラム

BRSimulator/Assets/Script at main · mtkbirdman/BRSimulator

Contribute to mtkbirdman/BRSimulator development by creating an account on GitHub.

github.com

↓その他の解説記事

【Unity】BR Simulatorの製作記事まとめ

Unityを使って鳥人間コンテストの滑空機部門を想定したフライトシミュレーターを製作するための記事まとめ

mtkbirdman.com

2022.06.15

それではいってみよう

Unityの物理演算の概要

Unityでは物理演算を行う際にRigidbodyというコンポーネントを使う

≫Rigidbody - Unity マニュアル

このRigidbodyに重量と慣性モーメントを設定し，スクリプトで力やトルクを加えることで，簡単に物理演算を実装することができる

≫Rigidbody-AddRelativeForce - Unity スクリプトリファレンス
≫Rigidbody-AddRelativeTorque - Unity スクリプトリファレンス

なので前回作ったプログラムのように複雑な運動方程式や時間積分を考える必要は一切なく，機体にはたらく3つの力と3つのモーメントだけを考えればいい

座標系については，空力計算の際は青本と同じく機体前方にX軸，右翼側にY軸，下向きにZ軸をとる

RigidbodyにAddRelativeForceやAddRelativeTorqueを使う際にはUnityの座標系（機体前方にX軸，上向きにY軸，左翼側にZ軸をとった左手系）に変換する

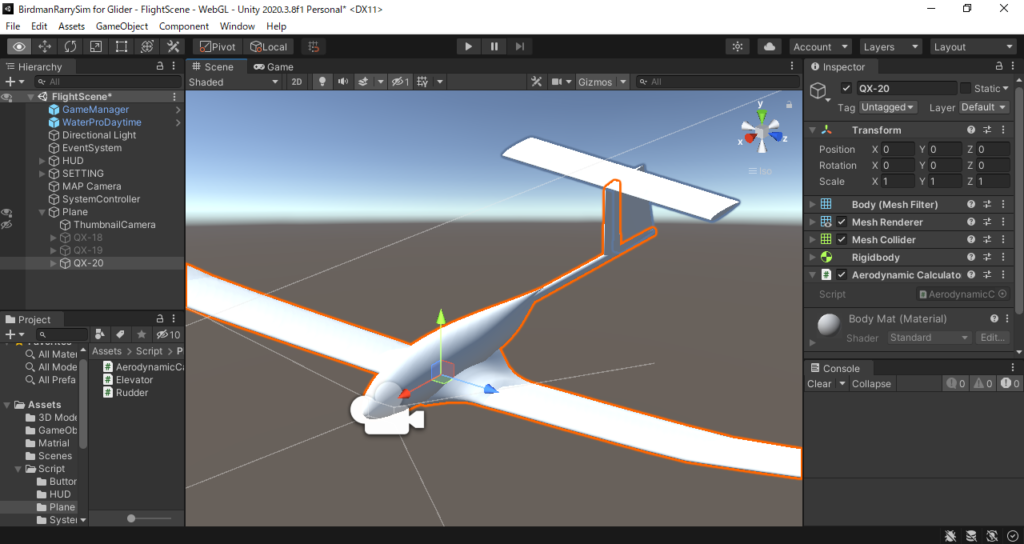
まとめると，Unityの物理演算に必要なのは以下の項目になる

• 重量
• 慣性モーメント
• 3方向の力 \({\bf F}=[X, Y, Z]\)
• 3方向のモーメント \({\bf F}=[L, M, N]\)
• 教科書の座標系とUnityの座標系の関係

一つずつ説明していく

質量・重心位置・慣性モーメント

質量と重心位置については値をそのまま設定すればいい

≫Rigidbody-mass - Unity スクリプトリファレンス
≫Rigidbody-centerOfMass - Unity スクリプトリファレンス

しかし，慣性モーメントに関してはひと手間かける必要がある

Unityにおいて慣性モーメントは次の2つの変数で設定する

≫Rigidbody-inertiaTensor - Unity スクリプトリファレンス
≫Rigidbody-inertiaTensorRotation - Unity スクリプトリファレンス

inertiaTensorは，重心に対する慣性主軸まわりの主慣性モーメントであり，inertiaTensorRotationは機体座標系に対する慣性主軸の回転を表すクォータニオンである

≫慣性モーメント - Wikipedia

つまり，どうにかしてモデルの慣性テンソルを求めたら，それを対角化して主慣性モーメントとその回転を求める必要がある

航空機の慣性テンソルは対称性を考慮すると以下の行列で表される（白本：式1.11）

\begin{eqnarray}
{\bf I}=\left[\begin{array}{ccc}
I_{xx}&0&I_{xz}\\
0&I_{yy}&0\\
I_{xz}&0&I_{zz}\\
\end{array}\right]
\end{eqnarray}

これを大学生の英知を使って対角化すると，固有値および固有ベクトルは次のように求まる

\begin{eqnarray}
\lambda_{1}&=&\frac{1}{2}(-\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}+I_{xx}+I_{zz})\\
\lambda_{2}&=&I_{yy}\\
\lambda_{3}&=&\frac{1}{2}(\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}+I_{xx}+I_{zz})\\
\\
v_{1}&=&\left[-\frac{-I_{xx}+C+\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}}{2I_{xz}},0,1\right]\\
v_{2}&=&\left[0,1,0\right]\\
v_{3}&=&\left[-\frac{-I_{xx}+I_{zz}-\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}}{2I_{xz}},0,1\right]\\
\end{eqnarray}

後は適当にExcelなどで計算すればいい

Excelを使って慣性テンソルから主慣性モーメントと慣性主軸を計算する

Excelを使って，慣性モーメントから主慣性モーメントと慣性主軸を計算する方法について説明する

mtkbirdman.com

2022.10.02

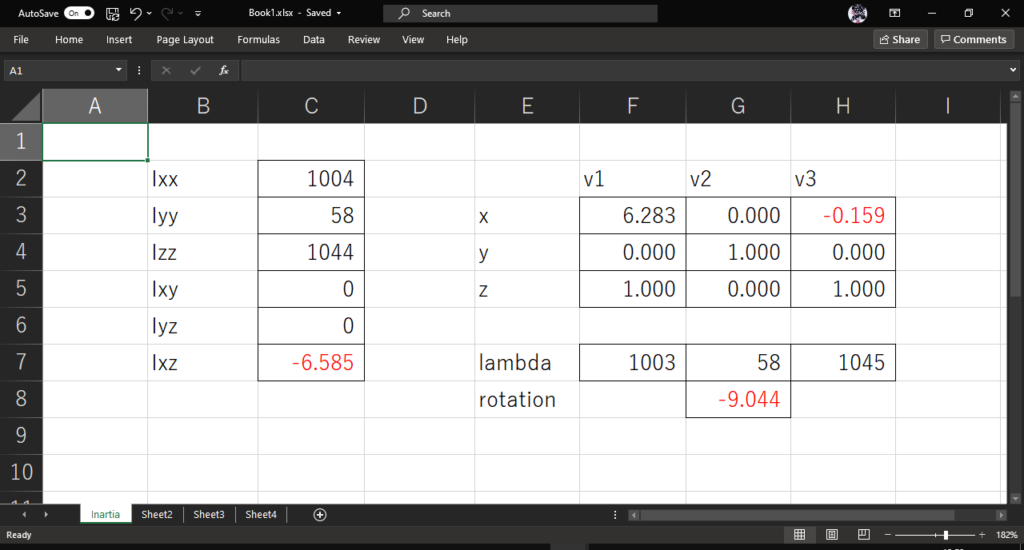
QX-20では，主慣性モーメントは\({\bf \lambda}=\left[1003, 58, 1045\right]\)で，慣性主軸は機体座標をy軸まわりに-9.044度回転させたものであることがわかる

そもそも重心位置と慣性テンソルの求め方がわからないという人はこちら
≫重量推算②

迎角と横滑り角 (\(\alpha\), \(\beta\))

機体の対地速度を\([u, v, w]\)，突風成分を\([u_{g}, v_{g}, w_{g}]\)とすると，機体の迎角\(\alpha\)と横滑り角\(\beta\)はそれぞれ次の式で表される（青本：式1.7-2）

\begin{eqnarray}
V&=&\sqrt{(u+u_{g})^{2}+(v+v_{g})^2+(w+w_{g})^{2}}\\
\alpha&=&\arctan{\frac{w+w_{g}}{u+u_{g}}}\\
\beta&=&\arcsin{\frac{v+v_{g}}{V}}\\
\end{eqnarray}

上記の式のとおり，今回の物理演算では，突風の影響は迎角・横滑り角の変化として考慮されている

突風成分

突風成分を\([u_{g}, v_{g}, w_{g}]\)とし，それぞれ各軸の正方向から吹いてくる場合を正とする

つまり，\(u_{g}\)は正対風が正，\(v_{g}\)は右から吹いてきたら正，\(w_{g}\)は上昇風が正である

また，今回の物理演算では風速勾配として1/7乗則を採用する
≫Wind Gradient

\begin{eqnarray}
V_{g}(h)=V_{0}\left(\frac{h}{h_{0}}\right)^{\frac{1}{7}}
\end{eqnarray}

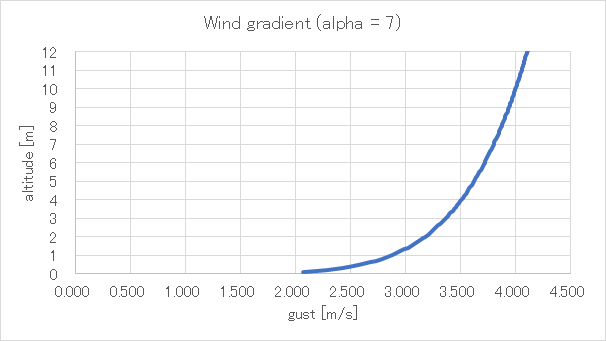
プラホの高さ(\(h_{0}=10.5\)[m])で\(V_{0}=4 \)[m/s]の風が吹いているときの風速\(V_{g}\)の分布は次のようになる

地面効果

地面効果の影響については，以下の論文にあるHoerner and Borstの式を参考にする
≫Lifting-Line Predictions for Induced Drag and Lift in Ground Effect

\begin{eqnarray}
\frac{(C_{D_{i}}/C_{L}^{2})_{h}}{(C_{D_{i}}/C_{L}^{2})_{\infty}}
=\frac{33(h/b)^{1.5}}{1+33(h/b)^{1.5}}
\end{eqnarray}

Hoerner and Borstの式は高度5m以上の範囲ではよく一致するが，5m以下では誘導抗力が小さくなりすぎ，高度0mで誘導抗力が0になってしまう

今回の物理演算では水面付近の精度を優先し，以下の式を用いる

\begin{eqnarray}
C_{L}(h) &\simeq& C_{L_{\infty}} \\
C_{D_{i}}(h)&=&C_{GE}(h)C_{D_{i_{\infty}}}\\
\end{eqnarray}

\begin{eqnarray}
C_{GE}(h) = \frac{C_{GE_{min}}+33(h/b)^{1.5}}{1+33(h/b)^{1.5}}\\
\end{eqnarray}

ここで，\(C_{GE_{min}}\)は\(\frac{(C_{D_{i}}/C_{L}^{2})_{h}}{(C_{D_{i}}/C_{L}^{2})_{\infty}}\)の最小値であり，QX-20では\(C_{GE_{min}}=0.283\)である

比較してみるとこんな感じになる

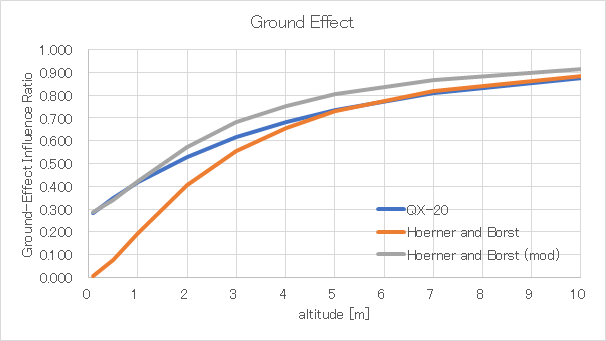
計算の負荷を下げるための近似なのである程度の誤差はしょうがない

鳥コン滑空機の地面効果について厳密に計算する方法についてはこちら
≫TR-797の解説

縦のつり合い

巡航状態では，力とモーメントは次のように釣り合っている

\begin{eqnarray}
C_{L_{0}}&=&C_{L_{w_{0}}}+\frac{S_{t}}{S_{w}}C_{L_{t_{0}}}\\
0&=&C_{m_{w_{0}}}+C_{L_{w_{0}}}h_{w}-V_{H}C_{L_{t_{0}}}\\
\end{eqnarray}

これより，巡航時の\(C_{L_{w_{0}}}\)と\(C_{L_{t_{0}}}\)は次のように求まる

\begin{eqnarray}
C_{L_{w_{0}}}&=&C_{L_{0}}-\frac{S_{t}}{S_{w}}C_{L_{t_{0}}}\\
C_{L_{t_{0}}}&=&\frac{C_{m_{w_{0}}}+C_{L_{0}}h_{w}}{V_{H}+\frac{S_{t}}{S_{w}}h_{w}}\\
\end{eqnarray}

縦の空気力とモーメントはこのつり合いをもとに計算していく

縦の空気力 \(X\)，\(Z\)

x軸方向にはたらく力\(X\)とz方向にはたらく力\(Z\)は次の式で表される

\begin{eqnarray}
X&=&\frac{1}{2}\rho V^{2} S_{w} C_{x}\\
Z&=&\frac{1}{2}\rho V^{2} S_{w} C_{z}\\
\\
C_{x}&=&-C_{D}\cos{\alpha}+C_{L}\sin{\alpha}\\
C_{z}&=&-C_{L}\cos{\alpha}-C_{D}\sin{\alpha}\\
\end{eqnarray}

まず，揚力係数\(C_{L}\)は次のように計算する

\begin{eqnarray}
C_{L}&=&C_{L_{w}}+\frac{S_{t}}{S_{w}}C_{L_{t}}\\
\\
C_{L_{w}}&=&C_{L_{w_{0}}}+a_{w}(\alpha-\alpha_{0})\\
C_{L_{t}}&=&C_{L_{t_{0}}}+a_{t}\left\{(\alpha-\alpha_{0})+(1-C_{GE}\frac{C_{L_{w}}}{C_{L_{w_{0}}}})\varepsilon_{0}+\delta_{e}\tau+\frac{l_{t}}{V}q\right\}\\
\end{eqnarray}

ここで，\((1-C_{GE}\frac{C_{L_{w}}}{C_{L_{w_{0}}}})\varepsilon_{0}\)の項は主翼の吹きおろしの変化を表し，次のように求められる

\begin{eqnarray}
\Delta \varepsilon&=&\varepsilon-\varepsilon_{0}
&=&C_{GE}\frac{C_{L_{w}}}{\pi e (AR)}-\frac{C_{L_{w_{0}}}}{\pi e (AR)}
&=&-(1-C_{GE}\frac{C_{L_{w}}}{C_{L_{w_{0}}}})\varepsilon_{0}
\end{eqnarray}

ただし，失速を表現するため\(|C_{L_{w}}|<C_{L_{max}}\)，\(|C_{L_{t}}|<C_{L_{max}}\)の制約を加える

次に，抗力係数\(C_{D}\)は次のように計算する

\begin{eqnarray}
C_{D}&=&C_{D_{p}}+C_{D_{i}}\\
\\
C_{D_{p}}&=&C_{D_{p_{0}}}\left\{1+\left(\frac{|\alpha|}{9}\right)^{3}\right\}\\
C_{D_{i}}&=&\frac{C_{L}^{2}}{\pi e (AR)}C_{GE}\\
\end{eqnarray}

ここで，\(1+\left(\frac{|\alpha|}{9}\right)^{3}\)は失速を表現するための係数で，QX-20のCDp-α線図を見ながら適当に決定した

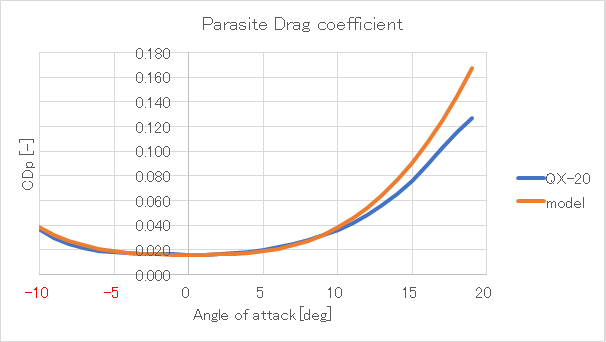
迎角が小さい範囲ではよく一致しているので良いんじゃなかろうか

縦のモーメント \(M\)

重心まわりのピッチングモーメント\(M\)は次のように表される

\begin{eqnarray}
M_{cg}&=&\frac{1}{2}\rho V^{2}S_{w}{\overline c}C_{m}\\
\\
C_{m}&=&C_{m_{w}}+C_{L_{w}}h_{w}-V_{H}C_{L_{t}}\\
\end{eqnarray}

ただし，主翼によるピッチングモーメント係数は一定（\(C_{m_{w}}=C_{m_{w_{0}}}=const.\)）とする

横・方向のつり合い

巡航状態では横・方向の力もモーメントも0なので，横・方向に関しては微小擾乱理論を用いる

鳥コン滑空機における横・方向の安定微係数の詳しい求め方についてはこちら

鳥コン滑空機における横・方向の微小擾乱理論

鳥コン滑空機のような大きな上反角を持つ機体に対する横・方向の微小擾乱理論について説明する

mtkbirdman.com

2021.06.01

安定微係数の単位は以下のとおり

\(C_{y_{\beta}}\)，\(C_{l_{\beta}}\)，\(C_{n_{\beta}}\)：[1/deg]
\(C_{y_{p}}\)，\(C_{y_{r}}\)，\(C_{l_{p}}\)，\(C_{l_{r}}\)，\(C_{n_{p}}\)，\(C_{n_{r}}\)：[1/rad]

横・方向の空気力 \(Y\)

機体に横向きにはたらく空気力\(Y\)は次の式で表される

\begin{eqnarray}
Y&=&\frac{1}{2}\rho V^{2}S_{w}C_{y}\\
\\
C_{y}&=&C_{y_{\beta}}\beta+C_{y_{p}}\frac{1}{180/\pi}\frac{pb}{2V}+C_{y_{r}}\frac{1}{180/\pi}\frac{rb}{2V}+C_{y_{\delta_{r}}}\delta_{r}\\
\end{eqnarray}

横・方向のモーメント \(L\)，\(N\)

ローリングモーメント\(L\)およびピッチングモーメント\(N\)はそれぞれ次の式で表される

\begin{eqnarray}
L&=&\frac{1}{2}\rho V^{2}S_{w}bC_{l}\\
N&=&\frac{1}{2}\rho V^{2}S_{w}bC_{n}\\
\\
C_{l}&=&C_{l_{\beta}}\beta+C_{l_{p}}\frac{1}{180/\pi}\frac{pb}{2V}+C_{l_{r}}\frac{1}{180/\pi}\frac{rb}{2V}+C_{l_{\delta_{r}}}\delta_{r}\\
C_{n}&=&C_{n_{\beta}}\beta+C_{n_{p}}\frac{1}{180/\pi}\frac{pb}{2V}+C_{n_{r}}\frac{1}{180/\pi}\frac{rb}{2V}+C_{n_{\delta_{r}}}\delta_{r}\\
\end{eqnarray}

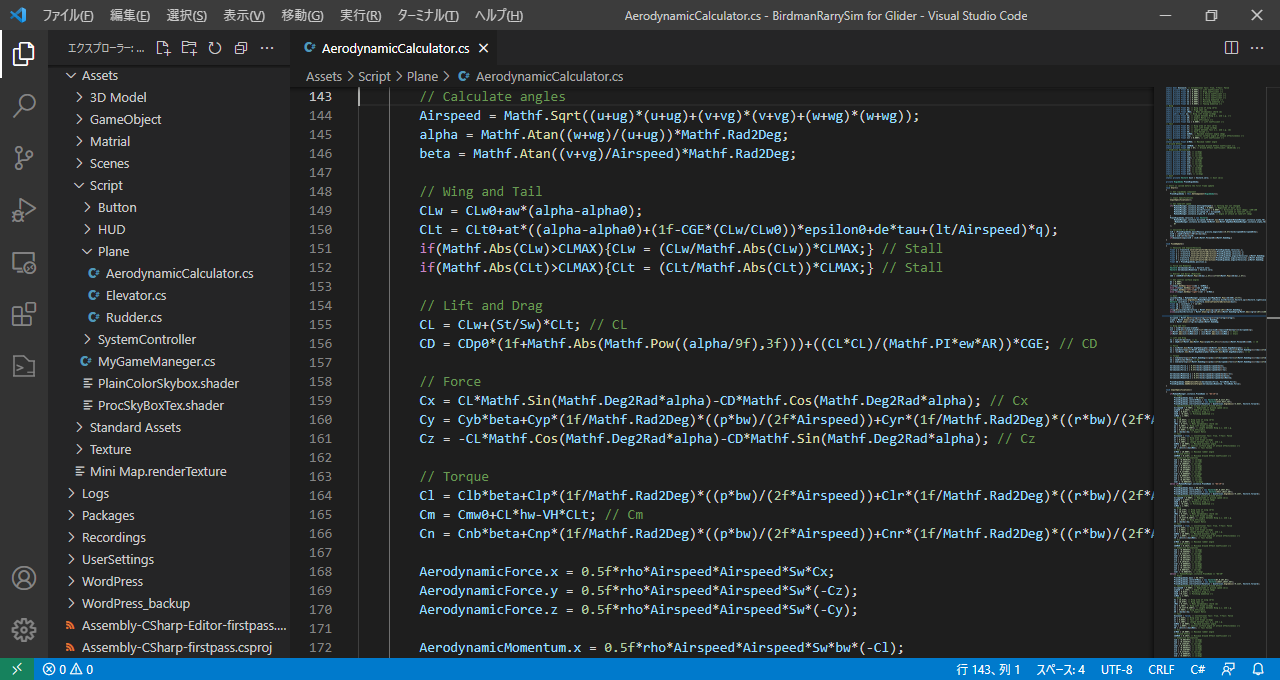
スクリプトの実装

プログラム全体についてはこちら

≫github.com/mtkbirdman.com/BirdmanRallySim/Plane/AerodynamicCalculator.cs

MyGameManeger.instanceについてはこちら

≫Unity 2Dアクションの作り方【ゲームマネージャーを作ろう】 _ ゲームの作り方！

かいつまんで説明していく

Start()

初期化を行うメソッド

≫MonoBehaviour-Start() - Unity スクリプトリファレンス

// Get rigidbody component
PlaneRigidbody = this.GetComponent<Rigidbody>();

// Input Specifications
InputSpecifications();

GameObject.GetComponentを使ってRigidbodyを取得し，InputSpecifications()で機体の諸元を取得する

≫GameObject-GetComponent - Unity スクリプトリファレンス

// Calculate CL at cluise
CL0 = (PlaneRigidbody.mass*Physics.gravity.magnitude)/(0.5f*rho*Airspeed0*Airspeed0*Sw);
CLt0 = (Cmw0+CL0*hw)/(VH+(St/Sw)*hw);
CLw0 = CL0-(St/Sw)*CLt0;
if(Downwash){epsilon0 = (CL0/(Mathf.PI*ew*AR))*Mathf.Rad2Deg;}

縦のつり合いに従ってつり合い状態における値を計算する

Downwashがtrueなら吹きおろしを計算し，falseなら吹きおろしは無視する（T字尾翼）

FixedUpdate()

固定時間（デフォルトでは0.02秒）おきに呼び出されるメソッド．物理演算に使用される

≫MonoBehaviour-FixedUpdate() - Unity スクリプトリファレンス

// Velocity and AngularVelocity
float u = transform.InverseTransformDirection(PlaneRigidbody.velocity).x;
float v = -transform.InverseTransformDirection(PlaneRigidbody.velocity).z;
float w = -transform.InverseTransformDirection(PlaneRigidbody.velocity).y;
float p = -transform.InverseTransformDirection(PlaneRigidbody.angularVelocity).x*Mathf.Rad2Deg;
float q = transform.InverseTransformDirection(PlaneRigidbody.angularVelocity).z*Mathf.Rad2Deg;
float r = transform.InverseTransformDirection(PlaneRigidbody.angularVelocity).y*Mathf.Rad2Deg;
float hE = PlaneRigidbody.position.y;

Rigidbody.velocityを使って対地速度を，Rigidbody.angularVelocityを使って角速度を求め，Transform.InverseTransformDirectionを使って機体軸まわりに変換している

≫Rigidbody-velocity - Unity スクリプトリファレンス
≫Rigidbody-angularVelocity - Unity スクリプトリファレンス
≫Transform-InverseTransformDirection - Unity スクリプトリファレンス

// Get control surface angles
de = 0.000f;
dr = 0.000f;
if(Input.GetKey("down")){de = -deMAX;}
else if(Input.GetKey("up")){de = deMAX;}
if(Input.GetKey("left")){dr = drMAX;}
else if(Input.GetKey("right")){dr = -drMAX;}

Input.GetKeyを使ってキーボード入力を取得し，エレベーター・ラダーそれぞれの舵角を設定する

≫Input-GetKey - Unity スクリプトリファレンス
≫KeyCode - Unity スクリプトリファレンス
≫一般的なゲーム入力 - Unity マニュアル

// Gust
LocalGustMag = MyGameManeger.instance.GustMag*Mathf.Pow((hE/hE0),1f/7f);
Gust = Quaternion.AngleAxis(MyGameManeger.instance.GustDirection,Vector3.up)*(Vector3.right*LocalGustMag);
Vector3 LocalGust = this.transform.InverseTransformDirection(Gust);
float ug = LocalGust.x + 1e-10f;
float vg = -LocalGust.z;
float wg = -LocalGust.y;
if(ug>0){LocalGustDirection = Mathf.Atan(vg/(ug+1e-10f))*Mathf.Rad2Deg;}
else{LocalGustDirection = Mathf.Atan(vg/(ug+1e-10f))*Mathf.Rad2Deg+vg/Mathf.Abs((vg+1e-10f))*180;}

LocalGustMagはWind Gradientを考慮した局所的な風速で，LocalGustDirectionは機体軸のx軸を0度として右翼側を正，左翼側を負として局所的な風向きを-180度～+180度で表している

Quaternion.AngleAxisは指定した角度だけ指定した軸まわりに回転させるクォータニオンを生成する

Unityでは，Quaternion*Vector3でベクトルを回転させることができる

Mathf.Atanの定義域が-90度～90度なので，最後の2行で-180度～+180度に変換している

≫Quaternion-AngleAxis - Unity スクリプトリファレンス
≫Quaternion-operator * - Unity スクリプトリファレンス
≫Vector3-up - Unity スクリプトリファレンス
≫Vector3-right - Unity スクリプトリファレンス
≫Mathf-Atan - Unity スクリプトリファレンス

// Calculate angles
Airspeed = Mathf.Sqrt((u+ug)*(u+ug)+(v+vg)*(v+vg)+(w+wg)*(w+wg));
alpha = Mathf.Atan((w+wg)/(u+ug))*Mathf.Rad2Deg;
beta = Mathf.Atan((v+vg)/Airspeed)*Mathf.Rad2Deg;

// Wing and Tail
CLw = CLw0+aw*(alpha-alpha0);
CLt = CLt0+at*((alpha-alpha0)+(1f-CGE*(CLw/CLw0))*epsilon0+de*tau+(lt/Airspeed)*q);
if(Mathf.Abs(CLw)>CLMAX){CLw = (CLw/Mathf.Abs(CLw))*CLMAX;} // Stall
if(Mathf.Abs(CLt)>CLMAX){CLt = (CLt/Mathf.Abs(CLt))*CLMAX;} // Stall

// Lift and Drag
CL = CLw+(St/Sw)*CLt; // CL        
CD = CDp0*(1f+Mathf.Abs(Mathf.Pow((alpha/9f),3f)))+((CL*CL)/(Mathf.PI*ew*AR))*CGE; // CD

迎角と横滑り角 (α, β)と縦の空気力 X，Zに従って計算する

if文を使ってそれぞれの揚力係数がCLMAXを超えないようにしている

≫Mathf-Rad2Deg - Unity スクリプトリファレンス

// Force
Cx = CL*Mathf.Sin(Mathf.Deg2Rad*alpha)-CD*Mathf.Cos(Mathf.Deg2Rad*alpha); // Cx       
Cy = Cyb*beta+Cyp*(1f/Mathf.Rad2Deg)*((p*bw)/(2f*Airspeed))+Cyr*(1f/Mathf.Rad2Deg)*((r*bw)/(2f*Airspeed))+Cydr*dr; // Cy       
Cz = -CL*Mathf.Cos(Mathf.Deg2Rad*alpha)-CD*Mathf.Sin(Mathf.Deg2Rad*alpha); // Cz

// Torque
Cl = Clb*beta+Clp*(1f/Mathf.Rad2Deg)*((p*bw)/(2f*Airspeed))+Clr*(1f/Mathf.Rad2Deg)*((r*bw)/(2f*Airspeed))+Cldr*dr; // Cl        
Cm = Cmw0+CL*hw-VH*CLt; // Cm       
Cn = Cnb*beta+Cnp*(1f/Mathf.Rad2Deg)*((p*bw)/(2f*Airspeed))+Cnr*(1f/Mathf.Rad2Deg)*((r*bw)/(2f*Airspeed))+Cndr*dr; // Cn

縦の空気力 X，Z，縦のモーメント M，横・方向の空気力 Y，横・方向のモーメント L，Nに従って計算する

AerodynamicForce.x = 0.5f*rho*Airspeed*Airspeed*Sw*Cx;
AerodynamicForce.y = 0.5f*rho*Airspeed*Airspeed*Sw*(-Cz);
AerodynamicForce.z = 0.5f*rho*Airspeed*Airspeed*Sw*(-Cy);

AerodynamicMomentum.x = 0.5f*rho*Airspeed*Airspeed*Sw*bw*(-Cl);
AerodynamicMomentum.y = 0.5f*rho*Airspeed*Airspeed*Sw*bw*Cn;
AerodynamicMomentum.z = 0.5f*rho*Airspeed*Airspeed*Sw*cMAC*Cm;

PlaneRigidbody.AddRelativeForce(AerodynamicForce, ForceMode.Force);
PlaneRigidbody.AddRelativeTorque(AerodynamicMomentum, ForceMode.Force);

Unityの物理演算の概要で説明したとおり，座標軸の違いに気を付けながら力，トルクを加える

≫Rigidbody-AddRelativeForce – Unity スクリプトリファレンス
≫Rigidbody-AddRelativeTorque – Unity スクリプトリファレンス

InputSpecifications()

機体の諸元を入力する

おわりに

Unityで鳥コン滑空機の物理演算を行った

歴代パイロットの評価も上々なのでうれしい限りである

記号

この記事で使った記号は以下のとおり

記号	変数名	単位	説明
\(\rho\)	rho	kg/m^3	空気密度
\(V\)	Airspeed	m/s	対気速度
\([u, v, w]\)	u, v, w	m/s	機体軸で表した対地速度ベクトル
\([p, q, r]\)	p, q, r	deg/s	各機体軸まわりの角速度
\([u_{g}, v_{g}, w_ {g}]\)	ug, vg, wg	m/s	突風ベクトル
\(h_{E}\)	hE	m	高度
\(\alpha\)	alpha	deg	迎角
\(\beta\)	beta	deg	横滑り角
\(C_{L}\)	CL	-	揚力係数
\(C_{D}\)	CD	-	抗力係数
\(C_{D_{p}}\)	CDp	-	有害抗力係数
\(C_{D_{i}}\)	-	-	誘導抗力係数
\(C_{x}\)	Cx	-	x方向の空気力係数
\(C_{y}\)	Cy	-	y方向の空気力係数
\(C_{z}\)	Cz	-	z方向の空気力係数
\(C_{l}\)	Cl	-	ローリングモーメント係数
\(C_{m}\)	Cm	-	ピッチングモーメント係数
\(C_{n}\)	Cn	-	ヨーイングモーメント係数
\(S\)	S	m^2	翼面積
\(b\)	b	m	スパン
\({\overline c}\)	cMAC	m	平均空力翼弦長
\(a\)	a	1/deg	揚力傾斜
\(h_{w}\)	hw	0.01%MAC	主翼空力中心-機体重心間距離
\(AR\)	AR	-	アスペクト比
\(e\)	e	-	翼効率
\(l_{t}\)	lt	m	水平尾翼空力中心-機体重心間距離
\(V_{H}\)	VH	-	水平尾翼容積比(\(=S_{t}l_{t}/S_{w}{\overline c}\))
\(\delta_{e}\)	de	deg	水平尾翼舵角
\(\tau\)	tau	-	舵面効率
\(\delta_{r}\)	dr	deg	垂直尾翼舵角
\(C_{GE}\)	CGE	-	地面効果係数

添え字	変数	単位	説明
\((~)_{0}\)	0	-	巡航状態
\((~)_{TO}\)	TO	-	離陸時
\((~)_{w}\)	w	-	主翼
\((~)_{t}\)	t	-	水平尾翼
\((~)_{f}\)	f	-	垂直尾翼
\((~)_{max}\)	MAX	-	最大値
\((~)_{min}\)	MIN	-	最小値
\((~)_{\beta}\)	b	1/deg	\(\beta\)による偏微分
\((~)_{p}\)	p	1/rad	\(p\)による偏微分
\((~)_{r}\)	r	1/rad	\(r\)による偏微分
\((~)_{\delta_{r}}\)	dr	1/deg	\(\delta_{r}\)による偏微分