Excelを使って，慣性テンソルから主慣性モーメントと慣性主軸を計算する方法について説明する
はじめに
この記事では，Excelを使って慣性テンソルから主慣性モーメントと慣性主軸を計算する方法について説明する
手順は以下のとおり
- エクセルシートに慣性テンソルのデータを貼り付ける
- 慣性テンソルの単位を変換する
- 主慣性モーメントおよび慣性主軸を計算する
- 慣性主軸の傾きを計算する
↓エクセルファイルのダウンロードはこちら
↓この記事で扱う慣性テンソルの求め方はこちら
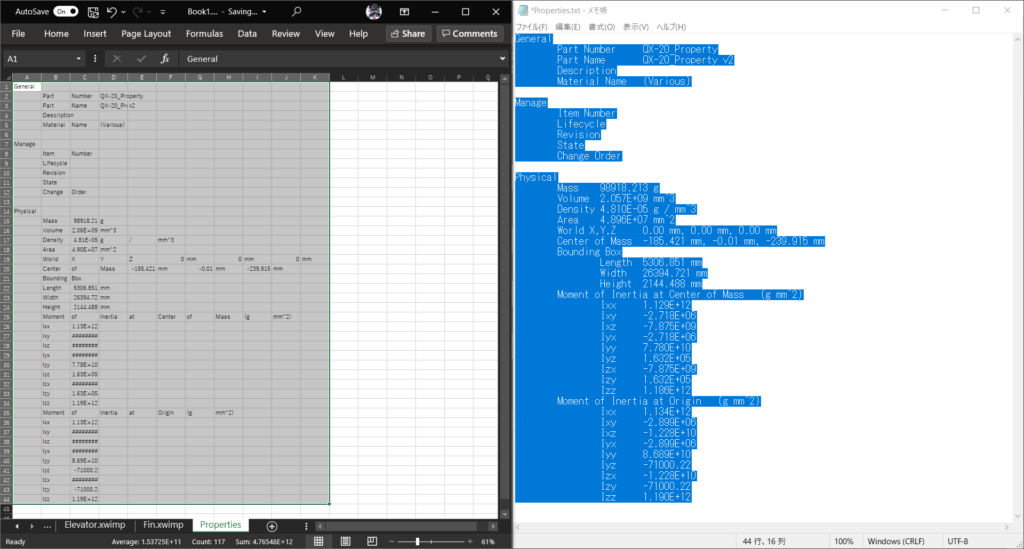
出力された慣性テンソルの値はこれ
General
Part Number QX-20_Property
Part Name QX-20_Property v2
Description
Material Name (Various)
Manage
Item Number
Lifecycle
Revision
State
Change Order
Physical
Mass 98918.213 g
Volume 2.057E+09 mm^3
Density 4.810E-05 g / mm^3
Area 4.896E+07 mm^2
World X,Y,Z 0.00 mm, 0.00 mm, 0.00 mm
Center of Mass -185.421 mm, -0.01 mm, -239.915 mm
Bounding Box
Length 5306.851 mm
Width 26394.721 mm
Height 2144.488 mm
Moment of Inertia at Center of Mass (g mm^2)
Ixx 1.129E+12
Ixy -2.718E+06
Ixz -7.875E+09
Iyx -2.718E+06
Iyy 7.780E+10
Iyz 1.632E+05
Izx -7.875E+09
Izy 1.632E+05
Izz 1.186E+12
Moment of Inertia at Origin (g mm^2)
Ixx 1.134E+12
Ixy -2.899E+06
Ixz -1.228E+10
Iyx -2.899E+06
Iyy 8.689E+10
Iyz -71000.22
Izx -1.228E+10
Izy -71000.22
Izz 1.190E+12
それではいってみよう
エクセルシートにプロパティのデータを貼り付ける
新しいシートを作成して，Fusion360で出力したプロパティを.txtファイルにしたものを貼り付ける
慣性モーメントの単位を変換する
Fusion360で出力された慣性テンソルの単位は[g mm^2]なので，これを[kg m^2]に変換する
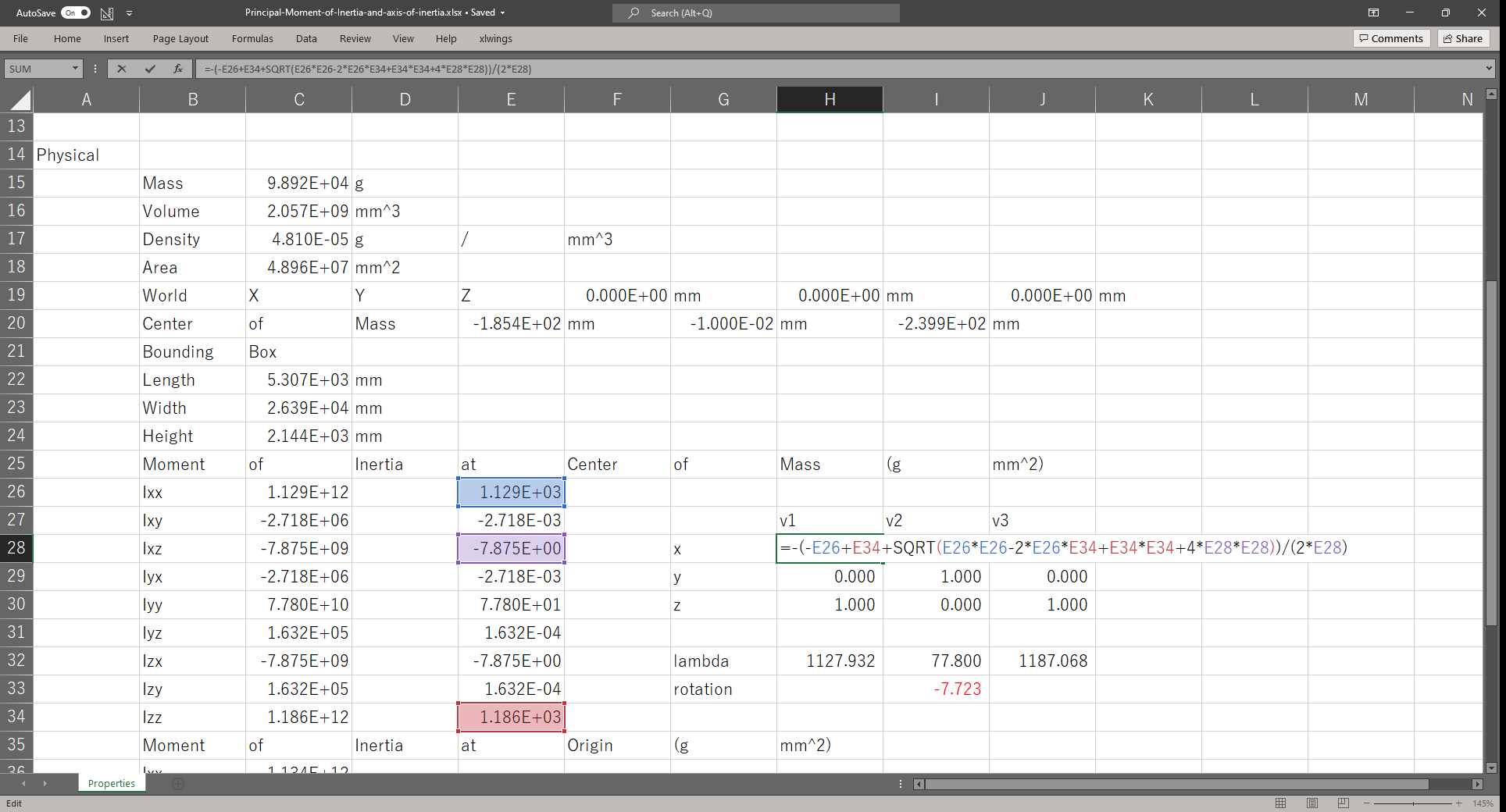
セルE26に以下の数式を入力し，セルE34までオートフィルを実行する
=C26*10^(-9)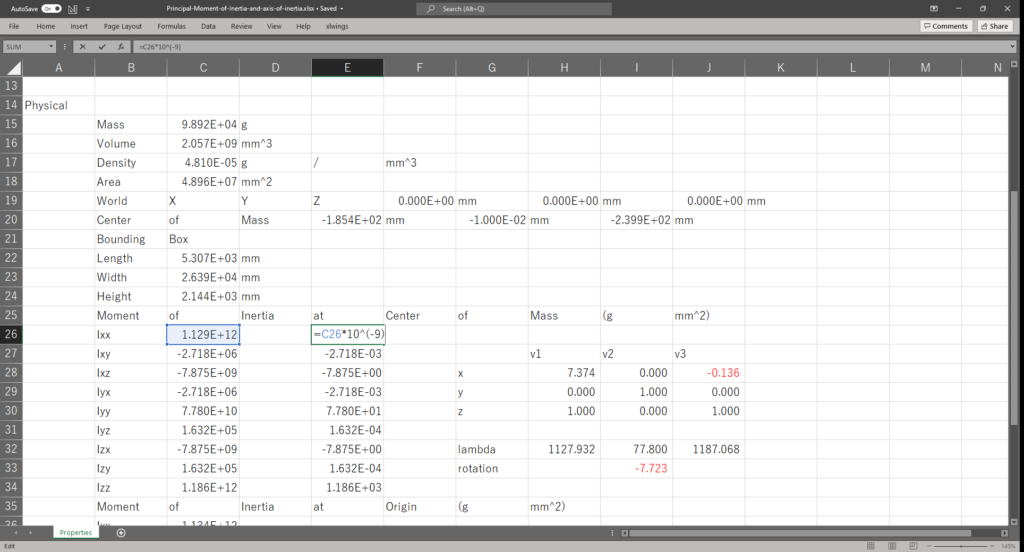
主慣性モーメントおよび慣性主軸を計算する
航空機の慣性テンソルは対称性を考慮すると以下の行列で表される（白本：式1.11）
\begin{eqnarray}
{\bf I}=\left[\begin{array}{ccc}
I_{xx}&0&I_{xz}\\
0&I_{yy}&0\\
I_{xz}&0&I_{zz}\\
\end{array}\right]
\end{eqnarray}
これを大学生の英知を使って対角化すると，固有値および固有ベクトルは次のように求まる
\begin{eqnarray}
\lambda_{1}&=&\frac{1}{2}(-\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}+I_{xx}+I_{zz})\\
\lambda_{2}&=&I_{yy}\\
\lambda_{3}&=&\frac{1}{2}(\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}+I_{xx}+I_{zz})\\
\\
v_{1}&=&\left[-\frac{-I_{xx}+I_{zz}+\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}}{2I_{xz}},0,1\right]\\
v_{2}&=&\left[0,1,0\right]\\
v_{3}&=&\left[-\frac{-I_{xx}+I_{zz}-\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}}{2I_{xz}},0,1\right]\\
\end{eqnarray}
慣性主軸
セルH28，セルJ28にそれぞれ以下の数式を入力し，慣性テンソルの固有ベクトル（慣性主軸）を計算する
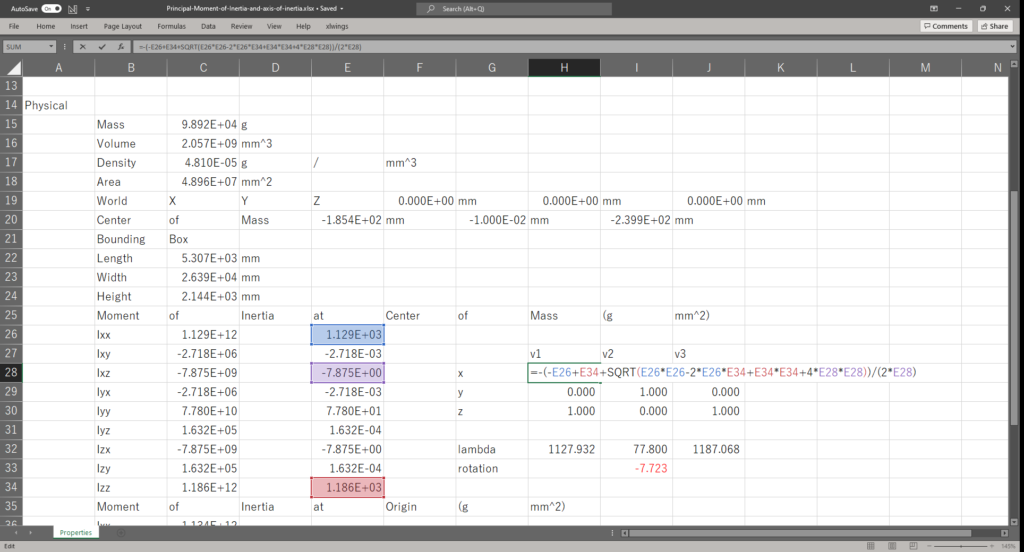
\begin{eqnarray}
v_{1}&=&\left[-\frac{-I_{xx}+I_{zz}+\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}}{2I_{xz}},0,1\right]\\
\\
v_{3}&=&\left[-\frac{-I_{xx}+I_{zz}-\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}}{2I_{xz}},0,1\right]\\
\end{eqnarray}
=-(-E26+E34+SQRT(E26*E26-2*E26*E34+E34*E34+4*E28*E28))/(2*E28)=-(-E26+E34-SQRT(E26*E26-2*E26*E34+E34*E34+4*E28*E28))/(2*E28)主慣性モーメント
セルH32，セルH33，セルH34にそれぞれ以下の数式を入力して主慣性モーメントを計算する
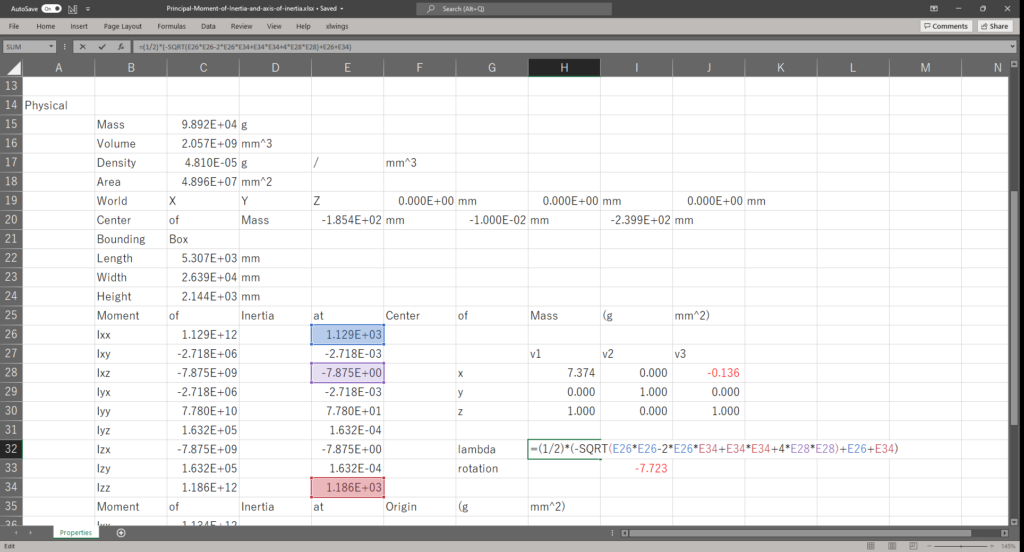
\begin{eqnarray}
\lambda_{1}&=&\frac{1}{2}(-\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}+I_{xx}+I_{zz})\\
\lambda_{2}&=&I_{yy}\\
\lambda_{3}&=&\frac{1}{2}(\sqrt{I_{xx}^{2}-2I_{xx}I_{zz}+I_{zz}^{2}+4I_{xz}^{2}}+I_{xx}+I_{zz})\\
\end{eqnarray}
=(1/2)*(-SQRT(E26*E26-2*E26*E34+E34*E34+4*E28*E28)+E26+E34)=E30=(1/2)*(SQRT(E26*E26-2*E26*E34+E34*E34+4*E28*E28)+E26+E34)慣性主軸の傾きを計算する
セルI33に以下の数式を入力して慣性主軸のy軸まわりの回転角[deg]を計算する
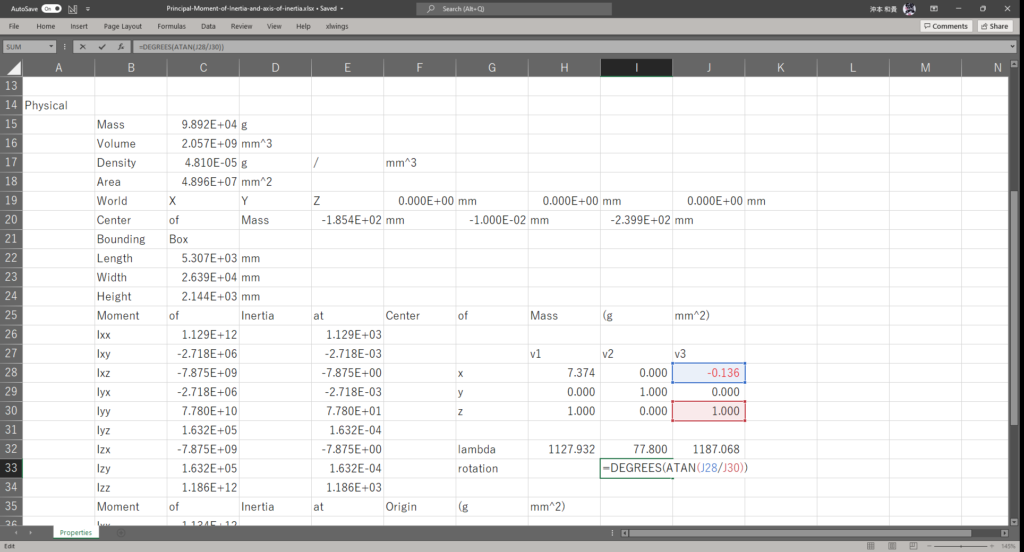
=DEGREES(ATAN(J28/J30))航空機は左右対称なので，慣性主軸は機体の対称面内で傾いているだけである
以上
おわりに
この記事では，Excelを使って慣性モーメントから主慣性モーメントと慣性主軸を計算する方法について説明した
やはり大学生の英知は素晴らしい
コメント