TR-797の解説

TR-797　”非平面翼の最適設計ー揚力と翼根曲げモーメントを与えた時の最小誘導抵抗ー”の解説を行う

概要
論文の解説
まとめ

概要

TR-797といえば鳥人間界隈の循環分布最適化のバイブルともいえるものである

実際の論文は以下からダウンロードできるので必ず一度読んでみてほしい(読んで理解し，プログラムで実装できればこの記事を読む必要はない )

≫非平面翼の最適設計-揚力と翼根曲げモーメントを与えた時の最小誘導抵抗-

この論文の結論だけを端的にいうと「ウィングレットをつけるよりもその分スパンを伸ばしたほうがいいよ」なのだが，人力飛行機については別の使い方ができる

プロペラ機については以下の記事を参考にするといい

≫人力飛行機の主翼設計を銀本より良くするたった一つの方法

≫「人力飛行機の主翼設計を銀本より良くするたった一つの方法」を使って人力飛行機を設計してみた。

≫人力飛行機を割と本気で設計してみた。第一報

一方，設計思想にもよるが，鳥コン滑空機において循環分布を崩してまで桁を軽量化する意味はあまりない（≫ 滑空機の最適重量についての考察）

ところがTR-797を使うともう少し面白いことができる

それは，「地面効果域での循環分布の最適化」である

論文の解説

論文の解説を行っていく

ここから先はすでに論文を読んだものとして話を進めていくので，手元に論文を置いておくといい

1. はじめに

この章を要約すると次のようになる

Wingletをつけると誘導抗力を減らせるよ
でもWingletを付けたら実質スパン伸ばしてない？
Wingletをつけるのとスパン伸ばすのどっちがいいの？
誘導抗力が小さくなったって構造重量増えたら意味なくない？
よし，じゃあ翼の伸展平面形と翼根曲げモーメントを同じにしてその2つを比べてみよう！

第一章はこんな感じ．次の章へ進む

2. 最適化問題の定式化

この章が今回の記事のメインテーマである

2.1 非平面翼にはたらく空気力の計算

この節の前半部分を要約すると次のようになる

翼理論では揚力面は多数の馬蹄渦の集合で表されるよ
誘導抗力は主翼の無限下流にあるTrefftz面に投影した後流渦にのみ依存するよ
アスペクト比が大きい翼では誘導抗力以外の翼にはたらく空気力もTrefftz面に投影した渦で考えても問題ないよ

ここら辺の議論は「航空力学の基礎第3版p.131」あたりにも書いてあるので参考にしてほしい

ちなみにTrefftz面というのはちょこっと調べた感じだとどうやら翼の無限下流にある面のことをそう呼ぶらしい

さて，揚力\(L\)，翼根曲げモーメント\(B\)，誘導抗力\(D_{i}\)は循環\(\Gamma\)を使って次のように表される

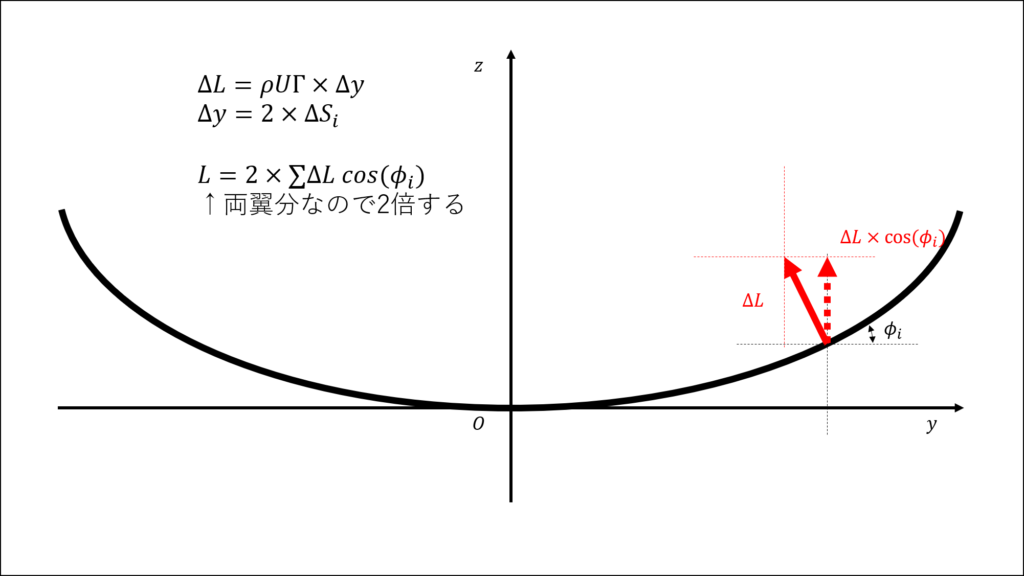
\begin{eqnarray}
L &=& 4\rho U \sum_{i=1}^{N} \Gamma_{i} cos{\phi_{i}} \Delta S_{i}
\tag{4} \\
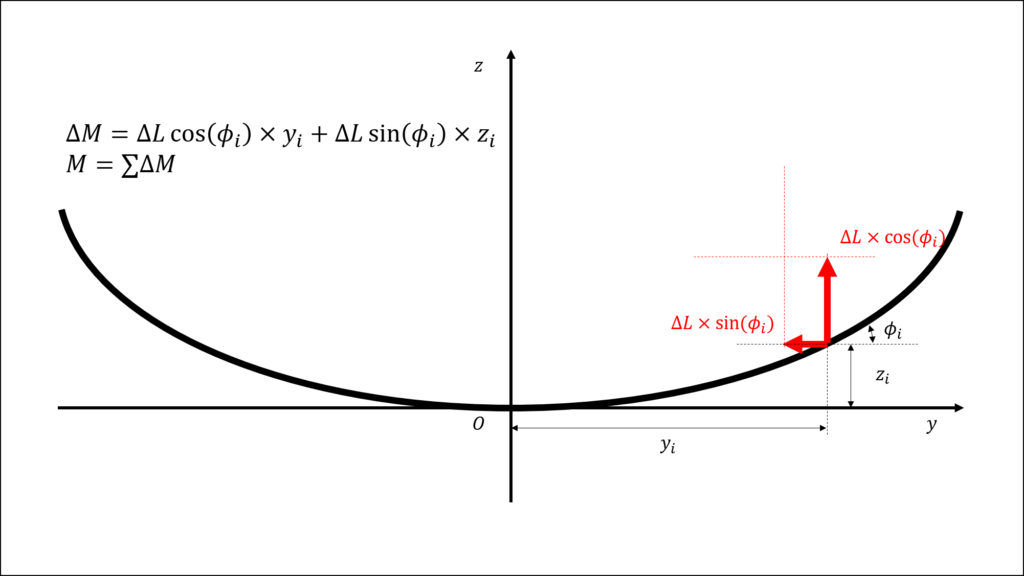
B &=& 2\rho U \sum_{i=1}^{N} \Gamma_{i} (y_{i}cos{\phi_{i}}+z_{i}sin{\phi_{i}}) \Delta S_{i}
\tag{5} \\
D_{i} &=& 2\rho U \sum_{i=1}^{N} \Gamma_{i} V_{ni} \Delta S_{i}
\tag{6}
\end{eqnarray}

ここで\(V_{ni}\)はBiot-Savartの法則によって計算される渦形によって誘起される速度で，次のように表される

\begin{eqnarray}
V_{ni} &=& \sum_{j=1}^{N} Q_{ij} \Gamma_{i}
\tag{7}
\end{eqnarray}

ちなみにこの速度\(V_{ni}\)は翼面上ではなく翼の無限下流にあるTrefftz面における速度なので，航空力学の基礎第3版p.43でいうとBiot-Savartの法則は渦糸が一方向に無限に伸びているときの式(2.65)ではなく渦糸が両方向無限に伸びている式(2.64)のほうである

\begin{eqnarray}
v &=& \frac{\Gamma}{2\pi h}
\tag{2.64} \\
v &=& \frac{\Gamma}{4\pi h}
\tag{2.65} \\
\end{eqnarray}

式(7)において，\(Q_{ij}\)はj番目のパネルとz軸を挟んで反対方向にあるｊ’番目のパネルに置かれた単位強さ当たりの渦対がi番目パネルの中心に誘起する垂直速度を表す影響係数（式(2.64)でいうと\(\frac{1}{2\pi h}\)）で，次の式で表される

\begin{eqnarray}
Q_{ij} &=& \frac{1}{2\pi}((-\frac{y'_{ij}-\Delta S_{j}}{{R_{+ij}}^2}+\frac{y'_{ij}+\Delta S_{j}}{{R_{-ij}}^2}) cos(\phi_{i}-\phi_{j}) \\
&& +(-\frac{z'_{ij}}{{R_{+ij}}^2}+\frac{z'_{ij}}{{R_{-ij}}^2}) sin(\phi_{i}-\phi_{j}) \\
&& +(-\frac{y''_{ij}-\Delta S_{j}}{{R'_{-ij}}^2}+\frac{y''_{ij}+\Delta S_{j}}{{R'_{+ij}}^2}) cos(\phi_{i}+\phi_{j}) \\
&& +(-\frac{z''_{ij}}{{R'_{-ij}}^2}+\frac{z''_{ij}}{{R'_{+ij}}^2}) sin(\phi_{i}+\phi_{j})) \\
\tag{8}
\end{eqnarray}

ここで

\begin{eqnarray}
y'_{ij} &=& (y_{i}-y_{j}) cos(\phi_{j})+(z_{i}-z_{j}) sin(\phi_{j})
\tag{9a} \\
z'_{ij} &=& -(y_{i}-y_{j}) sin(\phi_{j})+(z_{i}-z_{j}) cos(\phi_{j})
\tag{9b} \\
y''_{ij} &=& (y_{i}+y_{j}) cos (\phi_{j}) -(z_{i}-z_{j}) sin (\phi_{j})
\tag{9c} \\
z''_{ij} &=& (y_{i}+y_{j}) sin (\phi_{j}) +(z_{i}-z_{j}) cos (\phi_{j})
\tag{9d} \\
{R_{+ij}}^2 &=& (y'_{ij}-\Delta S_{j})^2+{z'_{ij}}^2
\tag{10a} \\
{R_{-ij}}^2 &=& (y'_{ij}+\Delta S_{j})^2+{z'_{ij}}^2
\tag{10b} \\
{R'_{+ij}}^2 &=& (y''_{ij}+\Delta S_{j})^2+{z''_{ij}}^2
\tag{10c} \\
{R'_{-ij}}^2 &=& (y''_{ij}-\Delta S_{j})^2+{z''_{ij}}^2
\tag{10d}
\end{eqnarray}

式(8)の\(Q_{ij}\)が式(2.64)における\(\frac{1}{2\pi h}\)に対応する係数であることを説明していく

式(8)の右辺第一項と第二項は右翼のｊ番目のパネルによる影響を，右辺第三項と第四項は左翼のj'番目のパネルによる影響を表しているのでひとまず右翼のｊ番目のパネルによる影響を考える

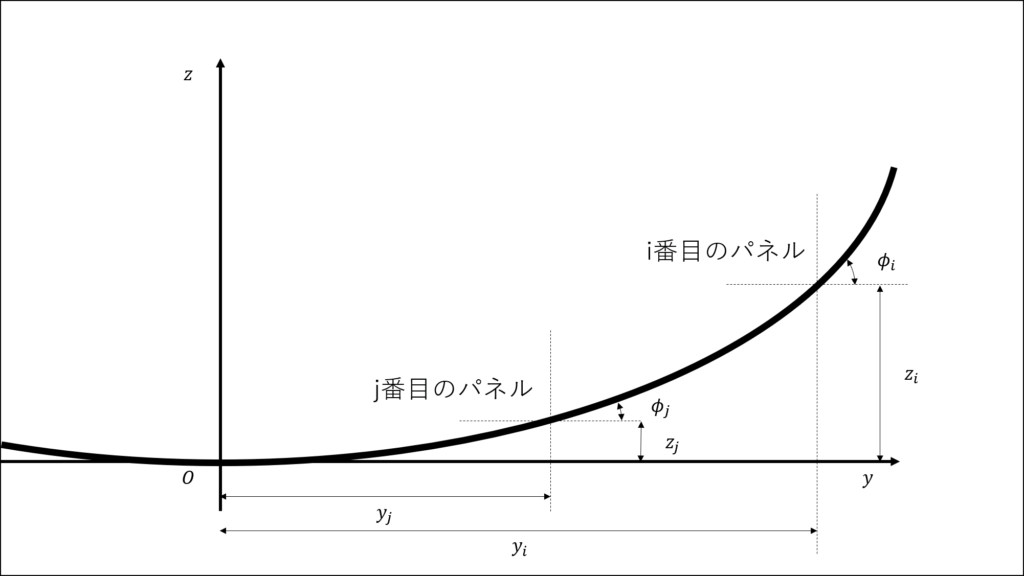
まずj番目のパネルを原点とする局所座標を考える

この局所座標ではi番目のパネルの座標は\((y_{i}-y_{j},z_{i}-z_{j})\)となる

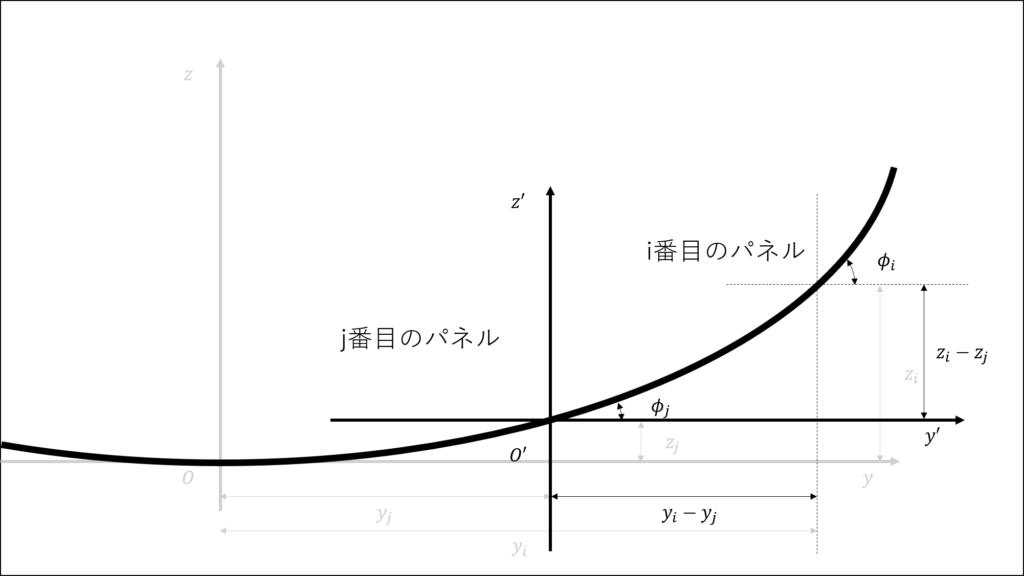
さらにこの座標系を\(\phi_{j}\)だけ回転させると，回転座標の公式よりi番目のパネルの座標は式(9a)，(9b)のようになる

\begin{eqnarray}
y'_{ij} &=& (y_{i}-y_{j}) cos(\phi_{j})+(z_{i}-z_{j}) sin(\phi_{j})
\tag{9a} \\
z'_{ij} &=& -(y_{i}-y_{j}) sin(\phi_{j})+(z_{i}-z_{j}) cos(\phi_{j})
\tag{9b} \\
\end{eqnarray}

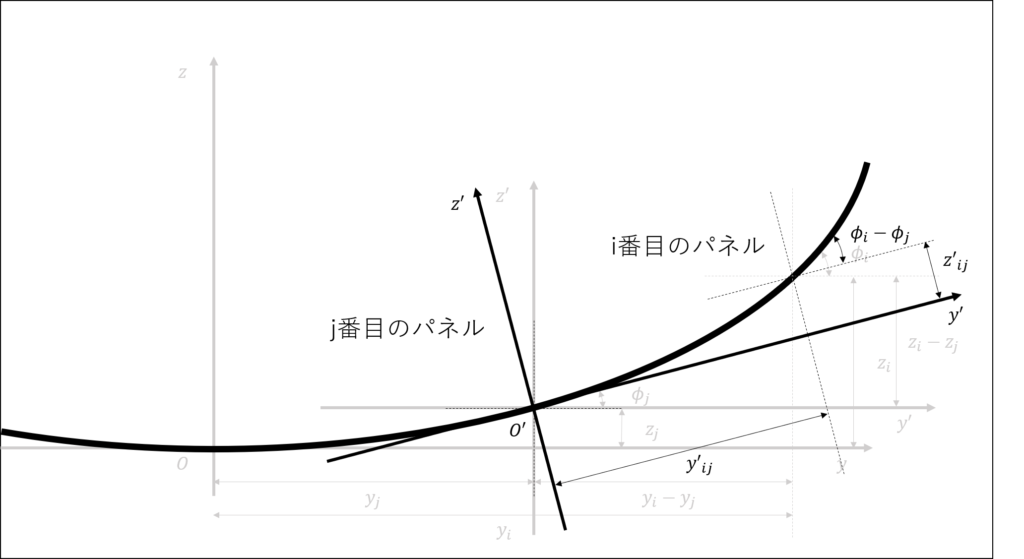
次に，j番目のパネルの右側から出てくる渦糸の循環の影響を考える

この渦糸は反時計回りに回っているため循環の符号は正であり，i番目のパネルの中心との距離は次の式で表される

\begin{eqnarray}
R_{+ij} &=& \sqrt{(y'_{ij}-\Delta S_{j})^2+{z'_{ij}}^2}
\tag{10a'}
\end{eqnarray}

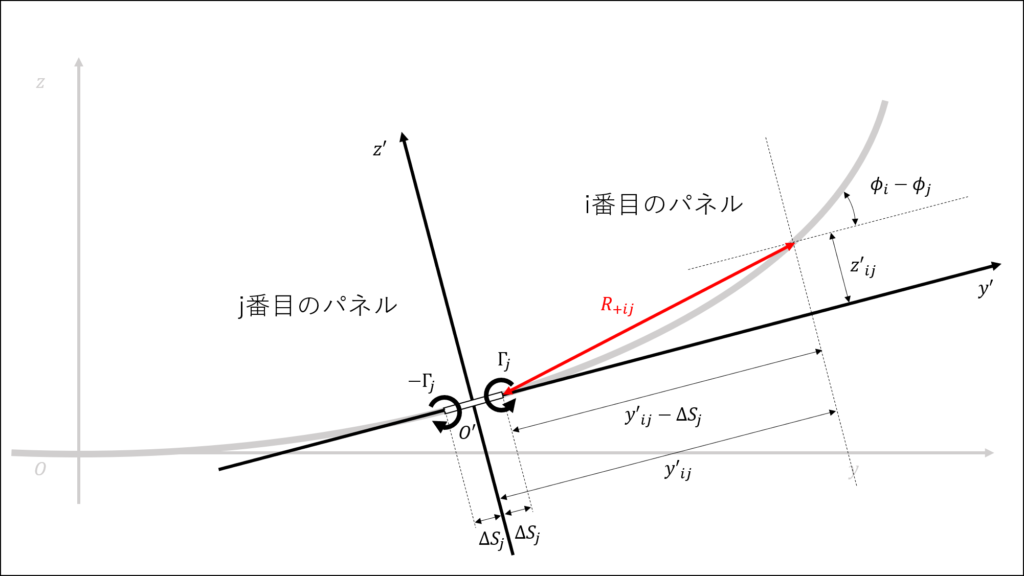
この循環によってi番目のパネルに垂直に誘導される速度を\(V_{+}\)とすると，式(2.64)より以下の式で表せる

\begin{eqnarray}
V_{+} &=& \frac{\Gamma_{j}}{2\pi R_{+ij}}
\end{eqnarray}

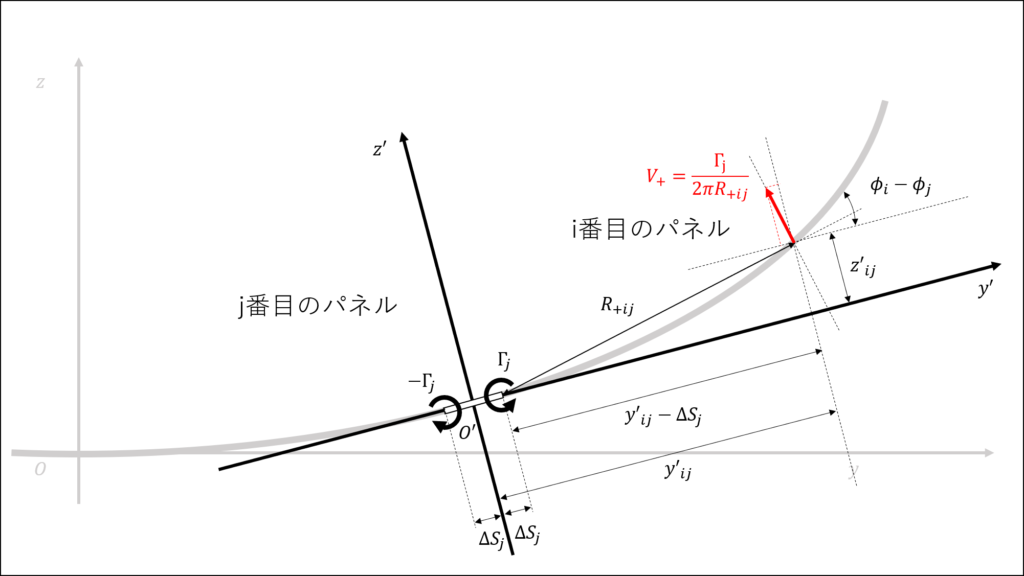
上図において，j番目のパネル右側とi番目のパネル中心を結んだ線(長さ\(R_{+ij}\))とy’軸のなす角を\(\theta\)とすると下の関係がわかる

\begin{eqnarray}
cos{\theta} &=& \frac{y'_{ij}-\Delta S_{j}}{R_{+ij}} \\
sin{\theta} &=& \frac{z'_{ij}}{R_{+ij}} \\
\end{eqnarray}

この関係を用いて，\(V_{+}\)をy’軸方向とz’軸方向に分解するとそれぞれ次のようになる

\begin{eqnarray}
V_{+y'} &=& V_{+} sin{\theta} = \frac{z'_{ij}}{{R_{+ij}}^2} \Gamma_{j} \\
V_{+z'} &=& V_{+} cos{\theta} = \frac{y'_{ij}-\Delta S_{j}}{{R_{+ij}}^2} \Gamma_{j} \\
\end{eqnarray}

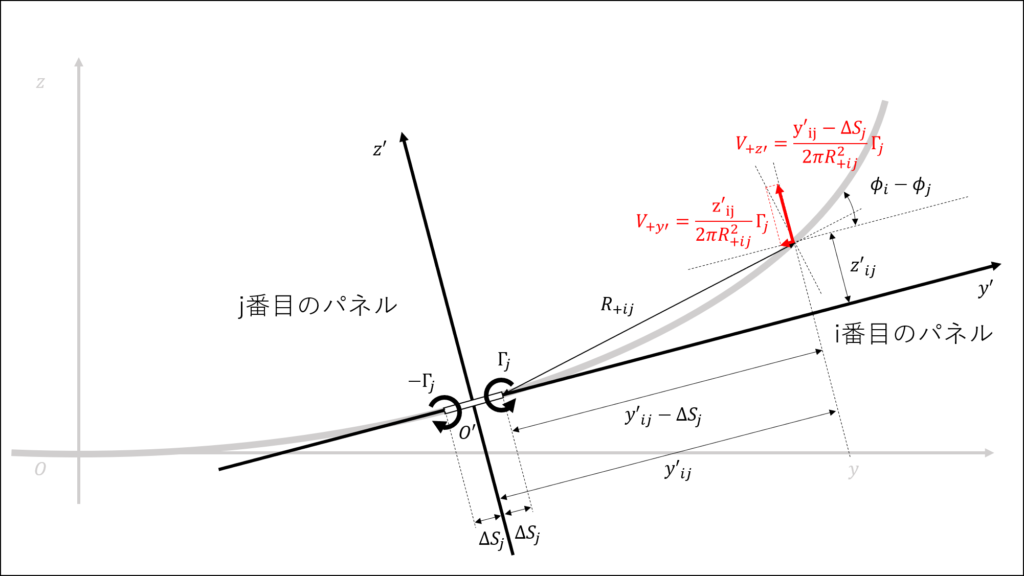
同様に，j番目のパネルの左側から出てくる渦糸によって誘起される速度を考えると次のようになる

\begin{eqnarray}
V_{-y'} &=& V_{+} sin{\theta'} = \frac{z'_{ij}}{{R_{-ij}}^2} \Gamma_{j} \\
V_{-z'} &=& V_{+} cos{\theta'} = \frac{y'_{ij}+\Delta S_{j}}{{R_{-ij}}^2} \Gamma_{j} \\
\end{eqnarray}

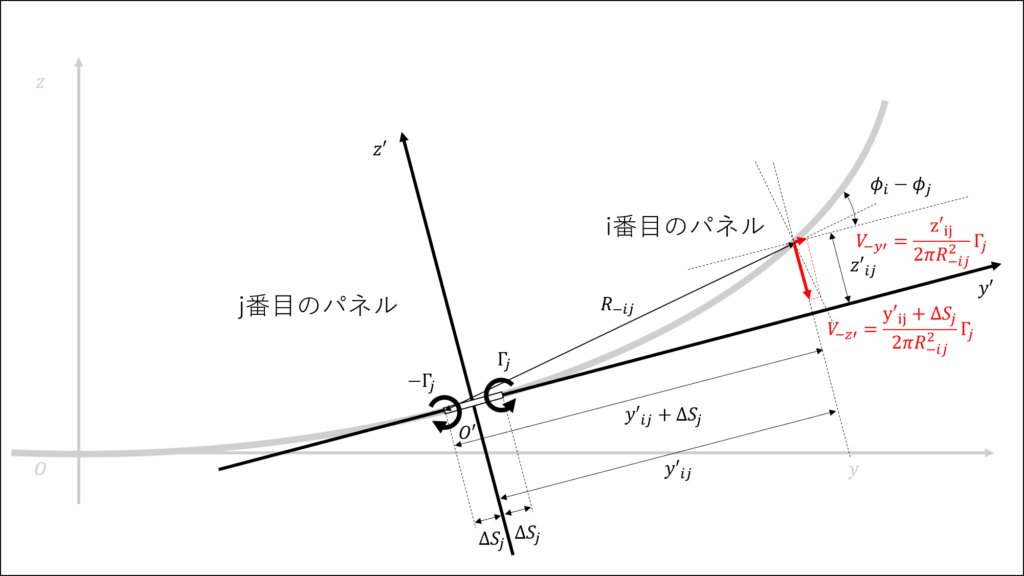
向きをを考慮するとj番目のパネルの両側から出る渦糸によってi番目のパネルの中心に誘起される速度のy'軸，z'軸方向成分はそれぞれ\(V_{y'}=-V_{+y'}+V_{-y'}\)，\(V_{z'}=V_{+z'}-V_{-z'}\) であり，これをi番目のパネルに対して垂直な方向に分解した速度\(V_{nij}\)は次のようになる

\begin{eqnarray}
V_{nij} &=& V_{y'} sin(\phi_{i}-\phi_{j})-V_{z'} cos(\phi_{i}-\phi_{j}) \\
&=& (-V_{+y'}+V_{-y'}) sin(\phi_{i}-\phi_{j})-(V_{+y'}-V_{-y'}) cos(\phi_{i}-\phi_{j}) \\
&=& \frac{\Gamma_{j}}{2\pi}((-\frac{y'_{ij}-\Delta S_{j}}{R_{+ij}^2}+\frac{y'_{ij}+\Delta S_{j}}{R_{-ij}^2}) cos(\phi_{i}-\phi_{j}) \\
&& +(-\frac{z'_{ij}}{R_{+ij}^2}+\frac{z'_{ij}}{R_{-ij}^2}) sin(\phi_{i}-\phi_{j}) \\
\tag{8'}
\end{eqnarray}

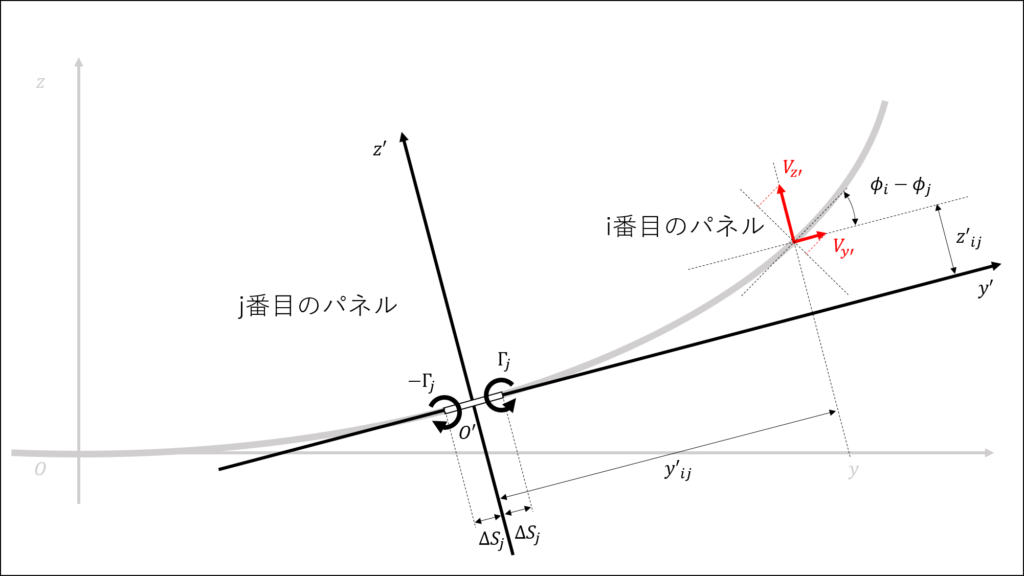
これで式(8)の右辺の第一項と第二項が求められた

左翼のj'番目のパネルについて考える

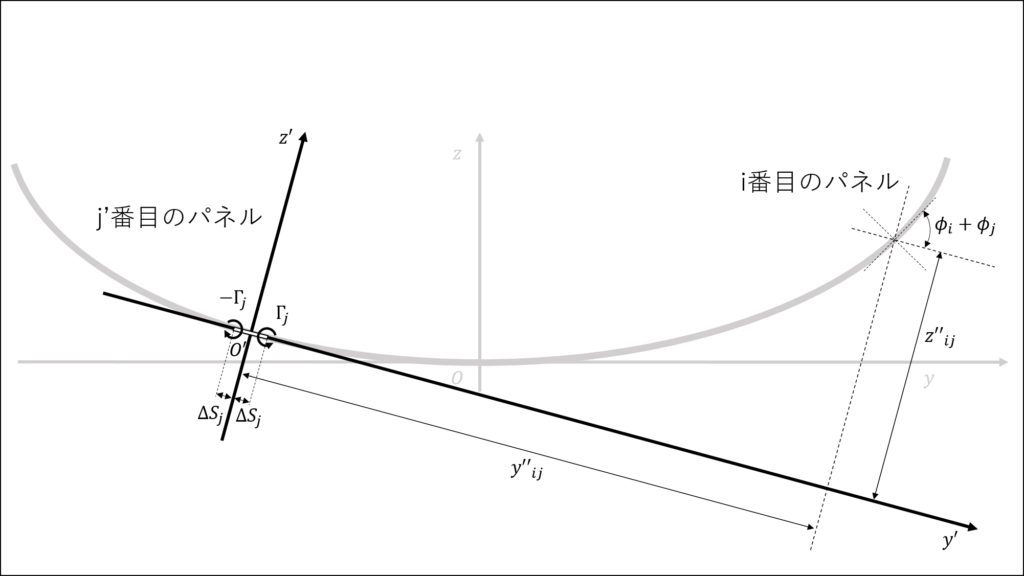
j'番目のパネルでは，j番目のパネルの式において\(y_{j} \to (-y_{j})\)，\(\phi_{j} \to (-\phi_{j})\)とすればよく，\(y''_{ij}\)，\(z''_{ij}\)は次の式で表される

\begin{eqnarray}
y''_{ij} &=& (y_{i}-(-y_{j})) cos(-\phi_{j})+(z_{i}-z_{j}) sin(-\phi_{j})
\tag{9c'} \\
z''_{ij} &=& -(y_{i}-(-y_{j})) sin(-\phi_{j})+(z_{i}-z_{j}) cos(-\phi_{j})
\tag{9d'} \\
\end{eqnarray}

j'番目のパネルの右側から出る渦糸とi番目のパネルの中心との距離が\(R'_{-ij}\)， j'番目のパネルの左側から出る渦糸と i番目パネルの中心との距離が\(R'_{+ij}\)であることに注意すると，これらは次の式で表される

\begin{eqnarray}
{R'_{+ij}}^2 &=& (y''_{ij}+\Delta S_{j})^2+{z''_{ij}}^2
\tag{10c} \\
{R'_{-ij}}^2 &=& (y''{ij}-\Delta S{j})^2+{z''_{ij}}^2
\tag{10d} \\
\end{eqnarray}

よってj'番目のパネルによってi番目のパネルの中心に垂直に誘起される速度は次のように表される

\begin{eqnarray}
V'_{nij} &=& \frac{\Gamma_{j}}{2\pi}((-\frac{y''_{ij}-\Delta S_{j}}{{R'_{-ij}}^2}+\frac{y''_{ij}+\Delta S_{j}}{{{R_{+ij}}}^2}) cos(\phi_{i}-(-\phi_{j})) \\
&& +(-\frac{z''_{ij}}{{R_{-ij}}^2}+\frac{z''_{ij}}{{R_{+ij}}^2}) sin(\phi_{i}-(-\phi_{j})) \\
\tag{8''}
\end{eqnarray}

これで式(8)の右辺第三項と第四項が求められた

\(Q_{ij}\)がBiot-Savartの法則の係数であることがわかっただろうか

2.1.\(\alpha\) 地面効果の考慮

ついでに地面効果も考慮しておく

地面効果を再現するには，地面を挟んで反対側に，翼面上にある循環と同じ強さ，逆向きの循環を配置すればよい（以下，鏡像とよぶ）

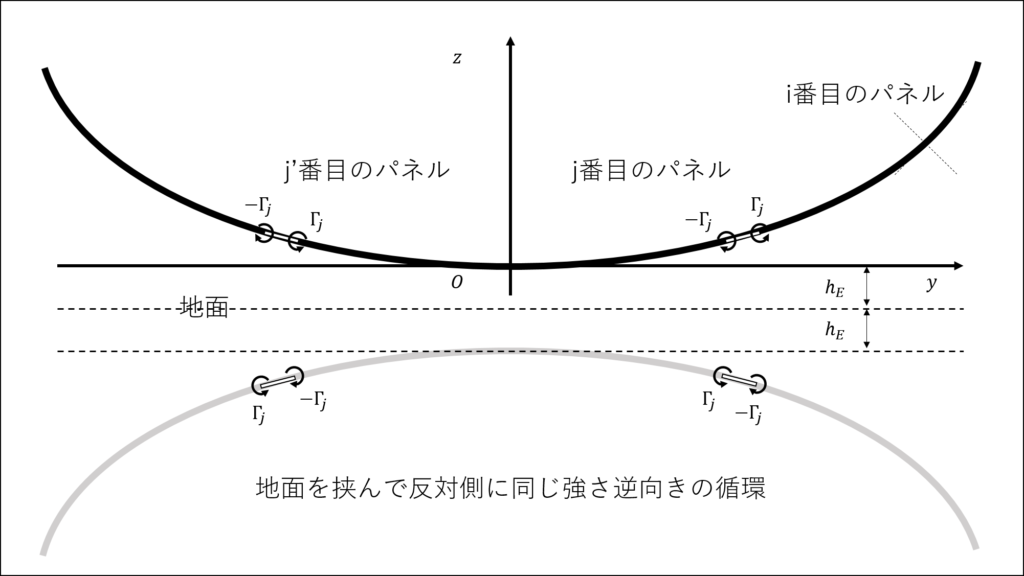
鏡像の循環がi番目のパネルに及ぼす影響係数を考える

右翼の鏡像の循環については，j番目のパネルの式を次のように変換する

\(y_{j} \to y_{j}\)
\(z_{j} \to (-z_{j}-2h_{E})\)
\(\phi_{j} \to (-\phi_{j})\)
\(\Gamma_{j} \to (-\Gamma_{j})\)

左翼の鏡像の循環については，j番目のパネルの式を次のように変換する

\(y_{j} \to (-y_{j})\)
\(z_{j} \to (-z_{j}-2h_{E})\)
\(\phi_{j} \to \phi_{j}\)
\(\Gamma_{j} \to (-\Gamma_{j})\)

よって，鏡像によるi番目のパネルの垂直方向の速度への影響係数\({Q_{ij}}_{mirror}\)は次のようになる

\begin{eqnarray}
{Q_{ij}}_{mirror} &=& \frac{1}{2\pi}(-(-\frac{{y'_{ij}}_{mirror}-\Delta S_{j}}{{{R_{+ij}}_{mirror}}^2}+\frac{{y'_{ij}}_{mirror}+\Delta S_{j}}{{{R_{-ij}}_{mirror}}^2}) cos(\phi_{i}-(-\phi_{j})) \\
&& -(-\frac{{z'_{ij}}_{mirror}}{{{R_{+ij}}_{mirror}}^2}+\frac{{z'_{ij}}_{mirror}}{{{R_{-ij}}_{mirror}}^2}) sin(\phi_{i}-(-\phi_{j})) \\
&& -(-\frac{{y''_{ij}}_{mirror}-\Delta S_{j}}{{{R'_{-ij}}_{mirror}}^2}+\frac{{y''_{ij}}_{mirror}+\Delta S_{j}}{{{R'_{+ij}}_{mirror}}^2}) cos(\phi_{i}-\phi_{j}) \\
&& -(-\frac{{z''_{ij}}_{mirror}}{{{R'_{-ij}}_{mirror}}^2}+\frac{{z''_{ij}}_{mirror}}{{{R'_{+ij}}_{mrror}}^2}) sin(\phi_{i}-\phi_{j})) \\
\end{eqnarray}

ここで，

\begin{eqnarray}
{y'_{ij}}_{mirror} &=& (y_{i}-y_{j}) cos(-\phi_{j})+(z_{i}-(z_{j}-2h_{E})) sin(-\phi_{j}) \\
{z'_{ij}}_{mirror} &=& -(y_{i}-y_{j}) sin(-\phi_{j})+(z_{i}-(z_{j}-2h_{E})) cos(-\phi_{j}) \\
{y''_{ij}}_{mirror} &=& (y_{i}+y_{j}) cos (\phi_{j}) +(z_{i}-(z_{j}-2h_{E}) sin (\phi_{j}) \\
{z''_{ij}}_{mirror} &=& -(y_{i}+y_{j}) sin (\phi_{j}) +(z_{i}-(z_{j}-2h_{E})) cos (\phi_{j}) \\
{{R_{+ij}}_{mirror}}^2 &=& ({y'_{ij}}_{mirror}-\Delta S_{j})^2+{{z'_{ij}}_{mirror}}^2 \\
{{R_{-ij}}_{mirror}}^2 &=& ({y'_{ij}}_{mirror}+\Delta S_{j})^2+{{z'_{ij}}_{mirror}}^2 \\
{{R'_{+ij}}_{mirror}}^2 &=& ({y''_{ij}}_{mirror}+\Delta S_{j})^2+{{z''_{ij}}_{mirror}}^2 \\
{{R'_{-ij}}_{mirror}}^2 &=& ({y''_{ij}}_{mirrro}-\Delta S_{j})^2+{{z''_{ij}}_{mirror}}^2 \\
\end{eqnarray}

ちなみにここらへんの数式はコピペを使いまくって書いているので符号間違いは大いにありうることを頭に入れておいてほしい

2.2 最適化問題の定式化

この章の前半ではいままで使ってきた変数を正規化している

かなりたくさんの変数や式が正規化されているが，必要なのは以下のものだけである

\begin{eqnarray}
\Delta \sigma_{i} &=& \frac{\Delta S_{i}}{l_e} \\
\eta_{i} &=& \frac{y_{i}}{l_{e}} \\
\zeta &=& \frac{z_{i}}{l_{e}} \\
q_{ij} &=& Q_{ij} l_{e} \\
\end{eqnarray}

\(Q_{ij}\)の単位は[1/m]なので正規化するときは\(l_{e}\)をかけることに注意する

これらの正規化された変数を使って次の変数を新たに定義する

\begin{eqnarray}
g_{i} &=& \frac{2 l_{e} \rho U \Gamma_{i}}{L}
\tag{19} \\
c_{i} &=& 2cos{\phi_{i}} \Delta \sigma
\tag{20} \\
b_{i} &=& \frac{3\pi}{2}(\eta_{i} cos{\phi_{i}}+\zeta_{i} sin{\phi_{i}})\Delta \sigma
\tag{21} \\
A_{ij} &=& \pi q_{ij} \Delta \sigma_{i}
\tag{22} \\
\end{eqnarray}

この変数を使うと，揚力，翼根曲げモーメント，誘導抗力に関する拘束条件が次のように表せる

\begin{eqnarray}
1 &=& \sum_{i=1}^N c_{i} g_{i} = {\bf c}^T \cdot {\bf g}
\tag{23} \\
\beta &=& \sum_{i=1}^N b_{i} g_{i} = {\bf b}^T \cdot {\bf g}
\tag{24} \\
\frac{1}{e} &=& \sum_{i=1}^N \sum_{j=1}^N g_{i} A_{ij} g_{j} = {\bf g}^T \cdot {\bf A} \cdot {\bf g}
\tag{25} \\
\end{eqnarray}

ちなみに上の式に\(g_{i}\)，\(c_{i}\)，\(b_{i}\)，\(A_{ij}\)を代入すると式(4’)，(5’)，(11’)になることを確認できる

翼の有害抗力は伸展平面形を固定しているため有害抗力の大きさはほぼ一定とみなせる．そのため，構造的制限\(\beta\)の下で\(\frac{1}{e}\)が最小となるような循環分布を求めればそれが最適な循環分布であることがわかる

2.3 最適化問題の解法

この節では，最適化問題を解くためのLagrange未定乗数法が説明されている

しかし，ぶっちゃけLagrange未定乗数法が何かさっぱりわからなくても，式(33)のN+2限連立1次方程式が解ければ問題ない

\begin{eqnarray}
\left[
\begin{array}{cccccccc}
2A_{11} & A_{21}+A_{12} & \ldots & \ldots & \ldots & A_{N1}+A_{1N} & -c_{1} & -b_{1} \\
A_{12}+A_{21} & 2A_{22} & & & & \vdots & -c_{2} & -b_{2} \\
\vdots & \vdots & \ddots & & & \vdots & \vdots & \vdots \\
A_{1i}+A_{i1} & \vdots & \ldots & 2A_{ii} & \ldots & \vdots & \vdots & \vdots \\
\vdots & \vdots & & & \ddots & \vdots & \vdots & \vdots \\
A_{1N}+A_{N1} & \ldots & \ldots & \ldots & \ldots & 2A_{NN} & -c_{N} & -b_{N} \\
-c_{1} & -c_{2} & \ldots & \ldots & \ldots & -c_{N} & 0 & 0 \\
-b_{1} & -b_{2} & \ldots & \ldots & \ldots & -b_{N} & 0 & 0 \\
\end{array}
\right]
\cdot \left[
\begin{array}{c}
g_{1} \\
g_{2} \\
\vdots \\
\vdots \\
\vdots \\
g_{N} \\
\mu_1 \\
\mu_2 \
\end{array}
\right]
= \left[
\begin{array}{c}
0 \\
0 \\
\vdots \\
\vdots \\
\vdots \\
0 \\
-1 \\
\beta \\
\end{array}
\right]
\end{eqnarray}