TR-797”非平面翼の最適設計-揚力と翼根曲げモーメントを与えた時の最小誘導抵抗-”のExcel VBAでの実装を行う
目的とフローチャート
論文の解説自体は前回(≫TR-797の解説)で行ったので,今回はExcel VBAで実装してみる
テンプレートファイルのダウンロード
エクセルシートの配置などの参考になるようにテンプレートファイルを添付しておく
※数式やマクロはすべて削除してあり,値も適当である
TemplateNO_TEXT_ver20191114.xlsx
前々回(≫重量推算②)の続きからやりたい人は,まずセルAW12:AW15に構造的制限の有無,翼に沿った長さ\(l_{e}\),パネルの反復\(\Delta S\),構造的制限\(\beta\)を入力,セルBB22:BB23に対気速度と高度を入力する
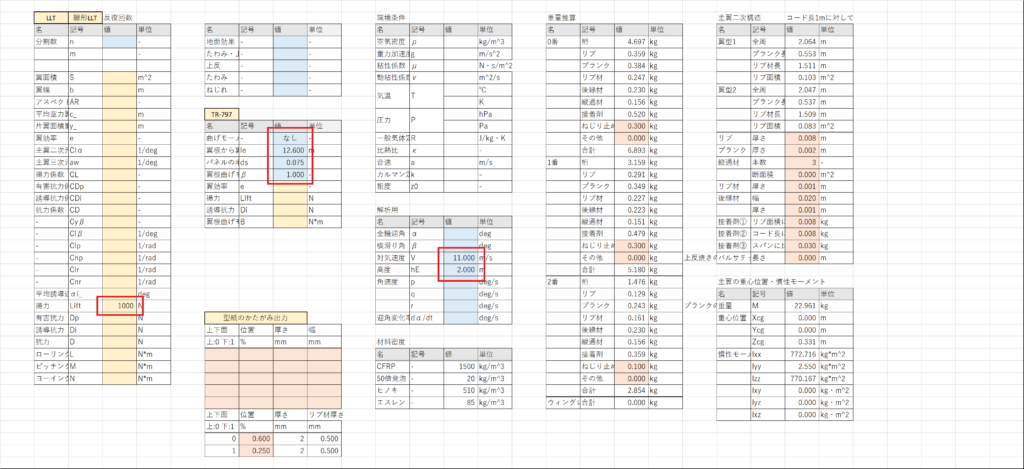
またAF列の45行目以下に,テンプレートシートから上反角分布をもってきておく
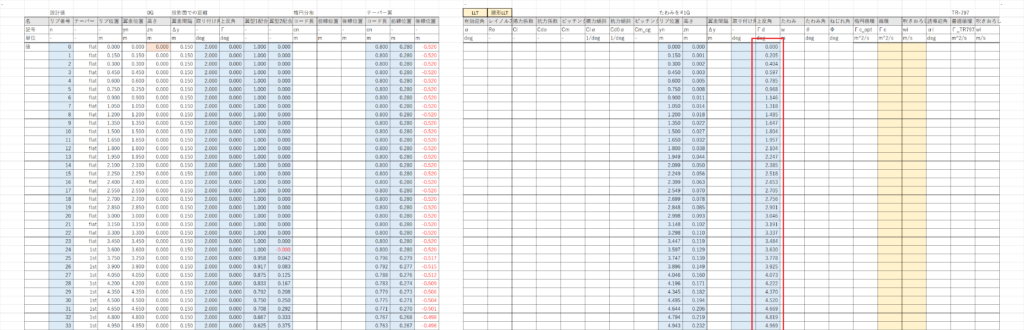
フローチャート
循環分布を最適化するまでのフローチャートを以下に示す
機体形状を定式化し,循環-吹きおろしの影響係数を求める.揚力のつり合い,翼根曲げモーメントの制限,誘導抗力が最小になるという条件を詰め込んだ連立一次方程式を解くことで循環分布が求まり,それをもとに誘導抗力などを計算する
どちらかというと渦格子法に近いプログラムである
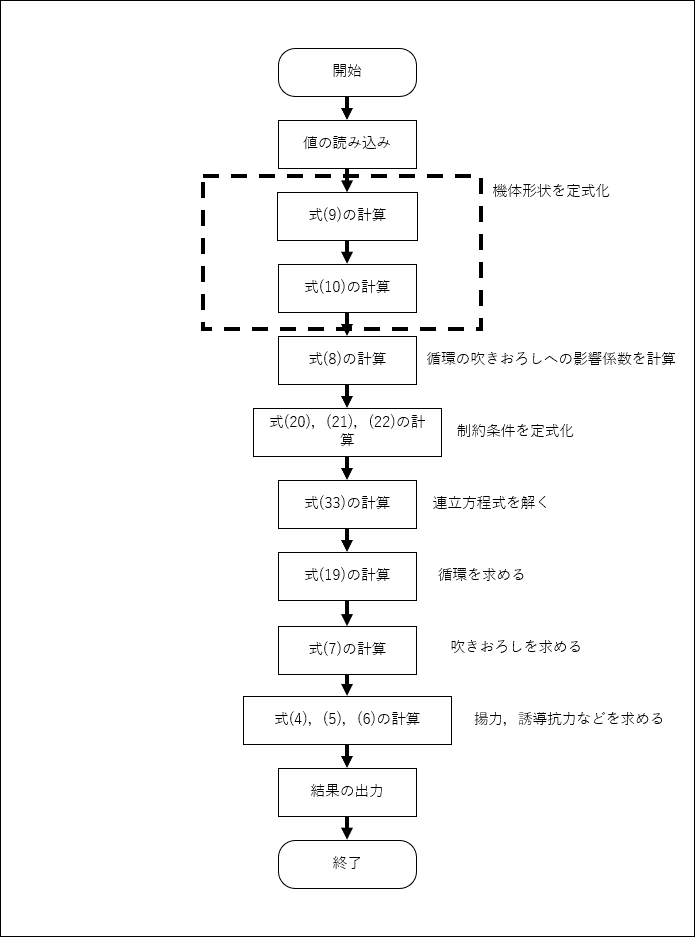
ソースコード全文はこれ
Function TR797(ByVal span_div As Integer, ByVal beta As Double, ByVal hE As Double) As Double()
'地面効果を考慮して,翼根の曲げモーメントに制約を設けた循環分布の最適化を行う
'参考文献:”非平面翼の最適設計-揚力と翼根曲げモーメントを与えた時の最小誘導抵抗- TR797 航空宇宙技術研究所”
'ワークシートの定義
Set sht1 = Sheets("主翼(sht1)")
Dim state As variables
'変数の宣言
Dim Aij() As Double: ReDim Aij(span_div - 1, span_div - 1) 'スパン荷重分布と誘導抵抗を結び付ける影響関数
Dim bi() As Double: ReDim bi(span_div - 1) 'スパン荷重分布と翼根曲げモーメントを関係づける影響関数
Dim BendingMoment As Double '翼根曲げモーメント
Dim ci() As Double: ReDim ci(span_div - 1) 'スパン荷重分布と全揚力とを関係づける影響関数
Dim Di As Double '誘導抗力
Dim e As Double 'スパン効率
Dim gi() As Double: ReDim gi(span_div - 1) 'スパン荷重分布を表す無次元ベクトル
Dim Lift As Double '必要な揚力
Dim le As Double '翼根から翼端までの翼の長さ(翼を水平面に投影したときの翼幅とは異なる)
Dim N As Integer '右翼をパネル分割したときの分割数(control point)
Dim Qij() As Double: ReDim Qij(span_div - 1, span_div - 1) 'スパン荷重分布と垂直誘導速度を結び付ける影響関数
Dim ds As Double 'パネルの半幅
Dim U As Double '一様流速度
Dim wi() As Double: ReDim wi(span_div - 1) '荷重曲線に垂直方向に誘導される速度
Dim circulation() As Double: ReDim circulation(span_div - 1) '循環分布
Dim rho As Double '一様流密度
Dim phi() As Double: ReDim phi(span_div - 1) '上反角分布 '上反角分布
'座標.p:prime,m:mirror
Dim y() As Double: ReDim y(span_div - 1)
Dim z() As Double: ReDim z(span_div - 1)
Dim yp() As Double: ReDim yp(span_div - 1, span_div - 1)
Dim zp() As Double: ReDim zp(span_div - 1, span_div - 1)
Dim ypp() As Double: ReDim ypp(span_div - 1, span_div - 1)
Dim zpp() As Double: ReDim zpp(span_div - 1, span_div - 1)
Dim ymp() As Double: ReDim ymp(span_div - 1, span_div - 1)
Dim zmp() As Double: ReDim zmp(span_div - 1, span_div - 1)
Dim ympp() As Double: ReDim ympp(span_div - 1, span_div - 1)
Dim zmpp() As Double: ReDim zmpp(span_div - 1, span_div - 1)
Dim Rpij() As Double: ReDim Rpij(span_div - 1, span_div - 1) 'パネル間の距離.R+ij
Dim Rmij() As Double: ReDim Rmij(span_div - 1, span_div - 1) 'パネル間の距離.R-ij
Dim Rpijp() As Double: ReDim Rpijp(span_div - 1, span_div - 1) 'パネル間の距離.R+ij
Dim Rmijp() As Double: ReDim Rmijp(span_div - 1, span_div - 1) 'パネル間の距離.R-ij
Dim Rpijm() As Double: ReDim Rpijm(span_div - 1, span_div - 1) 'パネル間の距離.R+ij
Dim Rmijm() As Double: ReDim Rmijm(span_div - 1, span_div - 1) 'パネル間の距離.R-ij
Dim Rpijmp() As Double: ReDim Rpijmp(span_div - 1, span_div - 1) 'パネル間の距離.R+ij
Dim Rmijmp() As Double: ReDim Rmijmp(span_div - 1, span_div - 1) 'パネル間の距離.R-ij
'その他
Dim output() As Double
Dim pi As Double '円周率
Dim rad As Double 'degからradへの変換係数
Dim matrix1() As Double
Dim matrix2() As Double
Dim answer() As Double
'カウンター
Dim i As Integer
Dim j As Integer
'ActiveWorkbook.Save 'まず上書き保存
Application.ScreenUpdating = False '画面更新の非表示
Application.DisplayAlerts = False '警告画面の非表示
With sht1
'値の読み込み
pi = 4 * Atn(1)
rad = pi / 180
Call ReadState(state, 1)
Lift = .Cells(26, 44) '必要な揚力
le = .Cells(13, 49) '翼根から翼端までの翼の長さ(翼を水平面に投影したときの翼幅とは異なる)
ds = .Cells(14, 49) 'パネルの半幅
U = state.Vair '一様流速度
rho = state.rho '一様流密度
'値の読み込み
For i = 0 To span_div - 1
y(i) = (1 / 2) * (.Cells(45 + i, 28) + .Cells(45 + i + 1, 28))
z(i) = (1 / 2) * (.Cells(45 + i, 29) + .Cells(45 + i + 1, 29))
phi(i) = rad * (1 / 2) * (.Cells(45 + i, 32) + .Cells(45 + i + 1, 32)) '上反角分布 [rad]
Next i
End With
'座標の計算
For i = 0 To span_div - 1
For j = 0 To span_div - 1
'オリジナルの計算
'右翼
yp(i, j) = (y(i) - y(j)) * Cos(phi(j)) + (z(i) - z(j)) * Sin(phi(j))
zp(i, j) = -(y(i) - y(j)) * Sin(phi(j)) + (z(i) - z(j)) * Cos(phi(j))
'左翼
ypp(i, j) = (y(i) + y(j)) * Cos(phi(j)) - (z(i) - z(j)) * Sin(phi(j))
zpp(i, j) = (y(i) + y(j)) * Sin(phi(j)) + (z(i) - z(j)) * Cos(phi(j))
'鏡像の計算
'右翼
ymp(i, j) = (y(i) - y(j)) * Cos(phi(i)) - (z(i) - (-z(j) - 2 * hE)) * Sin(phi(j))
zmp(i, j) = (y(i) - y(j)) * Sin(phi(j)) + (z(i) - (-z(j) - 2 * hE)) * Cos(phi(j))
'左翼
ympp(i, j) = (y(i) + y(j)) * Cos(phi(j)) + (z(i) - (-z(j) - 2 * hE)) * Sin(phi(j))
zmpp(i, j) = -(y(i) + y(j)) * Sin(phi(j)) + (z(i) - (-z(j) - 2 * hE)) * Cos(phi(j))
Next j
Next i
'R+ij,R-ijの計算
For i = 0 To span_div - 1
For j = 0 To span_div - 1
'オリジナルの計算
'右翼の計算
Rpij(i, j) = Sqr((yp(i, j) - ds) * (yp(i, j) - ds) + zp(i, j) * zp(i, j))
Rmij(i, j) = Sqr((yp(i, j) + ds) * (yp(i, j) + ds) + zp(i, j) * zp(i, j))
'左翼の計算
Rpijp(i, j) = Sqr((ypp(i, j) + ds) ^ 2 + zpp(i, j) ^ 2)
Rmijp(i, j) = Sqr((ypp(i, j) - ds) ^ 2 + zpp(i, j) ^ 2)
'鏡像の計算
'右翼の計算
Rpijm(i, j) = Sqr((ymp(i, j) - ds) ^ 2 + zmp(i, j) ^ 2)
Rmijm(i, j) = Sqr((ymp(i, j) + ds) ^ 2 + zmp(i, j) ^ 2)
'左翼の計算
Rpijmp(i, j) = Sqr((ympp(i, j) + ds) ^ 2 + zmpp(i, j) ^ 2)
Rmijmp(i, j) = Sqr((ympp(i, j) - ds) ^ 2 + zmpp(i, j) ^ 2)
Next j
Next i
'Qijの計算
For i = 0 To span_div - 1
For j = 0 To span_div - 1
Qij(i, j) = (-((yp(i, j) - ds) / (Rpij(i, j) * Rpij(i, j))) + ((yp(i, j) + ds) / (Rmij(i, j) * Rmij(i, j)))) * Cos(phi(i) - phi(j)) _
+ (-(zp(i, j) / (Rpij(i, j) * Rpij(i, j))) + (zp(i, j) / (Rmij(i, j) * Rmij(i, j)))) * Sin(phi(i) - phi(j)) _
+ (-((ypp(i, j) - ds) / (Rmijp(i, j) * Rmijp(i, j))) + ((ypp(i, j) + ds) / (Rpijp(i, j) * Rpijp(i, j)))) * Cos(phi(i) + phi(j)) _
+ (-(zpp(i, j) / (Rmijp(i, j) * Rmijp(i, j))) + (zpp(i, j) / (Rpijp(i, j) * Rpijp(i, j)))) * Sin(phi(i) + phi(j)) _
+ ((ymp(i, j) - ds) / (Rpijm(i, j) * Rpijm(i, j)) - (ymp(i, j) + ds) / (Rmijm(i, j) * Rmijm(i, j))) * Cos(phi(i) + phi(j)) _
+ (zmp(i, j) / (Rpijm(i, j) * Rpijm(i, j)) - zmp(i, j) / (Rmijm(i, j) * Rmijm(i, j))) * Sin(phi(i) + phi(j)) _
+ ((ympp(i, j) - ds) / (Rmijmp(i, j) * Rmijmp(i, j)) - (ympp(i, j) + ds) / (Rpijmp(i, j) * Rpijmp(i, j))) * Cos(phi(i) - phi(j)) _
+ (zmpp(i, j) / (Rmijmp(i, j) * Rmijmp(i, j)) - zmpp(i, j) / (Rpijmp(i, j) * Rpijmp(i, j))) * Sin(phi(i) - phi(j))
Qij(i, j) = Qij(i, j) * (1 / (2 * pi))
Next j
Next i
'Aij,bi,ci,qiの計算
For i = 0 To span_div - 1
For j = 0 To span_div - 1
Aij(i, j) = pi * Qij(i, j) * le * (ds / le)
Next j
bi(i) = ((3 * pi) / 2) * ((y(i) / le) * Cos(phi(i)) + (z(i) / le) * Sin(phi(i))) * (ds / le)
ci(i) = 2 * Cos(phi(i)) * (ds / le)
Next i
If beta = 0 Then '曲げモーメントの制約なし
'Lagrange未定乗数法の係数行列を計算
ReDim matrix1(span_div + 1 - 1, span_div + 1 - 1)
ReDim matrix2(span_div + 1 - 1)
For i = 0 To span_div - 1
For j = 0 To span_div - 1
matrix1(i, j) = Aij(j, i) + Aij(i, j)
Next j
Next i
For i = 0 To span_div - 1
matrix1(i, span_div) = -ci(i)
matrix1(span_div, i) = -ci(i)
Next i
matrix2(span_div) = -1
'境界条件の方程式を解いて循環を求める
answer = ans(span_div + 1, matrix1, matrix2)
Else
'Lagrange未定乗数法の係数行列を計算
ReDim matrix1(span_div + 2 - 1, span_div + 2 - 1)
ReDim matrix2(span_div + 2 - 1)
For i = 0 To span_div - 1
For j = 0 To span_div - 1
matrix1(i, j) = Aij(j, i) + Aij(i, j)
Next j
Next i
For i = 0 To span_div - 1
matrix1(i, span_div) = -ci(i)
matrix1(i, span_div + 1) = -bi(i)
matrix1(span_div, i) = -ci(i)
matrix1(span_div + 1, i) = -bi(i)
Next i
matrix2(span_div) = -1
matrix2(span_div + 1) = -beta
'境界条件の方程式を解いて循環を求める
answer = ans(span_div + 2, matrix1, matrix2)
End If
'循環の計算
For i = 0 To span_div - 1
circulation(i) = answer(i) * Lift / (2 * le * rho * U)
Next i
'誘導抗力の計算
Di = 0
BendingMoment = 0
For i = 0 To span_div - 1
For j = 0 To span_div - 1
Di = Di + 2 * rho * circulation(i) * Qij(i, j) * circulation(j) * ds
wi(i) = wi(i) + (1 / 2) * Qij(i, j) * circulation(j)
Next j
BendingMoment = BendingMoment + 2 * rho * U * circulation(i) * (y(i) * Cos(phi(i)) + z(i) * Sin(phi(i))) * ds
Next i
e = ((Lift * Lift) / (2 * pi * rho * U * U * le * le)) / Di
beta = BendingMoment / ((2 / (3 * pi)) * le * Lift)
With sht1
'結果の表示
ReDim output(4, 0)
output(0, 0) = beta
output(1, 0) = e
output(2, 0) = Lift
output(3, 0) = Di
output(4, 0) = BendingMoment
.Range("AW15:AW19") = output()
ReDim output(span_div, 1)
For i = 0 To span_div - 1
output(i, 0) = circulation(i)
output(i, 1) = wi(i)
Next i
output(span_div, 0) = 0
output(span_div, 1) = 0
TR797 = output()
End With
End Function
1つずつ解説していく
変数の宣言
今回は翼分割数span_div,構造的制限beta,高度hEを引数として,循環分布,吹きおろし分布を戻り値として返すFunctionとする
≫【VBA入門】Functionの使い方(呼び出し、引数、戻り値)
Function TR797(ByVal span_div As Integer, ByVal beta As Double, ByVal hE As Double) As Double()使用している変数を以下に示す
これからのプログラムはシートをまたいで実行されることが多い.そういうときはワークシートプロジェクトを定義する
≫【VBA入門】WorksheetsからWorksheetオブジェクトを取得し操作する
'ワークシートの定義
Set sht1 = Sheets("主翼(sht1)")
Dim state As variables
'変数の宣言
Dim Aij() As Double: ReDim Aij(span_div - 1, span_div - 1) 'スパン荷重分布と誘導抵抗を結び付ける影響関数
Dim bi() As Double: ReDim bi(span_div - 1) 'スパン荷重分布と翼根曲げモーメントを関係づける影響関数
Dim BendingMoment As Double '翼根曲げモーメント
Dim ci() As Double: ReDim ci(span_div - 1) 'スパン荷重分布と全揚力とを関係づける影響関数
Dim Di As Double '誘導抗力
Dim e As Double 'スパン効率
Dim gi() As Double: ReDim gi(span_div - 1) 'スパン荷重分布を表す無次元ベクトル
Dim Lift As Double '必要な揚力
Dim le As Double '翼根から翼端までの翼の長さ(翼を水平面に投影したときの翼幅とは異なる)
Dim N As Integer '右翼をパネル分割したときの分割数(control point)
Dim Qij() As Double: ReDim Qij(span_div - 1, span_div - 1) 'スパン荷重分布と垂直誘導速度を結び付ける影響関数
Dim ds As Double 'パネルの半幅
Dim U As Double '一様流速度
Dim wi() As Double: ReDim wi(span_div - 1) '荷重曲線に垂直方向に誘導される速度
Dim circulation() As Double: ReDim circulation(span_div - 1) '循環分布
Dim rho As Double '一様流密度
Dim phi() As Double: ReDim phi(span_div - 1) '上反角分布 '上反角分布
'座標.p:prime,m:mirror
Dim y() As Double: ReDim y(span_div - 1)
Dim z() As Double: ReDim z(span_div - 1)
Dim yp() As Double: ReDim yp(span_div - 1, span_div - 1)
Dim zp() As Double: ReDim zp(span_div - 1, span_div - 1)
Dim ypp() As Double: ReDim ypp(span_div - 1, span_div - 1)
Dim zpp() As Double: ReDim zpp(span_div - 1, span_div - 1)
Dim ymp() As Double: ReDim ymp(span_div - 1, span_div - 1)
Dim zmp() As Double: ReDim zmp(span_div - 1, span_div - 1)
Dim ympp() As Double: ReDim ympp(span_div - 1, span_div - 1)
Dim zmpp() As Double: ReDim zmpp(span_div - 1, span_div - 1)
Dim Rpij() As Double: ReDim Rpij(span_div - 1, span_div - 1) 'パネル間の距離.R+ij
Dim Rmij() As Double: ReDim Rmij(span_div - 1, span_div - 1) 'パネル間の距離.R-ij
Dim Rpijp() As Double: ReDim Rpijp(span_div - 1, span_div - 1) 'パネル間の距離.R+ij
Dim Rmijp() As Double: ReDim Rmijp(span_div - 1, span_div - 1) 'パネル間の距離.R-ij
Dim Rpijm() As Double: ReDim Rpijm(span_div - 1, span_div - 1) 'パネル間の距離.R+ij
Dim Rmijm() As Double: ReDim Rmijm(span_div - 1, span_div - 1) 'パネル間の距離.R-ij
Dim Rpijmp() As Double: ReDim Rpijmp(span_div - 1, span_div - 1) 'パネル間の距離.R+ij
Dim Rmijmp() As Double: ReDim Rmijmp(span_div - 1, span_div - 1) 'パネル間の距離.R-ij
'その他
Dim output() As Double
Dim pi As Double '円周率
Dim rad As Double 'degからradへの変換係数
Dim matrix1() As Double
Dim matrix2() As Double
Dim answer() As Double
'カウンター
Dim i As Integer
Dim j As Integerさすがに変数が増えてきて,動的変数を再定義するだけで行数がばかにならないので可読性を上げるために配列の宣言と動的変数の再定義を同じ行で行っている
値の読み込み
必要な値を読み込む
シートをまたいで値を読み込むときにはWithステートメントを使うとよい
≫【VBA入門】Withの使い方、入れ子(ネスト)で使う方法
With sht1
'値の読み込み
pi = 4 * Atn(1)
rad = pi / 180
Call ReadState(state, 1)
Lift = .Cells(26, 44) '必要な揚力
le = .Cells(13, 49) '翼根から翼端までの翼の長さ(翼を水平面に投影したときの翼幅とは異なる)
ds = .Cells(14, 49) 'パネルの半幅
U = state.Vair '一様流速度
rho = state.rho '一様流密度
'値の読み込み
For i = 0 To span_div - 1
y(i) = (1 / 2) * (.Cells(45 + i, 28) + .Cells(45 + i + 1, 28))
z(i) = (1 / 2) * (.Cells(45 + i, 29) + .Cells(45 + i + 1, 29))
phi(i) = rad * (1 / 2) * (.Cells(45 + i, 32) + .Cells(45 + i + 1, 32)) '上反角分布 [rad]
Next i
End With状態変数を読み込むときに使っている関数は次のようなものである
構造体については次の記事を参考にしてほしい
構造体は便利なのでこれからもどんどん使っていく
式(9)の計算
式(9)を計算する
\begin{eqnarray}
y'_{ij} &=& (y_{i}-y_{j}) cos(\phi_{j})+(z_{i}-z_{j}) sin(\phi_{j}) \\
z'_{ij} &=& -(y_{i}-y_{j}) sin(\phi_{j})+(z_{i}-z_{j}) cos(\phi_{j}) \\
y''_{ij} &=& (y_{i}+y_{j}) cos (\phi_{j}) -(z_{i}-z_{j}) sin (\phi_{j}) \\
z''_{ij} &=& (y_{i}+y_{j}) sin (\phi_{j}) +(z_{i}-z_{j}) cos (\phi_{j}) \\
{y'_{ij}}_{mirror} &=& (y_{i}-y_{j}) cos(-\phi_{j})+(z_{i}-(z_{j}-2h_{E})) sin(-\phi_{j}) \\
{z'_{ij}}_{mirror} &=& -(y_{i}-y_{j}) sin(-\phi_{j})+(z_{i}-(z_{j}-2h_{E})) cos(-\phi_{j}) \\
{y''_{ij}}_{mirror} &=& (y_{i}+y_{j}) cos (\phi_{j}) +(z_{i}-(z_{j}-2h_{E}) sin (\phi_{j}) \\
{z''_{ij}}_{mirror} &=& -(y_{i}+y_{j}) sin (\phi_{j}) +(z_{i}-(z_{j}-2h_{E})) cos (\phi_{j}) \\
\end{eqnarray}
'座標の計算
For i = 0 To span_div - 1
For j = 0 To span_div - 1
'オリジナルの計算
'右翼
yp(i, j) = (y(i) - y(j)) * Cos(phi(j)) + (z(i) - z(j)) * Sin(phi(j))
zp(i, j) = -(y(i) - y(j)) * Sin(phi(j)) + (z(i) - z(j)) * Cos(phi(j))
'左翼
ypp(i, j) = (y(i) + y(j)) * Cos(phi(j)) - (z(i) - z(j)) * Sin(phi(j))
zpp(i, j) = (y(i) + y(j)) * Sin(phi(j)) + (z(i) - z(j)) * Cos(phi(j))
'鏡像の計算
'右翼
ymp(i, j) = (y(i) - y(j)) * Cos(phi(i)) - (z(i) - (-z(j) - 2 * hE)) * Sin(phi(j))
zmp(i, j) = (y(i) - y(j)) * Sin(phi(j)) + (z(i) - (-z(j) - 2 * hE)) * Cos(phi(j))
'左翼
ympp(i, j) = (y(i) + y(j)) * Cos(phi(j)) + (z(i) - (-z(j) - 2 * hE)) * Sin(phi(j))
zmpp(i, j) = -(y(i) + y(j)) * Sin(phi(j)) + (z(i) - (-z(j) - 2 * hE)) * Cos(phi(j))
Next j
Next i式(10)の計算
式(10)を計算する
\begin{eqnarray}
{R_{+ij}}^2 &=& (y'_{ij}-\Delta S_{j})^2+{z'_{ij}}^2 \\ {R_{-ij}}^2 &=& (y'_{ij}+\Delta S_{j})^2+{z'_{ij}}^2 \\ {R'_{+ij}}^2 &=& (y''_{ij}+\Delta S_{j})^2+{z''_{ij}}^2 \\ {R'_{-ij}}^2 &=& (y''_{ij}-\Delta S_{j})^2+{z''_{ij}}^2 \\ {{R_{+ij}}_{mirror}}^2 &=& ({y'_{ij}}_{mirror}-\Delta S_{j})^2+{{z'_{ij}}_{mirror}}^2 \\
{{R_{-ij}}_{mirror}}^2 &=& ({y'{ij}}_{mirror}+\Delta S_{j})^2+{{z'_{ij}}_{mirror}}^2 \\{{R'_{+ij}}_{mirror}}^2 &=& ({y''_{ij}}_{mirror}+\Delta S_{j})^2+{{z''_{ij}}_{mirror}}^2 \\
{{R'_{-ij}}_{mirror}}^2 &=& ({y''_{ij}}_{mirrro}-\Delta S_{j})^2+{{z''_{ij}}_{mirror}}^2 \\
\end{eqnarray}
'R+ij,R-ijの計算
For i = 0 To span_div - 1
For j = 0 To span_div - 1
'オリジナルの計算
'右翼の計算
Rpij(i, j) = Sqr((yp(i, j) - ds) * (yp(i, j) - ds) + zp(i, j) * zp(i, j))
Rmij(i, j) = Sqr((yp(i, j) + ds) * (yp(i, j) + ds) + zp(i, j) * zp(i, j))
'左翼の計算
Rpijp(i, j) = Sqr((ypp(i, j) + ds) ^ 2 + zpp(i, j) ^ 2)
Rmijp(i, j) = Sqr((ypp(i, j) - ds) ^ 2 + zpp(i, j) ^ 2)
'鏡像の計算
'右翼の計算
Rpijm(i, j) = Sqr((ymp(i, j) - ds) ^ 2 + zmp(i, j) ^ 2)
Rmijm(i, j) = Sqr((ymp(i, j) + ds) ^ 2 + zmp(i, j) ^ 2)
'左翼の計算
Rpijmp(i, j) = Sqr((ympp(i, j) + ds) ^ 2 + zmpp(i, j) ^ 2)
Rmijmp(i, j) = Sqr((ympp(i, j) - ds) ^ 2 + zmpp(i, j) ^ 2)
Next j
Next i式(8)の計算
式(8)を計算する
\begin{eqnarray}
Q_{ij} &=& \frac{1}{2\pi}((-\frac{y'_{ij}-\Delta S_{j}}{{R_{+ij}}^2}+\frac{y'_{ij}+\Delta S_{j}}{{R_{-ij}}^2}) cos(\phi_{i}-\phi_{j}) \\
&& +(-\frac{z'_{ij}}{{R_{+ij}}^2}+\frac{z'_{ij}}{{R_{-ij}}^2}) sin(\phi_{i}-\phi_{j}) \\
&& +(-\frac{y''_{ij}-\Delta S_{j}}{{R'_{-ij}}^2}+\frac{y''_{ij}+\Delta S_{j}}{{R'_{+ij}}^2}) cos(\phi_{i}+\phi_{j}) \\
&& +(-\frac{z''_{ij}}{{R'_{-ij}}^2}+\frac{z''_{ij}}{{R'_{+ij}}^2}) sin(\phi_{i}+\phi_{j}) \\
&& -(-\frac{{y'_{ij}}_{mirror}-\Delta S_{j}}{{{R_{+ij}}_{mirror}}^2}+\frac{{y'_{ij}}_{mirror}+\Delta S_{j}}{{{R_{-ij}}_{mirror}}^2}) cos(\phi_{i}-(-\phi_{j})) \\
&& -(-\frac{{z'_{ij}}_{mirror}}{{{R_{+ij}}_{mirror}}^2}+\frac{{z'_{ij}}_{mirror}}{{{R_{-ij}}_{mirror}}^2}) sin(\phi_{i}-(-\phi_{j})) \\
&& -(-\frac{{y''_{ij}}_{mirror}-\Delta S_{j}}{{{R'_{-ij}}_{mirror}}^2}+\frac{{y''_{ij}}_{mirror}+\Delta S_{j}}{{{R'_{+ij}}_{mirror}}^2}) cos(\phi_{i}-\phi_{j}) \\
&& -(-\frac{{z''_{ij}}_{mirror}}{{{R'_{-ij}}_{mirror}}^2}+\frac{{z''_{ij}}_{mirror}}{{{R'_{+ij}}_{mrror}}^2}) sin(\phi_{i}-\phi_{j})) \\
\end{eqnarray}
頑張って入力しよう
'Qijの計算
For i = 0 To span_div - 1
For j = 0 To span_div - 1
Qij(i, j) = (-((yp(i, j) - ds) / (Rpij(i, j) * Rpij(i, j))) + ((yp(i, j) + ds) / (Rmij(i, j) * Rmij(i, j)))) * Cos(phi(i) - phi(j)) + (-(zp(i, j) / (Rpij(i, j) * Rpij(i, j))) + (zp(i, j) / (Rmij(i, j) * Rmij(i, j)))) * Sin(phi(i) - phi(j)) + (-((ypp(i, j) - ds) / (Rmijp(i, j) * Rmijp(i, j))) + ((ypp(i, j) + ds) / (Rpijp(i, j) * Rpijp(i, j)))) * Cos(phi(i) + phi(j)) + (-(zpp(i, j) / (Rmijp(i, j) * Rmijp(i, j))) + (zpp(i, j) / (Rpijp(i, j) * Rpijp(i, j)))) * Sin(phi(i) + phi(j)) + ((ymp(i, j) - ds) / (Rpijm(i, j) * Rpijm(i, j)) - (ymp(i, j) + ds) / (Rmijm(i, j) * Rmijm(i, j))) * Cos(phi(i) + phi(j)) + (zmp(i, j) / (Rpijm(i, j) * Rpijm(i, j)) - zmp(i, j) / (Rmijm(i, j) * Rmijm(i, j))) * Sin(phi(i) + phi(j)) + ((ympp(i, j) - ds) / (Rmijmp(i, j) * Rmijmp(i, j)) - (ympp(i, j) + ds) / (Rpijmp(i, j) * Rpijmp(i, j))) * Cos(phi(i) - phi(j)) + (zmpp(i, j) / (Rmijmp(i, j) * Rmijmp(i, j)) - zmpp(i, j) / (Rpijmp(i, j) * Rpijmp(i, j))) * Sin(phi(i) - phi(j))
Qij(i, j) = Qij(i, j) * (1 / (2 * pi))
Next j
Next iがんばった
式(20),(21),(22)の計算
式(20),(21),(22)を計算する
\begin{eqnarray}
c_{i} &=& 2cos{\phi_{i}} \Delta \sigma
\tag{20} \\
b_{i} &=& \frac{3\pi}{2}(\eta_{i} cos{\phi_{i}}+\zeta_{i} sin{\phi_{i}})\Delta \sigma
\tag{21} \\
A_{ij} &=& \pi q_{ij} \Delta \sigma_{i}
\tag{22} \\
\end{eqnarray}
'Aij,bi,ci,qiの計算
For i = 0 To span_div - 1
For j = 0 To span_div - 1
Aij(i, j) = pi * Qij(i, j) * le * (ds / le)
Next j
bi(i) = ((3 * pi) / 2) * ((y(i) / le) * Cos(phi(i)) + (z(i) / le) * Sin(phi(i))) * (ds / le)
ci(i) = 2 * Cos(phi(i)) * (ds / le)
Next i式(33)の計算
式(33)を計算する
\begin{eqnarray}
\left[
\begin{array}{cccccccc}
2A_{11} & A_{21}+A_{12} & \ldots & \ldots & \ldots & A_{N1}+A_{1N} & -c_{1} & -b_{1} \\
A_{12}+A_{21} & 2A_{22} & & & & \vdots & -c_{2} & -b_{2} \\
\vdots & \vdots & \ddots & & & \vdots & \vdots & \vdots \\
A_{1i}+A_{i1} & \vdots & \ldots & 2A_{ii} & \ldots & \vdots & \vdots & \vdots \\
\vdots & \vdots & & & \ddots & \vdots & \vdots & \vdots \\
A_{1N}+A_{N1} & \ldots & \ldots & \ldots & \ldots & 2A_{NN} & -c_{N} & -b_{N} \\
-c_{1} & -c_{2} & \ldots & \ldots & \ldots & -c_{N} & 0 & 0 \\
-b_{1} & -b_{2} & \ldots & \ldots & \ldots & -b_{N} & 0 & 0 \\
\end{array}
\right]
\cdot \left[
\begin{array}{c}
g_{1} \\
g_{2} \\
\vdots \\
\vdots \\
\vdots \\
g_{N} \\
\mu_1 \\
\mu_2 \\
\end{array}
\right]
= \left[
\begin{array}{c}
0 \\
0 \\
\vdots \\
\vdots \\
\vdots \\
0 \\
-1 \\
\beta \\
\end{array}
\right]
\end{eqnarray}
ここでは構造的制限の有無で場合分けし,構造的制限のない場合はN+1次元連立1次方程式を解いている
If beta = 0 Then '曲げモーメントの制約なし
'Lagrange未定乗数法の係数行列を計算
ReDim matrix1(span_div + 1 - 1, span_div + 1 - 1)
ReDim matrix2(span_div + 1 - 1)
For i = 0 To span_div - 1
For j = 0 To span_div - 1
matrix1(i, j) = Aij(j, i) + Aij(i, j)
Next j
Next i
For i = 0 To span_div - 1
matrix1(i, span_div) = -ci(i)
matrix1(span_div, i) = -ci(i)
Next i
matrix2(span_div) = -1
'境界条件の方程式を解いて循環を求める
answer = ans(span_div + 1, matrix1, matrix2)
Else
'Lagrange未定乗数法の係数行列を計算
ReDim matrix1(span_div + 2 - 1, span_div + 2 - 1)
ReDim matrix2(span_div + 2 - 1)
For i = 0 To span_div - 1
For j = 0 To span_div - 1
matrix1(i, j) = Aij(j, i) + Aij(i, j)
Next j
Next i
For i = 0 To span_div - 1
matrix1(i, span_div) = -ci(i)
matrix1(i, span_div + 1) = -bi(i)
matrix1(span_div, i) = -ci(i)
matrix1(span_div + 1, i) = -bi(i)
Next i
matrix2(span_div) = -1
matrix2(span_div + 1) = -beta
'境界条件の方程式を解いて循環を求める
answer = ans(span_div + 2, matrix1, matrix2)
End If式(19)の計算
連立方程式を解いて\({\bf g}\)が求まったので,それをもとに循環\({\bf \Gamma}\)を計算する
\begin{eqnarray}
g_{i} &=& \frac{2 l_{e} \rho U \Gamma_{i}}{L}
\end{eqnarray}
'循環の計算
For i = 0 To span_div - 1
circulation(i) = answer(i) * Lift / (2 * le * rho * U)
Next i式(7)の計算 式(4),(5),(6)の計算
循環\({\bf \Gamma}\)がわかったので,式(7)を用いて吹きおろしを計算する
\begin{eqnarray}
V_{ni} &=& \sum_{j=1}^{N} Q_{ij} \Gamma_{i} \\
\end{eqnarray}
ただしこの吹きおろしはTrefftz面での吹きおろしなので,翼面上での吹きおろしはこれの半分であることに注意する
最後に式(4),式(5),式(6)を計算する
\begin{eqnarray}
L &=& 4\rho U \sum_{i=1}^{N} \Gamma_{i} cos{\phi_{i}} \Delta S_{i} \\
B &=& 2\rho U \sum_{i=1}^{N} \Gamma_{i} (y_{i}cos{\phi_{i}}+z_{i}sin{\phi_{i}}) \Delta S_{i} \\
D_{i} &=& 2\rho U \sum_{i=1}^{N} \Gamma_{i} V_{ni} \Delta S_{i} \\
\end{eqnarray}
'誘導抗力の計算
Di = 0
BendingMoment = 0
For i = 0 To span_div - 1
For j = 0 To span_div - 1
Di = Di + 2 * rho * circulation(i) * Qij(i, j) * circulation(j) * ds
wi(i) = wi(i) + (1 / 2) * Qij(i, j) * circulation(j)
Next j
BendingMoment = BendingMoment + 2 * rho * U * circulation(i) * (y(i) * Cos(phi(i)) + z(i) * Sin(phi(i))) * ds
Next i
e = ((Lift * Lift) / (2 * pi * rho * U * U * le * le)) / Di
beta = BendingMoment / ((2 / (3 * pi)) * le * Lift)結果の出力
計算した結果を出力する
With sht1
'結果の表示
ReDim output(4, 0)
output(0, 0) = beta
output(1, 0) = e
output(2, 0) = Lift
output(3, 0) = Di
output(4, 0) = BendingMoment
.Range("AW15:AW19") = output()
ReDim output(span_div, 1)
For i = 0 To span_div - 1
output(i, 0) = circulation(i)
output(i, 1) = wi(i)
Next i
output(span_div, 0) = 0
output(span_div, 1) = 0
TR797 = output()
End With循環分布と吹きおろし分布を戻り値として返している
以上でプログラムの解説は終了である
プログラムの実行
それでは実際にプログラムを実行してみる
実行には次のコードを用いる
Sub 循環分布最適化()
'ワークシートの定義
Set sht1 = Sheets("主翼(sht1)")
Dim answer() As Double '循環分布
Dim startTime As Double
Dim endTime As Double
Dim processTime As Double
Application.ScreenUpdating = False '画面更新の非表示
Application.DisplayAlerts = False '警告画面の非表示
startTime = Timer '開始時間取得
'値の読み込み
span_div = sht1.Cells(33, 4) '右翼をパネル分割したときの分割数
beta = sht1.Cells(15, 49) '翼根曲げモーメントの制約を表すパラメーター
hE = sht1.Cells(23, 54) '高度
If sht1.Cells(12, 49) = "なし" Then beta = 0
answer() = TR797(span_div, 1, hE)
sht1.Range(sht1.Cells(45, 36), sht1.Cells(45 + span_div, 36)) = answer()
answer() = TR797(span_div, beta, hE)
sht1.Range(sht1.Cells(45, 40), sht1.Cells(45 + span_div, 41)) = answer()
'終了時間取得
endTime = Timer
'処理時間表示
processTime = endTime - startTime
MsgBox "計算が終了しました" & vbCrLf & "処理時間:" & processTime
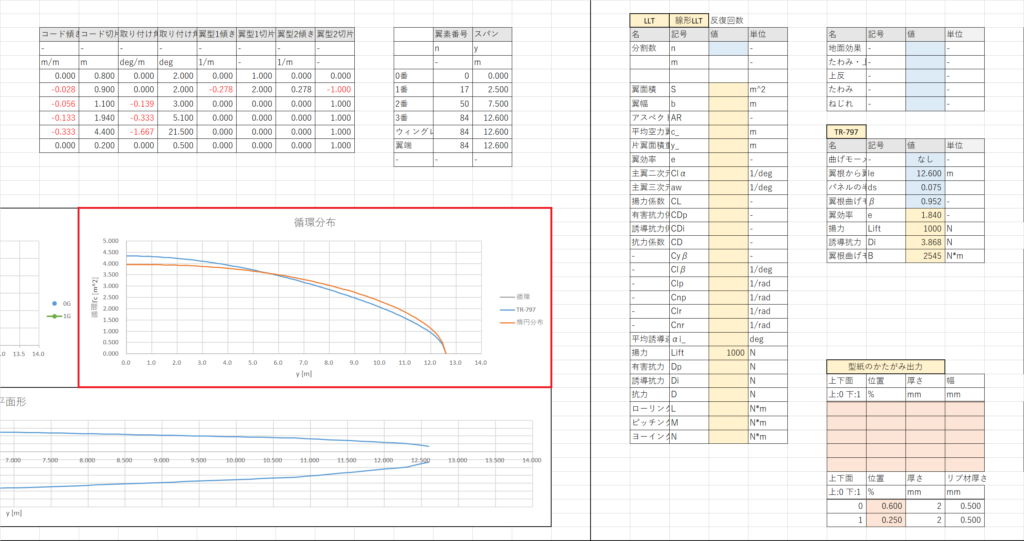
End Sub実際に実行してみると次のようになる
楕円分布よりもさらに翼根側に揚力が集中した循環分布が計算できた
まとめ
地面効果を含めた循環分布の最適化ができた
あとは煮るなり焼くなり好きに最適化しよう
↓次の記事
↓記事一覧





コメント
素晴らしいブログをありがとうございます.
冒頭の文字なしテンプレートではセルAW10は曲げモーメントとなっているのに対して
数値のみテンプレートとTR797マクロでのデータ取得位置はセルAW12以下が入力位置となっているため
初見だと混乱するかもしれません.
追伸失礼します.
主翼(sht1)でのセル位置です.
いつもありがとうございます!
ファイルを修正してアップしなおしました。