エクセルシートを用いて機体の重量および慣性モーメントの推算を行う
目的
今回の目的は,前回(≫重量推算①:設計シートの下準備)に引き続いて,エクセルシートを用いて機体の重量を推算することである
前回までで設計シートの下準備は終了したので,この記事では機体の各部の重量推算を行っていく
テンプレートファイルのダウンロード
エクセルシートの配置などの参考になるようにテンプレートファイルを添付しておく
※数式やマクロはすべて削除してあり,値も適当である
TemplateNO_TEXT_ver20191114.xlsx
重量推算
それでは実際に解説していく
機体重量
このシートでは,機体重量および慣性モーメントの推算を行う
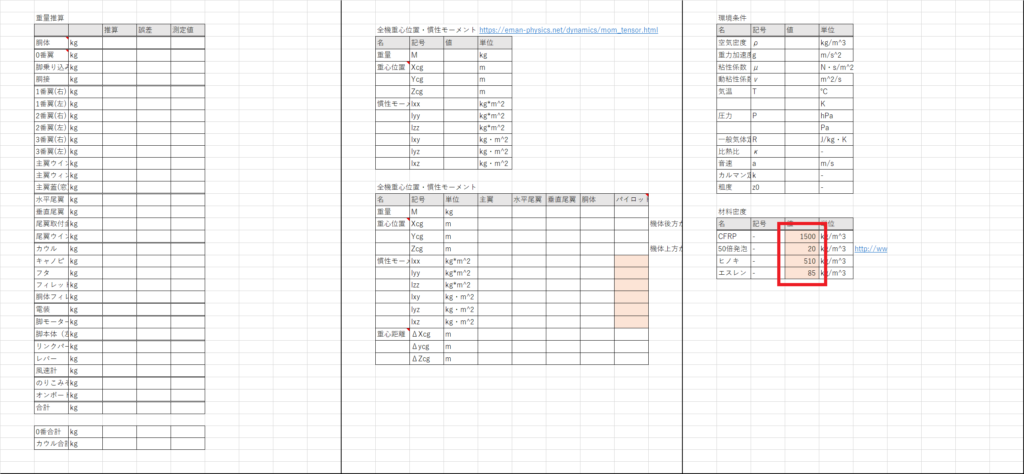
セルX20:X23に,機体に使う主な材料の密度を入力する
材料の密度は過去の機体データや実際に測定したものを利用する
スパー寸法
セルAR4に,機体重量シートからCFRPの密度を持ってくる
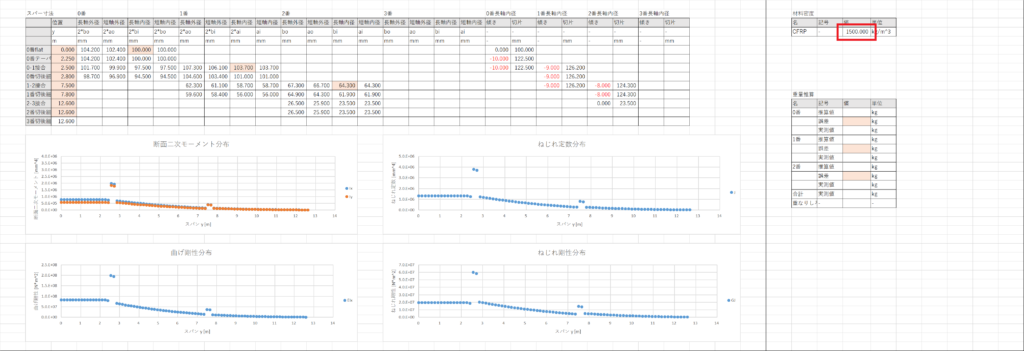
列AU~AWに断面積,列AX~AZに体積,列BA~BCに重量を計算し,列BDでリブ位置でのスパー重量の合計を計算する
- \((断面積)=\frac{\pi((長軸外径)(短軸外径)-(長軸内径)(短軸内径))}{4}\)
- \((体積)=(断面積)\times(翼素スパン)\)
- \((重量)=(体積)\times(密度)\)
該当するスパー以外のリブ位置では何も表示しないようにif関数を使って場合分けをしておく.例えば0番の断面積を計算するセルAU45には次のように入力する
=IF(T45="","",PI()*(T45*U45-V45*W45)/4)
セルAR13,AR16,AR19でそれぞれのスパーの重量を計算する
自作スパーの場合は積層時に重なりしろが発生するのでセルAR23に重なりしろ係数(>1.0)を入力し,理論値にかけておく
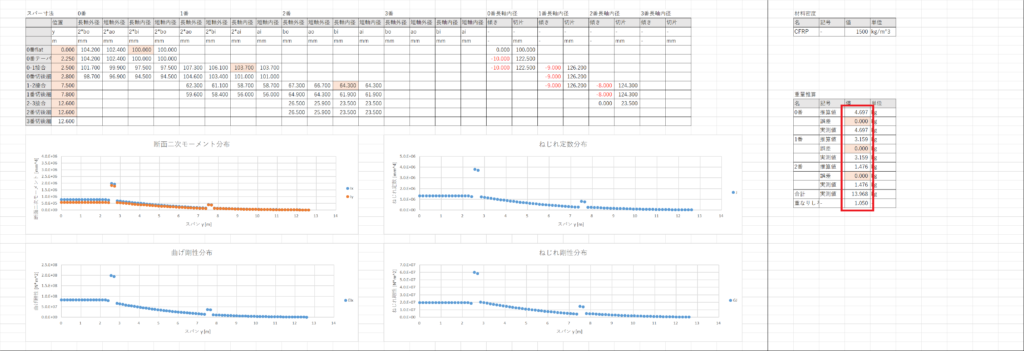
このシートはここまで
主翼
セルBB31:BB34に,機体重量シートから各部材の密度を持ってくる
セルBL12:BL21に,次の部材の寸法を入力する
- リブ厚さ[m]
- プランク厚さ[m]
- 縦通材本数および平均断面積[㎡]
- リブ材(リブキャップ)厚さ[m]
- 後縁材幅[m]および厚さ[m]
- 接着剤重量
ただし,接着剤重量は
- リブ面積(コード長の2乗)に比例するもの(接着剤①):リブー桁間の接着剤や後縁補強のバルサチップなど
- コード長に比例するもの(接着剤②):リブ材の接着剤やフィルム,プランクを貼るときの両面テープなど
- スパンに比例するもの(接着剤③):後縁材の接着剤やスパン方向に貼る両面テープ
に分類し,過去の機体重量データに合うような値を適当に決定した
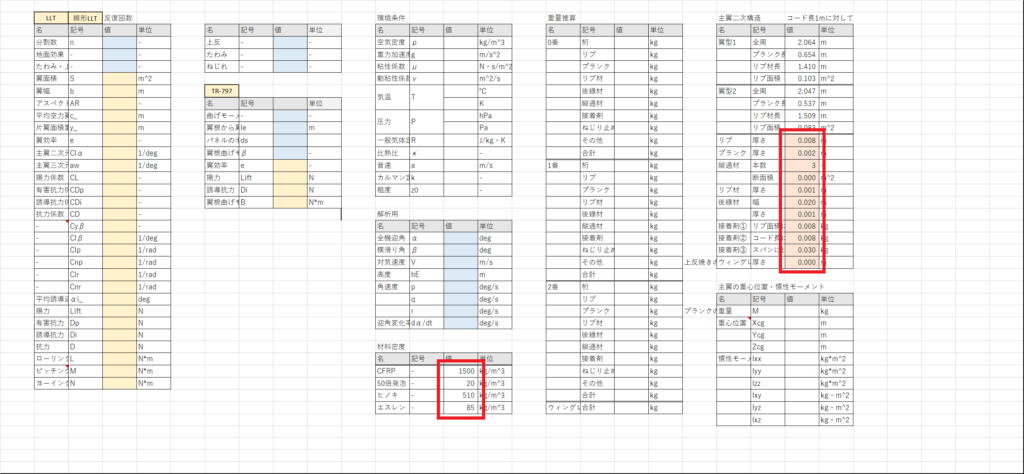
セルAL6:AL11に,スパー寸法シートから,各スパー接合部の位置をもってきて,翼素番号を計算する
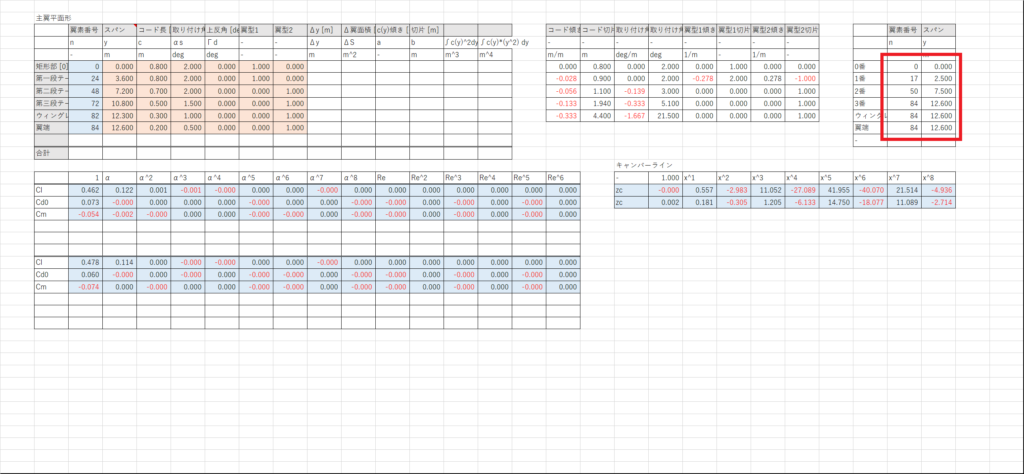
BA列の45行目以下に,リブ位置でのスパー番号を計算する
AK6:AK11で計算した翼素番号で場合分けするので,例えばセルBA45には次のように入力する
=IF(C45<$AK$7,"0",IF(C45<$AK$8,"1st",IF(C45<$AK$9,"2nd",IF(C45<$AK$10,"3rd","Winglet"))))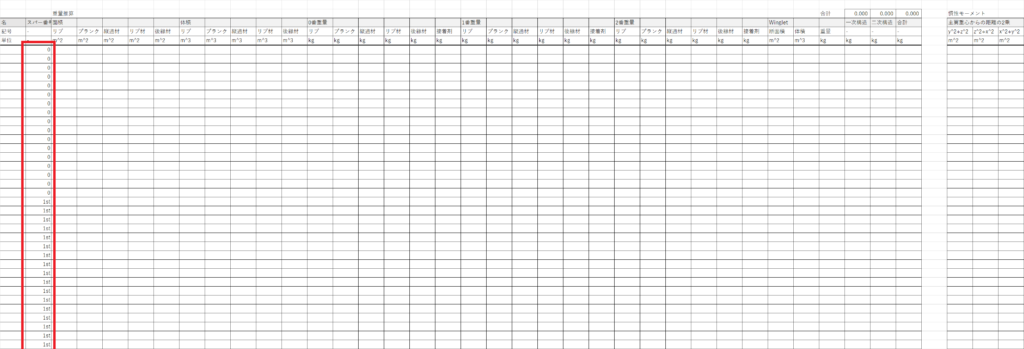
BB列~BK列の45行目以下で,それぞれの部材の断面積,体積を次のように計算する
面積
- \((リブ面積)=((翼型1リブ面積)\times(翼型1配合率)+(翼型2リブ面積)\times(翼型2配合率))\times(コード長)^2 \)
- \((プランク面積)=((翼型1プランク長さ)\times(翼型1配合率)+(翼型2プランク長さ)\times(翼型2配合率))\times(コード長)\times(プランク厚さ)\)
- \((縦通材面積)=(縦通材断面積)\times(本数)\)
- \((リブ材面積)=((翼型1リブ材長さ)\times(翼型1配合率)+(翼型2リブ材長さ)\times(翼型2配合率))\times(コード長)\times(リブ材厚さ)\)
- \((後縁材面積)=(後縁材幅)\times(後縁材厚さ)\)
体積
- リブ,リブ材:\((体積)=(面積)\times(リブ厚さ)\)
- プランク,縦通材,後縁材:\((体積)=(面積)\times(翼素スパン)\)
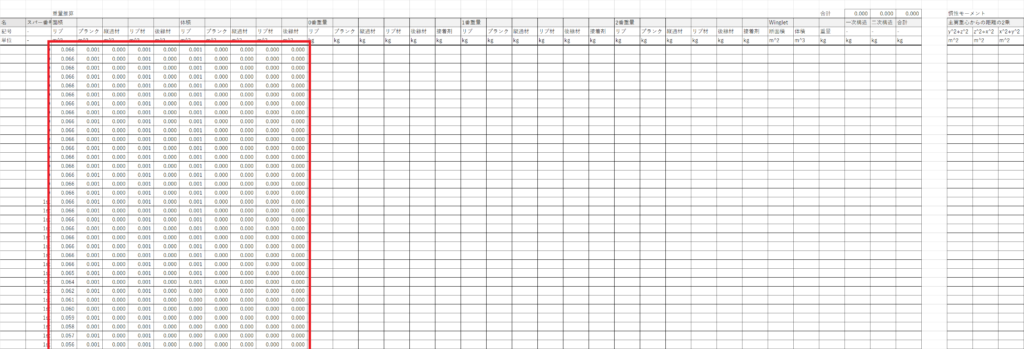
BL列~CC列の45行以下で各部材の重量\((=(体積)\times(密度))\)を計算する
ただし,接着剤は\((接着剤重量)=(接着剤①)\times(コード長)^2+(接着剤②)\times(コード長)+(接着剤③)\times(翼素スパン)\)で計算する
また,各翼ごとの重量を計算したいので,目的の翼ではないリブ位置では何も表示しないようにする
たとえば0番の接着剤重量を計算するBQ45には次のように入力する
=IF($BA45="0",$BL$19*P45*P45+$BL$20*P45+$BL$21*(F46-F45),"")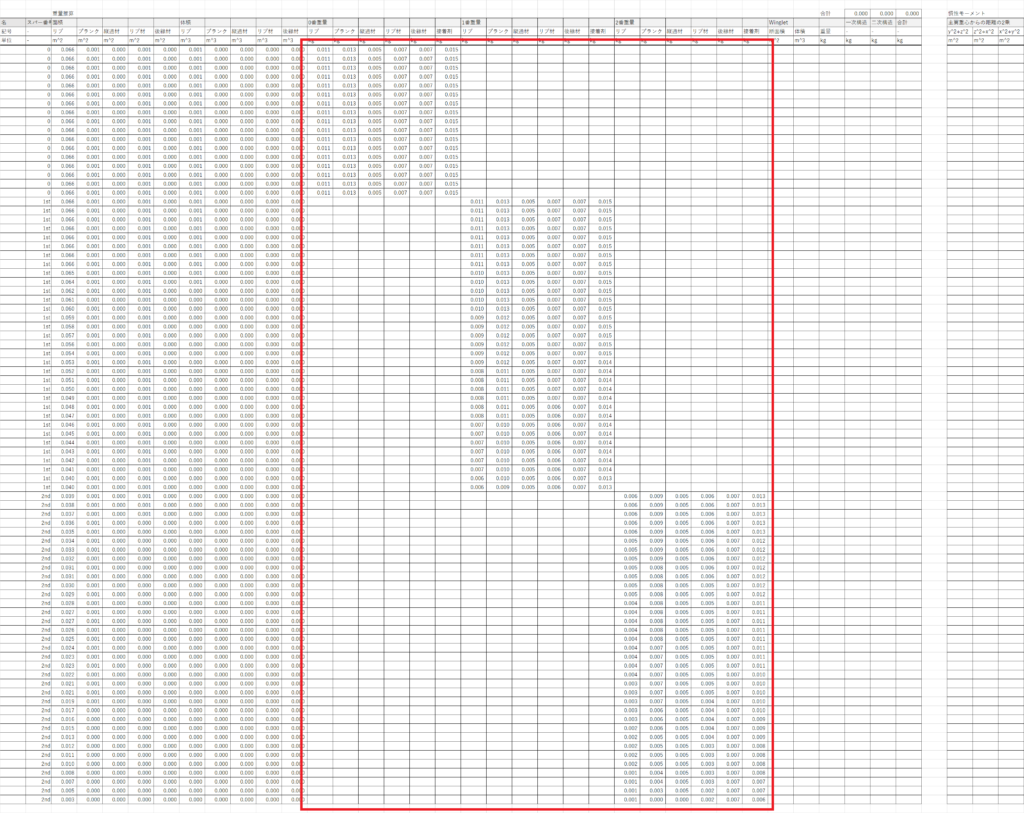
CH列の45行以下で二次構造の合計重量を計算する(SUM関数)
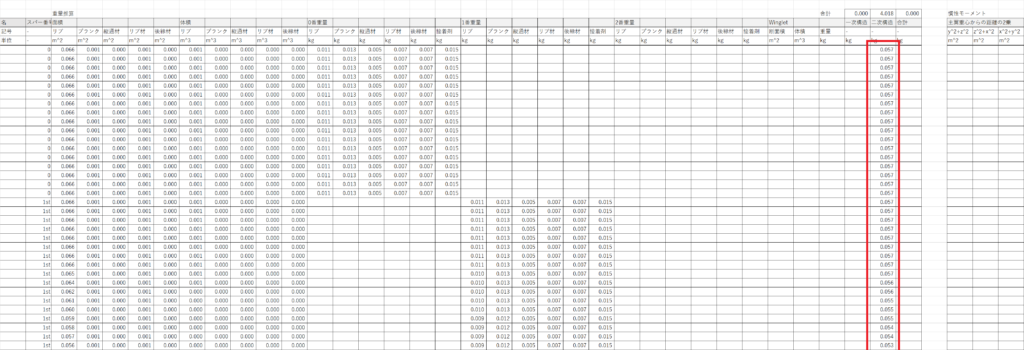
列CGにスパー寸法シートからスパー重量をもってきて,列CIで翼重量の合計を計算する

セルBG4:BG34に部材ごとの重量を計算し,セルBL26で主翼全体の重量を計算する
0番は半分しか計算していないので部材ごとの重量を2倍すること
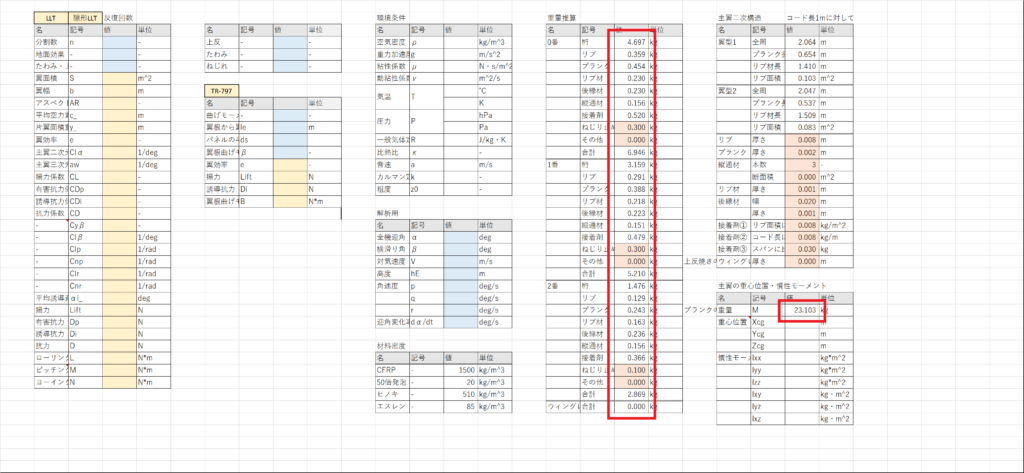
これで主翼の重量推算が終了した
ちなみにこれでようやく主翼の空力計算が行えるようになる
水平尾翼・垂直尾翼
主翼と同様に水平尾翼・垂直尾翼の重量推算を行う
セルBG20:BG27でスパーの重量推算を行うこと以外は主翼と同じなのでシートを見ればわかると思う
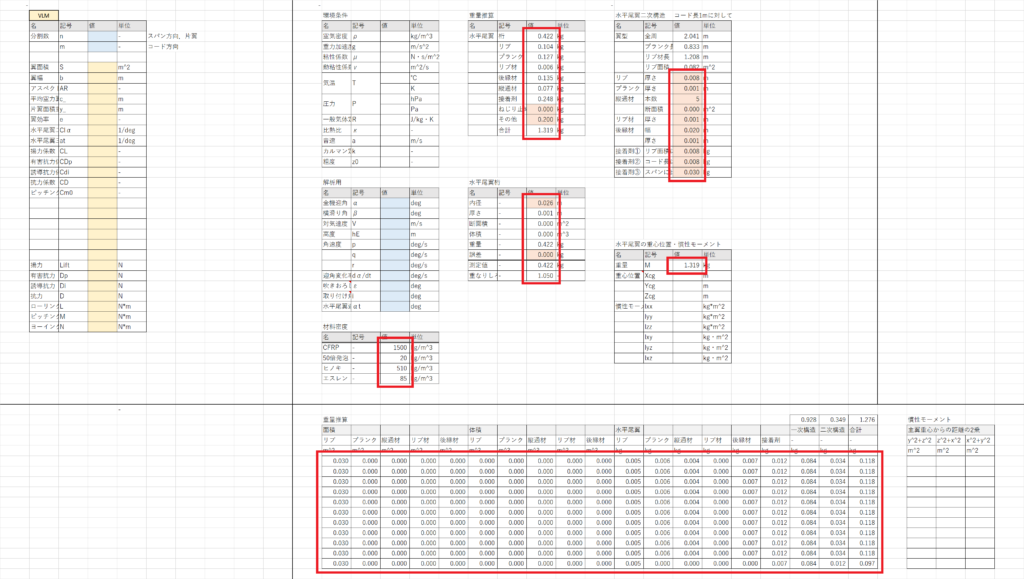
尾翼の重量推算はこれで終了した
胴体構造計算
このシートでは胴体構造の重量推算を行う
基本的にはスパー寸法のシートと同じなので見ればわかると思う
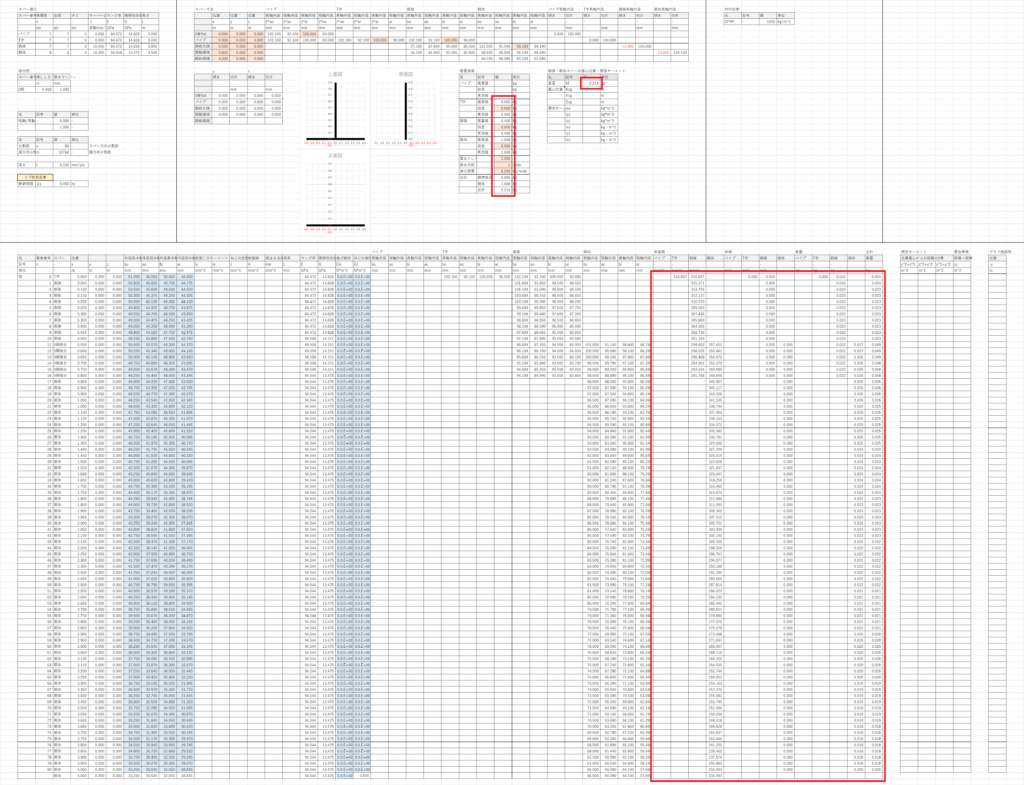
これで胴体構造の重量推算は終了した
機体重量
機体重量のシートに戻って全機の重量推算を行う
セルD4:D33に機体各部の重量の推算値を入力する
シート上で重量推算を行った主翼,水平尾翼,垂直尾翼,胴体はそれぞれのシートから推算値をもってきて,それ以外の部品は過去のデータから推算値を入力する
機体製作後に,E4:E33に誤差(推算値より重い場合を正)を入力し,F4:F33で測定値を計算する
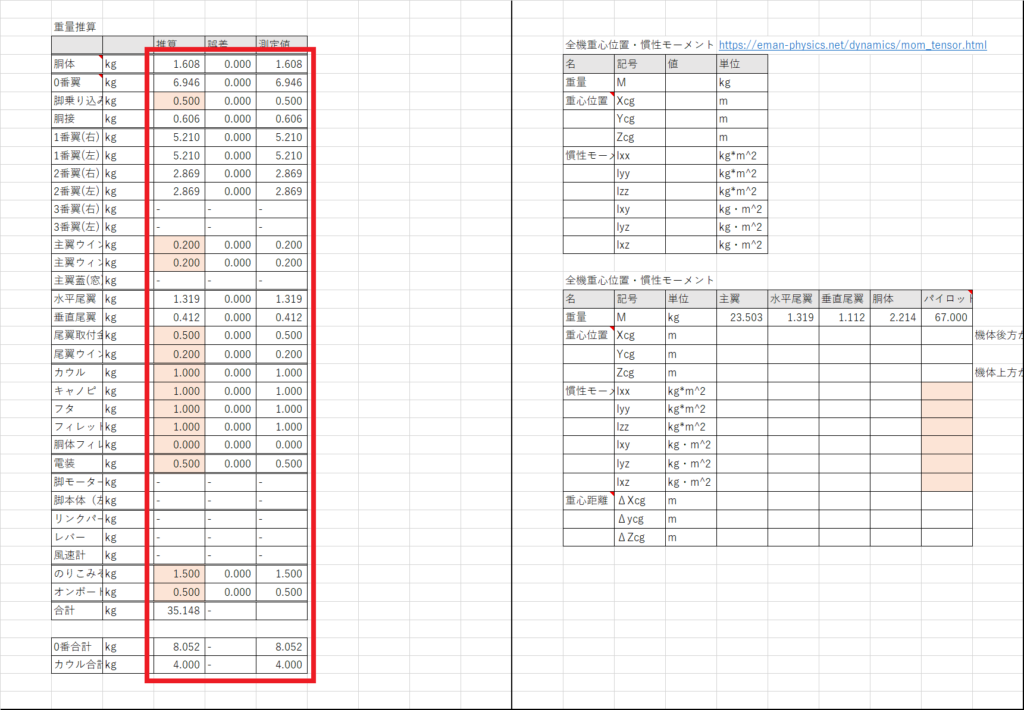
全機計算のシートのセルI5にパイロット重量を入力する
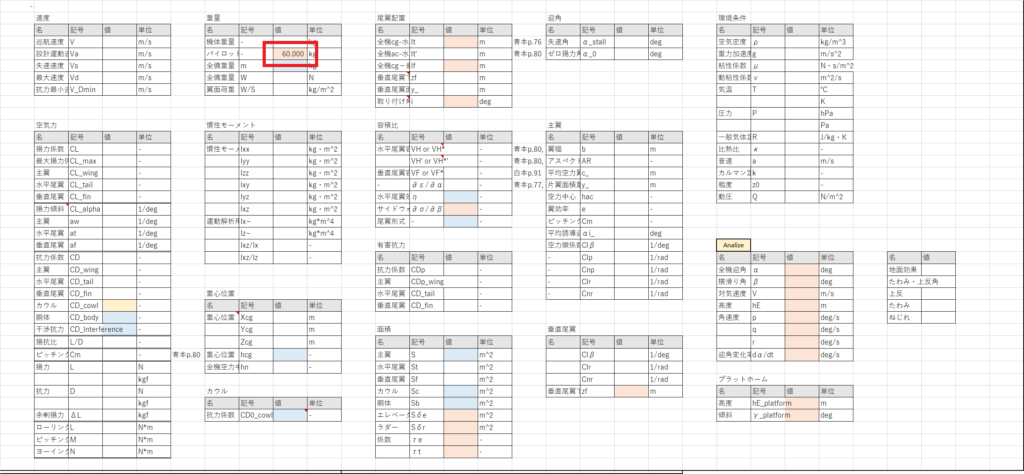
機体重量シートのセルO18:S18に機体各部の重量を持ってくる
- 主翼:0番翼,1番翼(左右),2番翼(左右),ウィングレット(左右)
- 水平尾翼:水平尾翼
- 垂直尾翼:垂直尾翼,尾翼取付金具,尾翼ウィングレット
- 胴体:胴体,胴接
- パイロット:パイロット,上にあげたもの以外すべて
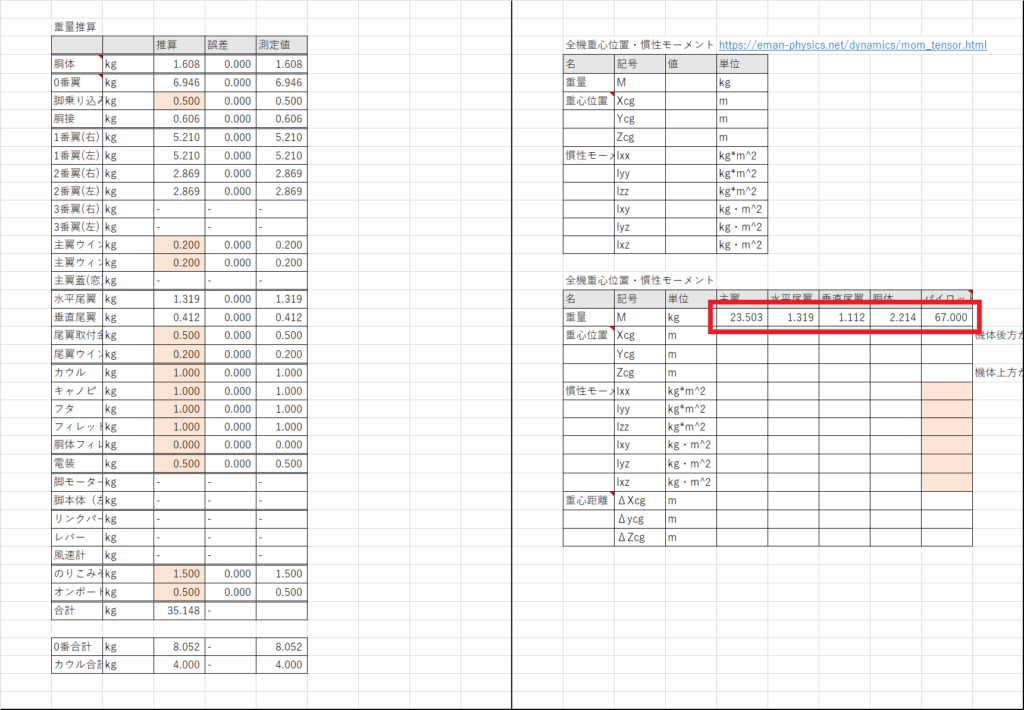
これで機体の重量推算は終了した
慣性モーメント
機体の各部の重量がわかったので慣性モーメントを計算することができる
慣性モーメントは機体の運動を解析するときに非常に重要な値である
原理
重心周りの慣性モーメントは次の公式で計算できる
\begin{eqnarray}
I_{xx} &=& \iiint (y^2+z^2) dm \\
I_{yy} &=& \iiint (z^2+x^2) dm \\
I_{zz} &=& \iiint (x^2+y^2) dm \\
I_{xy} &=& \iiint xy dm \\
I_{yz} &=& \iiint yz dm \\
I_{zx} &=& \iiint zx dm
\tag{1}
\end{eqnarray}
重心位置は次の公式で計算できる
\begin{eqnarray}
(X_cg,Y_cg,Z_cg) &=& \frac{\int (x,y,z) dm}{\int dm}
\tag{2}
\end{eqnarray}
平行軸の定理は次の式で表される
\begin{eqnarray}
I &=& I_{cg}+md^2
\tag{3}
\end{eqnarray}
これらの式を用いて全機の重心周りの慣性モーメントを計算する
積分式は微小要素の総和に変換して計算する
主翼
主翼の主翼の重心周りの慣性モーメントを計算する
現時点ではまだ主翼の空力計算を行っておらず主翼のたわみ量がわからないため,テンプレートシートから飛行時のたわみ量を列AB~ACの45行目以下にコピーする
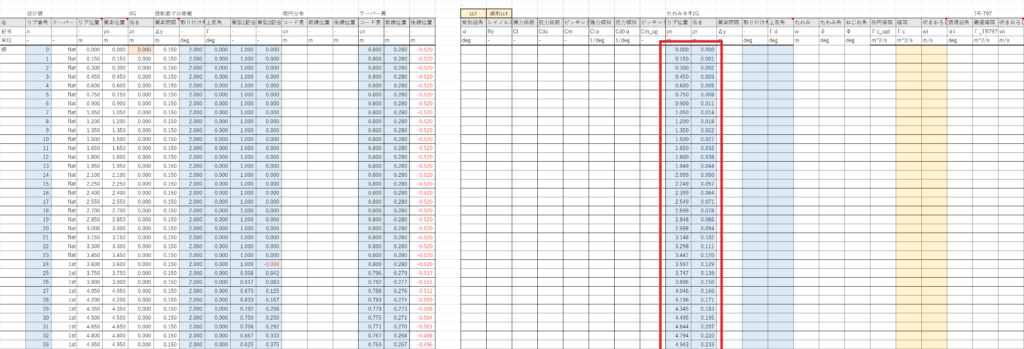
セルBL27:BL29で,主翼の重心位置を次の式で計算する
\begin{eqnarray}
(X_cg, Y_cg, Z_cg) &=& \frac{\sum (x_i, y_i, z_i) \Delta m_i}{\sum \Delta m_i}
\tag{2'}
\end{eqnarray}
重心位置の基準点(原点)は主翼桁中心とし,機体後方がx軸正,右翼側をy軸正,機体上方をz軸正とする
x方向の重心位置を計算するのは死ぬほど面倒くさい現実的ではないので0を入力,y方向の重心位置は一般的に0である
積の総和を計算するにはSUMPRODUCT関数を使うといい
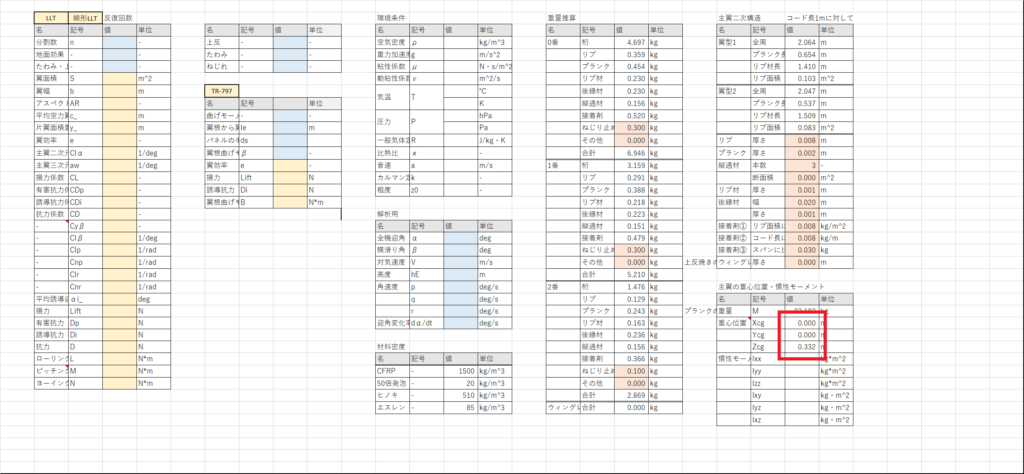
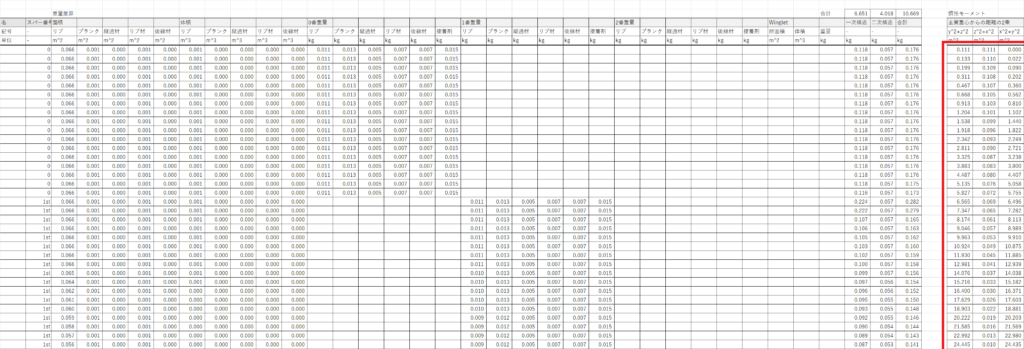
式(1)で慣性モーメントを計算するために,列CK~CMの45行目以下で重心位置からの距離の二乗を計算する
\begin{eqnarray}
I_{xx} &=& \sum (y_i^2+z_i^2) \Delta m \\
I_{yy} &=& \sum (z_i^2+x_i^2) \Delta m \\
I_{zz} &=& \sum (x_i^2+y_i^2) \Delta m \\
I_{xy} &=& \sum x_i y_i \Delta m \\
I_{yz} &=& \sum y_i z_i \Delta m \\
I_{zx} &=& \sum z_i x_i \Delta m
\tag{1'}
\end{eqnarray}
セルBL30:BL35で,慣性モーメントを計算する
左右対称なので\(I_{xy}=I_{yz}=0\),\(x=0\)なので\(I_{xz}=0\)であり,片翼分しか計算していないので対称性より\(I_{xx}, I_{yy}, I_{zz}\)の計算結果を2倍する
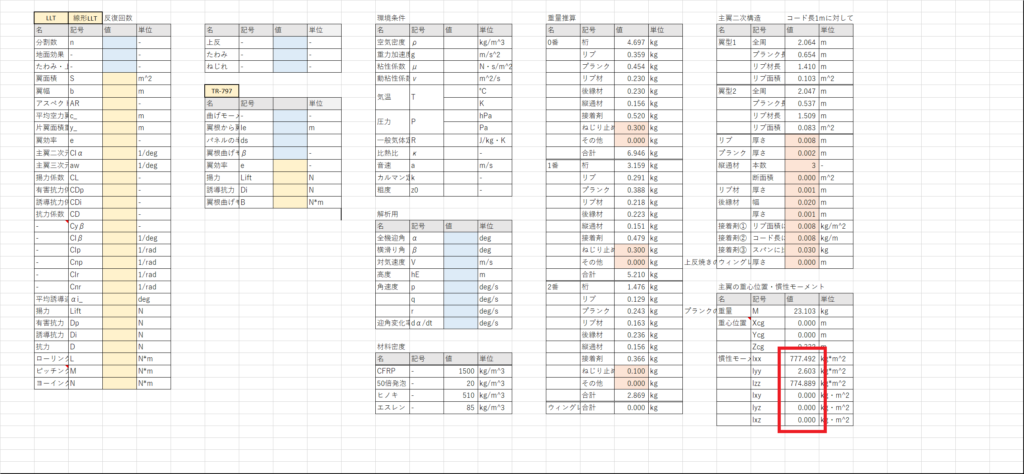
これで主翼の主翼の重心周りの慣性モーメントの計算は終了した
尾翼
尾翼の主翼桁中心からみた重心位置と重心周りの慣性モーメントを計算する
全機計算のシートのセルN4,N6,S33にそれぞれ全機cg-水平ac間距離,全機cg-垂直ac間距離,垂直尾翼下端位置(≒水平尾翼位置)を入力する
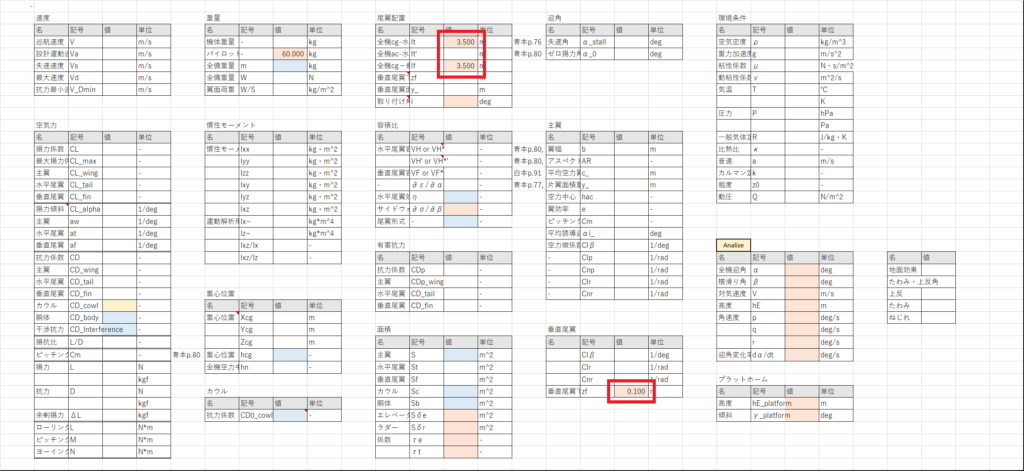
水平尾翼シートと垂直尾翼シートで水平尾翼の重心周りの慣性モーメントと重心位置を計算する
方法は主翼と同じなので見てもらえればわかると思う
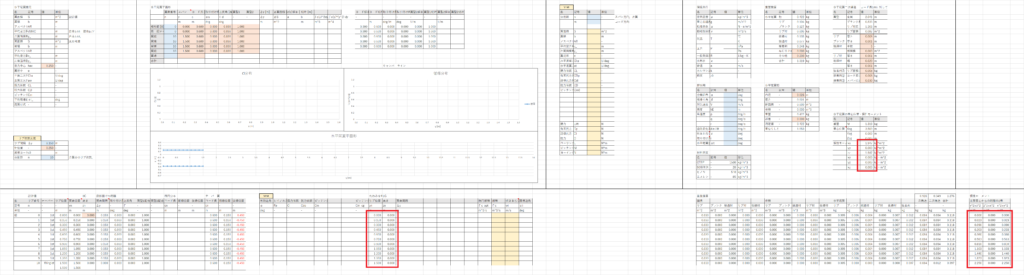
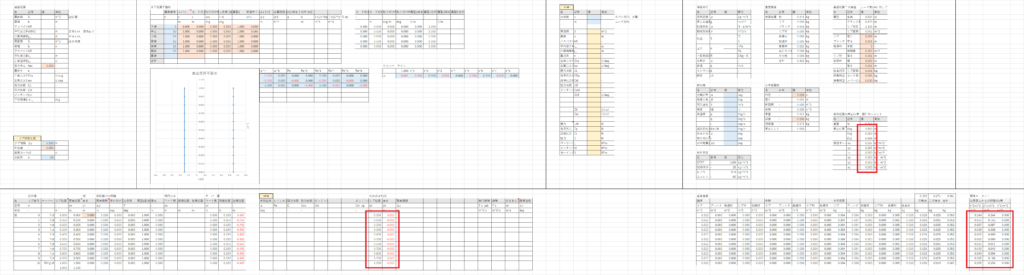
これで尾翼の主翼桁中心からみた重心位置と重心周りの慣性モーメントを計算が終了した
胴体構造計算
胴体構造の主翼桁中心から見た重心位置と,重心位置周りの慣性モーメントを計算する
計算方法は主翼,尾翼と同様なので見てもらえればわかると思う
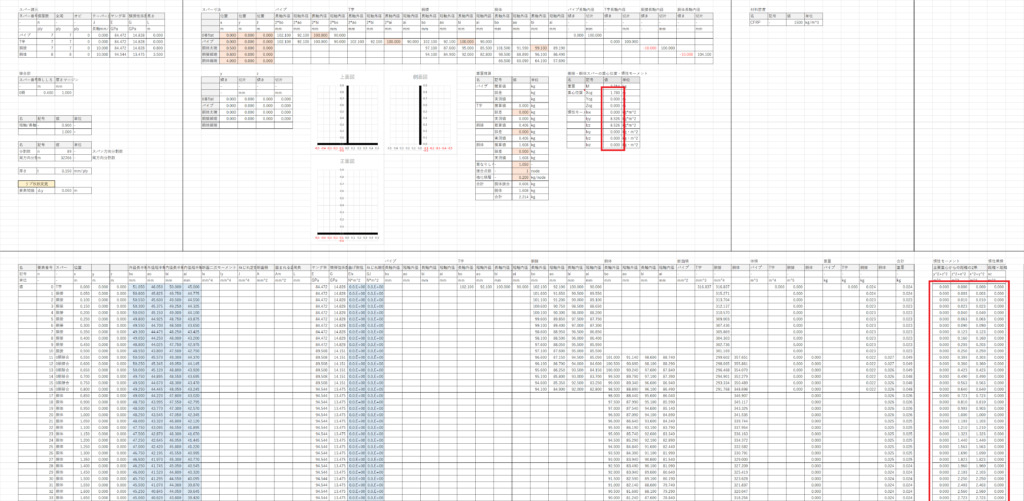
パイロット
パイロットの重心周りの慣性モーメントを計算する
今回はFusion360のフリー素材を使ってパイロットを再現し,プロパティ機能を使って慣性モーメントを計測する
上のサイトからダウンロードした球体関節人形を,パイロットと同じ身長になるよう拡大縮小し,飛行姿勢に近い体勢になるようジョイントを駆動する
今回は身長165㎝程になるようにした
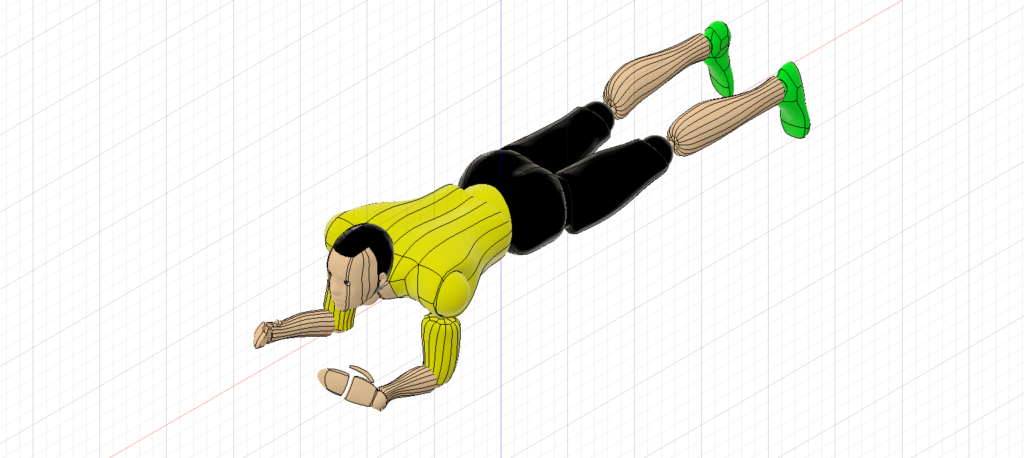
左側のウィンドウの一番上を右クリックし,プロパティを選択する
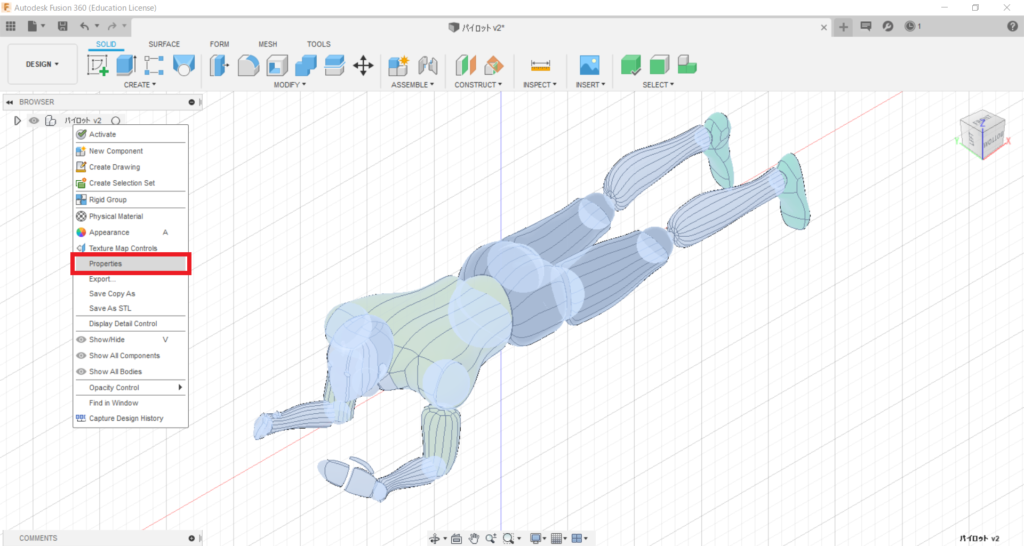
密度,重量,体積が出てくるので,パイロットの体重と同じになるようパイロットの密度を変更する
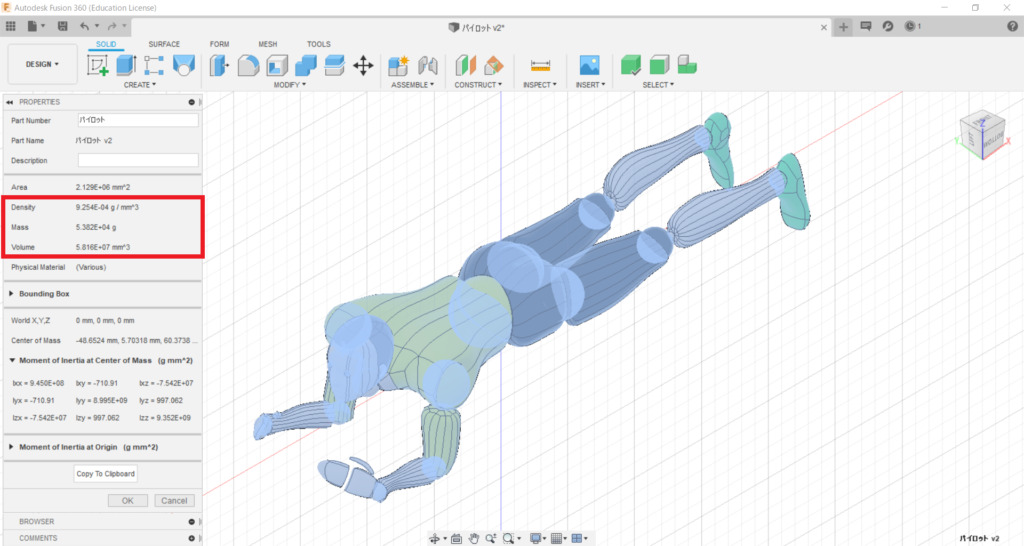
ここではパイロットの体重を60㎏にしたいので,密度を1.032 [g/㎤]とした
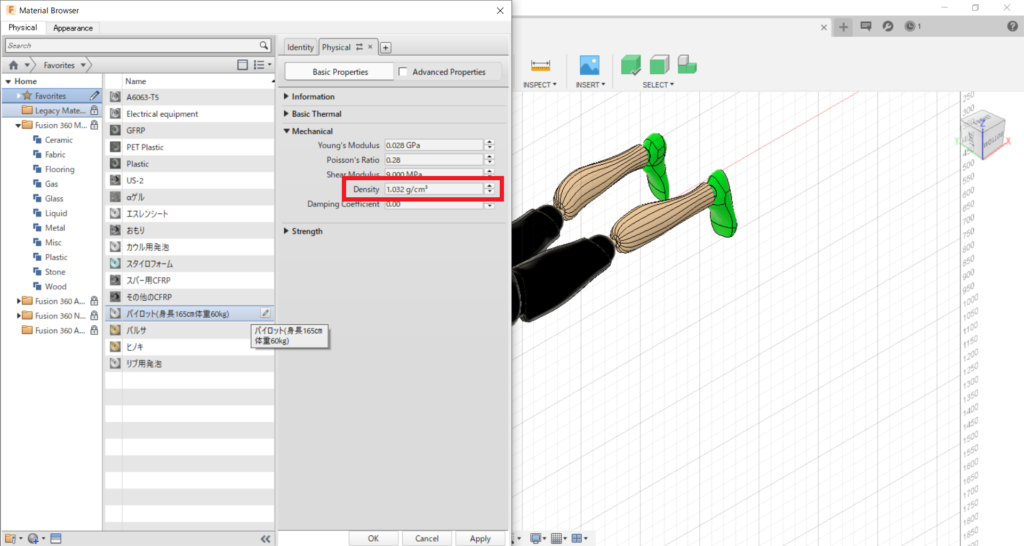
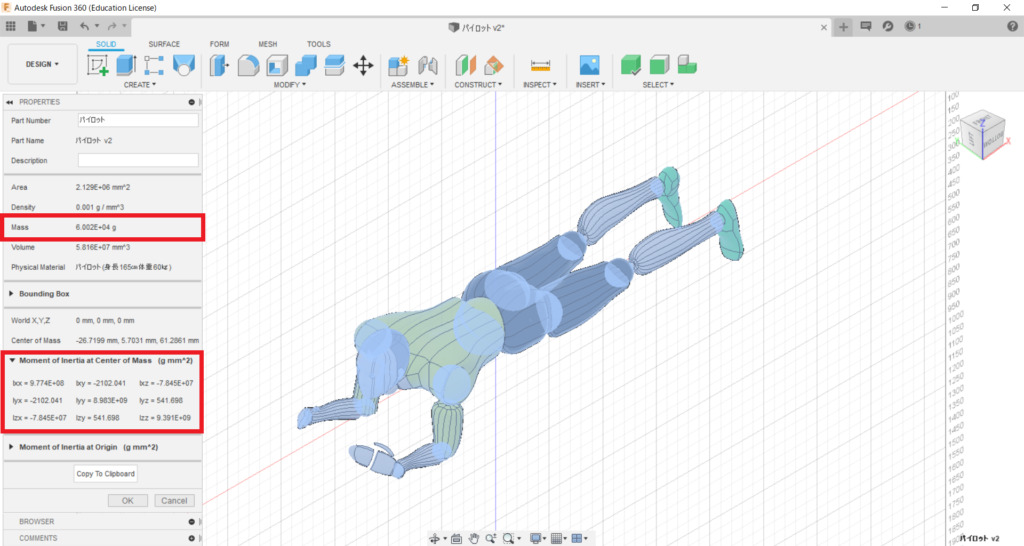
体重が60㎏になり,重心周りの慣性モーメントが出力された
パイロット v2
Area 2.129E+06 mm^2
Density 0.001 g / mm^3
Mass 6.002E+04 g
Volume 5.816E+07 mm^3
Physical Material パイロット(身長165㎝体重60㎏)
Bounding Box
Length 1770.576 mm
Width 493.559 mm
Height 462.699 mm
World X,Y,Z 0 mm, 0 mm, 0 mm
Center of Mass -26.7199 mm, 5.7031 mm, 61.2861 mm
Moment of Inertia at Center of Mass (g mm^2)
Ixx = 9.774E+08
Ixy = -2102.041
Ixz = -7.845E+07
Iyx = -2102.041
Iyy = 8.983E+09
Iyz = 541.698
Izx = -7.845E+07
Izy = 541.698
Izz = 9.391E+09
Moment of Inertia at Origin (g mm^2)
Ixx = 1.205E+09
Ixy = 9.144E+06
Ixz = 1.984E+07
Iyx = 9.144E+06
Iyy = 9.251E+09
Iyz = -2.098E+07
Izx = 1.984E+07
Izy = -2.098E+07
Izz = 9.436E+09Fuison360から出力された慣性モーメントを機体重量シートのS22:S27に入力し,パイロットの重心位置(≒乗り込み位置)を適当に入力する
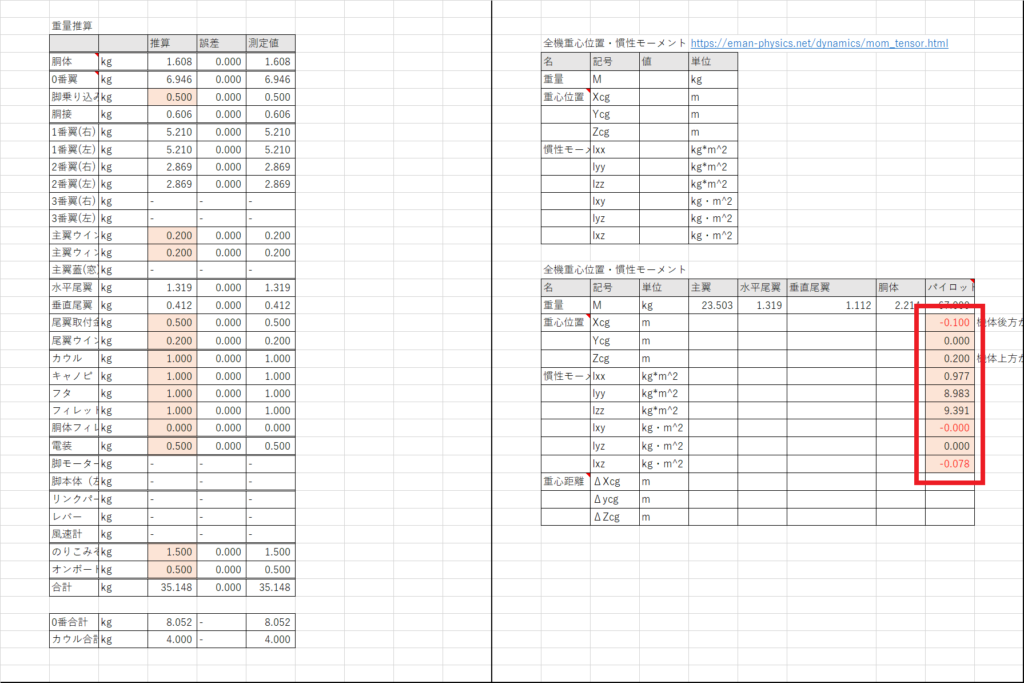
これでパイロットの重心周りの慣性モーメントの計算が終了した
機体重量
機体重量シートで全機の重心周りの慣性モーメントを計算する
セルO19:R27にそれぞれのシートから重心位置と重心周りの慣性モーメントを持ってくる
セルN5で全備重量を計算し,セルN6:N8で全機の重心位置を計算する.(特に意味はないが全機の重心位置がちょうど0になるようパイロットの乗り込み位置を微調整しておいた)
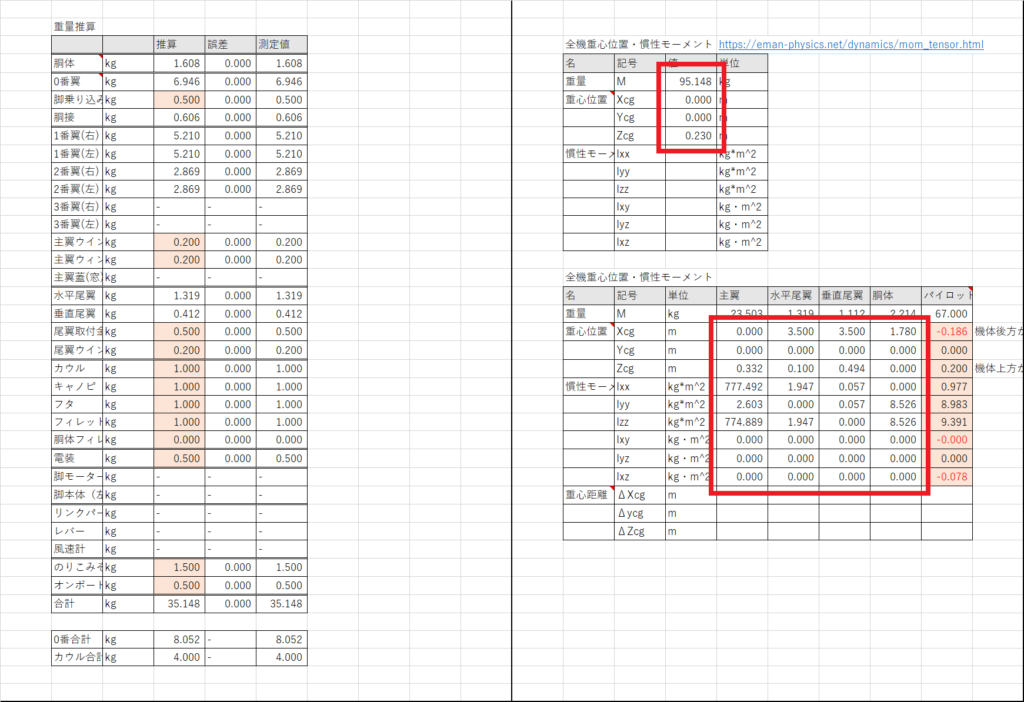
セルO28:S30で全機の重心位置とそれぞれの重心位置の距離の差を計算し,セルN9:N14で 平行軸の定理を使って全機の重心周りの慣性モーメントを計算する
\begin{eqnarray}
I &=& \sum (I_{cg_{i}}+m_i d_i^2)
\tag{3'}
\end{eqnarray}
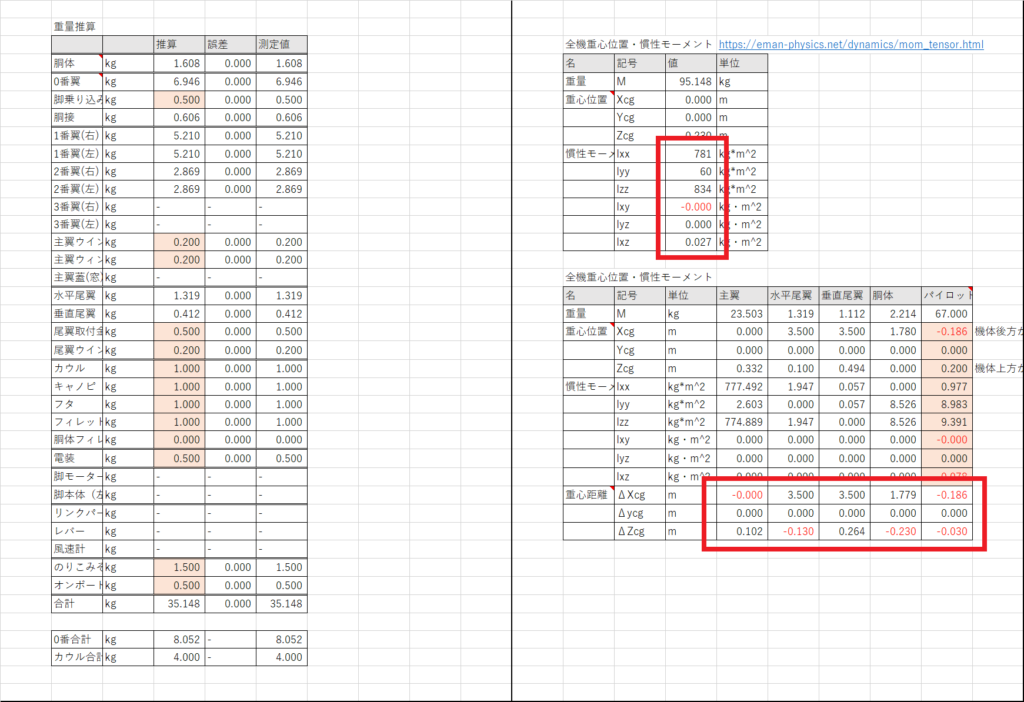
これで全機の重心周りの慣性モーメントの計算が終了した
テンプレートファイルのダウンロード
今回の記事で説明した数式が入ってリルエクセルシートを添付しておく
説明が不十分だった人は実際に自分で見て確認してほしい
※マクロは削除してある
まとめ
重量推算は毎年少しずつ修正を加えていくことでより精度を高めていくことができる
慣性モーメントは推算の域を出ないが,歴代の機体を計算して比較することで設計に生かすことができるのではと思う
頑張れ
↓次の記事
↓記事一覧





コメント