主翼の空力および構造計算を行うプログラムを作成する
揚力線理論や渦格子法を拡張したようなプログラムになる
目的
今回の目的は,主翼の空力計算を行うことである.
XFLR5で行う空力計算とは異なり,たわみやねじれも同時に計算する
循環分布の計算についてはTR-797と同じ方法をとるので,詳しくは次の記事(≫TR-797の実装)を参考にしてほしい
構造設計については次の本を参考にした
≫グライダーの製作(Ⅰ) 『木製ボックス桁』・・・(文献1)
また,非線形の空力計算については次の文献を参考にした
≫Non-Linear Lifting Line Implementation and Validation for Aerodynamic and Stability Analysis・・・(文献2)
空力微係数などの計算については次の文献を参考にした
≫航空機力学入門|加藤寛一郎・・・(文献3)
ちなみに本家XFLR5の空力計算は次の文献を参考にしている
≫ Method for calculating wing characteristics by lifting-line theory using nonlinear section lift data ・・・(文献4)
今回の記事では,文献1,文献2,文献3をもとに空気力を計算→翼のたわみとねじれを計算→空気力を計算→翼のたわみとねじれを計算→・・・を収束するまで行っていくことになる
また,参考文献を参照する際に助けとなるよう,式番号などはそれぞれの文献のものにそろえる
フローチャート
今回のプログラムのフローチャートを以下に示す
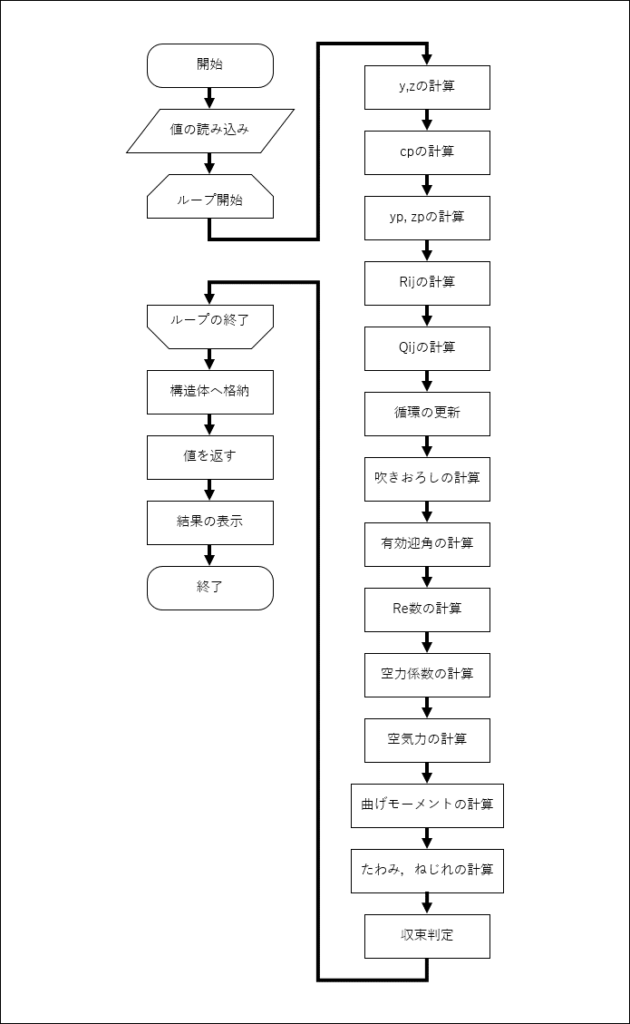
長い.それに尽きる
プログラムの解説
それでは実際に解説してく
テンプレートファイル
エクセルシートの配置などの参考になるようにテンプレートファイルを添付しておく
※数式やマクロはすべて削除してあり,値も適当である
TemplateNO_TEXT_ver20191114.xlsx
プログラムの構造
主翼の空力計算のプログラムは,引数を主翼の構造体Wing,状態変数の構造体state,設計シートへの出力の有無pとして,主翼の構造体に計算結果を返すFunctionとする
Public Function VLM_wing(p As Integer, ByRef Wing As Specifications, ByRef state As variables) As Specifications
(処理)
End Function設計シートのプログラム全般で使う構造体については次の記事(≫設計シートに使う構造体について)を参考にしてほしい
プログラムの全体の流れ
今回のプログラムはかなり長いので,可読性を上げるためにもそれぞれの処理はプロシージャに分けて行った
プログラムの全体は次のようになる
'LLT'
Call read_value_from_sheet(Wing, state, chord, chord_cp, dW(), setting_angle0(), foil_mixture, dihedral_angle0, Eix, GJ(), Cl_coef, Cdp_coef, Cm_coef)
'LLTの反復計算'
For iteration = 0 To iteration_max
Call calculation_yz(Wing, state, y, z, setting_angle0, setting_angle, phi, dihedral_angle0, dihedral_angle, theta)
Call calculation_cp(Wing, state, cp, y, z)
Call calculation_ypzp(Wing, state, yp, zp, ymp, zmp, cp, dihedral_angle)
Call calculation_Rij(Wing, state, ds, yp, zp, ymp, zmp, Rpij, Rmij, Rpijm, Rmijm)
Call calculation_Qij(Wing, state, ds, yp, zp, ymp, zmp, Rpij, Rmij, Rpijm, Rmijm, dihedral_angle, Qij)
Call update_circulation(Wing, state, iteration, coef, circulation, circulation_old)
Call calculation_downwash(Wing, state, circulation, Qij, alpha_induced, cp, wi)
Call calculation_alpha_effective(Wing, state, alpha_effective, alpha_induced, cp, dihedral_angle, setting_angle, alpha_max, alpha_min)
Call calculation_Re(Wing, state, Re, cp, chord_cp, Re_max, Re_min)
Call calculation_aerodynamic_coefficient(Wing, state, CL, Cdp, Cm_ac, a0, a1, Cda, Cm_cg, dN, dT, dL, dDp, dM_cg, dM_ac, cp, chord_cp, alpha_induced, alpha_effective, Re, dihedral_angle, foil_mixture, Cl_coef, Cdp_coef, Cm_coef)
Call calculation_Force(Wing, state, iteration, Lift, Induced_Drag, cp, circulation, dihedral_angle, wi, CL, chord_cp)
Call calculation_Moment(Wing, state, Bending_Moment, Bending_Moment_T, Shear_Force, Torque, dN, dT, dM_cg, dW, dihedral_angle, cp, y, z)
Call calculation_deflection(Wing, state, deflection, theta, phi, Bending_Moment, Torque, Eix, GJ)
Call change_mode(Wing, state, dihedral_angle, dihedral_angle0, deflection, theta, phi, dM_ac, dM_cg, Shear_Force, Bending_Moment, Bending_Moment_T, Torque)
'収束判定'
If iteration > 0 Then
If error > Abs((Lift(iteration) - Lift(iteration - 1)) / Lift(iteration - 1)) Then Exit For
End If
If p = 1 Then Application.StatusBar = "反復回数" & iteration & "回" & String(iteration, "■") 'ステータスバーに反復回数を表示'
DoEvents
Next iteration
Application.StatusBar = False
If iteration > iteration_max Then
iteration = iteration_max
End If
Call input_data_to_type(Wing, state, iteration, dihedral_angle, chord_cp, y, cp, a0, a1, Cda, dDp, dN, dT, dM_ac, CL, Cdp, Lift, Induced_Drag)
VLM_wing = Wing
If p = 1 Then
sht1.Range("AS2") = iteration
Call output_data_to_sheet(Wing, alpha_effective, Re, CL, Cdp, Cm_ac, a0, Cda, Cm_cg, setting_angle, dihedral_angle, circulation, wi, alpha_induced, y, z, deflection, theta, phi, Shear_Force, Bending_Moment, Torque, Bending_Moment_T)
End If
End Function引数が多すぎて逆に見づらくなっている気がしないでもない
変数の宣言
今回のプログラムで使う変数を以下に示す
'ワークシートの定義'
Set sht0 = Sheets("各種パラメータ(sht0)")
Set sht1 = Sheets("主翼(sht1)")
Set sht2 = Sheets("たわみ・ねじり(sht2)")
Set sht8 = Sheets("全機計算(sht8)")
Set sht20 = Sheets("スパー寸法(sht20)")
'LLTの変数の定義'
Const coef As Double = 0.1 '循環の更新に使う謎係数.収束は遅くなるが数学的に安定するらしい.'
Const iteration_max As Integer = 32767 - 1
Const error As Double = 10 ^ (-5) '誤差'
Const Re_max As Double = 1000000
Const Re_min As Double = 100000
Const alpha_max As Double = 20
Const alpha_min As Double = -10
'翼の幾何学形状'
Dim ds As Double: ds = Wing.dy / 2 'パネルの半幅 [m]'
Dim dz() As Double '高さの差 [m]'
Dim n_MAC As Integer '平均空力翼弦長のリブ番号'
Dim chord() As Double: ReDim chord(2 * Wing.span_div) 'コード長 [m]'
Dim setting_angle0() As Double: ReDim setting_angle0(2 * Wing.span_div - 1) '初期取り付け角 [deg]'
Dim setting_angle() As Double: ReDim setting_angle(2 * Wing.span_div - 1) '取り付け角 [deg]'
Dim dihedral_angle() As Double: ReDim dihedral_angle(2 * Wing.span_div - 1) '上反角 [deg].Γd.Dihedral'
Dim dihedral_angle0() As Double: ReDim dihedral_angle0(2 * Wing.span_div - 1) '初期上反角 [deg].Γd0.Dihedral'
Dim foil_mixture() As Double: ReDim foil_mixture(2 * Wing.span_div - 1, 1) '翼配合率'
Dim Eix() As Double: ReDim Eix(2 * Wing.span_div - 1) '曲げ剛性'
Dim GJ() As Double: ReDim GJ(2 * Wing.span_div - 1) 'ねじり剛性'
Dim chord_cp() As Double: ReDim chord_cp(2 * Wing.span_div - 1) 'コントロールポイントでのコード長 [m]'
Dim deflection() As Double: ReDim deflection(2 * Wing.span_div) 'たわみ [m]'
Dim theta() As Double: ReDim theta(2 * Wing.span_div) 'たわみ角 [deg]'
Dim phi() As Double: ReDim phi(2 * Wing.span_div) 'ねじれ角 [deg]'
Dim cp() As Double: ReDim cp(2, 2 * Wing.span_div - 1) 'i番目の要素のcontrol point [m]'
Dim y() As Double 'y座標.リブのスパン方向位置 [m].wing station'
Dim z() As Double 'z座標.高さ [m]'
Dim Z_cg As Double: Z_cg = sht8.Range("I28")
'翼の空力計算'
Dim Cl_coef(14, 1) As Double '揚力係数を表す多項式の係数'
Dim Cdp_coef(14, 1) As Double '有害抗力係数を表す多項式の係数'
Dim Cm_coef(14, 1) As Double 'ピッチングモーメント係数を表す多項式の係数'
Dim dynamic_pressure As Double: dynamic_pressure = Wing.dynamic_pressure '動圧の計算 [N/m^2]'
Dim alpha_induced() As Double: ReDim alpha_induced(2 * Wing.span_div - 1) '誘導迎角 [deg]'
Dim alpha_effective() As Double: ReDim alpha_effective(2 * Wing.span_div - 1) '有効迎角 [deg]'
Dim Re() As Double: ReDim Re(2 * Wing.span_div - 1) '局所レイノルズ数'
Dim CL() As Double: ReDim CL(2 * Wing.span_div - 1) '局所揚力係数'
Dim Cdp() As Double: ReDim Cdp(2 * Wing.span_div - 1) '局所有害抗力係数'
Dim Cm_ac() As Double: ReDim Cm_ac(2 * Wing.span_div - 1) '空力中心周りの局所ピッチングモーメント係数'
Dim Cm_cg() As Double: ReDim Cm_cg(2 * Wing.span_div - 1) '桁位置周りの局所ピッチングモーメント係数'
Dim a0() As Double: ReDim a0(2 * Wing.span_div - 1) 'α=0のときの揚力傾斜 [-]'
Dim a1() As Double: ReDim a1(2 * Wing.span_div - 1) '断面揚力傾斜 [1/deg]'
Dim Cda() As Double: ReDim Cda(2 * Wing.span_div - 1) '断面抗力傾斜 [1/deg]'
Dim circulation() As Double: ReDim circulation(2 * Wing.span_div - 1) '循環 [m^2/s].Γc.Circulation.2n×1行列'
Dim circulation_old() As Double: ReDim circulation_old(2 * Wing.span_div - 1) '循環 [m^2/s].Γc.Circulation.2n×1行列'
Dim wi() As Double: ReDim wi(2 * Wing.span_div - 1) '吹きおろし速度 [m/s]'
Dim Qij() As Double: ReDim Qij(2 * Wing.span_div - 1, 2 * Wing.span_div - 1) 'スパン荷重分布と垂直誘導速度を結び付ける影響関数'
'翼にはたらく力,モーメント'
Dim Lift() As Double: ReDim Lift(iteration_max + 1) '揚力 [N]'
Dim Induced_Drag() As Double: ReDim Induced_Drag(iteration_max + 1) '誘導抗力 [N]'
Dim dL() As Double: ReDim dL(2 * Wing.span_div - 1) '翼素揚力 [N]'
Dim dDp() As Double: ReDim dDp(2 * Wing.span_div - 1) '翼素有害抗力 [N]'
Dim dW() As Double: ReDim dW(2 * Wing.span_div - 1) '翼素重量[N]'
Dim dN() As Double: ReDim dN(2 * Wing.span_div - 1) 'N軸方向の力 [N]'
Dim dT() As Double: ReDim dT(2 * Wing.span_div - 1) 'T軸方向の力 [N]'
Dim dM_ac() As Double: ReDim dM_ac(2 * Wing.span_div - 1) '空力中心周りの翼素トルク [N*m]'
Dim dM_cg() As Double: ReDim dM_cg(2 * Wing.span_div - 1) '桁位置周りの翼素トルク [N*m]'
Dim Bending_Moment() As Double: ReDim Bending_Moment(2 * Wing.span_div) '曲げモーメント [N*m]'
Dim Bending_Moment_T() As Double: ReDim Bending_Moment_T(2 * Wing.span_div) 'T曲げモーメント [N*m]'
Dim Torque() As Double: ReDim Torque(2 * Wing.span_div) 'トルク [N*m]'
Dim Shear_Force() As Double: ReDim Shear_Force(2 * Wing.span_div) 'せん断力'
'座標.p:prime,m:mirror'
Dim yp() As Double: ReDim yp(2 * Wing.span_div - 1, 2 * Wing.span_div - 1)
Dim zp() As Double: ReDim zp(2 * Wing.span_div - 1, 2 * Wing.span_div - 1)
Dim ymp() As Double: ReDim ymp(2 * Wing.span_div - 1, 2 * Wing.span_div - 1)
Dim zmp() As Double: ReDim zmp(2 * Wing.span_div - 1, 2 * Wing.span_div - 1)
Dim Rpij() As Double: ReDim Rpij(2 * Wing.span_div - 1, 2 * Wing.span_div - 1) 'パネル間の距離.R+ij'
Dim Rmij() As Double: ReDim Rmij(2 * Wing.span_div - 1, 2 * Wing.span_div - 1) 'パネル間の距離.R-ij'
Dim Rpijm() As Double: ReDim Rpijm(2 * Wing.span_div - 1, 2 * Wing.span_div - 1) 'パネル間の距離.R+ij'
Dim Rmijm() As Double: ReDim Rmijm(2 * Wing.span_div - 1, 2 * Wing.span_div - 1) 'パネル間の距離.R-ij'
'一般'
Dim sum As Double
Dim tmp As Double
Dim num As Double
Dim pi As Double: pi = 4 * Atn(1) '円周率'
Dim rad As Double: rad = (pi / 180) 'degからradへの変換'
Dim deg As Double: deg = (180 / pi) 'radからdegへの変換'
Dim output() As Double '結果貼り付け用配列'
Dim Integral As Double '積分値'
Dim average As Double: average = 0 '収束判定用'
'カウンター'
Dim i As Integer
Dim j As Integer
Dim iteration As Integer行数の節約のために動的配列の大きさの宣言や値の計算は同じ行で行っている
Re_max,Re_min,alpha_max,apha_minは,繰り返し計算の途中で迎角やRe数がXFLR5であらかじめ計算した範囲を出てしまったときに起こる発散を防ぐための値である(≫XFLR5で二次元翼を解析して結果を出力する)
値の読み込み
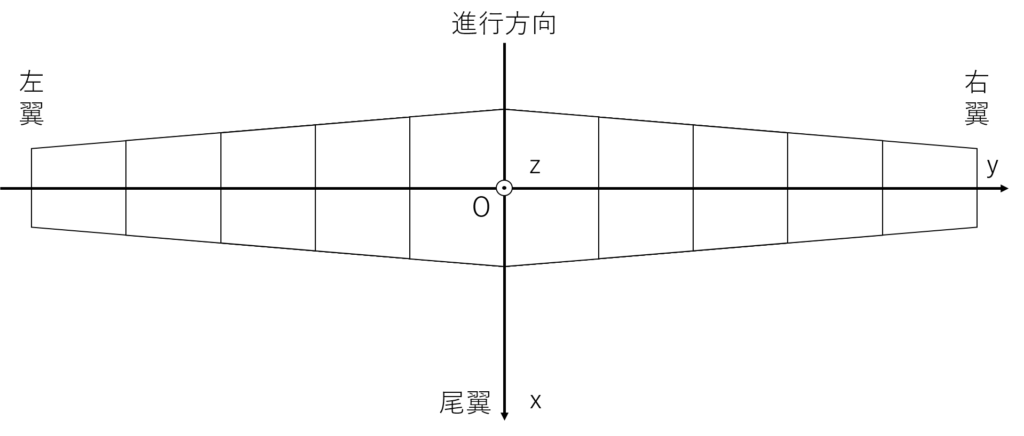
値の読み込みを行う前に,座標系の定義と番号の振り方を説明しておく
座標系については,機体後方をx軸正,右翼側をy軸正,機体上方をz軸正とする
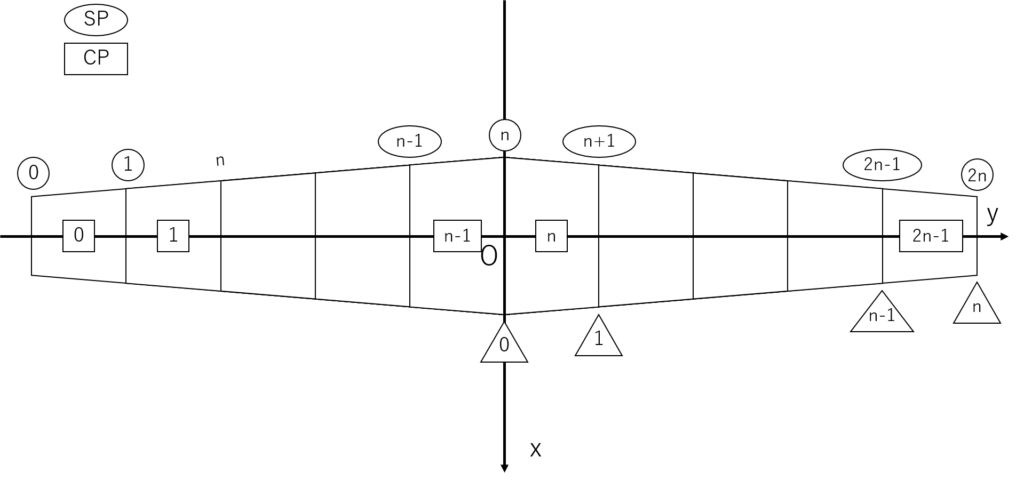
翼を有限このパネルに分割する計算法において,空気力や循環が働くとするパネルの中心をcontrol point (cp),パネルの境界をsurface point (sp)と呼ぶ
リブ枚数をn(翼中心のリブ番号が0,翼端のリブ番号がn)とすると,cp,spの番号は次のようになる
わかりにくいときは下のように小さなnで具体的に考えてみるといい
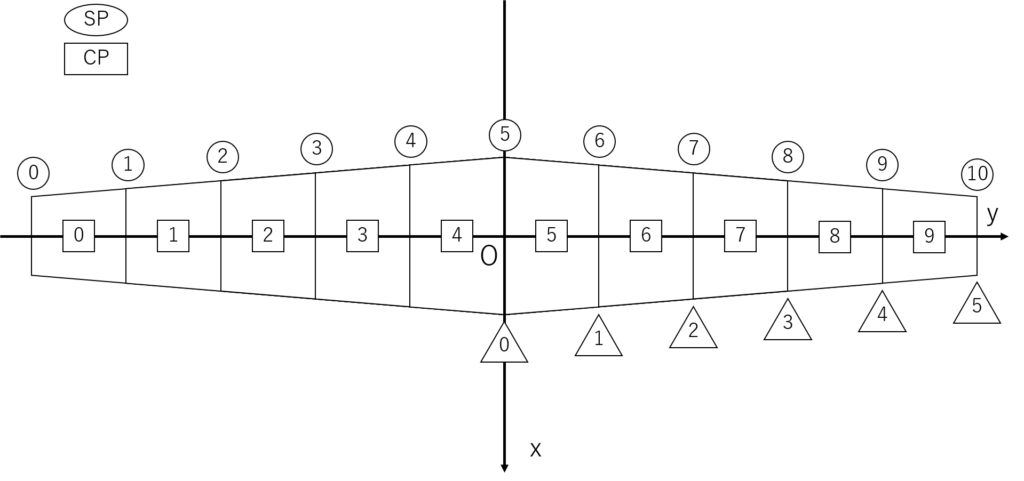
この番号をしっかり意識しながらシートから必要な値を読み込んでいく
Sub read_value_from_sheet(ByRef Wing As Specifications, ByRef state As variables, ByRef chord() As Double, ByRef chord_cp() As Double, ByRef dW() As Double, ByRef setting_angle0() As Double, ByRef foil_mixture() As Double, ByRef dihedral_angle0() As Double, ByRef Eix() As Double, ByRef GJ() As Double, ByRef Cl_coef() As Double, ByRef Cdp_coef() As Double, ByRef Cm_coef() As Double)
With Wing
'値の読み込み
'左翼端が0,右翼端が2*span_div
For i = 0 To .span_div
chord(.span_div + i) = sht1.Cells(45 + i, 16) '右翼の値
chord(.span_div - i) = chord(.span_div + i) '左翼の値
Next i
For i = 0 To .span_div - 1
'右翼の値
chord_cp(.span_div + i) = (1 / 2) * (chord(.span_div + i) + chord(.span_div + 1 + i))
dW(.span_div + i) = (1 / 2) * (sht2.Cells(45 + i, 14) + sht2.Cells(45 + i + 1, 14))
setting_angle0(.span_div + i) = (1 / 2) * (sht1.Cells(45 + i, 9) + sht1.Cells(45 + i + 1, 9))
foil_mixture(.span_div + i, 0) = (1 / 2) * (sht1.Cells(45 + i, 11) + sht1.Cells(45 + i + 1, 11))
foil_mixture(.span_div + i, 1) = (1 / 2) * (sht1.Cells(45 + i, 12) + sht1.Cells(45 + i + 1, 12))
dihedral_angle0(.span_div + i) = (1 / 2) * (sht1.Cells(45 + i, 10) + sht1.Cells(45 + i + 1, 10))
Eix(.span_div + i) = (1 / 2) * (sht2.Cells(45 + i, 12) + sht2.Cells(45 + i + 1, 12))
GJ(.span_div + i) = (1 / 2) * (sht2.Cells(45 + i, 13) + sht2.Cells(45 + i + 1, 13))
'左翼の値
chord_cp(.span_div - 1 - i) = (1 / 2) * (chord(.span_div - i) + chord(.span_div - 1 - i))
dW(.span_div - 1 - i) = dW(.span_div + i)
setting_angle0(.span_div - 1 - i) = setting_angle0(.span_div + i)
foil_mixture(.span_div - 1 - i, 0) = foil_mixture(.span_div + i, 0)
foil_mixture(.span_div - 1 - i, 1) = foil_mixture(.span_div + i, 1)
dihedral_angle0(.span_div - 1 - i) = -dihedral_angle0(.span_div + i) '左翼は負の値
Eix(.span_div - 1 - i) = Eix(.span_div + i)
GJ(.span_div - 1 - i) = GJ(.span_div + i)
Next i
For j = 0 To 1
For i = 0 To 14
Cl_coef(i, j) = sht1.Cells(21 + j * 3, 13 + i)
Cdp_coef(i, j) = sht1.Cells(22 + j * 3, 13 + i)
Cm_coef(i, j) = sht1.Cells(23 + j * 3, 13 + i)
Next i
Next j
End With
End Sub設計シート上で元々リブ位置(sp)で定義してある量は,cpの両側のspの値を平均している
このプロシージャについては以上である
繰り返し計算のループ
今回のプログラムでは循環分布を計算するために繰り返し計算を行う
For iteration = 0 To iteration_max
'(ループ内の処理)
If p = 1 Then Application.StatusBar = "反復回数" & iteration & "回" & String(iteration, "■") 'ステータスバーに反復回数を表示
DoEvents
Next iteration
Application.StatusBar = Falseループ内の最後の2行はエクセルシートの下のステータスバーに進捗状況を表示するコードと,Excel VBAあるあるの”応答なし”を防ぐためのコードである
y,zの計算
まず,Qijを計算するのに必要な値を順次計算していく
翼のたわみやねじれをもとに翼の各spの座標や取り付け角を更新する
Sub calculation_yz(ByRef Wing As Specifications, ByRef state As variables, ByRef y() As Double, ByRef z() As Double, ByRef setting_angle0() As Double, ByRef setting_angle() As Double, ByRef phi() As Double, ByRef dihedral_angle0() As Double, ByRef dihedral_angle() As Double, ByRef theta() As Double)
With Wing
ReDim y(2 * .span_div) 'リブのスパン方向位置 [m].wing station
ReDim z(2 * .span_div) '高さ [m]
'y,zを計算
'翼中心が0.翼端がspan_divisions
For i = 0 To .span_div - 1
'Γd,αsを更新
'左翼
setting_angle(.span_div - 1 - i) = setting_angle0(.span_div - 1 - i) + (1 / 2) * (phi(.span_div - i) + phi(.span_div - 1 - i)) '[deg]
dihedral_angle(.span_div - 1 - i) = dihedral_angle0(.span_div - 1 - i) - (1 / 2) * (theta(.span_div - i) + theta(.span_div - 1 - i)) '[deg] 左翼は負の値
'右翼
setting_angle(.span_div + i) = setting_angle0(.span_div + i) + (1 / 2) * (phi(.span_div + i) + phi(.span_div + 1 + i)) '[deg]
dihedral_angle(.span_div + i) = dihedral_angle0(.span_div + i) + (1 / 2) * (theta(.span_div + i) + theta(.span_div + 1 + i)) '[deg]
'左翼
y(.span_div - 1 - i) = y(.span_div - i) - .dy * Cos(-rad * dihedral_angle(.span_div - 1 - i))
z(.span_div - 1 - i) = z(.span_div - i) + .dy * Sin(-rad * dihedral_angle(.span_div - 1 - i))
'右翼
y(.span_div + 1 + i) = y(.span_div + i) + .dy * Cos(rad * dihedral_angle(.span_div + i))
z(.span_div + 1 + i) = z(.span_div + i) + .dy * Sin(rad * dihedral_angle(.span_div + i))
Next i
End With
End Sub翼の上反角はTR-797の実装のときと同じように,左翼では負の値になっていることに注意する
このプロシージャについては以上である
cpの計算
cpの座標を計算する
ただ平均をとるだけである
Sub calculation_cp(ByRef Wing As Specifications, ByRef state As variables, ByRef cp() As Double, ByRef y() As Double, ByRef z() As Double)
With Wing
'cpの計算
'左翼端が0,右翼端が2*span_div
For i = 0 To .span_div - 1
'cpの計算
'右翼
cp(0, .span_div + i) = 0
cp(1, .span_div + i) = (1 / 2) * (y(.span_div + i) + y(.span_div + i + 1))
cp(2, .span_div + i) = (1 / 2) * (z(.span_div + i) + z(.span_div + i + 1))
'左翼
cp(0, .span_div - 1 - i) = 0
cp(1, .span_div - 1 - i) = (1 / 2) * (y(.span_div - 1 - i) + y(.span_div - i))
cp(2, .span_div - 1 - i) = (1 / 2) * (z(.span_div - 1 - i) + z(.span_div - i))
Next i
End With
End Subこのプロシージャについては以上である
yp,zpの計算
yp,zpを計算する
基本的にはTR-797の実装のときと同じだが,今回のプログラムでは右翼と左翼のたわみなどは別々に計算するので,左翼のyp,zpを計算するときには左翼のy,zの値を使う
Sub calculation_ypzp(ByRef Wing As Specifications, ByRef state As variables, ByRef yp() As Double, ByRef zp() As Double, ByRef ymp() As Double, ByRef zmp() As Double, ByRef cp() As Double, ByRef dihedral_angle() As Double)
With Wing
'座標の計算
For j = 0 To 2 * .span_div - 1
For i = 0 To 2 * .span_div - 1
'オリジナルの計算
yp(i, j) = (cp(1, i) - cp(1, j)) * Cos(rad * dihedral_angle(j)) + (cp(2, i) - cp(2, j)) * Sin(rad * dihedral_angle(j))
zp(i, j) = -(cp(1, i) - cp(1, j)) * Sin(rad * dihedral_angle(j)) + (cp(2, i) - cp(2, j)) * Cos(rad * dihedral_angle(j))
'鏡像の計算
ymp(i, j) = (cp(1, i) - cp(1, j)) * Cos(-rad * dihedral_angle(j)) + (cp(2, i) - (-cp(2, j) - 2 * state.hE)) * Sin(-rad * dihedral_angle(j))
zmp(i, j) = -(cp(1, i) - cp(1, j)) * Sin(-rad * dihedral_angle(j)) + (cp(2, i) - (-cp(2, j) - 2 * state.hE)) * Cos(-rad * dihedral_angle(j))
Next i
Next j
End With
End Subこのプロシージャについては以上である
Rijの計算,Qijの計算
Rij,Qijを計算する
TR-797の実装のときと同じである
Sub calculation_Rij(ByRef Wing As Specifications, ByRef state As variables, ByVal ds As Double, ByRef yp() As Double, ByRef zp() As Double, ByRef ymp() As Double, ByRef zmp() As Double, ByRef Rpij() As Double, ByRef Rmij() As Double, ByRef Rpijm() As Double, ByRef Rmijm() As Double)
With Wing
'R+ij,R-ijの計算
For j = 0 To 2 * .span_div - 1
For i = 0 To 2 * .span_div - 1
'オリジナルの計算
Rpij(i, j) = Sqr((yp(i, j) - ds) * (yp(i, j) - ds) + zp(i, j) * zp(i, j))
Rmij(i, j) = Sqr((yp(i, j) + ds) * (yp(i, j) + ds) + zp(i, j) * zp(i, j))
'鏡像の計算
Rpijm(i, j) = Sqr((ymp(i, j) - ds) ^ 2 + zmp(i, j) ^ 2)
Rmijm(i, j) = Sqr((ymp(i, j) + ds) ^ 2 + zmp(i, j) ^ 2)
Next i
Next j
End With
End SubSub calculation_Qij(ByRef Wing As Specifications, ByRef state As variables, ByVal ds As Double, ByRef yp() As Double, ByRef zp() As Double, ByRef ymp() As Double, ByRef zmp() As Double, ByRef Rpij() As Double, ByRef Rmij() As Double, ByRef Rpijm() As Double, ByRef Rmijm() As Double, ByRef dihedral_angle() As Double, ByRef Qij() As Double)
With Wing
'Qijの計算
For j = 0 To 2 * .span_div - 1
For i = 0 To 2 * .span_div - 1
Qij(i, j) = (-((yp(i, j) - ds) / (Rpij(i, j) * Rpij(i, j))) + ((yp(i, j) + ds) / (Rmij(i, j) * Rmij(i, j)))) * Cos(rad * (dihedral_angle(i) - dihedral_angle(j))) + (-(zp(i, j) / (Rpij(i, j) * Rpij(i, j))) + (zp(i, j) / (Rmij(i, j) * Rmij(i, j)))) * Sin(rad * (dihedral_angle(i) - dihedral_angle(j))) + ((ymp(i, j) - ds) / (Rpijm(i, j) * Rpijm(i, j)) - (ymp(i, j) + ds) / (Rmijm(i, j) * Rmijm(i, j))) * Cos(rad * (dihedral_angle(i) + dihedral_angle(j))) + (zmp(i, j) / (Rpijm(i, j) * Rpijm(i, j)) - zmp(i, j) / (Rmijm(i, j) * Rmijm(i, j))) * Sin(rad * (dihedral_angle(i) + dihedral_angle(j)))
Next i
Next j
End With
End SubQijが計算できたので,循環分布がわかれば吹きおろし分布を計算できる
このプロシージャについては以上である
循環の更新
文献2の式(8)に従って循環分を更新する
\begin{eqnarray}
\Gamma_{input}=\Gamma_{old}+D(\Gamma_{new}-\Gamma_{old})
\tag{8}
\end{eqnarray}
ここで\(\Gamma_{input}\)は吹きおろしを計算するための循環分布,\(Gamma_{new}\)は新しく計算した循環分布,\(\Gamma_{old}\)は1つ前の循環分布,\(D\)はDampin factorで発散を防ぐための係数である
Sub update_circulation(ByRef Wing As Specifications, ByRef state As variables, ByVal iteration As Integer, ByVal coef As Double, ByRef circulation() As Double, ByRef circulation_old() As Double)
With Wing
'循環Γcの計算 @cp
For i = 0 To 2 * .span_div - 1
If iteration > 1 Then circulation(i) = circulation_old(i) + coef * (circulation(i) - circulation_old(i)) '循環Γcを更新
circulation_old(i) = circulation(i) '循環Γc_oldを更新
Next i
End With
End Sub繰り返し計算の最初(iteration=0)のときはまだ循環分布を計算していないためcirculationには何の値も入っていない
iteration=1のときはじめてcirculationに1回目の循環分布の値が入っており,circulation_oldにその値を格納できる
よって式(8)の方法で循環分布を更新できるのはcirculation_oldに1回目の循環分布が格納されているiteration=2のときであり,そのため場合分けを行っている
このプロシージャについては以上である
吹きおろしの計算
吹きおろし,誘導迎角,平均誘導迎角の計算を行う
Sub calculation_downwash(ByRef Wing As Specifications, ByRef state As variables, ByRef circulation() As Double, ByRef Qij() As Double, ByRef alpha_induced() As Double, ByRef cp() As Double, ByRef wi() As Double)
With Wing
'吹きおろしwi,誘導迎角αiの計算 @cp
ReDim wi(2 * .span_div - 1) '吹きおろし速度 [m/s]
.epsilon = 0
For i = 0 To 2 * .span_div - 1
For j = 0 To 2 * .span_div - 1
wi(i) = wi(i) + (1 / (4 * pi)) * Qij(i, j) * circulation(j)
Next j
'誘導迎角の計算
alpha_induced(i) = deg * Atn(wi(i) / (state.Vair - rad * state.r * cp(1, i)))
.epsilon = .epsilon + alpha_induced(i)
Next i
.epsilon = .epsilon / (2 * .span_div - 1) '主翼位置での平均吹きおろし角
End With
End Subこのプロシージャについては以上である
有効迎角の計算
ここからは循環分布を計算するために必要な値を順次計算していく
まず,有効迎角の計算を行う
特に意味はないが機体がロールしたときや横滑りを起こしたときの解析もできるようにしておく
各cpにおける有効迎角は次のように計算できる
\begin{eqnarray}
(有効迎角) &= & (全機迎角)+(取り付け角)-(誘導迎角)+(ロールによる影響)+(横滑りによる影響)
\end{eqnarray}
文献3によると,対気速度\(V\),横滑り角\(\beta\)で運動しているとき,上反角\(\Gamma_{dihedral_{i}}\)のcpに生じている吹き上げは次の式で表される
\begin{eqnarray}
V\sin{\beta}\sin({\Gamma_{dihedral_{i}}})
\tag{4.64'}
\end{eqnarray}
同じく,ロール角速度\(p\)で運動しているとき,スパン方向位置\(y_{i}\)にあるcpに生じている吹き上げは次の式で表される
\begin{eqnarray}
p y_{i}
\tag{4.74'}
\end{eqnarray}
また,ヨー角速度\(r\)で運動しているとき,スパン方向位置\(y_{i}\)にあるcpにおける対気速度は次の式で表される
\begin{eqnarray}
V-r y_{i}
\tag{4.92'}
\end{eqnarray}
よって,i番目のcpの有効迎角は次の式で計算できる
\begin{eqnarray}
\alpha_{effective}=\alpha+\alpha_{setting}-\alpha_{induced}
+\frac{V\sin{\beta}\sin({\Gamma_{dihedral_{i}}})}{V-r y_{i}}
+\frac{p y_{i}}{V-r y_{i}}
\end{eqnarray}
Sub calculation_alpha_effective(ByRef Wing As Specifications, ByRef state As variables, ByRef alpha_effective() As Double, ByRef alpha_induced() As Double, ByRef cp() As Double, ByRef dihedral_angle() As Double, ByRef setting_angle() As Double, ByRef alpha_max As Double, ByRef alpha_min As Double)
With Wing
'局所迎角α(誘導迎角は含まないの計算 @cp
'左翼端が0,右翼端が2*span_div
For i = 0 To .span_div - 1
'局所迎角 [deg]=全機迎角+取り付け角+誘導迎角+ロール角速度pによる影響を追加+横滑りによる影響を追加
'左翼の有効迎角の計算
num1 = .span_div - 1 - i
alpha_effective(num1) = state.alpha + setting_angle(num1) - alpha_induced(num1) + deg * Atn((rad * state.p * cp(1, num1)) / (state.Vair - rad * state.r * cp(1, num1))) + deg * Atn(state.Vair * Sin(rad * state.beta) * Sin(rad * dihedral_angle(num1)) / (state.Vair - rad * state.r * cp(1, num1)))
'右翼の有効迎角の計算
num2 = .span_div + i
alpha_effective(num2) = state.alpha + setting_angle(num2) - alpha_induced(num2) + deg * Atn((rad * state.p * cp(1, num2)) / (state.Vair - rad * state.r * cp(1, num2))) + deg * Atn(state.Vair * Sin(rad * state.beta) * Sin(rad * dihedral_angle(num2)) / (state.Vair - rad * state.r * cp(1, num2)))
Next i
For i = 0 To 2 * .span_div - 1
'計算が発散しないようにalphaを制限する.
If alpha_effective(i) > alpha_max Then alpha_effective(i) = alpha_max
If alpha_effective(i) < alpha_min Then alpha_effective(i) = alpha_min
Next i
End With
End Subすべての有効迎角を計算した後に,XFLR5であらかじめ計算した範囲をはみ出た迎角にたいして処理を行っている
このプロシージャについては以上である
Re数の計算
Re数の計算を行う
Sub calculation_Re(ByRef Wing As Specifications, ByRef state As variables, ByRef Re() As Double, ByRef cp() As Double, ByRef chord_cp() As Double, ByRef Re_max As Double, ByRef Re_min As Double)
With Wing
'Reの計算 @cp
'左翼端が0,右翼端が2*span_div
For i = 0 To 2 * .span_div - 1
Re(i) = ((state.Vair - rad * state.r * cp(1, i)) * chord_cp(i)) / state.mu 'レイノルズ数の計算
Next i
For i = 0 To 2 * .span_div - 1
'計算が発散しないようにRe数を制限する.
If Re(i) > Re_max Then Re(i) = Re_max
If Re(i) < Re_min Then Re(i) = Re_min
Next i
End With
End Subこのプロシージャについては以上である
空力係数の計算を行う
局所揚力係数をはじめとした空力係数,および局所揚力などの空気力を計算する
すでに翼型解析②:解析データを最小二乗法で多項式近似するで,二次元翼の空力係数を迎角,Re数の任意の次数の多項式で表したときの係数を求めてあるので,局所揚力係数\(C_{l}\),局所抗力係数\(C_{d_{p}}\),局所ピッチングモーメント係数\(C_{m_{ac}}\)は容易に計算できる
空力中心周り\(h_{ac}\)のピッチングモーメント係数\(C_{m_{ac}}\)と桁位置\(h_{spar}\)周りのピッチングモーメント係数\(C_{m_{cg}}\)の関係は次の式で表される
\begin{eqnarray}
Cm_{cg}=Cm_{ac}+C_{l}(h_{spar}-h_{ac})
\end{eqnarray}
さらにそこから各cpにはたらく空気力も次のように計算できる
\begin{eqnarray}
\Delta L_{i} &=& \frac{1}{2}\rho V^2 \Delta S_{i} C_{l_{i}} \\
\Delta D_{p_{i}} &=& \frac{1}{2}\rho V^2 \Delta S_{i} C_{d_{p_{i}}} \\
\Delta M_{ac_{i}} &=& \frac{1}{2}\rho V^2 \Delta S_{i} c_{i} C_{m_{ac_{i}}} \\
\Delta M_{cg_{i}} &=& \frac{1}{2}\rho V^2 \Delta S_{i} c_{i} C_{m_{cg_{i}}} \\
\Delta S_{i} &=& c_{cp_{i}} dy\cos({\Gamma_{dihedral_{i}}})
\end{eqnarray}
また,文献1のp.40にならって,空気力を構造軸(n-t軸)へ投影する
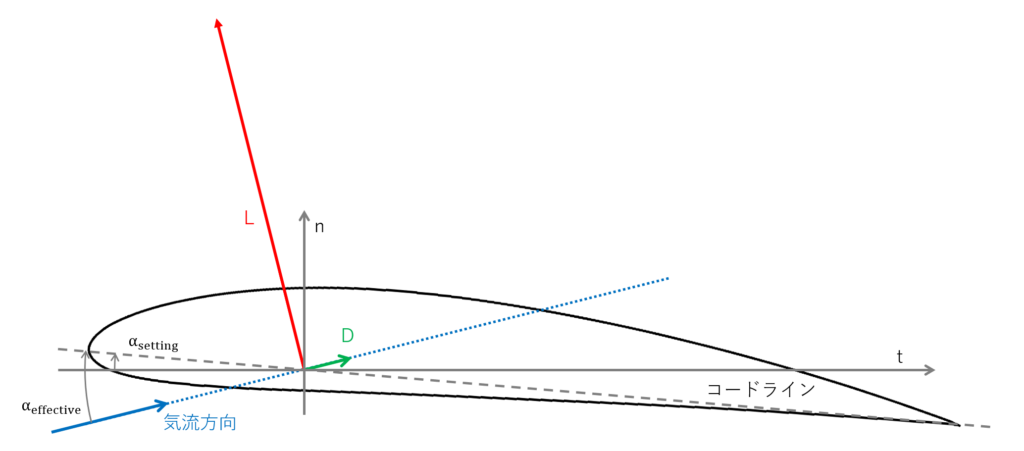
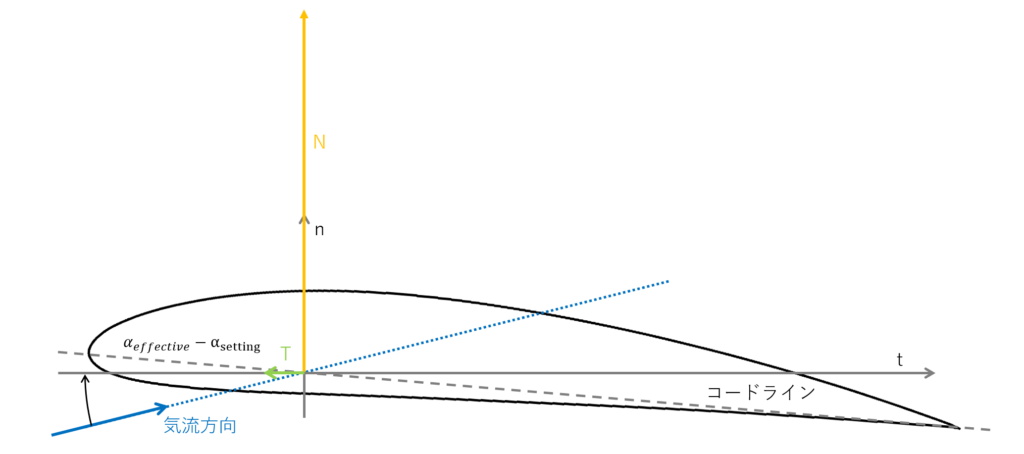
図より,空気力のN軸方向成分,T軸方向成分はそれぞれ次の式で表される
\begin{eqnarray}
N &=& L\cos{(\alpha_{effective}-\alpha_{setting})}+D_{p}\sin{(\alpha_{effective}-\alpha_{setting})} \\
T &=& -L\sin{(\alpha_{effective}-\alpha_{setting})}+D_{p}\cos{(\alpha_{effective}-\alpha_{setting})} \\
\tag{文献1,p.40}
\end{eqnarray}
Sub calculation_aerodynamic_coefficient(ByRef Wing As Specifications, ByRef state As variables, ByRef CL() As Double, ByRef Cdp() As Double, ByRef Cm_ac() As Double, ByRef a0() As Double, ByRef a1() As Double, ByRef Cda() As Double, ByRef Cm_cg() As Double, ByRef dN() As Double, ByRef dT() As Double, ByRef dL() As Double, ByRef dDp() As Double, ByRef dM_cg() As Double, ByRef dM_ac() As Double, ByRef cp() As Double, ByRef chord_cp() As Double, ByRef setting_angle() As Double, ByRef alpha_effective() As Double, ByRef Re() As Double, ByRef dihedral_angle() As Double, ByRef foil_mixture() As Double, ByRef Cl_coef() As Double, ByRef Cdp_coef() As Double, ByRef Cm_coef() As Double)
'Cd,Cm,dS,dL,dTの計算 @cp
ReDim CL(2 * Wing.span_div - 1) '局所揚力係数 @cp
ReDim Cdp(2 * Wing.span_div - 1) '局所有害抗力係数 @cp
ReDim Cm_ac(2 * Wing.span_div - 1) '局所ピッチングモーメント係数 @cp
For i = 0 To 2 * Wing.span_div - 1
a0(i) = foil_mixture(i, 0) * Cl_coef(0, 0) + foil_mixture(i, 1) * Cl_coef(0, 1) '迎角0度のときの揚力係数
a1(i) = foil_mixture(i, 0) * Cl_coef(1, 0) + foil_mixture(i, 1) * Cl_coef(1, 1) '断面揚力傾斜の計算 [1/deg]
Cda(i) = foil_mixture(i, 0) * Cdp_coef(1, 0) + foil_mixture(i, 1) * Cdp_coef(1, 1) '断面抗力傾斜の計算 [1/deg]
For j = 0 To 8
tmp = alpha_effective(i) ^ j
CL(i) = CL(i) + foil_mixture(i, 0) * Cl_coef(j, 0) * tmp + foil_mixture(i, 1) * Cl_coef(j, 1) * tmp
Cdp(i) = Cdp(i) + foil_mixture(i, 0) * Cdp_coef(j, 0) * tmp + foil_mixture(i, 1) * Cdp_coef(j, 1) * tmp
Cm_ac(i) = Cm_ac(i) + foil_mixture(i, 0) * Cm_coef(j, 0) * tmp + foil_mixture(i, 1) * Cm_coef(j, 1) * tmp
Next j
For j = 9 To 14
tmp = Re(i) ^ (j - 8)
CL(i) = CL(i) + foil_mixture(i, 0) * Cl_coef(j, 0) * tmp + foil_mixture(i, 1) * Cl_coef(j, 1) * tmp
Cdp(i) = Cdp(i) + foil_mixture(i, 0) * Cdp_coef(j, 0) * tmp + foil_mixture(i, 1) * Cdp_coef(j, 1) * tmp
Cm_ac(i) = Cm_ac(i) + foil_mixture(i, 0) * Cm_coef(j, 0) * tmp + foil_mixture(i, 1) * Cm_coef(j, 1) * tmp
Cda(i) = Cda(i) + foil_mixture(i, 0) * Cdp_coef(j, 0) * tmp + foil_mixture(i, 1) * Cdp_coef(j, 1) * tmp '断面抗力傾斜の計算 [1/deg]
Next j
Cm_cg(i) = Cm_ac(i) + CL(i) * (Wing.hspar - Wing.hac) 'ピッチングモーメントを空力中心回りから桁位置まわりに変換
'機体にはたらく空気力を計算
tmp = chord_cp(i) * Wing.dy * Cos(rad * dihedral_angle(i)) '翼素面積
Wing.dynamic_pressure = 0.5 * state.rho * (state.Vair - rad * state.r * cp(1, i)) ^ 2 '動圧
dL(i) = Wing.dynamic_pressure * tmp * CL(i) '翼素揚力
dDp(i) = Wing.dynamic_pressure * tmp * Cdp(i) '翼素抗力
dM_cg(i) = Wing.dynamic_pressure * tmp * chord_cp(i) * Cm_cg(i) '桁位置まわりの翼素ピッチングモーメント
dM_ac(i) = Wing.dynamic_pressure * tmp * chord_cp(i) * Cm_ac(i) '空力中心まわりの翼素ピッチングモーメント
'空気力を機体軸に対して分解
sum = rad * (alpha_effective(i) - setting_angle(i))
dN(i) = Wing.dynamic_pressure * tmp * (CL(i) * Cos(sum) - Cdp(i) * Sin(sum)) '機体上方を正
dT(i) = Wing.dynamic_pressure * tmp * (-CL(i) * Sin(sum) + Cdp(i) * Cos(sum)) '機体後方を正
Next i
End Subこのプロシージャについては以上である
空気力を計算する
循環分布,揚力,誘導抗力を計算する
循環\(\Gamma\),揚力\(L\),誘導抗力\(D_{i}\)はそれぞれ次のように計算できる
\begin{eqnarray}
\Gamma_{i} &=& \frac{1}{2}c_{i} V_{i} C_{l_{i}} \\
L &=& \sum \rho V_{i}\Gamma_{i}\Delta y\cos{(\Gamma_{dihedral_{i}})} \\
D_{i} &=& \sum \rho w_{i_{i}} \Gamma_{i} \Delta y \\
\end{eqnarray}
Sub calculation_Force(ByRef Wing As Specifications, ByRef state As variables, ByVal iteration As Double, ByRef Lift() As Double, ByRef Induced_Drag() As Double, ByRef cp() As Double, ByRef circulation() As Double, ByRef dihedral_angle() As Double, ByRef wi() As Double, ByRef CL() As Double, ByRef chord_cp() As Double)
'揚力,誘導抗力,循環の計算
For i = 0 To 2 * Wing.span_div - 1
circulation(i) = 0.5 * chord_cp(i) * (state.Vair - rad * state.r * cp(1, i)) * CL(i)
Lift(iteration) = Lift(iteration) + state.rho * (state.Vair - rad * state.r * cp(1, i)) * circulation(i) * Wing.dy * Cos(rad * dihedral_angle(i))
Induced_Drag(iteration) = Induced_Drag(iteration) + state.rho * wi(i) * circulation(i) * Wing.dy
Next i
End Subこれで循環分布を計算できた
このプロシージャについては以上である
曲げモーメントを計算する
最後に翼の変形量を求めるのに必要な値を順次計算していく
まず,翼にはたらく曲げモーメント,剪断力,トルクを計算する
これらの値がパネルの両端(sp)で定義される量であることに注意すると,i番目(左翼)のspにおける曲げモーメント\(M_{bending_{i}}\),剪断力\(F_{i}\),トルク\(M_{torque_{i}}\)は次のように計算できる
\begin{eqnarray}
M_{bending_{i}} &=& \sum_{j=1}^i ((\Delta N_{j-1}\cos{(\Gamma_{dihedral_{j-1}})}-\Delta W_{i})\times|y_{cp_{j-1}}-y_{i}|+\Delta N_{j-1}\sin{(\Gamma_{dihedral_{j-1}})}\times|z_{cp_{j-1}}-z_{i}|) \\
F_{i} &=& \sum_{j=1}^i (\Delta N_{j-1}\cos{(\Gamma_{dihedral_{j-1}})}-\Delta W_{i}) \\
M_{torque_{i}} &=& \sum_{j=1}^i (\Delta M_{torque_{j-1}}+\Delta T \times|z_{cp_{j-1}}-z_{i}|) \\
\end{eqnarray}
ここで,トルク計算の右辺第二項の\(\Delta T \times|z_{cp_{j-1}}-z_{i}|\)は,上反角が大きい機体における空気力のx軸方向成分とパネル同士のZ方向距離によるトルクである
XFLR5 Guidelinesのp.26にある次の記述
The only use for the sweep and thedihedral in this implementation of the LLT is for the calculation of the pitching moment coefficient Cm.
XFLR5 v6.02 Guidelines page26
(後退角および上反角はCmの計算にしか使わない) とはこのことである
Sub calculation_Moment(ByRef Wing As Specifications, ByRef state As variables, ByRef Bending_Moment() As Double, ByRef Bending_Moment_T() As Double, ByRef Shear_Force() As Double, ByRef Torque() As Double, ByRef dN() As Double, ByRef dT() As Double, ByRef dM_cg() As Double, ByRef dW() As Double, ByRef dihedral_angle() As Double, ByRef cp() As Double, ByRef y() As Double, ByRef z() As Double)
'曲げモーメント,ねじりモーメントを計算
ReDim Bending_Moment(2 * Wing.span_div) '曲げモーメント [N*m]
ReDim Bending_Moment_T(2 * Wing.span_div) '曲げモーメント [N*m]
ReDim Shear_Force(2 * Wing.span_div) 'せん断力
ReDim Torque(2 * Wing.span_div) 'トルク [N*m]
For i = 1 To Wing.span_div '翼端から翼根に向けてspのループ
For j = 1 To i '翼端からi番目の要素に向けてcpのループ
num1 = 2 * Wing.span_div - i: num2 = 2 * Wing.span_div - j
'上反角を考慮して曲げモーメントを計算.j>i.num1<num2
Bending_Moment(i) = Bending_Moment(i) + (dN(j - 1) * Cos(rad * dihedral_angle(j - 1)) - dW(j - 1)) * Abs(cp(1, j - 1) - y(i)) + dN(j - 1) * Sin(Abs(rad * dihedral_angle(j - 1))) * Abs(cp(2, j - 1) - z(i)) '左翼
Bending_Moment(num1) = Bending_Moment(num1) + (dN(num2) * Cos(rad * dihedral_angle(num2)) - dW(num2)) * Abs(cp(1, num2) - y(num1)) + dN(num2) * Sin(Abs(rad * dihedral_angle(num2))) * Abs(cp(2, num2) - z(num1)) '右翼
'T曲げモーメント.右にヨーイングする方向を正.
Bending_Moment_T(i) = Bending_Moment_T(i) + dT(j - 1) * Abs(cp(1, j - 1) - y(i)) '左翼
Bending_Moment_T(num1) = Bending_Moment_T(num1) + dT(num2) * Abs(cp(1, num2) - y(num1)) '右翼
Torque(i) = Torque(i) + dM_cg(j - 1) + dT(j - 1) * (cp(2, j - 1) - z(i)) '左翼
Torque(num1) = Torque(num1) + dM_cg(num2) + dT(num2) * (cp(2, num2) - z(num1)) '右翼
'剪断力
Shear_Force(i) = Shear_Force(i) + (dN(j - 1) * Cos(rad * dihedral_angle(j - 1)) - dW(j - 1)) '左翼
Shear_Force(num1) = Shear_Force(num1) + (dN(num2) * Cos(rad * dihedral_angle(num2)) - dW(num2)) '右翼
Next j
Next i
Bending_Moment(Wing.span_div) = 0.5 * Bending_Moment(Wing.span_div)
Bending_Moment_T(Wing.span_div) = 0.5 * Bending_Moment_T(Wing.span_div)
Torque(Wing.span_div) = 0.5 * Torque(Wing.span_div)
Shear_Force(Wing.span_div) = 0.5 * Shear_Force(Wing.span_div)
End Subこの計算方法だと翼中心の値が2倍になってしまうので,ループの外でその値を半分にする処理を行っている
このプロシージャについては以上である
たわみ,ねじれの計算
たわみ角,たわみ,ねじれ角の計算を行う
たわみ角\(\theta\),たわみ\(w\),ねじれ角\(\phi\)は次の式で計算できる
\begin{eqnarray}
\theta &=& \int \frac{M}{EI} dy \\
w &=& \int \theta dy \\
\phi &=& \int \frac{M_{torque}}{GJ} dy \\
\end{eqnarray}
Sub calculation_deflection(ByRef Wing As Specifications, ByRef state As variables, ByRef deflection() As Double, ByRef theta() As Double, ByRef phi() As Double, ByRef Bending_Moment() As Double, ByRef Torque() As Double, ByRef Eix() As Double, ByRef GJ() As Double)
Dim pi As Double: pi = 4 * Atn(1) '円周率
Dim rad As Double: rad = (pi / 180) 'degからradへの変換
Dim deg As Double: deg = (180 / pi) 'radからdegへの変換
'w,θ,Φの計算 @sp
'左翼端が0,右翼端が2*span_div
ReDim deflection(2 * Wing.span_div) 'たわみ [m]
ReDim theta(2 * Wing.span_div) 'たわみ角 [deg]
ReDim phi(2 * Wing.span_div) 'ねじれ角 [deg]
For i = 0 To Wing.span_div - 1 '翼中心から翼端へのループ
num1 = Wing.span_div - 1 - i
num2 = Wing.span_div + i
'たわみ角
theta(num1) = theta(num1 + 1) + (Bending_Moment(num1) / Eix(num1)) * Wing.dy '左翼
theta(num2 + 1) = theta(num2) + (Bending_Moment(num2 + 1) / Eix(num2)) * Wing.dy '右翼
'たわみ
deflection(num1) = deflection(num1 + 1) + theta(num1 + 1) * Wing.dy '左翼
deflection(num2 + 1) = deflection(num2) + theta(num2) * Wing.dy '右翼
'ねじれ角
phi(num1) = phi(num1 + 1) + (Torque(num1) * Wing.dy) / GJ(num1) '左翼
phi(num2 + 1) = phi(num2) + (Torque(num2 + 1) * Wing.dy) / GJ(num2) '右翼
Next i
'Φを[rad]から[deg]に変換
For i = 0 To 2 * Wing.span_div - 1
theta(i) = deg * theta(i) '[deg]への変換
phi(i) = deg * phi(i) '[deg]への変換
Next i
End Subこれで翼の変形量を計算できた
このプロシージャについては以上である
収束判定
ループ内の処理の最後に収束判定を行う
繰り返し計算の揚力の変化量があらかじめ指定した閾値を下回ったとき判定とみなす
'収束判定
If iteration > 0 Then
If error > Abs((Lift(iteration) - Lift(iteration - 1)) / Lift(iteration - 1)) Then Exit For
End Ifこれでループ内の処理は終了である
構造体へ格納
もろもろの値を計算して構造体へ格納する
\begin{eqnarray}
\Delta S_{i} &=& c_{cp_{i}}dy\cos{(\Gamma_{dihedral_{i}})} \\
S &=& \sum_{i=0}^{2n-1} \Delta S_{i} \\
\overline{c} &=& \frac{2}{S}\sum_{i=0}^{n-1} c_{i}^2 \Delta y \cos{(\Gamma_{dihedral_{i}})}
\tag{文献3(2.52)} \\
\overline{y} &=& \frac{2}{S}\sum_{i=0}^{n-1} c_{i}y_{i} \Delta y \cos{(\Gamma_{dihedral_{i}})}
\tag{文献3(2.54)} \\
AR &=& \frac{b^2}{S}
\tag{文献3(2.40)} \\
C_{l_{\alpha}} &=& \frac{\partial}{\partial\alpha}(\frac{\sum_{i=0}^{2n-1}\frac{1}{2}\rho V^2 \Delta S C_{l_{i}}}{\frac{1}{2}\rho V^2 S}) \\
&=& \frac{\sum_{i=0}^{2n-1} C_{l_{\alpha_{i}}} \Delta S_{i}}{S} \\
D_{p} &=& \sum_{i=0}^{2n-1} \Delta D_{p_{i}} \\
L &=& -\sum_{i=0}^{2n-1} dN_{i}\cos{(\Gamma_{dihedral_{i}})}\times y_{cp_{i}} \\
M_{ac} &=& \sum_{i=0}^{2n-1} \Delta M_{ac_{i}}+dT_{i}\times z_{cp_{i}} \\
M_{cg} &=& M_{ac}+L_{wing}\times(h_{spar}-h_{ac}-\Delta h) \\
N &=& \sum_{i=0}^{2n-1} dT_{i}\times y_{cp_{i}} \\
D &=& D_{i}+D_{p} \\
C_{L} &=& \frac{L}{\frac{1}{2}\rho V^2 S} \\
C_{D_{p}} &=& \frac{D_{p}}{\frac{1}{2}\rho V^2 S} \\
C_{D_{i}} &=& \frac{D_{i}}{\frac{1}{2}\rho V^2 S} \\
C_{D} &=& \frac{D}{\frac{1}{2}\rho V^2 S} \\
C_{m_{ac}} &=& \frac{M_{ac}}{\frac{1}{2}\rho V^2 S} \\
C_{m_{cg}} &=& \frac{M_{cg}}{\frac{1}{2}\rho V^2 S} \\
e &=& \frac{\frac{C_{L}^2}{\pi AR}}{C_{D_{i}}} \\
a_{w} &=& \frac{C_{l_{\alpha_{i}}}}{1+\frac{C_{l_{\alpha}}}{\pi AR}} \\
\end{eqnarray}
Sub input_data_to_type(ByRef Wing As Specifications, ByRef state As variables, ByRef iteration As Integer, ByRef dihedral_angle() As Double, ByRef chord_cp() As Double, ByRef y() As Double, ByRef cp() As Double, _
ByRef a0() As Double, ByRef a1() As Double, ByRef Cda() As Double, ByRef dDp() As Double, ByRef dN() As Double, ByRef dT() As Double, ByRef dM_ac() As Double, _
ByRef CL() As Double, ByRef Cdp() As Double, ByRef Lift() As Double, ByRef Induced_Drag() As Double)
Dim pi As Double: pi = 4 * Atn(1) '円周率
Dim rad As Double: rad = (pi / 180) 'degからradへの変換
Dim deg As Double: deg = (180 / pi) 'radからdegへの変換
Dim sinG As Double
Dim cosG As Double
Dim ycp As Double
Dim cdy As Double
'構造体に値を格納
With Wing
'chord_cp,dS,Sの計算
.S = 0
For i = 0 To 2 * .span_div - 1
.S = .S + chord_cp(i) * .dy * cos(rad * dihedral_angle(i)) '台形として計算.(上底+下底)×高さ÷2.スパーに沿った面積.xy平面への投影ではない.
Next i
'平均空力翼弦chord_mac
.chord_mac = 0
For i = 0 To .span_div - 1 '左翼のみで計算
.chord_mac = .chord_mac + chord_cp(i) * chord_cp(i) * .dy * cos(rad * dihedral_angle(i))
Next i
.chord_mac = (2 / .S) * .chord_mac
'片翼面積中心 [m]
.y_ = 0
For i = .span_div To 2 * .span_div - 1
.y_ = .y_ + chord_cp(i) * cp(1, i) * .dy * cos(rad * dihedral_angle(i))
Next i
.y_ = (2 / .S) * .y_
'翼面積,スパン,アスペクト比の計算
.b = 2 * y(2 * .span_div)
.AR = (.b * .b) / .S
'Cl,Cm,dDp,dT,a0,二次元揚力傾斜Cla[1/deg]の計算の計算 @cp
'翼中心が0.翼端がspan_divisions
.Cla = 0
For i = 0 To 2 * .span_div - 1
cdy = chord_cp(i) * .dy * cos(rad * dihedral_angle(i)) '有効翼素面積(xy平面への投影)
.Cla = .Cla + (a1(i) * cdy) / .S '二次元揚力傾斜 [1/deg]
Next i
'揚力L,誘導抗力Di,翼面積S,ローリングモーメントLの計算
'翼中心が0.翼端がspan_divisions
.Drag_parasite = 0: .L_roll = 0: .M_pitch = 0: .N_yaw = 0
For i = 0 To 2 * .span_div - 1
.Drag_parasite = .Drag_parasite + dDp(i)
.L_roll = .L_roll - dN(i) * cos(rad * dihedral_angle(i)) * cp(1, i) 'L [N*m]
.M_pitch = .M_pitch + dM_ac(i) + dT(i) * cp(2, i) 'M[N*m] 空力中心周り
.N_yaw = .N_yaw + dT(i) * cp(1, i) 'N [N*m]
Next i
.Lift = Lift(iteration)
.Drag_induced = Induced_Drag(iteration)
.Drag = .Drag_induced + .Drag_parasite
'翼効率e,揚力係数CL,誘導抗力係数CDi,三次元揚力傾斜 [1/deg]の計算
.CL = .Lift / (.dynamic_pressure * .S)
.Cdp = .Drag_parasite / (.dynamic_pressure * .S)
.CDi = .Drag_induced / (.dynamic_pressure * .S)
.CD = .Drag / (.dynamic_pressure * .S)
.Cm_ac = .M_pitch / (.dynamic_pressure * .S * .chord_mac) '空力中心周り
.e = ((.CL * .CL) / (pi * .AR)) / .CDi
.aw = rad * (deg * .Cla) / (1 + ((deg * .Cla) / (pi * .AR))) '[1/deg]
.M_pitch = .M_pitch + .Lift * .chord_mac * (.hspar - .hac - state.dh) '重心位置周り
.Cm_cg = .M_pitch / (.dynamic_pressure * .S * .chord_mac) '重心位置周り
'横・方向の安定微係数の計算
.Cyb = 0: .Cyp = 0: .Cyr = 0: .Clb = 0: .Clp = 0: .Clr = 0: .Cnb = 0: .Cnp = 0: .Cnr = 0
For i = .span_div To 2 * .span_div - 1 '右翼で計算して2倍
cdy = chord_cp(i) * .dy '翼素面積
sinG = sin(rad * dihedral_angle(i))
cosG = cos(rad * dihedral_angle(i))
ycp = cp(1, span_divisions + i)
zcp = cp(2, span_divisions + i)
Cx = CL(i) * sin(rad * state.alpha) - Cdp(i) * cos(rad * state.alpha)
Cxa = a1(i) * (1 / rad) * sin(rad * state.alpha) + CL(i) * cos(rad * state.alpha) - 0 * (1 / rad) * cos(rad * state.alpha) + Cdp(i) * sin(rad * state.alpha) '[1/rad]
.Cyb = .Cyb - (2 / .S) * a1(i) * sinG * sinG * cdy '[1/deg]
.Cyp = .Cyp - (4 / (.S * .b)) * a1(i) * (1 / rad) * sinG * cosG * ycp * cdy '[1/rad]
.Cyr = .Cyr + (8 / (.S * .b)) * CL(i) * sinG * ycp * cdy '[1/rad]
.Clb = .Clb - (2 / (.S * .b)) * a1(i) * sinG * (cosG * ycp + sinG * zcp) * cdy '[1/deg]
.Clp = .Clp - (4 / (.S * .b * .b)) * a1(i) * (1 / rad) * ycp * cosG * (cosG * ycp + sinG * zcp) * cdy '[1/rad]
.Clr = .Clr + (8 / (.S * .b * .b)) * CL(i) * ycp * (cosG * ycp + sinG * zcp) * cdy '[1/rad]
.Cnb = .Cnb - (2 / (.S * .b)) * Cxa * sinG * ycp * cdy * rad '[1/deg]
.Cnp = .Cnp - (4 / (.S * .b * .b)) * Cxa * ycp * ycp * cosG * cdy '[1/rad]
.Cnr = .Cnr + (8 / (.S * .b * .b)) * Cx * ycp * ycp * cdy '[1/rad]
Next i
End With
End Sub横・方向の安定微係数については次の記事を参照
このプロシージャについては以上である
値を返す
関数に値を返す
VLM_wing = Wing結果の表示
結果をシートに表示する
If p = 1 Then
sht1.Range("AS2") = iteration
Call output_data_to_sheet(Wing, alpha_effective, Re, CL, Cdp, Cm_ac, a0, Cda, Cm_cg, setting_angle, dihedral_angle, circulation, wi, alpha_induced, y, z, deflection, theta, phi, Shear_Force, Bending_Moment, Torque, Bending_Moment_T)
End Ifできる限り配列に格納してまとめて貼り付ける
Sub output_data_to_sheet(ByRef Wing As Specifications, ByRef alpha_effective() As Double, ByRef Re() As Double, ByRef CL() As Double, ByRef Cdp() As Double, ByRef Cm_ac() As Double, ByRef a0() As Double, ByRef Cda() As Double, ByRef Cm_cg() As Double, _
ByRef setting_angle() As Double, ByRef dihedral_angle() As Double, ByRef circulation() As Double, ByRef wi() As Double, ByRef alpha_induced() As Double, _
ByRef y() As Double, ByRef z() As Double, ByRef deflection() As Double, ByRef theta() As Double, ByRef phi() As Double, _
ByRef Shear_Force() As Double, ByRef Bending_Moment() As Double, ByRef Torque() As Double, ByRef Bending_Moment_T() As Double)
With Wing
'結果の出力
'吹きおろし,循環分布
ReDim output(.span_div, 19)
For i = 0 To .span_div - 1 '右翼
num = .span_div + i
output(i, 0) = alpha_effective(num)
output(i, 1) = Re(num)
output(i, 2) = CL(num)
output(i, 3) = Cdp(num)
output(i, 4) = Cm_ac(num)
output(i, 5) = a0(num)
output(i, 6) = Cda(num)
output(i, 7) = Cm_cg(num)
output(i, 10) = y(num) - y(num - 1)
output(i, 11) = setting_angle(num)
output(i, 12) = dihedral_angle(num)
output(i, 16) = sht1.Cells(45 + i, 36)
output(i, 17) = circulation(num)
output(i, 18) = wi(num)
output(i, 19) = alpha_induced(num)
Next i
For i = 0 To .span_div '右翼
num = .span_div + i
output(i, 8) = y(num)
output(i, 9) = z(num)
output(i, 13) = deflection(num)
output(i, 14) = theta(num)
output(i, 15) = phi(num)
Next i
sht1.Range(sht1.Cells(45, 20), sht1.Cells(45 + .span_div, 39)) = output
ReDim output(.span_div, 3)
For i = 0 To .span_div
num = .span_div + i
output(i, 0) = Shear_Force(num)
output(i, 1) = Bending_Moment(num)
output(i, 2) = Torque(num)
output(i, 3) = Bending_Moment_T(num)
Next i
sht2.Range(sht2.Cells(45, 18), sht2.Cells(45 + .span_div, 21)) = output
ReDim output(28, 0)
output(0, 0) = .S
output(1, 0) = .b
output(2, 0) = .AR
output(3, 0) = .chord_mac
output(4, 0) = .y_
output(5, 0) = .e
output(6, 0) = .Cla
output(7, 0) = .aw
output(8, 0) = .CL
output(9, 0) = .Cdp
output(10, 0) = .CDi
output(11, 0) = .CD
output(12, 0) = .Cyb
output(13, 0) = .Clb
output(14, 0) = .Clp
output(15, 0) = .Cnp
output(16, 0) = .Clr
output(17, 0) = .Cnr
output(18, 0) = .epsilon
output(19, 0) = .Lift
output(20, 0) = .Drag_parasite
output(21, 0) = .Drag_induced
output(22, 0) = .Drag
output(23, 0) = .L_roll
output(24, 0) = .M_pitch
output(25, 0) = .N_yaw
output(26, 0) = .Cyp
output(27, 0) = .Cyr
output(28, 0) = .Cnb
sht1.Range("AR7:AR35") = output
sht1.Range("D20") = .Cm_ac
End With
End Sub
これでプログラムについての解説は終了である
プログラムの実行
それでは実際にプログラムを実行してみる
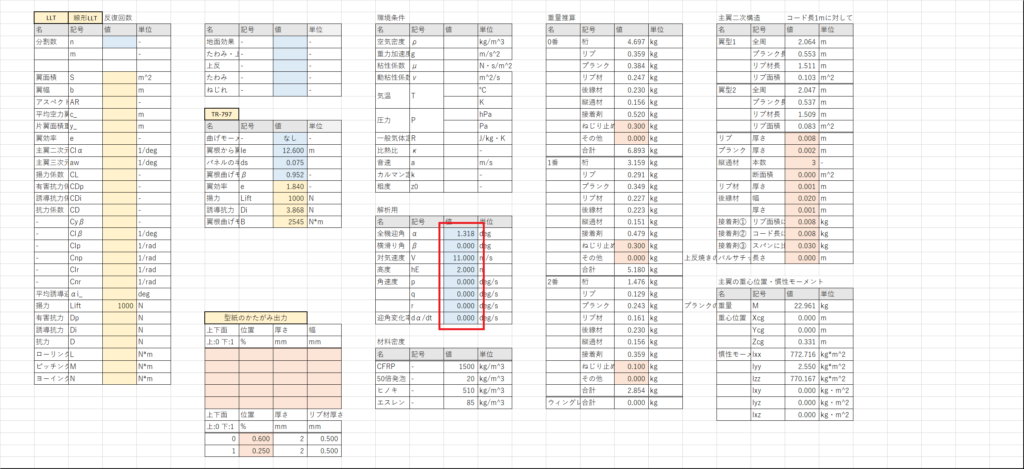
テンプレートファイルの下準備
前回(≫TR-797の実装)の続きからやりたい人は,まず主翼のシートのBB20:BB27に,解析の条件を入力する
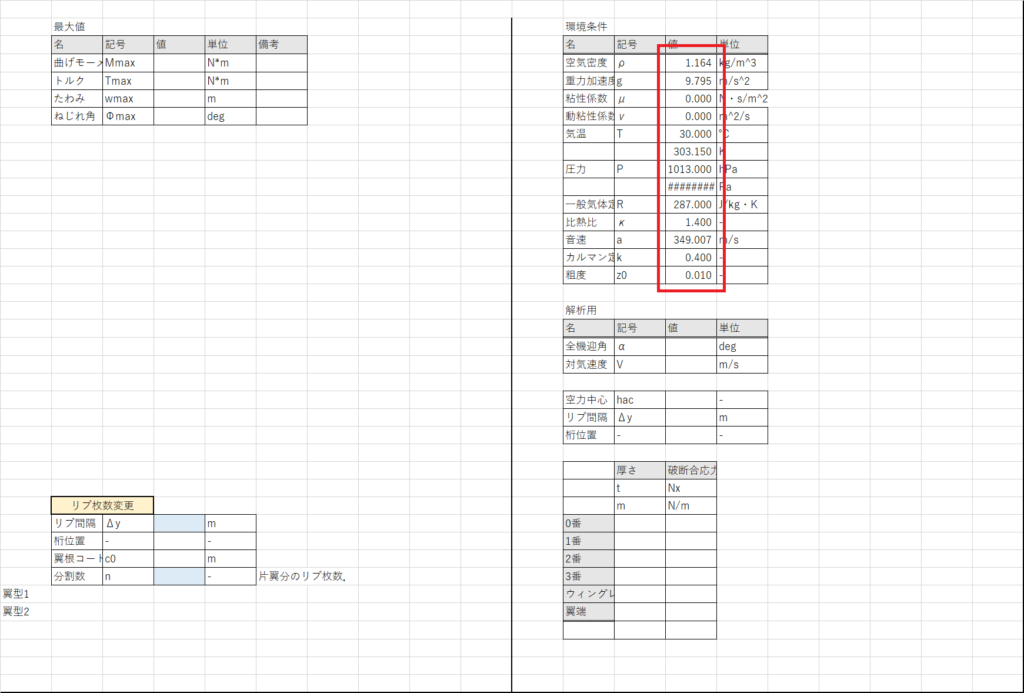
たわみ・ねじりのシートのN4:N16にもろもろの値を各種パラメータのシートから持ってくる
列L~列Nの45行目以下に,曲げ剛性,ねじれ剛性,翼重量をそれぞれスパー寸法のシートと主翼のシートから持ってくる
翼重量の単位は[N]なので,主翼重量に先ほど持ってきた重力加速度をかけておく
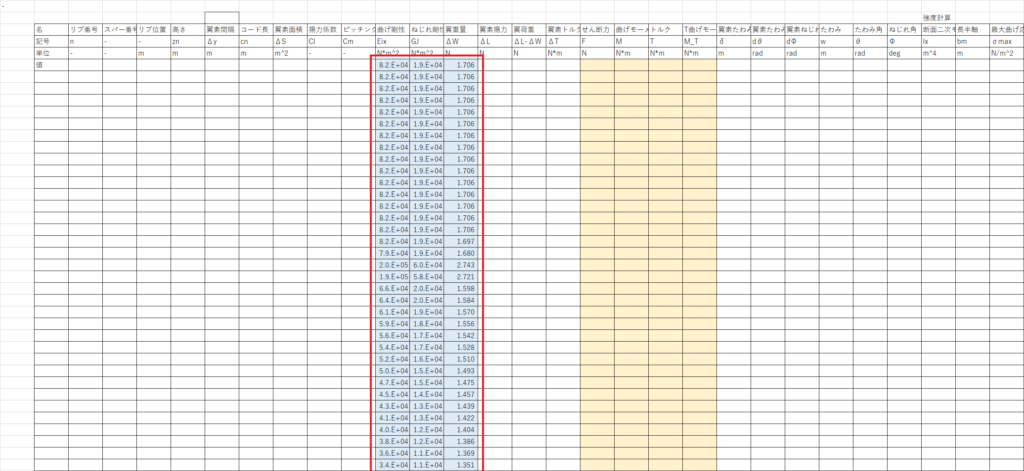
これで準備は完了である
実行結果
実行用のプログラムは例えば次のようなものになる
Sub 主翼計算()
Set sht1 = Sheets("主翼(sht1)")
Dim state As variables
Dim Wing As Specifications
Dim startTime As Double
Dim endTime As Double
Dim processTime As Double
'ActiveWorkbook.Save'まず上書き保存
Application.ScreenUpdating = False '画面更新の非表示
startTime = Timer '開始時間取得
'状態変数の読み込み
state = ReadState(state, 1)
Wing = Read_value(Wing, state, 1)
'LLTの計算
Wing = VLM_wing(1, Wing, state)
endTime = Timer '終了時間取得
processTime = endTime - startTime
MsgBox "計算が終了しました" & vbCrLf & "処理時間:" & processTime '処理時間表示
End Subこれを実行すれば,数秒で計算が終了する

たわみ・ねじれのシートにさらにいくつかの値を主翼シートから持ってくる
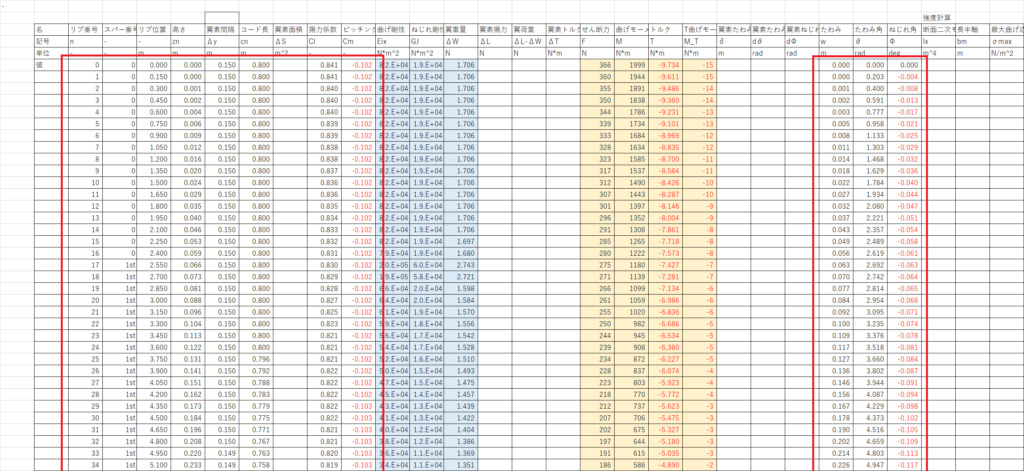
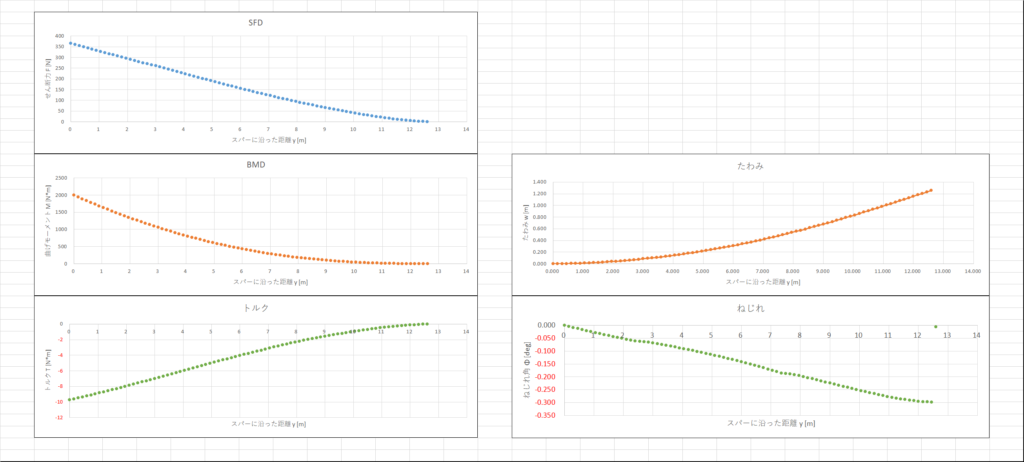
たわみやねじれ,SFDやBMDも表示できる
繰り返し回数
繰り返し回数による結果の変化を見てみる
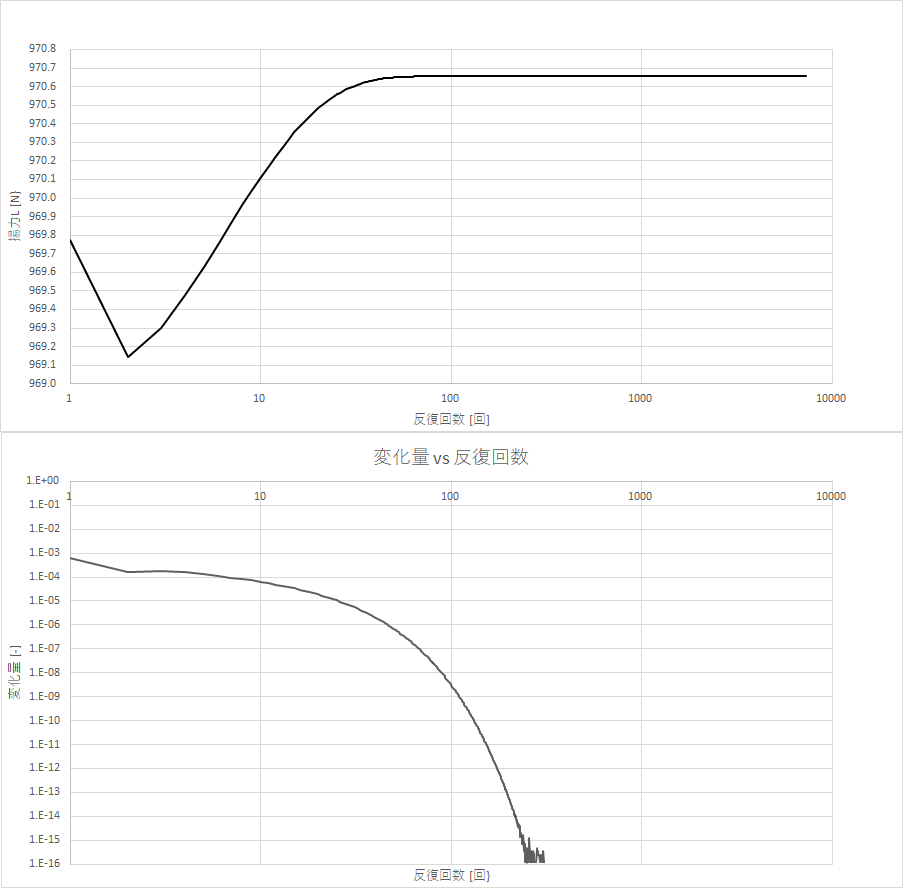
上図より,数十回の繰り返し計算で値が収束していることがわかる
下図を参考に変化量の閾値を決めるといい
XFLR5との比較
次の記事を参考にしてほしい
まとめ
Excel VBAで主翼の空力・構造計算のプログラムを作成した
XFLR5を使うよりもかなり時間の節約になるのではないかと思う
↓次の記事
↓記事一覧
【更新情報】20191219
- 重心周りのピッチングモーメントの式の間違いを修正
【追記】20200910 change_modeについて
change_modeのコードを以下に示す
どちらかというとデバッグ用のコードで,設計時の空力計算には必要ない
Sub change_mode(ByRef Wing As Specifications, ByRef state As variables, ByRef dihedral_angle() As Double, ByRef dihedral_angle0() As Double, ByRef deflection() As Double, ByRef theta() As Double, ByRef phi() As Double, ByRef dM_ac() As Double, ByRef dM_cg() As Double, ByRef Shear_Force() As Double, ByRef Bending_Moment() As Double, ByRef Bending_Moment_T() As Double, ByRef Torque() As Double)
With Wing
If sht1.Range("AW4") = "なし" Then
ReDim dihedral_angle0(2 * .span_div - 1) '初期上反角 [deg].Γd0.Dihedral
End If
If sht1.Range("AW5") = "なし" Then
ReDim deflection(2 * .span_div) 'たわみ [m]
ReDim theta(2 * .span_div) 'たわみ角 [deg]
End If
If sht1.Range("AW6") = "なし" Then
ReDim phi(2 * .span_div) 'ねじれ角 [deg]
End If
End With
End Sub主翼(sht1)のAW4~AW6の値をあり/なしに変更することによって,①初期上反がなかったら?②たわみがなかったら?③ねじれがなかったら?という場合の空力計算を行うことができる
例えば,設計シートの値とXFLR5の値を比較したいときには今回のプログラムのたわみとねじれの自動更新は必要ないので,AW5=”なし”,AW6="なし"として計算した結果を比較すればいい
【ミス修正】20200911
- メインプログラムの
input_data_to_typeの引数からZ_cgを削除
【ミス修正】20210602
- 横・方向の安定微係数の計算の仕方を修正






コメント
循環を求める式ですが、
$$
\Gamma_i=\frac 1 2 \bar c_i V_i {C_l}_i
$$
だと思います。
すずゆーさん、ご指摘ありがとうございます!
修正させていただきました。