翼型解析②：解析データを最小二乗法で多項式近似する

離散化された解析データを最小二乗法を用いて多項式近似する

目的とフローチャート
プログラムの解説
プログラムの実行
まとめ

目的とフローチャート

今回の目的は，前回（>翼型解析①：大量のテキストファイルをエクセルに読み込む）でExcelファイルに貼り付けた離散化された解析結果を最小二乗法を用いて多項式近似することである

こうすることで今後の空力計算において任意の迎角の揚力係数や抗力係数，ピッチングモーメント係数を計算できる

最小二乗法については次のサイトを参考にしてほしい

最小二乗法の行列表現：
主張1：行列\({\bf A}\)と列ベクトル\({\bf b}\)が与えられたときに
\(||{\bf Ax-b}||\)
を最小にする\({\bf x}\)を求める問題は非常に重要である。
主張2：\({\bf A^t A}\)が正則のとき上記の問題の解は唯一つである：
\({\bf x=(A^T A)^{-1} A^T b}\)
最小二乗法の行列表現（単回帰，多変数，多項式）

今回はCLをαの関数，CDとCmをαとReの関数として扱い，それぞれをαの8次式とRe数の6次式で表す（この次数は好きに決めていい）

例えばCDのデータがn個あったとき，i番目のデータについて

\(CD_i=C_0+C_1\alpha_i+C_2\alpha_i^2 +C_3\alpha_i^3 +C_4\alpha_i^4 +C_5\alpha_i^5 +C_6\alpha_i^6 +C_7\alpha_i^7+C_8\alpha_i^8 \\ \hspace{30pt}+D_1 Re_i+D_2 Re_i^2+D_3 Re_i^3+D_4 Re_i^4+D_5 Re_i^5+D_6 Re_i^6\)

n個のデータを行列にまとめると

\( \left[ \begin{array}{ccccccccccccccc} 1&\alpha_1&\ldots&\alpha_1^8&Re_1&\ldots&Re_1^6 \\ \vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots \\ 1&\alpha_n&\ldots&\alpha_n^8&Re_n&\ldots&Re_n^6 \end{array} \right] \left[ \begin{array}{c} C_0 \\ \vdots \\C_8\\D_1\\ \vdots \\D_6 \end{array} \right] =\left[ \begin{array}{c} CD_1 \\ \vdots \\CD_n \end{array} \right] \)

つまり

\begin{eqnarray} {\bf A}&=&\left[ \begin{array}{ccccccccccccccc} 1&\alpha_1&\ldots&\alpha_1^8&Re_1&\ldots&Re_1^6 \\ \vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots \\ 1&\alpha_n&\ldots&\alpha_n^8&Re_n&\ldots&Re_n^6 \end{array} \right] \\ {\bf x}&=&\left[ \begin{array}{c} C_0 \\ \vdots \\C_8\\D_1\\ \vdots \\D_6 \end{array} \right] \\ {\bf b}&=&\left[ \begin{array}{c} CD_1 \\ \vdots \\CD_n \end{array} \right] \end{eqnarray}

として \({\bf x=(A^T A)^{-1} A^T b}\) を求めればいい

マクロのフローチャートを以下に示す

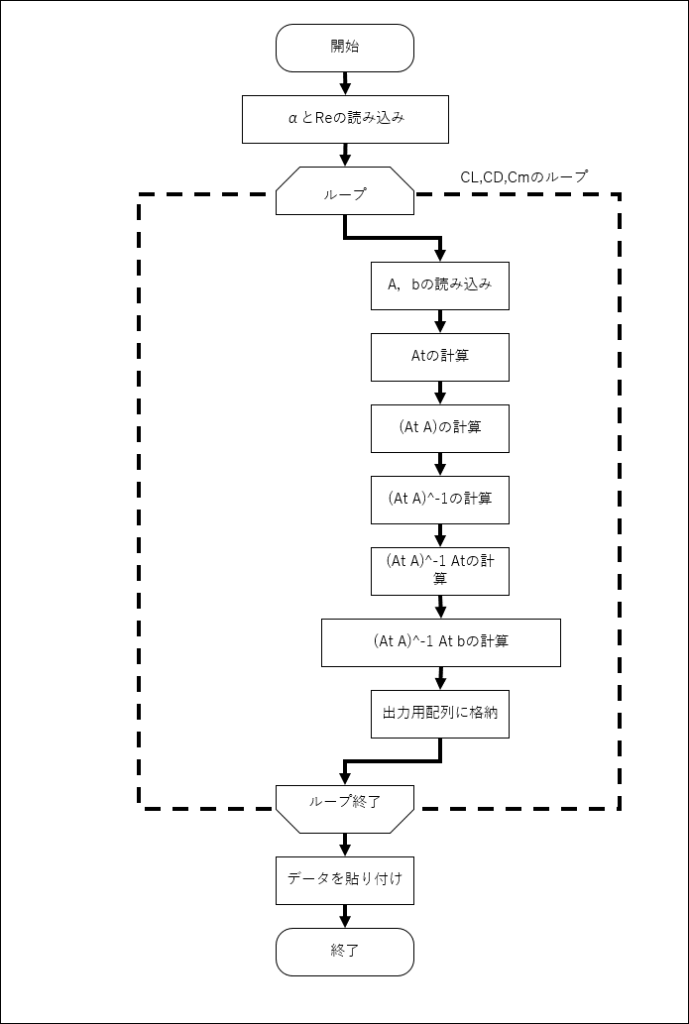
テンプレートファイルのダウンロード

エクセルシートの配置などの参考になるようにテンプレートファイルを添付しておく

※数式やマクロはすべて削除してあり，値も適当である

翼型解析シート

1 ファイル 1.14 MB

ダウンロード

プログラムの解説

それでは実際に解説していく

行列演算に使う関数は行列計算に関するExcelマクロで解説している

使用する変数

マクロに使用する変数を以下に示す

 '変数の宣言
 '多変数関数の最小二乗法
 Dim data1 As Integer 'XFRL5のデータの個数
 Dim data2 As Integer '多項式の項の数
 Dim alpha() As Double '迎角
 Dim Re() As Double 'レイノルズ数
 Dim matrix1() As Double 'A
 Dim matrix2() As Double 'At
 Dim matrix3() As Double '(At A)
 Dim matrix4() As Double '(At A)^-1
 Dim matrix5() As Double '(At A)^-1 At
 Dim matrix6() As Double 'b
 Dim matrix7() As Double '(At A)^-1 At b
 Dim output(2, 14) As Double '係数出力用の配列
 'カウンター
 Dim i As Integer
 Dim j As Integer
 Dim k As Integer

XFLR5の出力データ数data1がわからないのですべての配列を動的配列にしてプログラムの途中で大きさを宣言する

αとReの読み込み

XFLR5から出力したデータの個数を調べてから配列を宣言し，ループを作ってalpha()とRe()に格納していく

'値の読み込み
data1 = Cells(Rows.Count, 1).End(xlUp).Row - 12 + 1 '現在入っているデータの個数を取得

'配列の大きさの宣言
ReDim alpha(data1)
ReDim Re(data1)

'値の読み込み
For i = 0 To data1 - 1
    alpha(i) = Cells(12 + i, 1)
    Re(i) = Cells(12 + i, 5)
Next i

CL,CD,Cmのループ

それぞれについてほぼ同じ操作を行うので，3回ループを回すことでコードを短くする

For k = 0 To 2
    (k=0,1,2がそれぞれCL,CD,Cmに対応する)
Next k

\({\bf A,b}\)の読み込み

CLのみRe数の関数ではないので行列\({\bf A}\)の列の数を8にする（CDとCmの列の数は14）

行列\({\bf b}\) を読み込むときにkの値を使っている


    If k = 0 Then
        data2 = 8 'CL
    Else
        data2 = 14 'CD,Cm
    End If
    ReDim matrix1(data1, data2) 'A
    ReDim matrix6(data1, 0) 'b
    
    '多変数関数の配列の作成
    For i = 0 To data1 - 1
        For j = 0 To 8
            matrix1(i, j) = alpha(i) ^ j 'A
        Next j
        If k <> 0 Then
            For j = 9 To data2
                matrix1(i, j) = Re(i) ^ (j - 8) 'A
            Next j
        End If
        matrix6(i, 0) = Cells(12 + i, 2 + k) 'b
    Next i

それ以降の処理

見ればわかると思う

matrix2 = Transpose(data1 + 1, data2 + 1, matrix1) 'At
matrix3 = mult(matrix2, matrix1) '(At・A)
matrix4 = inverse(data2 + 1, matrix3) '(At A)^-1
matrix5 = mult(matrix4, matrix2) '(At A)^-1 At
matrix7 = mult(matrix5, matrix6) '(At A)^-1 At b
For i = 0 To data2
    output(k, i) = matrix7(i, 0)
Next i

ここまでがループの中の処理

データの貼り付け

これもまた見ればわかると思う

Range()とCells()をうまく使うといい

Range(Cells(3, 7), Cells(5, 7 + data2)) = output()

プログラムの実行

今回作成したプログラムを実際に実行してみる

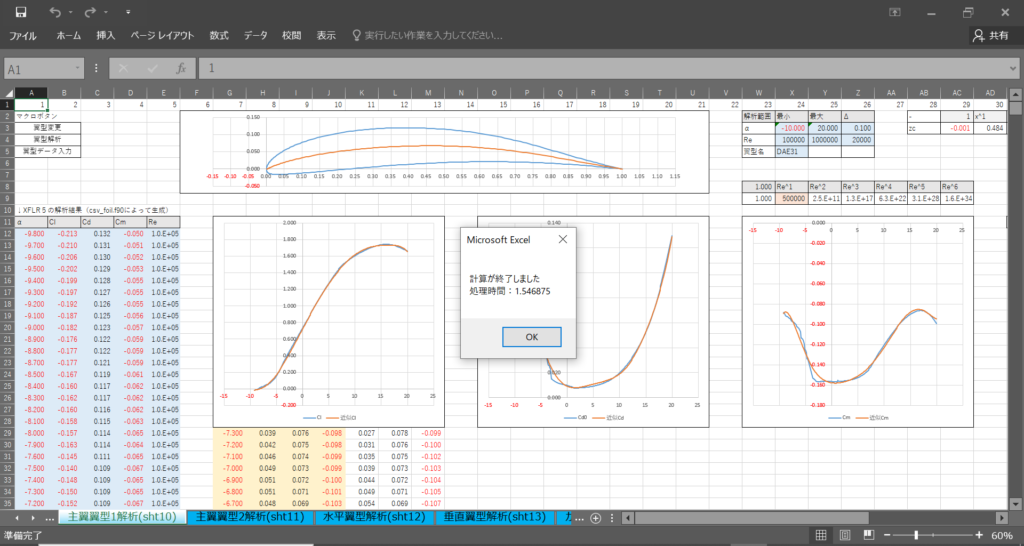
(上書き保存をしなければ)実行時間は約1.5秒だった

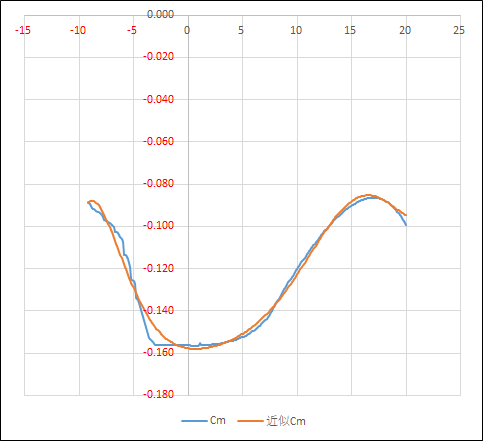
CL,CD,Cmの実際の値と多項式近似の値をRe=50'000で比較してみる

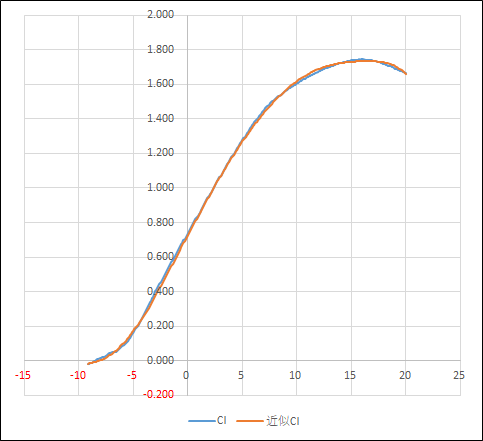
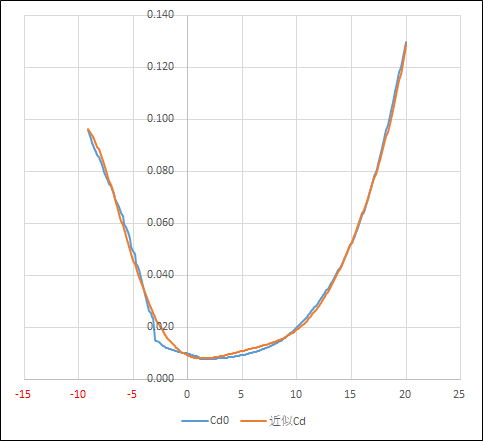
まとめ

今回の記事ではXFLR5で出力した結果を最小二乗法で多項式近似してみた

この近似で満足できるかは個人によって分かるかもしれない

~~満足できなかった人は他の補完曲線について勉強してみるといい~~
~~>補間法と最小二乗法~~（リンク切れ）

↓次の記事

↓前回の記事

↓記事一覧