渦格子法を用いた尾翼の空力計算

渦格子法を用いて水平尾翼，および垂直尾翼の空力計算を行う

目的

今回の目的は，渦格子法を用いて水平尾翼，および垂直尾翼の空力計算を行うことである

前回の記事(≫主翼の空力および構造計算)で扱ったアルゴリズムもいわば渦格子法の一種ではあるが，コード方向に1分割しかしていないためアスペクト比の大きい翼にしか適用できない

渦格子法のアルゴリズムは次の文献を参考にした

≫航空力学の基礎(第3版) p.147-156・・・(文献1)

そう，みんな大好き銀本の，誰もが読み飛ばしたであろう「3.12 揚力面理論」の内容である

式の導出や理論の説明などは文献1に詳しく書いてあるのでこの記事では割愛する

これ以降の説明は，傍らに銀本を置きながら聞くとわかりやすいだろう

フローチャート

結局は渦格子法なので， 前回の記事(≫主翼の空力および構造計算) や(≫TR-797の実装)のときと同じように，翼の形状を読み込んで循環分布と吹きおろしの関係を表す係数を求め，連立一次方程式を解いて循環分布を求めるという流れで計算を行っていく

フローチャートを以下に示す

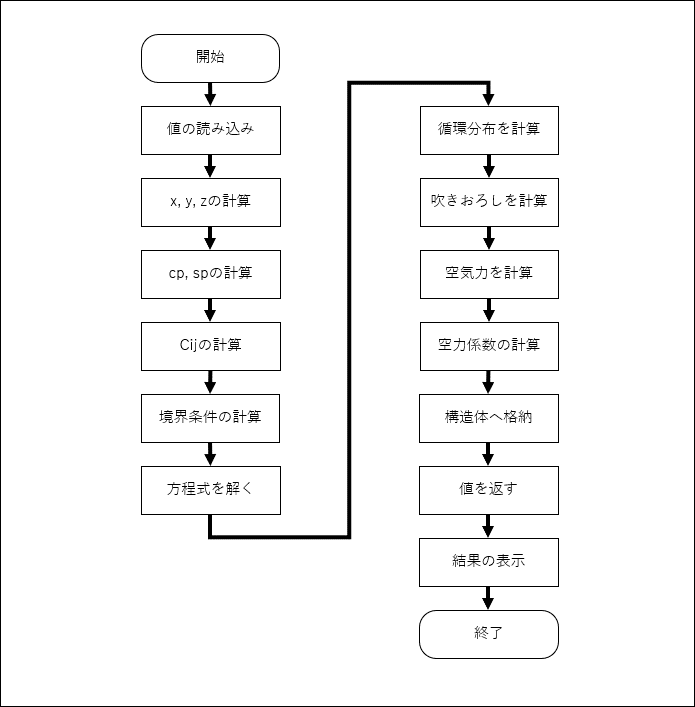
今回は線形を仮定して計算するので前回のような反復計算は行わない

プログラムの解説

それでは実際に解説していく

テンプレートファイル

エクセルシートの配置などの参考になるようにテンプレートファイルを添付しておく

※数式やマクロはすべて削除してあり，値も適当である

プログラムの構造

渦格子法の空力計算のプログラムは，引数を尾翼の構造体Tail (or Fin),状態変数の構造体state，設計シートへの出力の有無pとして，尾翼の構造体に計算結果を返すFunctionとする

Public Function VLM_tail(p As Integer, ByRef Tail As Specifications, ByRef state As variables) As Specifications
    (処理)
End Function

設計シートのプログラム全般で使う構造体については次の記事(≫設計シートに使う構造体について)を参考にしてほしい

プログラム全体の流れ

今回のプログラムもそれなりに長いので，可読性を上げるためにもそれぞれの処理はプロシージャに分けて行った

プログラムの全体は次のようになる

Public Function VLM_tail(p As Integer, ByRef Tail As Specifications, ByRef state As variables) As Specifications
Application.ScreenUpdating = False '画面更新の非表示
alpha_tail = state.alpha + (Tail.it + state.de) - Tail.epsilon '尾翼迎角 [deg]
alphat_tail = alpha_tail + Atn(state.q * rad * (Tail.lt / state.Vair)) * deg 'ピッチ角速度qの分だけ尾翼迎角を変化させる

'VLM
Call read_value_from_sheet(Tail, state, chord, chord_cp, Cl_coef, Cdp_coef, Cm_coef, zc_coef, sht3)
Call calculation_xyz(Tail, state, x, y, z, chord, zc_coef)
Call calculation_cp_sp(Tail, state, x, y, z, cp, sp1, sp2, dzdx)
Call calculation_Cij(Tail, state, cp, sp1, sp2, Cij)
Call calculation_BC(Tail, state, alpha_tail, matrix1, matrix2, Cij, dzdx)
circulation = ans(2 * Tail.span_div * Tail.chord_div, matrix1, matrix2) '境界条件の方程式を解いて循環を求める
Call calculation_circulation(Tail, state, circulation, circulation_chord)
Call calculation_downwash(Tail, state, wi, cp, sp1, sp2, circulation_chord, alpha_induced, alpha_effective, alpha_tail)
Call calculation_Force(Tail, state, wi, circulation_chord)
Call calculation_aerodynamic_coefficient(Tail, state, CL, Cdp, Cm_ac, a1, Cm_cg, dL, dDp, dM_cg, chord_cp, alpha_effective, Re, Cl_coef, Cdp_coef, Cm_coef)

Call input_data_to_type(Tail, state, chord_cp, y, cp, ds, dDp, dM_cg, a1)
VLM_tail = Tail '構造体に値を格納

If p = 1 Then Call output_data_to_sheet(Tail, alpha_effective, Re, CL, Cdp, Cm_ac, a1, Cm_cg, circulation_chord, wi, alpha_induced, y, z, cp)

End Function

主翼のプログラムよりはすっきりしている気がする

変数の宣言

今回のプログラムで使う変数を以下に示す

'ワークシートの定義2
Set sht3 = Sheets("水平尾翼(sht3)")
Set sht8 = Sheets("全機計算(sht8)")
'VLMの変数の定義
Dim alpha_tail As Double '尾翼迎角 [deg]
Dim foil_mixture() As Double: ReDim foil_mixture(Tail.span_div, 1) '翼配合率
Dim Cl_coef(14) As Double '揚力係数を表す多項式の係数
Dim Cdp_coef(14) As Double '有害抗力係数を表す多項式の係数
Dim Cm_coef(14) As Double 'ピッチングモーメント係数を表す多項式の係数
Dim zc_coef(8) As Double 'キャンバーラインを表すzc(x)の多項式の係数
Dim chord() As Double: ReDim chord(2 * Tail.span_div) 'コード長 [m]
Dim chord_cp() As Double: ReDim chord_cp(2 * Tail.span_div - 1) 'コード長 [m] 'コントロールポイントでのコード長 [m]
Dim ds() As Double: ReDim ds(Tail.span_div - 1) '翼素面積 [m^2]
Dim cp() As Double: ReDim cp(2, 2 * Tail.span_div * Tail.chord_div - 1) 'i番目の要素のcontrol point [m]
Dim sp1() As Double: ReDim sp1(2, 2 * Tail.span_div * Tail.chord_div - 1) 'i番目の要素のsurface point1 [m]
Dim sp2() As Double: ReDim sp2(2, 2 * Tail.span_div * Tail.chord_div - 1) 'i番目の要素のsurface point2 [m]
Dim x() As Double: ReDim x((2 * Tail.span_div + 1) * Tail.chord_div + 2 * Tail.span_div) 'x座標 [m]
Dim y() As Double: ReDim y((2 * Tail.span_div + 1) * Tail.chord_div + 2 * Tail.span_div) 'y座標 [m]
Dim z() As Double: ReDim z((2 * Tail.span_div + 1) * Tail.chord_div + 2 * Tail.span_div) 'z座標 [m]
Dim x0 As Double '原点のx座標 [m]
Dim y0 As Double '原点のy座標 [m]
Dim z0 As Double '原点のz座標 [m]
Dim dzdx() As Double: ReDim dzdx(2 * Tail.span_div * Tail.chord_div - 1) 'キャンバーラインの傾き @cp [-]
Dim Cij() As Double: ReDim Cij(2 * Tail.span_div * Tail.chord_div - 1, 2 * Tail.span_div * Tail.chord_div - 1) 'j番目のU字渦がi番目のcpに誘導する速度を表す係数
Dim dx1 As Double 'dx1=xi-x1j
Dim dx2 As Double 'dx2=xi-x2j
Dim dy1 As Double 'dy1=yi-y1j
Dim dy2 As Double 'dy2=yi-y2j
Dim r1 As Double 'r1=sqrt(dx1^2+dy1^2)
Dim r2 As Double 'r2=sqrt(dx2^2+dy2^2)
'翼にはたらく力，モーメント
Dim dL() As Double: ReDim dL(2 * Tail.span_div - 1) '翼素揚力 [N]
Dim dDp() As Double: ReDim dDp(2 * Tail.span_div - 1) '翼素有害抗力 [N]
Dim dM_cg() As Double: ReDim dM_cg(2 * Tail.span_div - 1) '翼素トルク [N*m]
'翼の空力計算
Dim alpha_induced() As Double: ReDim alpha_induced(2 * Tail.span_div - 1) '誘導迎角 [deg]
Dim alpha_effective() As Double: ReDim alpha_effective(2 * Tail.span_div - 1) '有効迎角 [deg]
Dim Re() As Double: ReDim Re(2 * Tail.span_div - 1) '局所レイノルズ数
Dim CL() As Double: ReDim CL(2 * Tail.span_div - 1) '局所揚力係数
Dim Cdp() As Double: ReDim Cdp(2 * Tail.span_div - 1) '局所有害抗力係数
Dim Cm_ac() As Double: ReDim Cm_ac(2 * Tail.span_div - 1) '局所ピッチングモーメント係数 空力中心回り
Dim Cm_cg() As Double: ReDim Cm_cg(2 * Tail.span_div - 1) '局所ピッチングモーメント係数 桁位置まわり
Dim Cla As Double '二次元揚力傾斜 [1/deg]
Dim a1() As Double: ReDim a1(2 * Tail.span_div - 1) '断面揚力傾斜 [1/deg]
Dim circulation() As Double '循環 [m^2/s]．Γc．Circulation
Dim circulation_chord() As Double: ReDim circulation_chord(2 * Tail.span_div - 1) 'コード方向の循環の和 [m^2/s]．Γc．Circulation
Dim wi() As Double: ReDim wi(2 * Tail.span_div - 1) '吹きおろし速度 [m/s]
'一般
Dim sum As Double
Dim pi As Double: pi = 4 * Atn(1) '円周率
Dim rad As Double: rad = (pi / 180) 'degからradへの変換
Dim deg As Double: deg = (180 / pi) 'radからdegへの変換
Dim output() As Double '結果貼り付け用配列
'ガウスの消去法に代入するための配列
Dim matrix1() As Double
Dim matrix2() As Double
'カウンター
Dim i As Integer
Dim j As Integer
Dim k As Integer
Dim num As Integer
Dim num1 As Integer
Dim num2 As Integer

行数の節約のために動的配列の大きさの宣言や値の計算は同じ行で行っている

値の読み込み

値の読み込みを行う前に，座標系の定義と番号の振り方を説明しておく

座標系については，機体後方をx軸正，右翼側をy軸正，機体上方をz軸正とする

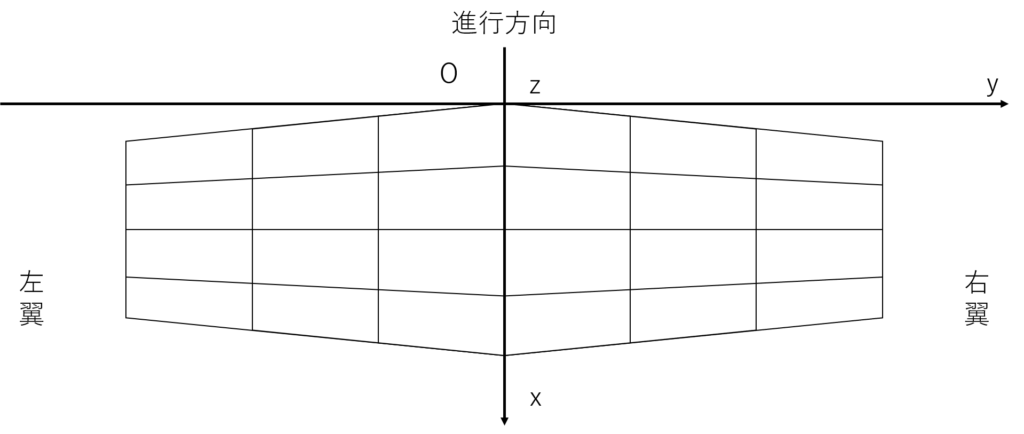
今回はスパン方向だけでなくコード方向にもパネルを分割する必要があるので，スパン方向の分割数をn，コード方向の分割数をmとする

格子点番号は次のようになる

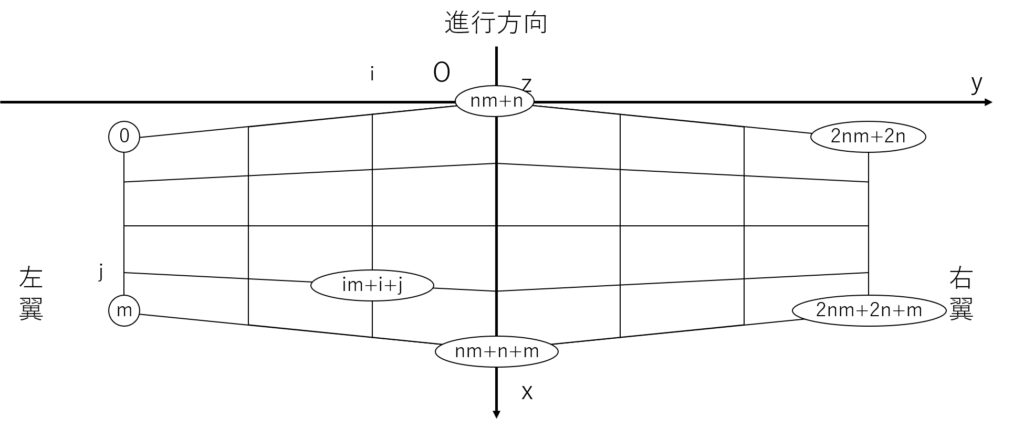
n=3，m=4とすると次のようになる

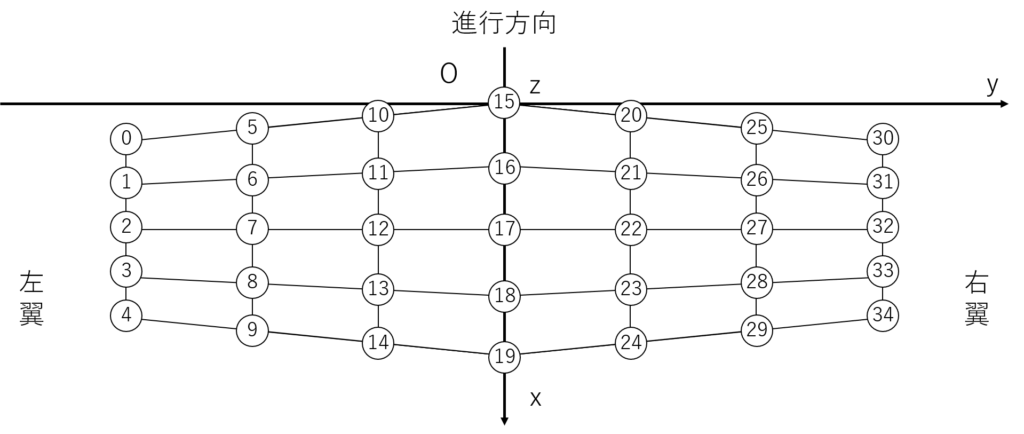
文献1によると今回のプログラムでは，control point (CP)はパネルの中央，前縁から後方3/4の点，sirface point (SP)はパネルの両端，前縁から後方1/4の点として定義されている

パネル番号は以下のようになる

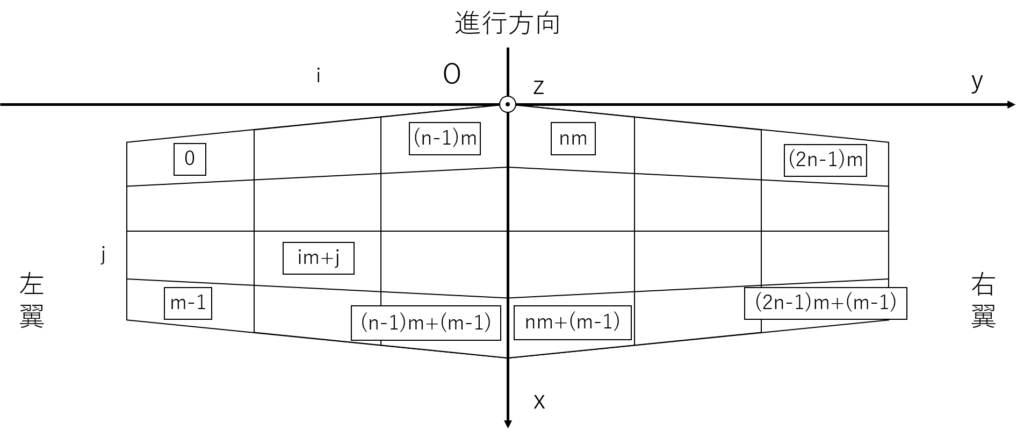
n=3，m=4とすると次のようになる

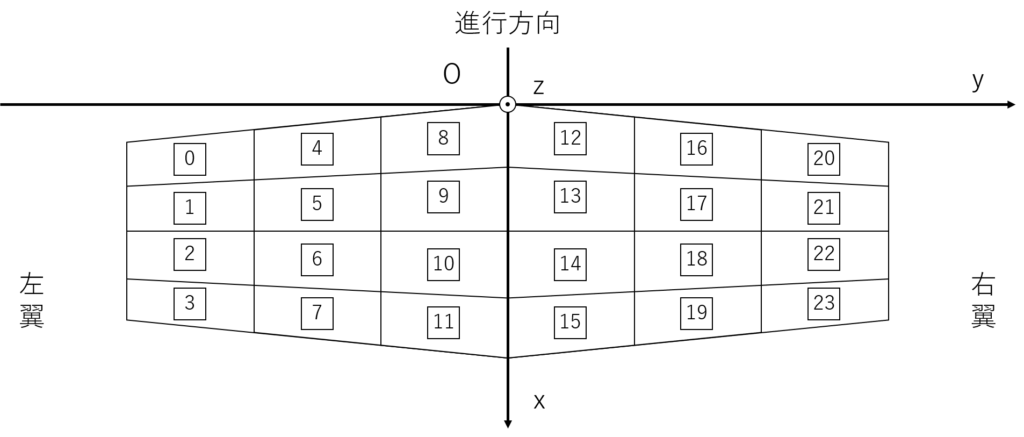
リブ番号は次のようになる

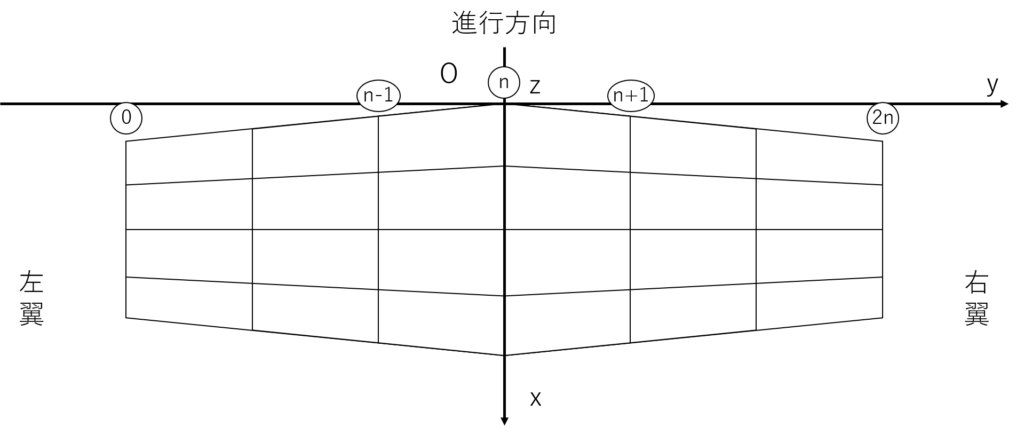
この番号を意識しながら値を読み込んでいく

Sub read_value_from_sheet(ByRef Tail As Specifications, ByRef state As variables, ByRef chord() As Double, ByRef chord_cp() As Double, ByRef Cl_coef() As Double, ByRef Cdp_coef() As Double, ByRef Cm_coef() As Double, ByRef zc_coef() As Double, ByRef sht As Worksheet)
With Tail
    '値の読み込み '尾翼中心が0，右翼端がspan_divisions
    For i = 0 To .span_div
        chord(.span_div - i) = sht.Cells(45 + i, 16)
        chord(.span_div + i) = chord(.span_div - i)
    Next i
    For i = 0 To 14
        Cl_coef(i) = sht.Cells(21, 13 + i)
        Cdp_coef(i) = sht.Cells(22, 13 + i)
        Cm_coef(i) = sht.Cells(23, 13 + i)
    Next i
    For i = 0 To 8
        zc_coef(i) = sht.Cells(22, 30 + i)
    Next i
    'chord_cpの計算 '尾翼中心が0，右翼端がspan_divisions-1
    For i = 0 To 2 * .span_div - 1
        chord_cp(i) = (chord(i) + chord(i + 1)) / 2
    Next i
End With
End Sub

zc_coef()は，翼型解析③：翼の寸法を計算するで計算した，キャンバーラインを最小二乗法で近似したときの係数となる

このプロシージャについては以上である

x，y，zの計算

格子点におけるx，y，z座標を計算する

なお，渦格子法において，翼型は次のように翼中心を結んだ折れ線として近似されていることに注意する

Sub calculation_xyz(ByRef Tail As Specifications, ByRef state As variables, ByRef x() As Double, ByRef y() As Double, ByRef z() As Double, ByRef chord() As Double, ByRef zc_coef() As Double)
With Tail
    'x,y,zを計算 '桁位置が原点 '左翼端が0，右翼端が2*span_divisions
    For i = 0 To 2 * .span_div
        For j = 0 To .chord_div
            num = i * .chord_div + i + j
            x(num) = -chord(i) * .hspar + chord(i) * (j / .chord_div)
            y(num) = .dy * (i - .span_div)
            For k = 0 To 8
                z(num) = z(num) + chord(i) * zc_coef(k) * ((j / .chord_div) ^ k)
            Next k
        Next j
    Next i
    x0 = x(.span_div * .chord_div + .span_div)
    y0 = y(.span_div * .chord_div + .span_div)
    z0 = z(.span_div * .chord_div + .span_div)
    '原点の位置を翼中心へ
    For i = 0 To 2 * .span_div * .chord_div + 2 * .span_div + .chord_div
        x(i) = x(i) - x0
        y(i) = y(i) - y0
        z(i) = z(i) - z0
    Next i
End With
End Sub

このプロシージャについては以上である

cp，spの計算

cp，spの座標を計算する

改めて，cp，sp1，sp2とは次のような点である

• cp：パネルの中央，前縁から後方3/4の点
• sp1：パネルの左端，前縁から後方1/4の点
• sp2：パネルの右端，前縁から後方1/4の点

格子点番号とパネル番号の関係は次のようになる

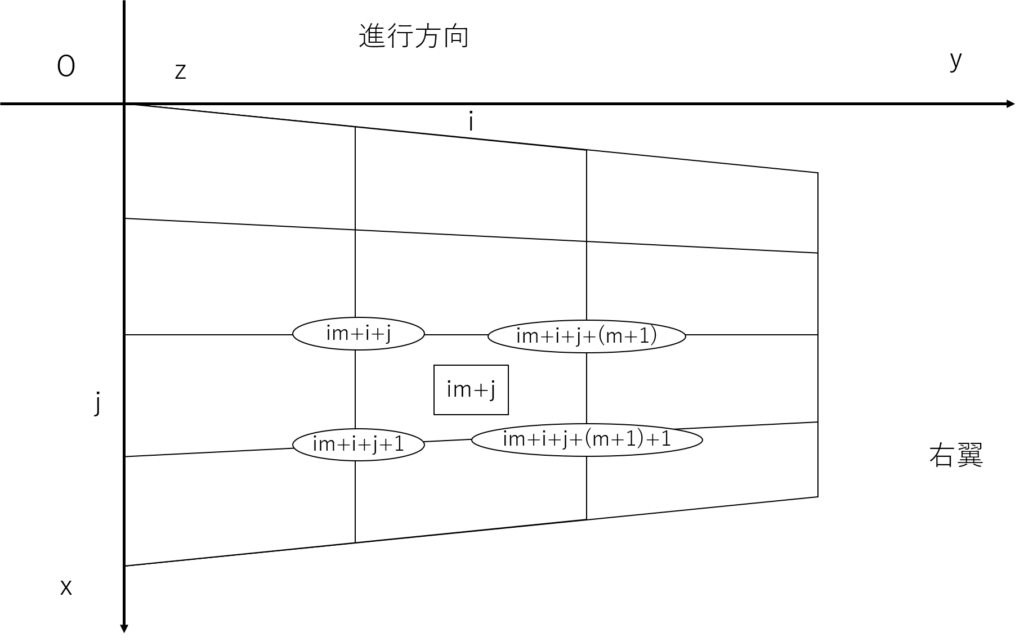
内分点の公式を使えばcp，sp1，sp2は計算できる

ついでにdz/dxも計算している

Sub calculation_cp_sp(ByRef Tail As Specifications, ByRef state As variables, ByRef x() As Double, ByRef y() As Double, ByRef z() As Double, ByRef cp() As Double, ByRef sp1() As Double, ByRef sp2() As Double, ByRef dzdx() As Double)
With Tail
    'sp,cp,dz/dxを計算
    For i = 0 To 2 * .span_div - 1
        For j = 0 To .chord_div - 1
            num1 = i * .chord_div + j 'cp
            num2 = i * .chord_div + i + j 'xyz
            '平面翼なのでz=0
            cp(0, num1) = ((x(num2) * 1 + x(num2 + 1) * 3) / 4 + (x(num2 + .chord_div + 1) * 1 + x(num2 + .chord_div + 2) * 3) / 4) / 2
            cp(1, num1) = ((y(num2) * 1 + y(num2 + 1) * 3) / 4 + (y(num2 + .chord_div + 1) * 1 + y(num2 + .chord_div + 2) * 3) / 4) / 2
            cp(2, num1) = 0
            sp1(0, num1) = (x(num2) * 3 + x(num2 + 1) * 1) / 4
            sp1(1, num1) = (y(num2) * 3 + y(num2 + 1) * 1) / 4
            sp1(2, num1) = 0
            sp2(0, num1) = (x(num2 + .chord_div + 1) * 3 + x(num2 + .chord_div + 2) * 1) / 4
            sp2(1, num1) = (y(num2 + .chord_div + 1) * 3 + y(num2 + .chord_div + 2) * 1) / 4
            sp2(2, num1) = 0
            dzdx(num1) = ((z(num2 + 1) + z(num2 + .chord_div + 2)) / 2 - (z(num2) + z(num2 + .chord_div + 1)) / 2) / ((x(num2 + 1) + x(num2 + .chord_div + 2)) / 2 - (x(num2) + x(num2 + .chord_div + 1)) / 2)
        Next j
    Next i
End With
End Sub

さりげなくたわみ，ねじれがないことを仮定しているのに気づいただろうか

尾翼は剛体なのである

このプロシージャについては以上である

Cijの計算

文献1(3.158)を計算する

文献1では右翼のみを計算しているが，座標番号などが逆にわかりにくいのでこの記事ではスパン全域にわたってCijを計算している

式をよく見ながら間違えずに入力するだけ

Sub calculation_Cij(ByRef Tail As Specifications, ByRef state As variables, ByRef cp() As Double, ByRef sp1() As Double, ByRef sp2() As Double, ByRef Cij() As Double)
With Tail
    'Cijを計算
    For i = 0 To 2 * .span_div * .chord_div - 1
        For j = 0 To 2 * .span_div * .chord_div - 1
            dx1 = cp(0, i) - sp1(0, j) 'dx1=xi-x1j
            dx2 = cp(0, i) - sp2(0, j) 'dx2=xi-x2j
            dy1 = cp(1, i) - sp1(1, j) 'dy1=yi-y1j
            dy2 = cp(1, i) - sp2(1, j) 'dy2=yi-y2j
            r1 = Sqr(dx1 ^ 2 + dy1 ^ 2) 'r1=sqrt(dx1^2+dy1^2)
            r2 = Sqr(dx2 ^ 2 + dy2 ^ 2) 'r2=sqrt(dx2^2+dy2^2)
            Cij(i, j) = (1 / (dx1 * dy2 - dy1 * dx2)) * (((dx1 - dx2) * dx1 + (dy1 - dy2) * dy1) / r1 - ((dx1 - dx2) * dx2 + (dy1 - dy2) * dy2) / r2) - (1 / dy1) * (1 + dx1 / r1) + (1 / dy2) * (1 + dx2 / r2)
        Next j
    Next i
End With
End Sub

このプロシージャについては以上である

境界条件の計算

文献1(3.169)に従って境界条件を計算する

文献1(3.163)で省略されたsinを省略せずに用いているが，どちらにせよ結果に大差はない

Sub calculation_BC(ByRef Tail As Specifications, ByRef state As variables, ByVal alpha_tail As Double, ByRef matrix1() As Double, ByRef matrix2() As Double, ByRef Cij() As Double, ByRef dzdx() As Double)
Dim pi As Double: pi = 4 * Atn(1) '円周率
Dim rad As Double: rad = (pi / 180) 'degからradへの変換
Dim deg As Double: deg = (180 / pi) 'radからdegへの変換
With Tail
    '境界条件の方程式を計算する
    ReDim matrix1(2 * .span_div * .chord_div - 1, 2 * .span_div * .chord_div - 1)
    ReDim matrix2(2 * .span_div * .chord_div - 1)
    For i = 0 To 2 * .span_div * .chord_div - 1
        For j = 0 To 2 * .span_div * .chord_div - 1
                matrix1(i, j) = Cij(i, j)
        Next j
    Next i
    For i = 0 To 2 * .span_div * .chord_div - 1
        matrix2(i) = -4 * pi * state.Vair * Sin((alpha_tail) * rad - dzdx(i))
    Next i
End With
End Sub

このプロシージャについては以上である

方程式を解く

文献1(3.169)の連立一次方程式を解く

使用しているソルバーについては次の記事(≫行列計算に関するExcelマクロ)を参考にしてほしい

'境界条件の方程式を解いて循環を求める
circulation = ans(2 * Tail.span_div * Tail.chord_div, matrix1, matrix2)

循環分布を計算

文献1(3.169)を解いたので，各パネルに配置された循環分布が求まった

吹きおろしを求めるために，コード方向のパネルの循環を足し合わせ，翼の後縁から後ろに流れていく循環の強さを求める

Sub calculation_circulation(ByRef Tail As Specifications, ByRef state As variables, ByRef circulation() As Double, ByRef circulation_chord() As Double)
With Tail
    '循環のコード方向の和を計算する
    For i = 0 To 2 * .span_div - 1
        For j = 0 To .chord_div - 1
            num1 = i * .chord_div + j 'cp
            circulation_chord(i) = circulation_chord(i) + circulation(num1)
        Next j
    Next i
End With
End Sub

このプロシージャについては以上である

吹きおろしを計算

スパン方向の循環分布が求まったので，吹きおろしを計算する

吹きおろしは文献1(2.65)，Biot-Savartの法則より次の式で計算できる

\begin{eqnarray}
w_{induced_{i}} &=& \sum_{j=0}^{2n-1} \frac{1}{4\pi}(\frac{1}{y_{sp1_{j}}-y_{cp_{i}}}-\frac{1}{y_{sp2_{j}}-y_{cp_{i}}})\Gamma_{j}
\end{eqnarray}

Sub calculation_downwash(ByRef Tail As Specifications, ByRef state As variables, ByRef wi() As Double, ByRef cp() As Double, ByRef sp1() As Double, ByRef sp2() As Double, ByRef circulation_chord() As Double, ByRef alpha_induced() As Double, ByRef alpha_effective() As Double, ByVal alpha_tail As Double)
Dim pi As Double: pi = 4 * Atn(1) '円周率
Dim rad As Double: rad = (pi / 180) 'degからradへの変換
Dim deg As Double: deg = (180 / pi) 'radからdegへの変換
With Tail
    '循環分布から吹きおろしを計算する
    For i = 0 To 2 * .span_div - 1
        For j = 0 To 2 * .span_div - 1 '左翼の循環による吹きおろし
            wi(i) = wi(i) + (1 / (4 * pi)) * (1 / (sp1(1, j * .chord_div) - cp(1, i * .chord_div)) - 1 / (sp2(1, j * .chord_div) - cp(1, i * .chord_div))) * circulation_chord(j)
        Next j
        alpha_induced(i) = deg * Atn(wi(i) / state.Vair)
        alpha_effective(i) = alpha_tail + alpha_induced(i)
    Next i
End With
End Sub

このプロシージャについては以上である

空気力を計算

循環分布，吹きおろしが計算できたので揚力，誘導抗力を計算する

負の循環が生じたときに誘導抗力が負になることを防ぐために\(D_{induced}\)の計算では絶対値を取っている

Sub calculation_Force(ByRef Tail As Specifications, ByRef state As variables, ByRef wi() As Double, ByRef circulation_chord() As Double)
With Tail
    '揚力，誘導抗力を計算する
    'wは下向きが正
    For i = 0 To 2 * .span_div - 1
        .Lift = .Lift + state.rho * state.Vair * circulation_chord(i) * .dy
        .Drag_induced = .Drag_induced + Abs(state.rho * wi(i) * circulation_chord(i) * .dy)
    Next i
End With
End Sub

このプロシージャについては以上である

空力係数の計算

空力係数を計算する

前回(≫主翼の空力および構造計算)と同様に行う

Sub calculation_aerodynamic_coefficient(ByRef Tail As Specifications, ByRef state As variables, ByRef CL() As Double, ByRef Cdp() As Double, ByRef Cm_ac() As Double, ByRef a1() As Double, ByRef Cm_cg() As Double, ByRef dL() As Double, ByRef dDp() As Double, ByRef dM_cg() As Double, ByRef chord_cp() As Double, ByRef alpha_effective() As Double, ByRef Re() As Double, ByRef Cl_coef() As Double, ByRef Cdp_coef() As Double, ByRef Cm_coef() As Double)
With Tail
    'Cl,Cm,dL,dDp,dTの計算 @cp '左翼端が0，右翼端が2*span_divisions-1
    For i = 0 To 2 * .span_div - 1
        Re(i) = state.Vair * chord_cp(i) * (1 / state.mu)
        For j = 0 To 8
            CL(i) = CL(i) + Cl_coef(j) * (alpha_effective(i) ^ j)
            Cdp(i) = Cdp(i) + Cdp_coef(j) * (alpha_effective(i) ^ j)
            Cm_ac(i) = Cm_ac(i) + Cm_coef(j) * (alpha_effective(i) ^ j)
        Next j
        For j = 9 To 14
            CL(i) = CL(i) + Cl_coef(j) * (Re(i) ^ (j - 8))
            Cdp(i) = Cdp(i) + Cdp_coef(j) * (Re(i) ^ (j - 8))
            Cm_ac(i) = Cm_ac(i) + Cm_coef(j) * (Re(i) ^ (j - 8))
        Next j
        Cm_cg(i) = Cm_ac(i) + CL(i) * (.hspar - .hac) '空力中心周りのピッチングモーメント係数を桁位置周りに換算
        dDp(i) = .dynamic_pressure * Cdp(i) * chord_cp(i) * .dy '翼素有害抗力．
        dM_cg(i) = .dynamic_pressure * chord_cp(i) * .dy * Cm_cg(i) * chord_cp(i) '翼素トルク
        a1(i) = Cl_coef(1) '断面揚力傾斜の計算 [1/deg]
    Next i
End With
End Sub

このプロシージャについては以上である

構造体へ格納

もろもろの値を計算して構造体に格納する

詳しくは前回の記事(≫主翼の空力および構造計算 )を参考にしてほしい

Sub input_data_to_type(ByRef Fin As Specifications, ByRef state As variables, ByRef chord_cp() As Double, ByRef y() As Double, ByRef cp() As Double, ByRef ds() As Double, _
                       ByRef dDp() As Double, ByRef dM_cg() As Double, ByRef a1() As Double)
Dim Plane As Specifications '構造体
Dim pi As Double: pi = 4 * Atn(1) '円周率
Dim rad As Double: rad = (pi / 180) 'degからradへの変換
Dim deg As Double: deg = (180 / pi) 'radからdegへの変換

'構造体に値を格納
With Fin
    
    'αe,Reの計算 @cp
    .S = 0
    For i = 0 To .span_div - 1
        'alphae(i) = alpha + alphat + alphai(i)
        ds(i) = chord_cp(i) * .dy
       .S = .S + ds(i)
    Next i
    
    '翼面積，スパン，アスペクト比の計算
    .b = y((.span_div + 1) * .chord_div + .span_div)
    .AR = (.b * .b) / .S
    
    
    '平均空力翼弦の計算
    .chord_mac = 0
    .Cla = 0
    For i = 0 To .span_div - 1
        .chord_mac = .chord_mac + chord_cp(i) * chord_cp(i) * .dy
        .Cla = .Cla + (2 * a1(i) * chord_cp(i) * .dy) / .S '二次元揚力傾斜 [1/deg]
    Next i
    .chord_mac = (1 / .S) * .chord_mac
    
    '片翼面積重心y_ [m]の計算
    .y_ = 0
    For i = 0 To .span_div - 1
        .y_ = .y_ + chord_cp(i) * cp(1, i * .chord_div) * .dy
    Next i
    .y_ = (1 / .S) * .y_
    
    '揚力L，誘導抗力Di，翼面積Sの計算
    .Drag_parasite = 0
    .M_pitch = 0
    For i = 0 To .span_div - 1
        '片翼分
        .Drag_parasite = .Drag_parasite + dDp(i)
        .N_yaw = .N_yaw + dM_cg(i)
    Next i
    .Drag = .Drag_parasite + .Drag_induced
    
    '翼効率e，揚力係数CLwing，誘導抗力係数CDiwingの計算
    .CL = .Lift / (.dynamic_pressure * .S)
    .Cdp = .Drag_parasite / (.dynamic_pressure * .S)
    .CDi = .Drag_induced / (.dynamic_pressure * .S)
    .CD = .Cdp + .CDi
    .Cm_ac = .M_pitch / (.dynamic_pressure * .S * .chord_mac)
    .e = Abs((.CL * .CL) / (.CDi * pi * .AR))
    .aw = (.Cla * deg) / (1 + ((.Cla * deg) / (pi * .AR))) * rad

    'モーメントの計算
    .L_roll = -.Lift * (.zf + .y_)
    .M_pitch = .M_pitch
    .N_yaw = .Lift * .lf
    
    '横・方向の安定微係数の計算
    Call Read_value(Plane, state, 8) '主翼平均空力翼弦長を読み込み
    .Cyb = -(.S / Plane.S) * .aw '[1/deg]
    .Cyp = -(.S / Plane.S) * .aw * (1 / rad) * (2 * (.zf + .y_) / Plane.b) '[1/rad]
    .Cyr = (.S / Plane.S) * .aw * (1 / rad) * (2 * .lf / Plane.b) '[1/rad]
    .Clb = .Cyb * ((.zf + .y_) / Plane.b)
    .Clp = .Cyp * ((.zf + .y_) / Plane.b)
    .Clr = .Cyr * ((.zf + .y_) / Plane.b)
    .Cnb = -.Cyb * (.lf / Plane.b)
    .Cnp = -.Cyp * (.lf / Plane.b)
    .Cnr = -.Cyr * (.lf / Plane.b)
    
End With
    
End Sub

横・方向の安定微係数については次の記事を参照

鳥コン滑空機における横・方向の微小擾乱理論

鳥コン滑空機のような大きな上反角を持つ機体に対する横・方向の微小擾乱理論について説明する

mtkbirdman.com

2021.06.01

このプロシージャについては以上である

値を返す

関数に値を返す

VLM_tail = Tail

結果の表示

結果をシートに表示する

If p = 1 Then Call output_data_to_sheet(Tail, alpha_effective, Re, CL, Cdp, Cm_ac, a1, Cm_cg, circulation_chord, wi, alpha_induced, y, z, cp)

できる限り配列に格納してまとめて貼り付ける

Sub output_data_to_sheet(ByRef Tail As Specifications, ByRef alpha_effective() As Double, ByRef Re() As Double, ByRef CL() As Double, ByRef Cdp() As Double, ByRef Cm_ac() As Double, ByRef a0() As Double, ByRef Cm_cg() As Double, _
                         ByRef circulation_chord() As Double, ByRef wi() As Double, ByRef alpha_induced() As Double, ByRef y() As Double, ByRef z() As Double, ByRef cp() As Double)

With Tail
    
    '結果の出力
    ReDim output(.span_div, 19)
    For i = 0 To .span_div - 1 '右翼
        output(i, 0) = alpha_effective(.span_div - 1 - i)
        output(i, 1) = Re(.span_div - 1 - i)
        output(i, 2) = CL(.span_div - 1 - i)
        output(i, 3) = Cdp(.span_div - 1 - i)
        output(i, 4) = Cm_ac(.span_div - 1 - i)
        output(i, 5) = 0
        output(i, 6) = 0
        output(i, 7) = Cm_cg(.span_div - 1 - i)
        output(i, 10) = .dy
        output(i, 16) = 0
        output(i, 17) = circulation_chord(.span_div - 1 - i)
        output(i, 18) = wi(.span_div - 1 - i)
        output(i, 19) = alpha_induced(.span_div - 1 - i)
    Next i
    For i = 0 To .span_div '右翼
        output(i, 8) = y(i * .chord_div + i)
        output(i, 9) = z(i * .chord_div + i)
        output(i, 11) = 0
        output(i, 12) = 0
        output(i, 13) = 0
        output(i, 14) = 0
        output(i, 15) = 0
    Next i
    sht3.Range(sht3.Cells(45, 20), sht3.Cells(45 + .span_div, 39)) = output
    
    ReDim output(28, 0)
    output(0, 0) = .S
    output(1, 0) = .b
    output(2, 0) = .AR
    output(3, 0) = .chord_mac
    output(4, 0) = .y_
    output(5, 0) = .e
    output(6, 0) = .Cla
    output(7, 0) = .aw
    output(8, 0) = .CL
    output(9, 0) = .Cdp
    output(10, 0) = .CDi
    output(11, 0) = .CD
    output(12, 0) = .Cyb
    output(13, 0) = .Clb
    output(14, 0) = .Clp
    output(15, 0) = .Cnp
    output(16, 0) = .Clr
    output(17, 0) = .Cnr
    output(18, 0) = .epsilon
    output(19, 0) = .Lift
    output(20, 0) = .Drag_parasite
    output(21, 0) = .Drag_induced
    output(22, 0) = .Drag
    output(23, 0) = .L_roll
    output(24, 0) = .M_pitch
    output(25, 0) = .N_yaw
    output(26, 0) = .Cyp
    output(27, 0) = .Cyr
    output(28, 0) = .Cnb
    sht3.Range("AR7:AR35") = output
    sht3.Range("D20") = .Cm_ac
    
End With

End Sub

これでプログラムについての解説は終了である

プログラムの実行

それでは実際にプログラムを実行してみる

テンプレートファイルの下準備

前回 (≫主翼の空力および構造計算 ) の続きからやりたい人は，まず全機計算のシートのセルN9に水平尾翼の取り付け角，セルN19に水平尾翼の形式(Conventional or T-tail)を入力する

セルS13、セルS15、セルN30にも適当な値を入力しておく

水平尾翼のシートのセルBB20:BB27に，解析の条件を入力し，セルBB28に水平尾翼位置での吹きおろし角を次のように入力する

=IF('全機計算(sht8)'!N19="Conventional",2*'主翼(sht1)'!AR25,0)

セルBB29に水平尾翼取り付け角をもってきて，セルBB30で水平尾翼迎角(=全機迎角＋取り付け角-吹きおろし角)を計算する

これで準備は完了である

実行結果

実行用のプログラムは例えば次のようなものになる

Sub 水平尾翼計算()
'ワークシートの定義
Set sht3 = Sheets("水平尾翼(sht3)")
Dim state As variables
Dim Tail As Specifications
Dim startTime As Double
Dim endTime As Double
Dim processTime As Double

'ActiveWorkbook.Save'まず上書き保存
Application.ScreenUpdating = False '画面更新の非表示
startTime = Timer '開始時間取得

state = ReadState(state, 3)　'状態変数の読み込み
Tail = Read_value(Tail, state, 3)

Tail = VLM_tail(1, Tail, state)　'VLMの計算

endTime = Timer '終了時間取得
processTime = endTime - startTime '処理時間表示
MsgBox "計算が終了しました" & vbCrLf & "処理時間：" & processTime

End Sub

これを実行すれば，0.数秒で計算が終了する

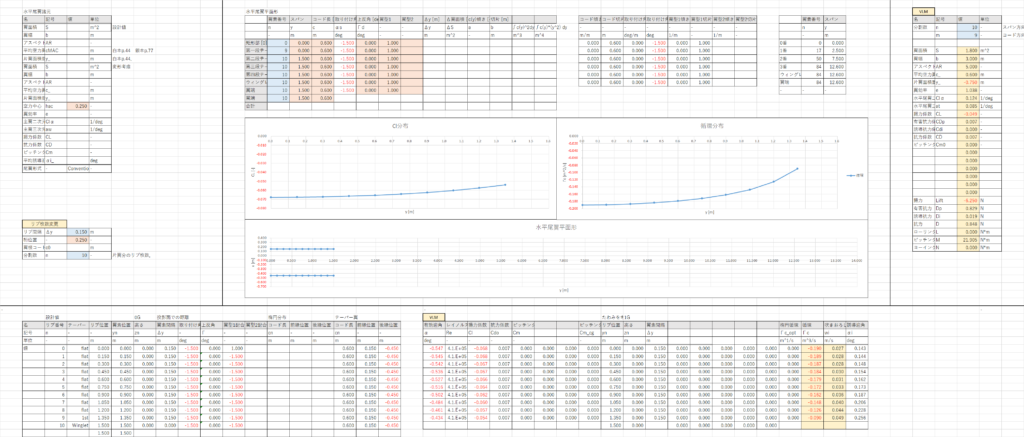
XFLR5との比較

次の記事を参考にしてほしい

≫設計シートとXFLR5の結果を比較する

まとめ

Excel VBAで渦格子法のプログラムを作成した

XFLR5を使うよりもかなり時間の節約になるのではないかと思う

垂直尾翼のコードもこれとほぼ同じものなので，自分で作ってみてほしい

↓次の記事

全機の計算

今まで作ったプログラムを用いて全機の計算を行う

mtkbirdman.com

2020.01.12

↓記事一覧

設計シート作りの記事一覧

設計シートを作りについて説明した記事の一覧

mtkbirdman.com

2021.06.13

【更新情報】20191219

1. 尾翼迎角alpha_tailにエレベータ舵角deに追加

【ミス修正】20200912

1. calculation_downwash，input_data_to_typeのサブプロシージャの中にpiの宣言を追加