鳥コン滑空機のような大きな上反角を持つ機体に対する横・方向の微小擾乱理論について説明する
はじめに
航空機の安定性解析では,微小擾乱理論と呼ばれる考え方が使われる
微小擾乱理論については以下の書籍が参考になる
通称:白本
通称:青本
安定微係数の推算については白本の第4章が,運動方程式の立式や微小擾乱方程式については青本の第1章・第2章・第3章がわかりやすい(わかりやすいとは言ってない)
ただし,白本の横・方向の安定微係数の推算(白本:p.89~)では以下の仮定が行われている
- 横方向の力\(Y\)については主翼の影響を無視(白本:P.91)
- 主翼の上反角\(\Gamma\)については小さいとし,スパン方向に一定(白本:p.93)
- 揚力係数\(C_{L_{0}}\),揚力傾斜\(a_{1}\)はスパン方向に一定(白本:p.93, 98)
これらの仮定を鳥コン滑空機に適用するには無理があるので,より厳密な安定微係数の推算方法を考えてみる
ただし,以下の仮定を採用する
- 翼の左右のたわみやねじれは等しく,フライトを通して一定である
- 胴体の影響は無視できる(鳥コン滑空機では主翼に比べて胴体がかなり小さいため)
横・方向の微小擾乱の概要
微小擾乱理論において,横向きにはたらく力\(Y\),ローリングモーメント\(L\),ヨーイングモーメント\(N\)はそれぞれ次のように表される(青本:p.22~25)
\begin{eqnarray}
Y&=&\frac{1}{2}\rho V^{2}SC_{y}\\
\\
C_{y}&=&C_{y_{\beta}}\beta+C_{y_{p}}\frac{pb}{2V}+C_{y_{r}}\frac{rb}{2V}+C_{y_{\delta_{r}}}\delta_{r}\\
\\
L&=&\frac{1}{2}\rho V^{2}SbC_{l}\\
N&=&\frac{1}{2}\rho V^{2}SbC_{n}\\
\\
C_{l}&=&C_{l_{\beta}}\beta+C_{l_{p}}\frac{pb}{2V}+C_{l_{r}}\frac{rb}{2V}+C_{l_{\delta_{r}}}\delta_{r}\\
C_{n}&=&C_{n_{\beta}}\beta+C_{n_{p}}\frac{pb}{2V}+C_{n_{r}}\frac{rb}{2V}+C_{n_{\delta_{r}}}\delta_{r}\\
\end{eqnarray}
なお,主翼が寄与する安定微係数の推算では,右翼の揚力増加に着目して計算し,それを2倍することによって主翼全体の安定微係数を計算する
\(\beta\)の影響
機体が速度\(V\),横滑り角\(\beta\)で飛行しているとき,横方向の速度\(v\)は次の式で表される(青本:p.21)
\begin{eqnarray}
v=V\sin{\beta}
\end{eqnarray}
上反角が\(\Gamma\)のとき,翼の迎角増加\(\Delta\alpha\)および揚力増加\(\Delta L\)は次の式で求まる(白本:p.93)
\begin{eqnarray}
\Delta \alpha &\simeq& \arctan{\frac{v\sin{\Gamma}}{V}}
\simeq \sin{\beta} \sin{\Gamma}
\simeq \beta \sin{\Gamma}\tag{1a} \\
\\
\Delta L &=& \frac{1}{2}\rho V^{2} \mathrm{dS} \Delta C_{L} \\
&=& \frac{1}{2}\rho V^{2} c\mathrm{dy} a_{1} \Delta \alpha \\
&=& \frac{1}{2}\rho V^{2} a_{1} \beta \sin{\Gamma} c \mathrm{dy} \tag{1b} \\
\end{eqnarray}
\(p\)の影響
機体が速度\(V\),ロール角速度\(p\)で飛行しているとき,スパン位置\(y\)における迎角増加\(\Delta \alpha\)は次の式で表される(白本:p.95)
\begin{eqnarray}
\Delta \alpha &=& \arctan{\frac{py\cos{\Gamma}}{V}}
\simeq \frac{py}{V}\cos{\Gamma} \tag{2a} \\
\end{eqnarray}
よって,翼素の揚力増加\(\Delta L\)は次の式で求まる
\begin{eqnarray}
\Delta L &=& \frac{1}{2}\rho V^{2} \mathrm{dS} \Delta C_{L} \\
&=& \frac{1}{2}\rho V^{2} c\mathrm{dy} a_{1} \Delta \alpha \\
&=& \frac{1}{2}\rho V^{2} a_{1} \frac{py}{V} \cos{\Gamma} c \mathrm{dy} \tag{2b} \\
\end{eqnarray}
\(r\)の影響
機体が速度\(V\),ヨー角速度\(r\)で飛行しているとき,スパン位置\(y\)における速度増加\(\Delta V\)は次の式で表される(白本:p.95)
\begin{eqnarray}
\Delta V = -ry \\
\end{eqnarray}
よって,翼素の揚力増加\(\Delta L\)は次の式で求まる
\begin{eqnarray}
\Delta L &=& \frac{1}{2}\rho (V-ry)^{2} \mathrm{dS} C_{L}-\frac{1}{2}\rho V^{2} \Delta S C_{L} \\
&=& \frac{1}{2}\rho \left\{(V-ry)^{2}-V^{2}\right\} c\mathrm{dy} C_{L} \\
&=& \frac{1}{2}\rho (2V-ry)(-ry) C_{L} c \mathrm{dy}\\
&\simeq& \frac{1}{2}\rho (-2Vry) C_{L} c \mathrm{dy} \tag{3} \\
\end{eqnarray}
\(\Delta \alpha\)の影響
迎角\(\alpha\)で飛行しているとき,x軸方向とz軸方向にはたらく力は次の式で表される(青本:p.23)
\begin{eqnarray}
X&=&\frac{1}{2}\rho V^{2} S C_{x}\\
Z&=&\frac{1}{2}\rho V^{2} S C_{z}\\
\\
C_{x}&=&C_{L}\sin{\alpha}-C_{D}\cos{\alpha}\\
C_{z}&=&-C_{L}\cos{\alpha}-C_{D}\sin{\alpha}\simeq-C_{L}\\
\end{eqnarray}
ここで,迎角が変化したときのx方向の力の増加\(\Delta X\)は次の式で表される
\begin{eqnarray}
\Delta C_{x}&=&\frac{\partial C_{x}}{\partial \alpha}\Delta \alpha\\
&=& \left(C_{L_{\alpha}}\sin{\alpha}+C_{L}\cos{\alpha}-C_{D_{\alpha}}\cos{\alpha}+C_{D}\sin{\alpha}\right)\Delta \alpha \\
&\simeq& \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right)\Delta \alpha \\
\\
\Delta X &=& \frac{1}{2}\rho V^{2} \mathrm{dS}\Delta C_{x}\\
&=& \frac{1}{2}\rho V^{2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right)\Delta \alpha c\mathrm{dy} \tag{4} \\
\end{eqnarray}
ただし,迎角の小さい範囲では\(C_{D}= const.\)(\(C_{D_{\alpha}}= 0\))とした
\(\Gamma\)の影響
上反角\(\Gamma\)は,横滑り角\(\beta\)によって迎角を増加させるだけではなく,揚力をyz平面内に傾けるはたらきがある
上反角\(\Gamma\)を持つ翼素に揚力\(L\)がはたらいているとき,y方向,z方向の力はそれぞれ次のように求まる
\begin{eqnarray}
Y&=&-L\sin{\Gamma} \tag{5}\\
Z&=&-L\cos{\Gamma} \tag{6}\\
\end{eqnarray}
\(C_{y_{\beta}}\)
\(C_{y_{\beta}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{y_{\beta}} = (C_{y_{\beta}})_{wing}+(C_{y_{\beta}})_{fin}\\
\end{eqnarray}
主翼の寄与\(C_{y_{\beta_{w}}}\)は式(1b),(5)より次のように求まる
\begin{eqnarray}
(Y)_{wing} &=& -2\int_{0}^{b/2} \Delta L \sin{\Gamma}\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho V^{2}a_{1} \beta \sin{\Gamma}^2 c\mathrm{dy} \\
\\
(C_{y})_{wing} &=& -\frac{2}{S} \int_{0}^{b/2} a_{1} \sin{\Gamma}^2 \beta c \mathrm{dy} \\
\\
(C_{y_{\beta}})_{wing} &=& -\frac{2}{S} \int_{0}^{b/2} a_{1} \sin{\Gamma}^2 c \mathrm{dy}\\
\end{eqnarray}
垂直尾翼の寄与\((C_{y_{\beta}})_{fin}\)は次の式で表される(白本:p.91)
\begin{eqnarray}
(C_{y_{\beta}})_{f}
=-\frac{S_{f}}{S}a_{f}\left(1-\frac{\partial\sigma}{\partial\beta}\right)
\simeq-\frac{S_{f}}{S}a_{f}
\end{eqnarray}
\(C_{y_{p}}\)
\(C_{y_{p}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{y_{p}} = (C_{y_{p}})_{wing}+(C_{y_{p}})_{fin}\\
\end{eqnarray}
主翼の寄与\((C_{y_{p}})_{wing}\)は式(2b),(5)より次のように求まる
\begin{eqnarray}
(Y)_{wing}
&=& -2\int_{0}^{b/2} \Delta L \sin{\Gamma}\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho V^{2} a_{1} \frac{py}{V} \sin{\Gamma}\cos{\Gamma}c \mathrm{dy} \\
\\
(C_{y})_{wing} &=& -\frac{2}{S} \int_{0}^{b/2} a_{1} \frac{py}{V} \sin{\Gamma}\cos{\Gamma} c\mathrm{dy} \\
&=& -\frac{4}{Sb} \int_{0}^{b/2} a_{1} \frac{pb}{2V} y\sin{\Gamma}\cos{\Gamma} c\mathrm{dy} \\
\\
(C_{y_{p}})_{wing} &=& -\frac{4}{Sb} \int_{0}^{b/2} a_{1} y\sin{\Gamma}\cos{\Gamma} c \mathrm{dy}\\
\end{eqnarray}
垂直尾翼の寄与\((C_{y_{p}})_{fin}\)は次の式で表される(白本:p.99)
\begin{eqnarray}
(C_{y_{p}})_{fin}
=-\frac{S_{f}}{S}a_{f}\left(\frac{2z_{fp}}{b}-\frac{\partial\sigma}{\partial {\hat p}}\right)
\simeq -\frac{S_{f}}{S}a_{f}\frac{2z_{f}}{b}
\end{eqnarray}
\(C_{y_{r}}\)
\(C_{y_{r}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{y_{r}} = (C_{y_{r}})_{wing}+(C_{y_{r}})_{fin}\\
\end{eqnarray}
主翼の寄与\((C_{y_{r}})_{wing}\)は式(3),(5)より次のように求まる
\begin{eqnarray}
(Y)_{wing}
&=& -2\int_{0}^{b/2} \Delta L \sin{\Gamma}\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho (-2Vry) C_{L}\sin{\Gamma} c\mathrm{dy}\\
\\
(C_{y})_{wing} &=& \frac{4}{S} \int_{0}^{b/2} C_{L} \frac{ry}{V} \sin{\Gamma} c\mathrm{dy} \\
&=& \frac{8}{Sb} \int_{0}^{b/2} C_{L} \frac{rb}{2V} y\sin{\Gamma} c\mathrm{dy} \\
\\
(C_{y_{r}})_{wing} &=& \frac{8}{Sb} \int_{0}^{b/2} C_{L} y\sin{\Gamma} c\mathrm{dy}\\
\end{eqnarray}
垂直尾翼の寄与\((C_{y_{r}})_{fin}\)は次の式で表される(白本:p.102)
\begin{eqnarray}
(C_{y_{r}})_{fin}=\frac{S_{f}}{S}a_{f}\left(\frac{2l_{f}}{b}+\frac{\partial \sigma}{\partial {\hat r}}\right)
\simeq \frac{S_{f}}{S}a_{f}\frac{2l_{f}}{b}
\end{eqnarray}
\(C_{y_{\delta_{r}}}\)
\(C_{y_{\delta_{r}}}\)は垂直尾翼の寄与のみであり,以下の式で求められる(白本:p.91)
\begin{eqnarray}
C_{y_{\delta_{r}}} = \frac{S_{f}}{S}a_{f}\tau
\end{eqnarray}
\(C_{l_{\beta}}\)
\(C_{l_{\beta}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{l_{\beta}} = (C_{l_{\beta}})_{wing}+(C_{l_{\beta}})_{fin}\\
\end{eqnarray}
主翼の寄与\((C_{l_{\beta}})_{wing}\)は式(1b),(5),(6)より次のように求まる(白本p.92~95)
\begin{eqnarray}
(L)_{wing}
&=& -2\int_{0}^{b/2} \left(\Delta L \cos{\Gamma}\times y + \Delta L \sin{\Gamma}\times z\right)\\
&=& -2\int_{0}^{b/2} \Delta L \left( y\cos{\Gamma}+z\sin{\Gamma} \right)\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho V^{2} a_{1} \beta \sin{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right)c \mathrm{dy} \\
\\
(C_{l})_{wing} &=& -\frac{2}{Sb} \int_{0}^{b/2} a_{1} \beta \sin{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right)c \mathrm{dy} \\
\\
(C_{l_{\beta}})_{wing} &=& -\frac{2}{Sb} \int_{0}^{b/2} a_{1} \sin{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy}\\
\end{eqnarray}
垂直尾翼の寄与\((C_{l_{\beta}})_{fin}\)は次の式で表される
\begin{eqnarray}
(C_{l_{\beta}})_{fin}=(C_{y_{\beta}})_{fin}\frac{z_{f}}{b}
=-\frac{S_{f}}{S}a_{f}\frac{z_{f}}{b}
\end{eqnarray}
\(C_{l_{p}}\)
\(C_{l_{p}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{l_{p}} = (C_{l_{p}})_{wing}+(C_{l_{p}})_{fin}\\
\end{eqnarray}
主翼の寄与\(C_{l_{p}}\)は,式(2b),(5),(6)より次のように求まる(白本:p.95)
\begin{eqnarray}
(L)_{wing}
&=& -2\int_{0}^{b/2} \Delta L \left( y\cos{\Gamma}+z\sin{\Gamma} \right)\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho V^{2} a_{1} \frac{py}{V} \cos{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
\\
(C_{l})_{wing}
&=& -\frac{2}{Sb} \int_{0}^{b/2} a_{1} \frac{py}{V} \cos{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
&=& -\frac{4}{Sb^{2}} \int_{0}^{b/2} a_{1} \frac{pb}{2V}y \cos{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
\\
(C_{l_{p}})_{wing} &=& -\frac{4}{Sb^{2}} \int_{0}^{b/2} a_{1} y \cos{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
\end{eqnarray}
垂直尾翼の寄与\((C_{l_{p}})_{fin}\)は次の式で表される
\begin{eqnarray}
(C_{l_{p}})_{fin}=(C_{y_{p}})_{fin}\frac{z_{f}}{b}
=-\frac{S_{f}}{S}a_{f}\frac{2z_{f}}{b}\frac{z_{f}}{b}
\end{eqnarray}
\(C_{l_{r}}\)
\(C_{l_{r}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{l_{r}} = (C_{l_{r}})_{wing}+(C_{l_{r}})_{fin}\\
\end{eqnarray}
主翼の寄与\(C_{l_{r_{w}}}\)は式(3),(5),(6)より次のように求まる(白本:p.99)
\begin{eqnarray}
(L)_{wing}
&=& -2\int_{0}^{b/2} \Delta L \left( y\cos{\Gamma}+z\sin{\Gamma} \right)\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho (-2Vry) C_{L} \left( y\cos{\Gamma}+z\sin{\Gamma} \right)c \mathrm{dy} \\
\\
(C_{l})_{wing}
&=& \frac{4}{Sb} \int_{0}^{b/2} C_{L} \frac{ry}{V} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
&=& \frac{8}{Sb^{2}} \int_{0}^{b/2} C_{L}\frac{rb}{2V} y \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
\\
(C_{l_{r}})_{wing} &=& \frac{8}{Sb^{2}} \int_{0}^{b/2} C_{L} y \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
\end{eqnarray}
垂直尾翼の寄与\((C_{l_{r}})_{fin}\)は次の式で表される(白本:p.101)
\begin{eqnarray}
(C_{l_{r}})_{fin}=(C_{y_{r}})_{fin}\frac{z_{f}}{b}
=\frac{S_{f}}{S}a_{f}\frac{2l_{f}}{b}\frac{z_{f}}{b}
\end{eqnarray}
\(C_{l_{\delta_{r}}}\)
\(C_{l_{\delta_{r}}}\)は垂直尾翼の寄与のみであり,以下の式で求められる
\begin{eqnarray}
C_{l_{\delta_{r}}} = C_{y_{\delta_{r}}}\frac{z_{f}}{b}
= \frac{S_{f}}{S}a_{f}\tau\frac{z_{f}}{b} \\
\end{eqnarray}
\(C_{n_{\beta}}\)
\(C_{n_{\beta}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{n_{\beta}} = (C_{n_{\beta}})_{wing}+(C_{n_{\beta}})_{fin}\\
\end{eqnarray}
主翼の寄与\((C_{n_{\beta}})_{wing}\)は式(1a),(4)より次のように求まる
\begin{eqnarray}
(N)_{wing}
&=& -2\int_{0}^{b/2} \Delta X \times y\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho V^{2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \beta \sin{\Gamma} yc \mathrm{dy} \\
\\
(C_{n})_{wing} &=& -\frac{2}{Sb} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \beta \sin{\Gamma} y c\mathrm{dy} \\
\\
(C_{n_{\beta}})_{wing} &=& -\frac{2}{Sb} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \sin{\Gamma} y c\mathrm{dy}\\
\end{eqnarray}
垂直尾翼の寄与\((C_{n_{\beta}})_{fin}\)は次の式で表される(白本:p.91)
\begin{eqnarray}
(C_{n_{\beta}})_{fin}=-(C_{y_{\beta}})_{fin}\frac{l_{f}}{b}=\frac{S_{f}}{S}a_{f}\frac{l_{f}}{b}
\end{eqnarray}
\(C_{n_{p}}\)
\(C_{n_{p}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{n_{p}} = (C_{n_{p}})_{wing}+(C_{n_{p}})_{fin}\\
\end{eqnarray}
主翼の寄与\((C_{n_{p}})_{wing}\)は式(2a),(4)より次のように求まる
\begin{eqnarray}
(N)_{wing}
&=& -2\int_{0}^{b/2} \Delta X \times y\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho V^{2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \frac{py}{V}\cos{\Gamma} yc \mathrm{dy} \\
\\
(C_{n})_{wing}
&=& -\frac{2}{Sb} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \frac{py}{V}\cos{\Gamma} y c\mathrm{dy} \\
&=& -\frac{4}{Sb^{2}} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \frac{pb}{2V}\cos{\Gamma} y^{2} c\mathrm{dy} \\
\\
(C_{n_{p}})_{wing} &=& -\frac{4}{Sb^{2}} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \cos{\Gamma} y^{2} c\mathrm{dy} \\
\end{eqnarray}
垂直尾翼の寄与\((C_{n_{p}})_{fin}\)は次の式で表される(白本:p.91)
\begin{eqnarray}
(C_{n_{p}})_{fin}=-(C_{y_{p}})_{fin}\frac{l_{f}}{b}
=\frac{S_{f}}{S}a_{f}\frac{2z_{f}}{b}\frac{l_{f}}{b}
\end{eqnarray}
\(C_{n_{r}}\)
\(C_{n_{r}}\)は主翼と垂直尾翼の寄与に分けられる
\begin{eqnarray}
C_{n_{r}} = (C_{n_{r}})_{wing}+(C_{n_{r}})_{fin}\\
\end{eqnarray}
主翼の寄与\((C_{n_{r}})_{wing}\)は式(3)の\(C_{L}\)を\(C_{x}\)とすると次のように求まる(白本:p.101)
\begin{eqnarray}
(N)_{wing}
&=& -2\int_{0}^{b/2} \Delta X \times y\\
&=& -2\int_{0}^{b/2} \frac{1}{2}\rho (-2Vry) C_{x} y c\mathrm{dy} \\
\\
(C_{n})_{wing}
&=& \frac{4}{Sb} C_{x} \frac{ry}{V} y c\mathrm{dy} \\
&=& \frac{8}{Sb^{2}} \int_{0}^{b/2} (C_{L}\sin{\alpha}-C_{D}\cos{\alpha}) \frac{rb}{2V} y^{2} c\mathrm{dy} \\
\\
(C_{n_{r}})_{wing} &=& \frac{8}{Sb^{2}} \int_{0}^{b/2} (C_{L}\sin{\alpha}-C_{D}\cos{\alpha}) y^{2} c\mathrm{dy} \\
\end{eqnarray}
垂直尾翼の寄与\((C_{n_{r}})_{fin}\)は次の式で表される(白本:p.101)
\begin{eqnarray}
(C_{n_{r}})_{fin}=(C_{y_{r}})_{fin}\frac{l_{f}}{b}
=-\frac{S_{f}}{S}a_{f}\frac{2l_{f}}{b}\frac{l_{f}}{b}
\end{eqnarray}
\(C_{n_{\delta_{r}}}\)
\(C_{n_{\delta_{r}}}\)は垂直尾翼の寄与のみであり,以下の式で求められる(白本:p.91)
\begin{eqnarray}
C_{n_{\delta_{r}}} = -(C_{y_{\delta_{r}}})_{fin}\frac{l_{f}}{b}
= -\frac{S_{f}}{S}a_{f}\tau\frac{l_{f}}{b} \\
\end{eqnarray}
おわりに
上反角\(\Gamma\)が大きい機体における横・方向の安定微係数を導出した
| 主翼の寄与 | 垂直の寄与 | |||
| \(C_{y_{\beta}}\) | = | \(-\frac{2}{S} \int_{0}^{b/2} a_{1} \sin{\Gamma}^2 c \mathrm{dy}\) | + | \(-\frac{S_{f}}{S_{w}}a_{f}\) |
| \(C_{y_{p}}\) | = | \(-\frac{4}{S_{w}b_{w}} \int_{0}^{b/2} a_{1} y\sin{\Gamma}\cos{\Gamma} c \mathrm{dy}\) | + | \(-\frac{S_{f}}{S_{w}}a_{f}\frac{2z_{f}}{b}\) |
| \(C_{y_{r}}\) | = | \(\frac{8}{S_{w}b_{w}} \int_{0}^{b/2} C_{L} y\sin{\Gamma} c\mathrm{dy}\) | + | \(\frac{S_{f}}{S_{w}}a_{f}\frac{2l_{f}}{b}\) |
| \(C_{y_{\delta_{r}}}\) | = | \(\) | + | \(\frac{S_{f}}{S_{w}}a_{f}\tau\) |
| \(C_{l_{\beta}}\) | = | \(-\frac{2}{S_{w}b_{w}} \int_{0}^{b/2} a_{1} \sin{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy}\) | + | \(-\frac{S_{f}}{S_{w}}a_{f}\frac{l_{f}}{b_{w}}\) |
| \(C_{l_{p}}\) | = | \(-\frac{4}{S_{w}b_{w}^{2}} \int_{0}^{b/2} a_{1} y \cos{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy}\) | + | \(-\frac{S_{f}}{S_{w}}a_{f}\frac{2z_{f}}{b}\frac{z_{f}}{b_{w}}\) |
| \(C_{l_{r}}\) | = | \(\frac{8}{S_{w}b_{w}^{2}} \int_{0}^{b/2} C_{L} y \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy}\) | + | \(\frac{S_{f}}{S_{w}}a_{f}\frac{2l_{f}}{b}\frac{z_{f}}{b_{w}}\) |
| \(C_{l_{\delta_{r}}}\) | = | \(\) | + | \(\frac{S_{f}}{S_{w}}a_{f}\tau\frac{z_{f}}{b_{w}}\) |
| \(C_{n_{\beta}}\) | = | \(-\frac{2}{S_{w}b_{w}} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \sin{\Gamma} y c\mathrm{dy}\) | + | \(\frac{S_{f}}{S_{w}}a_{f}\frac{l_{f}}{b_{w}}\) |
| \(C_{n_{p}}\) | = | \(-\frac{4}{S_{w}b_{w}^{2}} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \cos{\Gamma} y^{2} c\mathrm{dy}\) | + | \(\frac{S_{f}}{S_{w}}a_{f}\frac{2z_{f}}{b}\frac{l_{f}}{b_{w}}\) |
| \(C_{n_{r}}\) | = | \(\frac{8}{S_{w}b_{w}^{2}} \int_{0}^{b/2} (C_{L}\sin{\alpha}-C_{D}\cos{\alpha}) y^{2} c\mathrm{dy}\) | + | \(-\frac{S_{f}}{S_{w}}a_{f}\frac{2l_{f}}{b}\frac{l_{f}}{b_{w}}\) |
| \(C_{n_{\delta_{r}}}\) | = | \(\) | + | \(-\frac{S_{f}}{S_{w}}a_{f}\tau\frac{l_{f}}{b_{w}}\) |
ちなみにQX-20では以下のような値になったので,自分で計算するときは参考にしてほしい
| 主翼の寄与 | 垂直の寄与 | 合計 | |||||
| \(C_{y_{\beta}}\) | = | -0.002303 | + | -0.001268 | = | -0.003555 | [1/deg] |
| \(C_{y_{p}}\) | = | -0.454452 | + | -0.002691 | = | -0.455493 | [1/rad] |
| \(C_{y_{r}}\) | = | 0.126752 | + | 0.017427 | = | 0.143466 | [1/rad] |
| \(C_{y_{\delta_{r}}}\) | = | 0 | + | 0.000888 | = | 0.000888 | [1/deg] |
| \(C_{l_{\beta}}\) | = | -0.004041 | + | -0.000023 | = | -0.004049 | [1/deg] |
| \(C_{l_{p}}\) | = | -0.829663 | + | -0.000050 | = | -0.829690 | [1/rad] |
| \(C_{l_{r}}\) | = | 0.227676 | + | 0.000323 | = | 0.227736 | [1/rad] |
| \(C_{l_{\delta_{r}}}\) | = | 0 | + | 0.000016 | = | 0.000016 | [1/deg] |
| \(C_{n_{\beta}}\) | = | -0.000657 | + | 0.000152 | = | -0.000500 | [1/deg] |
| \(C_{n_{p}}\) | = | -0.133063 | + | 0.000323 | = | -0.132307 | [1/rad] |
| \(C_{n_{r}}\) | = | 0.003037 | + | -0.002090 | = | 0.000942 | [1/rad] |
| \(C_{n_{\delta_{r}}}\) | = | 0 | + | -0.000106 | = | -0.000106 | [1/deg] |
なお,上の説明では角度の単位を[rad]に統一しているが,実際に計算するときは角度,角速度,揚力傾斜の単位はそれぞれ[deg],[deg/s],[1/deg]であることに注意すること
「人力飛行機は方向安定が負」というのは教科書に載っていない発見である
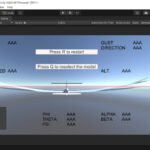
この式を用いて物理演算を行っているフライトシミュレーターはこちら
これらの値を実際に計算する設計シートはこちら




コメント
白本を参照しながら読んでいたのですが、白本では主翼スパンは全てbで表されているところ、こちらではbとbw二通りで表現されています。これはどちらも主翼スパンとして扱えばよろしいでしょうか?
コメントいただきありがとうございます!
bとbwはどちらも主翼スパンで間違いありません.
誤解を防ぐため,主翼面積はSw->S,主翼スパンはbw->bに統一して更新させていただきました.
こちらのサイトを参考に方向安定性のCnbを算出しようとしたのですが,機体に上反角がない場合は,(N)wingと(Cn)wingによる影響はないという考えでよろしいでしょうか.よろしくお願いいたします.
コメントいただきありがとうございます!
この記事では人力飛行機を対象にしているため省略していますが、主翼のCnβの寄与には、上反角の他に後退角によるものがあります。
白本には記載がありませんが、白本の参考文献であるDATCOMの1576ページに主翼の後退角によるCnβの計算式が載っています。必要に応じて参照してみてください(ただし、実験結果との比較はAR=6までしか記載されていませんが…)
≫ https://www.pdas.com/datcomrefs.html
(1番上のAFWAL-TR-83-3048)