鳥コン滑空機の最適重量についての考察

鳥コン滑空機の最適重量について，エネルギー保存則からアプローチして考えてみる

そもそも鳥コン滑空機の最適重量とは？

プロペラ機のチームはパイロットの出力を減らすために機体の軽量化に命を削っているが，滑空機はそうでもない．同じ大きさのプラスチックのボールと野球の硬式球，全力で投げてより遠くまで投げれるのはもちろん硬式球だ．重すぎても飛ばないし，軽すぎても飛ばない．

ちなみに鳥コン出場者ガイドブックには次にように書いてある．

機体の重量

　これはとても大事なことの一つです．重いと飛びませんし，軽く作り弱いと飛行中に壊れます．どこがちょうどよいかは難しいことですが，肝心な部分を強く作り，そうでないところは無駄を省いて軽く作る．これが飛行機設計の基本です．滑空機は材料を工夫して主翼面積22㎡の滑空機を35㎏以下で作れば理想です．

鳥人間コンテスト出場者ガイドブック　p.9

それでは実際に，滑空機の最適重量を計算してみる

エネルギー保存則から飛距離を導く

滑空機のエネルギー保存則

まず，滑空機のエネルギー保存則は

$$(スタート直後のエネルギー)-(着水直前のエネルギー)=(抵抗と風によってなされる仕事)$$

となる．これを数式で表すと

$$(\frac{1}{2}mV_0^2+mgh)-(\frac{1}{2}mV_s^2)=\int_s (D+W) ds$$

である．この式の各項について，順番に考えていく．

①左辺第一項 \(\frac{1}{2}mV_0^2\)

左辺第一項は機体がプラホから飛び立った直後に持っている運動エネルギーである

プラホを助走中の機体は，パイロットのダッシュ力と重力のプラホ斜面に平行な成分によって加速される．

機体に加わる外力を\(P\)，助走距離を\(L\) ，プラホの傾斜を\(\gamma_0\) とすると

\begin{eqnarray} V_0^2 &=& 2(\frac{P}{m}+g\sin \gamma_0 )L \\ V_0 &\cong& \sqrt{2\frac{P}{m}L} \end{eqnarray}

となる．（\(g\sin \gamma_0\)は微小として無視）

この\(V_0\)を左辺第一項に代入すると

$$\frac{1}{2}mV_0^2=PL$$

となる．

②左辺第2項 \(mgh\)

左辺第2項は機体がプラホから飛び出すときに持っている位置エネルギーである．見ての通りプラホの高さと機体重量に比例する

③左辺第3項 \(\frac{1}{2}mV_s^2\)

左辺第3項は機体が着水する直前に持っている運動エネルギーである

この運動エネルギーが一番小さくなるのは機体が失速速度で飛行しているときだが，実際の鳥コンを考えてみると失速迎角になる前にフェアリングかテールが着水してしまうので失速速度で飛行することはできない

そこで，全機の揚力傾斜を\(a_0\)，着水直前の機体の引き起こし角を\(\Delta\alpha\)とすると，着水直前の揚力係数の増加量\(\Delta C_L\)は

$$\Delta C_L=a_0\Delta\alpha$$

よって，着水時の運動エネルギーは，巡航速度を\(V\)，巡航時の揚力係数を\(C_L\)とすると

\begin{eqnarray} \frac{1}{2}mV_s^2 &=& \frac{1}{2}m\frac{mg}{\frac{1}{2}\rho S (C_L+\Delta C_L)}\\ &=& \frac{1}{2}m\frac{mg}{\frac{1}{2}\rho S C_L}\frac{1}{1+\frac{\Delta C_L}{C_L}}\\ &=& \frac{1}{2}mV^2 \frac{1}{1+\frac{\Delta C_L}{C_L}} \end{eqnarray}

となる

④右辺第一項 \(D\)

機体に働く抗力\(D\)は，有害抗力係数を\(C_{D_p}\)，誘導抗力係数を\(C_{D_i}=\frac{C_L^2}{\pi AR}\)，主翼のスパンを\(b\)，アスペクト比を\(AR=\frac{b^2}{S}\)とすると

\begin{eqnarray} D&=&\frac{1}{2}\rho V^2 S C_{D_p}+\frac{1}{2}\rho V^2 S C_{D_i}\\&=&\frac{1}{2}\rho V^2 S C_{D_p}+\frac{1}{2}\rho V^2 S \frac{C_L^2}{\pi AR}\\&=&\frac{1}{2}\rho V^2 S C_{D_p}+\frac{2(mg)^2}{\pi\rho b^2 V^2} \end{eqnarray}

⑤右辺第2項 \(W\)

風が機体に加える力\(W\)は，風による迎角変化で傾いた揚力の一部であると考える．（向きは抗力\(D\)と同じ向きを正）

正対風を\(u_g\)による迎角変化\(\Delta\alpha_g\)は，経路角を\(\gamma\)とすると

\begin{eqnarray}\Delta\alpha_g=\frac{-u_g\sin{\gamma}}{V}\cong\frac{-u_g\gamma}{V}\cong-\frac{u_g}{V}\frac{D}{L} \end{eqnarray}

よって，風が機体に加える力\(W\)は

$$ W=-L\sin{\Delta\alpha_g}\cong-L\Delta\alpha_g=\frac{u_g}{V}D $$

また，\(D+W=(1+\frac{u_g}{V})D\)となる

⑥経路積分 \(\int_s ds\)と飛距離 \(R\)の関係

右辺において，\(D+W\)が一定なら

$$ \int_s (D+W)ds=(D+W)\int_s ds $$

ここで，\(\cos{\gamma}=\frac{\int_s ds}{R}\cong1\)より，

$$ \int_s ds\cong R $$

よって右辺は

$$ \int_s (D+W) ds\cong(D+W)R $$

また，\(\gamma\cong\tan{\gamma}=\frac{h}{R}\)より

$$ R\cong\frac{h}{\gamma} $$

⑦風による経路角への影響

無風のとき，対気速度と対地速度は等しく，対地速度\(u\)，沈下速度\(w\)はそれぞれ

\begin{eqnarray} u&=&V\cos{\gamma}\cong V\\w&=&V\sin{\gamma} \end{eqnarray}

であり，経路角は

$$ \gamma\cong\ \tan{\gamma}=\frac{w}{u}\cong\frac{w}{V} $$

正対風\(u_g\)があると，対地速度と沈下速度は

\begin{eqnarray} u&=&V\cos{\gamma}-u_g\cong V-u_g\\w&=&V\sin{\gamma} \end{eqnarray}

となり，地面に対する経路角は

$$ \gamma\cong\ \tan{\gamma}\cong\frac{w}{V-u_g} $$

よって，経路角に正対風の影響を考慮すると

$$ \gamma\to\gamma\frac{V}{V-u_g} $$

⑥より，飛距離\(R\)は

$$ R\cong\frac{h}{\gamma}\to\frac{h}{\gamma}\frac{V-u_g}{V}=R (1-\frac{u_g}{V}) $$

飛距離を表す式

①～⑦をまとめて，飛距離\(R\)について整理すると

$$ R=(1-\frac{u_g}{V})\frac{PL+mgh-\frac{1}{2}mV^2 \frac{1}{1+\frac{\Delta C_L}{C_L}}}{ (1+\frac{u_g}{V})(\frac{1}{2}\rho V^2 S C_{D_p}+\frac{2(mg)^2}{\pi\rho b^2 V^2})} $$

これで，エネルギー保存則から飛距離を表す式を導くことができた

結果と考察

それでは実際にExcelを使って機体重量と飛距離の関係を見てみる．

なお，機体のデータとしては以下を用いた

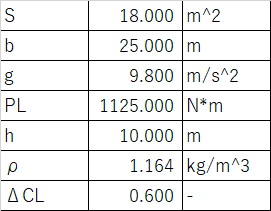
正対風を\(ug=-1.0 m/s, 1.5 m/s, 4.0 m/s\)として，計算した結果を以下に示す

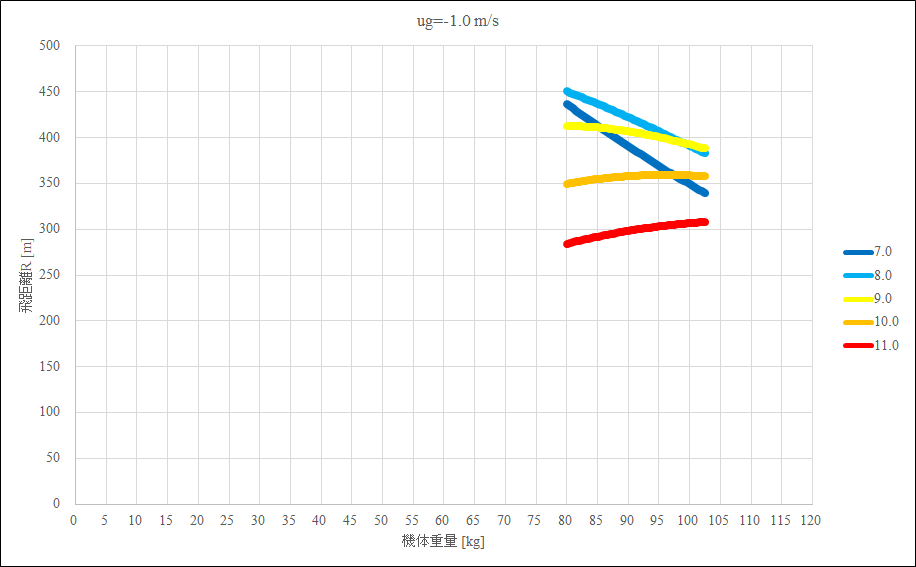
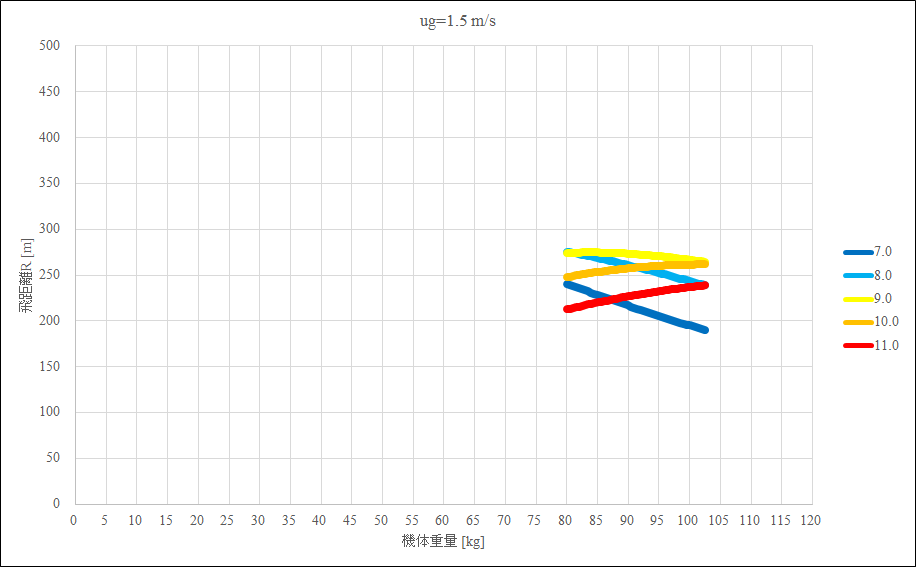
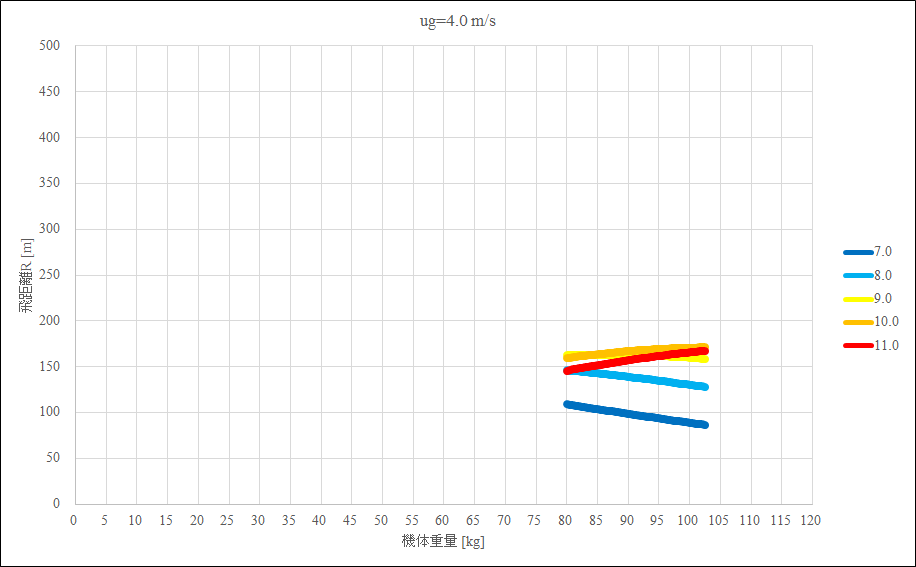
これらのグラフから，以下のことが読み取れる

• 正対風が強いと飛距離が小さくなる
• 正対風が強いほど高速機が有利になる
• 低速機なら低翼面荷重，高速機なら高翼面荷重が有利
• 低翼面荷重高速機はもったいない，高翼面荷重低速機はかなり損

このように，正対風の強さと巡航速度によって最適重量は変わることがわかる

ただし，この式には鳥コン滑空機には欠かせない次の要素が欠けている

• 飛行速度は高度の関数であること．高速機は低い高度しか飛べない
• 飛行高度によって風の強さが異なること．（Wind Gradient，接地境界層）
• 地面効果
• 発進時のエネルギーロス（速度不足による高度のロス）

高速機は発進時には対気速度が不足していることが多く，高度を落として速度を稼がなければならない（いわゆるダイブ飛行）．低い高度を飛べば，正対風も弱まり，地面効果によって誘導抗力も小さくなる．

よって実際の最適重量は，この式で求めたよりも高速機よりになると考えられる．

まとめ

滑空機の最適重量は，その日の風や機体の巡航速度によって大きく異なる

低翼面荷重低速機で背風に乗って棒飛びをするか，高翼面荷重高速機でダイブして正対風の中を駆け抜けるかは設計思想とパイロットの好みしだいとなる

>>実際に使用したExcelファイルのダウンロードはこちらから

使用した文字の定義