遺伝的アルゴリズム(GA: Genetic Algorithm)を用いて,鳥コン滑空機の飛行経路最適化を試みた
鳥コン滑空機においては,縦の運動(高度の操作,ダイブor棒飛び)だけでなく横・方向の運動(風上に飛ぶのではなく背風に乗った飛行)も重要であるため,6自由度の運動を考える
計算コストを鑑みて,縦の運動は非線形,横・方向の運動は線形(微小擾乱)として扱う
今回作成したプログラムによって,鳥コン滑空機の定石とされるいくつかのフライトの有用性を数値計算を用いて確認することができた
ただし,機体の空力計算を行う上での近似が琵琶湖でのフライトに即していない部分も多い
プログラム言語は,本体のソルバーにFortran90,プレ・ポスト処理にExcel VBAを用いた
ソースコードはGitHubにて公開しているので,必要な人はダウンロードしてほしい
≫mtkbirdman.com/GA_NLFS
はじめに
鳥コン滑空機では,「正対風ならダイブ,背風なら棒飛び」,「旋回して風を背負って飛んだ方が飛距離が伸びる」などの,長距離フライトを達成するためのセオリーが存在する
今回の目的は,それらのセオリーを6自由度の運動方程式解くことによるシミュレーションで確認することである
理論
NLFS6
6自由度非線形フライトシミュレーターNLFS6(: 6 degree of freedom Non-Linear Flight Simulator)について説明する
参考にしたのは次の文献
・・・文献1
式番号や細かい記号の定義,式の導出や説明などは文献1を参考にしてほしい
6自由度運動方程式
文献1のp.16より,航空機の運動方程式は次のようになる
\(並進運動方程式\)
\begin{eqnarray}
\dot{u}&=&-\frac{q}{(180/\pi)}w&+\frac{r}{(180/\pi)}v&-g\sin{\theta}&+\frac{\rho V^2 S}{2m}C_{x}\\
\dot{v}&=&-\frac{r}{(180/\pi)}u&+\frac{p}{(180/\pi)}w&-g\cos{\theta}\sin{\phi}&+\frac{\rho V^2 S}{2m}C_{y}\\
\dot{w}&=&-\frac{p}{(180/\pi)}v&+\frac{q}{(180/\pi)}u&-g\cos{\theta}\cos{\phi}&+\frac{\rho V^2 S}{2m}C_{z}\
\tag{1.4-1}
\end{eqnarray}
\(回転運動方程式\)
\begin{eqnarray}
\dot{p}&=&\frac{\frac{L}{I_{x}}+\frac{I_{xz}}{I_{x}}\frac{N}{I_{z}}}{1-\frac{I_{xz}^2}{I_{x}I_{z}}}\\
\dot{q}&=&\frac{M}{I_{y}}\\
\dot{r}&=&\frac{\frac{N}{I_{z}}+\frac{I_{xz}}{I_{z}}\frac{L}{I_{x}}}{1-\frac{I_{xz}^2}{I_{x}I_{z}}}
\tag{1.4-4}
\end{eqnarray}
ここで,
\begin{eqnarray}
L&=&(I_{y}-I_{z})\frac{qr}{(180/\pi)}+I_{xz}\frac{pq}{(180/\pi)}+\frac{\rho V^2 S b}{2}(\frac{180}{\pi})C_{l}\\
M&=&(I_{z}-I_{x})\frac{rp}{(180/\pi)}+I_{xz}\frac{r^{2}-p^{2}}{(180/\pi)}+\frac{\rho V^2 S \overline{c}}{2}(\frac{180}{\pi})C_{m}\\
N&=&(I_{x}-I_{y})\frac{pq}{(180/\pi)}+I_{xz}\frac{qr}{(180/\pi)}+\frac{\rho V^2 S b}{2}(\frac{180}{\pi})C_{n}
\tag{1.4-2}
\end{eqnarray}
ただし,推力に関する項は取り除いてある
この式を導くにあたって用いた仮定は「機体が左右対称である\((I_{xy}=I_{yz}=0)\)」のみなので,式(1.4-1)と式(1.4-4)の微分方程式を解くことによって航空機の運動をシミュレーションすることができる
機体姿勢と地球座標上の軌跡
空間上の機体姿勢はヨー角\(\psi\),ピッチ角\(\theta\),ロール角\(\phi\)によって表される
絶対座標系で記述されたベクトルを機体座標系に変換するには,ベクトルをヨー方向に\(\psi\)→ピッチ方向に\(\theta\)→ロール方向に\(\phi\)と順番に回転させればよい
逆に,機体座標系で記述されたベクトルを絶対座標系に変換するには,ベクトルをロール方向に\(\phi\)→ピッチ方向に\(\theta\)→ヨー方向に\(\psi\)と順番に回転させればよい
よって,機体座標系における対地速度\([u, v, w]^{T}\)から絶対座標系における対地速度\([\dot{X_{E}}, \dot{Y_{E}}, \dot{h_{E}}]^{T}\)への変換は次のようになる
\begin{eqnarray}
\left[\begin{array}{c}
\dot{X_{E}}\\
\dot{Y_{E}}\\
\dot{h_{E}}
\end{array}\right]=
\left[\begin{array}{lll}
\cos{\theta}\cos{\psi}&\sin{\phi}\sin{\theta}\cos{\psi}-\cos{\phi}\sin{\psi}&\cos{\phi}\sin{\theta}\cos{\psi}+\sin{\phi}\sin{\psi}\\
\cos{\theta}\sin{\psi}&\sin{\phi}\sin{\theta}\sin{\psi}+\cos{\phi}\cos{\psi}&\cos{\phi}\sin{\theta}\sin{\psi}-\sin{\phi}\cos{\psi}\\
\sin{\theta}&-\sin{\phi}\cos{\theta}&-\cos{\phi}cos{\theta}
\end{array}\right]
\left[\begin{array}{c}
u\\
v\\
w
\end{array}\right]
\tag{1.5-9}
\end{eqnarray}
式(1.5-9)を使って,式(1.4-1)で計算した\([u, v, w]^{T}\)を\([\dot{X_{E}}, \dot{Y_{E}}, \dot{h_{E}}]^{T}\)に変換する
機体姿勢角と機体軸まわりの角速度
機体軸まわりの角速度\([p, q, r]^{T}\)を機体姿勢角速度\([\dot{\phi}, \dot{\theta}, \dot{\psi}]^{T}\)へ変換する式は次のように表される
\begin{eqnarray}
\dot{\phi}&=&p+(r\cos{\phi}+q\sin{\phi})\tan{\theta}\\
\dot{\theta}&=&q\cos{\phi}-r\sin{\phi}\\
\dot{\psi}&=&\frac{r\cos{\phi}+q\sin{\phi}}{\cos{\theta}}
\tag{1.6-9}
\end{eqnarray}
式(1.6-9)を使って,式(1.4-4)で計算した\([p, q, r]^{T}\)を\([\dot{\phi}, \dot{\theta}, \dot{\psi}]^{T}\)に変換する
迎角,横滑り角,経路角
文献1で扱う突風(gust)は,次のような近似を行っている
- 突風は空間に固定(frozen)されている
- 突風は機体の進行方向にのみ大きさが変化する
- 突風の大きさはステップ上に変化する
このとき,x軸,y軸,z軸の負の方向の突風成分を\([u_{g}, v_{g}, w_{g}]^{T}\)とすると,迎角\(\alpha\),横滑り角\(\beta\)は次のように表される
\begin{eqnarray}
V&=&\sqrt{(u+u_{g})^{2}+(v+v_{g})^{2}+(w+w_{g})^{2}}\\
\alpha&=&\left( \frac{180}{\pi} \right) \arctan{\frac{w+w_{g}}{u+u_{g}}}\\
\beta&=&\left( \frac{180}{\pi} \right) \arcsin{\frac{v+v_{g}}{V}}
\tag{1.7-2}
\end{eqnarray}
突風成分の正負をもう一度確認しておく
- \(u_{g}\):正対風が正
- \(v_{g}\):右翼側から吹いてくる風が正
- \(w_{g}\):上昇風が正
飛行経路角\(\gamma\)を速度ベクトル\([u, v, w]^{T}\)と水平面のなす角とすると,無風のときピッチ角\(\theta\)と迎角\(\alpha\)を用いて次のように表される
\begin{eqnarray}
\gamma=\theta-\alpha
\tag{1.8-6}
\end{eqnarray}
風がある場合は式(1.8-6)は成り立たないので,飛行経路角\(\gamma\)を対地速度ベクトル\([u, v, w]^{T}\)と水平面のなす角とすると,次のように表される
\begin{eqnarray}
\gamma=\theta-\left( \frac{180}{\pi} \right) \arctan{\frac{w}{u}}
\tag{1.8-6’}
\end{eqnarray}
正直この式があっているかどうかはわからないが,飛行中のパイロットが感じ取れるのは対地速度ベクトルと水平面のなす角だと思うので,式(1.8-6’)を使うことにする
空力係数
6自由度の運動方程式(1.4-1),(1.4-4)を見てみると,運動方程式を解くために必要な空力係数は\(C_{x}\),\(C_{y}\),\(C_{z}\),\(C_{l}\),\(C_{m}\),\(C_{n}\)の6つであり,それらを決定する変数は\(V\),\(\alpha\),\(\beta\),\(p\),\(q\),\(r\),\(\delta e\),\(\delta r\),\(\delta h\),\(h_{E}\)の10個である.多い
これら6つの空力係数を数値計算によって求めることは可能であり(≫全機の計算),初期のNLFS6では実際にすべてのタイムステップにおいて6つの空力係数をすべて計算していた
もちろん各タイムステップで6つの空力係数をすべて計算する方が正確ではあるが,かなり時間がかかってしまう.(例えば初期のNLFS6では1フライトの計算に数分,最適化には1週間以上かかった)
そこで,6つの空力係数を以下のように近似する
\begin{eqnarray}
C_{x}&=&C_{x}(V,\alpha,h_{E})\\
C_{y}&=&C_{y_{\beta}}\beta+C_{y_{\delta r}}\delta r\\
C_{z}&=&C_{z}(V,\alpha,h_{E})
\tag{1.8-4',5'}\\
C_{l}&=&C_{l_{\beta}}\beta+\frac{b}{2V}\left( C_{l_{p}}\frac{p}{(180/\pi)}+C_{l_{r}}\frac{r}{(180/\pi)} \right)+C_{l_{\delta r}}\delta r\\
C_{m}&=&C_{m}(V,\alpha,h_{E})+\frac{\overline{c}}{2V}C_{m_{q}}\frac{q}{(180/\pi)}+C_{m_{\delta e}}\delta e+C_{m_{\delta h}}\delta h\\
C_{n}&=&C_{n_{beta}}\beta+\frac{b}{2V}\left( C_{n_{p}}\frac{p}{(180/\pi)}+C_{n_{r}}\frac{r}{(180/\pi)} \right)+C_{n_{\delta r}}\delta r
\tag{1.8-9}\\
\end{eqnarray}
ここで\(C_{x}(V,\alpha,h_{E})\),\(C_{z}(V,\alpha,h_{E})\),\(C_{m}(V,\alpha,h_{E})\)は,あらかじめ適切な範囲・ステップで計算された大量のデータに最小二乗法を施して得られた近似多項式で,次のように表される
\begin{eqnarray}
C_{x,z,m}(V,\alpha,h_{E})&=&(a_{0}+a_{1}V)(b_{0}+b_{1}\alpha+\cdots+b_{6}\alpha^{6})(c_{0}+c_{1}h_{E}+\cdots+c_{6}h_{E}^{5})
\end{eqnarray}
実際に最小二乗法で求めるのはこの式を展開したときの各項の係数なので,\(C_{x}(V,\alpha,h_{E})\),\(C_{z}(V,\alpha,h_{E})\),\(C_{m}(V,\alpha,h_{E})\)それぞれに84個のパラメータが存在することになる.多い
近似を行うことによって,6つの空力係数はたかだか1度の多項式の計算のみで求めることができるようになり,大幅な計算時間の短縮が可能になる
ただし,近似を行ったことによる弊害は以下に挙げるようなものがある
- 横滑り角\(\beta\)などによる抗力の増加は無視
- 操舵\(\delta e\),\(\delta r\)による抗力の増加は無視
- 多項式近似は範囲の端で精度が落ちる
横滑りによる抗力の増加\(C_{D_{\beta}}\)には,カウルの抗力増加に加えて,上反角がついた翼が横滑りすることによって崩れた循環分布による誘導抗力も含まれる
以下にQX-20の主翼の\(C_{D_{i}}-\beta\)線図を示す
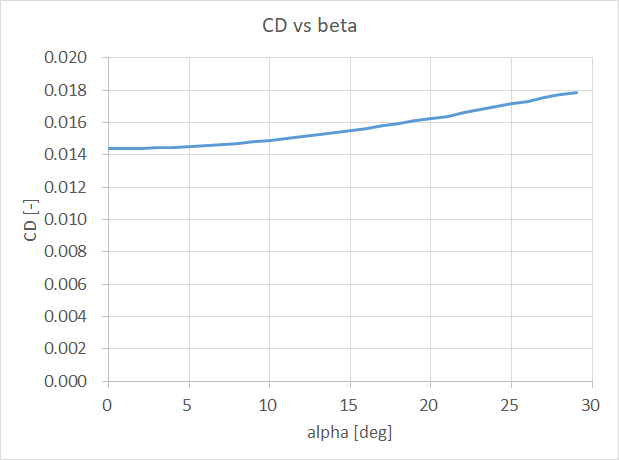
↓より最新の見解はこちら
舵角の定義
機体の操縦は縦をエレベーターor重心移動,横・方向をラダーで行う
エレベーター舵角\(\delta e\)[deg],ラダー\(\delta r\)[deg],重心移動距離\(\delta h\)[%MAC]はそれぞれ,機体に負のモーメントを発生させる方向を正とする.
まとめると次のようになる
- \(\delta e\):機体の頭を下げるときの操作が正
- \(\delta r\):機首を左に振るときの操作が正
- \(\delta h\):重心を前に動かす操作が正
数値積分
数値積分にはAdams-Bashforth法を用いる
≫線型多段法#2次のアダムス・バッシュフォース(Adams-Bashforth)法 - Wikipedia
Adams-Bashforth法は次の式で表される
\begin{eqnarray}
x_{n+2}=x_{n+1}+\frac{3\dot{x}_{n+1}-\dot{x}_{n}}{2}\Delta t
\end{eqnarray}
機体の制御
機体の制御はPID制御で行う
≫PID制御 - Wikipedia
現代制御理論を使った最適制御とか,文献1に載っているダイナミックインバージョン制御とかいろいろやってみたが,結局PID制御が最強だった.Simple is the Best.
縦方向の制御は目標とする経路角\(\gamma_{target}\)を与え,横・方向の制御は目標とするバンク角\(\phi_{tagert}\)を与える
縦方向のフライトは①ダイブ(\(\gamma_{target}=\gamma_{dive}\))→②定常滑空(\(\gamma_{target}=\gamma_{cruise}\))の2つのフェーズ,横・方向の制御は①定常滑空(\(\phi_{target}=0\))→②バンク(\(\phi_{target}=\phi_{bank}\))→③定常滑空(\(\phi_{target}=0\))の3つのフェーズに分けられ,それぞれ独立している
終了判定
解析の終了は以下のように行った
- 時間切れ:最大反復回数に達する.(\({\sf iteration=iteration_{max}}\))
- 失速:失速迎角を超える.(\({\sf alpha>alpha_{stall}}\))
- 着水:着水高度を下回る.(\({\sf hE<hE_{water}}\))
- 逆走:ヨー角の絶対値が90度を超える.(\({\sf abs(psi)>90}\))
今回の解析では\({\sf alpha_{stall}=18.0}\)[deg],\({\sf hE_{water}=0.3}\)[m]としている
逆走の条件は絶対座標系における対地速度の条件\(\frac{dX_{E}}{dt}<0\)でもいい.というか記事を書きながら思ったがこっちのほうが良い
計算は面倒なのでやり直さない
遺伝的アルゴリズム
概要
遺伝的アルゴリズムについては,以下のサイトを参考にした
≫【初心者向け】Re_ゼロから始める遺伝的アルゴリズム【人工知能】 - Qiita
≫遺伝的アルゴリズム_(Genetic Algorithm)を始めよう!
このサイトを見ながらOne-Max問題を解くプログラムを自分で作ってみればだいたい理解できるのではないかと思う
すごくざっくりいうと,『いろいろ良さそうなやつを試してみて一番良かったやつを採用』するアルゴリズムで,必ずしも絶対的な最適解ではないことに注意してほしい
最適化するパラメータ
以下の17個のパラメータを最適化する
- プラホ発進時の姿勢角\([\phi,\theta,\psi]^{T}\)
- 引き起こし時刻\(t_{pull up}\)
- バンク開始時刻\(t_{bank start}\)
- バンク終了時刻\(t_{bank end}\)
- ダイブ角\(\gamma_{dive}\)
- 定常滑空角\(\gamma_{cruise}\)
- バンク角\(\phi_{bank}\)
- PID制御パラメータ\(PID_{lon_{dive}}\),\(PID_{lon_{cruise}}\),\(PID_{lat_{cruise}}\),\(PID_{lat_{bank}}\)
いろいろと試した結果,これに落ち着いた
遺伝子の評価には飛距離を用いる
実装
NLFS6と遺伝的アルゴリズムのプログラムにはFortran90を使用し,プレ処理,ポスト処理にはExcel VBAを用いた
Fortran90のプログラムはGitHubで共有しているので参考にしてほしい
Fortran90を使ったことがなくてもC言語やExcel VBAの経験があれば,この記事とコメントアウトを参考にしながら読むぶんには問題ないと願う
NLFS6
NLFS6の実装について説明する
プレ処理
プレ処理では以下の3つのテキストファイルを準備する
- LIST.txt
- NLFS.txt
- Plane.txt
List.txtには上で述べた遺伝的アルゴリズムのパラメータ,NLFS.txtにはフライトシミュレーターの解析条件,Plane.txtには空力係数を計算する上で必要な値が書き込まれている
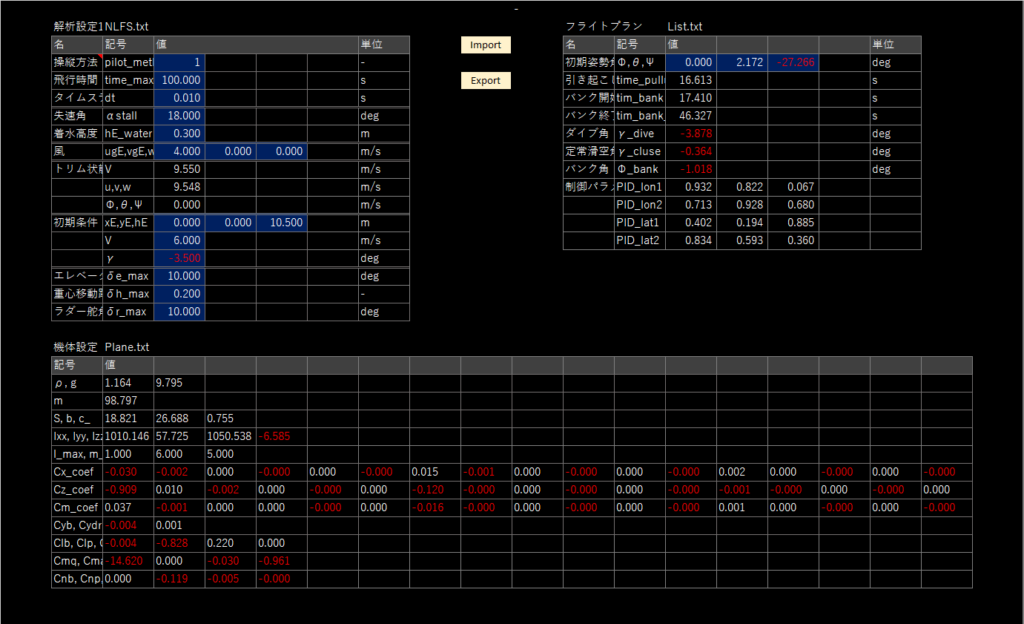
これらのテキストファイルを設計シートに組み込んだExcel VBAのマクロによって作成する
多項式モデルを作る際の訓練データは,\(V=5\sim15\)[m/s],\(\alpha=-10\sim20\)[deg],\(h_{E}=0\sim15\)[deg]をそれぞれ30分割して全機計算を行った29’791個のデータを使用した
ソルバー
プログラム1行1行の解説をしていたらきりがないので,ここではフローチャートのみ説明を行う
まず,飛行解析のプログラムのフローチャートを示す
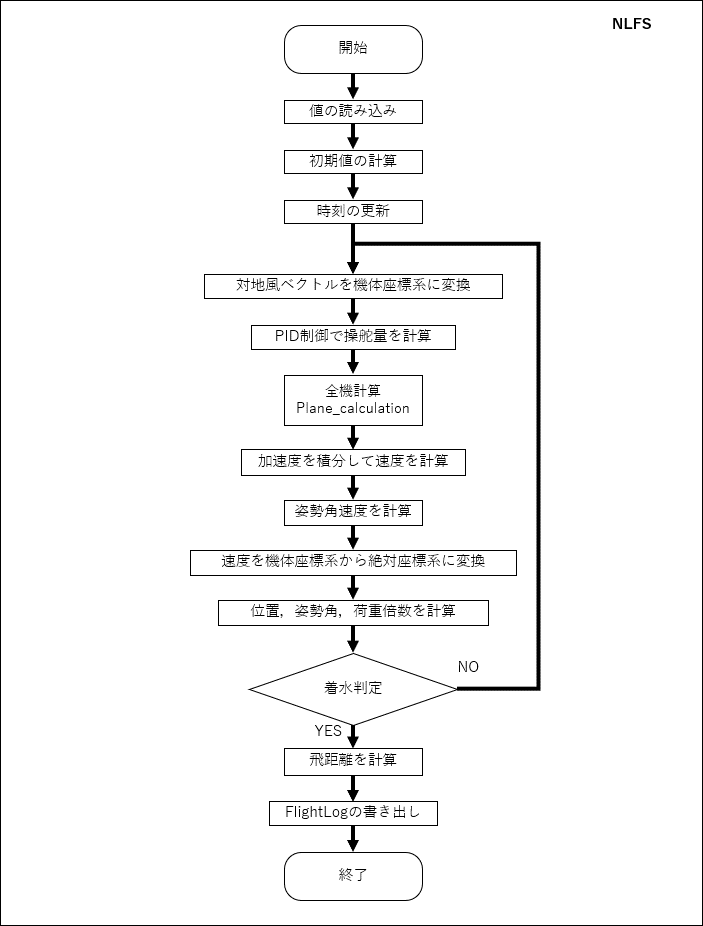
全機計算を行うプログラムのフローチャートを以下に示す
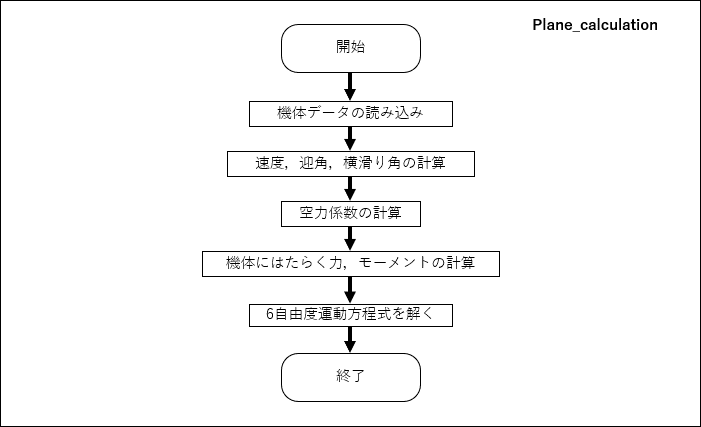
ポスト処理
フライトの結果が書きだされたCSVファイルFlightlog.txtとそのときの遺伝子が書きだされたLIST.txtを設計シートに読み込み,グラフを表示する
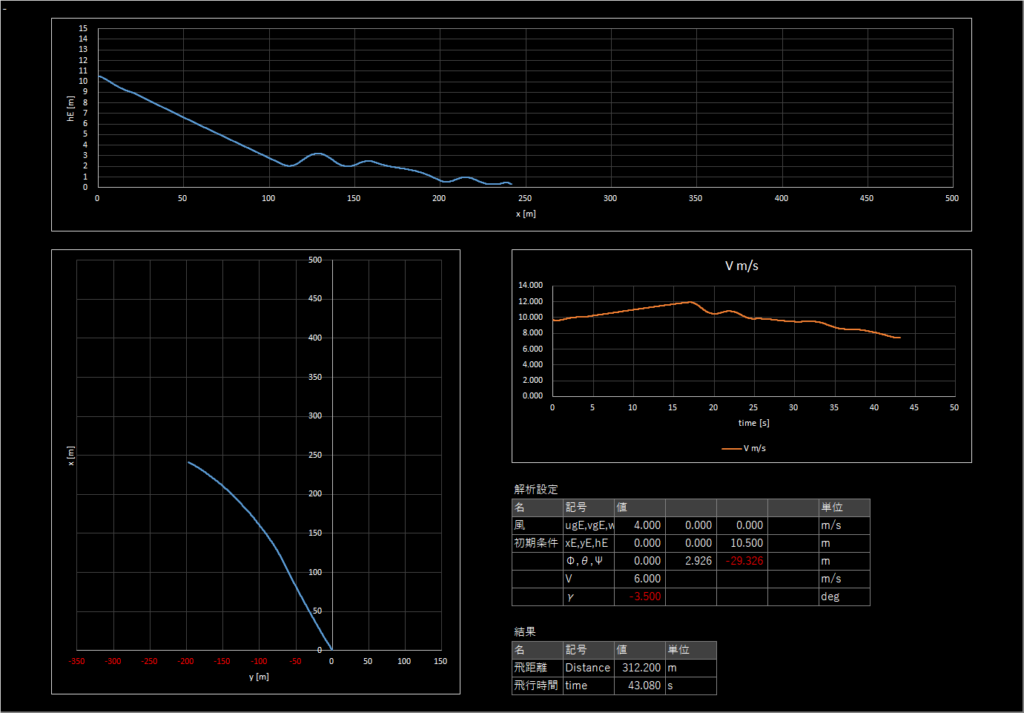
プログラムについては特に説明しないが,Excelは結果を表示するソフトとして使う分にはかなり使い勝手がいいと思う
遺伝的アルゴリズム
遺伝的アルゴリズムのプログラムについては,下の記事のコードをFortarnで書き直しただけなので,ここではフローチャートと遺伝的アルゴリズムのパラメーターのみ紹介する
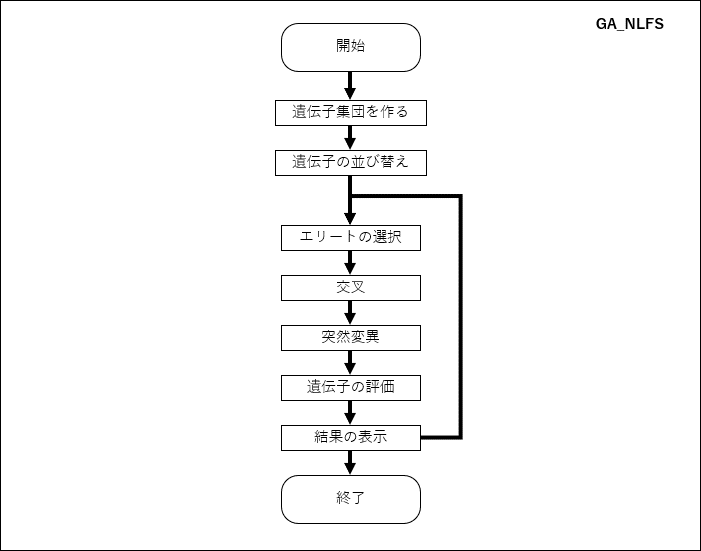
パラメーターは以下のように設定した
- 符号:実数値エンコーディング
- 選択:エリート主義
- 交叉:二点交叉(or 一様交叉)
- 突然変異:摂動(0.0~2.0倍)
- 世代:定常状態モデル
- 1世代の個体数:90
- エリート選択数:30
- 世代数:90
- 個体突然変異率:0.05
- 遺伝子突然変異率:0.02
結果
今回の計算は,すべてQX-20のデータをもとに計算している
QX-20がどんな機体かについては次の記事を参考にしてほしい
≫QX-20設計資料③:概念設計
いくつか明らかに学習が足りていなかったり,局所解に入っていそうなものもあるが再計算するのが面倒なのであえてそのまま載せている
自分でプログラムを動かしてやってみてほしい
プレ計算
プレ計算における多項式回帰の精度を確認しておく
左から,
\(\alpha=1.0\)[deg],\(h_{E}=0.194\)[m]のときの\(C_{x,z,m}-V\)線図,
\(V=9.67\)[m/s],\(h_{E}=0.194\)[m]のときの\(C_{x,z,m}-\alpha\)線図,
\(V=9.67\)[m/s],\(\alpha=1.0\)[deg]のときの\(C_{x,z,m}-h_{E}\)線図
である
いろいろと多項式回帰の特徴量をいじってみたが,これが一番良さそうだった
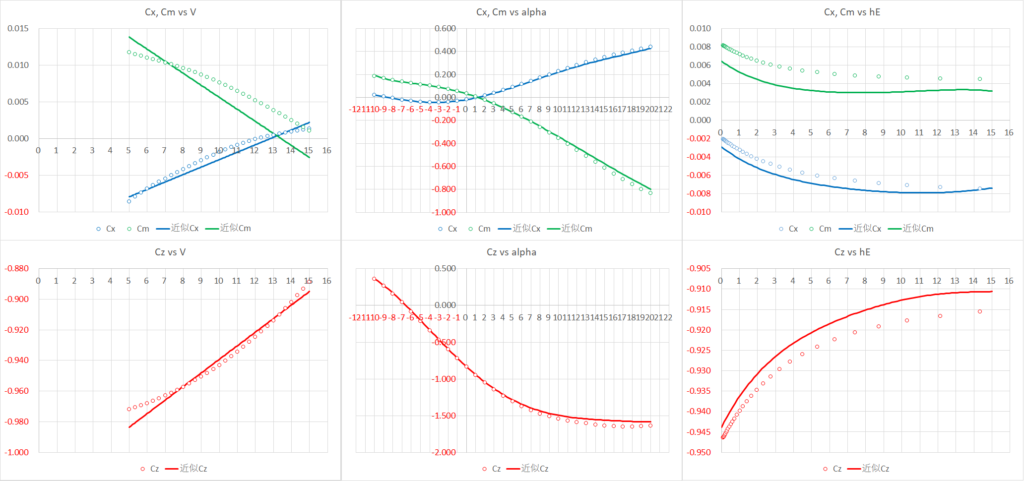
それなりに関数の値を予測できていると思う.異論は認める
このグラフを見ると,\(V=15.00\)[m/s],\(h_{E}=5.311\)[m]のときの\(C_{m}-\alpha\)線図なんて全然予測できていないような気がするが,実際にグラフを見てみると意外とそうでもなかったりする
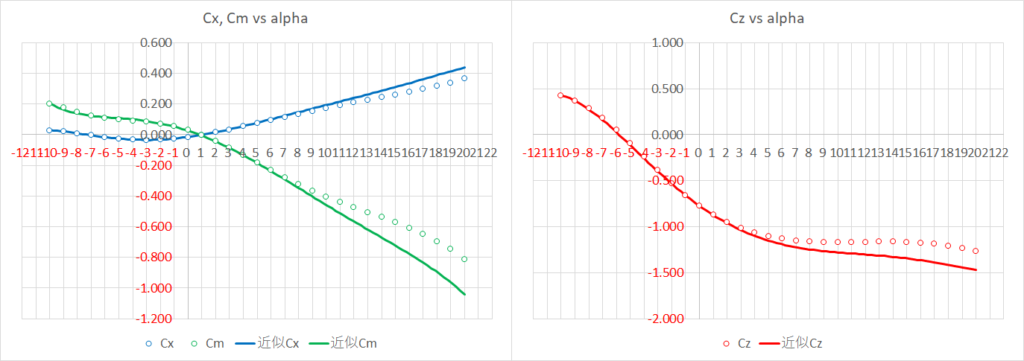
異論は認め(ry
制御なし
まず,NLFS6の性能を確かめるために,機体の制御を行わずに巡航状態に近い速度および経路角を初期値として計算してみる
| Case | 初速 [m/s] | 初期経路角 [deg] | 風速 [m/s] | 風向 | 制御 | 最適化 | 備考 |
| 1-1 | 9.75 | -1.40 | 0.0 | - | なし | なし | |
| 1-2 | 9.75 | -1.40 | 0.0 | - | なし | なし | 初期バンク角-1.0[deg] |
| 1-3 | 9.75 | -1.40 | 2.0 | 3時 | なし | なし |
Case1-1
それっぽく飛ぶ
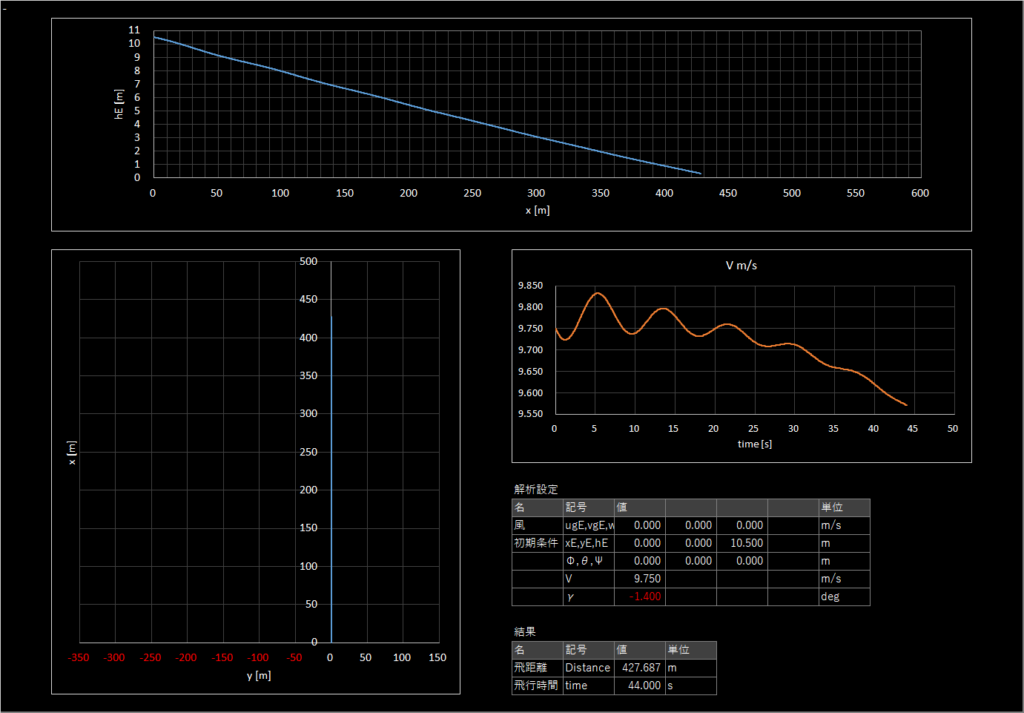
Case1-2
緩やかに発散しながら左方向へ飛んでいる
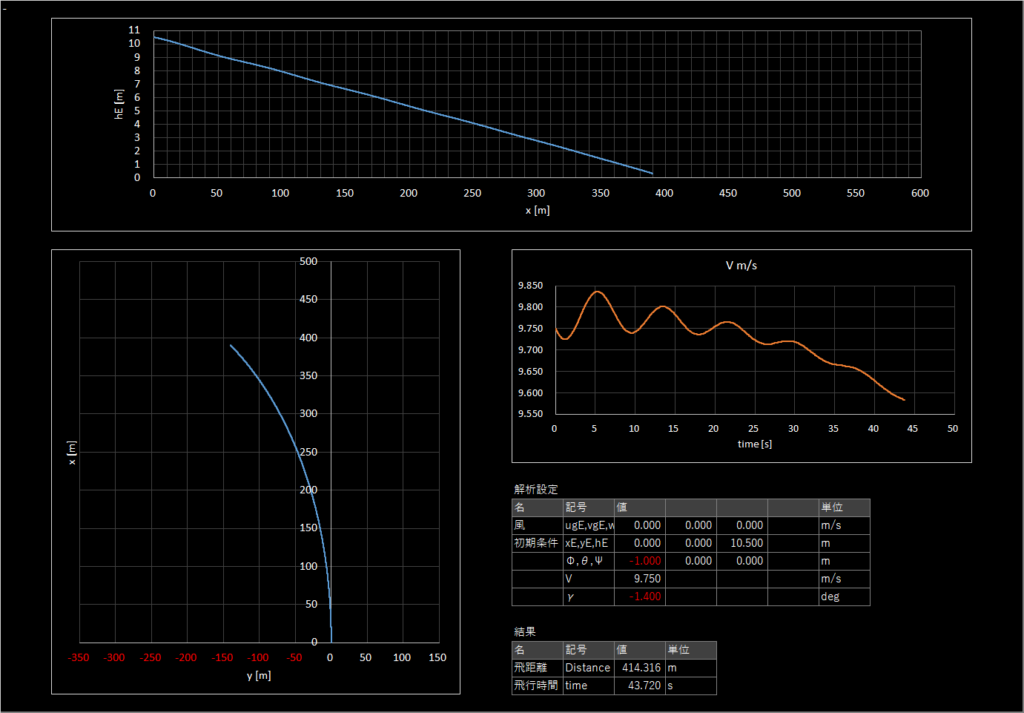
Case1-3
最初左にバンクした後,揺り戻しされて右の方へ飛んでいく
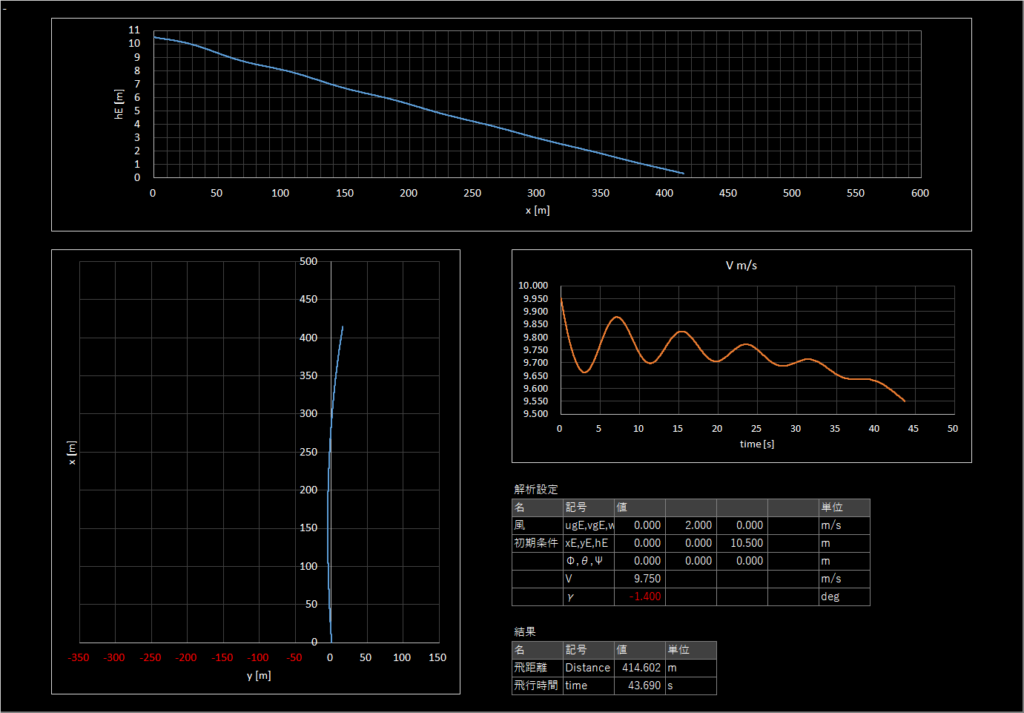
正対風のみ
いろいろな強さの正対風を与えて飛行経路の最適化を行った結果を示す
| Case | 初速 [m/s] | 初期経路角 [deg] | 風速 [m/s] | 風向 | 制御 | 最適化 | 飛距離[m] |
| 2-1 | 6.0 | -3.5 | 4.0 | 12時 | あり | あり | 301.581 |
| 2-2 | 6.0 | -3.5 | 2.0 | 12時 | あり | あり | 341.439 |
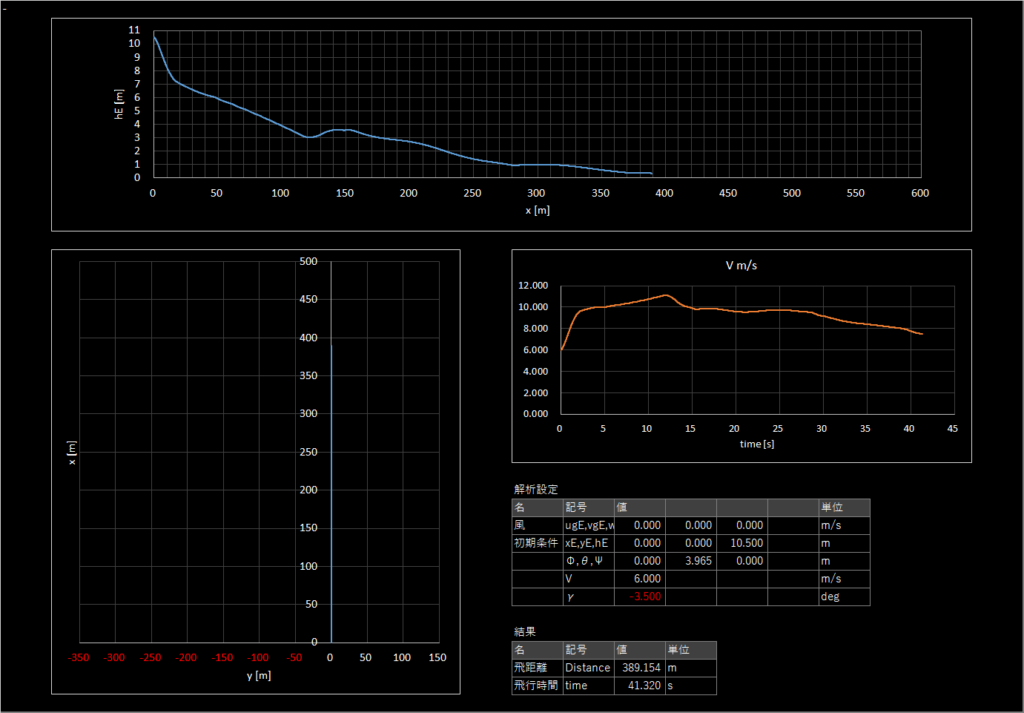
| 2-3 | 6.0 | -3.5 | 0.0 | - | あり | あり | 389.154 |
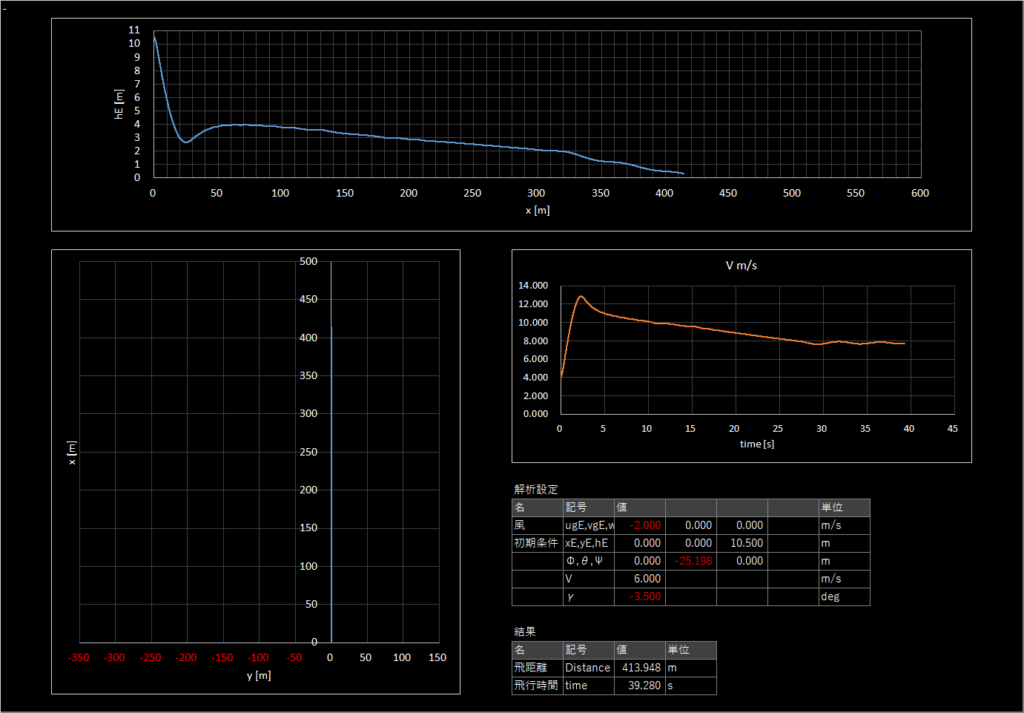
| 2-4 | 6.0 | -3.5 | -2.0 | 12時 | あり | あり | 413.948 |
正対風に向かって飛ぶことがいかに無謀かがよくわかる結果となっている
また,横風成分が全くない場合の旋回はただ飛距離をロスするだけなので,どれも直進する解になっていることにも注目してほしい
2-1
ダイブ角-3.0[deg]で水面ぎりぎりまで降下して引き起こし,水平飛行をする解が得られた
非常に緩やかなダイブといえる
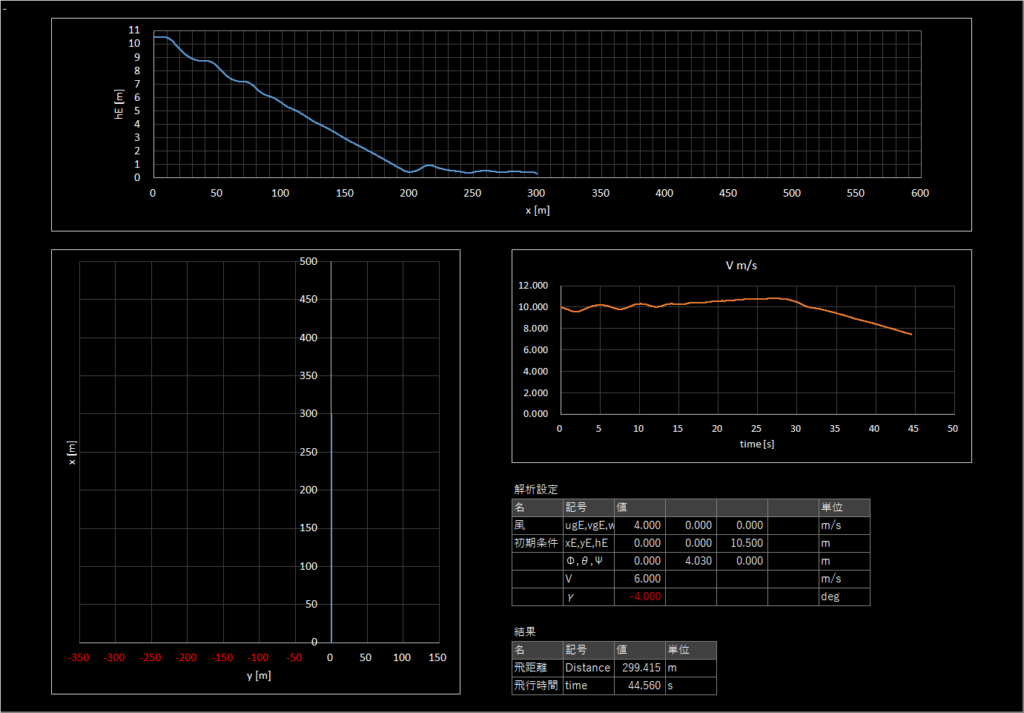
2-2
プラホ上で正対風2m/sというほぼ理想的な状況
定常滑空の操縦が下手なのは学習が足りていないため
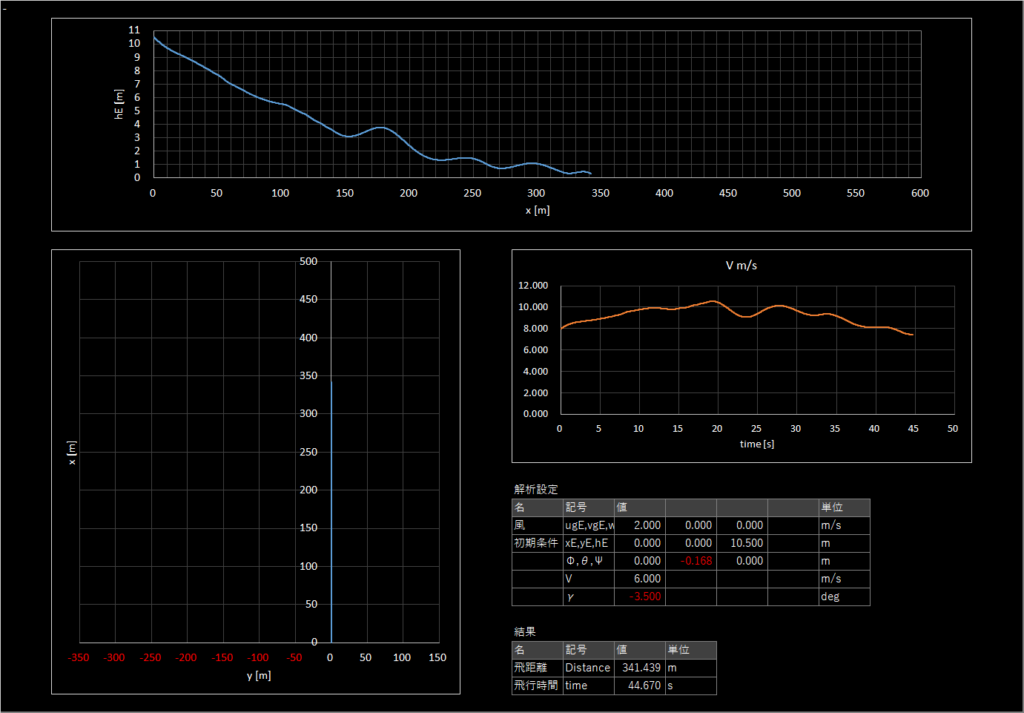
2-3
無風
対気速度が足りておらずプラホから出た直後に高度を落として加速している
2-4
背風
引き起こした後の対気速度がかなり遅い
背風では棒飛びのほうが良いことがわかる
横風
風速を4.0m/sに固定して,風向を変化させて計算してみる
Case3-1はCase2-1と同じものである
飛距離を見るに,Case3-3は局所解に陥ってしまっていると思われる
同じ風速でも風向きと操縦次第で飛距離が150mも変わってしまうのが鳥人間コンテスト滑空機部門なのである
| Case | 初速 [m/s] | 初期経路角 [deg] | 風速 [m/s] | 風向 [deg] | 制御 | 最適化 | 飛距離[m] |
| 3-1 | 6.0 | -3.5 | 4.0 | 0 | あり | あり | 301.581 |
| 3-2 | 6.0 | -3.5 | 4.0 | 15 | あり | あり | 408.033 |
| 3-3 | 6.0 | -3.5 | 4.0 | 30 | あり | あり | 386.233? |
| 3-4 | 6.0 | -3.5 | 4.0 | 45 | あり | あり | 440.001 |
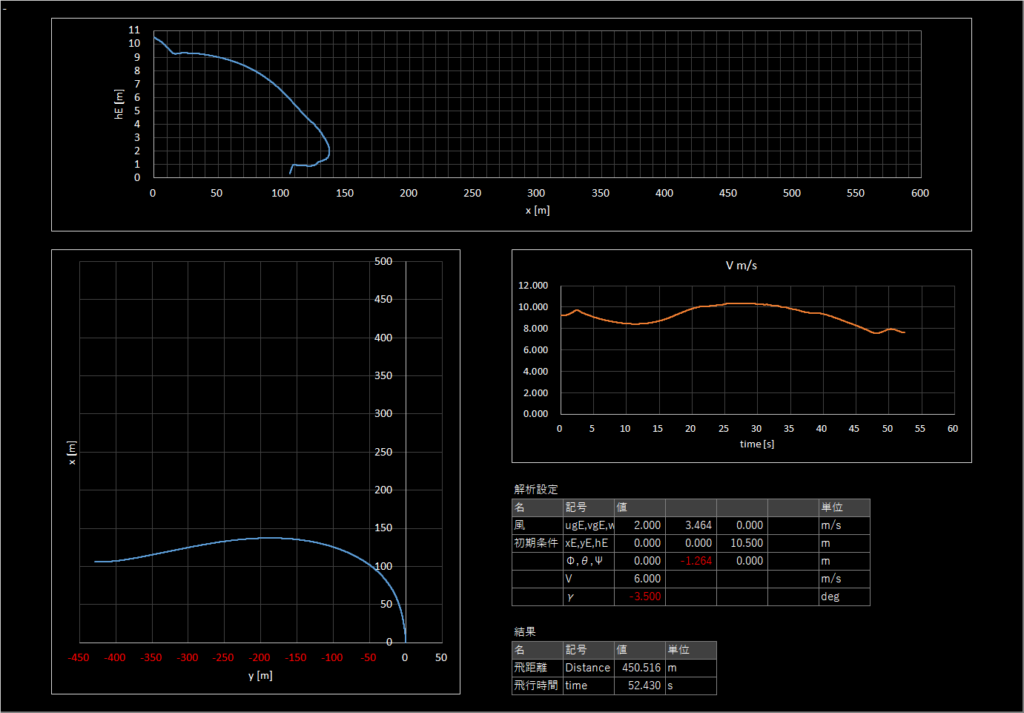
| 3-5 | 6.0 | -3.5 | 4.0 | 60 | あり | あり | 450.516 |
Case3-2
危険飛行区域侵入につき失格であるが,風の力を一身に受けて飛んでいることがわかる
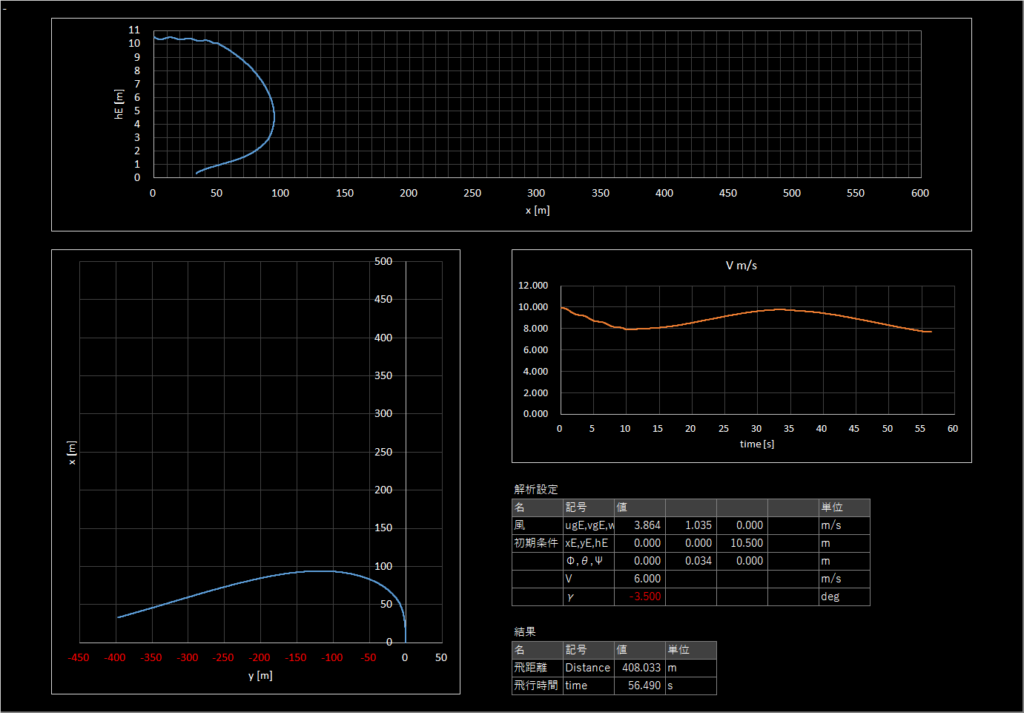
3-3
局所解に陥ったため旋回が不十分で飛距離が伸びていない
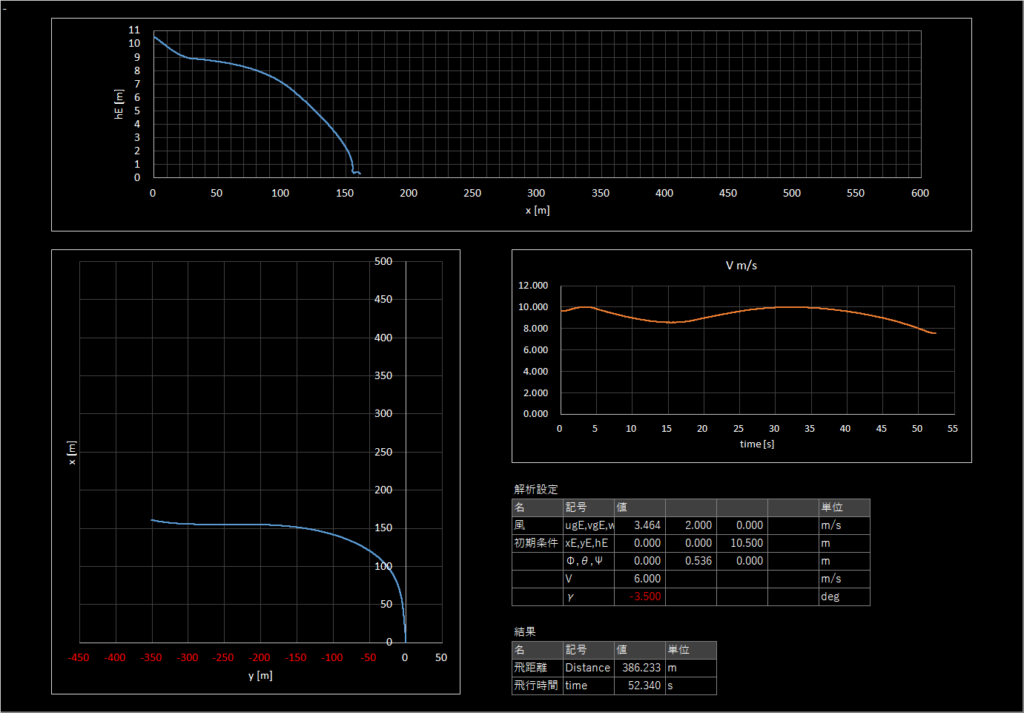
3-4
良いフライト
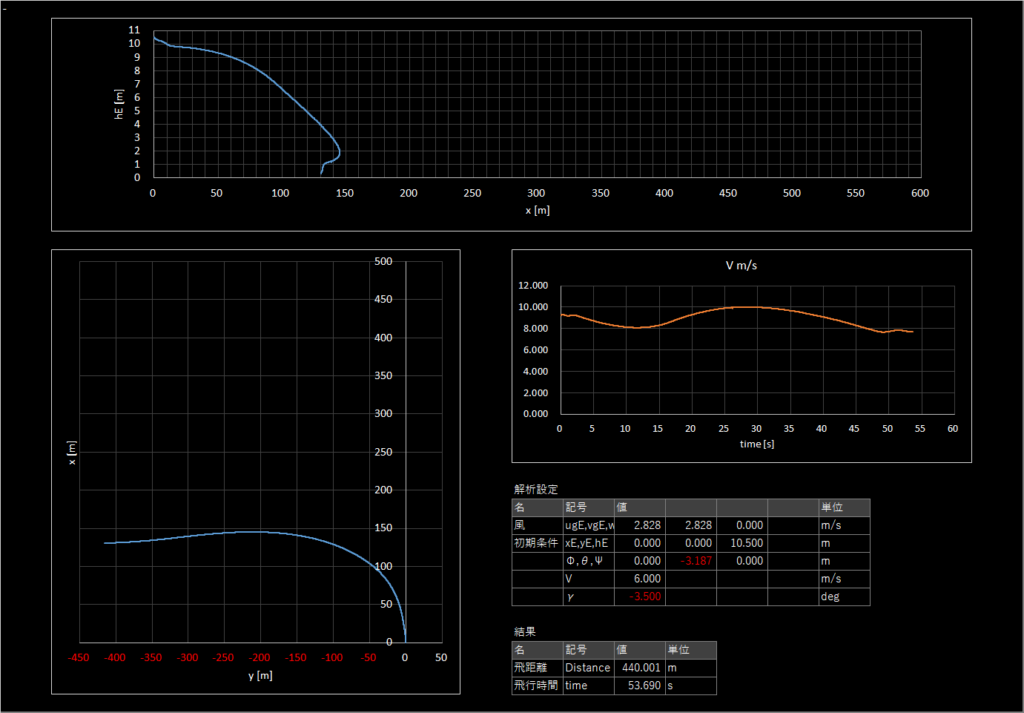
3-5
良いフライト
結論
遺伝的アルゴリズムと6自由度フライトシミュレーターによって,鳥コン滑空機のセオリーと呼ばれるものを数値的に検証することができた
ただし,Case3-3のように,遺伝的アルゴリズムで得られる解は局所的な最適解であることに注意しなければならない
↓より最新の見解はこちら
おまけ:実際にやってみよう!
サンプルコードとエクセルファイルを使って最適化を行う手順を説明する
準備するもの
NLFS6_ver1.f90
≫https://github.com/mtkbirdman/mtkbirdman.com
Excelファイル
Fortran実行環境
プレ処理
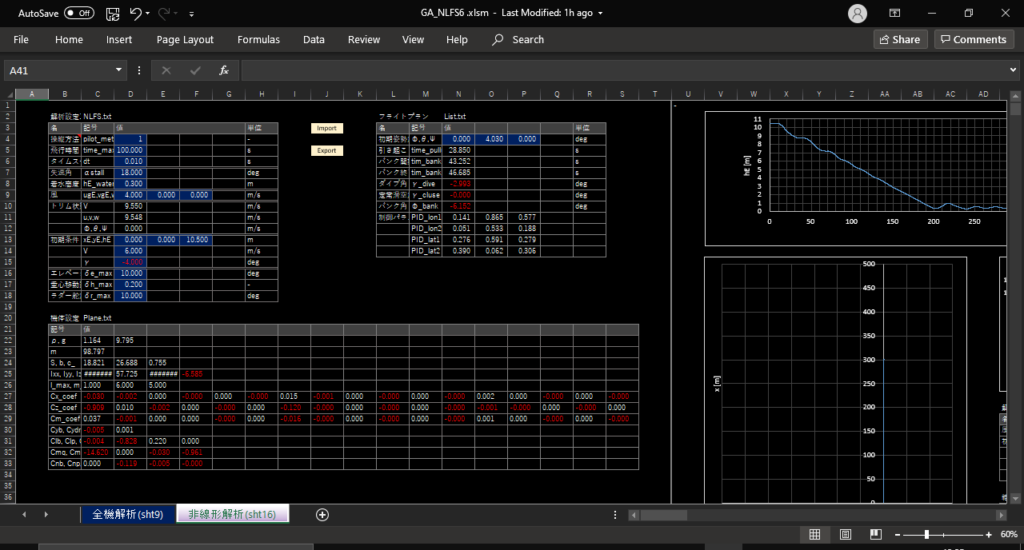
①下図の赤枠に,前もって計算した訓練データを入力する.(今回はQX-20のデータが既に入力されている)

②マクロ”Fit”を実行して多項式モデルの係数を計算する
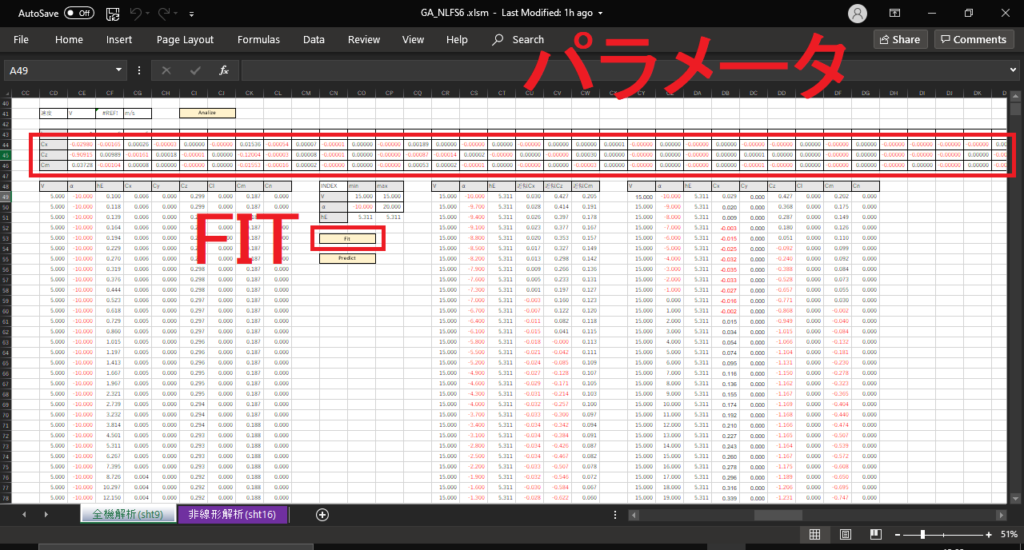
図の赤枠にINDEXを入力して,マクロ”Predict"を実行すれば上のグラフで訓練データと予測値を確認できる
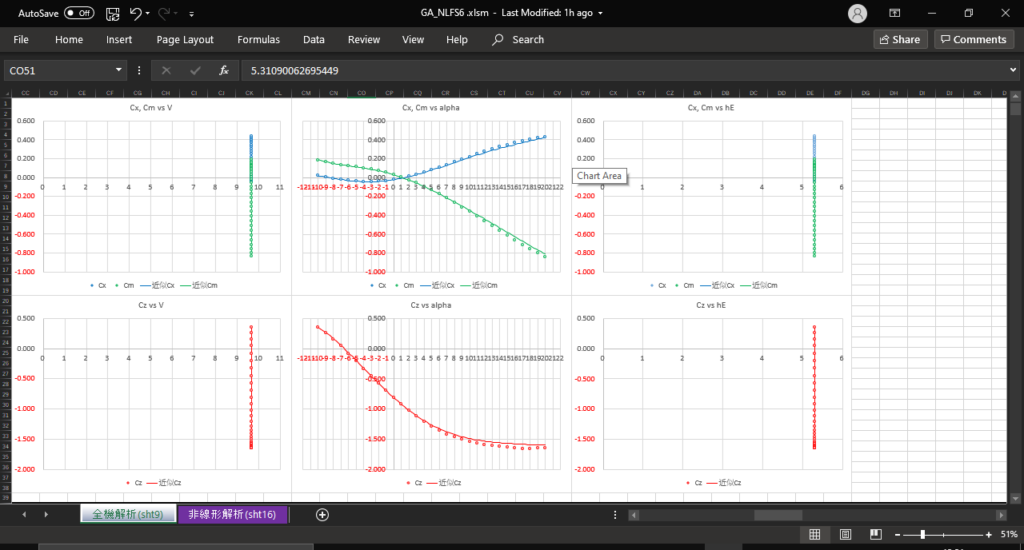
③青色のセルに必要な値を入力して,マクロ”Export"を実行すればLIST.txt,NLFS.txt,Plane.txtが作られる
プログラムの実行
VS codeのターミナルを開いてNLFS6_ver1.f90をコンパイル,実行する
>gfortran NLFS6_ver1.f90
プログラムを実行すると「What Analysis?」と表示されるので,1フライトの計算のみ行いたいなら「0」を,最適化を行いたいなら「1」を入力する
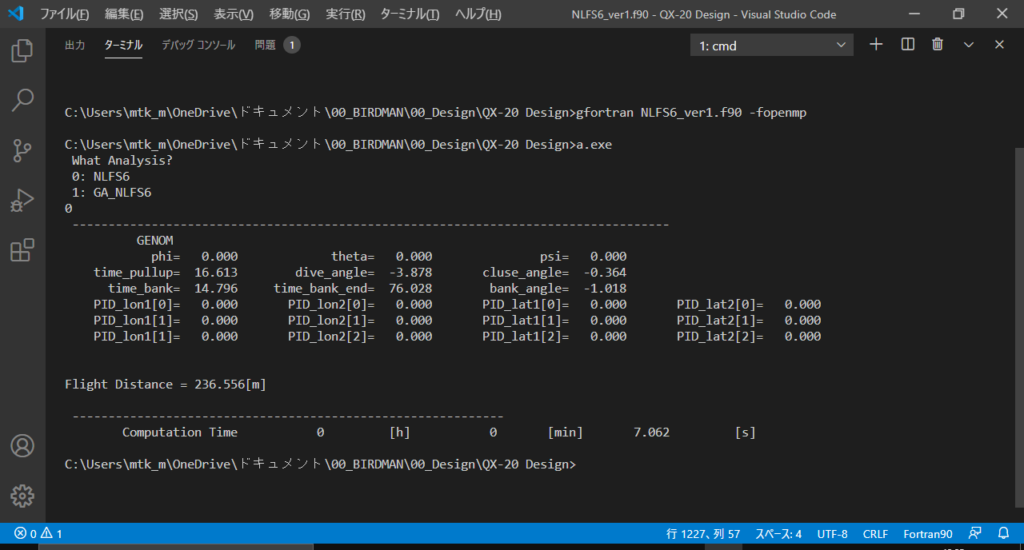
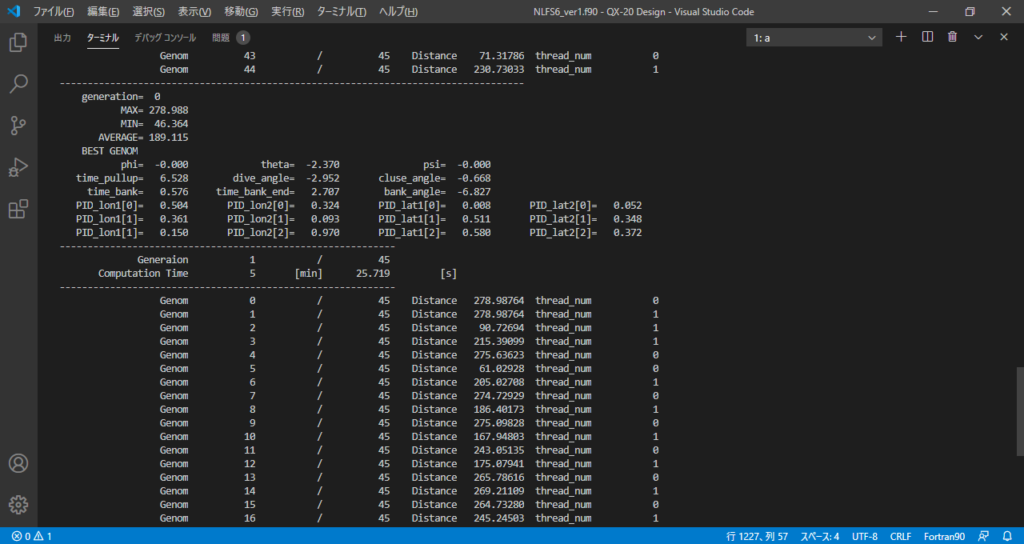
1フライトの計算なら数十秒,最適化には数時間~半日かかる
ポスト処理
マクロ”Import"を実行すれば,FLIGHTLOG.txtとLIST.txtに書かれた結果をExcelファイルに書き込むことができる
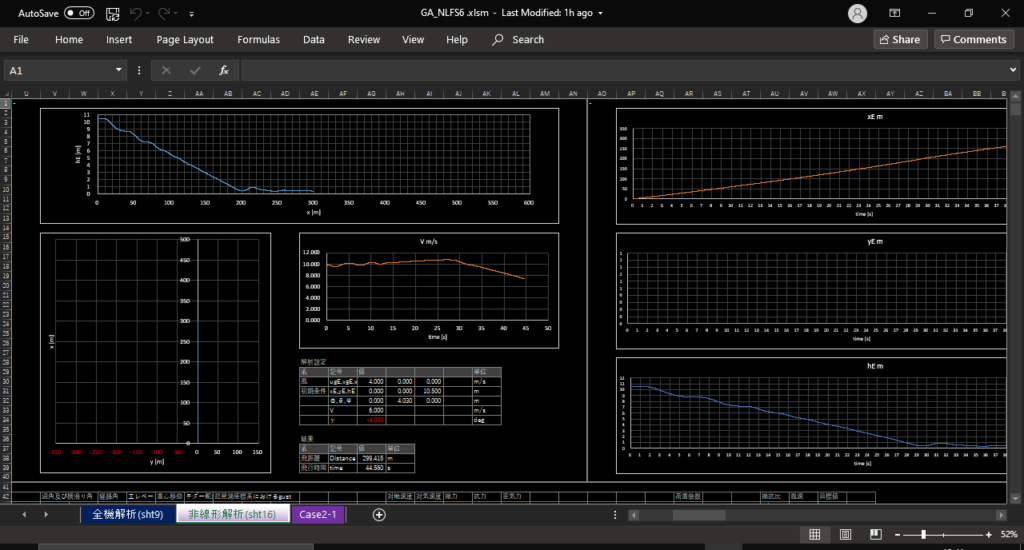
最適化のプログラムでは,1世代終えるごとにその世代で最も優秀な遺伝子のFLIGHTLOG.txtを書きだすので,プログラム実行中に”Import"することで途中経過を確認できる

コメント