C言語を使って境界要素法(パネル法)で二次元翼を解析するプログラムを作成する
≫C言語でCFD入門①:ポテンシャル流れの差分解法
≫C言語でCFD入門②:粘性流れの差分解法
≫C言語でCFD入門③:ポテンシャル流れの有限要素解析
≫C言語でCFD入門④:境界要素法による二次元翼型解析
この記事で説明したソースコードはGithubにアップしてある
≫mtkbirdman.com/CFD/
はじめに
C言語を使って境界要素法(パネル法)で二次元翼を解析するプログラムを作成する
参考にしたのは次の文献
CFDについては前回までと同様に文献1を参考にしていく
理論の説明などは参考文献を参照してもらった方が間違いなくわかりやすいので,この記事では主にプログラムの実装について説明する
『流れの数値解析入門』のC言語版サンプルコードだとでも思ってほしい
また,この記事では虚数単位には\(i\)を用いる
↓C言語の勉強はこの本が圧倒的におすすめ
int main(void)の意味からポインタまで,コードを書きながら一通り独学できる名著
理論概要
境界要素法とは
境界要素法(Boundary Element Method:BEM)とは,文献1に次のように書いてある
境界要素法は,領域の境界上の未知関数の積分により領域内の現象を表現できる場合に,境界条件を満足するような未知関数を求めることにより解く方法で,広くポテンシャル問題の解法として用いられる.
境界要素法 - Wikipedia
ここでは吹き出しや渦を物体内部に配置し,それらの特異点の強さ,位置を物体表面が特異点により誘起された一つの閉じた流線と一致するように決定することにより,任意形状の物体まわりのポテンシャル流れが求められる,特異点解法と呼ばれる方法について解説する.
ちょっと何言ってるかわからないが,要するに翼の表面に渦を配置して,翼表面で誘起される速度の法線方向成分が0になるような境界条件で渦の強さを求めればいい
以前作った渦格子法のプログラムと考え方はよく似ている
≫渦格子法を用いた尾翼の空力計算
ちなみに,みんな大好きXFLR5に組み込まれている二次元翼解析ソフトのXFOILで使われている手法でもある.以下のサイトの記事も参考にするといいかもしれない
≫Xfoilの背景_中で何をしているのか?
≫パネル法の簡単な解説 - 留年ポンコツまるけーのブログ
≫2次元翼型まわりの流れ解析・翼型最適化 実践編 - A Plane On The Sand
今回のプログラムでは複素ポテンシャルをゴリゴリ使うので,復習がてら頑張ってほしい
離散渦の複素ポテンシャル
n個の渦を複素平面上の点\(z_{j}~(j=1,\cdots,n)\)に循環\(\Gamma_{j}~(j=1,\cdots,n)\)で配置すると,\(j\)番目の渦による複素ポテンシャル\(W_{j}(z)\)は次のようになる
\begin{eqnarray}
W_{j}(z)=-\frac{i\Gamma_{j}}{2\pi}\ln{(z-z_{j})}
\tag{4.8}
\end{eqnarray}
複素ポテンシャル\(W_{j}\)の導関数は共役複素速度\(u_{j}-iv_{j}\)であり,次のようになる
\begin{eqnarray}
\frac{W_{j}(z)}{dz}=-\frac{i\Gamma_{j}}{2\pi}\frac{1}{z-z_{j}}=u_{j}-iv_{j}
\tag{4.9}
\end{eqnarray}
これをn個の渦について重ね合わせて,一様流\(U~(u_{0}, v_{0})\)の共役複素速度\({\overline U}~(=u_{0}-iv_{0})\)を重ね合わせると次のようになる
\begin{eqnarray}
\frac{W(z)}{dz}={\overline U}-\frac{i\Gamma_{j}}{2\pi}\sum_{j=1}^{n}\frac{1}{z-z_{j}}=(u_{0}+u)-i(v_{0}+v)
\tag{4.11}
\end{eqnarray}
分布渦の複素ポテンシャル
上で述べたような離散的な渦にはいろいろと問題があるので(文献1参照),面に渦を連続的に配置した分布渦について考える
図4.7のように,翼面上に座標\(s\)をとり,単位長さ当たりの循環\(\gamma(s)\)が配置された長さ\(L\)の平板翼を考える
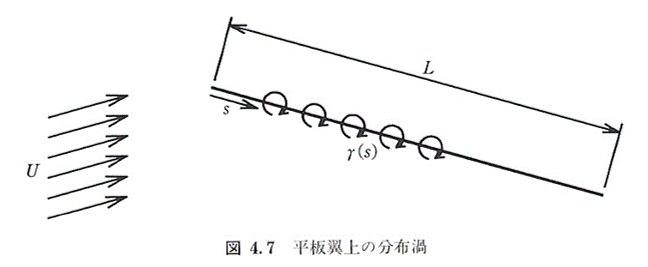
平板翼上の参照点\(z_{ref}\)における速度\(u_{ref}\)は,一様流と平板翼上のすべての渦によって誘起される速度の重ね合わせによって次のように表される
\begin{eqnarray}
{\overline u_{ref}}={\overline U}-\frac{i}{2\pi}\int_{0}^{L}\frac{\gamma(s)}{z_{ref}-z_{j}}ds
\tag{4.23}
\end{eqnarray}
平板翼上の参照点\(z_{ref}\)における法線方向のベクトルを\(n_{ref}\)とすると,誘起される速度\(u_{ref}\)が\(z_{ref}\)において法線方向成分を持たないための条件は次のように表される
\begin{eqnarray}
Re[{\overline u_{ref}}\cdot n_{ref}]=0
\tag{4.24}
\end{eqnarray}
式(4.23)を境界条件式(4.24)に代入すると,今回解くべき\(\gamma(s)\)についての積分方程式が得られる
\begin{eqnarray}
Re[{\overline U}\cdot n_{ref}]+\frac{1}{2\pi}\int_{0}^{L}Im\left[\frac{\gamma(s)}{z_{ref}-z_{j}}\right]ds=0
\tag{4.25}
\end{eqnarray}
この積分方程式に加えて,「翼の後縁がよどみ点になるように循環を決定する」というクッタ条件も適用する
式(4.24)の意味が分からない人は複素数の復習をしよう
≫複素数平面の基本的な公式集 _ 高校数学の美しい物語
積分方程式の離散化
式(4.25)の積分方程式は解析的に解くことができないので有限幅に分割して離散化して解く
そのためにまず,図4.8のように,翼面をn分割し,各要素をその両端の座標\(z_{j}\),\(z_{j+1}~(j=1,\cdots,n)\)を結ぶ線分で置き換えて考える.
※節点\(j\)は\(j=1,\cdots,n+1\)であることに注意
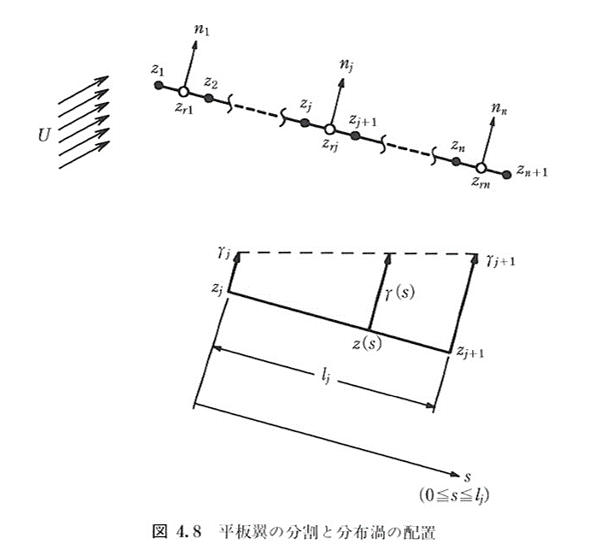
節点\(j\)上で分布渦の強さ\(\gamma_{j}\)を考え,参照点\(z_{ref_{j}}\)は各要素の中点に取る
\begin{eqnarray}
z_{ref_{j}}=\frac{z_{j+1}+z_{j}}{2}
\tag{4.29}
\end{eqnarray}
\(j\)番目の要素線分上の任意の点において,座標\(z(s)\),循環\(\gamma(s)\)は\(s~(0\leq s\leq l_{j})\)を用いて次のように補完される
\begin{eqnarray}
z(s)=z_{j}+\frac{s}{l_{j}}(z_{j+1}-z_{j})
\tag{4.26} \\
\gamma(s)=\gamma_{j}+\frac{s}{l_{j}}(\gamma_{j+1}-\gamma_{j})
\tag{4.27}
\end{eqnarray}
ここで,\(l_{j}\)はj番目の要素線分の長さである
\begin{eqnarray}
l_{j}=|z_{j+1}-z_{j}|
\tag{4.28}
\end{eqnarray}
これらを用いて,離散化された積分方程式を導出する
\(j\)番目の要素上の分布渦によって\(k\)番目の参照点\(z_{ref_{k}}\)に誘起される速度\(du_{k,j}~(k=1,\ldots,n~~j=1,\cdots,n)\)は次の式で表される
\begin{eqnarray}
d{\overline u_{k,j}}=-\frac{i}{2\pi}\int_{0}^{l_{j}}\frac{\gamma(s)}{z_{ref_{k}}-z_{j}}ds
\tag{4.30}
\end{eqnarray}
式(4.30)に,式(4.26)~式(4.28)を代入して積分し,\(\gamma_{j}\),\(\gamma_{j+1}\)について整理すると次のようになる
\begin{eqnarray}
{\overline u_{k,j}}=S_{k,j}^{(1)}\gamma_{j}+S_{k,j}^{(2)}\gamma_{j+1}
\tag{4.33}
\end{eqnarray}
ただし,\(S_{k,j}^{(1)}\),\(S_{k,j}^{(2)}\)は次の式で表される
\begin{eqnarray}
S_{k,j}^{(1)}&=&\frac{il_{j}}{2\pi(z_{j+1}-z_{j})}\left(-1+\frac{z_{j+1}-z_{ref_{k}}}{z_{j+1}-z_{j}}\ln{\frac{z_{j+1}-z_{ref_{k}}}{z_{j}-z_{ref_{k}}}}\right)
\tag{4.34a}\\
S_{k,j}^{(2)}&=&\frac{il_{j}}{2\pi(z_{j+1}-z_{j})}\left(+1-\frac{z_{j}-z_{ref_{k}}}{z_{j+1}-z_{j}}\ln{\frac{z_{j+1}-z_{ref_{k}}}{z_{j}-z_{ref_{k}}}}\right)
\tag{4.34b}
\end{eqnarray}
式(4.33)を翼面上のすべての分布渦\(j\)について足し合わせて,一様流の速度\(U\)と重ね合わせると参照点\(z_{ref_{k}}\)における速度\(u_{k}\)は次のようになる
\begin{eqnarray}
{\overline u_{k}}&=&{\overline U}+\sum_{j=1}^{n}{\overline u_{k,j}}\\
&=&{\overline U}+\sum_{j=1}^{n}(S_{k,j}^{(1)}\gamma_{j}+S_{k,j}^{(2)}\gamma_{j+1})\\
&=&{\overline U}+S_{k,1}^{(1)}\gamma_{1}+\sum_{j=2}^{n}(S_{k,j}^{(1)}+S_{k,j-1}^{(2)})\gamma_{j}+S_{k,n}^{(2)}\gamma_{n+1}~~~~(k=1,\cdots,n)
\tag{4.36}
\end{eqnarray}
ここで,\(k\)番目の要素線分に対する法線方向の単位ベクトル\(n_{k}\)は次のように表される
\begin{eqnarray}
n_{k}=\frac{z_{k+1}-z_{k}}{l_{k}}\frac{1}{i}~~~~(k=1,\cdots,n)
\tag{4.37}
\end{eqnarray}
よって,式(4.36)と式(4.37)を式(4.24)の境界条件\(Re[{\overline u_{k}}\cdot n_{k}]=0\)に代入すると,解くべき積分方程式(4.25)は次の式で表すことができる
\begin{eqnarray}
\sum_{j=1}^{n+1}A_{k,j}\gamma_{j}=B_{k}~~~~(k=1,\cdots,n)
\tag{4.39}
\end{eqnarray}
ただし,\(A_{k,j}\),\(B_{k}\)は次のように表される
\begin{eqnarray}
A_{k,1}&=&Re[S_{k,1}^{(1)}\cdot n_{k}]&(j=1&k=1,\cdots,n)
\tag{4.40a}\\
A_{k,j}&=&Re[(S_{k,j-1}^{(2)}+S_{k,j}^{(1)})\cdot n_{k}]&(j=2,\cdots,n&k=1,\cdots,n)
\tag{4.40b}\\
A_{k,1}&=&Re[S_{k,n}^{(2)}\cdot n_{k}]&(j=n+1&k=1,\cdots,n)
\tag{4.40c}\\
B_{k}&=&Re[{\overline U}\cdot n_{k}]&(k=1,\cdots,n)
\tag{4.40d}\\
\end{eqnarray}
これによって今回解くべき積分方程式(4.25)を離散化して式(4.39)を導くことができた
翼後縁におけるクッタ条件
任意の翼型においては,翼面は図4.12のように分割される
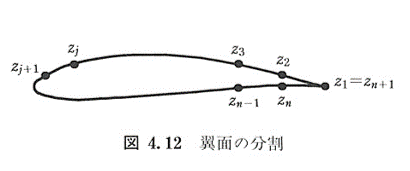
「翼の後縁がよどみ点になるように循環を決定する」というクッタ条件を「翼の上下面の流れが後縁で滑らかに合流し流れ去る」=「後縁を回り込む流れが存在しない」と考えると,クッタ条件は次の式で表すことができる
\begin{eqnarray}
\gamma_{1}+\gamma_{n+1}=0
\tag{4.46}
\end{eqnarray}
連立一次方程式の導出
離散化された積分方程式(4.39)とクッタ条件の式(4.46)を組み合わせたものが今回解くべき連立一次方程式である
\begin{eqnarray}
\left[\begin{array}{ccccc}
A_{1,1}&\cdots&\cdots&\cdots&A_{1,n+1}\\
\vdots& &\ddots& &\vdots\\
A_{n,1}&\cdots&\cdots&\cdots&A_{n,n+1}\\
1&0&\cdots&0&1
\end{array}\right]
\left[\begin{array}{c}
\gamma_{1}\\
\vdots\\
\gamma_{n}\\
\gamma_{n+1}
\end{array}\right]=
\left[\begin{array}{c}
B_{1}\\
\vdots\\
B_{n}\\
0
\end{array}\right]
\tag{4.47}
\end{eqnarray}
式(4.47)の連立方程式を解くことで,翼面上の分布渦\(\gamma\)を求めることができる
流れ場の任意の点における速度
流れ場の任意の点\(z\)における速度\({\overline u}\)を求めるには,式(4.36)の\(z_{ref}\)を\(z_{ref}\rightarrow z\)とすればよい
\begin{eqnarray}
{\overline u}&=&{\overline U}+S_{1}^{(1)}\gamma_{1}+\sum_{j=2}^{n}(S_{j}^{(1)}+S_{j}^{(2)})\gamma_{j})+S_{n}^{(2)}\gamma_{n+1}
\tag{4.42}\\
S_{j}^{(1)}&=&\frac{il_{j}}{2\pi(z_{j+1}-z_{j})}\left(-1+\frac{z_{j+1}-z}{z_{j+1}-z_{j}}\ln{\frac{z_{j+1}-z}{z_{j}-z}}\right)
\tag{4.43a}\\
S_{j}^{(2)}&=&\frac{il_{j}}{2\pi(z_{j+1}-z_{j})}\left(+1-\frac{z_{j}-z}{z_{j+1}-z_{j}}\ln{\frac{z_{j+1}-z}{z_{j}-z}}\right)
\tag{4.34b}
\end{eqnarray}
式(4.47)を解いて分布渦の強さ\(\gamma\)が求まれば,\({\overline u}=u-iv\)より流れ場の任意の点の速度を求めることができる
プログラムの解説①:BEM_P_main.c
それでは実際に作成したプログラムの解説を行う
今回は,データの入出力を主に行うBEM_P_main.cと境界要素法でCl,Cmの計算を主に行うBEM_P.cの2つのプログラムを作成した
ソースコードはGithubも参照
≫mtkbirdman.com/CFD/BEM_P_main.c
≫mtkbirdman.com/CFD/BEM_P.h
≫mtkbirdman.com/CFD/BEM_P.c
C言語における複素数の扱い
C言語には複素数の型が存在し,だいたいのことはできる
詳しくは次のサイトを参考にしてほしい
≫3 複素数と複素関数
main関数
main関数のフローチャートとソースコードを以下に示す
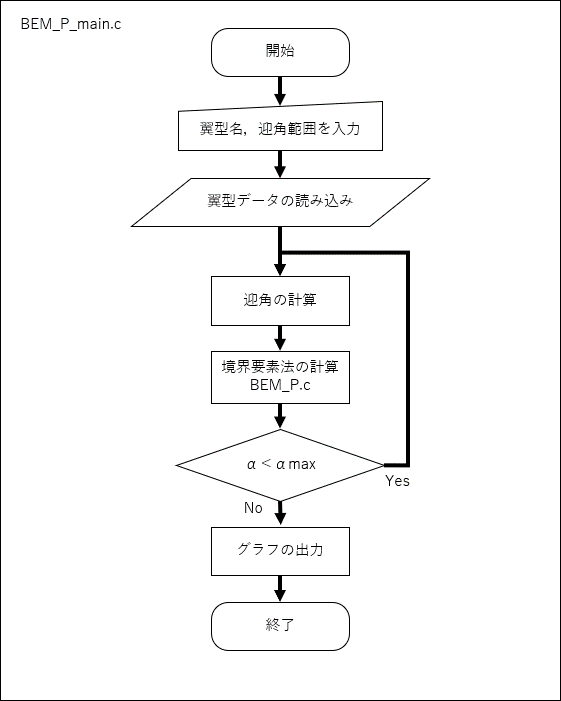
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<stdbool.h>
#include<time.h>
#include<complex.h>
#include<unistd.h>
#include"solver.h" //Header file of skyline_method
#include"BEM_P.h" //Header file of BEM
#define GNUPLOT_PATH "C:/gnuplot/bin/gnuplot.exe" //PATH for gnuplot.exe
int main(void){
FILE *fp;
/*--Constant--*/
double U0=1.0;
char OutputFile_name[64]="Output.txt";
char title[64]="Cm vs alpha";
/*--Variables--*/
double _Complex *z_foil;
char foil_name[256],file_name[256],file_format[]=".txt";
double alpha,amin,amax,da;
int nodes;
int n;
/*--Input foil name--*/
printf("Input foil name\n>>");
fgets(foil_name,sizeof(foil_name),stdin);
foil_name[strlen(foil_name)-1]='\0';
sprintf(file_name,"%s%s",foil_name,file_format); //Concatinate foil_name & file_format
printf("Input amin,amax,da\n>>");
scanf("%lf,%lf,%lf",&amin,&amax,&da);
Check_FileSize(file_name,&nodes);
z_foil=(double _Complex *)malloc(sizeof(double _Complex)*(nodes+1)); //Allocate matrix
Input_Airfoil(file_name,nodes,z_foil);
if((fp=fopen(OutputFile_name,"w"))==NULL){exit(EXIT_FAILURE);}else{fclose(fp);} //Renew output file
n=0;
while(alpha<amax){
alpha=amin+da*n;
Analize_foil(OutputFile_name,nodes,z_foil,U0,alpha);
n++;
}
plot_polar(title,OutputFile_name);
return 0;
}26∼32行目で翼型名と解析する迎角範囲をキーボードから入力し,翼型データが入っているファイル名と出力するグラフタイトルを作っている
≫1行の文字列として入力する - 苦しんで覚えるC言語
≫文字列処理関数 - 苦しんで覚えるC言語
34行目のCheck_FileSize関数で翼型の節点数を調べ,35行目で翼型座標を格納するdouble型の複素数配列z_foilを動的に宣言,36行目のInput_Airfoil関数でz_foilに翼型座標を格納する
40∼45行目のループで,入力した迎角範囲の解析を行う
Analize_foil関数は,計算した迎角,Cl,Cmの値を出力ファイルに書き加えていくので,あらかじめ38行目で出力ファイルをまっさらに作り直しておく
47行目のplot_polar関数で出力ファイルを開き,Gnuplotでグラフを描画する
入力する翼型座標データ
入力する翼型座標データを以下に示す
XFLR5で出力したので,1行目に翼型名が入り,2行目以降に後縁から上面を通って1周するデータである
NACA4412_36dat
1.00024 0.00000
0.95708 0.01152
0.87033 0.03243
0.78077 0.05087
0.69050 0.06644
0.60001 0.07918
0.50949 0.08864
0.41954 0.09458
0.33148 0.09572
0.24556 0.09058
0.16255 0.07821
0.08675 0.05817
0.03514 0.03614
0.01190 0.01992
0.00449 0.01121
0.00218 0.00726
0.00067 0.00355
0.00000 0.00000
0.00024 -0.00347
0.00146 -0.00693
0.00365 -0.01033
0.00679 -0.01360
0.01091 -0.01668
0.02284 -0.02234
0.05727 -0.02927
0.12637 -0.03213
0.21492 -0.02947
0.30793 -0.02449
0.40015 -0.01980
0.49263 -0.01564
0.58568 -0.01143
0.67914 -0.00756
0.77206 -0.00443
0.86537 -0.00214
0.95560 -0.00049
1.00024 0.00000Check_FileSize関数
ソースコードを以下に示す
void Check_FileSize(char *file_name,int *nodes){
FILE *fp; //fp:file pointer
char foil_data[256];
int i,j;
//Open file
*nodes=-1;
if((fp=fopen(file_name,"r"))==NULL){ //Failed
fprintf(stderr,"Not Found %s.",file_name);
exit(EXIT_FAILURE);
}else{ //Success
while(fgets(foil_data,sizeof(foil_data),fp)!=NULL){
*nodes=*nodes+1;
} //Read the data to the last row
}
fclose(fp);
*nodes=*nodes-1;
return;
}1行目から最終行まで読み込んで行数を数えるだけ
Input_Airfoil関数
ソースコードを以下に示す
void Input_Airfoil(char *file_name,int nodes,double _Complex *z_foil){
FILE *fp; //fp:file pointer
char foil_data[256],*ch;
int i,n;
double x,y,val[1024][4];
//Open file
n=0;
if((fp=fopen(file_name,"r"))==NULL){ //Failed
fprintf(stderr,"Not Found %s.",file_name); //Standard error output
exit(EXIT_FAILURE); //Program abnormal termination
}else{ //Success
while(fgets(foil_data,sizeof(foil_data),fp)!=NULL){ //Read the data to the last row
ch=strtok(foil_data," \n"); //Separate the first value by a delimiter
for(i=0;i<256;i++){
if(ch==NULL){ //End of string
break;
}else{
val[n][i]=atof(ch); //Convert a read value from char to double
}
ch=strtok(NULL," \n"); //Separate the next value
}
n++; //Update file size
}
}
fclose(fp); //Close file
for(n=0;n<=nodes;n++){
x=val[n+1][0];y=val[n+1][1];
z_foil[n]=x+I*y;
}
return;
}7~26行目でファイルからデータを読み込んで,28~31行目でz_foilに値を格納している
ファイルからの読み込みについては次の記事を参照してほしい
≫C言語でGnuplotを使って翼型を描く
plot_polar関数
ソースコードを以下に示す
void plot_polar(char *title,char *file_name){
FILE *gp; //gp:gnuplot pointer
/*--Constant--*/
double xmin=-5,xmax=15,ymin=-0.14,ymax=0.01;
char plot1[256]="using 1:3 with lines linewidth 2";
/*--Variables--*/
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){exit(EXIT_FAILURE);}
//Send comands to gnuplot
fprintf(gp,"set title '%s'\n",title);
fprintf(gp,"unset key\n"); //Hide legend
fprintf(gp,"set zeroaxis\n");
fprintf(gp,"set xrange [%f:%f]\n",xmin,xmax); //Set ranges
fprintf(gp,"set yrange [%f:%f]\n",ymin,ymax);
fprintf(gp,"set size square\n"); //Set aspect ratio
//Plot graphic
fprintf(gp,"plot '%s' %s\n",file_name,plot1);
fflush(gp);system("pause");fprintf(gp, "exit\n");_pclose(gp); //Close Gnuplot
return;
}Analize_foil関数によって出力されたファイルをGnuplotで出力する
データファイルをGnuplotで出力するやり方については次のサイトを参照してほしい
≫gnuplotコマンド集 - 二次元グラフの描画
グラフの範囲などの設定はお好みでどうぞ
プログラムの解説②:BEM_P.c
境界要素法でCl,Cmの計算を行うBEM_P.cについて説明する
軸になるのはmain関数で出てきたAnalize_foil関数である
Analize_foil関数
Analize_foil関数のフローチャートとソースコードを以下に示す
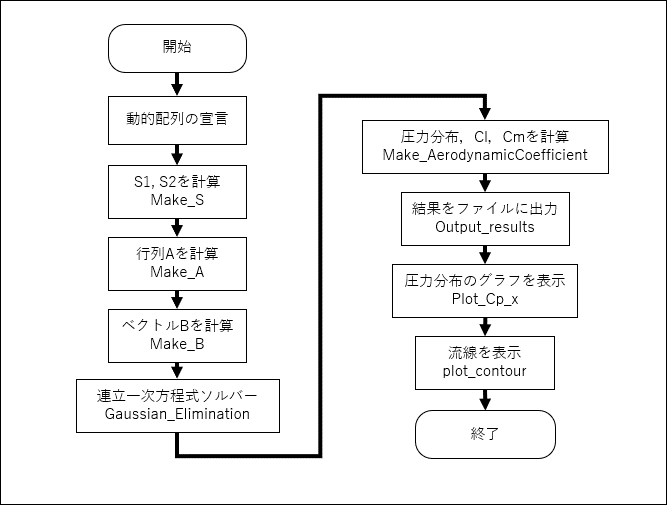
void Analize_foil(char *OutputFile_name,int nodes,double _Complex *z_foil,double U0,double alpha){
/*--Constant--*/
int kmax=40; //kmax:number of streamline
double xmin=-0.5,xmax=1.5,ymin=-0.5,ymax=0.5; //graph range
char title[64];
/*--Variables--*/
double _Complex **S1,**S2;
double _Complex *S1_base,*S2_base;
double _Complex U_inf=U0*cos(alpha*(M_PI/180))-I*U0*sin(alpha*(M_PI/180)); //Uniform flow
double **A,*B;
double *gamma,*l,*Cp; //gamma:circulation, l:length, Cp:pressure coefficient
double *A_base;
double Cl,Cm; //Cl:Lift coefficient, Cm:piching moment coefficient
char foil_name[256]="sample",file_name[256],file_format[]=".txt";
int i,j,k,n;
/*--Allocate Matrix--*/
S1=(double _Complex **)malloc(sizeof(double _Complex *)*(nodes+1));S1_base=(double _Complex *)malloc(sizeof(double _Complex)*(nodes+1)*(nodes+1));for(n=0;n<=nodes;n++){S1[n]=S1_base+(nodes+1)*n;}
S2=(double _Complex **)malloc(sizeof(double _Complex *)*(nodes+1));S2_base=(double _Complex *)malloc(sizeof(double _Complex)*(nodes+1)*(nodes+1));for(n=0;n<=nodes;n++){S2[n]=S2_base+(nodes+1)*n;}
l=(double *)malloc(sizeof(double)*nodes); //value at z_ref
Cp=(double *)malloc(sizeof(double)*nodes); //value at z_ref
A=(double **)malloc(sizeof(double *)*(nodes+1));A_base=(double *)malloc(sizeof(double)*(nodes+1)*(nodes+1));for(n=0;n<=nodes;n++){A[n]=A_base+(nodes+1)*n;}
B=(double *)malloc(sizeof(double)*(nodes+1));
gamma=(double *)malloc(sizeof(double)*(nodes+1));
Make_S(nodes,l,z_foil,S1,S2);
Make_A(nodes,l,A,z_foil,S1,S2);
Make_B(nodes,l,B,U_inf,z_foil);
Gaussian_Elimination(nodes,A,B);for(n=0;n<=nodes;n++){gamma[n]=B[n];}
Make_AerodynamicCoefficient(nodes,alpha,&Cl,&Cm,l,gamma,Cp,U_inf,z_foil);
Output_resluts(OutputFile_name,alpha,Cl,Cm);
strcpy(title,"Cp vs x");
plot_Cp_x(title,nodes,Cp,z_foil);
strcpy(title,"Stream line");
plot_contour(title,kmax,nodes,xmin,xmax,ymin,ymax,l,gamma,U_inf,z_foil);
return;
}17~24行目で動的配列の宣言を行っている
節点は0~nのn+1個で,要素線分の長さlと圧力分布Cpは要素線分の中点で定義するので,要素数は0~n-1のn個である
圧力分布のグラフの表示と流線の表示は必ずしも必要ではないので,この記事の最後におまけとしてソースコードを載せておく
Make_S関数
式(4.28)で要素線分の長さl,式(4.29)で参照点の座標z_ref,式(4.34)でS1,S2を計算する
\begin{eqnarray}
l_{j}&=&|z_{j+1}-z_{j}|
\tag{4.28}\\
z_{ref_{j}}&=&\frac{z_{j+1}+z_{j}}{2}
\tag{4.29}\\
S_{k,j}^{(1)}&=&\frac{il_{j}}{2\pi(z_{j+1}-z_{j})}\left(-1+\frac{z_{j+1}-z_{ref_{k}}}{z_{j+1}-z_{j}}\ln{\frac{z_{j+1}-z_{ref_{k}}}{z_{j}-z_{ref_{k}}}}\right)
\tag{4.34a}\\
S_{k,j}^{(2)}&=&\frac{il_{j}}{2\pi(z_{j+1}-z_{j})}\left(+1-\frac{z_{j}-z_{ref_{k}}}{z_{j+1}-z_{j}}\ln{\frac{z_{j+1}-z_{ref_{k}}}{z_{j}-z_{ref_{k}}}}\right)
\tag{4.34b}
\end{eqnarray}
ソースコードを以下に示す
void Make_S(int nodes,double *l,double _Complex *z_foil,double _Complex **S1,double _Complex **S2){
double _Complex z_ref[nodes];
int i,j,k,n;
//Make l & z_ref
for(i=0;i<nodes;i++){
l[i]=cabsf(z_foil[i+1]-z_foil[i]); //eq(4.28)
z_ref[i]=(z_foil[i]+z_foil[i+1])/2; //eq(4.29)
}
//Make S1 & S2 eq(4.34)
for(k=0;k<nodes;k++){
for(j=0;j<nodes;j++){
S1[k][j]=((I*l[j])/(2*M_PI*(z_foil[j+1]-z_foil[j])))*(-1+(z_foil[j+1]-z_ref[k])/(z_foil[j+1]-z_foil[j])*clogf((z_foil[j+1]-z_ref[k])/(z_foil[j]-z_ref[k])));
S2[k][j]=((I*l[j])/(2*M_PI*(z_foil[j+1]-z_foil[j])))*(+1-(z_foil[j]-z_ref[k])/(z_foil[j+1]-z_foil[j])*clogf((z_foil[j+1]-z_ref[k])/(z_foil[j]-z_ref[k])));
}
}
return;
}打ち間違いにさえ気を付ければ,そこまで難しくない
Make_A関数
式(4.37)で要素線分に対する法線ベクトルz_nを計算し,式(4.40)で係数Aを計算する
\begin{eqnarray}
n_{k}&=&\frac{z_{k+1}-z_{k}}{l_{k}}\frac{1}{i}&(k&=&1,\cdots,n)
\tag{4.37}\\
A_{k,1}&=&Re[S_{k,1}^{(1)}\cdot n_{k}]&(j&=&1&k=1,\cdots,n)
\tag{4.40a}\\
A_{k,j}&=&Re[(S_{k,j-1}^{(2)}+S_{k,j}^{(1)})\cdot n_{k}]&(j&=&2,\cdots,n&k=1,\cdots,n)
\tag{4.40b}\\
A_{k,1}&=&Re[S_{k,n}^{(2)}\cdot n_{k}]&(j&=&n+1&k=1,\cdots,n)
\tag{4.40c}
\end{eqnarray}
配列Aのn行目には式(4.46)のクッタ条件を代入する
\begin{eqnarray}
\gamma_{1}+\gamma_{n+1}=0
\tag{4.46}
\end{eqnarray}
ソースコードを以下に示す
void Make_A(int nodes,double *l,double **A,double _Complex *z_foil,double _Complex **S1,double _Complex **S2){
double _Complex z_n[nodes+1]; //n:normal
int i,j,k,n;
//Make z_n
for(i=0;i<nodes;i++){
z_n[i]=((z_foil[i+1]-z_foil[i])/l[i])*(1/I); //eq(4.29)
}
//Make A eq(4.40)
for(k=0;k<nodes;k++){
for(j=0;j<=nodes;j++){
if(j==0){
A[k][j]=crealf(S1[k][j]*z_n[k]);
}else if(j==nodes){
A[k][j]=crealf(S2[k][j-1]*z_n[k]);
}else{
A[k][j]=crealf((S2[k][j-1]+S1[k][j])*z_n[k]);
}
}
}
A[nodes][0]=1;A[nodes][nodes]=1; //Kutta condition
return;
}これも難しくはない
Make_B関数
式(4.37)で要素線分に対する法線ベクトルz_nを計算し,式(4.40)で係数Bを計算する
\begin{eqnarray}
B_{k}&=&Re[{\overline U}\cdot n_{k}]&(k=1,\cdots,n)
\tag{4.40d}\\
\end{eqnarray}
これにもn行目にクッタ条件の式(4.46)を代入してある
ソースコードを以下に示す
void Make_B(int nodes,double *l,double *B,double _Complex U_inf,double _Complex *z_foil){
double _Complex z_n[nodes+1]; //n:normal
int i,j,k,n;
//Make z_n
for(i=0;i<nodes;i++){
z_n[i]=((z_foil[i+1]-z_foil[i])/l[i])*(1/I); //eq(4.29)
}
//Make B eq(4.40d)
for(k=0;k<nodes;k++){
B[k]=-crealf(U_inf*z_n[k]);
}
B[nodes]=0; //Kutta Condition
return;
}特に難しくない
Gaussian_Elimination関数
連立一次方程式\({\bf A\gamma=B}\)の係数行列AとベクトルBが求まったので,ガウスの消去法で解を求める
ソースコードは次の記事(≫大規模疎行列に対する連立一次方程式のソルバー:Skyline法)の最後に乗っているので,必要なら参考にしてほしい
Make_AerodynamicCoefficient関数
渦分布\(\gamma\)が求まったので,翼表面の速度から圧力分布Cpを計算し,圧力を翼面全体にわたって積分することで揚力係数Clとピッチングモーメント係数Cmを計算する
一様流の速度を\(U_{0}\),迎角を\(\alpha\)とし,\(j\)番目の要素の長さを\(l_{j}\),傾き\(\theta_{j}=\arg{(z_{j+1}-z_{j})}\),要素線分上の参照点\(z_{ref_{j}}=x_{ref_{j}}+iy_{ref_{j}}\)における速度を\(U_{j}\)とすると,圧力係数\(C_{p_{j}}\),揚力係数\(C_{l}\),ピッチングモーメント係数\(C_{m}\)は次の式で表される
\begin{eqnarray}
C_{p_{j}}&=&\left\{1-\left(\frac{U_{j}}{U_{0}}\right)^{2}\right\} \\
C_{l}&=&\sum_{j=0}^{n}(p_{n_{j}}\cos{\alpha}-p_{t_{j}}\sin{\alpha}) \\
C_{m}&=&\sum_{j=0}^{n}(-p_{n_{j}}(x_{ref_{j}}-x_{\frac{1}{4}})+p_{t_{j}}y_{ref_{j}})
\end{eqnarray}
ただし,ピッチングモーメント係数\(C_{m}\)は1/4弦点\(z_{\frac{1}{4}}=0.25+0i\)まわりで計算し,\(p_{n_{j}}\),\(p_{t_{j}}\)は要素にはたらく圧力を翼弦に対して垂直・水平成分に分解したものである
\begin{eqnarray}
p_{n_{j}}&=&C_{p_{j}}l_{j}\cos{\theta_{j}} \\
p_{t_{j}}&=&-C_{p_{j}}l_{j}\sin{\theta_{j}}
\end{eqnarray}
ソースコードを以下に示す
void Make_AerodynamicCoefficient(int nodes,double alpha,double *Cl,double *Cm,double *l,double *gamma,double *Cp,double _Complex U_inf,double _Complex *z_foil){
/*--Constant--*/
double scale=1.0+pow(10,-10),rad=M_PI/180;
double _Complex z_qtr=0.25+I*0; //qtr:quarter
/*--Variables--*/
double _Complex z_ref[nodes];
double _Complex uv;
double U0=cabs(U_inf),U;
double theta,pt,pn; //n:normal t:tangent
double x,y;
int i,j,k,n;
//Make z_ref
for(n=0;n<nodes;n++){
z_ref[n]=(z_foil[n]+z_foil[n+1])/2; //eq(4.29)
z_ref[n]=z_ref[n]*scale;
}
//Calculation Cp
for(n=0;n<nodes;n++){
Make_uv(nodes,l,gamma,U_inf,&uv,z_ref[n],z_foil);
U=cabs(uv);
Cp[n]=(1-(U/U0)*(U/U0));
}
//Calculation Cl, Cm
*Cl=0;*Cm=0;
for(n=0;n<nodes;n++){
theta=carg(z_foil[n+1]-z_foil[n]);
pn=Cp[n]*l[n]*cos(theta);pt=-Cp[n]*l[n]*sin(theta);
x=crealf(z_ref[n]-z_qtr);y=cimagf(z_ref[n]-z_qtr);
*Cl=*Cl+pn*cos(rad*alpha)-pt*sin(rad*alpha);
*Cm=*Cm-pn*x+pt*y;
}
return;
}13~17行目でz_refを計算している.なぜかそのままだと値がバグるので,ほんのわずかに拡大するための係数scaleをかけている
19~24行目で圧力分布を計算し,26~34行目で揚力係数とピッチングモーメント係数を計算している
21行目のMake_uv関数は参照点の座標\(z_{ref}\)を引数として渡すと,その点での共役複素速度\({\overline u_{ref}}\)を返してくれる関数で,次に説明する
Make_uv関数
式(4.43)で係数S1,S2を計算し,式(4.42)で共役複素速度uvを計算する
\begin{eqnarray}
{\overline u}&=&{\overline U}+S_{1}^{(1)}\gamma_{1}+\sum_{j=2}^{n}(S_{j}^{(1)}+S_{j}^{(2)})\gamma_{j})+S_{n}^{(2)}\gamma_{n+1}
\tag{4.42}\\
S_{j}^{(1)}&=&\frac{il_{j}}{2\pi(z_{j+1}-z_{j})}\left(-1+\frac{z_{j+1}-z}{z_{j+1}-z_{j}}\ln{\frac{z_{j+1}-z}{z_{j}-z}}\right)
\tag{4.43a}\\
S_{j}^{(2)}&=&\frac{il_{j}}{2\pi(z_{j+1}-z_{j})}\left(+1-\frac{z_{j}-z}{z_{j+1}-z_{j}}\ln{\frac{z_{j+1}-z}{z_{j}-z}}\right)
\tag{4.34b}
\end{eqnarray}
ソースコードを以下に示す
void Make_uv(int nodes,double *l,double *gamma,double _Complex U_inf,double _Complex *uv,double _Complex z_ref,double _Complex *z_foil){
double _Complex S1_uv[nodes+1],S2_uv[nodes+1];
int k;
//eq.(4.43)
for(k=0;k<nodes;k++){
S1_uv[k]=((I*l[k])/(2*M_PI*(z_foil[k+1]-z_foil[k])))*(-1+(z_foil[k+1]-z_ref)/(z_foil[k+1]-z_foil[k])*clogf((z_foil[k+1]-z_ref)/(z_foil[k]-z_ref)));
S2_uv[k]=((I*l[k])/(2*M_PI*(z_foil[k+1]-z_foil[k])))*(+1-(z_foil[k]-z_ref)/(z_foil[k+1]-z_foil[k])*clogf((z_foil[k+1]-z_ref)/(z_foil[k]-z_ref)));
}
//eq.(4.42)
*uv=U_inf+S1_uv[0]*gamma[0]+S2_uv[nodes-1]*gamma[nodes];
for(k=1;k<nodes;k++){
*uv=*uv+(S2_uv[k-1]+S1_uv[k])*gamma[k];
}
return;
}見てのとおりである
Output_resluts関数
計算したCl,Cmをファイルに出力する
ソースコードを以下に示す
void Output_resluts(char *OutputFile_name,double alpha,double Cl,double Cm){
FILE *fp;
if((fp=fopen(OutputFile_name,"a"))==NULL){ //Failed
fprintf(stderr,"Not Found %s.",OutputFile_name);exit(EXIT_FAILURE);
}else{ //Success
fprintf(fp,"%f\t%f\t%f\n",alpha,Cl,Cm);
}
fclose(fp);
printf("alpha=%6.3f Cl=%6.3f Cm=%6.3f\n",alpha,Cl,Cm);
}プログラムの実行
それでは実際にプログラムを実行した結果を示す
>> gcc BEM_P_main.c BEM_P.c solver.c
>> a.exe
Input foil name
>>NACA4412
Input amin,amax,da
>>0,5,5
alpha= 0.000 Cl= 0.505 Cm=-0.108
続行するには何かキーを押してください . . .
続行するには何かキーを押してください . . .
alpha= 5.000 Cl= 1.105 Cm=-0.117
続行するには何かキーを押してください . . .
続行するには何かキーを押してください . . .
続行するには何かキーを押してください . . .
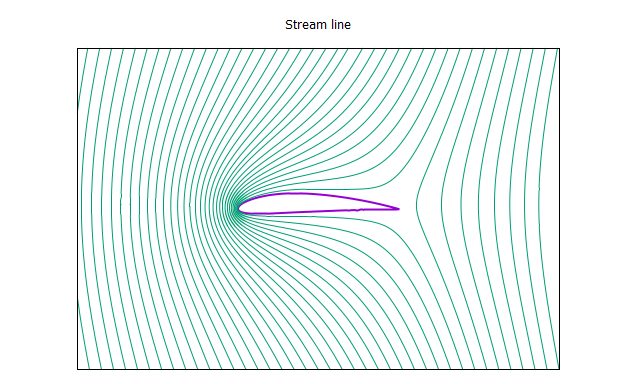
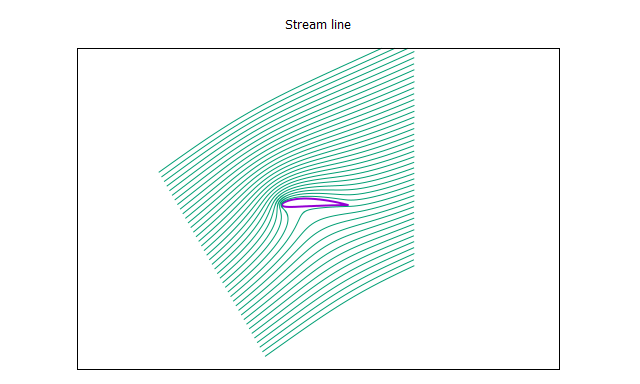
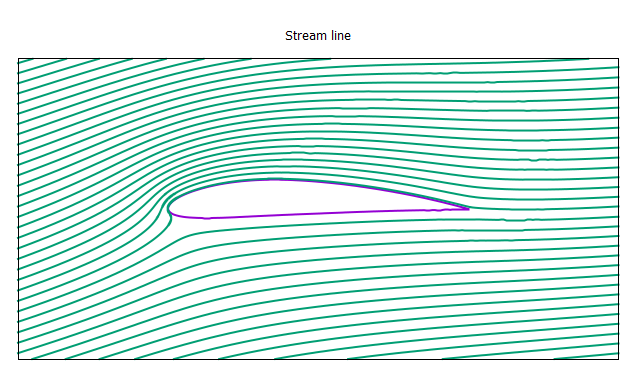
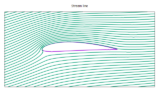
>>翼型:NACA4412
迎角:5 [deg]
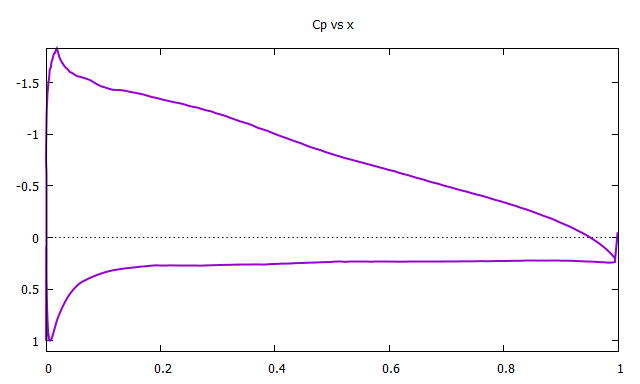
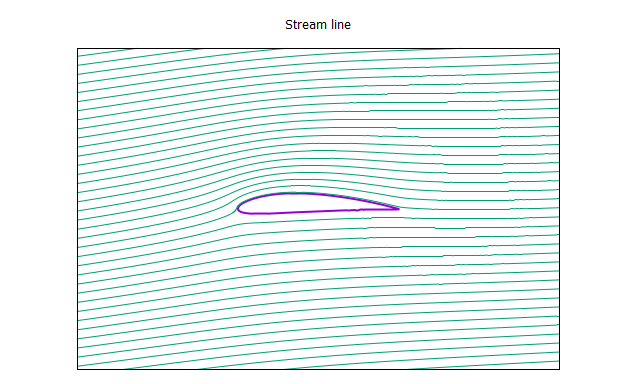
なんとなくそれっぽい圧力分布と流線が得られた
次は迎角の範囲を指定してCl-αとCm-αを見てみる
翼型:NACA4412
迎角:-5~15 [deg], step 1 [deg]
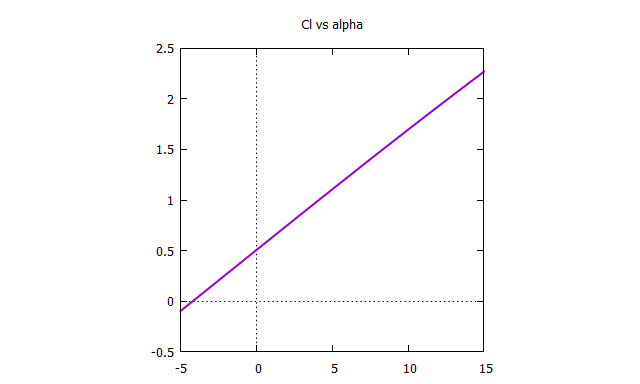
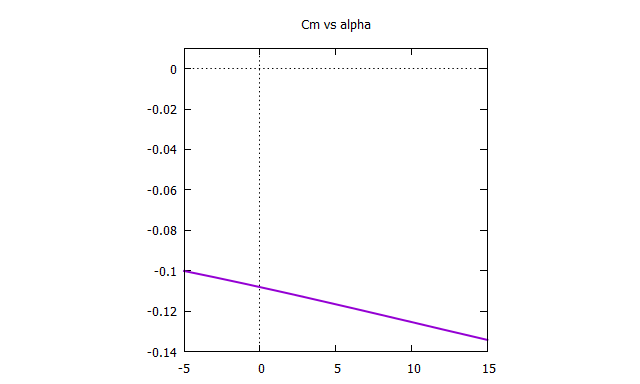
失速してないのはポテンシャル流れなのでしょうがないとして,それっぽい値を得ることができた
XFLR5との比較
上の結果を,XFLR5での解析結果と比較してみる
まずは圧力分布から
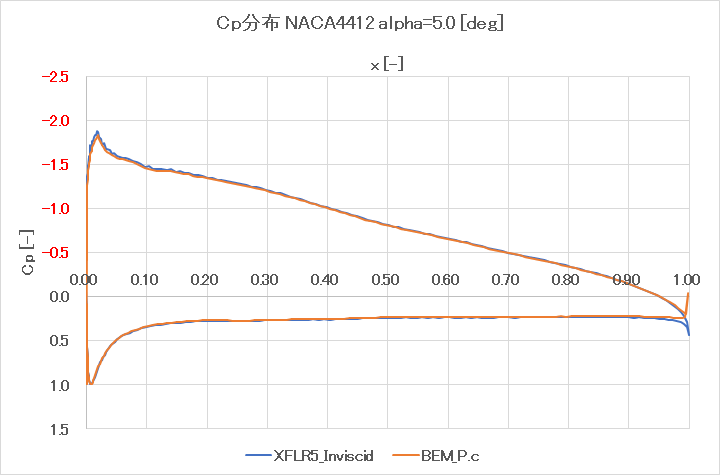
ばっちり一致した
次はClとCm.こちらはXFLR5で非粘性の結果を出力するやり方がわからなかったので粘性との比較
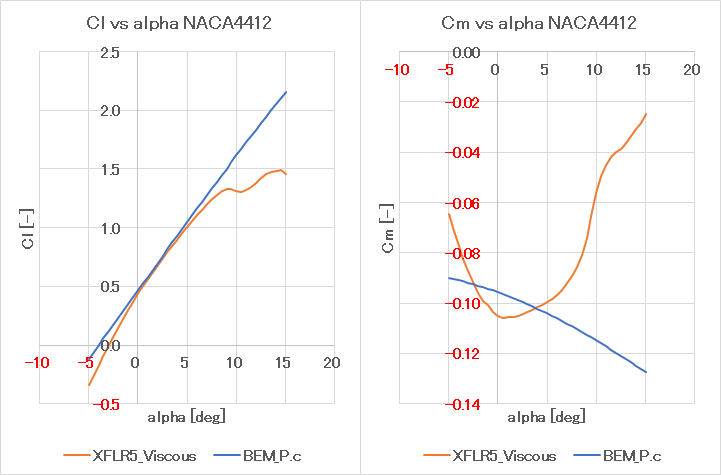
非粘性同士で比較したらきれいに一致しそうな雰囲気を感じる
おまけ①
ポテンシャル流れなので,迎角90[deg]とかいう狂った流れも計算できる
ちなみにこのときCl=6.295.クッタ条件が頑張りすぎである.
おまけ②
ピッチングモーメント係数の計算の基準点を1/4弦点ではなく空力中心にすれば,「空力中心回りのピッチングモーメントは迎角によらず一定」っぽい結果が得られる
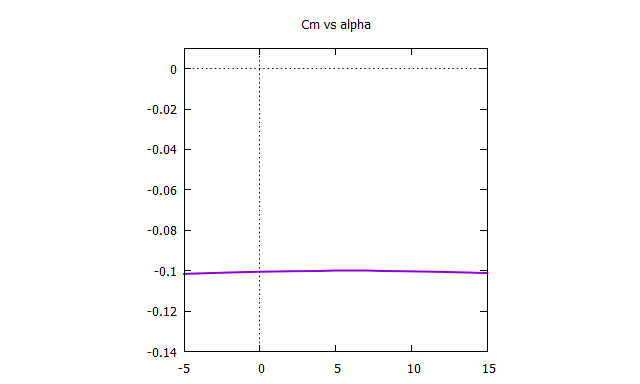
NACA4412なら\(z_{ac}=0.265+0i\)くらい
まとめ
境界要素法を使って任意の翼まわりの流体解析を行うことができた
もし余裕があれば粘性にも手を出してみたい
↓関連記事
おまけ
Gnuplotで結果を表示するプログラムのソースコードを紹介する
plot_contour関数
境界要素法で流線を描く方法は,いままでの差分法や有限要素法とは異なる
境界要素法では任意の位置での速度が得られるので,図5.4のように,流体粒子になったつもりで微小時間間隔dt後の位置を順次計算しながら微小直線を書き進めていく
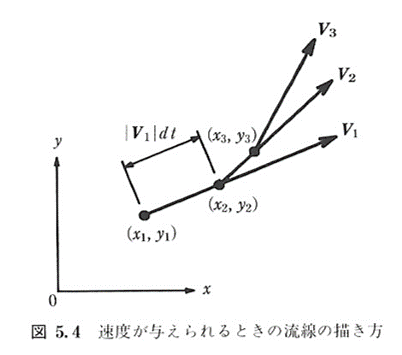
曲率が大きい部分ではdtを小さくするなどの工夫をすれば,より狂いの少ない流線が描ける
ソースコードを以下に示す
void plot_contour(char *title,int kmax,int nodes,double xmin,double xmax,double ymin,double ymax,double *l,double *gamma,double _Complex U_inf,double _Complex *z_foil){
FILE *gp; //gp:gnuplot pointer
/*--Constant--*/
double dt0=(1.0/cabs(U_inf))*0.01,dtheta_max=100000;
double rad=M_PI/180;
/*--Variables--*/
double _Complex z_ref,S1_uv[nodes+1],S2_uv[nodes+1];
double _Complex uv;
double alpha=atan(-cimagf(U_inf)/creal(U_inf)); //AOA
double dl1,dl2,x0,y0,x1,x2,y1,y2;
double dt; //time step
double theta,theta0,dtheta; //angle of stream line
double x,y,u,v;
char plot1[256],plot2[256];
int i,j,k,n;
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){exit(EXIT_FAILURE);}
//Send comands to gnuplot
fprintf(gp,"set title '%s'\n",title);
fprintf(gp,"set xrange [%f:%f]\n",xmin,xmax); //Set ranges
fprintf(gp,"set yrange [%f:%f]\n",ymin,ymax);
fprintf(gp,"unset xtics\nunset ytics\n");
fprintf(gp,"unset key\n"); //Hide legend
fprintf(gp,"set size ratio %f\n",(ymax-ymin)/(xmax-xmin)); //Set aspect ratio
//Plot graphic
strcpy(plot1,"'-' with lines linewidth 2");
strcpy(plot2,"'-' with lines linewidth 2");
fprintf(gp, "plot %s,%s\n",plot1,plot2);
//Plot Airfoil
for(n=0;n<=nodes;n++){
fprintf(gp,"%f\t%f\n",crealf(z_foil[n]),cimagf(z_foil[n]));
}
fprintf(gp,"e\n"); //End of array
//Plot Contour
if(alpha>0){
x0=xmin;y0=ymin;
dl1=fabs((ymax-ymin)*cos(alpha));dl2=fabs((xmax-xmin)*sin(alpha));
}else{
x0=xmin;y0=ymax;
dl1=fabs((xmax-xmin)*sin(alpha));dl2=fabs((ymax-ymin)*cos(alpha));
}
x1=x0-dl1*sin(alpha);y1=y0+dl1*cos(alpha);
x2=x0+dl2*sin(alpha);y2=y0-dl2*cos(alpha);
for(k=0;k<=kmax;k++){
//Set x,y
x=x1*((double)(k)/(double)(kmax))+x2*((double)(kmax-k)/(double)(kmax));
y=y1*((double)(k)/(double)(kmax))+y2*((double)(kmax-k)/(double)(kmax));
fprintf(gp,"%f\t%f\n",x,y);
//calculate stream line
theta0=alpha;
do{
z_ref=x+y*I;
Make_uv(nodes,l,gamma,U_inf,&uv,z_ref,z_foil);
u=crealf(uv),v=-cimagf(uv);
//Adjust dt
theta=atan(v/u);
dtheta=fabs((theta-theta0)/dt);if(dtheta>dtheta_max){dtheta=dtheta_max;}
dt=dt0*(1/(1+dtheta*dtheta));
//calculate x,y
x=x+u*dt;y=y+v*dt;
fprintf(gp,"%f\t%f\n",x,y);
theta0=theta;
}while(x<xmax);
fprintf(gp,"\n"); //End of array
}
fprintf(gp,"e\n"); //End of array
fflush(gp);system("pause");fprintf(gp, "exit\n");_pclose(gp); //Close Gnuplot
return;
}40~48行目で一様流の迎角alphaに垂直かつ描画範囲の端の点を通る面を計算し,50~53行目でその面をkmax等分する点を流線の開始点としている
60~63行目では流線の角度の変化率を計算し,変化率の大きいところでは時間間隔dtを小さくするような修正を加えている
plot_Cp_x関数
圧力分布を表示する関数
ソースコードを以下に示す
void plot_Cp_x(char *title,int nodes,double *Cp,double _Complex *z_foil){
FILE *gp; //gp:gnuplot pointer
/*--Constant--*/
double xmin=0,xmax=1.0;
/*--Variables--*/
double _Complex z_ref[nodes];
double ymin,ymax;
char plot1[256],plot2[256];
int i,j,k,n;
//Make z_ref, ymin, ymax
for(n=0;n<nodes;n++){
z_ref[n]=(z_foil[n]+z_foil[n+1])/2; //eq(4.29)
if(ymin>Cp[n]){ymin=Cp[n];}
if(ymax<Cp[n]){ymax=Cp[n];}
}
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){exit(EXIT_FAILURE);}
//Send comands to gnuplot
fprintf(gp,"set title '%s'\n",title);
fprintf(gp,"set xrange [%f:%f]\n",xmin,xmax); //Set ranges
fprintf(gp,"set yrange [%f:%f] reverse\n",ymax,ymin);
fprintf(gp,"unset key\n"); //Hide legend
fprintf(gp,"set zeroaxis\n");
//Plot graphic
strcpy(plot1,"'-' with lines linewidth 2");
fprintf(gp, "plot %s\n",plot1);
//Plot Cp vs x
for(n=0;n<nodes;n++){
fprintf(gp,"%f\t%f\n",crealf(z_ref[n]),Cp[n]);
}
fprintf(gp,"e\n"); //End of array
fflush(gp);system("pause");fprintf(gp, "exit\n");_pclose(gp); //Close Gnuplot
return;
}


コメント