C言語を使ってポテンシャル流れを差分解法で求めるプログラムを作成する
≫C言語でCFD入門①:ポテンシャル流れの差分解法
≫C言語でCFD入門②:粘性流れの差分解法
≫C言語でCFD入門③:ポテンシャル流れの有限要素解析
≫C言語でCFD入門④:境界要素法による二次元翼型解析
この記事で説明したソースコードはGithubにアップしてある
≫mtkbirdman.com/CFD/
はじめに
C言語を使ってポテンシャル流れを差分解法で求めるプログラムを作成する
参考にしたのは次の文献(文献1)
普通にわかりやすいし,Pascalのサンプルコードも載っているので実装にも移しやすい
理論の説明などは参考文献を参照してもらった方が間違いなくわかりやすいので,この記事では主にプログラムの実装について説明する
『流れの数値解析入門』のC言語版サンプルコードだとでも思ってほしい
↓C言語の勉強はこの本が圧倒的におすすめ
int main(void)の意味からポインタまで,コードを書きながら一通り独学できる名著
インストールについてはこちら
理論概要
差分法
そもそも差分法とは,ウィキペディアによると次のようなものである.
数値解析における有限差分法(ゆうげんさぶんほう、英: finite-difference methods; FDM)あるいは単に差分法は、微分方程式を解くために微分を有限差分近似(差分商)で置き換えて得られる差分方程式で近似するという離散化手法を用いる数値解法である。18世紀にオイラーが考案したと言われる[1]。
差分法 - Wikipedia
今日ではFDMは偏微分方程式の数値解法として支配的な手法である[2]。
今回実装する差分法については,文献1で次のように説明されている
差分法の考え方では,対称とする流れ場の領域を網の目(格子)に分割し,それぞれの格子内で流れの微分方程式を差分化すると全体としては連立方程式となり,これを解けば流れ場が得られる.
流れの数値解析入門 p.26
差分方程式の誘導
流れ関数を\(\psi\)とすると,2次元非圧縮ポテンシャル流れを規定するラプラスの方程式は次のようになる
\begin{eqnarray}
\frac{\partial^2 \psi}{\partial x^2}+\frac{\partial^2 \psi}{\partial y^2}=0
\tag{2.8}
\end{eqnarray}
図2.2のように流れ場を格子状に分割して,格子点\((i, j)\)における流れ関数\(\psi_{i, j}\)を定義する
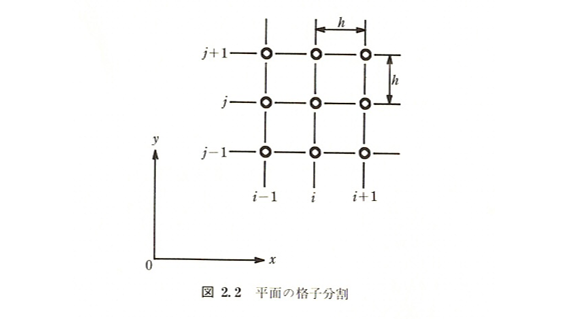
式(2.8)を差分方程式に変換して整理すると,次の連立一次方程式になる
\begin{eqnarray}
\psi_{i,j}=\frac{\psi_{i+1,j}+\psi_{i-1,j}+\psi_{i}{j+1}+\psi_{i,j-1}}{4}
\tag{2.11}
\end{eqnarray}
どんな複雑な式が出てくるのかと思いきや,周囲4点の流れ関数の平均をとるだけだった
式(2.11)の差分方程式を解くことによって,流れ場全体の流れ関数を求めることができる
連立一次方程式の解法
式(2.11)の連立一次方程式を解くために,反復法の一つであるガウス・ザイデル法を用いる
≫ガウス=ザイデル法 - Wikipedia
といってもやることは難しくなく,\(i\),\( j\)の小さい格子点から順番に計算していき,\(\psi_{i, j}\)の値が収束したら計算を終了する
k回目の計算で求められた値を\(\psi^{(k)}_{i, j}\)とすると,\(i, j\)の小さい格子点から順番に計算していくので,\(\psi^{(k+1)}_{i, j}\)を求める式は次のようになる
\begin{eqnarray}
\psi^{(k+1)}_{i,j}=\frac{\psi^{(k)}_{i+1,j}+\psi^{(k+1)}_{i-1,j}+\psi^{(k)}_{i,j+1}+\psi^{(k+1)}_{i,j-1}}{4}
\tag{2.12}
\end{eqnarray}
k+1回目の計算ではk回目の計算結果とk+1回目の計算結果の両方が使われることになる.そのため1回目の計算のときは,通常の格子点には適当な初期値(通常0)を与えておく
境界条件
今回の計算では,領域の境界に適当な\(\psi\)を与える
解析例:ステップを超える流れ
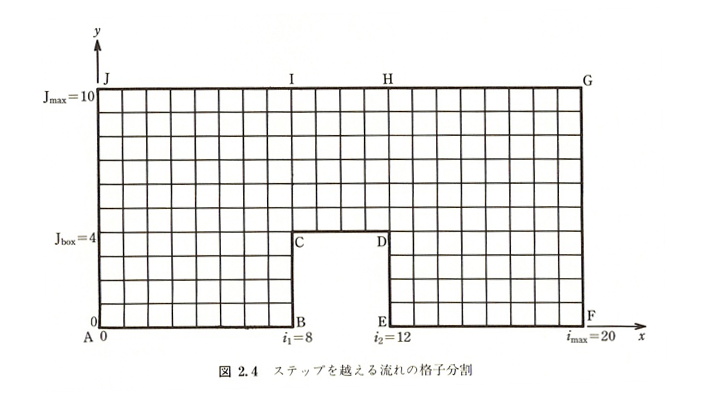
図2.4に示すようなステップを超える流れの計算を行う
解析範囲:0≦x≦2,0≦y≦1
境界条件:辺GJ → \(\psi=1.0\)
辺JA,FG → \(\psi=y\)
辺AB,BC,CD,DE,EF → \(\psi=0\)
imax,jmax,i1,i2,jboxの値は定数で指定する
プログラムの解説
上で述べたように差分法のプログラム自体は全く難しくない.今回のプログラムで一番難しかったのは流線を可視化するプログラムだった
フローチャートとソースコード
今回のプログラムのフローチャートを以下に示す
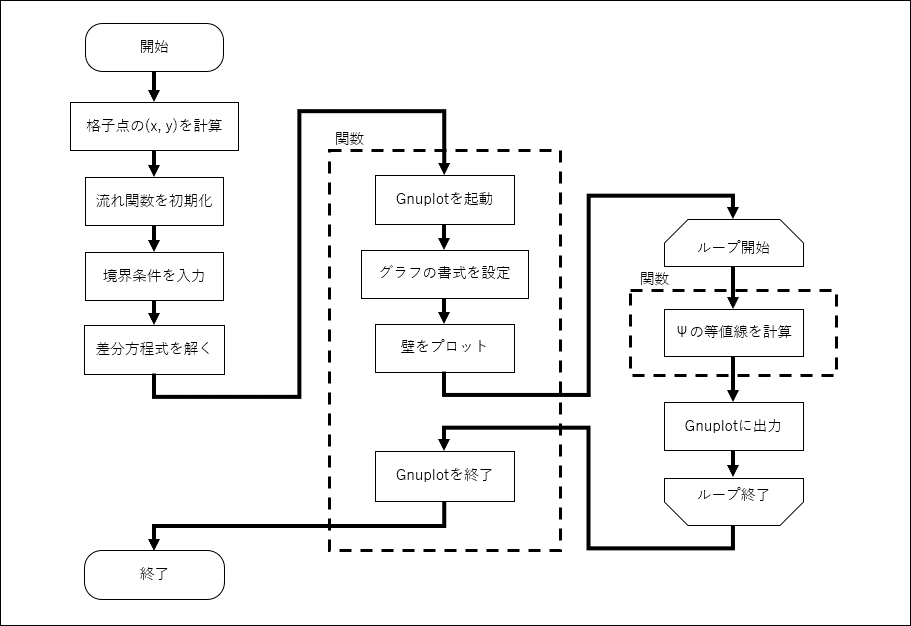
結果をGnuplotに出力する部分と,\(\psi\)の等値線(=流線)を計算するプログラムは別の関数を作った
それでは実際に解説していく
ソースコードはGithubも参照
≫mtkbirdman.com/CFD/FDM_P.c
#includeとプロトタイプ宣言
最初に次のヘッダーファイル(*.h)をincludeして,今回のプログラムで使う関数のプロトタイプ宣言を行う
≫自作関数を作る - 苦しんで覚えるC言語
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<stdbool.h>
#define GNUPLOT_PATH "C:/gnuplot/bin/gnuplot.exe" //PATH for gnuplot.exe
void contour(int imax,int jmax,double,double z[imax+1][jmax+1],double xy[imax+1][jmax+1][2],double cntr[][2],int *,int *);
void plot_results(int imax,int jmax,int,int,int,double,double,double,double,double z[imax+1][jmax+1],double xy[imax+1][jmax+1][2]);C言語で関数に配列を引数として渡すときは,配列の各次元の要素数も引数として与え,配列の各次元の要素数も指定しなければいけない(ただし1つ目の次元の要素数は省略可)
≫C言語の引数に多次元配列を渡す - Qiita
main関数
main関数全体を以下に示す
int main(void){
int imax=200,jmax=100,i1=80,i2=120,jbox=40,n_max=10000;
double xmin=0,xmax=2,ymin=0,ymax=1;
double xy[imax+1][jmax+1][2];
double psi_max=1.0,eps=0.00001,e_max,psi[imax+1][jmax+1],ds,s,dpsi;
int i,j,k,n;
//格子点の(x,y)を計算
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
xy[i][j][0]=(xmax-xmin)*((double)i/(double)imax);
xy[i][j][1]=(ymax-ymin)*((double)j/(double)jmax);
}
}
//流れ関数の初期化
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
psi[i][j]=0;
}
}
//境界条件の入力
for(i=0;i<=imax;i++){ psi[i][0]=0; } //底壁
for(j=0;j<=jbox;j++){ psi[i1][j]=0; } //ステップ左面
for(i=i1;i<=i2;i++){ psi[i][jbox]=0; } //ステップ上面
for(j=0;j<=jbox;j++){ psi[i2][j]=0; } //ステップ右面
for(i=0;i<=imax;i++){ psi[i][jmax]=psi_max; } //境界上端
ds=psi_max/jmax;
for(j=0;j<=jmax;j++){
s=ds*j;
psi[0][j]=s; //境界左端
psi[imax][j]=s; //境界右端
}
//ガウス=ザイデル法
n=0;
do{
e_max=eps; //最大誤差の初期値を設定
for(i=1;i<imax;i++){
if(i<i1||i>i2){ //ステップ外
for(j=1;j<jmax;j++){
dpsi=(psi[i+1][j]+psi[i-1][j]+psi[i][j+1]+psi[i][j-1])/4-psi[i][j];
psi[i][j]=psi[i][j]+dpsi; //式(2.12)を計算
if(fabs(dpsi)>e_max){e_max=fabs(dpsi);} //最大誤差を更新
}
}else{ //ステップ上
for(j=jbox+1;j<jmax;j++){
dpsi=(psi[i+1][j]+psi[i-1][j]+psi[i][j+1]+psi[i][j-1])/4-psi[i][j];
psi[i][j]=psi[i][j]+dpsi;
if(fabs(dpsi)>e_max){e_max=fabs(dpsi);} //update maximum error
}
}
}
n++; //nを更新
fprintf(stderr,"\r[%3d][%5.4f]",n,e_max); //進捗表示
}while(e_max>eps && n<n_max); //収束条件
printf("\nGauss-Seidel method iteration>>%d\n",n);
plot_results(imax,jmax,i1,i2,jbox,xmin,xmax,ymin,ymax,psi,xy);
return 0;
}変数の宣言
次のような変数を宣言した
int imax=200,jmax=100,i1=80,i2=120,jbox=40,n_max=10000;
double xmin=0,xmax=2,ymin=0,ymax=1;
double xy[imax+1][jmax+1][2];
double psi_max=1.0,eps=0.00001,e_max,psi[imax+1][jmax+1],ds,s,dpsi;
int i,j,k,n;とくに注意することはない
格子点の(x,y)を計算
格子点におけるx座標とy座標の値を計算する
実数値の計算にint型が入るときはとりあえずdouble型に変換しておいた方がミスが減る
≫型の変換 - 苦しんで覚えるC言語
//格子点の(x,y)を計算
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
xy[i][j][0]=(xmax-xmin)*((double)i/(double)imax);
xy[i][j][1]=(ymax-ymin)*((double)j/(double)jmax);
}
}流れ関数の初期化
境界条件の入力
境界条件に従って流れ関数を初期化し,境界条件を入力する
境界条件:辺GJ → \(\psi=1.0\)
辺JA,FG → \(\psi=y\)
辺AB,BC,CD,DE,EF → \(\psi=0\)
//流れ関数の初期化
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
psi[i][j]=0;
}
}
//境界条件の入力
for(i=0;i<=imax;i++){ psi[i][0]=0; } //底壁
for(j=0;j<=jbox;j++){ psi[i1][j]=0; } //ステップ左面
for(i=i1;i<=i2;i++){ psi[i][jbox]=0; } //ステップ上面
for(j=0;j<=jbox;j++){ psi[i2][j]=0; } //ステップ右面
for(i=0;i<=imax;i++){ psi[i][jmax]=psi_max; } //境界上端
ds=psi_max/jmax;
for(j=0;j<=jmax;j++){
s=ds*j;
psi[0][j]=s; //境界左端
psi[imax][j]=s; //境界右端
}差分方程式を解く
式(2.12)に従って,差分方程式を解く
\begin{eqnarray}
\psi^{(k+1)}_{i,j}=\frac{\psi^{(k)}_{i+1,j}+\psi^{(k+1)}_{i-1,j}+\psi^{(k)}_{i,j+1}+\psi^{(k+1)}_{i,j-1}}{4}
\tag{2.12}
\end{eqnarray}
ステップ上とそれ以外の部分で場合分けしてi,jのループを回して式(2.12)を計算する.境界条件が定められている格子点の計算は行わない
ループの中で計算した\(\psi\)の変化量\(\Delta \psi\)の絶対値があらかじめ定めた閾値を下回るか,反復数が設定した最大値を超えた場合にループを終了する
//ガウス=ザイデル法
n=0;
do{
e_max=eps; //最大誤差の初期値を設定
for(i=1;i<imax;i++){
if(i<i1||i>i2){ //ステップ外
for(j=1;j<jmax;j++){
dpsi=(psi[i+1][j]+psi[i-1][j]+psi[i][j+1]+psi[i][j-1])/4-psi[i][j];
psi[i][j]=psi[i][j]+dpsi; //式(2.12)を計算
if(fabs(dpsi)>e_max){e_max=fabs(dpsi);} //最大誤差を更新
}
}else{ //ステップ上
for(j=jbox+1;j<jmax;j++){
dpsi=(psi[i+1][j]+psi[i-1][j]+psi[i][j+1]+psi[i][j-1])/4-psi[i][j];
psi[i][j]=psi[i][j]+dpsi;
if(fabs(dpsi)>e_max){e_max=fabs(dpsi);}
}
}
}
n++; //nを更新
fprintf(stderr,"\r[%3d][%5.4f]",n,e_max); //進捗表示
}while(e_max>eps && n<n_max); //収束条件
printf("\nGauss-Seidel method iteration>>%d\n",n);ループの前に最大誤差e_maxに初期値を与えているが,e_maxの初期値によらず1度は\(\psi\)を計算してほしいのでdo-while文を使っている
≫【C言語入門】while文とdo-while文の使い方(break、continue文) _ 侍エンジニア塾ブログ(Samurai Blog) - プログラミング入門者向けサイト
また,21行目では計算の進捗を表示している
≫コンソールによるプログレス表示 - コンソール制御 - 碧色工房
ここまでで流体解析は終了である
関数 plot_results
流体解析した結果を表示するための関数plot_results()を作る
コード全体を以下に示す
void plot_results(int imax,int jmax,int i1,int i2,int jbox,double xmin,double xmax,double ymin,double ymax,double psi[imax+1][jmax+1],double xy[imax+1][jmax+1][2]){
FILE *gp; //gp:gnuplot pointer
double xy_contour[2][2],psi0;
char plot1[256],plot2[256];
int i,j,k,n;
int *ip,*jp;
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){ //Start gnuplot with pipe
fprintf(stderr,"Not Found %s.",GNUPLOT_PATH); //Standard error output
exit(EXIT_FAILURE); //Program abnormal termination
}
//Send comands to gnuplot
fprintf(gp,"set xrange [%f:%f]\n",xmin,xmax); //Set ranges
fprintf(gp,"set yrange [%f:%f]\n",ymin,ymax);
fprintf(gp,"set xtics 0.1\nset ytics 0.1\n");
fprintf(gp,"set grid \n");
fprintf(gp,"set size ratio %f\n",(ymax-ymin)/(xmax-xmin)); //Set aspect ratio
//Plot graphic
strcpy(plot1,"'-' with lines linewidth 2");
strcpy(plot2,"'-' with lines linewidth 2");
fprintf(gp, "plot %s, %s\n",plot1,plot2);
//Plot Wall
fprintf(gp,"%f\t%f\n",xy[0][0][0],xy[0][0][1]);
fprintf(gp,"%f\t%f\n",xy[i1][0][0],xy[i1][0][1]);
fprintf(gp,"%f\t%f\n",xy[i1][jbox][0],xy[i1][jbox][1]);
fprintf(gp,"%f\t%f\n",xy[i2][jbox][0],xy[i2][jbox][1]);
fprintf(gp,"%f\t%f\n",xy[i2][0][0],xy[i2][0][1]);
fprintf(gp,"%f\t%f\n",xy[imax][0][0],xy[imax][0][1]);
fprintf(gp,"e\n"); //End of array
//Plot streamline
ip=&i;jp=&j;
for(k=1;k<=10;k++){
i=0;j=0;
psi0=0.1*(double)k;
while(i<imax || j<jmax){
contour(imax,jmax,psi0,psi,xy,xy_contour,ip,jp);
fprintf(gp,"%f\t%f\n",xy_contour[0][0],xy_contour[0][1]);
fprintf(gp,"%f\t%f\n",xy_contour[1][0],xy_contour[1][1]);
}
fprintf(gp,"\n");
}
fprintf(gp,"e\n"); //End of array
fflush(gp); //Spit out the data stored in the buffer (required)
system("pause");
fprintf(gp, "exit\n"); //Terminate gnuplot
_pclose(gp); //Close Gnuplot
return;
}Gnuplotの使い方については次の記事(≫C言語でGnuplotを使って翼型を描く)で詳しく説明しているのでそちらを参考にしてほしい
ここでは流線を描くプログラムについて説明する
流線を描く
流線を描くプログラムを以下に示す
//流線を描く
ip=&i;jp=&j; //i,jのメモリをポインタip,jpに格納する
for(k=1;k<=10;k++){ //値の違う流線のループ
i=0;j=0;
psi0=0.1*(double)k; //Ψ0の計算
while(i<imax || j<jmax){
contour(imax,jmax,0.1*(double)k,psi,xy,xy_contour,ip,jp); //ポインタip,jpを引数として渡す
fprintf(gp,"%f\t%f\n",xy_contour[0][0],xy_contour[0][1]);
fprintf(gp,"%f\t%f\n",xy_contour[1][0],xy_contour[1][1]);
}
fprintf(gp,"\n");
}
fprintf(gp,"e\n"); //End of array一番外側のkのループは値の異なる\(\psi\)のループで,複数の流線を描いている
\(\psi\)の等値線を計算する関数contourは,ある\(\psi_{0}\)を与えると小さいi, jから順番に格子を調べていき,最初に見つけた等値線と格子の交点の座標(1格子分)とその格子番号(i, j)を返してくれるので,その等値線をGnuplotに出力する.
その後再び(i, j)の続きから調べていき,関数contourが返してくる等値線を出力する.これを繰り返し,最終的にすべての格子を調べ終えると,関数contourは(imax, jmax)を返してくれるのでwhile文の繰り返しを終了する
ここで重要なのは,(i, j)のループを続きから回すために,前回の(i, j)の値を関数に渡して,格子を調べた後に(i, j)の値を書き換えて返してもらうことである
そのためにint型のポインタ変数ip, jpを宣言し,それぞれにi, jのメモリを格納してから関数contourに渡している.(要するに参照渡し)
≫&つけが必要な変数の正体 - 苦しんで覚えるC言語
関数contour
格子を順番に調べて,格子と等値線の交点,格子点番号を返す関数contourのコードを以下に示す
void contour(int imax,int jmax,double z0,double z[imax+1][jmax+1],double xy[imax+1][jmax+1][2],double cntr[][2],int *ip,int *jp){
double x1,x2,x3,x4,y1,y2,y3,y4,z1,z2,z3,z4;
double x_tmp[4],y_tmp[4];
bool b1,b2,b3,b4;
int i,j,k,n,num1=0,num2=0;
//格子を調べる
for(i=0;i<imax;i++){
if(i>=*ip){ //続きから調べる
for(j=0;j<jmax;j++){
if(!(i==*ip && j<=*jp)){ //続きから調べる
//格子点におけるx,y,zを計算する
x1=xy[i][j][0];y1=xy[i][j][1];z1=z[i][j];
x2=xy[i+1][j][0];y2=xy[i+1][j][1];z2=z[i+1][j];
x3=xy[i+1][j+1][0];y3=xy[i+1][j+1][1];z3=z[i+1][j+1];
x4=xy[i][j+1][0];y4=xy[i][j+1][1];z4=z[i][j+1];
//格子の各辺上にz0があるかどうか判定する
b1=(z1<=z0 && z0<=z2) || (z2<=z0 && z0<=z1);
b2=(z2<=z0 && z0<=z3) || (z3<=z0 && z0<=z2);
b3=(z3<=z0 && z0<=z4) || (z4<=z0 && z0<=z3);
b4=(z4<=z0 && z0<=z1) || (z1<=z0 && z0<=z4);
//辺上のz0について(x,y)を線形補完する
if(b1){
x_tmp[0]=x1+((z0-z1)/(z2-z1))*(x2-x1);
y_tmp[0]=y1;
}
if(b2){
x_tmp[1]=x2;
y_tmp[1]=y2+((z0-z2)/(z3-z2))*(y3-y2);
}
if(b3){
x_tmp[2]=x3+((z0-z3)/(z4-z3))*(x4-x3);
y_tmp[2]=y3;
}
if(b4){
x_tmp[3]=x4;
y_tmp[3]=y4+((z0-z4)/(z1-z4))*(y1-y4);
}
//格子に等値線がまたがっているとき
if(b1 && b2){num1=0;num2=1;}
if(b2 && b3){num1=1;num2=2;}
if(b3 && b4){num1=2;num2=3;}
if(b4 && b1){num1=3;num2=0;}
if(b1 && b3){num1=0;num2=2;}
if(b4 && b2){num1=3;num2=1;}
if(num1!=num2){
//(x,y)を返す
cntr[0][0]=x_tmp[num1];
cntr[0][1]=y_tmp[num1];
cntr[1][0]=x_tmp[num2];
cntr[1][1]=y_tmp[num2];
goto OUT; //それ以降のループをすべて飛ばす
}
}
}
}
}
OUT:
*ip=i;*jp=j; //ip,jpのポインタ値を更新する
return;
}i, jのループの中でまず格子点上のx, y, zの値を計算する(13~16行目)
計算したzをもとに,格子の各辺上にz0があるかどうかを判断する(18~21行目)
ここで使っているb1~b4はbool型と呼ばれているもので,右辺の条件式が真ならtrueを,偽ならfalseを格納する
≫ブーリアン型#C言語 - Wikipedia
辺上にz0があればその座標を線形補完する(23∼38行目)
格子の4辺のうち2つの辺上にz0があれば格子に等値線がまたがっているということなので,配列cntrに座標を入れて,それ以降のループを飛ばす(39∼52行目)
ループをすべて飛ばすにはbreak文ではなくgoto文を使うといい
≫break文
最後にip,jpをi, jの値で更新する(59行)
プログラムの実行
プログラムを実行する
>> gcc FDM_P.c
>> a.exe
[4205][0.0000]
Gauss-Seidel method iteration>>4205
続行するには何かキーを押してください . . .
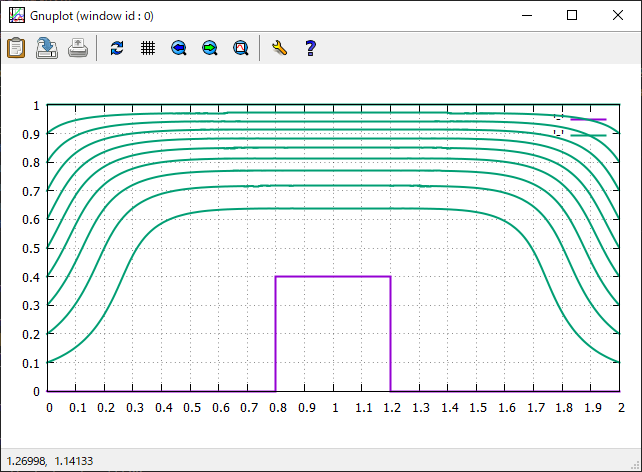
>>実際にプログラムを実行してみると,ステップを超えるポテンシャル流れの流線が表示されていることがわかる
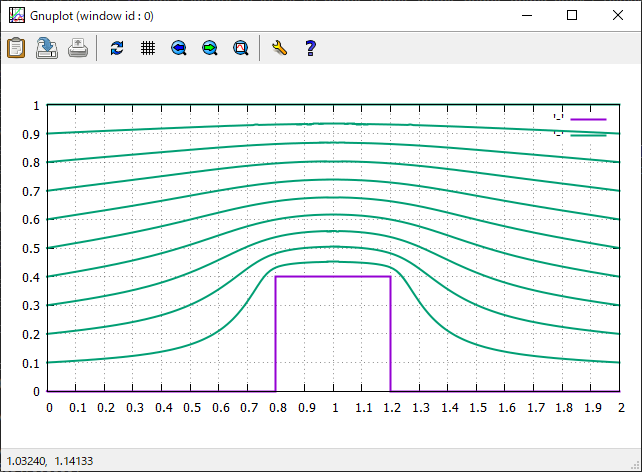
ちなみに,ガウス=ザイデル法の反復回数が不十分だと下のような結果になる
まとめ
等値線を描くプログラムにてこずったが,差分法を使ったポテンシャル流れの解析プログラムを書くことができた
↓次の記事

コメント