C言語を使って有限要素法でポテンシャル流れを解析するプログラムを作成する
≫C言語でCFD入門①:ポテンシャル流れの差分解法
≫C言語でCFD入門②:粘性流れの差分解法
≫C言語でCFD入門③:ポテンシャル流れの有限要素解析
≫C言語でCFD入門④:境界要素法による二次元翼型解析
この記事で説明したソースコードはGithubにアップしてある
≫mtkbirdman.com/CFD/
はじめに
C言語を使って有限要素法でポテンシャル流れを解析するプログラムを作成する
参考にしたのは次の文献(文献1および文献2)
CFDについては前回までと同様に文献1を参考にしていく
有限要素法については,構造解析ではあるが文献2がソースコード付きで非常にわかりやすいのでそちらを参考にしていく
今回作成するコードは文献2がベースとなる
↓C言語の勉強はこの本が圧倒的におすすめ
int main(void)の意味からポインタまで,コードを書きながら一通り独学できる名著
理論概要
基礎方程式から解くべき連立一次方程式を導出するまでの長い長い説明は文献1に譲り,ここでは必要最低限の内容のみ説明する
有限要素法
有限要素法とは,Wikipediaに次のように書いてある
有限要素法(ゆうげんようそほう、英語: Finite Element Method, FEM)は数値解析手法の一つ。解析的に解くことが難しい微分方程式の近似解を数値的に得る方法の一つであり[1]、Turner-Clough-Martin-Toppによって導入された[2]。方程式が定義された領域を小領域(要素)に分割し、各小領域における方程式を比較的単純で共通な補間関数で近似する[1]。構造力学分野で発達し、他の分野でも広く使われている手法。
有限要素法 - Wikipedia
流れ場を有限個の微小な要素(格子)に分割して方程式を解くのは差分法と同じだが,有限要素法は差分法に比べて,どんな複雑な形状にも対応できるというメリットを持つ
今回は最も簡単な要素である三角形一次要素を用いる
基礎方程式と境界条件
2次元ポテンシャル流れでは,流れ関数\(\psi\)は次のラプラスの式を満足する
\begin{eqnarray}
\frac{\partial^2 \psi}{\partial x^2}+\frac{\partial^2 \psi}{\partial y^2}
\tag{3.2}
\end{eqnarray}
これを図3.2に示すような境界条件で解くことを考える
\begin{eqnarray}
\psi={\overline \psi},~~~~(基本境界条件:S1)
\tag{3.4a}\\
\frac{\partial \psi}{\partial n}=f,~~~~(自然境界条件:S2)
\tag{3.4b}\\
\end{eqnarray}
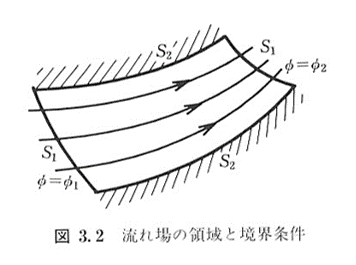
基本境界条件(固体壁や自由表面)では境界上の解の値そのものが与えられ,自然境界条件(流入/流出境界)では境界上での法線方向の流れ関数の変化率が与えられる
もちろん境界S1と境界S2を合わせたものが境界全周になる
ガラーキン法による重み付き残差法
式(3.2)の偏微分方程式を近似的に解くと,得られた解は誤差を持つことになる
そこで,次の式のように重み関数\(w(x, y)\)を用いてこの誤差をできるだけ小さくすることを考える
\begin{eqnarray}
\int \int_{A}\left(\frac{\partial^2 \psi}{\partial x^2}+\frac{\partial^2 \psi}{\partial y^2}\right)wdxdy=0
\tag{3.5}
\end{eqnarray}
このような方法を重み付き残差法という
重み関数\(w(x, y)\)の形にはいろいろなものがあるが,次の式のように重み関数\(w(x, y)\)を未知関数\(\psi\)と同じ形に仮定する方法をガラーキン法という
\begin{eqnarray}
w(x, y)=\psi^{*}
\tag{3.9}
\end{eqnarray}
重み関数の定義式(3.9)を式(3.5)に代入して,その式にグリーンの定理を適用してごちゃごちゃすると次の重み付き残差方程式が得られる
\begin{eqnarray}
\int \int_{A}\left(\frac{\partial \psi}{\partial x}\frac{\partial \psi^{*}}{\partial x}+\frac{\partial \psi}{\partial y}\frac{\partial \psi^{*}}{\partial y}\right)dxdy=\int_{S2}\frac{\partial \psi}{\partial n}\psi^{*}ds
\tag{3.11}
\end{eqnarray}
この式(3.11)から,有限要素法で解くべき連立一次方程式が導かれる
要素分割と係数行列
今回扱う有限要素法では,流れ場を適当な大きさの三角形の要素に分割する.分割した三角形の頂点を節点といい,節点上で流れ関数の値を考える
要素と節点にはそれぞれ要素番号,節点番号が通しで振られている
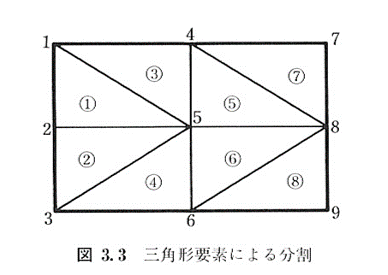
1つの三角形要素に着目して,局所節点番号1,2,3を与える.(この局所節点番号は流れ場全体での節点番号p,q,rに対応しているとする)
要素内の点P\((x, y)\)における流れ関数は次のように線形補完される
\begin{eqnarray}
\psi(x,y)=\alpha_{1}+\alpha_{2}x+\alpha_{3}y
\tag{3.12}
\end{eqnarray}
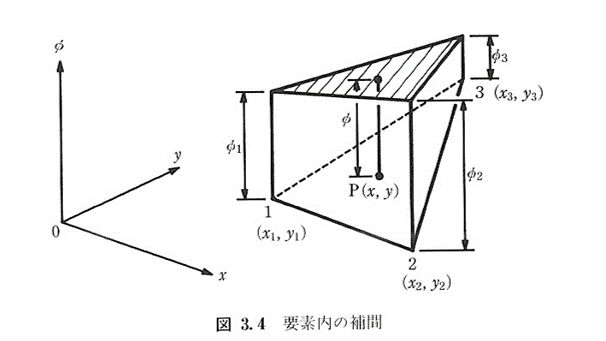
この式(3.12)の定義式を式(3.11)に代入してむちゃくちゃ式変形すると,1つの要素についての式(3.11)の左辺の積分は次のように計算できる
\begin{eqnarray}
I_{e}=\int \int_{A_{e}}\left(\frac{\partial \psi}{\partial x}\frac{\partial \psi^{*}}{\partial x}+\frac{\partial \psi}{\partial y}\frac{\partial \psi^{*}}{\partial y}\right)dxdy={\bf \psi^{*T}k\psi}
\tag{3.29}
\end{eqnarray}
ただし,局所節点番号でのx座標,y座標および流れ関数を\(x_{1}\),\(x_{2}\),\(x_{3}\),\(y_{1}\),\(y_{2}\),\(y_{3}\),\(\psi_{1}\),\(\psi_{2}\),\(\psi_{3}\)とし,
\begin{eqnarray}
{\bf k}&=&\left[\begin{array}{rrr}
k_{11}&k_{12}&k_{13}\\
k_{21}&k_{22}&k_{23}\\
k_{31}&k_{32}&k_{33}\\
\end{array}\right]
\tag{3.30}\\
k_{ij}&=&\frac{1}{4A}(a_{i}a_{j}+b_{i}b_{j})~~~(i,j=1,2,3)
\tag{3.31}\\
A&=&\frac{1}{2}\{(x_{2}-x_{1})(y_{3}-y_{1})-(x_{3}-x_{1})(y_{2}-y_{3})\}\\ \\
{\bf a}&=&\left[\begin{array}{r}
a_{1}\\a_{2}\\a_{3}
\end{array}\right]=-\left[\begin{array}{r}
x_{2}-x_{3}\\x_{3}-x_{1}\\x_{1}-x_{2}
\end{array}\right],~~~~
{\bf b}=\left[\begin{array}{r}
b_{1}\\b_{2}\\b_{3}
\end{array}\right]=\left[\begin{array}{r}
y_{2}-y_{3}\\y_{3}-y_{1}\\y_{1}-y_{2}
\end{array}\right]
\tag{3.22}\\
{\bf \psi}&=&\left[\begin{array}{r}
\psi_{1}\\ \psi_{2}\\ \psi_{3}
\end{array}\right],~~~~
{\bf \psi^{*}}=\left[\begin{array}{r}
\psi^{*}_{1}\\ \psi^{*}_{2}\\ \psi^{*}_{3}
\end{array}\right]
\tag{3.23}\\
\end{eqnarray}
である.式(3.29)の\({\bf k}\)を要素係数行列と呼ぶ
要素係数行列から全体係数行列へ
全体の節点数をn,局所節点番号1,2,3は流れ場全体での節点番号p,q,rに対応しているとして,次のベクトルを考える
\begin{eqnarray}
{\bf \Psi}=\left[\begin{array}{c}
\psi_{1}\\ \psi_{2}\\ \vdots\\ \psi_{n}
\end{array}\right],~~~~
{\bf \Psi^{*}}=\left[\begin{array}{c}
\psi^{*}_{1}\\ \psi^{*}_{2}\\ \vdots\\ \psi^{*}_{n}
\end{array}\right]
\tag{3.25}
\end{eqnarray}
式(3.25)のベクトルを用いて式(3.11)の左辺の積分を表すと,式(3.29)は次のように変形される
\begin{eqnarray}
I_{e}=[\psi^{*}_{1},\psi^{*}_{2},\ldots,\psi^{*}_{n}]\left[\begin{array}{ccccccc}
\ddots && \vdots && && \vdots && && \vdots && \\
\ldots && k_{pp} && \ldots && k_{pq} && \ldots && k_{pr} && \ldots \\
&& \vdots && \ddots && \vdots && && \vdots && \\
\ldots && k_{qp} && \ldots && k_{qq} && \ldots && k_{qr} && \ldots \\
&& \vdots && && \vdots && \ddots && \vdots && \\
\ldots && k_{rp} && \ldots && k_{rq} && \ldots && k_{rr} && \ldots \\
&& \vdots && && \vdots && && \vdots && \ddots\\
\end{array}\right]\left[\begin{array}{c}
\psi_{1}\\
\psi_{2}\\
\vdots \\
\psi_{n}\\
\end{array}\right]
\tag{3.33}
\end{eqnarray}
ここで,中央のn×nの行列は,\(k_{ij}~(i,j=p,q,r)\)が与えられている部分以外の値はすべて0である
式(3.33)をすべての要素について足し合わせると,最終的に式(3.11)の左辺の積分は次のようになる
\begin{eqnarray}
\int \int_{A}\left(\frac{\partial \psi}{\partial x}\frac{\partial \psi^{*}}{\partial x}+\frac{\partial \psi}{\partial y}\frac{\partial \psi^{*}}{\partial y}\right)dxdy={\bf \Psi^{*T}K\Psi}
\tag{3.38}
\end{eqnarray}
ただし,\({\bf K}\)はすべての要素について要素係数行列を足し合わせたもの(\({\bf K=\sum k}\))であり,全体係数行列と呼ぶ
自然境界条件
S2境界に面している要素の長さ\(l\)の辺23で,自然境界条件として\(\frac{\partial \psi}{\partial n}=f\)が与えられているとする
この要素についての式(3.11)の右辺の積分は,いろいろ計算したのち次のようになる
\begin{eqnarray}
\int_{S2}\frac{\partial \psi}{\partial n}\psi^{*}ds =
[\psi^{*}_{1},\psi^{*}_{2},\psi^{*}_{3}]
\left[\begin{array}{c}
0\\
\frac{fl}{2}\\
\frac{fl}{2}\\
\end{array}\right]={\bf\psi^{*}f}
\tag{3.43}
\end{eqnarray}
式(3.25)で定義した\(\Psi^{*}\)を用いて式(3.43)を書き直すと次にようになる
\begin{eqnarray}
\int_{S2}\frac{\partial \psi}{\partial n}\psi^{*}ds= [\psi^{*}_{1},\psi^{*}_{2},\ldots,\psi^{*}_{n}]
\left[\begin{array}{c}
\vdots\\
0\\
\vdots\\
\frac{fl}{2}\\
\vdots\\
\frac{fl}{2}\\
\vdots\\
\end{array}\right]
\tag{3.44}
\end{eqnarray}
式(3.43)の\({\bf f}\)をすべてのS2境界について足し合わせたベクトル\({\bf F}=\sum{\bf f}\)を用いると,式(3.11)の右辺は次のようになる
\begin{eqnarray}
\int_{S2}\frac{\partial \psi}{\partial n}\psi^{*}ds ={\bf \Psi^{*T}F}
\tag{3.46}
\end{eqnarray}
連立一次方程式の導出
式(3.38),式(3.46)より,式(3.11)の重み付き残差方程式は次のように書き換えられる
\begin{eqnarray}
{\bf \Psi^{T}K\Psi}&=&{\bf \Psi^{T}F}
\tag{3.47} \\ \\
{\bf K\Psi}&=&{\bf F}
\tag{3.49}
\end{eqnarray}
式(3.49)の連立一次方程式を解くことによって,すべての節点における流れ関数\(\psi\)を求めることができる
基本境界条件の処理
S1境界上では,節点\(m\)上での流れ関数\(\psi_{m}={\overline\psi_{m}}\)が与えられている
よって,連立方程式(3.49)の\(i\)行目に次のような変形を加える
- \(i\neq m\)なら,\(\psi_{m}\)に\({\overline\psi_{m}}\)を代入して右辺に移項する
- \(i=m\)なら,\(\psi_{m}\)以外の項をすべて0にし,\(F_{i}={\overline\psi_{m}}\)とする
\begin{eqnarray}
\begin{array}{cccccccccccclll}
K_{i1}\psi_{1}&+&K_{i2}\psi_{2}&+&\ldots&+&0&+&\ldots&+&K_{in}\psi_{n}&=&F_{i}-K_{im}{\overline\psi_{m}}&\hspace{10pt}&(i\neq m)\\
0&+&0&+&\ldots&+&\psi_{m}&+&\ldots&+&0&=&{\overline\psi_{m}}&\hspace{10pt}&(i=m)
\end{array}
\tag{3.51}
\end{eqnarray}
具体的には,係数行列\({\bf K}\)と右辺のベクトル\({\bf F}\)に対して次の処理を行う
\begin{eqnarray}
K_{mm}&=&1\\
K_{mp}&=&0,~K_{pm}=0\hspace{10pt}(p=1,\ldots,n;p\neq m)\\
F_{m}&=&{\overline\psi_{m}}\\
F_{p}&=&F_{p}-K_{pm}{\overline\psi_{m}}\hspace{10pt}(p=1,\ldots,n;p\neq m)
\tag{3.53}
\end{eqnarray}
次の文献にも詳しい記述があるので,気になる人は参考にしてほしい
≫≫第10回 連立一次方程式の数値解法―skiline法、反復法
ポテンシャル流れの有限要素解析例
今回のプログラムでは,以下の図1に示すような逆ステップを超える流れについて解析を行う
文献1と同じ形状であるが,番号の始まり(0から)と要素番号の振り方が異なるので注意してほしい
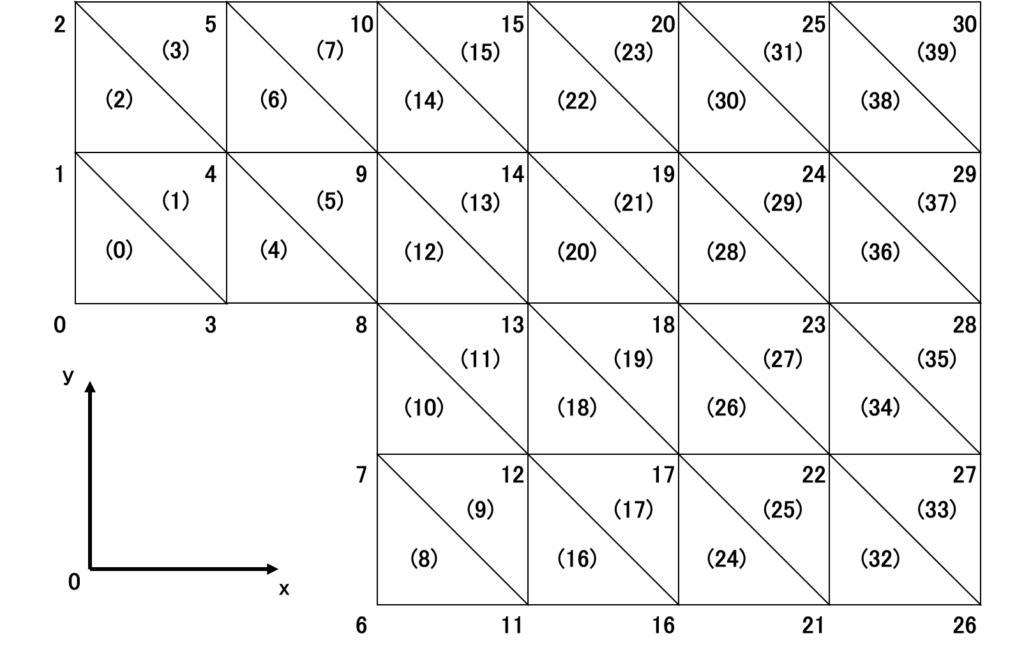
数字が節点番号,( )内の数字が要素番号
流入/流出境界上では自然境界条件を\(\frac{\partial \psi}{\partial n}=0\)とし,上下の壁面では基本境界条件として流れ関数の値を指定する
プログラムの解説①:FEM_CreateData.c
「入力データを変えれば計算部分のプログラムの変更は必要ない」という有限要素法のメリットを生かすために,入力データ生成用のプログラムFEM_CreateData.cと計算用のプログラムFEM_P.cを作成する
今後違う形状の流れ場を計算したい時は,FEM_CreateData.cのみを作り替えればよい
フローチャートとソースコード
FEM_CreateData.cのフローチャートとソースコードを以下に示す
そこまで長いプログラムではないのでmain関数だけで完結させている
このプログラム内では,x方向のカウンターに\(i\),y方向のカウンターに\(j\)を使用している
三角形一次要素を用いるので要素自由度dof_elm=3に設定する
ソースコードはGithubも参照
≫mtkbirdman.com/CFD/FEM_P_CreateData.c
#include<stdio.h>
#include<stdbool.h>
int main(void){
FILE *output;
/*--Constance--*/
int imax=6,jmax=4,ib=2,jb=2; //i:couner for x, j:counter for y
int dof_elm=3; //dof:Degree of Freedom, elm:elments
double xmin=0,xmax=0.6,ymin=0,ymax=0.4;
double psi_max=1.0,psi_min=0;
/*--Variables--*/
int nodes=(imax+1)*(jmax+1)-1-ib*jb,elm=(imax*jmax-ib*jb)*2-1; //b:box
int n_S1=2*imax+1+(jb-1),n_S2=(jmax+1)*2-jb; //S1:Essential boundary, S2:Natural boundary
double xy[nodes+1][2],f_S1[nodes+1],f_S2[nodes+1];
double f,l; //f:dpsi/dn at S2, l:length of S2
bool b_S1[nodes+1]; //If S1 is fixed,boolean->True
int cnct[elm+1][dof_elm]; //cnct:Connectivity
double dx=(xmax-xmin)/(double)imax,dy=(ymax-ymin)/(double)jmax;
int i,j,j0,k,n,e,nb,eb;
//Create Mesh
n=0;
for(i=0;i<=imax;i++){
j0=0;
if(i<ib){j0=jb;}
for(j=j0;j<=jmax;j++){
xy[n][0]=dx*i;
xy[n][1]=dy*j;
n++;
}
}
//Create connectivity
for(i=0;i<imax;i++){
nb=ib*jb;eb=2*ib*jb;j0=jmax+1;
if(i<ib){nb=(i+1)*jb;eb=2*(i+1)*jb;}
if(i<ib-1){j0=(jmax+1-jb);}
for(j=0;j<jmax;j++){
e=2*i*jmax+2*j-eb;
n=i*jmax+i+j-nb;
if(!(i<ib&&j<jb)){
cnct[e][0]=n;cnct[e][1]=n+j0;cnct[e][2]=n+1;
cnct[e+1][0]=n+j0+1;cnct[e+1][1]=n+1;cnct[e+1][2]=n+j0;
}
}
}
//Create Essential boundary conditions(S1) & Natural boundary conditions(S2)
for(n=0;n<=nodes;n++){f_S1[n]=0;f_S2[n]=0;b_S1[n]=false;}
for(i=0;i<=imax;i++){
j0=0;nb=ib*jb;eb=2*ib*jb;
if(i<ib){nb=(i+1)*jb;eb=2*(i+1)*jb;j0=jb;}
for(j=j0;j<=jmax;j++){
//S1
n=i*jmax+i+j-nb;
if(j==j0){f_S1[n]=psi_min;b_S1[n]=true;} //psi=0
if(i==ib&&(j0<j&&j<=jb)){f_S1[n]=psi_min;b_S1[n]=true;} //psi=0
if(j==jmax){f_S1[n]=psi_max;b_S1[n]=true;} //psi=psi_max*/
//S2
e=2*i*jmax+2*j-eb;
f=0;
l=dy;
if((i==0||i==imax-1)&&j<jmax){
f_S2[cnct[e][2]]=f_S2[cnct[e][2]]+(f*l)/2.0;
f_S2[cnct[e][0]]=f_S2[cnct[e][0]]+(f*l)/2.0;
}
}
}
//Output mesh data
output=fopen("FEM_data.dat","w");
fprintf(output,"%d,%d,%d,%d\n",imax,jmax,ib,jb);
fprintf(output,"%f,%f,%f,%f\n",xmin,xmax,ymin,ymax);
fprintf(output,"%d,%d,%d\n",nodes,elm,dof_elm);
for(n=0;n<=nodes;n++){fprintf(output,"%f,%f\n",xy[n][0],xy[n][1]);}
for(e=0;e<=elm;e++){fprintf(output,"%d,%d,%d\n",cnct[e][0],cnct[e][1],cnct[e][2]);}
for(n=0;n<=nodes;n++){fprintf(output,"%f,%d,%f\n",f_S1[n],b_S1[n],f_S2[n]);}
fclose(output);
return 0;
}格子点座標の計算(21~31行目)
格子点座標については,特に難しいことはしていない
51∼52行目で,ステップの上とそれ以外でjのループの開始を場合分けしていることに注意してほしい
配列cnctの計算(33~46行目)
配列cnctとはconnectivityの略で,ある要素eの局所節点番号n'と全体節点番号nを結び付ける配列である
\begin{eqnarray}
{\sf cnct[e][n']}={\sf n}
\end{eqnarray}
図1の要素番号と節点番号とにらめっこしていると,i,jにおける節点番号nとそれに隣接する要素番号eは次のようになることがわかる
\begin{eqnarray}
{\sf n}&=&{\sf i*jmax+i+j-nb}\\
{\sf e}&=&{\sf 2*i*jmax+2*j-eb}\\
\end{eqnarray}
ただし,nb,eb,j0は次のように与えられる
\begin{eqnarray}
\begin{array}{llll}
{\sf nb}&=&{\sf (i+1)*jb}&{\sf (i<ib)}\\
&=&{\sf ib*jb}&{\sf (ib\leq i)}\\ \\
{\sf eb}&=&{\sf 2*(i+1)*jb}&{\sf (i<ib)}\\
&=&{\sf 2*ib*jb}&{\sf (ib\leq i)}\\ \\
{\sf j0}&=&{\sf (jmax+1)-jb}&{\sf (i<ib-1)}\\
&=&{\sf jmax+1}&{\sf (ib-1\leq i)}
\end{array}
\end{eqnarray}
図に示すと以下のようになる
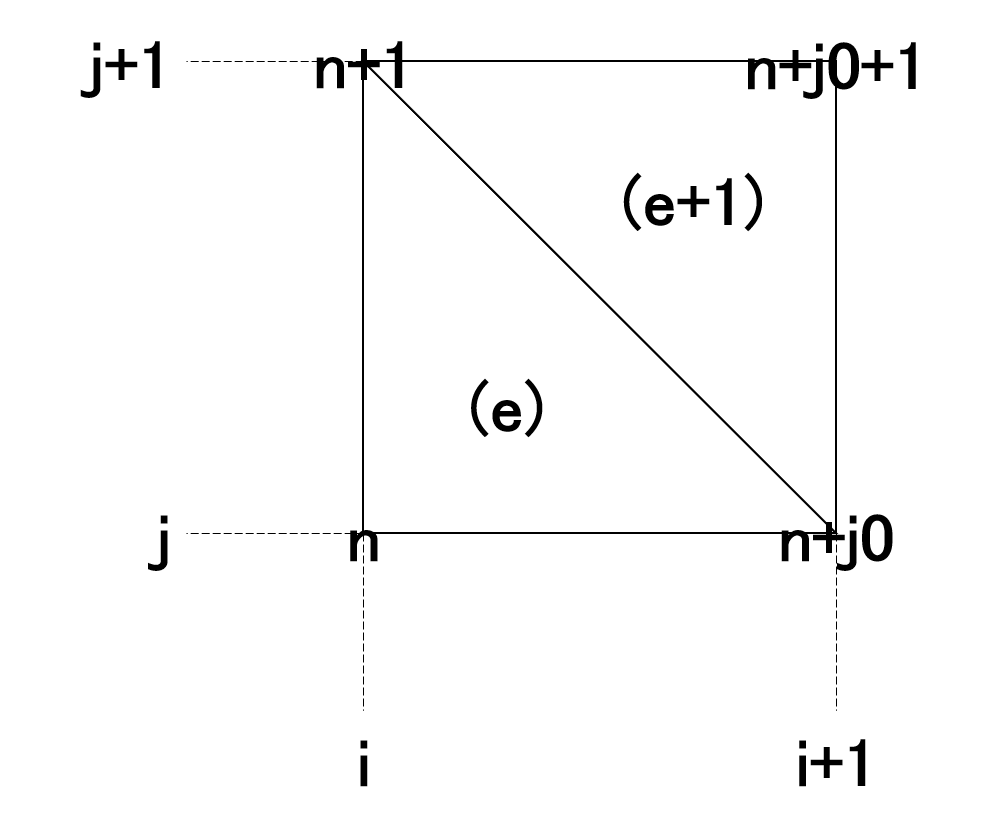
このi,j,n,eの関係を用いて配列cnctを計算している
境界条件f_S1,f_S2の計算(48~68行目)
基本境界条件f_S1と自然境界条件f_S2を計算している
ここで使用しているbool型配列b_S1は,配列f_S1[ i ]に格納されている値0がただの初期値0なのか基本境界条件\(\psi_{i}=0\)なのかを判断するための配列である
配列f_S1[ i ]に基本境界条件が設定されていればb_S1[ i ]=trueを,そうでなければb_S1[ i ]=falseを格納する
データの出力(70~78行目)
上で計算したデータはカンマ区切りのdatファイルで出力する
作成されたデータは次のようになる
bool型配列b_S1は整数型としてしか書き出せないのでtrueなら1,falseなら0となる
6,4,2,2
0.000000,0.600000,0.000000,0.400000
30,39,3
0.000000,0.200000
0.000000,0.300000
0.000000,0.400000
0.100000,0.200000
0.100000,0.300000
0.100000,0.400000
0.200000,0.000000
0.200000,0.100000
0.200000,0.200000
0.200000,0.300000
0.200000,0.400000
0.300000,0.000000
0.300000,0.100000
0.300000,0.200000
0.300000,0.300000
0.300000,0.400000
0.400000,0.000000
0.400000,0.100000
0.400000,0.200000
0.400000,0.300000
0.400000,0.400000
0.500000,0.000000
0.500000,0.100000
0.500000,0.200000
0.500000,0.300000
0.500000,0.400000
0.600000,0.000000
0.600000,0.100000
0.600000,0.200000
0.600000,0.300000
0.600000,0.400000
0,3,1
4,1,3
1,4,2
5,2,4
3,8,4
9,4,8
4,9,5
10,5,9
6,11,7
12,7,11
7,12,8
13,8,12
8,13,9
14,9,13
9,14,10
15,10,14
11,16,12
17,12,16
12,17,13
18,13,17
13,18,14
19,14,18
14,19,15
20,15,19
16,21,17
22,17,21
17,22,18
23,18,22
18,23,19
24,19,23
19,24,20
25,20,24
21,26,22
27,22,26
22,27,23
28,23,27
23,28,24
29,24,28
24,29,25
30,25,29
0.000000,1,0.000000
0.000000,0,0.000000
1.000000,1,0.000000
0.000000,1,0.000000
0.000000,0,0.000000
1.000000,1,0.000000
0.000000,1,0.000000
0.000000,1,0.000000
0.000000,1,0.000000
0.000000,0,0.000000
1.000000,1,0.000000
0.000000,1,0.000000
0.000000,0,0.000000
0.000000,0,0.000000
0.000000,0,0.000000
1.000000,1,0.000000
0.000000,1,0.000000
0.000000,0,0.000000
0.000000,0,0.000000
0.000000,0,0.000000
1.000000,1,0.000000
0.000000,1,0.000000
0.000000,0,0.000000
0.000000,0,0.000000
0.000000,0,0.000000
1.000000,1,0.000000
0.000000,1,0.000000
0.000000,0,0.000000
0.000000,0,0.000000
0.000000,0,0.000000
1.000000,1,0.000000プログラムの解説②:FEM_P.c
入力データの準備ができたので,有限要素法の計算を行う
フローチャート
main関数のフローチャートを以下に示す
配列には動的配列を使用し,メイン関数内でallocateを行う
そのため,ファイルからのデータの読み込みを2回に分け,①配列の大きさを読み込み→②動的配列をallocate→③動的配列にデータを読み込み,としている
連立一次方程式のソルバーにはskyline法を用いているので,必要な人は次の記事を参考にしてほしい
≫大規模疎行列に対する連立一次方程式のソルバー:Skyline法
ソースコードはGithubも参照
≫mtkbirdman.com/CFD/FEM_P.c
main関数
main関数のソースコードを以下に示す
特に難しいことはしていない
int main(void){
FILE *input;
clock_t start,end;
int imax,jmax,ib,jb;
double xmin,xmax,ymin,ymax;
int nodes,elm,dof_elm,Ksize;
double **xy,*xy_base,*f_S1,*f_S2;
double *K,*F,**uv,*uv_base;
bool *b_S1;
int **cnct,*cnct_base,*nd,*nmin;
int i,j,k,n,e;
start=clock();
Input_data1(&imax,&jmax,&ib,&jb,&dof_elm,&xmin,&xmax,&ymin,&ymax,&nodes,&elm);
/*--Allocate Matrix--*/
xy=(double **)malloc(sizeof(double *)*(nodes+1));xy_base=(double *)malloc(sizeof(double)*(nodes+1)*2);for(n=0;n<=nodes;n++){xy[n]=xy_base+2*n;}
cnct=(int **)malloc(sizeof(int *)*(elm+1));cnct_base=(int *)malloc(sizeof(int)*(elm+1)*(dof_elm));for(e=0;e<=elm;e++){cnct[e]=cnct_base+dof_elm*e;}
uv=(double **)malloc(sizeof(double *)*(elm+1));uv_base=(double *)malloc(sizeof(double)*(elm+1)*2);for(e=0;e<=elm;e++){uv[e]=uv_base+2*e;}
f_S1=(double *)malloc(sizeof(double)*(nodes+1));
f_S2=(double *)malloc(sizeof(double)*(nodes+1));
b_S1=(bool *)malloc(sizeof(bool)*(nodes+1));
nmin=(int *)malloc(sizeof(int)*(nodes+1));for(n=0;n<=nodes;n++){nmin[n]=n;}
nd=(int *)malloc(sizeof(int)*(nodes+1));
Input_data2(nodes,elm,xy,cnct,f_S1,b_S1,f_S2);
Make_nd_nmin(nodes,elm,dof_elm,&Ksize,cnct,nd,nmin);
/*--Allocate Matrix--*/
K=(double *)malloc(sizeof(double)*(Ksize+1));for(n=0;n<=Ksize;n++){K[n]=0;}
Make_K(nodes,elm,dof_elm,Ksize,cnct,nd,nmin,xy,K);
Set_BoundaryCondition(nodes,nd,nmin,b_S1,K,f_S1,f_S2,&F);
skyline_method(nodes,Ksize,nd,nmin,K,F);
Make_uv(elm,dof_elm,cnct,xy,F,uv);
end=clock();
/*--Output resluts--*/
Output_results(imax,jmax,ib,jb,nodes,elm,dof_elm,cnct,xmin,xmax,ymin,ymax,F,xy,uv);
plot_results(imax,jmax,ib,jb,nodes,elm,cnct,xmin,xmax,ymin,ymax,F,xy,uv);
plot_sparse(nodes,nmin);
printf("\n/--Specification--/\nnodes=%3d element=%3d Ksize=%3d\n",nodes,elm,Ksize);
printf("Time >> %f\n",(end-start)/(double)CLOCKS_PER_SEC);
return 0;
}【変数の説明】
start, end:計算開始/終了時間
imax, jmax, ib, jb:x方向,y方向のカウンターの最大値とステップの位置
xmin, xmax, ymin, ymax:x方向,y方向の範囲(最大値/最小値)
nodes, elm, dof_elm:節点数,要素数,要素内自由度(節点数)
Ksize:係数行列の大きさ(skyline法)
xy:格子点座標
f_S1, f_S2:基本境界条件S1,自然境界条件S2
K, F:全体係数行列(skyline法),右辺のベクトル
b_S1:基本境界条件S1の判断用
cnct:局所節点番号と全体の節点番号を結び付ける配列
nd, nmin:次の記事(≫大規模疎行列に対する連立一次方程式のソルバー:Skyline法)を参照
Input_data1関数,Input_data2関数
Input_data1関数,Input_data2関数のソースコードを以下に示す
void Input_data1(int *imax,int *jmax,int *ib,int *jb,int *dof_elm,double *xmin,double *xmax,double *ymin,double *ymax,int *nodes,int *elm){
FILE *input;
input=fopen("FEM_data.dat","r");
fscanf(input,"%d,%d,%d,%d",imax,jmax,ib,jb);
fscanf(input,"%lf,%lf,%lf,%lf",xmin,xmax,ymin,ymax);
fscanf(input,"%d,%d,%d,%d",nodes,elm,dof_elm);
fclose(input);
return;
}void Input_data2(int nodes,int elm,double **xy,int **cnct,double *f_S1,bool *b_S1,double *f_S2){
FILE *input;
char tmp[64];
int i,j,k,n,e;
input=fopen("FEM_data.dat","r");
for(i=0;i<3;i++){fgets(tmp,sizeof(tmp),input);} //Skip rows 1~3
for(n=0;n<=nodes;n++){fscanf(input,"%lf,%lf",&xy[n][0],&xy[n][1]);}
for(e=0;e<=elm;e++){fscanf(input,"%d,%d,%d",&cnct[e][0],&cnct[e][1],&cnct[e][2]);}
for(n=0;n<=nodes;n++){fscanf(input,"%lf,%d,%lf",&f_S1[n],&b_S1[n],&f_S2[n]);}
fclose(input);
return;
}今回はカンマ区切りのdatファイルなので,データの読み込みにはfscanf関数を使っている
≫テキストファイルの読み書き - 苦しんで覚えるC言語
2回目のデータ読み込みでは,ファイルの最小の3行を読み込む必要はないため,for文を3回まわして読み込みをスキップしている
どちらの関数でも,関数内で読み込んだ値を書き換えてmain関数に返す必要があるため,引数としてそれぞれの変数のアドレスを渡している.(配列の場合は先頭のアドレス)
動的配列の宣言
今回のプログラムで一番時間がかかったのがここなので,少し詳しく解説する
2次元配列を動的に宣言する方法は,以下のサイトを参考にした.(実際に採用したのは文献3の2つ目の方法)
≫配列を自由自在に作る - 苦しんで覚えるC言語
≫C言語で2次元配列を動的に割り当てる4つの方法 - FLYING・・・文献3
m行n列の行列\({\bf A}\)の値を格納するdouble型の2次元配列Aを動的に宣言するには次のようにする必要がある
①double型のポインタ変数へのポインタ**Aとdouble型のポインタ*A_baseを宣言する
double **A,*A_base;**Aをきちんと*(*A)と書いてもいいが,めんどくさいので省略されることが多い
②mallocを使って,double型のポインタをm個保存する領域と,double型の変数をm×n個保存する領域を確保する
A=(double **)malloc(sizeof(double *)*m);
A_base=(double *)malloc(sizeof(double)*n);malloc関数は確保した領域の先頭のアドレスを返すので,Aにはdouble型のポインタをm個保存できる領域の先頭のアドレス,A_baseにはdouble型の変数をm×n個保存できる領域の先頭のアドレスが格納される
実際に配列の値が保存されるのはA_baseで確保したメモリ領域で,1行目,2行目,・・・と1列のメモリ領域に各行の値が順番に保存される
③Aが持つm個のポインタ変数に,A_baseで確保したメモリ領域の中で各行の先頭の値が保存されるメモリのアドレスを格納する
for(i=0;i<m;i++){
A[i]=A_base+n*i;
}これにより,A[ i ]には行列\({\bf A}\)のi行1列目の成分\(A_{i1}\)の値が保存されているアドレスが格納され,A[ i ][ j ]によってi行j列目の成分\(A_{ij}\)の値にアクセスできる
配列nd,nminを計算
skyline行列の計算に必要なndとnminを計算する
ソースコードを以下に示す
void Make_nd_nmin(int nodes,int elm,int dof_elm,int *Ksize,int **cnct,int *nd,int *nmin){
int i,j,k,n,e;
//Make nmin
for(e=0;e<=elm;e++){
for(i=0;i<dof_elm;i++){
for(j=0;j<dof_elm;j++){
if(nmin[cnct[e][i]]>cnct[e][j]){
nmin[cnct[e][i]]=cnct[e][j];
}
}
}
}
//Make Ksize & nd
k=0;
for(i=0;i<=nodes;i++){
for(j=i;j>=nmin[i];j--){
if(i==j){nd[i]=k;}
k++;
}
}
k--;
*Ksize=k;
return;
}4~13行目のnminの計算では,要素番号eの要素において要素係数行列のi,j成分が全体係数行列のcnct[e][ i ],cnct[e][ j ]成分になることを利用して,cnct[e][ i ]行目の非ゼロの要素を持つ最小の列を更新している
15~24行目のndの計算では,1行目から最終行までの行のループの中で,i行i列目からi行nmin[ i ]列までのループを回すことによってskyline行列の大きさKsizeとndを計算している
係数行列Kの計算
まず,すべての要素について要素係数行列を計算し,それらを足し合わせて全体係数行列を計算する
今回も全体係数行列の下三角部分のみをskyline行列にして計算する
ソースコードを以下に示す
void Make_K(int nodes,int elm,int dof_elm,int Ksize,int **cnct,int *nd,int *nmin,double **xy,double *K){
double Ke[elm][dof_elm][dof_elm];
double xx[dof_elm],yy[dof_elm],Area;
double x1,x2,x3,y1,y2,y3;
int i,j,k,n,e,Ksize0,Ki,Kj;
//Make Ke
for(e=0;e<=elm;e++){
//x1~x3,y1~y3
x1=xy[cnct[e][0]][0];x2=xy[cnct[e][1]][0];x3=xy[cnct[e][2]][0];
y1=xy[cnct[e][0]][1];y2=xy[cnct[e][1]][1];y3=xy[cnct[e][2]][1];
//xx,yy
xx[0]=-(x2-x3);xx[1]=-(x3-x1);xx[2]=-(x1-x2);
yy[0]=y2-y3;yy[1]=y3-y1;yy[2]=y1-y2;
Area=0.5*((x2-x1)*(y3-y1)-(x3-x1)*(y2-y3));
//Ke
for(i=0;i<dof_elm;i++){
for(j=0;j<dof_elm;j++){
Ke[e][i][j]=(xx[i]*xx[j]+yy[i]*yy[j])/(4*Area);
}
}
}
//Sum Ke -> Make K
for(e=0;e<=elm;e++){
for(i=0;i<dof_elm;i++){
for(j=0;j<dof_elm;j++){
Ki=cnct[e][i];Kj=cnct[e][j];
if(Ki>=Kj){
n=nd[Ki]+Ki-Kj;
K[n]=K[n]+Ke[e][i][j];
}
}
}
}
return;
}7∼23行目の要素係数行列Keの計算は上で説明した式(3.22),(3.23),(3.30),(3.31)の通り
24∼35行目で要素係数行列Keを足し合わせて全体係数行列Kを求めるときに,全体係数行列のi,j成分がskyline行列のnd[ i ]+i-j番目の要素に対応しているという関係を利用している
≫大規模疎行列に対する連立一次方程式のソルバー:Skyline法
境界条件処理
式(3.51),(3.53)に従って基本境界条件の処理を行う
全体係数行列の対称性を利用して,下三角行列の処理しか行っていない
ソースコードを以下に示す
void Set_BoundaryCondition(int nodes,int *nd,int *nmin,bool *b_S1,double *K,double *f_S1,double *f_S2,double *(*F)){
int i,j,k,ji,ij,n;
for(i=0;i<=nodes;i++){ //Loop for row
if(b_S1[i]){ //f_S1[i] is Essential B.C.
for(j=i+1;j<=nodes;j++){ //Loop for Lji (j>i)
ji=nd[j]+j-i;
if(nmin[j]<=i){
f_S2[j]=f_S2[j]-f_S1[i]*K[ji];
}else{
f_S2[j]=f_S2[j];
}
}
for(j=nmin[i];j<i;j++){ //Loop for Uji=Lij (j<i)
ij=nd[i]+i-j;
f_S2[j]=f_S2[j]-f_S1[i]*K[ij];
}
//Set the component of a row/column where a Essential boundary condition exists to 0
for(j=i+1;j<=nodes;j++){ //Loop for Lji (j>i)
ji=nd[j]+j-i;
if(nmin[j]<=i){
K[ji]=0;
}
}
for(j=nmin[i];j<i;j++){ //Loop for Uji=Lij (j<i)
ij=nd[i]+i-j;
K[ij]=0;
}
K[nd[i]]=1;
f_S2[i]=f_S1[i];
}
}
*F=f_S2;
return;
}6~13行目と19∼24行目で,\(K_{pm}~(p=m+1,\ldots,n)\)の値を利用する処理を行っているが,下図のように行によってはm列の値が0でskyline行列に記憶されていない可能性があるので,nmin[p]で場合分けする必要がある.
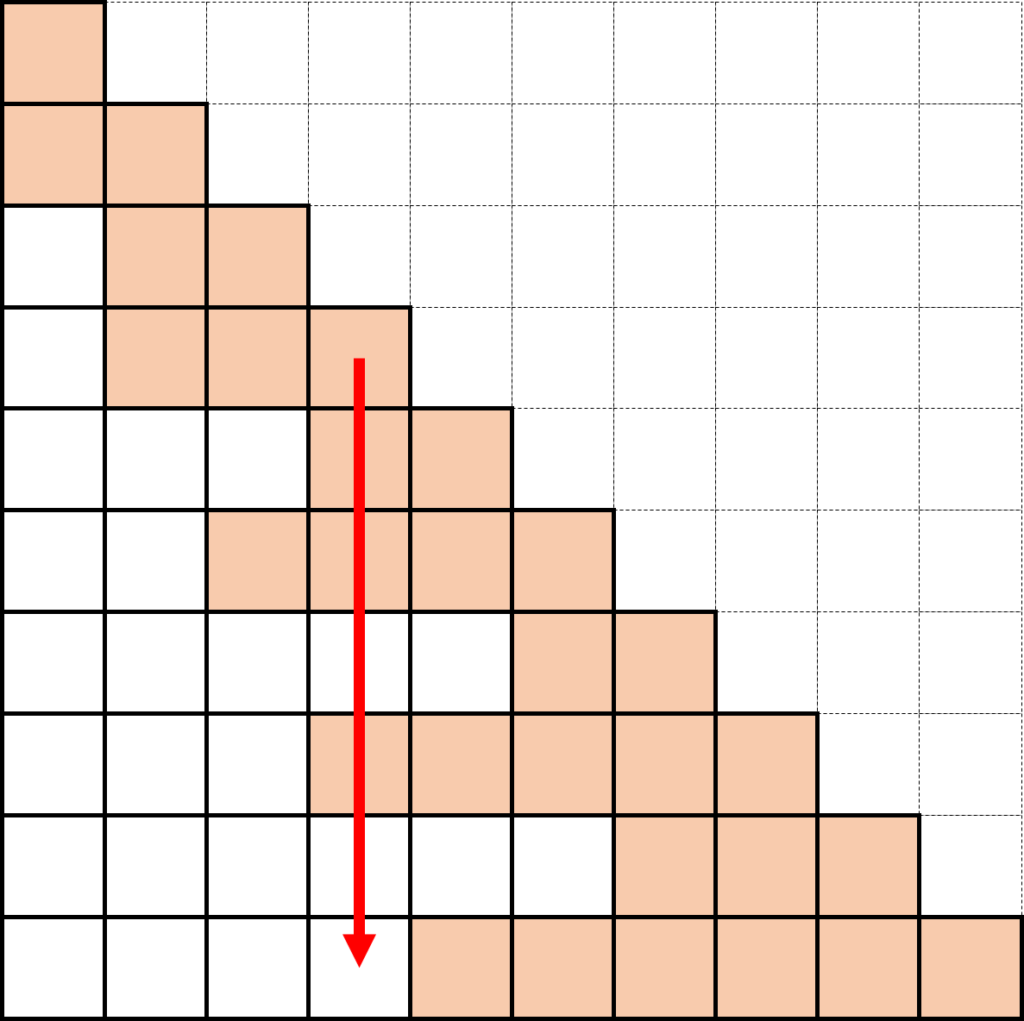
連立一次方程式を解く
連立一次方程式のソルバーにはskyline法を用いる.詳しくは次の記事を参考にしてほしい
≫大規模疎行列に対する連立一次方程式のソルバー:Skyline法
結果の出力
結果の出力に関しては,これまで使用してきた関数を三角形要素用に書き換えた.記事の最後にソースコードを乗せておくので参考にしてほしい
≫C言語でCFD入門①:ポテンシャル流れの差分解法
≫C言語でCFD入門②:粘性流れの差分解法
プログラムの実行
プログラムを実行する
>> gcc FEM_P_CreateData.c
>> a.exe
>> gcc FEM_P.c solver.c
>>a.exe
続行するには何かキーを押してください . . .
set arrow from 0.033333,0.233333 to 0.083818,0.233333
[...]
set arrow from 0.366667,0.166667 to 0.388
403,0.155279
set arrow from 0.333333,0.233333 to 0.367375,0.221945
[...]
set arrow from 0.566667,0.366667 to 0.594572,0.366667
続行するには何かキーを押してください . . .
続行するには何かキーを押してください . . .
/--Specification--/
nodes= 30 element= 39 Ksize=157
Time >> 0.000000
>>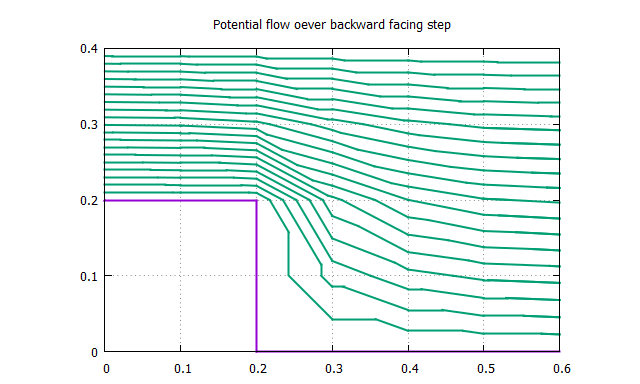
かなりメッシュは荒いが,それっぽい結果が出力できた
次に,筆者のPCの限界まで要素数を増やして実行してみる
≫ imax=24,jmax=16,ib=8,jb=8
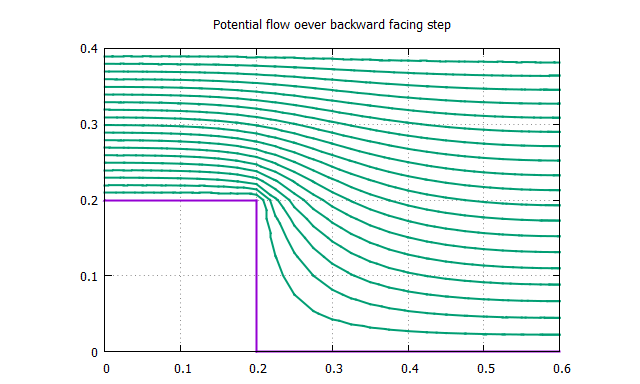
そこそこなめらかな流線を得ることができた
ちなみに,このときの節点数,要素数,skyline行列の要素数は次のようになった
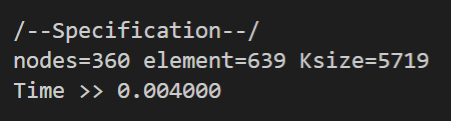
節点数が360なので,全体係数行列を普通の2次元配列に格納した場合は360×360=129'600ものメモリが必要になるが,skyline行列を使用したことによって5'719に抑えられている
全体係数行列の非ゼロの要素を可視化してみても,以下にskyline行列が大事かが理解できるかと思う
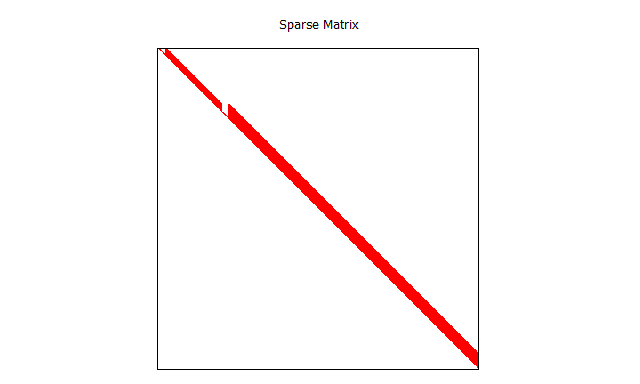
まとめ
今回は有限要素法によるポテンシャル流れの解析プログラムを製作した
筆者自身2年前に構造解析でFEMに挑戦したことがあるが,そのときはあまりの難しさに途中で挫折してしまった
2年越しのFEMリベンジを果たせたので非常に満足である
この1か月の過ごし方
— いーそー (@mtk_birdman) April 9, 2020
次回は有限要素法による粘性流れの解析プログラムに挑戦する
↓次の記事
おまけ
contour関数
等高線を表示する関数
void contour(int elm,int **cnct,double z0,double *z,double **xy,double cntr[][2],int *ep){ //Draw contour of z0
double x1,x2,x3,y1,y2,y3,z1,z2,z3;
double x_tmp[3],y_tmp[3];
bool b1,b2,b3;
int n1,n2,n3;
int i,j,k,n,e,num1=0,num2=0;
//Scan elements
for(e=*ep;e<=elm;e++){
n1=cnct[e][0];n2=cnct[e][1];n3=cnct[e][2];
x1=xy[n1][0];y1=xy[n1][1];z1=z[n1];
x2=xy[n2][0];y2=xy[n2][1];z2=z[n2];
x3=xy[n3][0];y3=xy[n3][1];z3=z[n3];
b1=(z1<=z0 && z0<=z2) || (z2<=z0 && z0<=z1);
b2=(z2<=z0 && z0<=z3) || (z3<=z0 && z0<=z2);
b3=(z3<=z0 && z0<=z1) || (z1<=z0 && z0<=z3);
if(b1){
x_tmp[0]=x1+((z0-z1)/(z2-z1))*(x2-x1);
y_tmp[0]=y1+((z0-z1)/(z2-z1))*(y2-y1);
}
if(b2){
x_tmp[1]=x2+((z0-z2)/(z3-z2))*(x3-x2);
y_tmp[1]=y2+((z0-z2)/(z3-z2))*(y3-y2);
}
if(b3){
x_tmp[2]=x3+((z0-z3)/(z1-z3))*(x1-x3);
y_tmp[2]=y3+((z0-z3)/(z1-z3))*(y1-y3);
}
if(b1 && b2){num1=0;num2=1;}
if(b2 && b3){num1=1;num2=2;}
if(b3 && b1){num1=2;num2=0;}
if(num1!=num2){
cntr[0][0]=x_tmp[num1];
cntr[0][1]=y_tmp[num1];
cntr[1][0]=x_tmp[num2];
cntr[1][1]=y_tmp[num2];
break;
}
}
*ep=e+1;
return;
}plot_results関数
Gnuplotで流線を表示する関数
void plot_results(int imax,int jmax,int ib,int jb,int nodes,int elm,int **cnct,double xmin,double xmax,double ymin,double ymax,double *z,double **xy){
FILE *gp; //gp:gnuplot pointer
double xy_contour[2][2],z0,zmin=0,zmax=0;
char plot1[256],plot2[256],title[64]="Potential flow oever backward facing step";
int i,j,k,n,e,nb,eb,j0,kmax=20;
int *ep;
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){exit(EXIT_FAILURE);}
//Send comands to gnuplot
fprintf(gp,"set title '%s'\n",title);
fprintf(gp,"set xrange [%f:%f]\n",xmin,xmax); //Set ranges
fprintf(gp,"set yrange [%f:%f]\n",ymin,ymax);
fprintf(gp,"set xtics 0.1\nset ytics 0.1\n");
fprintf(gp,"set grid \n");
fprintf(gp,"unset key\n"); //Hide legend
fprintf(gp,"set size ratio %f\n",(ymax-ymin)/(xmax-xmin)); //Set aspect ratio
//Plot graphic
strcpy(plot1,"'-' with lines linewidth 2");
strcpy(plot2,"'-' with lines linewidth 2");
fprintf(gp, "plot %s, %s\n",plot1,plot2);
//Plot Wall
for(i=0;i<=ib;i++){
nb=ib*jb;if(i<ib){nb=(i+1)*jb;}
n=i*jmax+i+jb-nb;
fprintf(gp,"%f\t%f\n",xy[n][0],xy[n][1]);
}
fprintf(gp,"\n");
for(j=0;j<=jb;j++){
n=ib*jmax+ib+j-ib*jb;
fprintf(gp,"%f\t%f\n",xy[n][0],xy[n][1]);
}
fprintf(gp,"\n");
for(i=ib;i<=imax;i++){
n=i*jmax+i+0-ib*jb;
fprintf(gp,"%f\t%f\n",xy[n][0],xy[n][1]);
}
fprintf(gp,"e\n"); //End of array
//Plot contour
for(n=0;n<=nodes;n++){
if(zmin>z[n]){zmin=z[n];}
if(zmax<z[n]){zmax=z[n];}
}
ep=&e;
for(k=1;k<kmax;k++){
e=0;
z0=zmin+(zmax-zmin)*((double)k/(double)kmax);
while(e<=elm){
contour(elm,cnct,z0,z,xy,xy_contour,ep);
fprintf(gp,"%f\t%f\n",xy_contour[0][0],xy_contour[0][1]);
fprintf(gp,"%f\t%f\n",xy_contour[1][0],xy_contour[1][1]);
fprintf(gp,"\n");
}
}
fprintf(gp,"e\n"); //End of array
fflush(gp); //Spit out the data stored in the buffer (required)
system("pause");
fprintf(gp, "exit\n"); //Terminate gnuplot
_pclose(gp); //Close Gnuplot
return;
}plot_sparse関数
skyline行列を可視化する関数
void plot_sparse(int nmax,int *nmin){
FILE *gp; //gp:gnuplot pointer
double xy_contour[2][2],z0,zmin=0,zmax=0;
char plot1[64],plot2[64],plot3[64],title[64]="Sparse Matrix";
int i,j,k,n,kmax=30;
int *ip,*jp;
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){
fprintf(stderr,"Not Found %s.",GNUPLOT_PATH);
exit(EXIT_FAILURE);
}
//Send comands to gnuplot
fprintf(gp,"set title '%s'\n",title);
fprintf(gp,"set xrange [%f:%f]\n",0,(double)(nmax+1));
fprintf(gp,"set yrange [%f:%f]\n",0,(double)(nmax+1));
fprintf(gp,"unset xtics\n");fprintf(gp,"unset ytics\n");
fprintf(gp,"set style fill solid\n");
fprintf(gp,"unset key\n"); //Hide legend
fprintf(gp,"set size square\n");
//Plot graphic
strcpy(plot1,"'-' with boxes linetype rgbcolor 'red'");
strcpy(plot2,"'-' with boxes linetype rgbcolor 'white'");
fprintf(gp, "plot %s,%s\n",plot1,plot2);
//Plot Skyline
for(k=0;k<=nmax;k++){
fprintf(gp,"%f\t%f\n",(double)k+0.5,(double)((nmax+1)-nmin[k]));
fprintf(gp,"\n");
}
fprintf(gp,"e\n"); //End of array
for(k=0;k<=nmax;k++){
fprintf(gp,"%f\t%f\n",(double)k+0.5,(double)((nmax+1)-(k+1)));
fprintf(gp,"\n");
}
fprintf(gp,"e\n"); //End of array
fflush(gp);
system("pause");
fprintf(gp,"exit\n");
_pclose(gp);
return;
}plot_vector関数
速度ベクトルを可視化する関数
void plot_vector(int imax,int jmax,int ib,int jb,int nodes,int elm,int dof_elm,int **cnct,double xmin,double xmax,double ymin,double ymax,double **xy,double **uv){
FILE *gp; //gp:gnuplot pointer
double coef=0.01;
double xy_contour[2][2],xg,yg;
char plot1[256],plot2[256],title[64]="Potential flow oever backward facing step";
int i,j,k,n,e,nb,eb,j0,kmax=20;
int *ep;
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){exit(EXIT_FAILURE);}
//Send comands to gnuplot
fprintf(gp,"set title '%s'\n",title);
fprintf(gp,"set xrange [%f:%f]\n",xmin,xmax); //Set ranges
fprintf(gp,"set yrange [%f:%f]\n",ymin,ymax);
fprintf(gp,"set xtics 0.1\nset ytics 0.1\n");
fprintf(gp,"set grid \n");
fprintf(gp,"unset key\n"); //Hide legend
fprintf(gp,"set size ratio %f\n",(ymax-ymin)/(xmax-xmin)); //Set aspect ratio
//Plot vector
for(e=0;e<=elm;e++){
xg=0;yg=0;
for(n=0;n<dof_elm;n++){
xg=xg+xy[cnct[e][n]][0];
yg=yg+xy[cnct[e][n]][1];
}
xg=xg/(double)dof_elm;yg=yg/(double)dof_elm;
printf("set arrow from %f,%f to %f,%f\n",xg,yg,xg+coef*uv[e][0],yg+coef*uv[e][1]);
fprintf(gp,"set arrow from %f,%f to %f,%f\n",xg,yg,xg+coef*uv[e][0],yg+coef*uv[e][1]);
}
//Plot graphic
strcpy(plot1,"'-' with lines linewidth 2");
fprintf(gp, "plot %s\n",plot1);
//Plot Wall
for(i=0;i<=ib;i++){
nb=ib*jb;if(i<ib){nb=(i+1)*jb;}
n=i*jmax+i+jb-nb;
fprintf(gp,"%f\t%f\n",xy[n][0],xy[n][1]);
}
fprintf(gp,"\n");
for(j=0;j<=jb;j++){
n=ib*jmax+ib+j-ib*jb;
fprintf(gp,"%f\t%f\n",xy[n][0],xy[n][1]);
}
fprintf(gp,"\n");
for(i=ib;i<=imax;i++){
n=i*jmax+i+0-ib*jb;
fprintf(gp,"%f\t%f\n",xy[n][0],xy[n][1]);
}
fprintf(gp,"e\n"); //End of array
fflush(gp); //Spit out the data stored in the buffer (required)
system("pause");
fprintf(gp, "exit\n"); //Terminate gnuplot
_pclose(gp); //Close Gnuplot
return;
}
コメント