C言語を使って粘性流れを差分解法で求めるプログラムを作成する
≫C言語でCFD入門①:ポテンシャル流れの差分解法
≫C言語でCFD入門②:粘性流れの差分解法
≫C言語でCFD入門③:ポテンシャル流れの有限要素解析
≫C言語でCFD入門④:境界要素法による二次元翼型解析
この記事で説明したソースコードはGithubにアップしてある
≫mtkbirdman.com/CFD/
はじめに
前回に続いて,C言語を使って粘性流れを差分解法で求めるプログラムを作成する
参考にしたのは次の文献
普通にわかりやすいし,Pascalのサンプルコードも載っているので実装にも移しやすい
理論の説明などは参考文献を参照してもらった方が間違いなくわかりやすいので,この記事では主にプログラムの実装について説明する
『流れの数値解析入門』のC言語版サンプルコードだとでも思ってほしい
↓C言語の勉強はこの本が圧倒的におすすめ
int main(void)の意味からポインタまで,コードを書きながら一通り独学できる名著
理論概要
非圧縮性流れの差分解法には,変数を流速\(u, v\)および圧力\(p\)にとるu-p法と変数を渦度\(\zeta\)と流れ関数\(\psi\)にとるζ-Ψ法がある
今回は,計算量の少なさと流線・等渦度線の可視化のしやすさからζ-Ψ法による解析を行う
基礎方程式
2次元ナビエ・ストークスの運動方程式は次の式で表される
\begin{eqnarray}
\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac{1}{\rho}\frac{\partial p}{\partial x}+\nu(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2})
\tag{2.13} \\
\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac{1}{\rho}\frac{\partial p}{\partial y}+\nu(\frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2})
\tag{2.14} \\
\end{eqnarray}
連続の式は次のように表される
\begin{eqnarray}
\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0
\tag{2.18}
\end{eqnarray}
これら2つの式を渦度と流れ関数を用いて表すことを考える
ここで,渦度\(\zeta(x, y; t)\)および流れ関数\(\psi(x, y; t)\)は次のように表される
\begin{eqnarray}
\zeta&=&\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}
\tag{2.15} \\
u&=&\frac{\partial \psi}{\partial y} \\
v&=&-\frac{\partial \psi}{\partial x}
\tag{2.17}
\end{eqnarray}
2次元ナビエストークス方程式の式(2.13)を\(y\)で,式(2.14)を\(x\)で微分し差をとることによって圧力項を消去し,式(2.15)を代入して整理すると次の式を得る
\begin{eqnarray}
\frac{\partial \zeta}{\partial t}+u\frac{\partial \zeta}{\partial x}+v\frac{\partial \zeta}{\partial y}=\nu(\frac{\partial^2 \zeta}{\partial x^2}+\frac{\partial^2 \zeta}{\partial y^2})
\tag{2.16}
\end{eqnarray}
式(2.16)を渦度輸送方程式という
これに流れ関数の定義式(2.17)を代入することによって次の式を得る
\begin{eqnarray}
\frac{\partial \zeta}{\partial t}+\frac{\partial \psi}{\partial y}\frac{\partial \zeta}{\partial x}-\frac{\partial \psi}{\partial x}\frac{\partial \zeta}{\partial y}=\nu(\frac{\partial^2 \zeta}{\partial x^2}+\frac{\partial^2 \zeta}{\partial y^2})
\tag{2.19}
\end{eqnarray}
連続の式(2.18)は流れ関数の定義により自動的に満たされ,渦度の式(2.15)に流れ関数の定義式(2.17)を代入すると次の式を得る
\begin{eqnarray}
\frac{\partial^2 \psi}{\partial x^2}+\frac{\partial^2 \psi}{\partial y^2}=-\zeta
\tag{2.20}
\end{eqnarray}
式(2.20)を流れ関数\(\psi(x, y; t)\)に関するポアソン方程式という
以上で,2次元ナビエストークス方程式と連続の式は渦度\(\zeta(x, y; t)\)および流れ関数\(\psi(x, y; t)\)に関する方程式(2.19),(2.20)に変換できた
渦度と流れ関数の差分方程式
図2.6のように流れ場を\(x\),\(y\)方向の長さがそれぞれ\(\Delta x\),\(\Delta y\)の格子で分割し,格子点番号を\((i, j)\)で表す
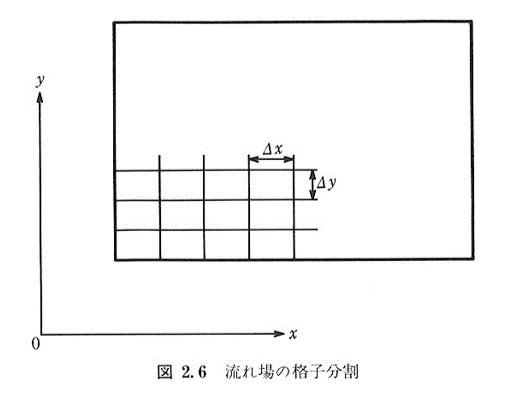
また,時間ステップを\(\Delta t\)とし,時刻\(t=t_{0}+n\Delta t\)における格子点位置\((i, j)\)の渦度\(\zeta\),流れ関数\(\psi\)の値をそれぞれ\(\zeta^{(n)}_{i, j}\),\(\psi^{(n)}_{i, j}\)と表す
式(2.19),(2.20)を差分化して整理すると次のようになる
\begin{align}
\zeta^{(n+1)}_{i, j}=&\zeta^{(n)}_{i, j}-\frac{\Delta t}{4\Delta x\Delta y}
\left\{
(\psi^{(n)}_{i, j+1}-\psi^{(n)}_{i, j-1})(\zeta^{(n)}_{i+1, j}-\zeta^{(n)}_{i-1, j})
-(\psi^{(n)}_{i+1, j}-\psi^{(n)}_{i-1, j})(\zeta^{(n)}_{i, j+1}-\zeta^{(n)}_{i, j-1})
\right. \\
&\left.
+\frac{\nu\Delta t}{\Delta x^2}(\zeta^{(n)}_{i-1, j}-2\zeta^{(n)}_{i, j}+\zeta^{(n)}_{i+1, j})
+\frac{\nu\Delta t}{\Delta y^2}(\zeta^{(n)}_{i, j-1}-2\zeta^{(n)}_{i, j}+\zeta^{(n)}_{i, j+1})
\right\}
\tag{2.26} \\
\psi^{(n+1)}_{i, j}=&\frac{1}{2(\Delta x^2+\Delta y^2)}
\left\{
(\psi^{(n+1)}_{i, j-1}+\psi^{(n+1)}_{i, j+1})\Delta x^2+(\psi^{(n+1)}_{i-1, j}+\psi^{(n+1)}_{i+1, j})\Delta y^2+\zeta^{(n+1)}_{i, j}\Delta x^2\Delta y^2
\right\}
\tag{2.28} \\
\end{align}
式(2.26),(2.28)を解くことによって流れ場の解析を行う
渦度と流れ関数の境界条件
渦度\(\zeta\)と流れ関数\(\psi\)の境界条件は,図2.9のようにすべての境界上で値そのものまたは法線方向の勾配が与えられていればよい
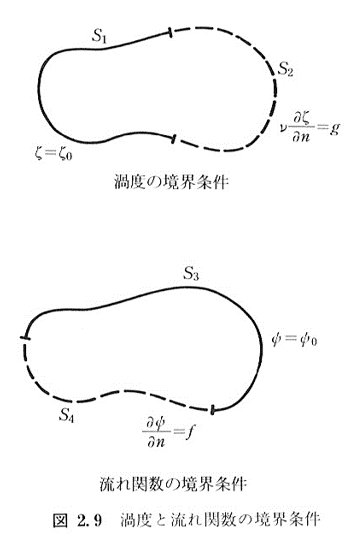
具体的な例を以下に示す
流れ関数\(\psi\)の境界条件
(1)流線に沿う境界(固体壁面上)
\begin{eqnarray}
\psi=\psi_{0}
\tag{2.32}
\end{eqnarray}
(2)流入/流出断面上で速度分布が与えられた境界
x軸方向に\(u(y)\)のような速度分布を持った流れでは,流れ関数の定義により\(u=\frac{\partial \psi}{\partial y}\)なので,流れ関数\(\psi\)は次の式で与えられる
\begin{eqnarray}
\psi=\int^{y}_{a} u(y) dy
\tag{2.33}
\end{eqnarray}
また,速度分布が与えられてなくても,流れが境界に垂直に流入/流出するときは次の関係式が使える
\begin{eqnarray}
\frac{\partial \psi}{\partial n}=0
\tag{2.35}
\end{eqnarray}
つまり,境界に対して流れ方向に隣接する点での値を,境界上での値として代入すればよい
渦度\(\zeta\)の境界条件
(1)壁面上の境界
固定した壁面上では流れは静止しており,その近傍では流れは壁に垂直であることを考慮すると,壁面上での渦度\(\zeta\)の境界条件は近似的に次のように与えられる
\begin{eqnarray}
\zeta(0)=\frac{2}{dy^2}(\psi(0)-\psi(dy))
\tag{2.39}
\end{eqnarray}
ここで,\(dy\)は壁面からの距離である
このことから,流れ関数と渦度を用いて粘性流れを解く場合には時間ステップごとに流れ関数\(\psi\)を用いて渦度\(\zeta\)の境界条件を計算しなおす必要がある
(2)流入/流出境界
流入/流出断面上で速度分布が与えられている場合は,渦度の定義より境界上の渦度\(\zeta\)の値を決定する
\begin{eqnarray}
\zeta=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}=\frac{\partial^2 \psi}{\partial x^2}-\frac{\partial^2 \psi}{\partial y^2}
\tag{2.40}
\end{eqnarray}
あるいは,流れが垂直に流入/流出するなら,流れ方向に隣接する点での値を境界での値として代入する
(3)自由表面
自由表面では壁面に沿う流れで壁面摩擦がはたらかないので,渦度\(\zeta\)の境界条件は次のようになる
\begin{eqnarray}
\zeta=0
\end{eqnarray}
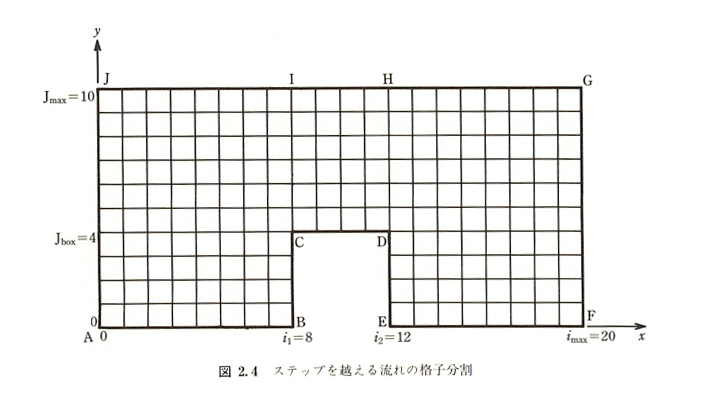
解析例:ステップを超える流れ
図2.4に示すようなステップを超える流れの計算を行う.(前回≫C言語でCFD入門①:ポテンシャル流れの差分解法と同じ)
プログラムの解説
出てくる数式は複雑だが,打ち間違えさえしなければプログラムはそこまで難しくない
フローチャート
プログラム全体のフローチャートを以下に示す
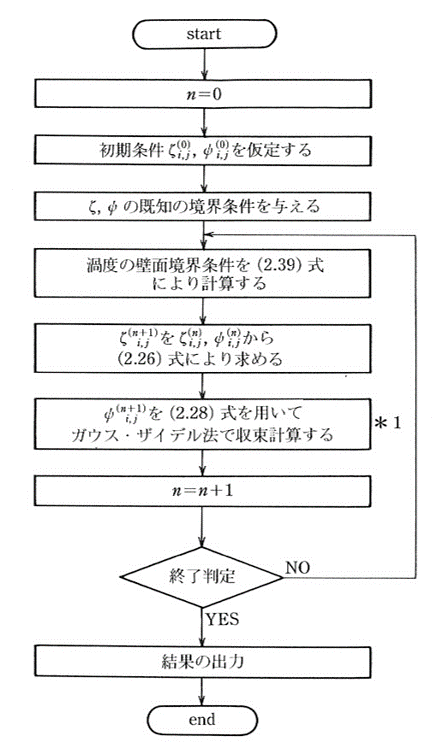
式(2.28)より\(\phi^{(n+1)}_{i, j}\)を求める際には,ポテンシャル流れと同様にガウス=ザイデル法を用いる
ソースコードはGithubも参照
≫mtkbirdman.com/CFD/FDM_N.c
#include
最初に次のヘッダーファイル(*.h)をincludeする
今回はmain関数で使う関数をmain関数の前に記述するのでプロトタイプ宣言は行わない
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<stdbool.h>
#define GNUPLOT_PATH "C:/gnuplot/bin/gnuplot.exe" //PATH for gnuplot.exemain関数
main関数のコードを示す
今回は処理をできる限り関数に分けたので,main関数はすっきりした
一様流速はpsi_max,レイノルズ数は動粘性係数nu,タイムステップはクーラン数couの値をいじることによって設定する
上で示したフローチャートと見比べてみてほしい
int main(void){
int imax=20,jmax=10,i1=8,i2=12,jbox=4,n_max=5000,np_max=50000;
double xmin=0,xmax=2,ymin=0,ymax=1;
double psi_max=0.05,eps_p=0.001,eps_z=0.001,e_max;
double cou=0.1; //cou:Courant number
double nu=0.01; //nu:Kinematic viscosity coefficient
double dx=(xmax-xmin)/(double)imax,dy=(ymax-ymin)/(double)jmax;
double xy[imax+1][jmax+1][2];
double psi[imax+1][jmax+1]; //流れ関数
double zeta[imax+1][jmax+1]; //渦度
double V0=psi_max/(dy*jmax); //一様流速
double Re=V0*(dy*jbox)/nu; //Re数
double dt=cou*(dx/V0); //タイムステップ
double psi0=psi_max,zeta0=V0/(dy*jmax); //流れ関数,渦度の基準値
double dx2=dx*dx,dy2=dy*dy,dx2dy2=dx2*dy2;
double ez_max,*pt=&ez_max;
int i,j,k,n=0;
printf("Re=%f\n",Re);
printf("dt=%f\n",dt);
Create_Mesh(imax,jmax,dx,dy,xy); //格子点座標計算
Initialize(imax,jmax,i1,i2,jbox,psi_max,psi,zeta); //初期化
Fixed_BoundaryCondition(imax,jmax,i1,i2,jbox,psi_max,psi,zeta); //固定境界条件入力
do{
printf("\riteration %d",n); //進捗表示
ez_max=0;
Variable_BoundaryCondition(imax,jmax,i1,i2,jbox,dx,dy,psi,zeta); //可変境界条件入力
Solve_VorticityTransportEquation(imax,jmax,i1,i2,jbox,nu,dt,dx,dy,pt,psi,zeta); //渦度輸送方程式を解く
GauseSeidelMethod(imax,jmax,i1,i2,jbox,np_max,eps_p,psi0,dx,dy,psi,zeta); //ガウス=ザイデル法
ez_max=ez_max/zeta0;
n++;
}while(ez_max>eps_p && n<n_max); //収束判定
printf("\n");
Output(imax,jmax,psi,zeta); //結果のファイル出力
plot_results(imax,jmax,i1,i2,jbox,xmin,xmax,ymin,ymax,psi,xy); //Gnuplotへ出力
return 0;
}収束判定に用いる\(\zeta\)の最大修正量ez_maxは,Solve_VorticityTransportEquation関数内で書き換える必要があるため,double型のポインタ変数ptを宣言し,参照渡しを行っている
Create_Mesh関数
格子点位置(x,y)を計算する
void Create_Mesh(int imax,int jmax,double dx,double dy,double xy[imax+1][jmax+1][2]){
int i,j,k,n;
//格子点座標の計算
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
xy[i][j][0]=dx*i;
xy[i][j][1]=dy*j;
}
}
return;
}Initialize関数
渦度\(\zeta\),流れ関数\(\psi\)を初期化する
void Initialize(int imax,int jmax,int i1,int i2,int jbox,double psi_max,double psi[imax+1][jmax+1],double zeta[imax+1][jmax+1]){
FILE *input;
double val[4][1024];
char str[32],*ch;
int i,j,j0,k,n;
printf("Initialize by data file? (y/n)\n>>");
fgets(str,sizeof(str),stdin);
if(strcmp(str,"y\n")==0){ //ファイルから初期値を入力
strcpy(str,"\0");
printf("Input file name\n>>");
fgets(str,sizeof(str),stdin); //ファイル名を入力
str[strlen(str)-1]='\0';
if((input=fopen(str,"r"))==NULL){
fprintf(stderr,"Not Found %s.",str);
exit(EXIT_FAILURE);
}else{
strcpy(str,"\0");
while(fgets(str,sizeof(str),input)!=NULL){
ch=strtok(str," \n");
for(i=0;i<256;i++){
if(ch==NULL){
break;
}else{
val[n][i]=atof(ch);
}
ch=strtok(NULL," \n");
}
n++;
}
}
fclose(input);
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
psi[i][j]=val[i*jmax+i+j][0];
zeta[i][j]=val[i*jmax+i+j][1];
}
}
}else{ //一様流として初期値を入力
for(i=0;i<=imax;i++){
j0=0;
if(i1<i&&i<i2){j0=jbox;} //ステップ上かどうかで場合分け
for(j=j0;j<=jmax;j++){
psi[i][j]=psi_max*((double)j)/((double)jmax);
zeta[i][j]=0;
}
}
}
return;
}9行目で,キーボードからの入力によってファイルを参照するかどうかの場合分けを行っているが,fgets関数では取得した文字列の最後に改行コード\nがつくことに注意する
10~38行目のファイルからのデータの読み込みは次の記事(≫C言語でGnuplotを使って翼型を描く)を参考にしてほしい
40~47行目では,ファイルから初期値を入力しない場合に,一様流を想定した初期値を代入している
41~42行目では,ステップ内部の格子点に初期値を設定しないよう,iの値で場合分けを行っている
Fixed_BoundaryCondition関数
固定境界条件を設定する
void Fixed_BoundaryCondition(int imax,int jmax,int i1,int i2,int jbox,double psi_max,double psi[imax+1][jmax+1],double zeta[imax+1][jmax+1]){
int i,j;
for(i=0;i<=imax;i++){ psi[i][0]=0; } //底壁
for(j=0;j<=jbox;j++){ psi[i1][j]=0; } //ステップ左面
for(i=i1;i<=i2;i++){ psi[i][jbox]=0; } //ステップ上面
for(j=0;j<=jbox;j++){ psi[i2][j]=0; } //ステップ右面
for(i=0;i<=imax;i++){ psi[i][jmax]=psi_max; } //自由表面
for(i=0;i<=imax;i++){ zeta[i][jmax]=0; } //自由表面
return;
}4~8行目では,壁面上での流れ関数\(\psi\)の境界条件を入力している
\begin{eqnarray}
\psi=\psi_{0}
\tag{2.32}
\end{eqnarray}
9行目では,自由表面での渦度\(\zeta\)の境界条件を入力している
\begin{eqnarray}
\zeta=0
\end{eqnarray}
Variable_BoundaryCondition関数
可変境界条件を設定する
void Variable_BoundaryCondition(int imax,int jmax,int i1,int i2,int jbox,double dx,double dy,double psi[imax+1][jmax+1],double zeta[imax+1][jmax+1]){
double dx2=dx*dx,dy2=dy*dy,dx2dy2=dx2*dy2;
int i,j;
for(i=1;i<i1;i++){zeta[i][0]=(2.0/dy2)*(psi[i][0]-psi[i][1]);} //底壁
for(j=1;j<jbox;j++){zeta[i1][j]=(2.0/dy2)*(psi[i1][j]-psi[i1-1][j]);} //ステップ左面
for(i=i1;i<=i2;i++){zeta[i][jbox]=(2.0/dy2)*(psi[i][jbox]-psi[i][jbox+1]);} //ステップ上面
for(j=1;j<jbox;j++){zeta[i2][j]=(2.0/dy2)*(psi[i2][j]-psi[i2-1][j]);} //ステップ右面
for(i=i2+1;i<imax;i++){zeta[i][0]=(2.0/dy2)*(psi[i][0]-psi[i][1]);} //底面
for(j=0;j<=jmax;j++){
psi[0][j]=psi[1][j];zeta[0][j]=zeta[1][j]; //流入境界
psi[imax][j]=psi[imax-1][j];zeta[imax][j]=zeta[imax-1][j]; //流出境界
}
return;
}5~9行目で,壁面上の渦度\(\zeta\)の境界条件を入力している
\begin{eqnarray}
\zeta(0)=\frac{2}{dy^2}(\psi(0)-\psi(dy))
\tag{2.39}
\end{eqnarray}
10~13行目では,流入/流出境界上での流れ関数\(\psi\)および渦度\(\zeta\)の値を,流れが垂直に流入/流出するとし,流れ方向に隣接する値を境界上での値として代入している
Solve_VorticityTransportEquation関数
式(2.26)を使って\(\zeta^{(n+1)}_{i, j}\)を計算する
\begin{align}
\zeta^{(n+1)}_{i, j}=&\zeta^{(n)}_{i, j}-\frac{\Delta t}{4\Delta x\Delta y}
\left\{
(\psi^{(n)}_{i, j+1}-\psi^{(n)}_{i, j-1})(\zeta^{(n)}_{i+1, j}-\zeta^{(n)}_{i-1, j})
-(\psi^{(n)}_{i+1, j}-\psi^{(n)}_{i-1, j})(\zeta^{(n)}_{i, j+1}-\zeta^{(n)}_{i, j-1})
\right. \\
&\left.
+\frac{\nu\Delta t}{\Delta x^2}(\zeta^{(n)}_{i-1, j}-2\zeta^{(n)}_{i, j}+\zeta^{(n)}_{i+1, j})
+\frac{\nu\Delta t}{\Delta y^2}(\zeta^{(n)}_{i, j-1}-2\zeta^{(n)}_{i, j}+\zeta^{(n)}_{i, j+1})
\right\}
\tag{2.26} \\
\end{align}
void Solve_VorticityTransportEquation(int imax,int jmax,int i1,int i2,int jbox,double nu,double dt,double dx,double dy,double *e_max,double psi[imax+1][jmax+1],double zeta[imax+1][jmax+1]){
double dx2=dx*dx,dy2=dy*dy,dx2dy2=dx2*dy2;
double dt4dxdy=dt/(4*dx*dy),ndtdx2=(nu*dt)/dx2,ndtdy2=(nu*dt)/dy2;
double zeta0[imax+1][jmax+1],dzeta;
int i,j,j0;
//zetaをzeta0にコピーする
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
zeta0[i][j]=zeta[i][j];
}
}
//式(2.26)を計算する
for(i=1;i<imax;i++){
j0=1;
if(i1<=i&&i<=i2){j0=jbox+1;} //ステップ上かどうかで場合分け
for(j=j0;j<jmax;j++){
dzeta=-dt4dxdy*((psi[i][j+1]-psi[i][j-1])*(zeta0[i+1][j]-zeta0[i-1][j])-(psi[i+1][j]-psi[i-1][j])*(zeta0[i][j+1]-zeta0[i][j-1]))+ndtdx2*(zeta0[i-1][j]-2*zeta0[i][j]+zeta0[i+1][j])+ndtdy2*(zeta0[i][j-1]-2*zeta0[i][j]+zeta0[i][j+1]);
zeta[i][j]=zeta0[i][j]+dzeta;
if(fabs(dzeta)>*e_max){*e_max=fabs(dzeta);} //最大更新量の計算
}
}
return;
}式(2.26)の\(\zeta^{(n+1)}_{i, j}\)の計算では\(\zeta^{(n)}_{i, j}\)を用いるため,zeta[i][j]を書き換えながらループを回すことができない
8~12行目でzeta[i][j]を別の配列zeta0[i][j]にコピーして,zeta0[i][j]を\(\zeta^{(n+1)}_{i, j}\)の計算で使うことによって上の問題を解決している
15~16行目では,Initialize関数と同様に,ステップ内部の格子点を計算しないようiの値で場合分けを行っている
GauseSeidelMethod関数
ガウス=ザイデル法によって\(\phi^{(n+1)}_{i, j}\)を計算する
ガウス=ザイデル法については次の記事(≫C言語でCFD入門①:ポテンシャル流れの差分解法)を参考にしてほしい
void GauseSeidelMethod(int imax,int jmax,int i1,int i2,int jbox,int np_max,double eps_p,double psi0,double dx,double dy,double psi[imax+1][jmax+1],double zeta[imax+1][jmax+1]){
double dx2=dx*dx,dy2=dy*dy,dx2dy2=dx2*dy2;
double r2dx2pdy2=1/(2*(dx2+dy2));
double dpsi,e_max;
int i,j,j0,n=0;
//ガウス=ザイデル法
do{
e_max=0;
for(j=0;j<=jmax;j++){ //流入/流出境界条件の更新
psi[0][j]=psi[1][j];zeta[0][j]=zeta[1][j];
psi[imax][j]=psi[imax-1][j];zeta[imax][j]=zeta[imax-1][j];
}
for(i=1;i<imax;i++){
j0=1;
if(i1<=i&&i<=i2){j0=jbox+1;}
for(j=j0;j<jmax;j++){
dpsi=r2dx2pdy2*((psi[i][j-1]+psi[i][j+1])*dx2+(psi[i-1][j]+psi[i+1][j])*dy2+zeta[i][j]*dx2dy2)-psi[i][j];
psi[i][j]=psi[i][j]+dpsi;
if(fabs(dpsi)>e_max){e_max=fabs(dpsi);} //最大更新量の計算
}
}
n++;
e_max=e_max/psi0;
}while(e_max>eps_p && n<np_max);
}10~13行目で,流入/流出境界上での\(\zeta\),\(\psi\)の値を代入しなおしている
Output関数
\(\zeta\)と\(\psi\)の計算結果をテキストファイル(*.txt)で出力する
≫テキストファイルの読み書き - 苦しんで覚えるC言語
特に難しいことはしていない
void Output(int imax,int jmax,double psi[imax+1][jmax+1],double zeta[imax+1][jmax+1]){
FILE *output;
double val[4][1024];
char str[32],*ch;
int i,j,k,n;
output=fopen("output_FDM_N.txt","w");
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
fprintf(output,"%f\t%f\n",psi[i][j],zeta[i][j]);
}
}
fclose(output);
return;
}plot_results関数
計算結果をGnuplotで出力する
いくつか変更点があるが,元のプログラムについては次の記事(≫C言語でCFD入門①:ポテンシャル流れの差分解法)を参考にしてほしい
void plot_results(int imax,int jmax,int i1,int i2,int jbox,double xmin,double xmax,double ymin,double ymax,double z[imax+1][jmax+1],double xy[imax+1][jmax+1][2]){
FILE *gp; //gp:gnuplot pointer
double xy_contour[2][2],z0,zmin=0,zmax=0;
char plot1[256],plot2[256],title[32]="Streamlines at Re=2";
int i,j,k,n,kmax=30;
int *ip,*jp;
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){ //Start gnuplot with pipe
fprintf(stderr,"Not Found %s.",GNUPLOT_PATH); //Standard error output
exit(EXIT_FAILURE); //Program abnormal termination
}
//Send comands to gnuplot
fprintf(gp,"set title '%s'\n",title);
fprintf(gp,"set xrange [%f:%f]\n",xmin,xmax); //Set ranges
fprintf(gp,"set yrange [%f:%f]\n",ymin,ymax);
fprintf(gp,"set xtics 0.1\nset ytics 0.1\n");
fprintf(gp,"set grid \n");
fprintf(gp,"set size ratio %f\n",(ymax-ymin)/(xmax-xmin)); //Set aspect ratio
//Plot graphic
strcpy(plot1,"'-' with lines linewidth 2");
strcpy(plot2,"'-' with lines linewidth 2");
fprintf(gp, "plot %s, %s\n",plot1,plot2);
//Plot Wall
fprintf(gp,"%f\t%f\n",xy[0][0][0],xy[0][0][1]);
fprintf(gp,"%f\t%f\n",xy[i1][0][0],xy[i1][0][1]);
fprintf(gp,"%f\t%f\n",xy[i1][jbox][0],xy[i1][jbox][1]);
fprintf(gp,"%f\t%f\n",xy[i2][jbox][0],xy[i2][jbox][1]);
fprintf(gp,"%f\t%f\n",xy[i2][0][0],xy[i2][0][1]);
fprintf(gp,"%f\t%f\n",xy[imax][0][0],xy[imax][0][1]);
fprintf(gp,"e\n"); //End of array
//Plot contour
for(i=0;i<=imax;i++){
for(j=0;j<=jmax;j++){
if(zmin>z[i][j]){zmin=z[i][j];}
if(zmax<z[i][j]){zmax=z[i][j];}
}
}
ip=&i;jp=&j;
for(k=1;k<=kmax;k++){
i=0;j=0;
z0=zmin+(zmax-zmin)*((double)k/(double)kmax);
while(i<imax || j<jmax){
contour(imax,jmax,z0,z,xy,xy_contour,ip,jp);
fprintf(gp,"%f\t%f\n",xy_contour[0][0],xy_contour[0][1]);
fprintf(gp,"%f\t%f\n",xy_contour[1][0],xy_contour[1][1]);
fprintf(gp,"\n");
}
}
fprintf(gp,"e\n"); //End of array
fflush(gp); //Spit out the data stored in the buffer (required)
system("pause");
fprintf(gp, "exit\n"); //Terminate gnuplot
_pclose(gp); //Close Gnuplot
return;
}15行目でグラフのタイトルを設定する
37~42行目でzの最小値と最大値を求める
46行目で,zの最小値から最大値までの範囲をkmax等分するようにz0の値を設定する
51行目で,改行コード\nの位置をwhile文の中に移動することで,閉じた等値線を描けるようにした
contour関数
与えられたzの等値線を描く
詳しくは次の記事(≫C言語でCFD入門①:ポテンシャル流れの差分解法)を参考にしてほしい
プログラムの実行
プログラムを実行する
>> gcc FDM_N.c
>> a.exe
Re=20.000000
dt=0.020000
Initialize by data file? (y/n)
>>n
iteration 346
続行するには何かキーを押してください . . .
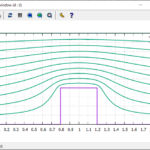
>>レイノルズ数をRe=2,20に設定してプログラムを実行してみる
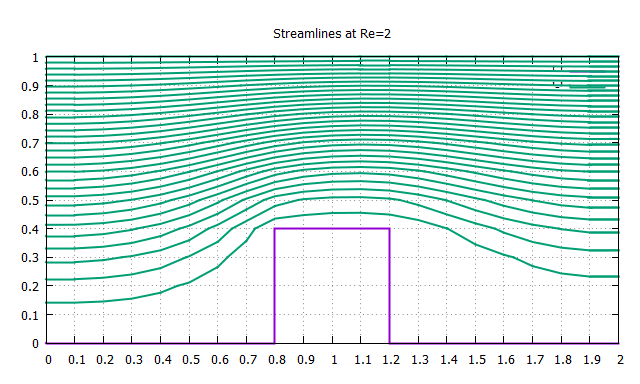
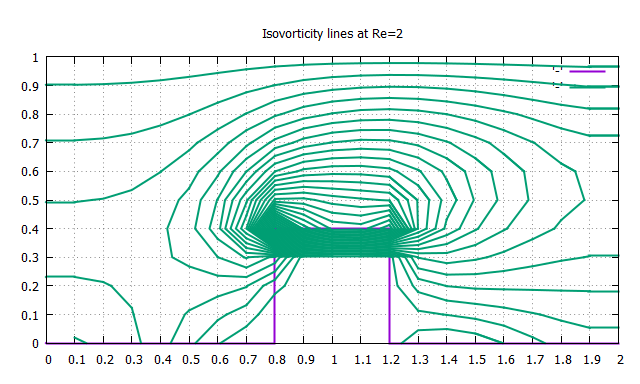
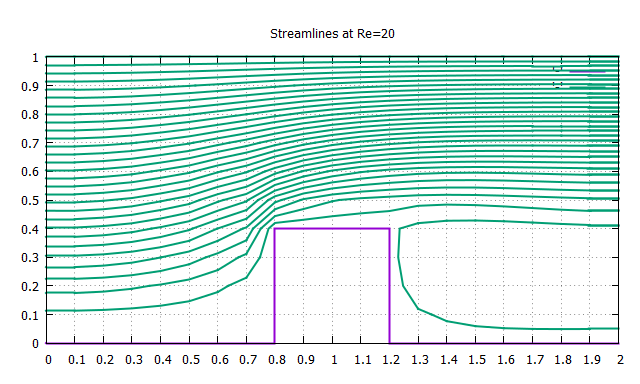
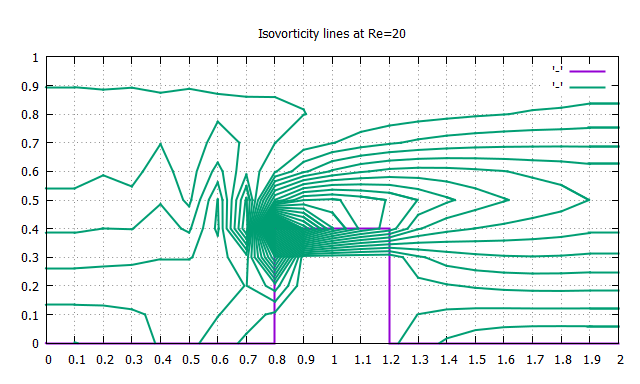
粘性の影響でステップ前後の流れに非対称性が生じたことが確認できる
ちなみにレイノルズ数が大きくなると流れが非定常になり計算結果が収束しなくなるので,一定の時間間隔で結果を出力するなどの工夫が必要になる
まとめ
ポテンシャル流れに続いて粘性流れのプログラムを作ることができた
次は有限要素法による流体解析プログラムに挑戦する
↓次の記事

コメント