大規模疎行列に対する連立一次方程式のソルバーであるSkyline法をC言語で実装する
流体解析や構造解析で有限要素法を使うときに,省メモリ・高速化に役立つ
この記事で説明したソースコードはGithubにアップしてある
≫mtkbirdman.com/CFD/
はじめに
疎行列
疎行列についてWikipediaでは次のように書いてある
疎行列(そぎょうれつ、英: sparse matrix)とは、成分のほとんどが零である行列のことをいう。スパース行列とも言う。 有限差分法、有限体積法、有限要素法などで離散化された偏微分方程式は一般に疎行列を係数行列とした連立一次方程式となる。
疎行列 - Wikipedia
数値解析の分野では、疎行列を前提とした解法が多い。疎行列であれば格納方式を工夫することで次元数を増やすことができる上に、ベクトル-行列積が比較的低計算量で求められるためである。
有限要素法の係数行列は要素数は非常に大きい(数万×数万)のにその成分のほとんどが0なので,行列の要素全てを記憶しているとメモリのほとんどが無駄になる
また,メモリのアクセスに関しても無駄が多く,計算時間も非常に大きくなる
一般に有限要素法の係数行列は実対称行列であり,0でない要素を持つのは行列の対角成分の付近なので,それを考慮して配列に値を格納することによって省メモリ・高速化が可能になる
その格納方法の一つが,今回扱うSkyline法である
Skyline法
Skyline法については,以下の資料を参考にした
≫非線形有限要素法特論 Nonlinear Finite-element-Method _ UTokyo OpenCourseWare・・・文献1の掲載元
≫第10回 連立一次方程式の数値解法―skiline法、反復法・・・文献1
さすが天下の東京大学,講義資料を公開するとは器が大きい
ちなみにこういうのもある
≫DOWNLOAD -ダウンロード- __ SPACE・・・文献2の掲載元
≫SPACE で学ぶ構造力学入門 骨組編Ⅲ 第5章・・・文献2
Skyline法では2次元配列である係数行列の値を以下のような順番で1次元配列(skyline行列)に格納する
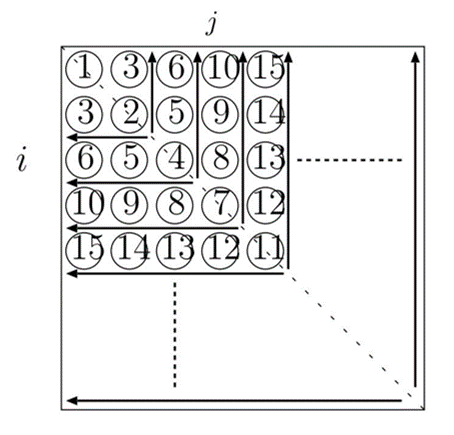
値が0の要素は配列に格納しないため,すべての値を格納し終わったときのskyline行列を図に示すと以下のようになる
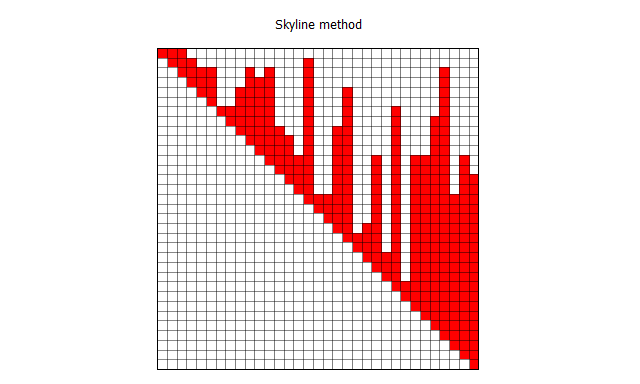
この図の形が,立ち並ぶ高層ビルの輪郭線に見えることからSkyline法というらしい.非常にオシャレである
skyline法を扱うために,次の2つの1次元配列:\(nd_{i}\),\(n_{min_{i}}\)を定義する
\(nd_{i}\):n_diagonal_i
\(nd_{i}\)は,元の係数行列のi行目の対角項の値がskyline行列の何番目の要素に格納されているかを格納している配列である
要素数は元の係数行列の行数(=列数)に一致する
\(nd_{i}\)を使えば,元の係数行列の\((i, j)\)の要素はskyline行列の\(nd_{i}+i-j\)の要素としてアクセスできる
\(n_{min_{i}}\):n_minimum_i
\(n_{min_{i}}\)は,元の係数行列のi行目において,非ゼロの要素が入っている最小の列数jを格納した一次元配列である
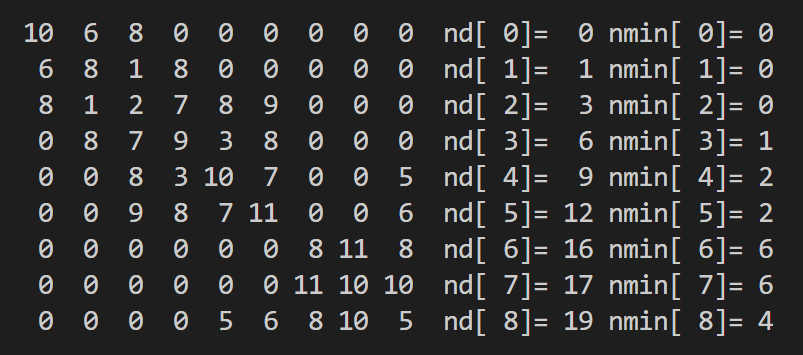
skyline行列の例
以下に,係数行列の例と\(nd_{i}\),\(n_{min_{i}}\)の値を示す
アルゴリズム概要
Skyline法による連立一次方程式ソルバーのアルゴリズムを説明する.詳しくは文献1を参考にしてほしい
やっていること自体はLDU分解で,修正コレスキー分解と言ったりもするらしい
≫コレスキー分解 - Wikipedia
アルゴリズムの概要は次のようになる
- 係数行列\({\bf K}\)をLDU分解する
- 下三角行列\({\bf L}\)を使って前進代入を行う
- 上三角行列\({\bf U}\)を使って後退代入を行う
ちなみに文献1では上三角行列に注目して列のループを回しているが,筆者は文献2のように下三角行列に注目して行のループを回す方が理解しやすかった
どちらでも結果に影響はないが,これからの説明およびプログラムは文献1をベースにしつつ下三角行列に注目して行っていく
LDU分解
連立一次方程式の係数行列\({\bf K}\)は下三角行列\({\bf L}\),対角行列\({\bf D}\),上三角行列\({\bf U}\)を用いて次のように分解できる
\begin{eqnarray}
{\bf K}={\bf L}{\bf D}{\bf U}
\tag{1}
\end{eqnarray}
有限要素法では一般に係数行列\({\bf K}\)は実対称行列なので式(1)は次のようになる
\begin{eqnarray}
{\bf K}&=&{\bf L}{\bf D}{\bf L^{T}}
\tag{2} \\
{\bf L}&=&{\bf U^{T}}
\end{eqnarray}
ただし,下三角行列\({\bf L}\)および上三角行列\({\bf U}\)の対角項の値はすべて1である
式(1)を行列の成分で表すと次のようになる
\begin{eqnarray}
K_{ij}&=&L_{ij}D_{jj}~~~(j=n_{min_{i}})
\tag{3}\\
K_{ij}&=&\sum_{k=max(n_{min_{i}},n_{min_{j}})}^{i-1}L_{ik}D_{kk}U_{kj}+L_{ij}D_{jj}~~~(j=n_{min_{i}}\ldots i-1)
\tag{4}\\
K_{ii}&=&\sum_{k=n_{min_{i}}}^{i-1}L_{ik}D_{kk}U_{ki}+D_{ii}~~~(i=j)
\tag{5}\\
\end{eqnarray}
式(3)~(5)を使い,次のように下三角行列\({\bf L}\),対角行列\({\bf D}\),上三角行列\({\bf U}(={\bf L^{T}})\)を求めていく
- 1行目(i=1)
式(3)より,\(D_{11}=K_{11}/L_{11}\)を計算する.定義より\(L_{11}=1\) - 2行目(i=2)
式(3)より,\(L_{21}=K_{21}/D_{11}\)を計算する
式(5)より,\(D_{22}=K_{22}-L_{21}D_{11}U_{12}\)を計算する - 3行目~最終行(i=3~n)
式(4)より\(L_{ij}\)を計算する.\((j<i)\)
式(5)より\(D_{ii}\)を計算する
前進代入・後退代入
LDU分解によって,\({\bf K}={\bf L}{\bf D}{\bf U}\)となる下三角行列\({\bf L}\),対角行列\({\bf D}\),上三角行列\({\bf U}\)が得られた
ここで解を求めたい連立一次方程式\({\bf Kx}={\bf b}\)を次のように変形する
\begin{eqnarray}
{\bf LDUx}&=&{\bf b}\\
{\bf Ly}&=&{\bf b}~~~({\bf DUx}={\bf y})
\tag{6}\\
{\bf Ux}&=&{\bf (D^{-1}y)}
\tag{7}\\
\end{eqnarray}
式(6)の方程式は前進代入,式(7)の方程式は後退代入によって解くことができ,最終的に解\({\bf x}\)が求められる
式(6),式(7)の方程式を成分を用いて表して整理すると次のようになる
\begin{eqnarray}
y_{i}=b_{i}-\sum_{k=1}^{i-1}L_{ik}x_{k}
\tag{6'}\\
x_{i}=\frac{y_{i}}{D_{ii}}-\sum_{k=n}^{i+1}U_{ik}y_{k}
\tag{7'}\\
\end{eqnarray}
プログラムの実装
ランダムな値を要素に持つ配列\({\bf A}\),\({\bf b}\)についての連立一次方程式\({\bf Ax}={\bf b}\)をガウスの消去法とskyline法で解き,計算時間を比較するプログラムを作る
ガウスの消去法とskyline行列の可視化プログラムについてはこの記事の最後にソースコードを乗せておくので参考にしてほしい
ガウスの消去法やskyline法は今後いろいろなプログラムで使うことになるので,ソースファイルを分割しヘッダーファイルをincludeしている
≫最小限の分割 - 苦しんで覚えるC言語
main関数
メイン関数のソースコードを以下に示す
ソースコードはGithubも参照
≫mtkbirdman.com/CFD/test_solver.c
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<string.h>
#include"solver.h"
#define GNUPLOT_PATH "C:/gnuplot/bin/gnuplot.exe" //PATH for gnuplot.exe
void plot_results(int nmax,int nmin[nmax+1]);
int main(void){
clock_t s1,s2,e1,e2;
int nmax=32,amax=10;
double b[nmax+1],b2[nmax+1],x[nmax+1];
double *L,*L2,**A,*Ap,*b1;
int nd[nmax+1],nmin[nmax+1]; //n_diagonal,n_min
int i,j,k,j0,ssize; //skyline_size
int ij,ji,n;
A=(double **)malloc(sizeof(double *)*(nmax+1));Ap=(double *)malloc(sizeof(double)*(nmax+1)*(nmax+1));for(n=0;n<=nmax;n++){A[n]=Ap+(nmax+1)*n;}
b1=(double *)malloc(sizeof(double)*(nmax+1));
for(i=0;i<=nmax;i++){for(j=0;j<=nmax;j++){A[i][j]=0;}} //Initialize A
//Create random matrix
ssize=0;
srand((int)time(NULL));
for(i=0;i<=nmax;i++){
j0=rand() % (i+1); //j0=nd[i]
for(j=j0;j<=i;j++){
A[i][j]=rand() % (amax+1)+1;
ssize++;
}
b[i]=rand() % (amax+1);
}
ssize--;
//Make A symmetry
for(i=0;i<=nmax;i++){
for(j=0;j<i;j++){
A[j][i]=A[i][j];
}
}
L=malloc(sizeof(double)*(ssize+1)); //Allocate L
//Convert A to L
k=0;
for(i=0;i<=nmax;i++){
for(j=i;j>=0;j--){
nmin[i]=0;
if(A[i][j]==0){
nmin[i]=j+1; //Make nmin
break;
}else{
L[k]=A[i][j];
}
if(i==j){nd[i]=k;} //Make nd
k++;
}
}
//Show A, nd and nmin
printf("\n");for(i=0;i<=nmax;i++){for(j=0;j<=nmax;j++){printf("%2.0f ",A[i][j]);}printf(" nd[%2d]=%3d nmin[%2d]=%2d\n",i,nd[i],i,nmin[i]);}printf("\n");
for(i=0;i<=nmax;i++){b1[i]=b[i];b2[i]=b[i];} //Copy b to b1, b2
s1=clock();
Gaussian_Elimination(nmax,A,b1);
e1=clock();s2=clock();
skyline_method(nmax,ssize,nd,nmin,L,b2);
e2=clock();
//Show reslut
for(j=0;j<=nmax;j++){printf("b1[%3d]=%7.3f b2[%3d]=%7.3f\n",j,b1[j],j,b2[j]);}
printf("\nGaussian Elimination\nMatrix size >> %d\nTime >> %f\n",(nmax+1)*(nmax+1),(e1-s1)/(double)CLOCKS_PER_SEC);
printf("\nSkyline method\nMatrix size >> %d\nTime >> %f\n",ssize,(e2-s2)/(double)CLOCKS_PER_SEC);
plot_results(nmax,nmin);
free(L);
return 0;
}20~37行目で,ランダムな要素を持つ行列を生成している
行列\({\bf A}\)は実対称行列なので,下三角の成分のみ計算し,32∼37行で上三角部分に値を代入している
24行目で,列のループの最初の値j0をランダムに決定することによって,skylineっぽい行列になるようにしている
関数rand,srandについては次のサイトを参考にした
≫【C言語入門】乱数(rand)の使い方 _ 侍エンジニア塾ブログ(Samurai Blog) - プログラミング入門者向けサイト
また,行列\({\bf A}\)をつくるときにskyline行列の要素数ssizeを計算しておき,38行目でskyline行列\({\bf L}\)の要素数を定義している
≫配列を自由自在に作る - 苦しんで覚えるC言語
40~54行目で,2次元配列Aを1次元配列Lに格納し,ついでにndとnminを計算している
skyline_method関数
skyline法のソースコードを以下に示す
ソースコードはGithubも参照
≫mtkbirdman.com/CFD/solver.c
≫mtkbirdman.com/CFD/solver.h
メモリ節約のため,\({\bf K}\),\({\bf L}\),\({\bf D}\)はすべて配列Lに,\({\bf b}\),\({\bf x}\),\({\bf y}\)はすべて配列bに格納されており,\({\bf U}={\bf L^{T}}\)を利用している
int max(int a,int b){
if(a>=b){return a;}
if(a<b){return b;}
}void skyline_method(int nmax,int ssize,int nd[nmax+1],int nmin[nmax+1],double L[ssize+1],double b[nmax+1]){
double tmp;
int i,j,k,ik,jk,ij,ki;
//LDU decomposition
for(i=0;i<=nmax;i++){
if(i==0){
L[0]=L[0]; //D11=K11
}else if(i==1){
if(nd[2]==3){
L[2]=L[2]/L[0]; //L21=K21/D11
L[1]=L[1]-L[2]*L[0]*L[2]; //D22=K22-L21*D11*U12
}else{
L[1]=L[1];
}
}else{ //i>2
for(j=nmin[i];j<i;j++){
tmp=0;
for(k=max(nmin[i],nmin[j]);k<j;k++){ //i>j
ik=nd[i]+i-k;
jk=nd[j]+j-k;
tmp=tmp+L[ik]*L[jk]; //SUM{(Lik*Dkk)*Ljk}
}
ij=nd[i]+i-j;
L[ij]=L[ij]-tmp; //(Lij*Djj)=Kij-SUM{(Lik*Dkk)*Ljk}
}
for(j=nmin[i];j<i;j++){
ij=nd[i]+i-j;
L[ij]=L[ij]/L[nd[j]]; //Lij=(Lij*Djj)/Djj
}
tmp=0;
for(k=nmin[i];k<i;k++){
ik=nd[i]+i-k;
tmp=tmp+L[ik]*L[ik]*L[nd[k]]; //SUM{Lik*Lik*Dkk}
}
L[nd[i]]=L[nd[i]]-tmp; //Dii=Kii-SUM{Lik*Lik*Dkk}
}
}
//Forward substitution
for(i=0;i<=nmax;i++){
if(i==0){
b[i]=b[i]; //y0=b0
}else{
for(k=nmin[i];k<i;k++){
ik=nd[i]+i-k;
b[i]=b[i]-L[ik]*b[k]; //yi=bi-SUM{Lik*xk}
}
}
}
//Backward substitution
for(i=0;i<=nmax;i++){
b[i]=b[i]/L[nd[i]]; //xi=yi/Dii
}
for(i=nmax;i>=0;i--){
if(i==nmax){
b[i]=b[i]; //bn=xn
}else{
for(k=nmax;k>i;k--){
ki=nd[k]+k-i;
if(nmin[k]<=i){
b[i]=b[i]-L[ki]*b[k]; //xj=xj-Lij*bi
}else{
b[i]=b[i];
}
}
}
}
return;
}10∼15行目では,\(K_{21}=0\)だった場合の場合分けをしている
17∼30行目で式(4)より\(L_{ij}\)を計算している
\begin{eqnarray}
L_{ij}&=&(K_{ij}-\sum_{k=max(n_{min_{i}},n_{min_{j}})}^{i-1}L_{ik}D_{kk}U_{kj})/D_{jj}~~~(j=n_{min_{i}}\ldots i-1)
\tag{4'}
\end{eqnarray}
31∼36行目で式(5)より\(D_{ii}\)を計算している
\begin{eqnarray}
D_{ii}&=&K_{ii}-\sum_{k=n_{min_{i}}}^{i-1}L_{ik}D_{kk}U_{ki}~~~(i=j)
\tag{5'}
\end{eqnarray}
i行目で列のループ(j, k)を回すときは,nmin[i]を利用して要素が0の成分にはアクセスしないようにしている
40∼50行目では式(6’)によって前進代入を計算し,52∼69行目では式(7’)により後退代入を計算している
\begin{eqnarray}
y_{i}=b_{i}-\sum_{k=1}^{i-1}L_{ik}x_{k}
\tag{6'}\\
x_{i}=\frac{y_{i}}{D_{ii}}-\sum_{k=n}^{i+1}U_{ik}y_{k}
\tag{7'}\\
\end{eqnarray}
後退代入では列を固定して行のループを回しているので,62~66行目の場合分けによって要素が0の成分にはアクセスしないようにしている
プログラムの実行
プログラムを実行する
>> gcc test_solver.c solver.c
>> a.exe
b1[ 0]=-17.101 b2[ 0]=-17.101
b1[ 1]= 48.112 b2[ 1]= 48.112
b1[ 2]= 23.697 b2[ 2]= 23.697
b1[ 3]=-34.804 b2[ 3]=-34.804
b1[ 4]= 42.971 b2[ 4]= 42.971
b1[ 5]=-17.069 b2[ 5]=-17.069
b1[ 6]=-16.525 b2[ 6]=-16.525
b1[ 7]=-14.113 b2[ 7]=-14.113
b1[ 8]= 54.425 b2[ 8]= 54.425
b1[ 9]=-37.410 b2[ 9]=-37.410
b1[ 10]=-47.623 b2[ 10]=-47.623
b1[ 11]=-11.733 b2[ 11]=-11.733
b1[ 12]= 32.436 b2[ 12]= 32.436
b1[ 13]=-34.861 b2[ 13]=-34.861
b1[ 14]= 13.501 b2[ 14]= 13.501
b1[ 15]= 28.949 b2[ 15]= 28.949
b1[ 16]= 6.321 b2[ 16]= 6.321
b1[ 17]= -2.730 b2[ 17]= -2.730
b1[ 18]= 66.333 b2[ 18]= 66.333
b1[ 19]=-47.872 b2[ 19]=-47.872
b1[ 20]= 62.088 b2[ 20]= 62.088
b1[ 21]= 17.264 b2[ 21]= 17.264
b1[ 22]=-17.930 b2[ 22]=-17.930
b1[ 23]=-64.718 b2[ 23]=-64.718
b1[ 24]=-50.483 b2[ 24]=-50.483
b1[ 25]= 19.270 b2[ 25]= 19.270
b1[ 26]= 49.967 b2[ 26]= 49.967
b1[ 27]=-55.449 b2[ 27]=-55.449
b1[ 28]= -1.428 b2[ 28]= -1.428
b1[ 29]= 8.147 b2[ 29]= 8.147
b1[ 30]= 45.224 b2[ 30]= 45.224
b1[ 31]= -9.207 b2[ 31]= -9.207
b1[ 32]=-13.221 b2[ 32]=-13.221
Gaussian Elimination
Matrix size >> 1089
Time >> 0.000000
Skyline method
Matrix size >> 344
Time >> 0.000000
続行するには何かキーを押してください . . .
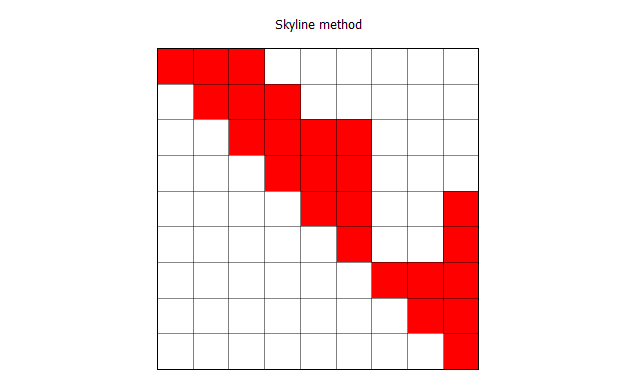
>>筆者のパソコンの限界であるnmax=500としてプログラムを実行してみると実行結果は次のようになった
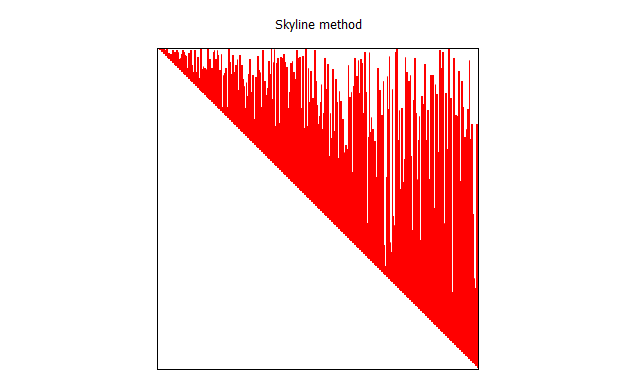
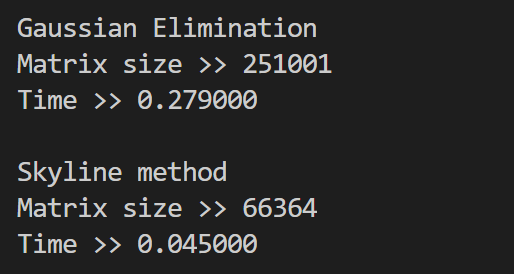
nmax=500という小さな配列だが,ガウスの消去法と比較してskyline法ではメモリの大きさは約4分の1,計算時間は約6分の1になった
ガウスの消去法のメモリの大きさと計算時間は要素数の2乗で増加していくので,nmaxが数万や数十万になればskyline法の有用性はより顕著になる
まとめ
有限要素法などのプログラムをつくるときに今回作ったskyline法のソルバーを使っていきたい
おまけ
ソースコードはGithubも参照
≫mtkbirdman.com/CFD/solver.c
≫mtkbirdman.com/CFD/solver.h
Gaussian_Elimination関数
void Gaussian_Elimination(int nmax,double **A,double *b){
double pivot,p;
int i,j,ii,jj;
for(i=0;i<=nmax;i++){
pivot=A[i][i];
for(j=i;j<=nmax;j++){
A[i][j]=A[i][j]/pivot;
}
b[i]=b[i]/pivot;
for(ii=i+1;ii<=nmax;ii++){
pivot=A[ii][i];
for(jj=i;jj<=nmax;jj++){
A[ii][jj]=A[ii][jj]-pivot*A[i][jj];
}
b[ii]=b[ii]-pivot*b[i];
}
}
for(i=nmax-1;i>=0;i--){
for(j=i+1;j<=nmax;j++){
b[i]=b[i]-A[i][j]*b[j];
}
}
return;
}plot_resluts関数
void plot_results(int nmax,int nmin[nmax+1]){
FILE *gp; //gp:gnuplot pointer
double xy_contour[2][2],z0,zmin=0,zmax=0;
char plot1[64],plot2[64],plot3[64],title[32]="Skyline method";
int i,j,k,n,kmax=30;
int *ip,*jp;
//Start Gnuplot comand
if((gp=_popen(GNUPLOT_PATH,"w"))==NULL){
fprintf(stderr,"Not Found %s.",GNUPLOT_PATH);
exit(EXIT_FAILURE);
}
//Send comands to gnuplot
fprintf(gp,"set title '%s'\n",title);
fprintf(gp,"set xrange [%f:%f]\n",0,(double)(nmax+1));
fprintf(gp,"set yrange [%f:%f]\n",0,(double)(nmax+1));
fprintf(gp,"unset xtics\n");fprintf(gp,"unset ytics\n");
fprintf(gp,"set style fill solid\n");
fprintf(gp,"unset key\n"); //Hide legend
fprintf(gp,"set size square\n");
//fprintf(gp,"set grid linetype 1 linecolor 'black'\n");
//Plot graphic
strcpy(plot1,"'-' with boxes linetype rgbcolor 'red'");
strcpy(plot2,"'-' with boxes linetype rgbcolor 'white'");
//fprintf(gp, "plot %s,%s\n",plot1,plot2);
strcpy(plot3,"'-' with lines linetype rgbcolor 'white' linewidth 0.1");
fprintf(gp, "plot %s,%s,%s\n",plot1,plot2,plot3);
//Plot Skyline
for(k=0;k<=nmax;k++){
fprintf(gp,"%f\t%f\n",(double)k+0.5,(double)((nmax+1)-nmin[k]));
fprintf(gp,"\n");
}
fprintf(gp,"e\n"); //End of array
for(k=0;k<=nmax;k++){
fprintf(gp,"%f\t%f\n",(double)k+0.5,(double)((nmax+1)-(k+1)));
fprintf(gp,"\n");
}
fprintf(gp,"e\n"); //End of array
for(k=0;k<=nmax;k++){
fprintf(gp,"%f\t%f\n",(double)k,0);
fprintf(gp,"%f\t%f\n",(double)k,(double)(nmax+1));
fprintf(gp,"\n");
}
for(k=0;k<=nmax;k++){
fprintf(gp,"%f\t%f\n",0,(double)k);
fprintf(gp,"%f\t%f\n",(double)(nmax+1),(double)k);
fprintf(gp,"\n");
}
fprintf(gp,"e\n"); //End of array
fflush(gp);
printf("\n");
system("pause");
fprintf(gp, "exit\n");
_pclose(gp);
return;
}
コメント