DATCOM 2.2.2 に基づいて、翼平面形の諸元を計算する。
はじめに
DATCOM 2.2.2 に基づいて、翼平面形の諸元を計算する。
PDFのページは235ページ
一般的な翼の平面形の諸元
一般的な翼の平面形の諸元は以下の式で計算する。
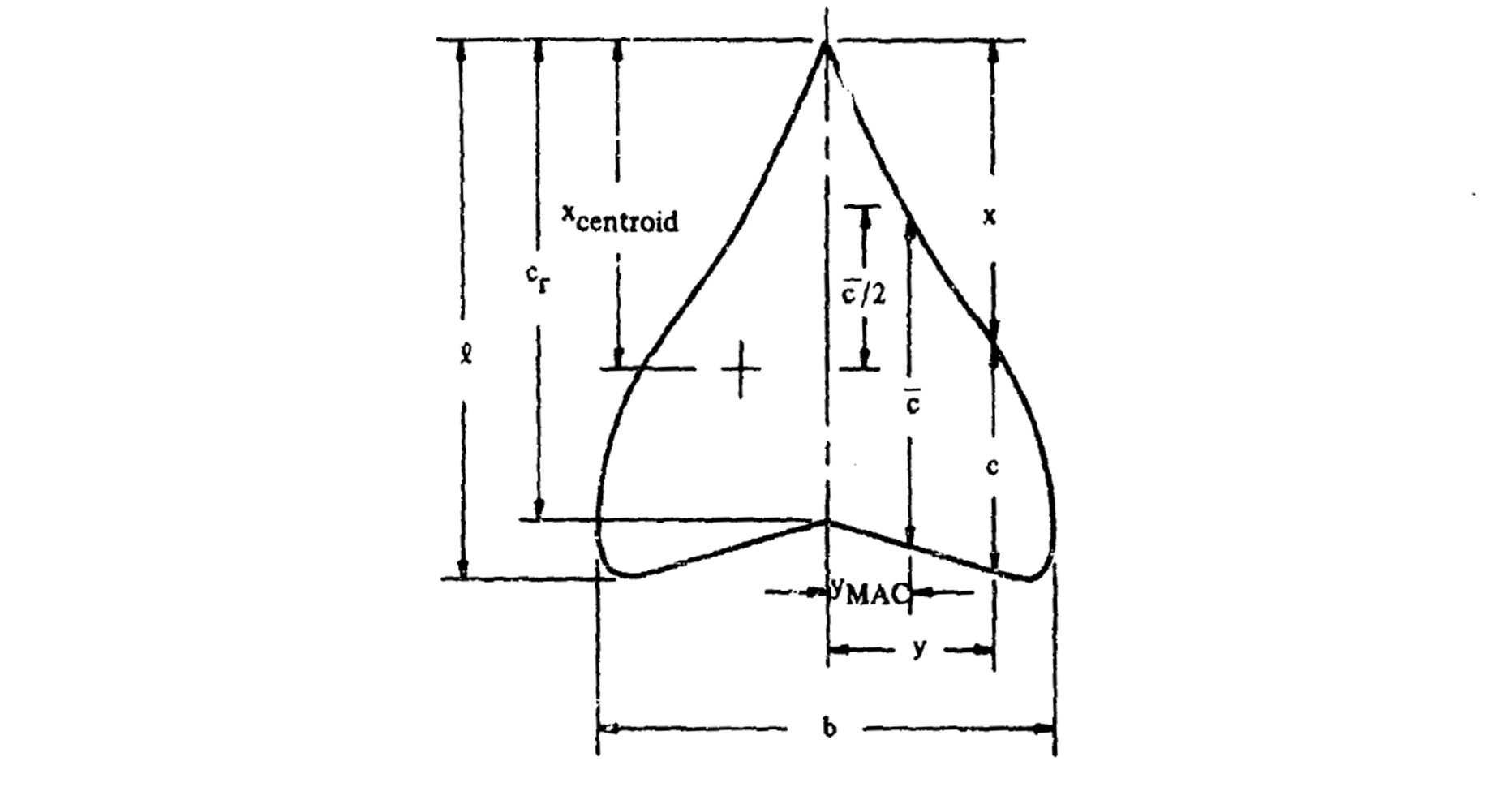
| 文字 | 単位 | 説明 |
| \(A\) | - | アスペクト比。 |
| \(b\) | m | スパン。 |
| \(b/l\) | - | wing-slenderness parameter |
| \(c\) | m | スパン位置\(y\)におけるコード長。 対称面と平行に定義する。 |
| \(\overline{c}\) | m | 平均空力翼弦長。(MAC) |
| \(c_{r}\) | m | 翼根コード長。 |
| \(l\) | m | 翼の全長。 |
| \(S\) | ㎡ | 翼面積。 |
| \(x\) | m | スパン位置\(y\)における前縁位置。 |
| \(y\) | m | 対称面から垂直に測ったスパン位置。 |
| \(y_{_{MAC}}\) | m | MACのスパン方向位置。 翼の面積重心位置と等価。 |
ここで
\begin{align}
A&=\frac{b^2}{S} \\\\
\overline{c}&=\frac{2}{S}\int_{0}^{b/2}{c^2 ~\mathrm{dy}} \\\\
S&=2\int_{0}^{b/2}{c ~\mathrm{dy}} \\\\
y_{_{MAC}}&=\frac{2}{S}\int_{0}^{b/2}{cy ~\mathrm{dy}}
\end{align}
単純なテーパー翼の平面形の諸元
単純なテーパー翼の平面形の諸元は以下の式で計算する。
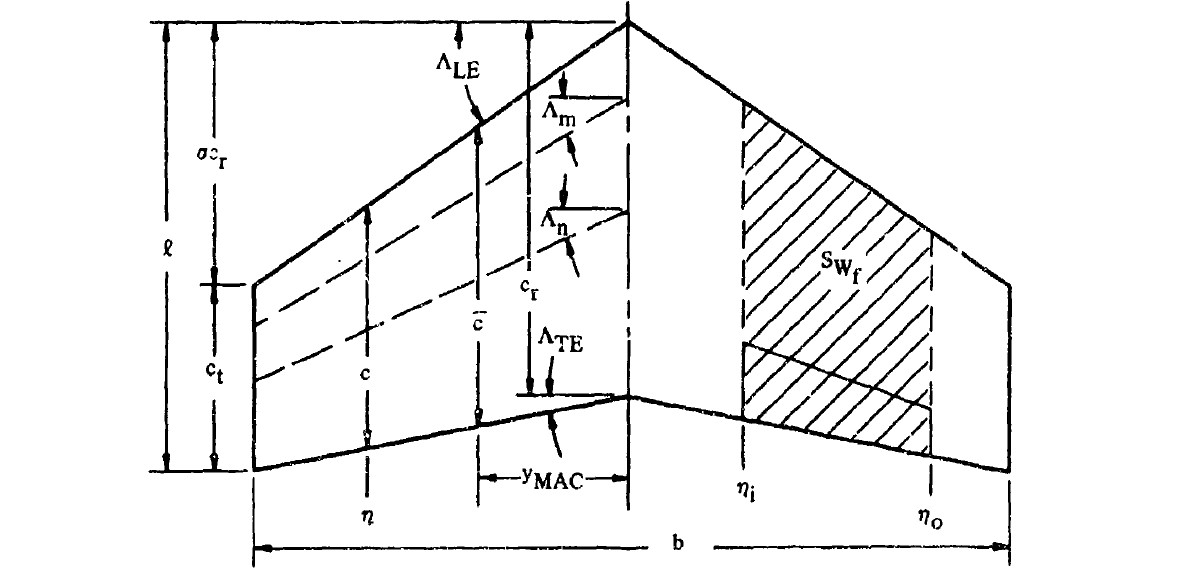
| 文字 | 単位 | 説明 |
| \(A\) | - | アスペクト比。 |
| \(b\) | m | スパン。 |
| \(c\) | m | スパン位置\(y\)におけるコード長。 対称面と平行に定義する。 |
| \(\overline{c}\) | m | 平均空力翼弦長。(MAC) |
| \(c_{r}\) | m | 翼根コード長。 |
| \(c_{t}\) | m | 翼端コード長 |
| \(m\)、\(n\) | - | 無次元化されたコード方向位置。 LE=0、TE=1 |
| \(l\) | m | 翼の全長。 |
| \(S\) | ㎡ | 翼面積。 |
| \(x\) | m | スパン位置\(y\)における前縁位置。 |
| \(y\) | m | 対称面から垂直に測ったスパン位置。 |
| \(y_{_{MAC}}\) | m | MACのスパン方向位置。 翼の面積重心位置と等価。 |
| \(\eta\) | - | 無次元化されたスパン方向位置。 \(\eta=y/(b/2)\) |
| \(\lambda\) | - | テーパー比。 |
| \(\Lambda_{_{LE}}\) | deg | 前縁後退角。 |
| \(\Lambda_{_{TE}}\) | deg | 後縁後退角。 |
| \(\Lambda_{_m}\)、\(\Lambda_{_n}\) | deg | 任意のコード方向位置における後退角。 |
ここで
\begin{align}
A&=\frac{b^2}{S}=\frac{2b}{c_{r}\left(1+\lambda\right)} \\\\
c&=c_{r}\left\{1+\left(\lambda-1\right)\frac{|y|}{b/2}\right\} \\\\
\overline{c}&=\frac{2}{S}\int_{0}^{b/2}{c^2 ~\mathrm{dy}}=\frac{2}{3}c_{r}\frac{1+\lambda+\lambda^2}{1+\lambda} \\\\
S&=2\int_{0}^{b/2}{c ~\mathrm{dy}}=\frac{b}{2}c_{r}\left(1+\lambda\right) \\\\
y_{_{MAC}}&=\frac{2}{S}\int_{0}^{b/2}{cy ~\mathrm{dy}}=\frac{1}{3}\frac{1+2\lambda}{1+\lambda}\frac{b}{2} \\\\
\tan{\Lambda_{n}}&=\tan{\Lambda_{m}}-\frac{4}{A}\left[\left(n-m\right)\frac{1-\lambda}{1+\lambda}\right] \\\\
\end{align}
reference
-
制限
-
おわりに
DATCOM 2.2.2 に基づいて、翼平面形の諸元を計算した。
↓次




コメント