DATCOM 4.1.1.2 に基づいて、2次元翼の揚力傾斜を計算する。
はじめに
DATCOM 4.1.1.2 に基づいて、2次元翼の揚力傾斜を計算する。
PDFのページは471ページ
Method 2
臨界マッハ数以下の2次元翼の揚力傾斜\(\left(c_{l_{\alpha}}\right)_{_M}\)は以下の式で計算する。
\begin{align}
\left(c_{l_{\alpha}}\right)_{_M}&=\frac{1.05}{\beta}\left[\frac{c_{l_{\alpha}}}{\left(c_{l_{\alpha}}\right)_{theory}}\right]\left(c_{l_{\alpha}}\right)_{theory}
\tag{4.1.1.2-a} \\\\
\left(c_{l_{\alpha}}\right)_{theory}&=6.28+4.7\left(t/c\right)\left[1+0.00375\phi_{TE}\right] ~\mathrm{[1/rad]} \\\\
\beta&=\sqrt{1-M^2}
\end{align}
ここで
| 文字 | 単位 | 説明 |
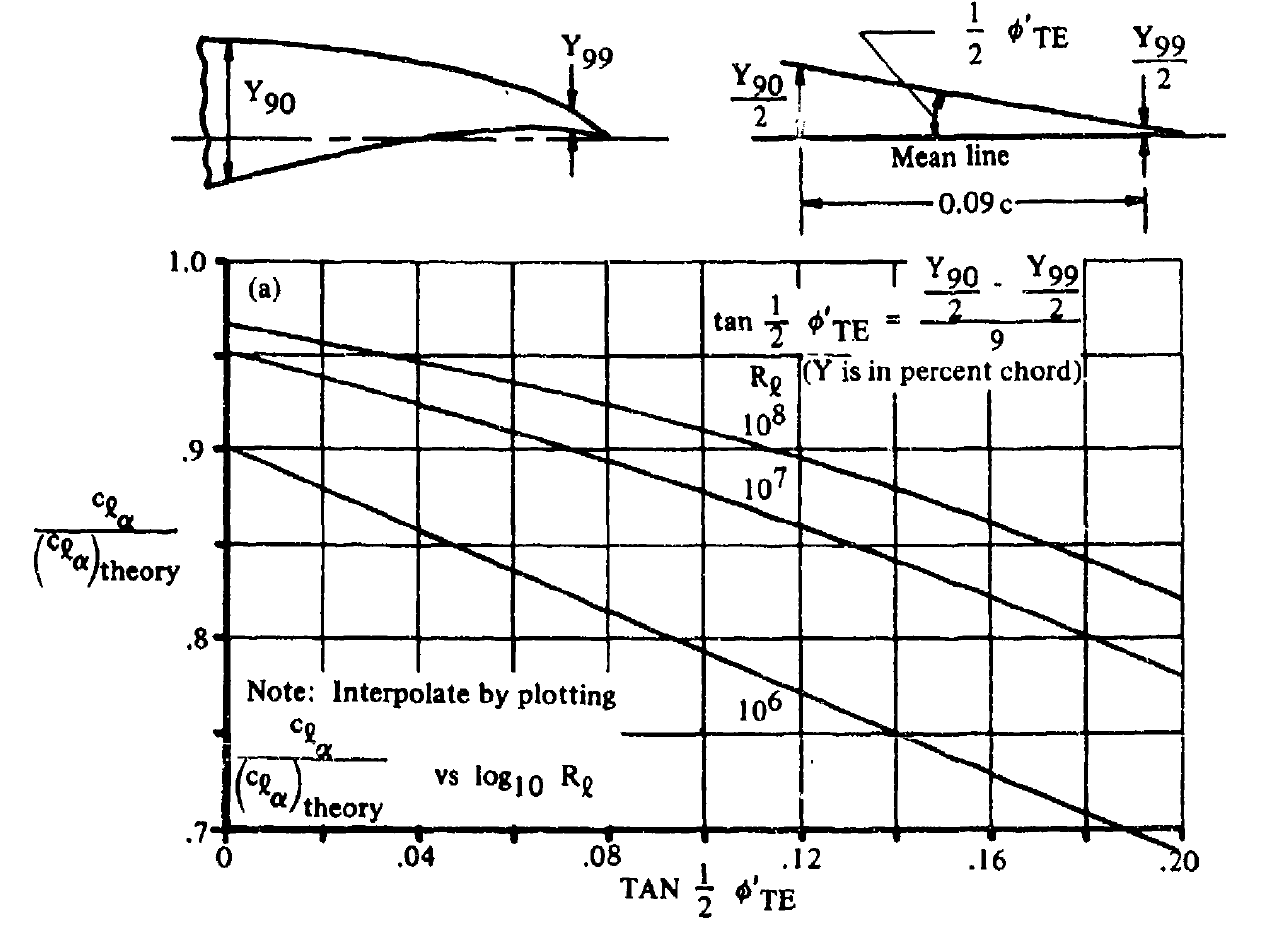
| \(\left[\frac{c_{l_{\alpha}}}{\left(c_{l_{\alpha}}\right)_{theory}}\right]\) | - | 経験的な補正係数。 figure 4.1.1.2-8aから求める。 |
| \(\left(c_{l_{\alpha}}\right)_{theory}\) | - | 2次元揚力傾斜の理論値。 後縁角の大きさにはあまり影響を受けないため、 \(\phi_{TE}=20\) [deg]を定数として採用する。(この手法の上限) |
| \(\beta\) | - | Prandtl–Glauert compressibility correction factor |
| \(t/c\) | - | 最大翼厚比。 |
reference

制限
この手法における注意点は以下の通り
- 乱流遷移点は前縁で固定されていること。
- 翼厚は20%以下であること。
- 臨界マッハ数以下であること。
- 流れは剥離していないこと。
Sample
OpenVSPのExample FileにあるPod Planeについて、実際に計算してみる。
↓計算に使用したエクセルファイル(マクロ付き)
ここで、NACA4字系列のキャンバーラインから翼上下面までの距離は以下の式で表される。
\begin{align}
y_{t}(x)=5\left(\frac{t}{c}\right)\left(0.2969\sqrt{x}-0.126x-0.3516x^2+0.2843x^3-0.1015x^4\right)
\end{align}
↓計算結果
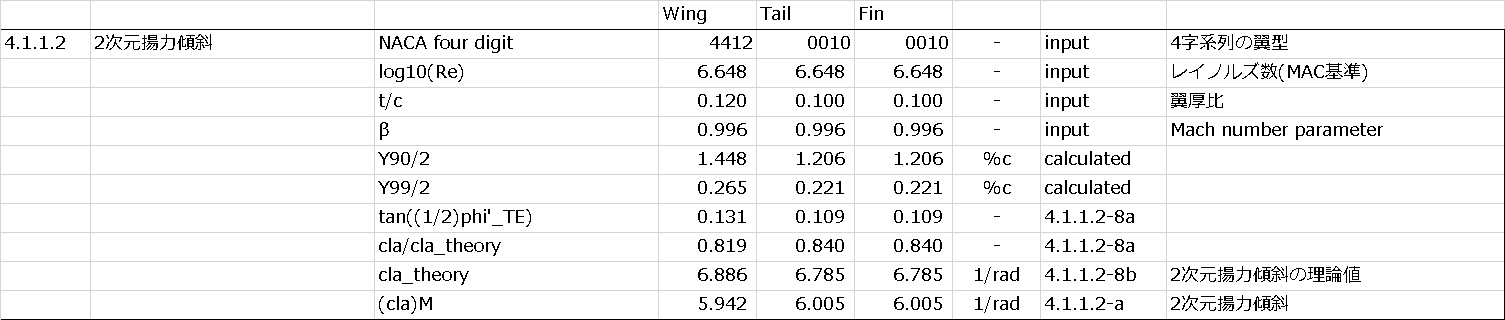
以上
おわりに
DATCOM 4.1.1.2 に基づいて、2次元翼の揚力傾斜を計算した。
↓次








コメント