DATCOM 4.1.3.2 に基づいて、3次元揚力傾斜を計算する。
はじめに
DATCOM 4.1.3.2 に基づいて、3次元揚力傾斜を計算する方法について説明する。
PDFは501ページ
Method 1
Straight Taperd Wingの3次元揚力傾斜は以下の式で表される。
\begin{align}
&C_{L_{\alpha}}=\frac{2\pi A}{2+\sqrt{\frac{A^2}{\kappa^2}\left(\beta^2+\tan{\Lambda_{c/2}}^2\right)+4}} \\\\\\
&\beta=\sqrt{1-M^2} \\\\
&\kappa=\frac{\left(c_{l_\alpha}\right)_{_M}}{\left(2\pi/\beta\right)}
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(A\) | - | アスペクト比。(垂直尾翼の場合は両翼あるとして計算する) DATCOM 2.2.2で計算する。 |
| \(\Lambda_{c/2}\) | deg | c/2ライン後退角。 DATCOM 2.2.2で計算する。 |
| \(\beta\) | - | Prandtl–Glauert compressibility correction factor |
| \(M\) | - | マッハ数 |
| \(\kappa\) | - | 2次元揚力傾斜の係数。 |
| \(\left(c_{l_{\alpha}}\right)_{_M}\) | 1/rad | あるマッハ数における2次元揚力傾斜 DATCOM 4.1.1.2で計算する。 |
ちなみに、この式において\(M\ll 1\)、\(\Lambda_{c/2}=0\)、\(\left(A^2/\kappa^2\right) \gg 1\)とすると
\begin{align}
C_{L_{\alpha}}
&=\frac{2\pi A}{2+\sqrt{\frac{A^2}{\kappa^2}\left(\beta^2+\tan^2{\Lambda_{c/2}}\right)+4}}
\simeq \frac{2\pi A}{2+\sqrt{\frac{A^2}{\kappa^2}+4}} \\\\
&\simeq \frac{2\pi A}{2+\frac{A}{\kappa}}
=\frac{2\pi\kappa}{\frac{2\pi\kappa}{\pi A}+1}=\frac{\left(c_{l_{\alpha}}\right)_{_M}}{1+\frac{\left(c_{l_{\alpha}}\right)_{_M}}{\pi A}}
\end{align}
となり、見慣れた白本の計算式になる。
reference
制限
この手法における注意点は以下の通り
- Straight Taperd Wingであること。(DATCOMの定めるNon-Straight-Taper Wingの例はSketch(a)を参照。)
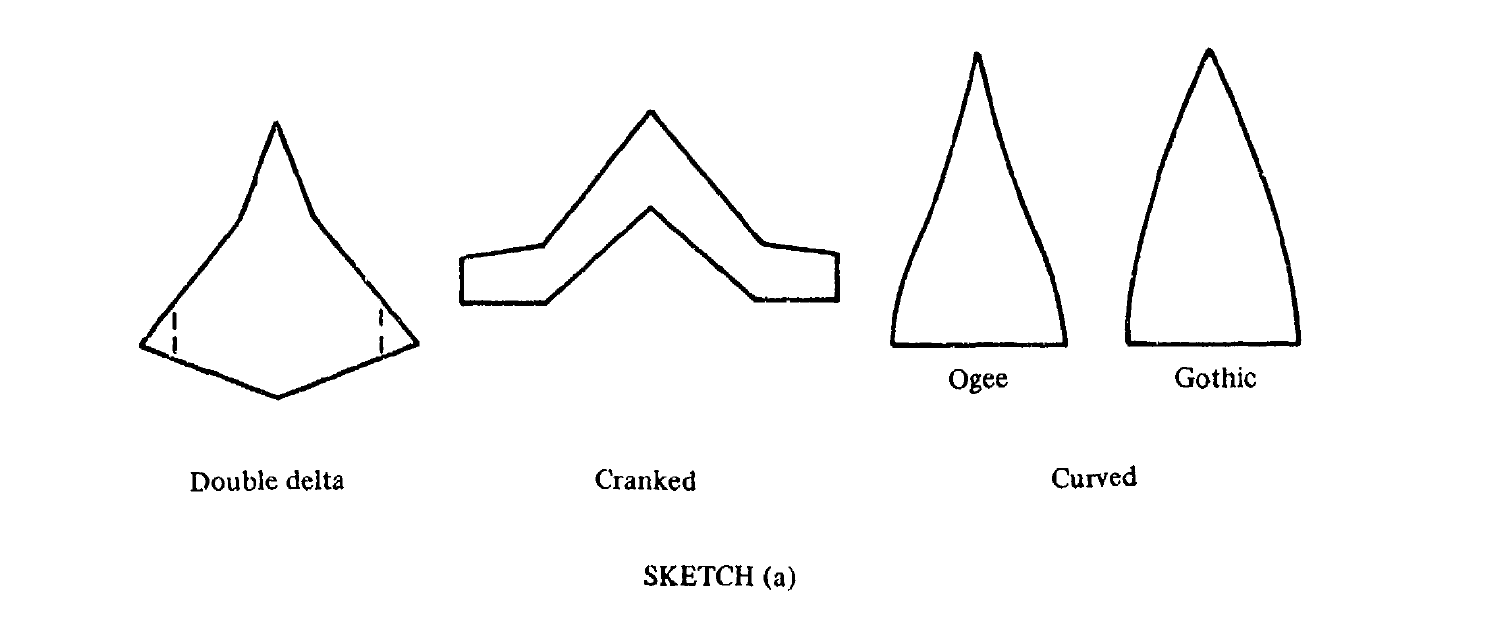
Sample
OpenVSPのExample FileにあるPod Planeについて、実際に計算してみる
↓計算に使用したエクセルファイル(マクロ付き)
↓計算結果

以上
おわりに
DATCOM 4.1.3.2 に基づいて、3次元揚力傾斜を計算した。
↓次
4.3.1.2







コメント