DATCOM 4.1.1 に基づいて、二次元翼のDesign Lift Coefficientを計算する。
はじめに
DATCOM 4.1.1 に基づいて、二次元翼のDesign Lift Coefficientを計算する。
Design Lift Coefficient \(c_{l_{i}}\)とは、翼前縁にあたる流れの向きが翼前縁のキャンバーラインと一致するときの2次元揚力係数である。ちなみに、\(c_{l}=c_{l_{i}}\)のとき、翼に働く抗力は最小になる。
PDFのページは461ページ
Method
DATCOMの2次元翼の性能の推算はNACAの実験データ(smooth-leading edge、\(Re=9\times 10^6\))に基づいているため、基本的に使用する翼型はNACAの4字系列、5字系列、6字系列を前提としている
二次元翼のdesign lift coefficient \(c_{l_{i}}\)およびそのときの迎角\(\alpha_{i}\)は、TABLE 4.1.1-Dの対応する値にキャンバーの比を掛けて計算する。(6字系列は\(c_{l_{i}}\)の比をかける)
例えば、NACA4412の\(c_{l_{i}}\)、\(\alpha_{i}\)を計算するには、TABLE 4.1.1-DのFour-Digit Seriesの64の行の値に注目して、
\begin{align}
c_{l_{i}}&=0.76 \times \frac{4}{6}=0.506 \\\\
\alpha_{i}&=0.74 \times \frac{4}{6}=0.493 ~\mathrm{[deg]}
\end{align}
とすればよい(NACA4字系列は1文字目が最大キャンバーの大きさを表す)
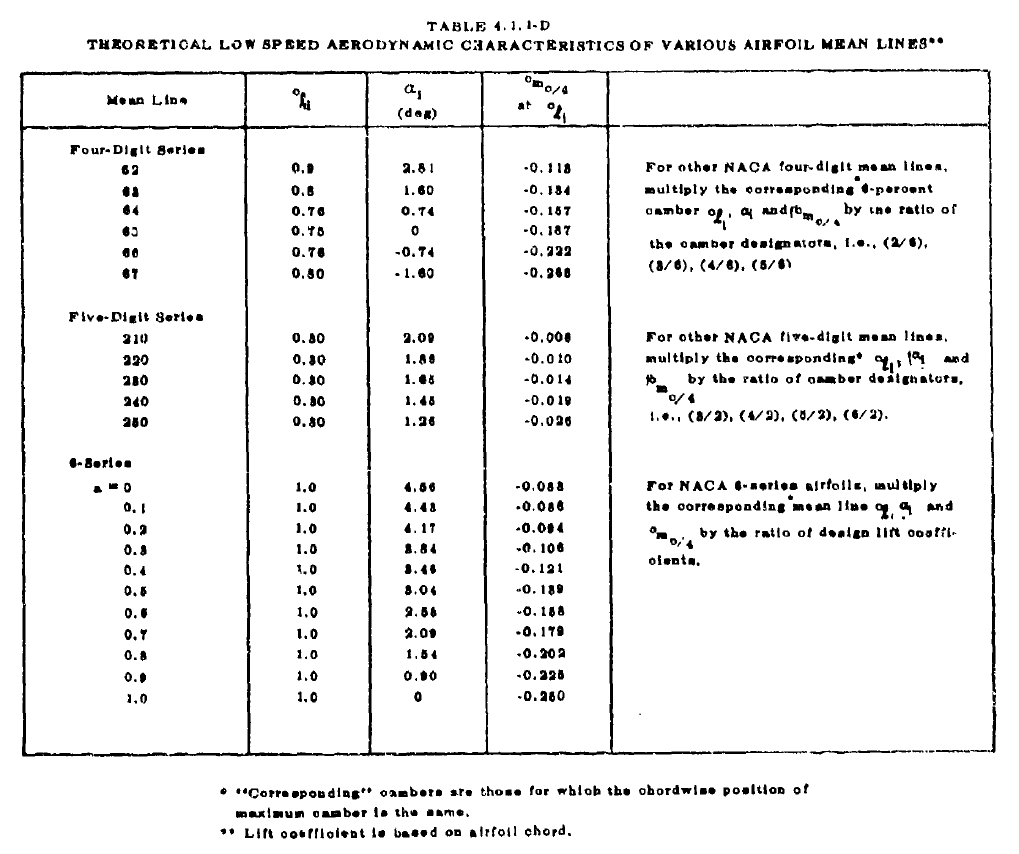
文字が潰れて最高に読みにくいので、4字系列だけ文字起こししたのがこれ
| Mean Line | \(c_{l_{i}}\) | \(\alpha_{i}\) [deg] | \(c_{m_{c/4}}\) at \(c_{l_{i}}\) |
| 62 | 0.9 | 2.81 | -0.113 |
| 63 | 0.8 | 1.60 | -0.134 |
| 64 | 0.76 | 0.74 | -0.157 |
| 65 | 0.73 | 0 | -0.187 |
| 66 | 0.76 | -0.74 | -0.222 |
| 67 | 0.8 | -1.60 | -0.266 |
いちおうXFLR5でも計算して、近い値が出たので間違いはないはず
reference
制限
-
Sample
OpenVSPのExample FileにあるPod Planeについて、実際に計算してみる
↓計算に使用したエクセルファイル(マクロ付き)
主翼翼型:NACA4412
尾翼翼型:NACA0010
↓計算結果

以上
おわりに
DATCOM 4.1.1 に基づいて、二次元翼のdesign lift coefficientを計算した。
↓次







コメント