2023年の鳥人間コンテストに出場したTeam Tinkerの2人乗り鳥コン滑空機 Gemini-X の設計についてまとめる
はじめに
2023年の鳥人間コンテストに出場したTeam Tinkerの2人乗り鳥コン滑空機 Gemini-X についての設計資料をまとめる
この記事をもとに、今後2人乗り鳥コン滑空機に挑戦してくれるチームが増えれば何よりである
↓設計の手順についてはQX-20の引継ぎ資料を参照
設計要求およびコンセプト
↓参考
まずは、機体に対する設計要求を明確にする
Team Tinkerの活動目的からフローダウンされた設計要求は以下の通り
まず第一に、社会人チームにしかできないような面白い機体を作ろう、ということになった
ただし、週末しか活動できない社会人チームでも1~2年で製作を完了させる必要がある
上記2点の設計要求を満たす機体として、2人乗り鳥コン滑空機を提案した
設計コンセプト
2人乗り鳥コン滑空機の設計コンセプトは以下の通り
- お手軽ど変態機
- 鳥コン滑空機の王道である「重く、硬く、速く」を追求した機体
それぞれについて説明する
お手軽ど変態機
鳥人間コンテスト滑空機部門にはこれまでも無尾翼機、先尾翼機、複葉機、結合翼機、羽ばたき機などのロマンあふれる機体が登場し、大会を盛り上げてきた
2人乗り鳥コン滑空機も例にもれずド級の変態機であるが、ほかの形態と比較して以下のような特徴がある
つまり、2人乗り鳥コン滑空機はその独自性の割には設計/製作の手間の増加が少なく、非常にコスパの良い変態機なのである
上記の特徴とTeam Tinkerのメンバーのスキルを鑑みて、「いけるんじゃね?」となって製作が決定した
鳥コン滑空機の王道
これについては以下のPDFがまとめられていてわかりやすいので、頭を空っぽにして読んでみてほしい
いろいろ言いたいことがあるのはお察しするが、それはひとまず置いておこう
2人乗り滑空機の可能性についての詳細な議論については、この記事の最後で行う
2人乗り滑空機のコンセプトは現役時代に思いついたものである
まさかこんな形で実現するとは夢にも思っていなかったが...
やっぱり次の時代は双胴滑空機だな
— いーそー (@mtk_birdman) October 14, 2020
スパン35m,翼面積30㎡,全備重量150㎏で初速7m/sくらいのやつ
圧倒的初速と位置エネルギーを持った化け物滑空機が琵琶湖を蹂躙する様を見てみたい
まとめ
というわけで、設計要求およびコンセプトは以下のとおり決定した
概念設計
↓参考
設計要求とコンセプトが決まったので、その設計要求を満たすような機体形状を概念設計のフェーズで考えていく
決めるべき項目は以下の通り
- 桁の調達
- 翼配置と胴体数
- 速度と翼面荷重
- 操縦方法
概念設計が完了すれば機体の初期三面図(ポンチ絵)を書くことができるようになる
桁の調達
まずはOBチームが一番苦労する桁の調達を行った
幸い今回は現役の倉庫にQX-16の桁が眠っていたので、ありがたくそれを頂戴することにした
ちなみにQX-16は九大の低翼左右非対称シリーズの中でも異色の機体で、胴体桁がまっすぐ後方に伸びている
https://www.q-birdman.jp/history/images/qx-16.pdf
そのため、Gemini-Xに対する「なんで胴体桁が非対称なんですか?」という質問への回答は「よく分からんけどなぜか貰った桁が非対称だった」である
なんにせよ使える桁が手に入ったのは非常にありがたく、協力してもらった現役にはとても感謝している
別に胴体桁がどこについていようが、重心さえ合わせれば飛行機は飛ぶのである
翼配置と胴体数
次に、機体の翼配置と胴体数を検討した
翼配置は高翼/低翼の2択、胴体数は単胴/双胴の2択なので、計4パターンの検討を行った
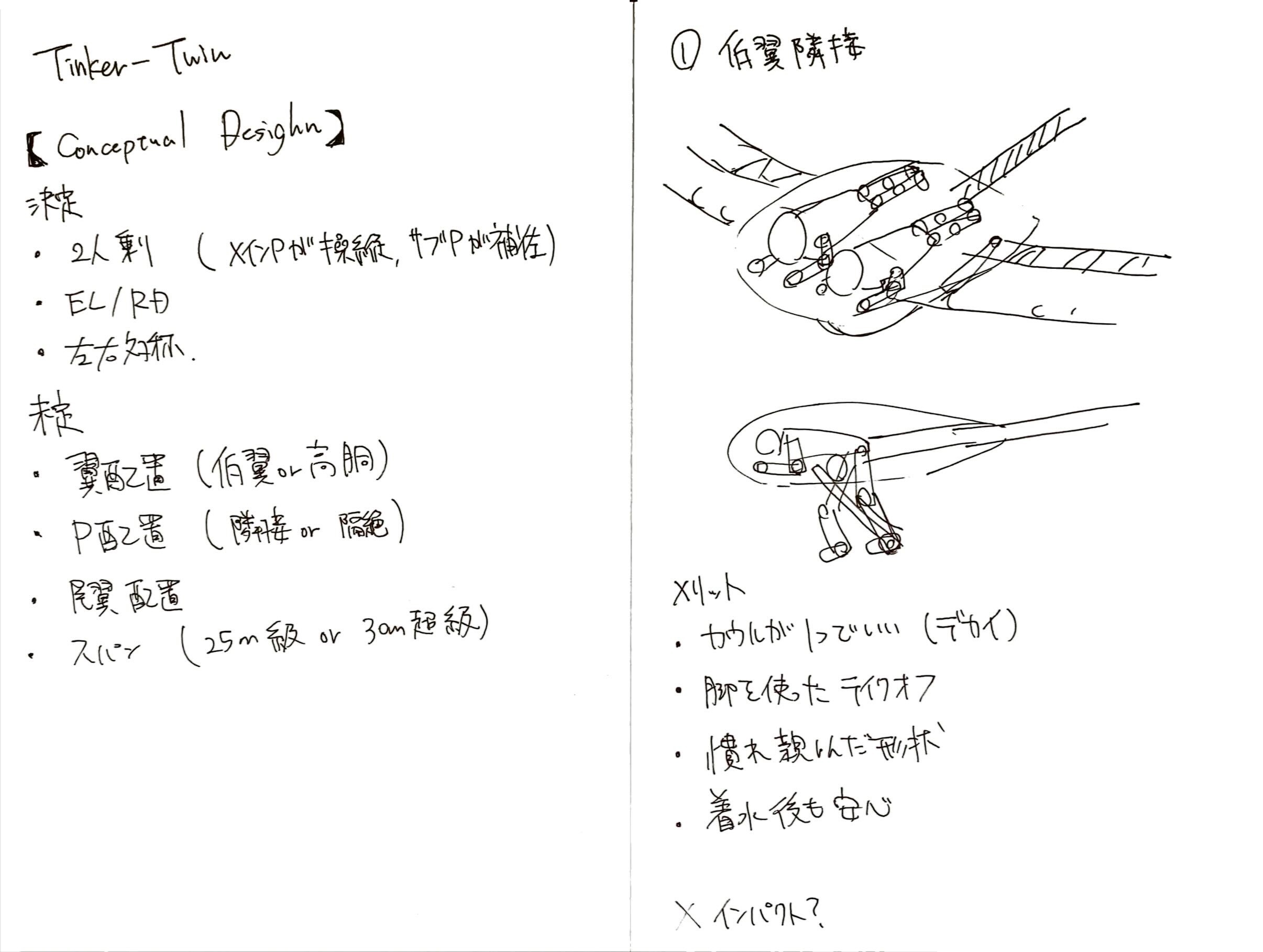
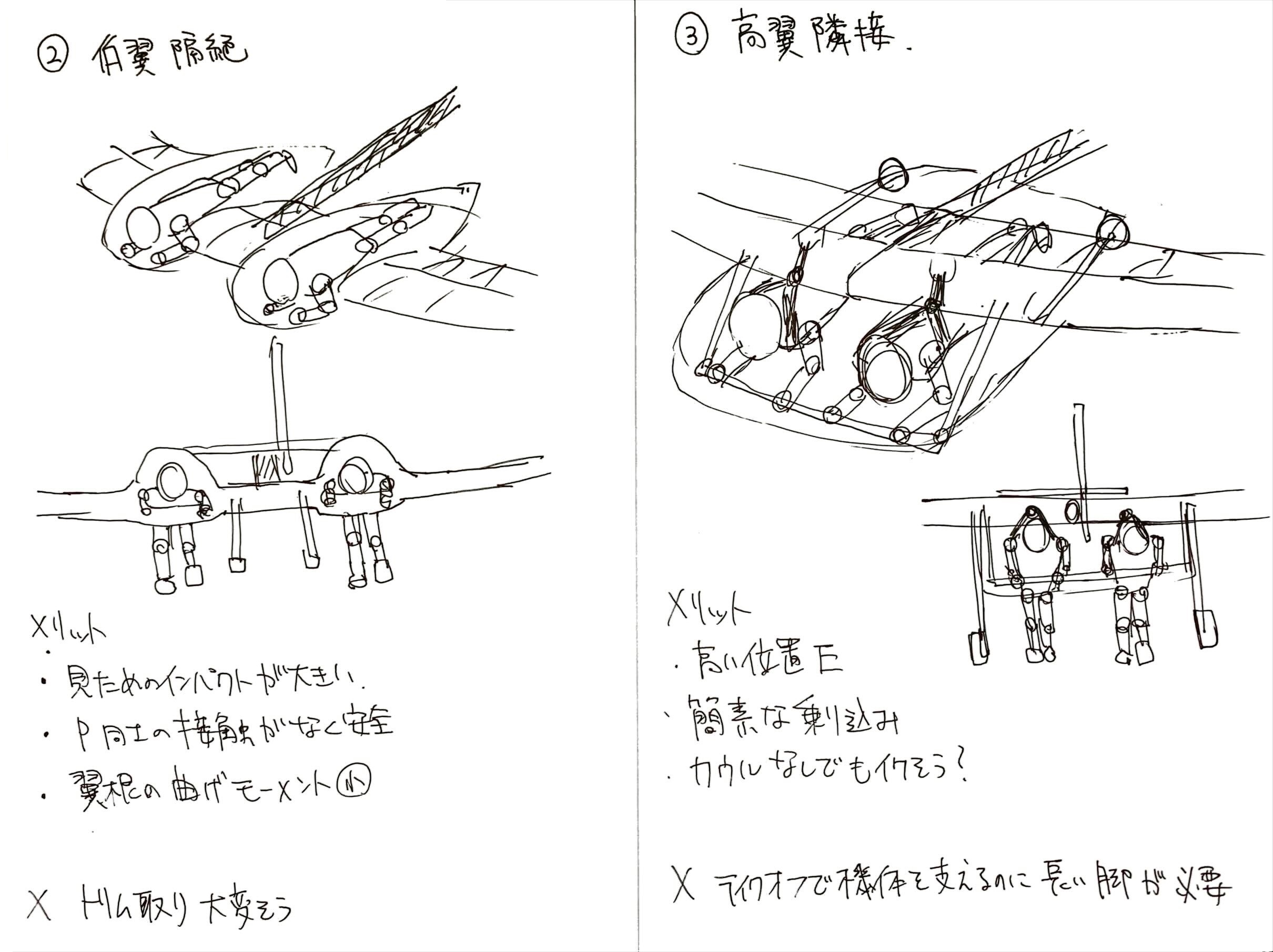
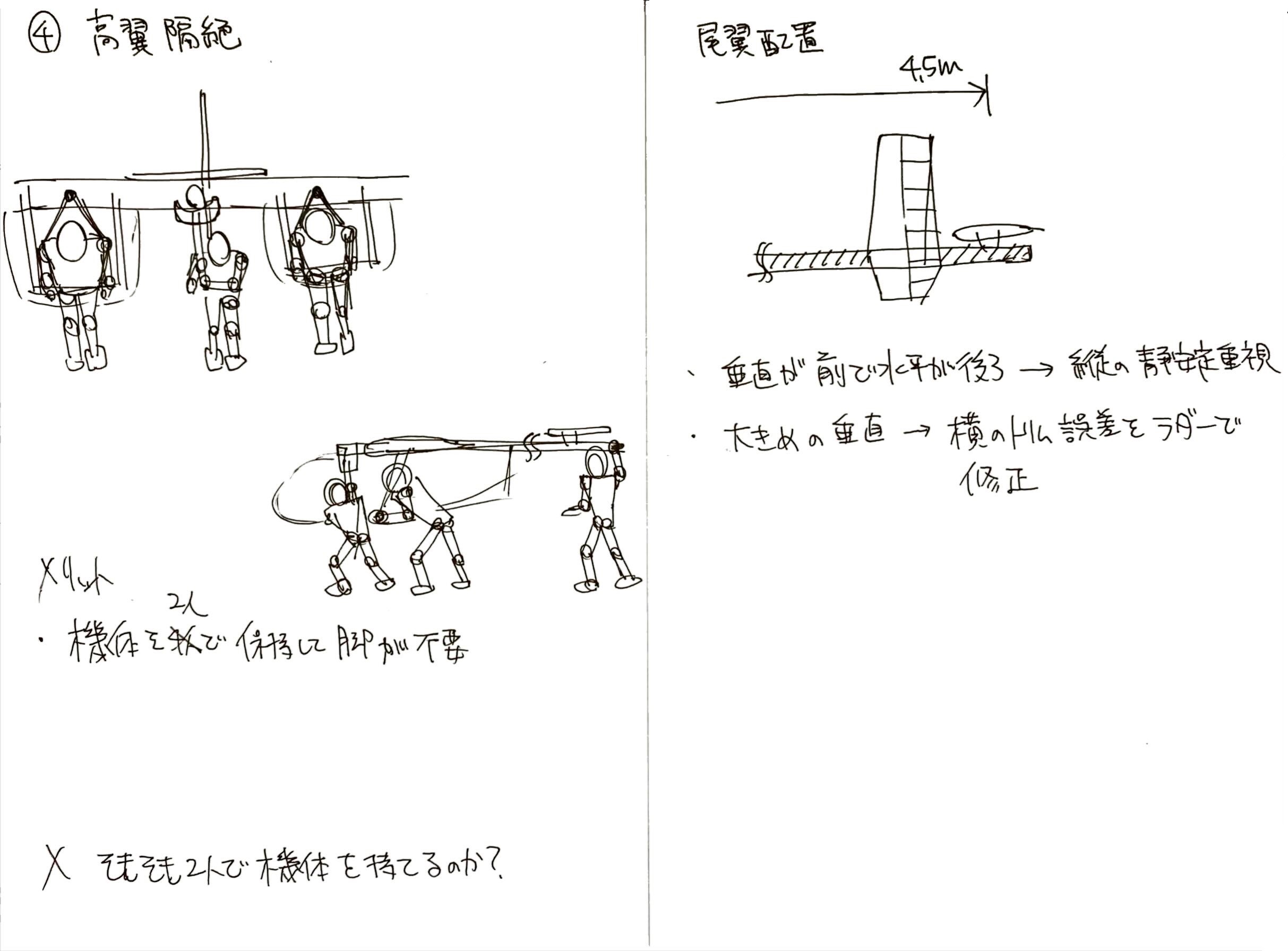
検討の結果、4つのパターンのうち「高翼双胴」が選ばれた
| 低翼単胴 | 低翼双胴 | 高翼単胴 | 高翼双胴 | |
| 見た目のインパクト | × | 〇 | × | 〇 |
| 安全性の高さ | △ | 〇 | × | 〇 |
| 翼根の曲げ荷重の小ささ | × | 〇 | × | 〇 |
| 機体保持の容易さ | × | × | △ | 〇 |
| 位置エネルギーの大きさ | × | × | 〇 | 〇 |
| コックピットの簡易さ | × | × | 〇 | 〇 |
| カウル有無による見た目 | × | × | 〇 | 〇 |
メリットおよび懸念点は以下の通り
双胴にすることで見た目のインパクトがすごいことになるのは言わずもがなだが、パイロット同士の距離を離し、かつそれぞれをカウルで保護することで、着水時の安全性を高めることもできる
また、高翼にすることで、パイロット2人が機体を支えられるようになり、テイクオフ時に脚が不要になることに加え、高翼の吊り下げ式にすることでコックピットフレームの構造も簡略化することができる
最悪カウルの製作が間に合わなかった場合でも、高翼配置ならハンググライダーのような見た目となり、ある程度サマになりそうだとも考えていた
このように、高翼配置は全体として工数の削減が期待できる形態である
設計的にも、双胴にすることで翼根の曲げモーメントを軽減することが可能になり(旅客機のエンジンが主翼の真ん中についているのと同じ理由)、機体全体の重心位置も高くなるので設計コンセプトにもよりマッチする機体になる
一方、懸念点の方は高翼双胴に限った話ではなく、2人乗り鳥コン滑空機全体に関する懸念点である(結果から言うと、横の重心も合わせられたし2人で機体を支えたまま息を合わせて乗り込めたしカウルは2個作れたことになるのだが...)
パイロットが何人どこに乗っていようが、重心さえ合わせれば飛行機は飛ぶのである
速度と翼面荷重
ざっくりした機体の形状が決まったので、鳥コン滑空機で最も重要な指標である速度と翼面荷重を検討した
上記のような理由から、Gemini-Xは低翼面荷重低速機(純棒飛び機)を目指すことにした
琵琶湖のいつもの風(湖から陸に3~4m/s)のなかで無理なくテイクオフし、乗り込みさえすればあとは勝手に飛んでくれるような機体のイメージである
今後もしどこかの誰かが2人乗り鳥コン滑空機を引き継いでくれるなら、この機体をベースに少しずつ高翼面荷重高速機側に寄せていけばいいと思う
操縦方法
操縦方法について、設計当初はエレベーター+ラダーを想定していたが、パイロットの意向により重心移動+ラダーに変更した
「2人乗り滑空機で重心移動の操縦なんてできるの?」という質問に対しては「できた」が回答になる
なにせ当日のフライトの離陸後の緩やかな機首上げは重心移動によるものである
実際、ハンググライダーのタンデム飛行の画像を検索すればパイロットが横並びに搭乗しているものも出てくるので、両パイロットがハング経験者であれば、無線の通信などを通して簡単な操縦は可能なのだと思う(トリムの維持など)
ただし、操縦の混乱を避けるため、重心移動およびラダー操作については左側に搭乗している機長が行うこととした
まとめ
というわけで、概念設計は以下のとおり決定した
基本設計
↓参考
基本設計では、概念設計で決まった内容をもとに、機体重量、主翼面積、巡航速度などの主要諸元を決定する
決めるべき項目は以下の通り
- 重量
- 翼面荷重
- 主翼面積
- 速度
- 揚力係数
- スパン
- アスペクト比
なお、それぞれの項目は互いに影響しあっているため、何度も何度も繰り返しループを行い値を調整していく必要がある
重量
全備重量は機体の重量とパイロットの重量の合計だが、基本設計の段階ではまだ具体的な値はわからないので、ある程度の推算値を設定して設計をすすめていく
機体については、QX-16の実績値35kgに対して、2人乗りへの改修による増分を10kgと見積もって、機体重量45kgとした(翼面積の増大と2つ目のカウルの追加)
パイロットについては、この段階ではまだ決まっていなかったので、65kg×2人とした
結果、全備重量の推算値は175kgとなり、この重量をもとに基本設計を行った
翼面荷重と主翼面積
機体重量が決まったので、次は翼面荷重を設定していく
翼面荷重については概念設計にて「低翼面荷重低速機」となっているので、5.0kg/㎡程度に設定した
翼面荷重=全備重量/主翼面積なので、全備重量と翼面荷重が決まったことにより主翼面積は自動的に35㎡になる
速度と巡航CL
速度についても概念設計にて「低翼面荷重低速機」となっているので、8.0m/s程度に設定した
滑空機部門の機体にしてはかなりの低速機である(現役時代のトレンドは10~11m/s程度)
テイクオフ時の対地速度がおよそ5~6m/s程度だといわれているので、プラホ上で2~3m/sの正対風が吹けば容易にテイクオフすることができる(プラホ傾斜が3.5度あることを考えるとさらに余裕がある)
揚力係数CLについても、決定した重量・速度・翼面積から計算すると CL=1.3 程度なので、翼型を選定するうえでも特に困ることはない(みんな大好きDAEシリーズの翼型のL/D最大となるCLが1.3程度)
スパン/アスペクト比
スパンについては、QX-16の桁(およそ25m)を再利用することを踏まえて決定する必要がある
製作性および性能の観点から、15m級、25m級、30m級、の3つの案を検討した
| スパン | 備考 |
| 15m | 〇 工数がダントツで少ない 〇 短スパンで構造的に楽 〇 運用が楽(5m×3分割) × コード長2mの矩形翼が爆誕する |
| 25m | 〇 工数、構造的に中間案 〇 翼根コード長1.5mで許容範囲内 |
| 30m | 〇 高アスペクト比で性能がいい × 工数の増加 × 運用が大変になる(5m×5分割+α) × そもそも記録狙いの機体ではない × 構造的にしんどい |
変態機といえばスパンを切り詰めて製作と設計を楽にするのが王道だが、さすがに2人乗り滑空機でスパンを15mにするのはしんどかったので、QX-16と同程度の25m級とした
アスペクト比はおよそ18程度になる
まとめ
上記のようなことを考えつつ、以下に示すいつもの表とにらめっこしながら最終的な数値を決定した
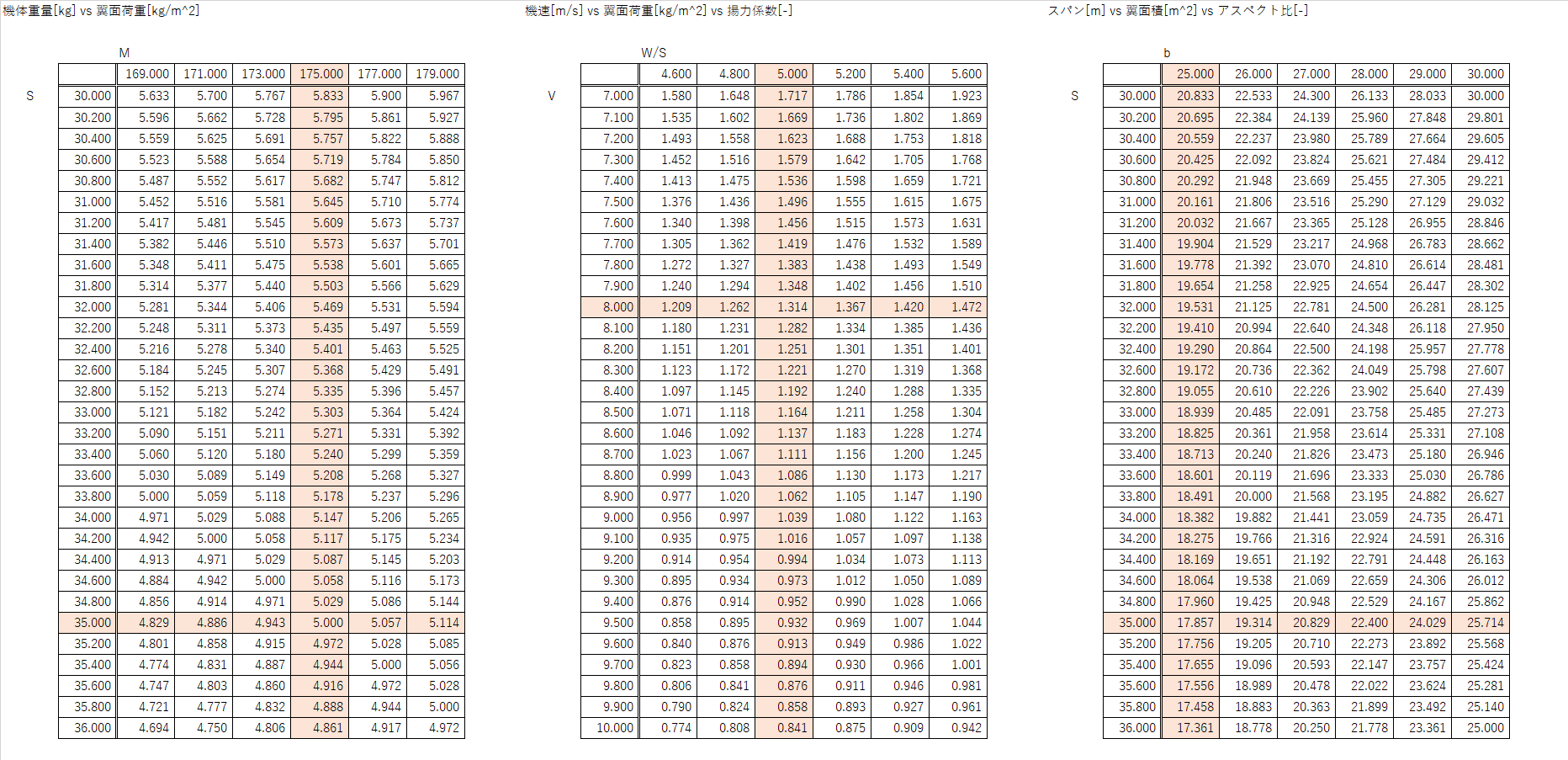
結果的に、基本設計によってGemini-Xの主要諸元は以下のように決定した
詳細設計
基本設計が完了したので、基本設計で設定した主要諸元を満たすように各部の詳細設計を行っていく
- 主翼
- 水平尾翼と垂直尾翼
- 胴体とカウル
それぞれについて説明していく
主翼
↓参考
主翼の詳細設計では以下のことを決定する
- 翼型
- 平面形と主桁構造
翼型
翼型については、定常滑空において CL=1.3 と大きめなので、みんな大好きDAEをベースにし、SD8040を50%ほど混合することで、以下の翼型を作成した
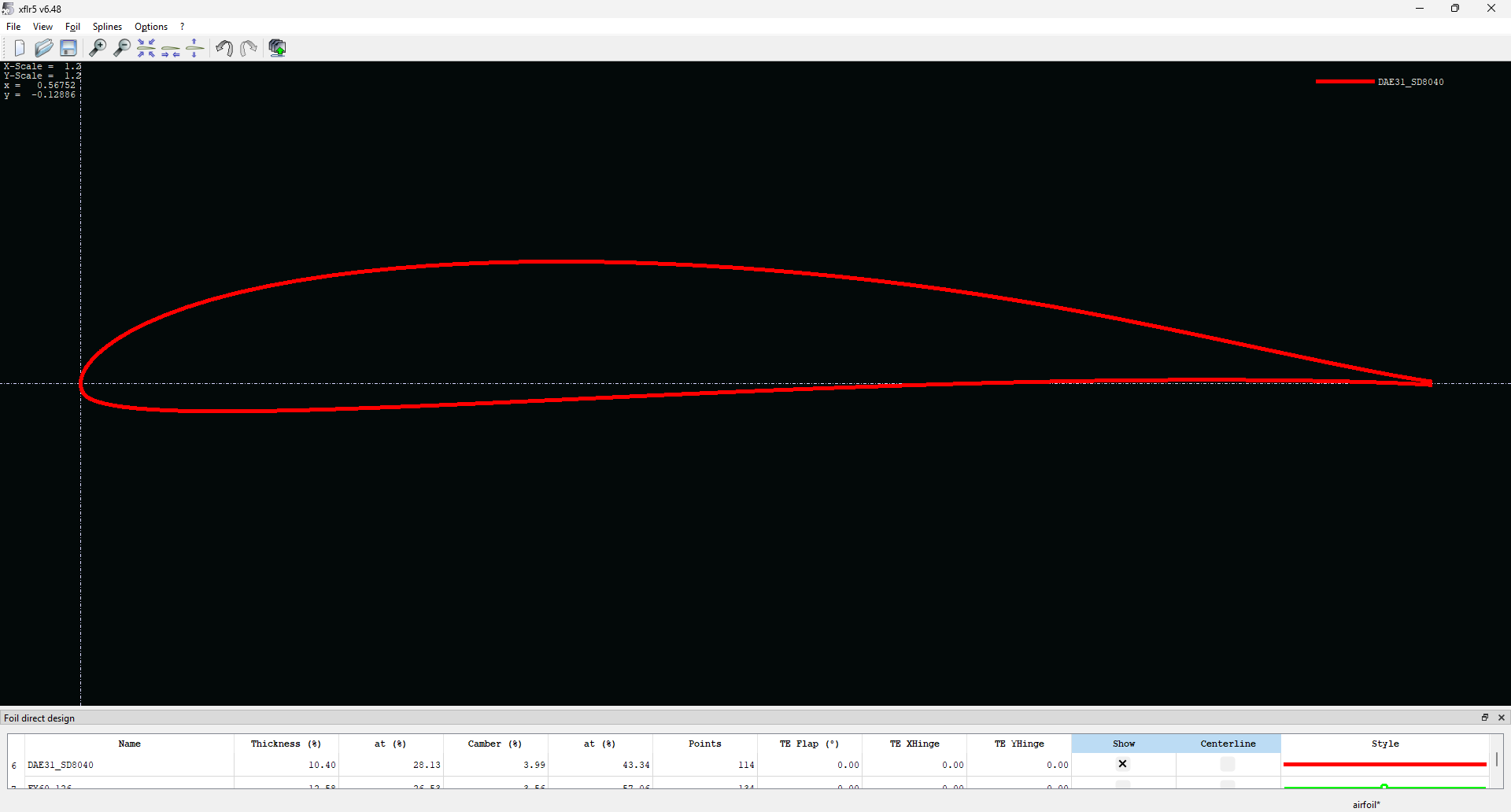
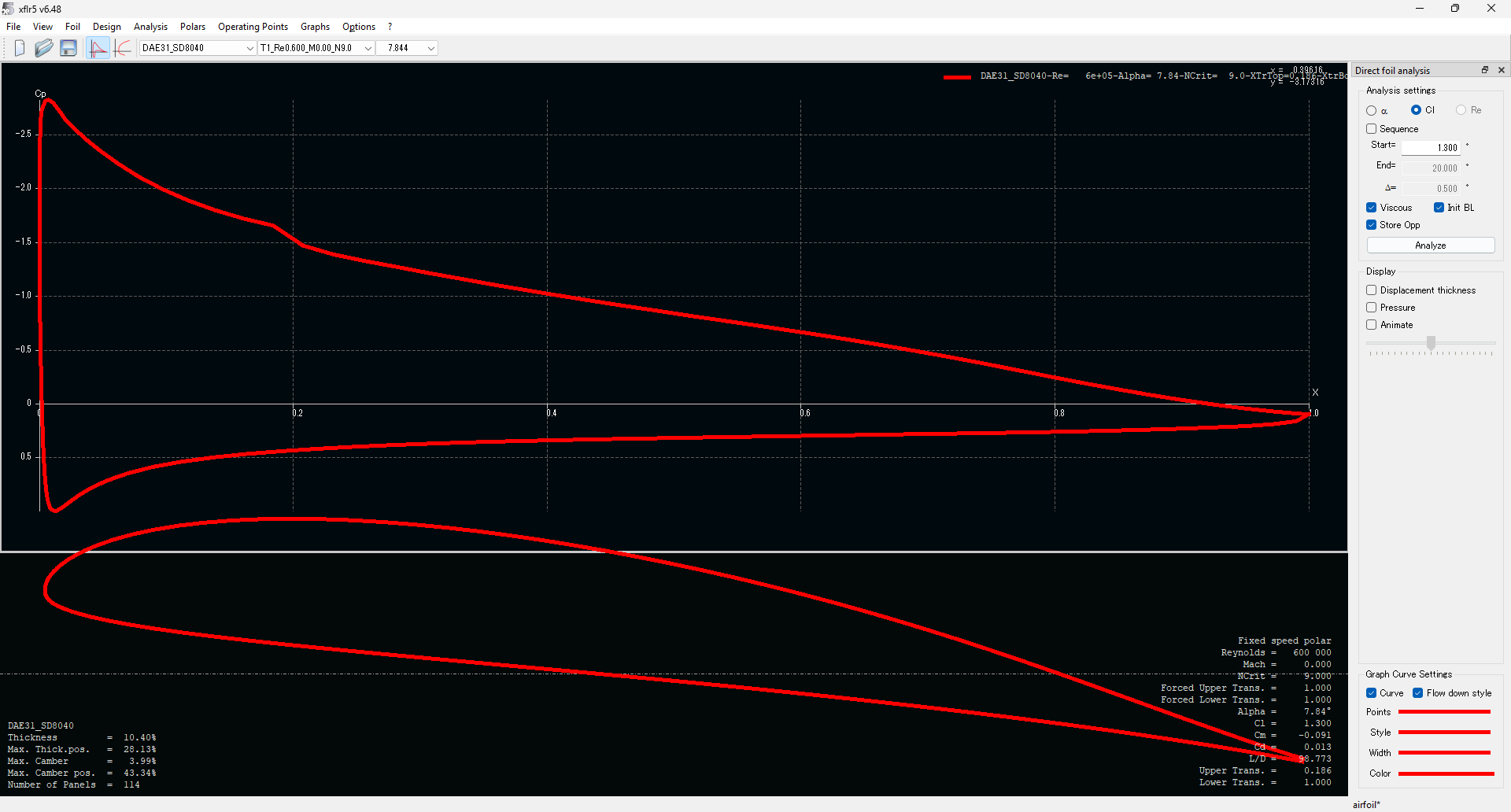
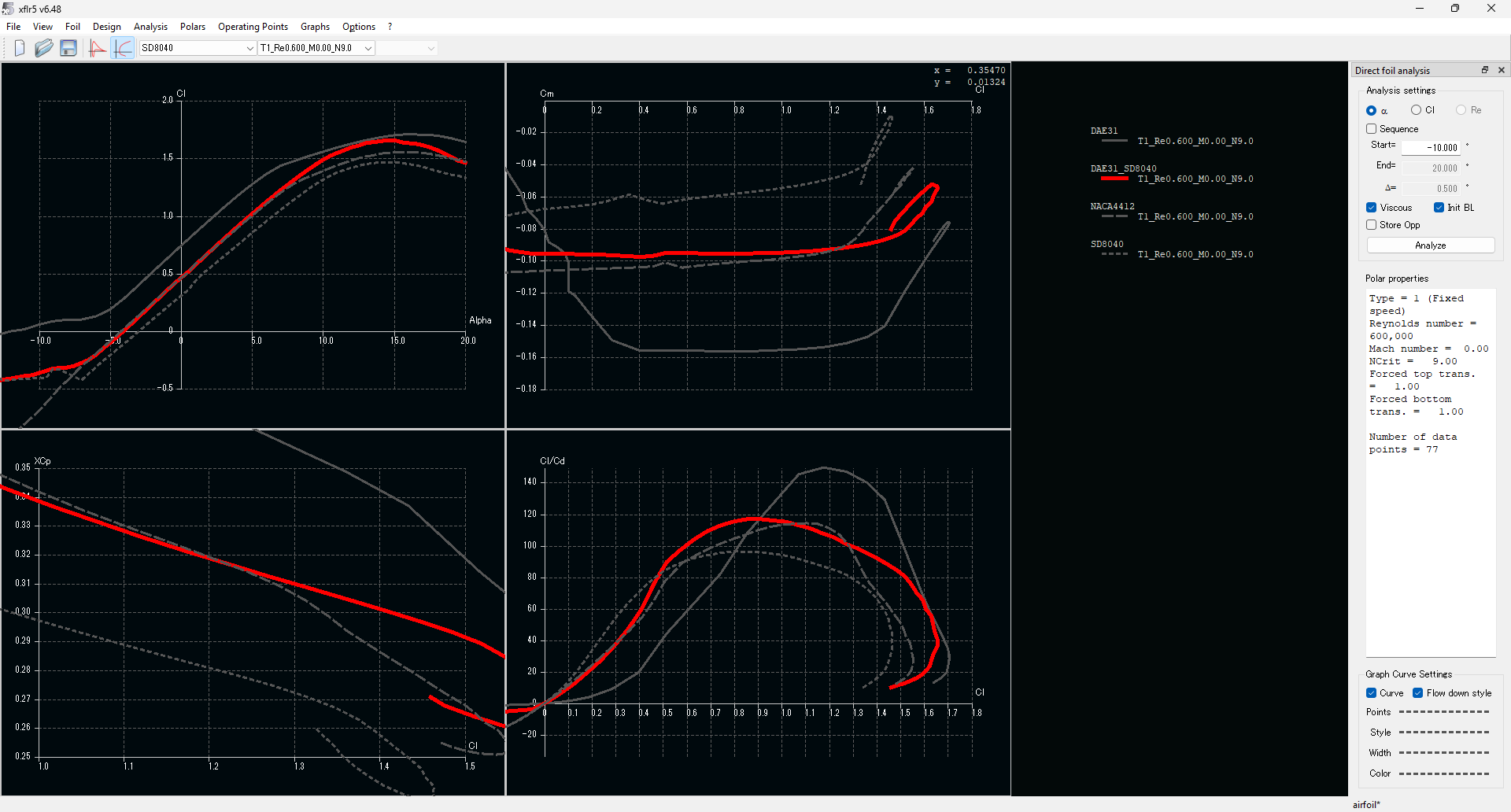
採用理由は以下の通り
翼型に関しては時間をかけずにさっさと決めてしまうのがいいと思う
その他諸元はこんな感じ
形状
- 最大翼厚:10.40%
- 最大翼厚位置:28.13%
at CL=1.3(定常滑空)
- Cd:0.013
- Cm:-0.091
- L/D:98.773
- alpha:7.84 deg
- Xcp:30.97%
ほしい方はこちらからどうぞ
DAE31_SD8040
1.0000000 0.0012431
0.9904697 0.0026837
0.9725228 0.0057755
0.9505702 0.0099410
0.9260226 0.0148756
0.9001607 0.0202506
0.8736981 0.0258547
0.8469767 0.0315367
0.8204112 0.0371364
0.7940940 0.0425754
0.7680428 0.0477910
0.7422295 0.0527303
0.7165386 0.0573702
0.6908477 0.0617192
0.6651639 0.0657782
0.6395030 0.0695282
0.6138305 0.0729686
0.5881180 0.0760954
0.5623332 0.0789284
0.5365785 0.0814442
0.5107204 0.0836625
0.4849278 0.0855738
0.4591519 0.0871593
0.4333993 0.0884213
0.4077167 0.0893457
0.3821175 0.0899178
0.3566066 0.0901242
0.3312427 0.0899502
0.3060334 0.0893675
0.2810124 0.0883643
0.2562370 0.0869067
0.2317368 0.0849784
0.2076273 0.0825428
0.1839449 0.0795712
0.1608393 0.0760359
0.1384541 0.0719171
0.1170323 0.0672118
0.0968964 0.0619532
0.0784346 0.0562332
0.0621150 0.0502635
0.0483041 0.0443056
0.0370326 0.0386032
0.0280570 0.0333166
0.0209758 0.0284848
0.0153818 0.0240926
0.0109674 0.0200531
0.0074838 0.0162854
0.0047587 0.0127342
0.0026805 0.0093548
0.0016173 0.0071842
0.0011850 0.0061183
0.0008220 0.0050630
0.0005276 0.0040198
0.0003009 0.0029919
0.0001403 0.0019808
0.0000416 0.0009842
0.0000000 0.0000000
0.0000125 -0.0009754
0.0000827 -0.0019467
0.0002158 -0.0029180
0.0004183 -0.0038917
0.0007016 -0.0048590
0.0010778 -0.0058076
0.0015572 -0.0067265
0.0021402 -0.0076068
0.0028244 -0.0084396
0.0036068 -0.0092182
0.0044817 -0.0099432
0.0054414 -0.0106159
0.0064800 -0.0112396
0.0087852 -0.0123676
0.0128185 -0.0138514
0.0176669 -0.0151554
0.0235816 -0.0163584
0.0309699 -0.0175036
0.0404580 -0.0185879
0.0529320 -0.0195596
0.0692682 -0.0203548
0.0895678 -0.0208254
0.1128817 -0.0208887
0.1380175 -0.0205819
0.1640720 -0.0199932
0.1906884 -0.0191900
0.2176322 -0.0182448
0.2447246 -0.0171944
0.2719545 -0.0160559
0.2993030 -0.0148587
0.3267163 -0.0136179
0.3542210 -0.0123493
0.3817550 -0.0110712
0.4092263 -0.0097997
0.4366968 -0.0085550
0.4641490 -0.0073287
0.4914911 -0.0061477
0.5188200 -0.0050202
0.5461163 -0.0039483
0.5733850 -0.0029401
0.6006575 -0.0019948
0.6278577 -0.0011172
0.6550029 -0.0003326
0.6822066 0.0003732
0.7093305 0.0009967
0.7364060 0.0015193
0.7634301 0.0019364
0.7903833 0.0022334
0.8172663 0.0023988
0.8440910 0.0024189
0.8708644 0.0022927
0.8974326 0.0020077
0.9237162 0.0015576
0.9488349 0.0009558
0.9715325 0.0001858
0.9900658 -0.0006593
1.0000000 -0.0012431
平面形と主桁構造
平面形と主桁構造については、基本設計で決まった主翼面積35㎡、スパン25mを満たしつつ、以下のことを考えながら設計した
とりあえず1番の特徴はフライングワイヤを採用したことである
QX-16の桁はもちろん単座滑空機のために設計されたものなので、そのままでは2人分の荷重を支えることはできない(たわみが大きくなりすぎる)
どれだけ揚力を内側に寄せてもたわみを抑えることができなかったので、鳥コン滑空機でありながらフライングワイヤを採用することにした(現役時代含めて初めての要素)
フライングワイヤの取り付け位置はとりあえず頑丈そうな1番翼と2番翼の接合部とし、パイロットについても機体中心からある程度離して配置することで、翼根の曲げモーメントを緩和するよう設計した
パイロットとフライングワイヤの効果を反映するために、設計シートに鉛直下向き荷重をかける魔改造を施して計算を行った
結果はこんな感じ
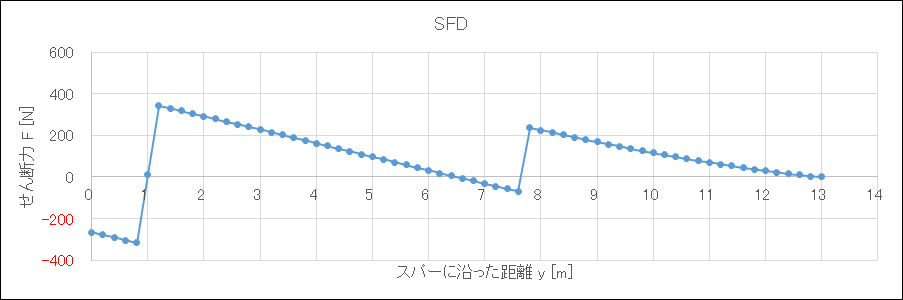
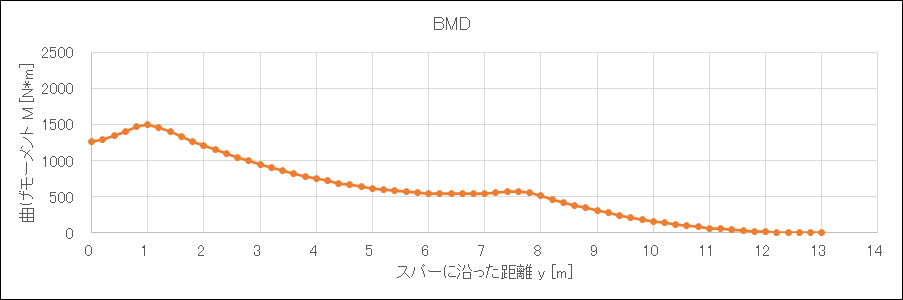
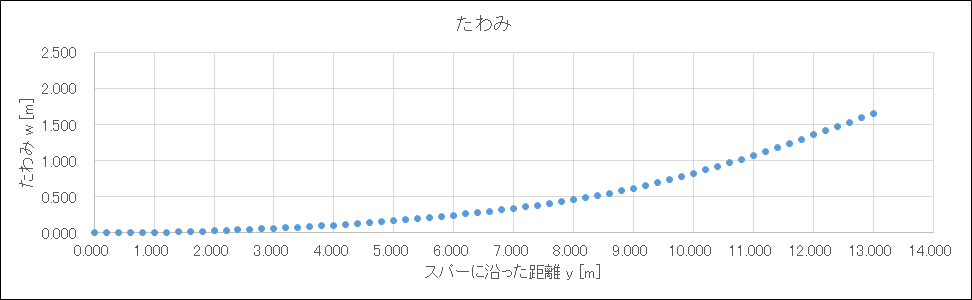
フライングワイヤおよびパイロットによって翼根の曲げモーメントは大きく抑えられ、なんなら1人乗り鳥コン滑空機よりも小さい値になった(QX-20の翼根曲げモーメントの設計値は約2,000 Nm)
翼端のたわみも1.5mほどに抑えられ、全体的な翼のしなり具合もまあいい感じになった

もう一つの大きな特徴は、風圧中心に主桁を置いたことである
通常の鳥コン滑空機だとテイクオフ(~6.0 m/s)→ 定常滑空(10~11 m/s)→ 着水(8 m/s~)というように広い速度域で飛行するので、速度によって移動する風圧中心に主桁を置くことはできない
それに対して、Gemini-Xは定常滑空速度8.0 m/s の純棒飛び機なので、風圧中心の移動を考えずに主桁を配置し、ねじりモーメントを抑制することにした(逆にいうとこの時点で完全にダイブしない/できない機体にしてしまったので、無風や背風のコンディションなら即棄権することになる)
結果、コード長は1.5倍近くになっているものの、翼端のねじれ角は0.2度以下に抑えることができた
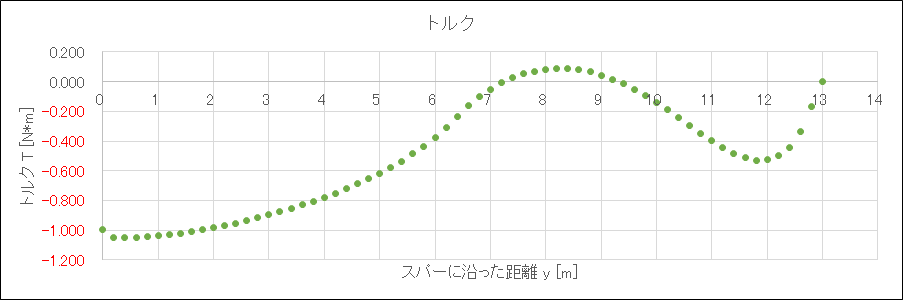
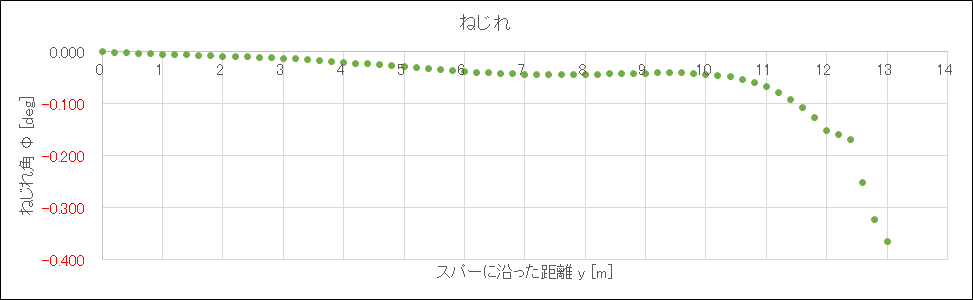
あとは主翼製作ができるだけ楽になるように矩形部をできるだけ大きく、テーパー段数をできるだけ少なく、それでいて平面図ができるだけダサくならないぎりぎりのラインを目指して頑張ってコード長を決定した
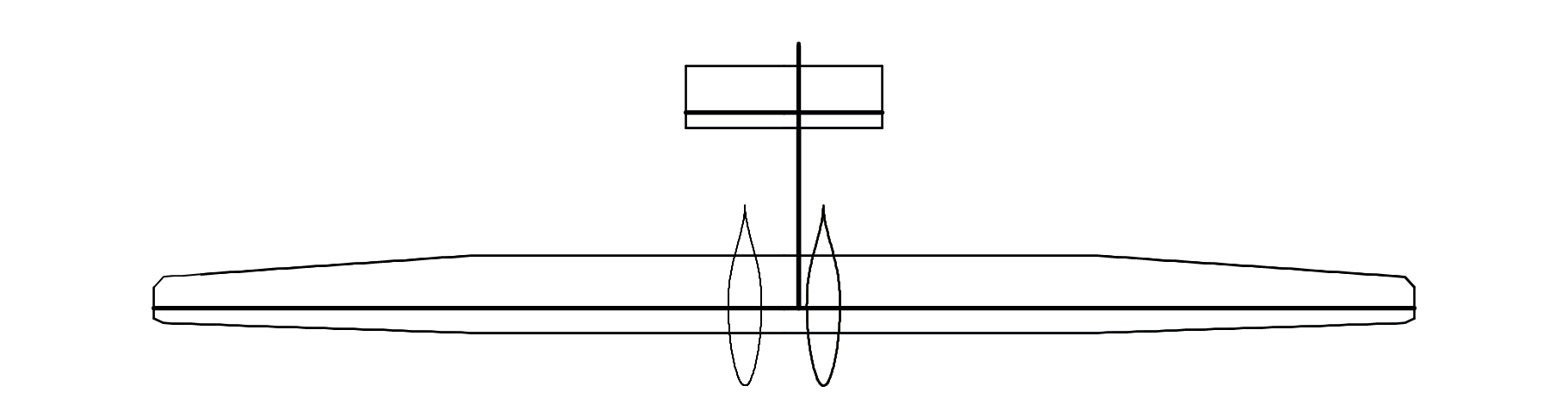
空力的ねじり下げや幾何的ねじり下げは管理が面倒なので採用していない
主翼の諸元はこんな感じ
水平尾翼と垂直尾翼
↓参考
水平尾翼と垂直尾翼については、QX-16の桁を流用する都合上、尾翼マウントの位置が変更できないので、それぞれの翼面積を変更するだけになった
Gemini-XではQX-16に比べて主翼面積がほぼ2倍になっているので、水平尾翼面積と垂直尾翼面積もQX-16からほぼ2倍になるようにした(QX-16と同じモーメントアームのまま容積比を維持するため)
水平尾翼の平面形については製作を楽にするために矩形とし、垂直尾翼の平面形は見た目がかっこよくなるように良い感じのテーパーを付けた
例のごとく、水平尾翼のスパンについては、大会会場のテントの中で機体を組み立てる都合上あまり長くすることができないので(今回は4.0m)、コード長1.2mというそこらの主翼よりもコード長の長いクソデカ水平尾翼が爆誕した
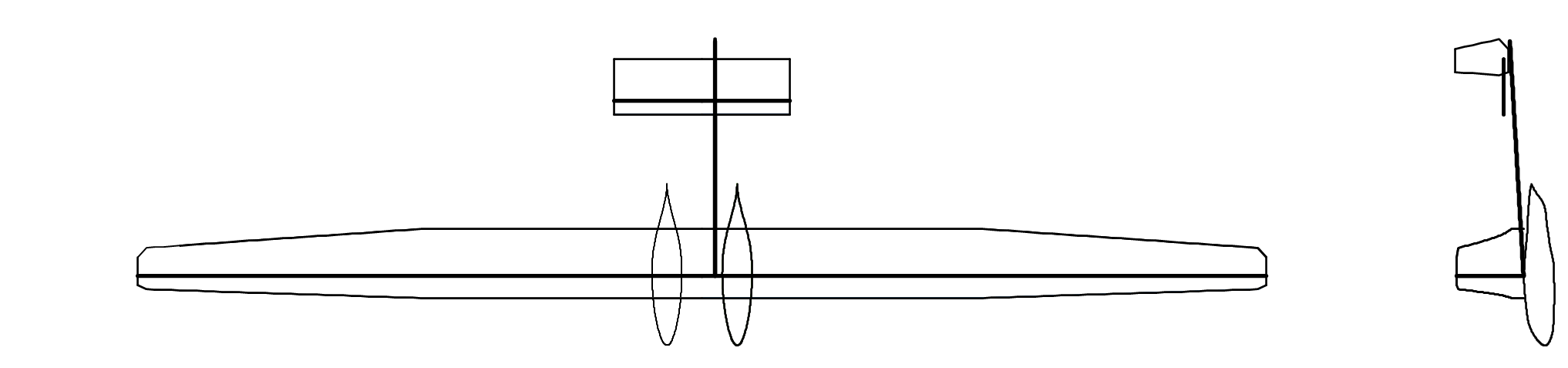
三面図で見るとあまりバランスの違和感はないが、そもそも主翼翼根のコード長が1.5mあるので、それと比較して水平尾翼の大きさにあまり違和感がないことに違和感を覚えるべきである
翼型についてはいつも通り水平尾翼にNACA0012、垂直尾翼にNACA0009を使った
水平尾翼のNACA0012に関してはコード長1.2mで翼厚12%だとかなり見た目的に分厚い翼になってしまったが、さすがに不確定要素の多い2人乗り鳥コン滑空機で失速特性の悪い薄翼を水平尾翼に採用することはできなかった
その他諸元についてはこんな感じ
胴体とカウル
↓参考
胴体とカウルについては、以下のようなことを考えた
あとはお任せしているうちに素晴らしいフレームとカウルが完成していた
カウルがないときのイメージがこんな感じ↓だったので、カウルを取り付けることができて本当によかったと思う
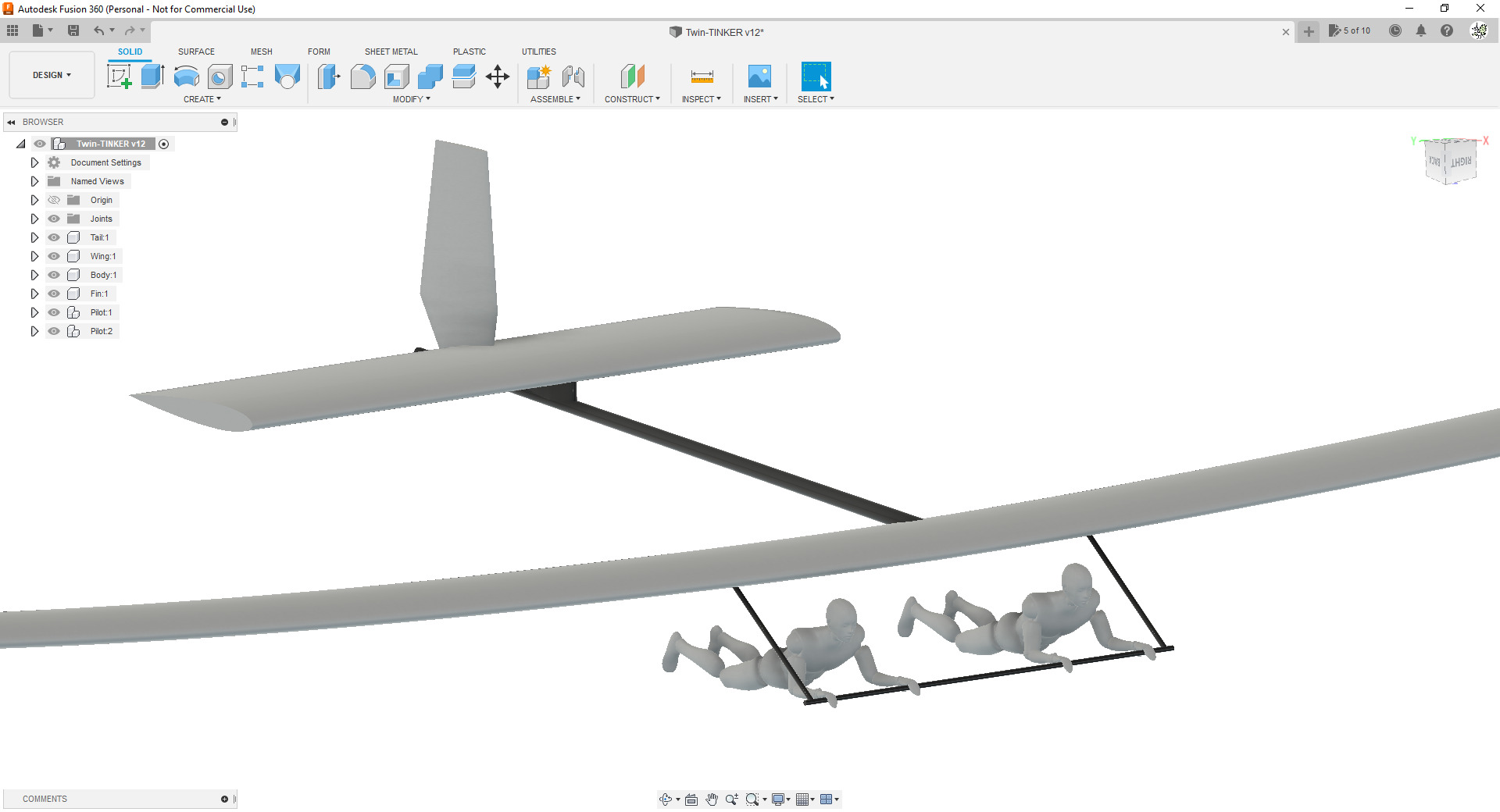
「カウルは機体の顔」という表現を改めて深く実感することになった
パイロットの体重差については、当日の測定で左の機長が62kg、右の副機長が71kgだったので、機長側に8.5kgのバラストを搭載して体重差を相殺した(琵琶湖の砂を入れた2Lペットボトル約2.5本分)
まとめ
Gemini-Xの詳細設計を経て、三面図はこんな感じなった
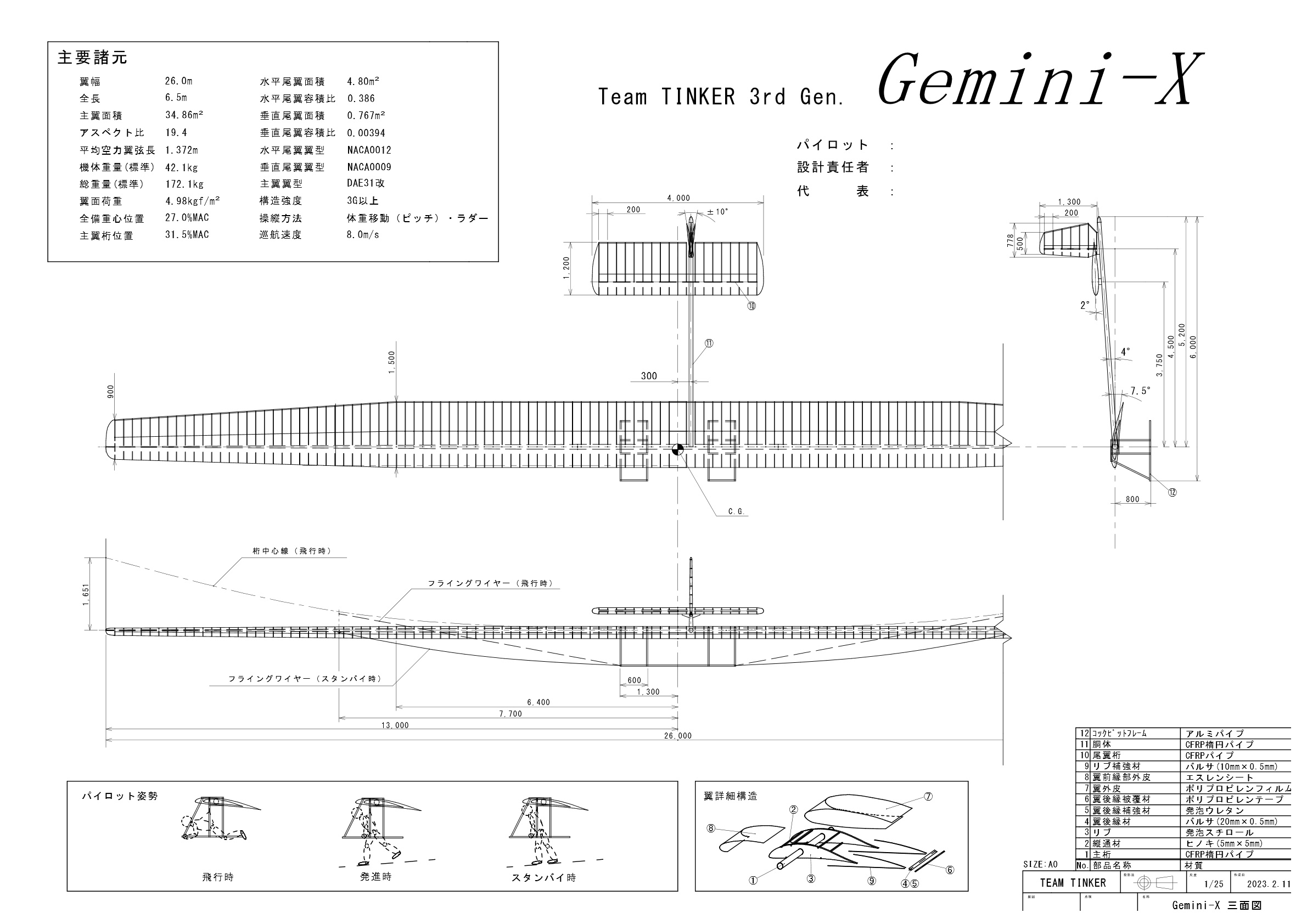
その他諸元は以下の通り
2人乗りのぶん機体の慣性モーメントもかなり大きいので、安定して飛んでくれるんじゃないかと思う
以上で「乗り込みさえすればあとはまっすぐ飛んでくれる機体」の設計の説明は終了である
テイクオフ
ここからは、2人乗り滑空機の肝である「乗り込みさえすれば…」についての考え方を説明する
概念設計時に挙げられていたテイクオフに関する2人乗り滑空機の懸念点は以下の通り
結論から言うと、これらの懸念点は「吊り下げ式にすると解決する」のだが、これをより理解するために、鳥コン滑空機で現在採用されているコックピット形式について比較しながら説明していく
- 高翼乗り込み式
- 脚付き乗り込み式
- 吊り下げ式
それではいってみよう
高翼乗り込み式
高翼乗り込み式のテイクオフのポイントは以下の通り
上記について各フェーズごとに説明する
(筆者は高翼機のフライトチーム経験がないので、コメントあればお願いします)
スタンバイ
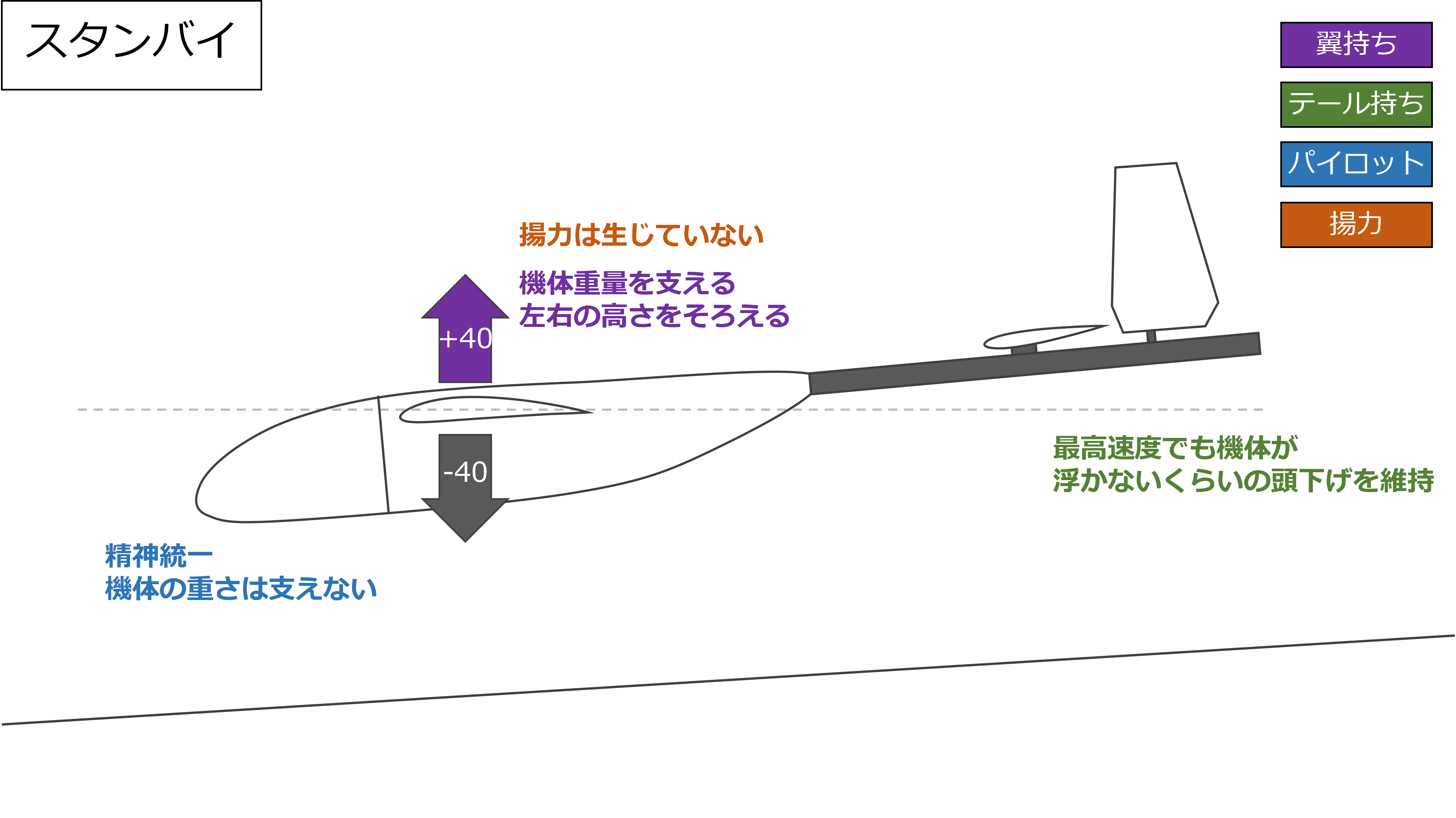
高翼機のスタンバイでは、翼持ちが機体の重量を支え、機体のバンクが水平になるように左右の高さをそろえる
このとき、パイロットは機体の重量をほとんど負担しない
高翼乗り込み式では、機体を下向きに引っ張るような力をほとんどかけることができないので、機体を持ち上げるような強い突風が吹くと容易に機体だけがあおられてしまう
例えば、速度9m/sの機体で全備重量の4割が機体重量だった場合、迎角0度でも5.7m/sの風で機体は完全に宙に浮いてしまう
テールを不用意に下げて迎角が大きくなっていればなおさらである
そのため、テール持ちは揚力が発生しないようにテールを高く保つ必要がある
走り出し
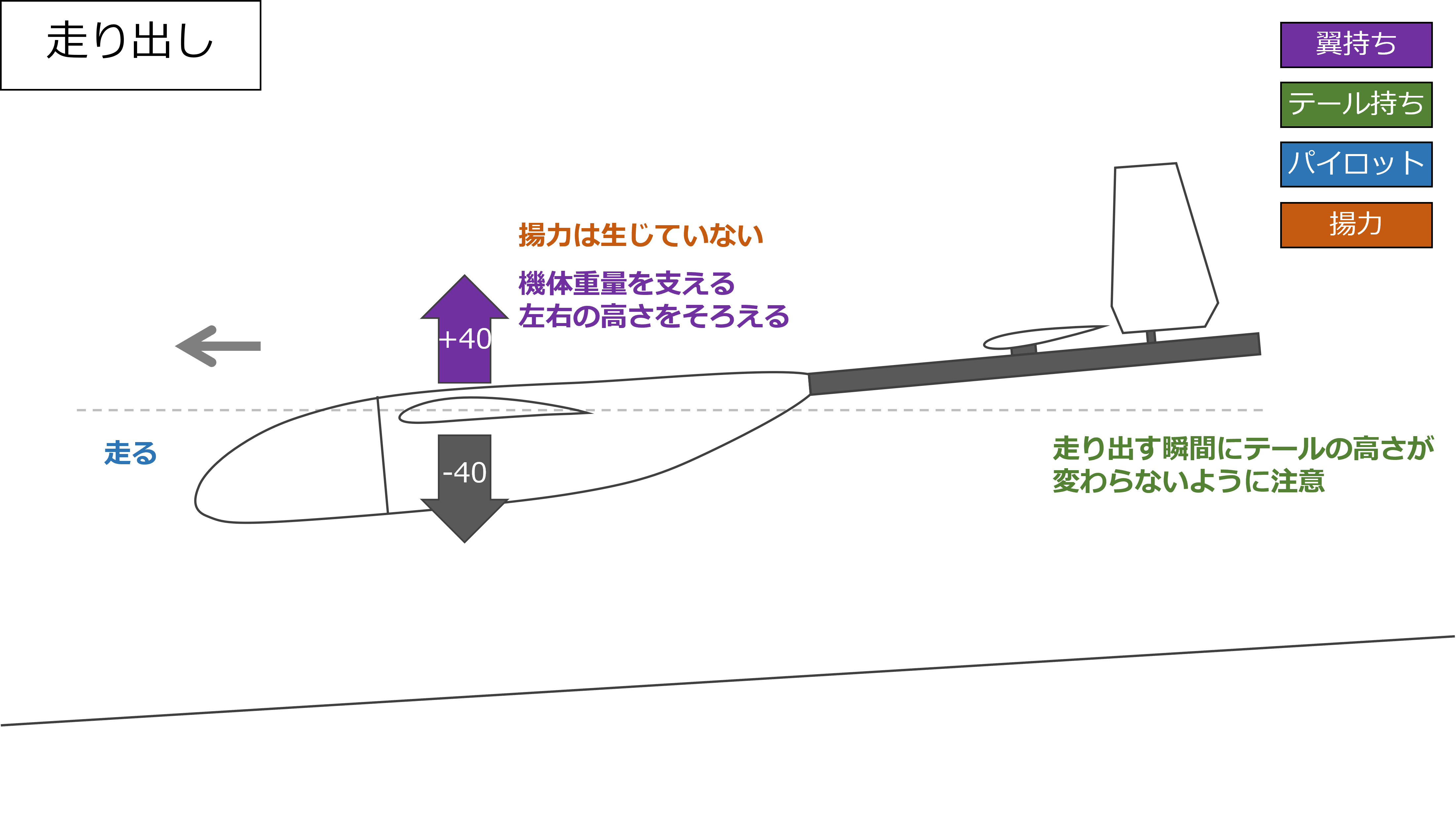
走り出したタイミングでも翼持ちとテール持ちのやることは変わらないが、静から動に移るタイミングで生じる姿勢や力の変化などで、スタンバイ時に調整した高さが乱れてしまうことがあるので注意する
パイロットはひたすら全力で走って機体を加速する
初速はあればあるほどいい
加速
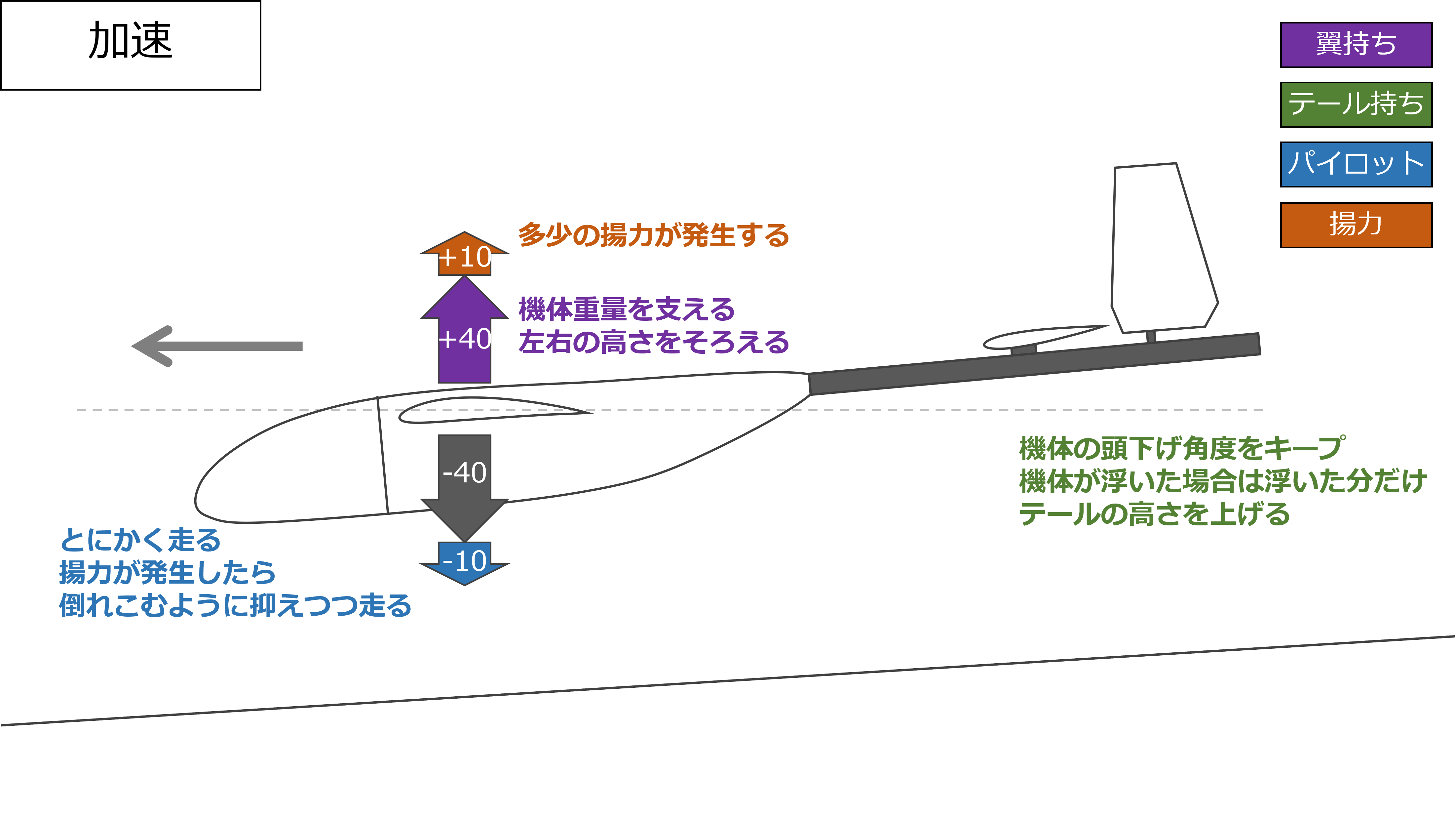
加速のフェーズでも翼持ちのやることは変わらないが、機体が横風などにあおられて機体がバンクした場合、片方の翼持ちに機体重量が集中することになるので、潰されないように注意する
加速するにつれて多少の揚力が発生しだすので、テール持ちは機体を浮かさないように頭下げをキープする
万が一機体が浮いてしまった場合、テール持ちは主翼とテールの相対的な位置(機体のピッチ角)をキープするようにテールを滑らかに上げる
パイロットはひたすら走り、機体が浮きそうになった場合は前に倒れこむようにして走って何とか浮きを抑える
完全に機体が浮いて足がプラホから離れてしまった場合は腕力と気合で乗り込む
風が吹いている場合は、プラットホームに当たった風が吹き上げてプラホ端で上昇風となっていることがあるので、翼端がプラホから出るタイミングは特に機体のバンクや不意の浮上に注意が必要である
機体が突風にあおられてバンクしながら浮いてしまった場合は、機体が傾いた方向にテールを振ることによってロールを制御できる(\(L_{r}\)を使う)
テイクオフ
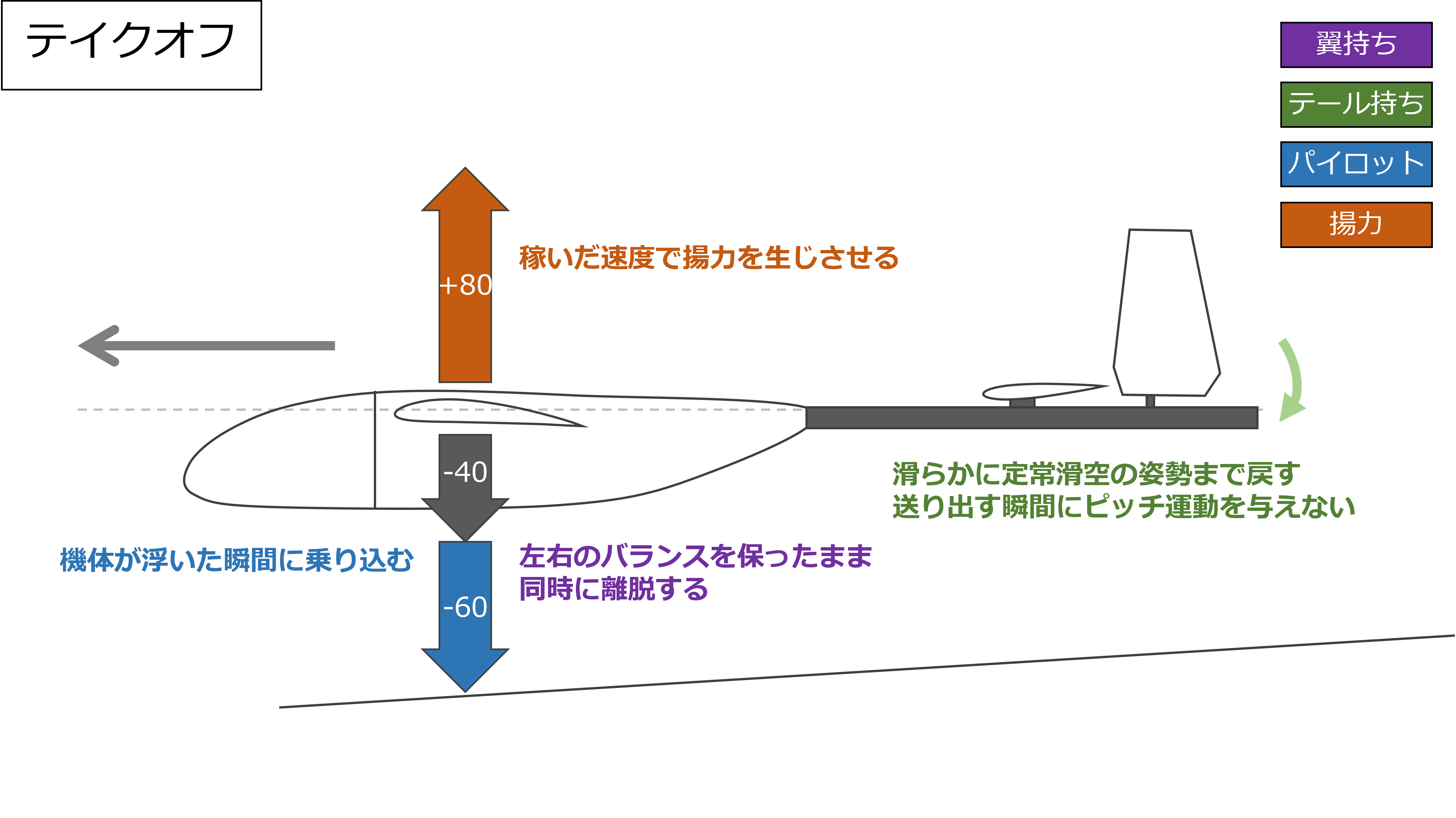
機体が最高速度に到達してテイクオフのタイミングになったら、翼持ちは左右のバランスを保ったまま同時に離脱する
翼持ちが離脱するタイミングに合わせてテール持ちはテールを滑らかに定常滑空の姿勢にまで戻し、機体にピッチ運動を与えないようにして真っ直ぐに送り出す(紙飛行機を飛ばすようなイメージ)
翼持ちが離脱してテール持ちがテールを下げたタイミングで、パイロットは浮いた機体に走って飛び乗る
「翼持ちが機体を支えている状態」から「揚力が機体とパイロットを支えている状態」へと滑らかに遷移させるイメージである
風と初速が十分にあればそのまままっすぐ飛ぶことができるし、速度が足りない場合は若干のダイブを行うことになる
高翼機で一番シビアなのがこの遷移のタイミングを翼持ち、テール持ち、パイロットの間で完璧に合わせることなので、フライトチームでひたすら練習を繰り返し、息を合わせることが必要になる
正対風が強い場合にテールを上げたまま水面に突き刺すように機体を送り出すテイクオフ方法があるが、重心移動方式の場合は注意する必要がある
というのも、重心移動方式のピッチの操舵力は(揚力)×(重心移動量)なので、過度に頭下げをした状態で飛び出すと、マイナス迎角で揚力ゼロ、重心移動が全く効かない、という状況になりうる
フライト映像で翼が全く撓んでいないままダイブして着水する機体などがこの現象に該当するが、この場合はもはやパイロットにはどうしようもない
エレベーター操舵の場合は主翼の揚力がゼロでも尾翼に空気が当たっていれば操縦できるので、上記のようなテイクオフ方法でも問題ない
まとめ
高翼・乗り込み式のテイクオフは翼持ち、テール持ち、パイロットがそれぞれの役割を完璧に果たす必要がある難易度の高い(たくさん練習が必要な)方法である
2人乗り滑空機の視点から見ると、パイロットが機体に飛び乗ったタイミングで機体にかかる荷重が瞬間的に増えるため、左右のパイロットの乗り込みタイミングをかなりシビアに合わせる必要があり、現実的ではない
脚付き乗り込み式
脚付き乗り込み式のテイクオフのポイントは以下の通り
上記について各フェーズごとに説明する
スタンバイ
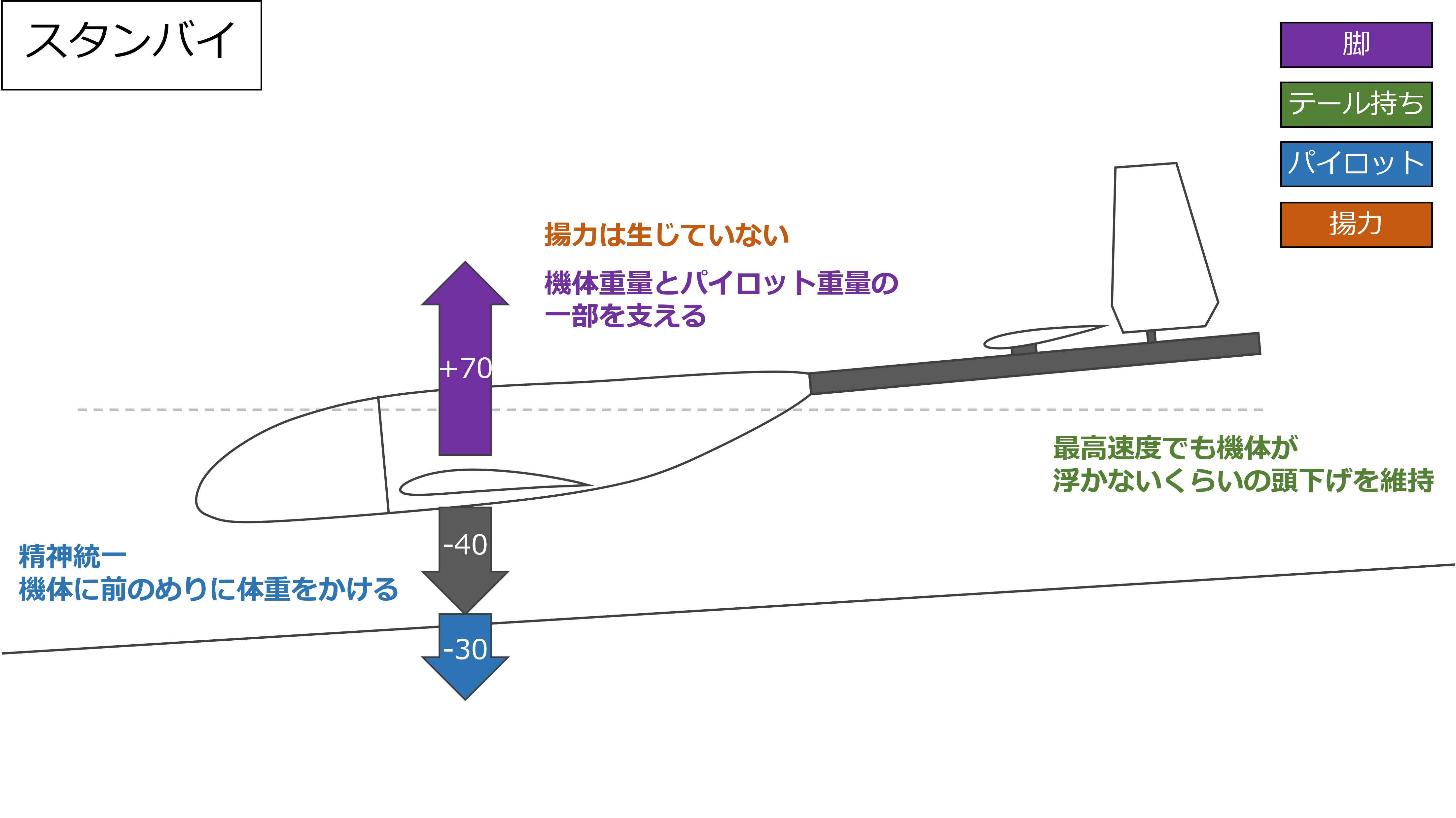
脚付きのスタンバイでは、左右の脚の長さによって機体の高さや水平が固定されるので、プラホ上での機体の高さ調整は必要ない
パイロットは機体に体重をかけてダッシュしやすい前傾姿勢を作る
このとき、脚の接地点が重心より前にある場合はテールが重くなり、脚の接地点が重心より後ろにある場合は機体を前転させる力がかかるので、テール持ちはこのような力を相殺しつつ、理想的な角度にテールを維持する
機体には機体の自重に加えてパイロットの体重も一部かかっているため、突風で機体があおられてしまうことはほとんどない
走り出し
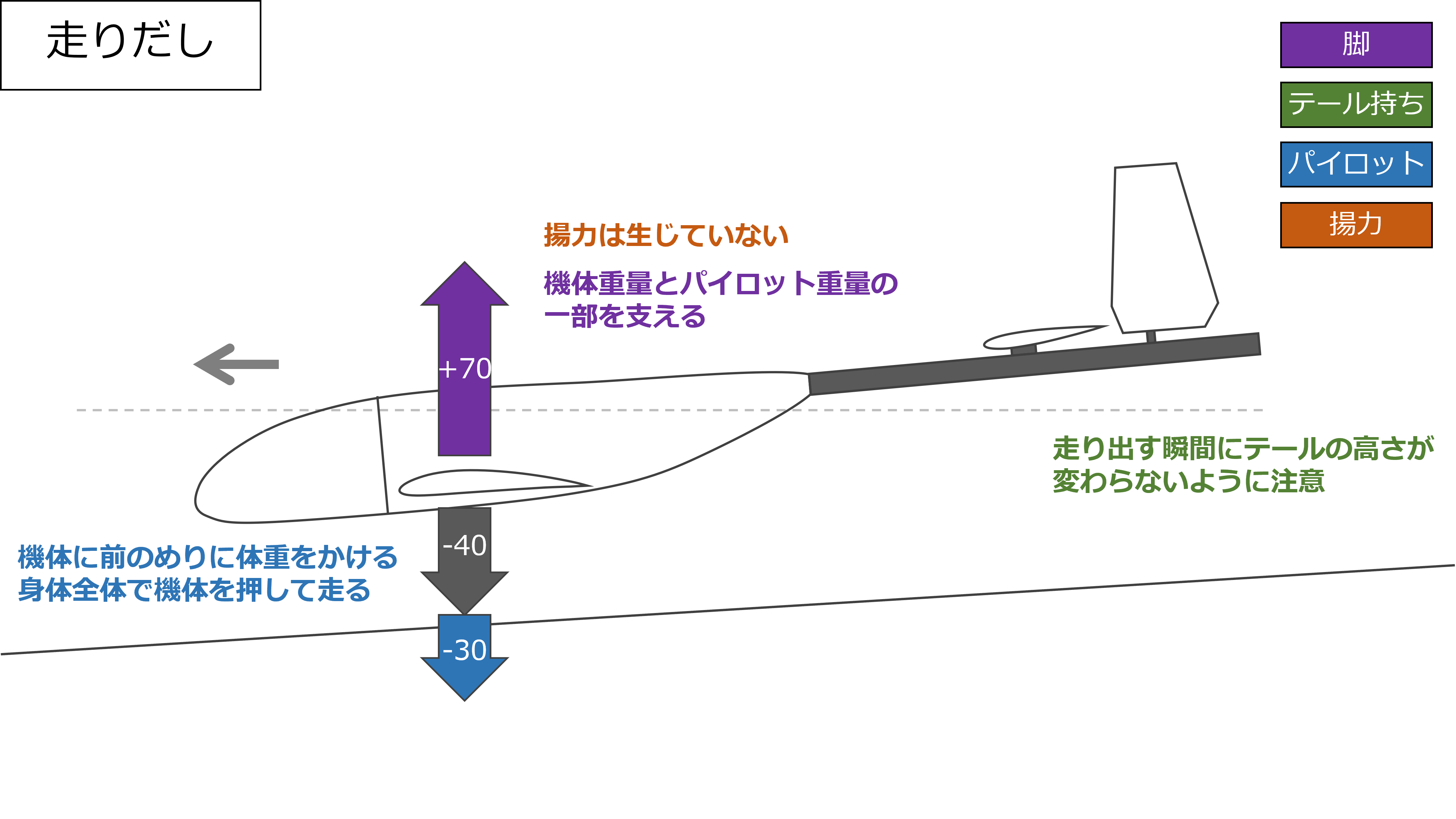
走り出しのフェーズについては高翼乗り込み式と大きな違いはなく、静から動に移るタイミングの姿勢や力の変化についてはテール持ちだけが注意しておけばいい
パイロットはひたすら全力で走って機体を加速する
初速はあればあるほどいい
加速
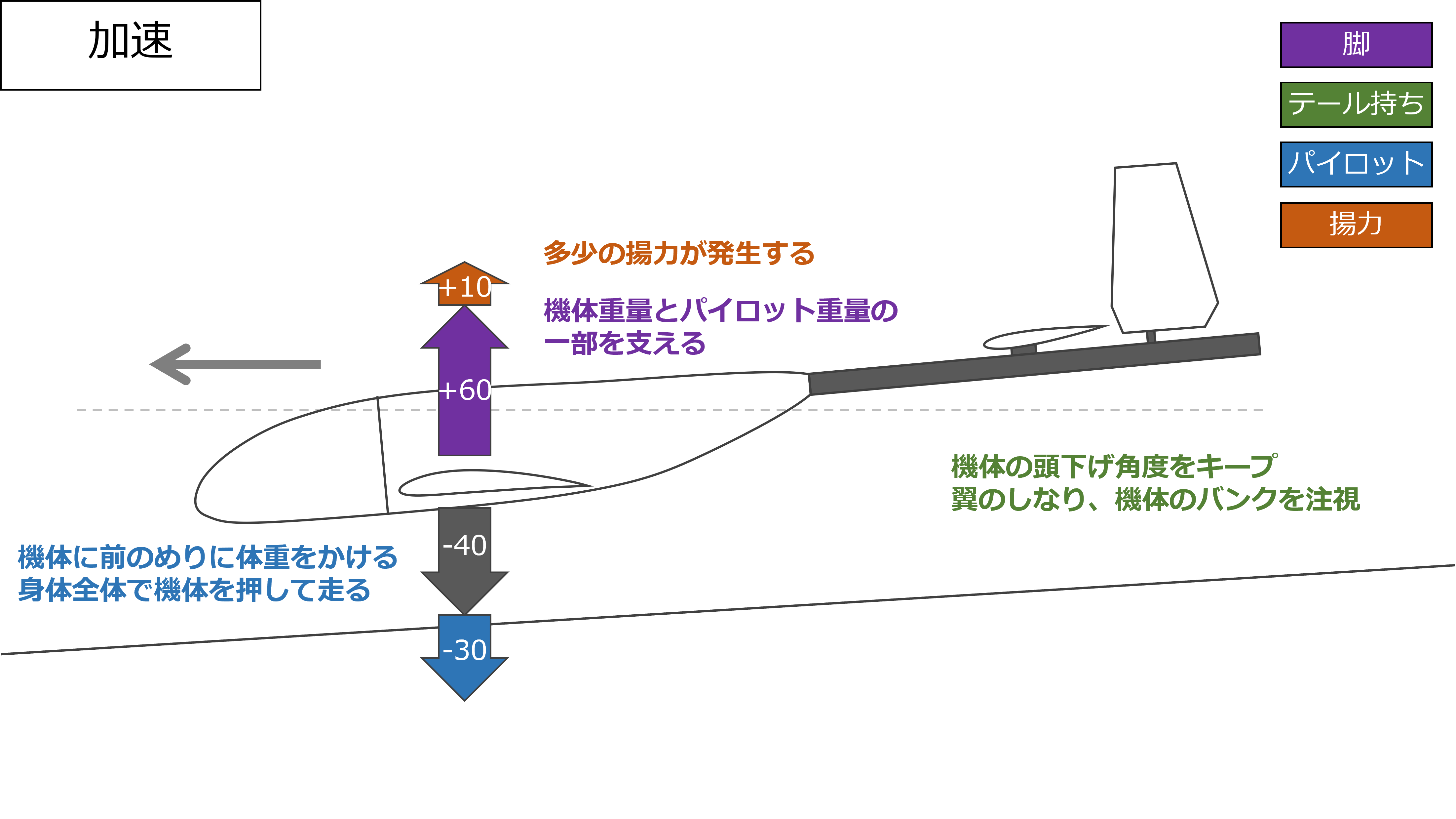
加速のフェーズにおいてもあまり考えることはなく、とにかく全力で走ればいい
機体にはそれなりの下向きの力がかかっているため途中で浮いてしまうことはほとんどないが、テール持ちが不用意にテールを下げる+プラホ端の吹き上げをくらう のコンボが決まると浮いてしまうこともある(実体験)
特に、機体がバンクしながら浮いてしまった場合はパイロットにはどうすることもできないので、テール持ちが速やかに機体をヨーイングさせてバンクに対処する必要がある
逆にいうと、テールの角度さえキープしておけば機体のバンクや不意の浮上のことを考えなくていいというのが脚付きのメリットだったりする
テイクオフ
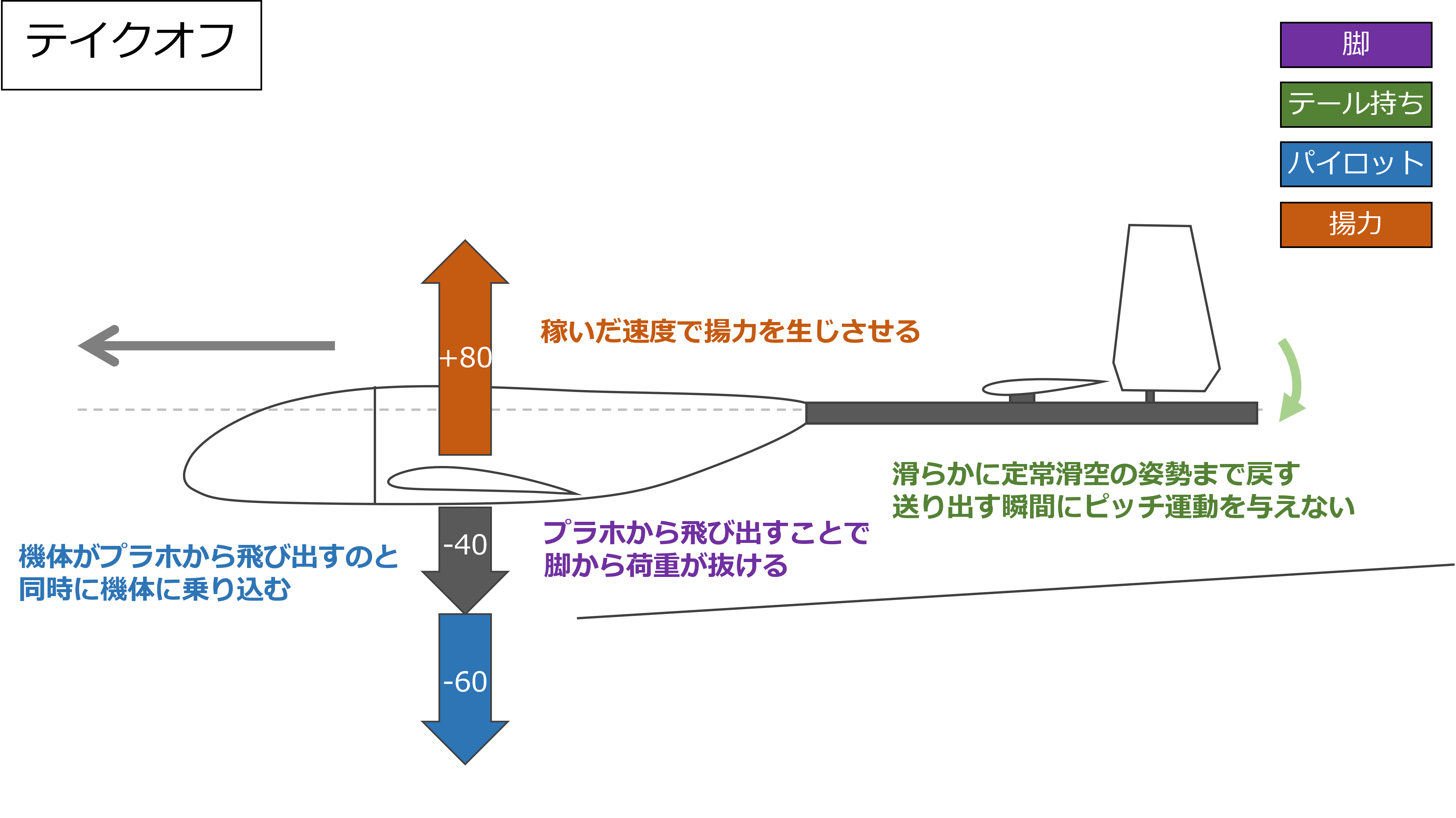
テイクオフのタイミングについては高翼乗り込み式とやや異なる
「脚が機体とパイロットを支えている状態」から「揚力が機体とパイロットを支えている状態」への遷移という点では発想は同じだが、任意のタイミングで離脱できる翼持ちと違い、脚はプラホ端から飛び出す瞬間に荷重が抜けることになる
なので、テール持ちがテールを下げて揚力を発生させるタイミングも、パイロットが機体に乗り込むタイミングも、この脚がプラホから飛び出すタイミングに合わせる必要がある
高翼乗り込み式ではフライトチームのメンバー間でタイミングを合わせることが重要であるため「走り出してから何歩でテイクオフする」といった練習が可能になるが、脚付き乗り込み式の場合は脚がプラホから飛び出すタイミングにすべてを合わせる必要があるため、「走り出してから何歩」という練習の仕方よりも、「プラホ端から何m」という指標で練習する必要がある
まとめ
脚付き乗り込み式は、機体の自重を脚で支えることによって機体の高さやバンクに気を取られずに全力ダッシュでテイクオフすることができる方式である
2人乗り滑空機の視点から見ると、機体重量+2人分の荷重を支えられる脚の設計/製作や格納システムの実装による工数の増加などがネックとなって採用を見送った
吊り下げ式
吊り下げ式のテイクオフのポイントは以下の通り
上記について各フェーズごとに説明する(基本的にハンググライダーのテイクオフと同じ思想となる)
スタンバイ
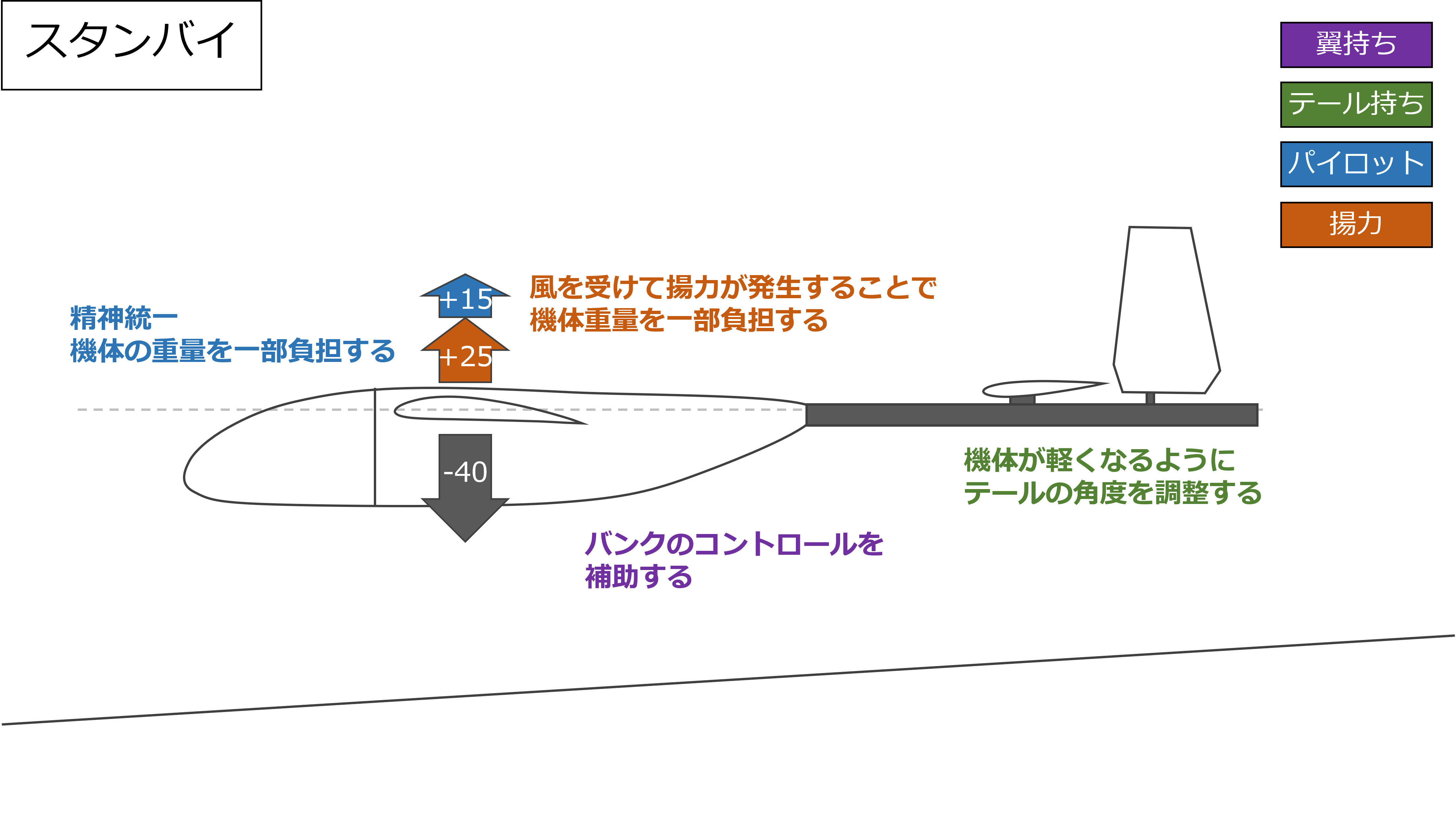
吊り下げ式が乗り込み式と大きく異なるのは、パイロットがハーネスを介して機体に接続されているため、機体を下向きに引っ張る力を加えられる点である
乗り込み式の場合は機体が浮いてしまった場合に抑える手段がほぼないため、テールを高く保持して揚力を発生させないようにしていたが、吊り下げ式の場合は機体が浮いてしまった場合でもパイロットが体重をかけることで比較的容易に浮きを抑えることができるため、機体の重量を支えるための揚力を積極的に利用することができる
スタンバイ中はパイロットが機体重量を支えつつ、テールの高さを良い感じに調整して揚力でも機体を支えられるようにする
翼持ちに関しては機体が傾いた際に補助する程度でいい
走り出し
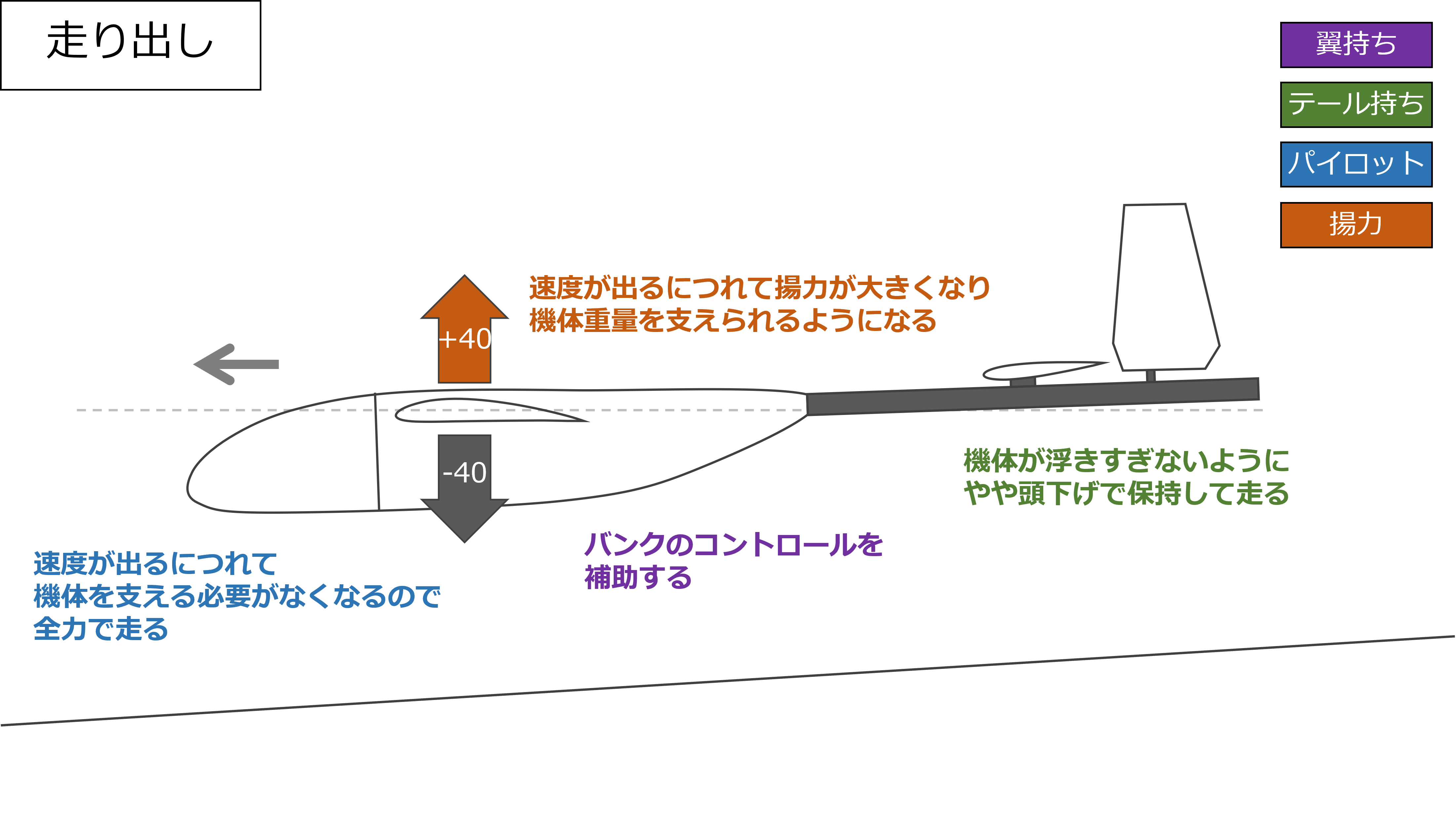
走り出してある程度速度が出ると揚力だけで機体を支えられるようになるので、パイロットは全力で走ることに注力する
テール持ちはあまり機体が浮きすぎないよう、定常滑空もしくはやや下げくらいでテールを保持したまま走る
翼持ちは機体がバンクしないように補助を行う
加速
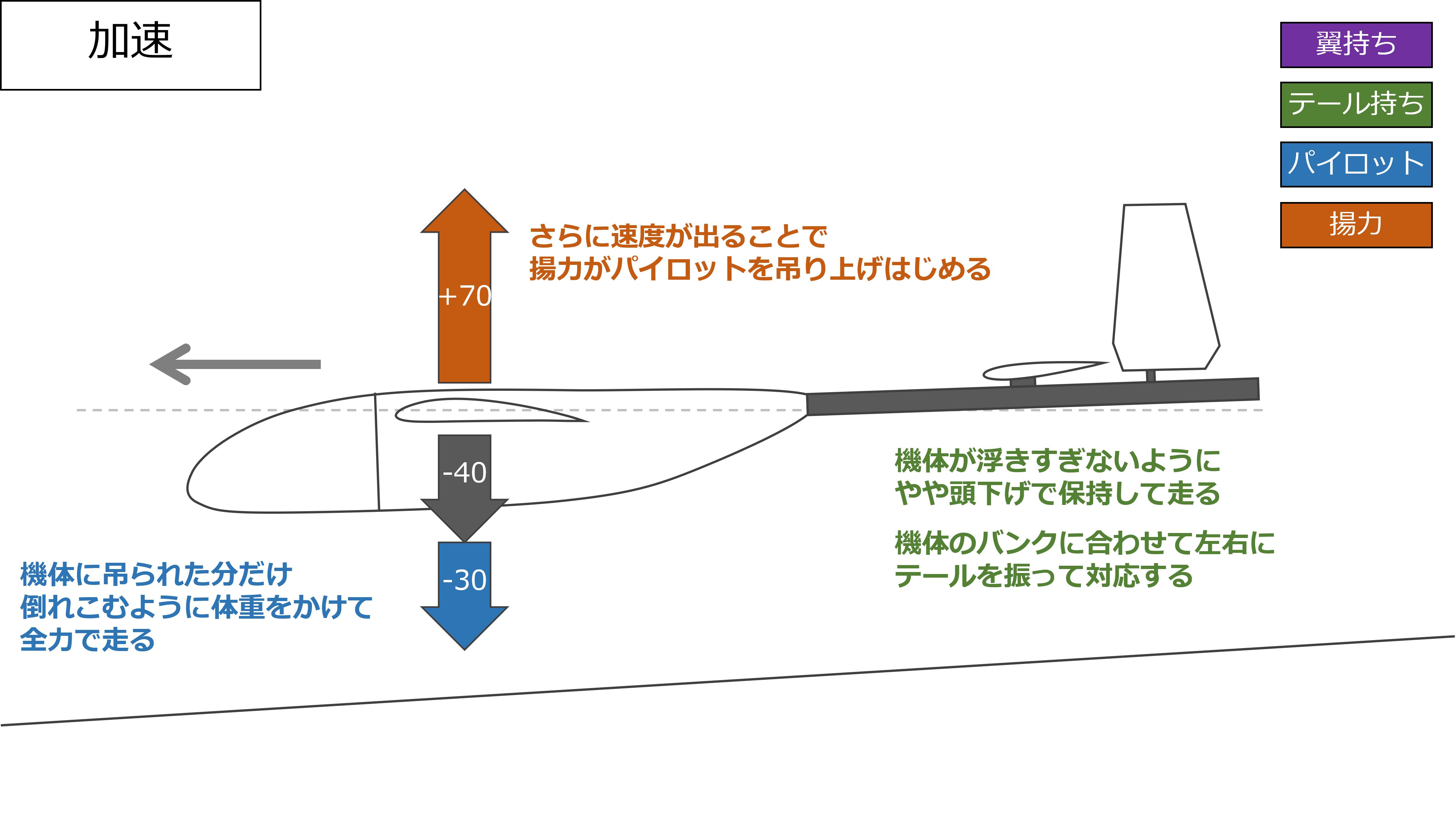
加速フェーズではさらに揚力が大きくなり、パイロットを吊り上げ始める
パイロットは機体に吊り上げられた分だけ倒れこむようにハーネスに体重をかけて全力で走る
テール持ちはパイロットが吊り上げられすぎないようにテールの高さを調整しつつ走り、機体がバンクした場合はテールを左右に振ることでバンクを修正する(\(L_{r}\)を使う)
例えば機体が左にバンクした場合はテールを左に振りながら(機体を右にヨーイングさせながら)走ることで、左翼の速度が増加して揚力が大きくなり、左バンクを修正することができる
吊られる→体重をかけて加速する→さらに吊られる→さらに体重をかける を繰り返すことで、徐々に「揚力が機体とパイロットを支えている状態」へと遷移していっている
テイクオフ
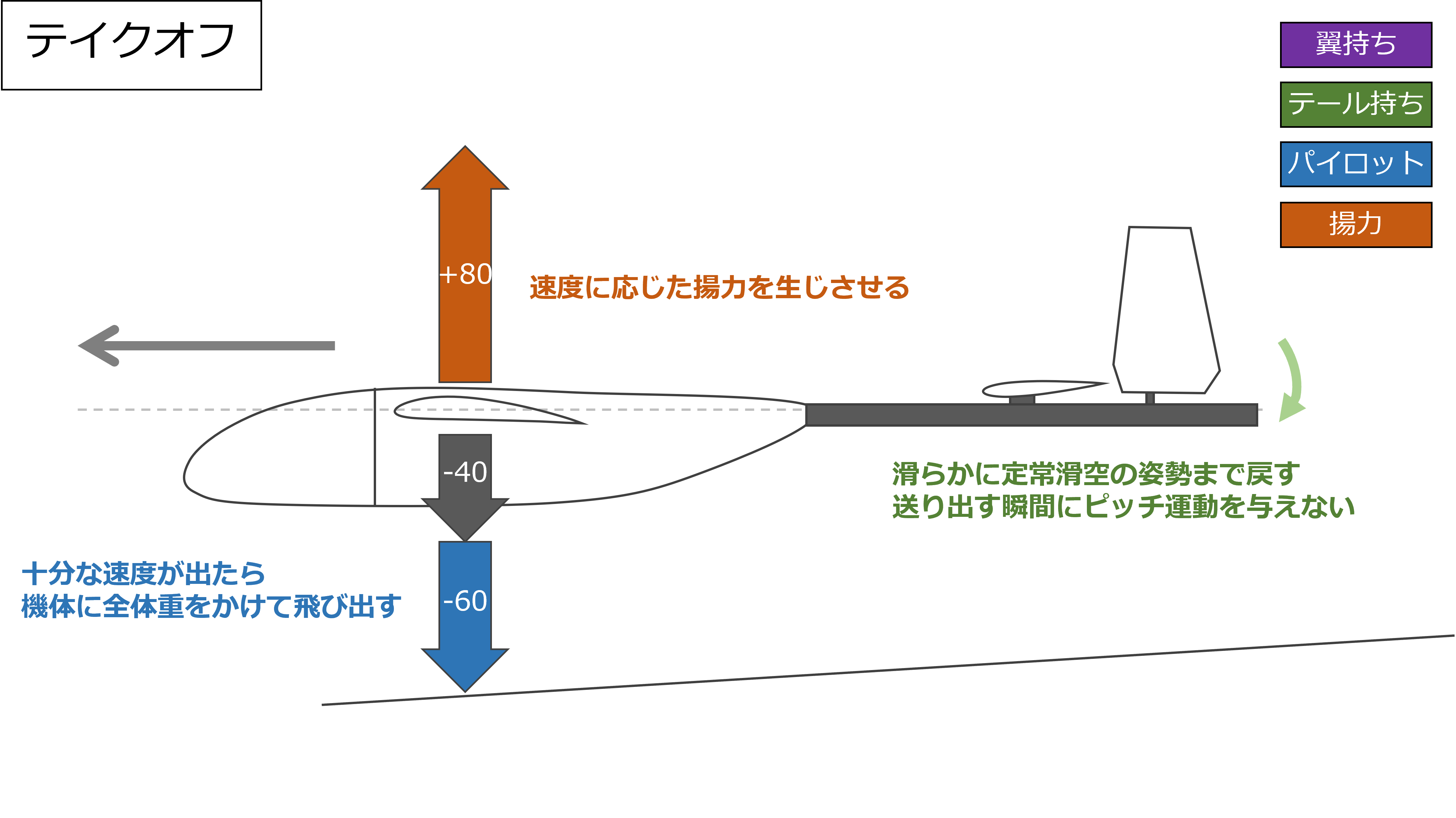
十分に機体が加速したら、パイロットは機体に全体重をかけて飛び出す
テール持ちはパイロットが飛び出すタイミングに合わせてテールを滑らかに下げて定常滑空の姿勢にして機体を送りだす
まとめ
吊り下げ式はハンググライダーと同様のテイクオフ方法なので、ハンググライダーで練習をした鳥コンパイロットとの相性は抜群に良い
2人乗り滑空機の視点から見ると、テイクオフの懸念点を以下のように解消できる
そもそも吊り上げ式は徐々にパイロットが揚力に吊られていくので、「乗り込みのタイミング」という概念が存在しない
加速のフェーズで連続的にパイロットの乗り込み度合いが増加していき、テイクオフのタイミングで乗り込みが完了することになる
もちろん最終的に「パイロットが全体重を機体に預けるタイミング」は存在するが、それが多少ずれたところで左右のパイロット重量のバランスは 左P:右P=100:0 のようにはならず、左P:右P=100:95 のようになるので、左右のバランスが大きく崩れることはない
乗り込みのタイミングをそこまで気にしなくていい、という点は2人乗り滑空機で吊り下げ式を採用する大きなメリットである
吊り下げ式では2人のパイロットに加えて揚力でも機体を支えることができるので、2人乗り滑空機の機体重量が大きくなっても機体保持に問題はない
ここで重要になってくるのが「機体重量に対する翼面荷重」という指標である
2人乗り滑空機は全備重量の増加を補うために大きな主翼が必要になるが、ここでの全備重量の増加分は主に2人目のパイロットの重量であり、機体重量に大きな増加はない
結果として、「機体重量に対する翼面荷重」がかなり小さくなるため、プラホ上のわずかな風でも大きな揚力を得ることができるようになる
例えば、速度10m/s、機体重量40kg、パイロット重量60kgという鳥コン滑空機と、同じ速度、機体重量でパイロットが60kg×2人の鳥コン滑空機を比較してみる
プラホ上で4m/sの風が吹いた場合、前者の機体では 100kg×0.4×0.4=16kg の揚力が発生し、パイロットが支える荷重は 40kg-16kg=24kg となる
一方、後者の機体では 160kg×0.4×0.4=25.6kg の揚力が発生し、パイロット1人が支える荷重は (40kg-25.6kg)÷2=7.2kg となる
揚力で支えられることで大きく軽減された機体重量をさらに2人のパイロットで分担できるので、上記の例に示したように、1人乗りと比較してパイロットが支えるべき機体重量を3分の1以下にまで減らすことが可能になる
2人乗り鳥コン滑空機の「機体が自分自身を持ち上げてくれる」という性質は、テイクオフだけでなく湖岸の運搬などでもかなり役に立つ性質だと思う
鳥コン滑空機のテイクオフは、機体の姿勢、速度、風などの時事刻々と変化する複雑な状況に対して、常に最適な動きを選択し続けるプロセスである
状況の組み合わせは多岐にわたり、失敗する要因も各チーム、機体、当日のコンディションによって千差万別となる
そのような特性を持ったテイクオフというプロセスの成功率をできる限り高めるためには、PFMEAの手法が効果的なのではないかと思う
PFMEAをやるにあたって必要な過去事例については、鳥コン出場特典のDVDに毎年20チーム弱のテイクオフ映像が収録されているので、10年分くらい見直せば大抵の故障モードはカバーできると思う
テイクオフの安定性に悩むチームは検討してみてもいいかもしれない
おわりに
2023年の鳥人間コンテストに出場したTeam Tinkerの2人乗り鳥コン滑空機 Gemini-X の設計についてまとめた
2人乗り鳥コン滑空機というコンセプトの実現可能性はフライトをもって実証され、今回出場したTeam Tinker 第3世代は無事に解散した
次のTeam Tinkerの集結がいつになるかは神のみぞ知るが、おそらく次回の機体はまた別のコンセプトに挑戦することになると思う
Gemini-Xを参考に今後も多くのチームが新しいコンセプトに挑戦し、琵琶湖に新たな風をふかしてくれることを心待ちにしている
↓審査員特別賞受賞!

↓おまけ
2人乗り鳥コン滑空機の可能性
ここからはさらにもう少し踏み込んで「2人乗り鳥コン滑空機」の今後の可能性について議論していく
もちろん今回のTeam TinkerのGemini-Xのような実証機レベルの機体では、現在のハイレベルな滑空機部門には到底太刀打ちできないので、「もし現在の鳥コン滑空機部門のレベルにまで高度に洗練された2人乗り機が完成したらどこまで飛べるのか?」という問いに対して話を進めていく
鳥コン滑空機設計者各位は一度ここで記事を閉じて、上記の問いに対する自分なりの答えを用意してみてほしい
これから自分の機体を設計するための良い頭の体操になると思う
↓参考
それではいってみよう
結論
筆者の結論は以下の通り
詳しく解説していく
飛距離に影響を与える要素
この記事の最初の方でも説明した通り、ぶっちゃけ速度と翼面荷重を同じにすれば1人乗りと2人乗りの機体は空力的にはほぼ変わらない
滑空機部門の飛距離を考える上で最も重要な鳥コン滑空機のエネルギー保存則は以下の式で表される
\begin{equation}
(スタート直後のエネルギー)-(着水直前のエネルギー)=(抵抗と風によってなされる仕事)
\end{equation}
これを数式で表すと次のようになる
\begin{equation}
(mgh+\frac{1}{2}mV_0^2)-(\frac{1}{2}mV_s^2)=\int_s (D+W) ds
\end{equation}
左辺のエネルギー項はすべて全備重量に比例するため、2人乗りにすることによって利用可能なエネルギーが約2倍になるという説明は間違ってはいない
しかし、全備重量が約2倍になると主翼面積も約2倍になり、右辺の抗力項も約2倍となるので、結局エネルギーの増分は抗力の増分によってほぼ打ち消されてしまう
ただし、ここで「約2倍」とか「ほぼ打ち消される」と表現している点が重要で、鳥コン滑空機においては全備重量(あるいは主翼面積)に比例しない要素がいくつか存在する
それらの要素に対して2人乗りというコンセプトがどのように影響を与えるのかをしっかりと考える必要がある
※右辺の「風からなされる仕事」については翼面荷重の大きさと飛行速度によって決まるため、2人乗りにしたからといって変化するものではない、と思っている、知らんけど
全備重量あるいは主翼面積に比例せず、かつ2人乗りにすることによって変化する要素は以下の通り
- カウルの抗力
- テイクオフ時の運動エネルギー
- スパン
それぞれについて説明していく
カウルの抗力
2人乗りになることでカウルが2つ必要になるため、カウルの抗力は2倍になる
初っ端から定量的な評価が難しい要素だが、ざっくり抗力の増加を推算してみる
一般的な従来型鳥コン滑空機をイメージする
揚力 L=1,000N、全機 L/D=40 とすると全機の抗力は 1,000N÷40=25N になる
この全機抗力は、翼の有害抗力、翼の誘導抗力、それ以外の有害抗力(≒カウルの抗力)に分けられる
翼の有害抗力については、XFLR5の3D解析などを参考にすると L/D=80 程度らしいので、翼の有害抗力の実数値は 1000N÷80=12N ほどである
翼の誘導抗力については、ざっくり揚力係数を0.9、アスペクト比を40とすると下式のとおり L/D=140 程度になるので、翼の誘導抗力の実数値は 1000N÷140=7N ほどである
\begin{align} \frac{L}{D_{i}}&=\frac{L}{L\varepsilon}=\frac{1}{\varepsilon} = \frac{1}{C_{L}/\pi AR} \\ &=\frac{1}{0.9/40\pi}\simeq 140 \end{align}
以上より、カウルの抗力の実数値は 25N-(12N+7N)=6N と見積もることができる
カウルの抗力はカウルの大きさと形状によって決まるため、2人乗り滑空機の場合は単純に6Nほど全機抗力が増加することになる
これが2人乗り滑空機の飛距離減少要因なので、これ以外の要素の飛距離上昇分がこれを上回ればよい
テイクオフ時の運動エネルギー
テイクオフ時の運動エネルギーは加速力×助走距離で与えられる
\begin{align} (運動エネルギー)&=(なされた仕事) \\ &=(力)\times(距離) \end{align}
センシティブな内容なのであえて曖昧な表現を用いるが、2人乗りにすることでテイクオフ時の加速力を2倍にすることができるため、運動エネルギーも2倍にすることができる
全機抗力が1.7倍ほど増加するのに対して、運動エネルギーは2倍ほど増加することになるので、ここの0.3倍の差分が2人乗り滑空機の飛距離増加要因になる
\begin{align} &\left\{ \begin{array} \\ \frac{1}{2} m {V_{0}}^{2} &=& PL \\ \frac{1}{2}(1.7m) {V’_{0}}^{2} &=& (2P)L \\ \end{array}\right. \\ \\ \rightarrow \quad& V’_{0}=\sqrt{\frac{2}{1.7}}V_{0} \simeq 1.085V_{0} \end{align}
ちなみに従来型鳥コン滑空機の初速は5〜6m/sと言われているので、機体重量を100kgとすればテイクオフ時の運動エネルギーは1,500Nm程度である
よって、2人乗り滑空機の全備重量に比例しない運動エネルギーの増加(初速の増加によるもの)は 1500Nm×0.3=450Nm 程度になる
スパン
先述したとおり、2人乗り滑空機では2人のパイロットに加えて揚力でも機体重量を支えることができるため、従来型鳥コン滑空機よりも重い機体を実現することができる
新たに獲得した機体重量の余剰を何に割り当てるかは設計者の好みによるが、今回はスパンの増加に割り当てることを考えてみる
誘導抗力の実数値はスパンの二乗に反比例するので、スパンを大きくすることで誘導抗力を小さくることができる
\begin{align} D_{i}&=\frac{1}{2}\rho V^2 S C_{D_{i}} = \frac{1}{2}\rho V^2 S \frac{C_{L}^2}{\pi AR} = \frac{2(mg)^2}{\rho \pi b^2 V^2} \end{align}
人力プロペラ部門の2人乗りの先駆者の機体を見るに、スパン40mほどまでなら琵琶湖で運用可能だと思われる
例として、従来型鳥コン滑空機を全備重量100kgでスパン28m、2人乗り鳥コン滑空機を全備重量170kgでスパン40mとすると、下式の通り誘導抗力は従来型鳥コン滑空機から1.4倍ほどしか増加しないことになる
\begin{align} D’_{i}&= \frac{2(1.7mg)^2}{\rho \pi (1.43b)^2 V^2} \simeq 1.41D_{i} \end{align}
力学的エネルギーが1.7倍ほど増加するのに対して、誘導抗力は1.4倍ほどしか増加しないことになるので、ここの0.3倍の差分が2人乗り滑空機の飛距離増加要因になる
まとめ
以上の考察を、具体的な数値例で計算してみる
なお、飛距離の計算は以下の式による
$$ R=\frac{PL+mgh-\frac{1}{2}mV^2 \frac{1}{1+\Delta C_L/C_L}}{(\frac{1}{2}\rho V^2 S C_{D_p}+\frac{2(mg)^2}{\pi\rho b^2 V^2})} $$
結果は以下の通り
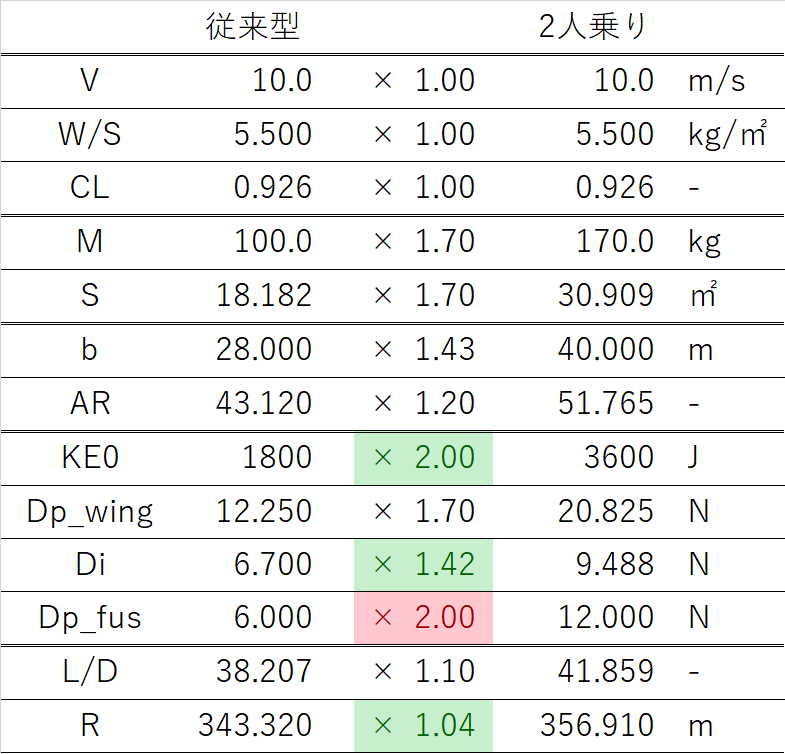
上記より、従来型鳥コン滑空機をそのまま2人乗りに改修するだけで、+4%の飛行距離増加を達成しうる可能性があることがわかった
たったの4%?と思うかもしれないが、2人乗りという圧倒的な変態性をもってしてなおコンセプトの段階で定量的に従来型に対する優位性が示せているという点は評価できるのではないかと思う(もちろん前提にいろいろ無理があるかもしれないが)
毎年似たような機体ばかりで面白くない!という過激派設計者は、独創性満載なのに記録更新まで狙えてしまう2人乗り滑空機というど変態機にぜひ挑戦してみてほしい
Gemini-X 設計シート
Gemini-Xの設計シートはこれ(マクロ付き)
DAE31_SD8040
1.0000000 0.0012431
0.9904697 0.0026837
0.9725228 0.0057755
0.9505702 0.0099410
0.9260226 0.0148756
0.9001607 0.0202506
0.8736981 0.0258547
0.8469767 0.0315367
0.8204112 0.0371364
0.7940940 0.0425754
0.7680428 0.0477910
0.7422295 0.0527303
0.7165386 0.0573702
0.6908477 0.0617192
0.6651639 0.0657782
0.6395030 0.0695282
0.6138305 0.0729686
0.5881180 0.0760954
0.5623332 0.0789284
0.5365785 0.0814442
0.5107204 0.0836625
0.4849278 0.0855738
0.4591519 0.0871593
0.4333993 0.0884213
0.4077167 0.0893457
0.3821175 0.0899178
0.3566066 0.0901242
0.3312427 0.0899502
0.3060334 0.0893675
0.2810124 0.0883643
0.2562370 0.0869067
0.2317368 0.0849784
0.2076273 0.0825428
0.1839449 0.0795712
0.1608393 0.0760359
0.1384541 0.0719171
0.1170323 0.0672118
0.0968964 0.0619532
0.0784346 0.0562332
0.0621150 0.0502635
0.0483041 0.0443056
0.0370326 0.0386032
0.0280570 0.0333166
0.0209758 0.0284848
0.0153818 0.0240926
0.0109674 0.0200531
0.0074838 0.0162854
0.0047587 0.0127342
0.0026805 0.0093548
0.0016173 0.0071842
0.0011850 0.0061183
0.0008220 0.0050630
0.0005276 0.0040198
0.0003009 0.0029919
0.0001403 0.0019808
0.0000416 0.0009842
0.0000000 0.0000000
0.0000125 -0.0009754
0.0000827 -0.0019467
0.0002158 -0.0029180
0.0004183 -0.0038917
0.0007016 -0.0048590
0.0010778 -0.0058076
0.0015572 -0.0067265
0.0021402 -0.0076068
0.0028244 -0.0084396
0.0036068 -0.0092182
0.0044817 -0.0099432
0.0054414 -0.0106159
0.0064800 -0.0112396
0.0087852 -0.0123676
0.0128185 -0.0138514
0.0176669 -0.0151554
0.0235816 -0.0163584
0.0309699 -0.0175036
0.0404580 -0.0185879
0.0529320 -0.0195596
0.0692682 -0.0203548
0.0895678 -0.0208254
0.1128817 -0.0208887
0.1380175 -0.0205819
0.1640720 -0.0199932
0.1906884 -0.0191900
0.2176322 -0.0182448
0.2447246 -0.0171944
0.2719545 -0.0160559
0.2993030 -0.0148587
0.3267163 -0.0136179
0.3542210 -0.0123493
0.3817550 -0.0110712
0.4092263 -0.0097997
0.4366968 -0.0085550
0.4641490 -0.0073287
0.4914911 -0.0061477
0.5188200 -0.0050202
0.5461163 -0.0039483
0.5733850 -0.0029401
0.6006575 -0.0019948
0.6278577 -0.0011172
0.6550029 -0.0003326
0.6822066 0.0003732
0.7093305 0.0009967
0.7364060 0.0015193
0.7634301 0.0019364
0.7903833 0.0022334
0.8172663 0.0023988
0.8440910 0.0024189
0.8708644 0.0022927
0.8974326 0.0020077
0.9237162 0.0015576
0.9488349 0.0009558
0.9715325 0.0001858
0.9900658 -0.0006593
1.0000000 -0.0012431NACA0009
1.0000000 0.0009450
0.9901774 0.0019724
0.9702755 0.0040166
0.9470241 0.0063434
0.9229643 0.0086844
0.8987629 0.0109733
0.8745303 0.0132015
0.8502843 0.0153692
0.8260287 0.0174772
0.8017656 0.0195266
0.7774967 0.0215175
0.7532237 0.0234501
0.7289480 0.0253237
0.7046715 0.0271373
0.6803957 0.0288895
0.6561224 0.0305781
0.6318533 0.0322006
0.6075902 0.0337540
0.5833350 0.0352345
0.5590897 0.0366378
0.5348564 0.0379590
0.5106374 0.0391925
0.4864351 0.0403319
0.4622524 0.0413702
0.4380922 0.0422995
0.4139581 0.0431107
0.3898541 0.0437941
0.3657850 0.0443385
0.3417562 0.0447317
0.3177746 0.0449597
0.2938485 0.0450068
0.2699883 0.0448552
0.2462075 0.0444844
0.2225236 0.0438707
0.1989606 0.0429863
0.1755518 0.0417979
0.1523461 0.0402656
0.1294196 0.0383406
0.1069011 0.0359641
0.0850405 0.0330718
0.0643875 0.0296285
0.0518278 0.0270688
0.0460908 0.0257462
0.0407954 0.0244168
0.0359620 0.0230974
0.0316062 0.0218064
0.0277294 0.0205580
0.0242935 0.0193560
0.0212534 0.0182024
0.0185621 0.0170971
0.0161766 0.0160354
0.0140568 0.0150125
0.0121636 0.0140226
0.0104694 0.0130601
0.0089511 0.0121203
0.0075858 0.0111977
0.0063589 0.0102876
0.0052589 0.0093863
0.0042741 0.0084896
0.0033984 0.0075943
0.0026275 0.0066985
0.0019572 0.0057998
0.0013868 0.0048979
0.0009172 0.0039941
0.0005477 0.0030896
0.0002753 0.0021900
0.0000961 0.0013031
0.0000068 0.0004323
0.0000068 -0.0004323
0.0000961 -0.0013031
0.0002753 -0.0021900
0.0005477 -0.0030896
0.0009172 -0.0039941
0.0013868 -0.0048979
0.0019572 -0.0057998
0.0026275 -0.0066985
0.0033984 -0.0075943
0.0042741 -0.0084896
0.0052589 -0.0093863
0.0063589 -0.0102876
0.0075858 -0.0111977
0.0089511 -0.0121203
0.0104694 -0.0130601
0.0121636 -0.0140226
0.0140568 -0.0150125
0.0161766 -0.0160354
0.0185621 -0.0170971
0.0212534 -0.0182024
0.0242935 -0.0193560
0.0277294 -0.0205580
0.0316062 -0.0218064
0.0359620 -0.0230974
0.0407954 -0.0244168
0.0460908 -0.0257462
0.0518278 -0.0270688
0.0643875 -0.0296285
0.0850405 -0.0330718
0.1069011 -0.0359641
0.1294196 -0.0383406
0.1523461 -0.0402656
0.1755518 -0.0417979
0.1989606 -0.0429863
0.2225236 -0.0438707
0.2462075 -0.0444844
0.2699883 -0.0448552
0.2938485 -0.0450068
0.3177746 -0.0449597
0.3417562 -0.0447317
0.3657850 -0.0443385
0.3898541 -0.0437941
0.4139581 -0.0431107
0.4380922 -0.0422995
0.4622524 -0.0413702
0.4864351 -0.0403319
0.5106374 -0.0391925
0.5348564 -0.0379590
0.5590897 -0.0366378
0.5833350 -0.0352345
0.6075902 -0.0337540
0.6318533 -0.0322006
0.6561224 -0.0305781
0.6803957 -0.0288895
0.7046715 -0.0271373
0.7289480 -0.0253237
0.7532237 -0.0234501
0.7774967 -0.0215175
0.8017656 -0.0195266
0.8260287 -0.0174772
0.8502843 -0.0153692
0.8745303 -0.0132015
0.8987629 -0.0109733
0.9229643 -0.0086844
0.9470241 -0.0063434
0.9702755 -0.0040166
0.9901774 -0.0019724
1.0000000 -0.0009450
NACA0012
1.0000000 0.0012600
0.9895501 0.0027168
0.9698930 0.0054072
0.9462635 0.0085579
0.9204961 0.0118944
0.8939013 0.0152339
0.8670254 0.0185054
0.8400497 0.0216879
0.8130321 0.0247764
0.7859930 0.0277696
0.7589419 0.0306668
0.7318852 0.0334669
0.7048287 0.0361677
0.6777776 0.0387662
0.6507375 0.0412585
0.6237141 0.0436394
0.5967131 0.0459028
0.5697408 0.0480414
0.5428037 0.0500467
0.5159088 0.0519090
0.4890637 0.0536172
0.4622769 0.0551590
0.4355578 0.0565204
0.4089170 0.0576860
0.3823670 0.0586384
0.3559221 0.0593585
0.3295999 0.0598251
0.3034217 0.0600144
0.2774144 0.0598999
0.2516124 0.0594524
0.2260622 0.0586388
0.2008287 0.0574230
0.1760080 0.0557658
0.1517526 0.0536284
0.1283155 0.0509816
0.1133427 0.0489327
0.1061168 0.0478282
0.0990964 0.0466742
0.0923073 0.0454762
0.0857821 0.0442416
0.0795456 0.0429769
0.0736155 0.0416906
0.0680134 0.0403925
0.0627514 0.0390910
0.0578273 0.0377929
0.0532395 0.0365059
0.0489795 0.0352357
0.0450295 0.0339851
0.0413728 0.0327573
0.0379888 0.0315538
0.0348560 0.0303742
0.0319554 0.0292187
0.0292659 0.0280861
0.0267694 0.0269746
0.0244504 0.0258830
0.0222924 0.0248093
0.0202817 0.0237511
0.0184076 0.0227070
0.0166581 0.0216749
0.0150240 0.0206523
0.0134981 0.0196381
0.0120723 0.0186300
0.0107408 0.0176260
0.0094991 0.0166251
0.0083423 0.0156254
0.0072668 0.0146253
0.0062705 0.0136240
0.0053507 0.0126203
0.0045059 0.0116130
0.0037355 0.0106024
0.0030385 0.0095877
0.0024144 0.0085693
0.0018636 0.0075486
0.0013856 0.0065262
0.0009803 0.0055038
0.0006475 0.0044839
0.0003865 0.0034688
0.0001945 0.0024618
0.0000684 0.0014676
0.0000057 0.0004874
0.0000000 0.0000000
0.0000057 -0.0004874
0.0000684 -0.0014676
0.0001945 -0.0024618
0.0003865 -0.0034688
0.0006475 -0.0044839
0.0009803 -0.0055038
0.0013856 -0.0065262
0.0018636 -0.0075486
0.0024144 -0.0085693
0.0030385 -0.0095877
0.0037355 -0.0106024
0.0045059 -0.0116130
0.0053507 -0.0126203
0.0062705 -0.0136240
0.0072668 -0.0146253
0.0083423 -0.0156254
0.0094991 -0.0166251
0.0107408 -0.0176260
0.0120723 -0.0186300
0.0134981 -0.0196381
0.0150240 -0.0206523
0.0166581 -0.0216749
0.0184076 -0.0227070
0.0202817 -0.0237511
0.0222924 -0.0248093
0.0244504 -0.0258830
0.0267694 -0.0269746
0.0292659 -0.0280861
0.0319554 -0.0292187
0.0348560 -0.0303742
0.0379888 -0.0315538
0.0413728 -0.0327573
0.0450295 -0.0339851
0.0489795 -0.0352357
0.0532395 -0.0365059
0.0578273 -0.0377929
0.0627514 -0.0390910
0.0680134 -0.0403925
0.0736155 -0.0416906
0.0795456 -0.0429769
0.0857821 -0.0442416
0.0923073 -0.0454762
0.0990964 -0.0466742
0.1061168 -0.0478282
0.1133427 -0.0489327
0.1283155 -0.0509816
0.1517526 -0.0536284
0.1760080 -0.0557658
0.2008287 -0.0574230
0.2260622 -0.0586388
0.2516124 -0.0594524
0.2774144 -0.0598999
0.3034217 -0.0600144
0.3295999 -0.0598251
0.3559221 -0.0593585
0.3823670 -0.0586384
0.4089170 -0.0576860
0.4355578 -0.0565204
0.4622769 -0.0551590
0.4890637 -0.0536172
0.5159088 -0.0519090
0.5428037 -0.0500467
0.5697408 -0.0480414
0.5967131 -0.0459028
0.6237141 -0.0436394
0.6507375 -0.0412585
0.6777776 -0.0387662
0.7048287 -0.0361677
0.7318852 -0.0334669
0.7589419 -0.0306668
0.7859930 -0.0277696
0.8130321 -0.0247764
0.8400497 -0.0216879
0.8670254 -0.0185054
0.8939013 -0.0152339
0.9204961 -0.0118944
0.9462635 -0.0085579
0.9698930 -0.0054072
0.9895501 -0.0027168
1.0000000 -0.0012600
import os
import win32api
import numpy as np
from xfoil import XFoil
from xfoil.model import Airfoil
import xlwings as xw
xf = XFoil() # Create an instance of the XFoil class
@xw.func
def define(wb_path, airfoil_name):
# Read airfoil
with open(os.path.join(wb_path,airfoil_name+".dat"), "r") as f:
airfoil = f.readlines() # Read an airfoil in the same format as XFLR5 (.dat)
airfoil = [line.split() for line in airfoil] # Split strings by tab
airfoil = np.array(airfoil[1:],dtype='float64') # Convert strings in list to numpy array
xf.airfoil = Airfoil(airfoil[:,0],airfoil[:,1]) # Airfoil: Instance of the Airfoil class
# Difine analysis
xf.M = 0 # float: Mach number.
xf.n_crit = 9 # float: Critical amplification ratio
xf.xtr = (1, 1) # tuple(float, float): Top and bottom flow trip x/c locations
xf.max_iter = 100 # int: Maximum number of iterations
xf.repanel # Re-panel airfoil
@xw.func
def xf_a(alpha, Re):
xf.reset_bls # Reset the boundary layers to be reinitialized on the next analysis
xf.Re = Re # float: Reynolds number
cl, cd, cm, cp = xf.a(alpha) # Analyze airfoil at a fixed angle of attack
return cl, cd, cm, cp
@xw.func
def xf_wing(wb_path, airfoil_name, alpha,Re):
alpha = np.array(alpha).reshape(-1) # np.shape = (span_div,)
Re = np.array(Re).reshape(-1)
cl = np.zeros_like(alpha)
cd = np.zeros_like(alpha)
cm = np.zeros_like(alpha)
cp = np.zeros_like(alpha)
define(wb_path, airfoil_name)
for n in range(alpha.shape[0]):
xf.reset_bls # Reset the boundary layers to be reinitialized on the next analysis
xf.Re = Re[n] # float: Reynolds number
cl[n], cd[n], cm[n], cp[n] = xf.a(alpha[n]) # Analyze airfoil at a fixed angle of attack
cl[n] = cl[n-1] if np.isinf(cl[n]) else cl[n]
cd[n] = cd[n-1] if np.isinf(cd[n]) else cd[n]
cm[n] = cm[n-1] if np.isinf(cm[n]) else cm[n]
return cl, cd, cm, cp
def msg_box(msg):
wb = xw.Book.caller()
win32api.MessageBox(wb.app.hwnd,str(msg))
if __name__ == "__main__":
#wb = xw.Book("myproject.xlsm")
#macro = wb.macro('SampleCall')
#macro()
define("./","NACA4412")
xf_a(0,100000)
なお、マクロを動かすにはxfoilのpythonライブラリをExcelにアドインとして追加する必要がある
以上
フライトの振り返り
Gemini-Xのフライトについて振り返る
トピックは以下の2つ
桁折れ
今大会のGemini-Xの桁折れは「フライングワイヤが全く機能していなかったこと」が原因だと推察している。
フライト映像を見てみると、フライングワイヤは緩んで風になびいており、翼端のたわみ量も設計値の1.5mよりかなり大きくなっていることが分かる。(垂直尾翼のスパンが1.2mなので、映像を見る限り3.5m強はたわんでいる)
実際、設計シートでフライングワイヤなしで荷重倍数1.0の解析を行うと、翼端のたわみは3.0mほどになる(下図のたわみもフライト時のたわみの大きさとかなり近いように見える)

このフライングワイヤが全く機能していない状態でも最大応力説を用いた強度解析では桁が折れるまでにまだ余裕はあったが、材料力学の範疇を大きく超えるたわみ量になったこと、桁が7年近く倉庫で眠っていたこと、自作であること、などが影響した結果、圧縮側の上面が座屈して桁折れしてしまったのではないかと考えられる
そもそもQX-16の桁が当時の設計の2倍近い荷重を支えて数秒間定常滑空をしたこと自体が驚異的ではあるが
今回はQX-16の桁を使いまわしたためにフライングワイヤを採用することになったが、もし次があるのなら単純に2人乗り用の片持ち桁を設計する必要がある
速すぎ
もうひとつの問題は、8.0m/sの純棒飛び機を設計したはずなのに速度が出過ぎてしまったことである
当日のフライトは若干ダイブ気味に飛行しているので、対気速度も8.0m/sより大きくなっていたはずである
フライト映像を見るに対地速度で11.0m/s程度、ダイブの落差から計算しても同様に11.0m/s程度は出ていたと推定できる
この速度は機体重量に換算すると約300kg越えなので、いくら何でも速すぎることになる
揚力係数に換算すると CL=0.7 程度なので、主翼リブの取り付け角を盛大に間違えていたのではないとすると、主翼の二次構造が変形してしまっていた可能性がある
桁のねじりについては桁位置を風圧中心におくことで対策することができたが、それでもリブ自身には上に折れ曲がるような荷重がはたらいている
リブを上に折れ曲がるような荷重によって主翼の二次構造が変形した結果、翼型のキャンバーがなくなり、揚力係数が小さくなってしまったのではないかと考えられる
今回は主翼の製作工数を考えて、QX-16ごろの主翼二次構造を踏襲したが、もし次があるのなら、コード長の増加に合わせた適切な二次構造を模索して行く必要がある











コメント