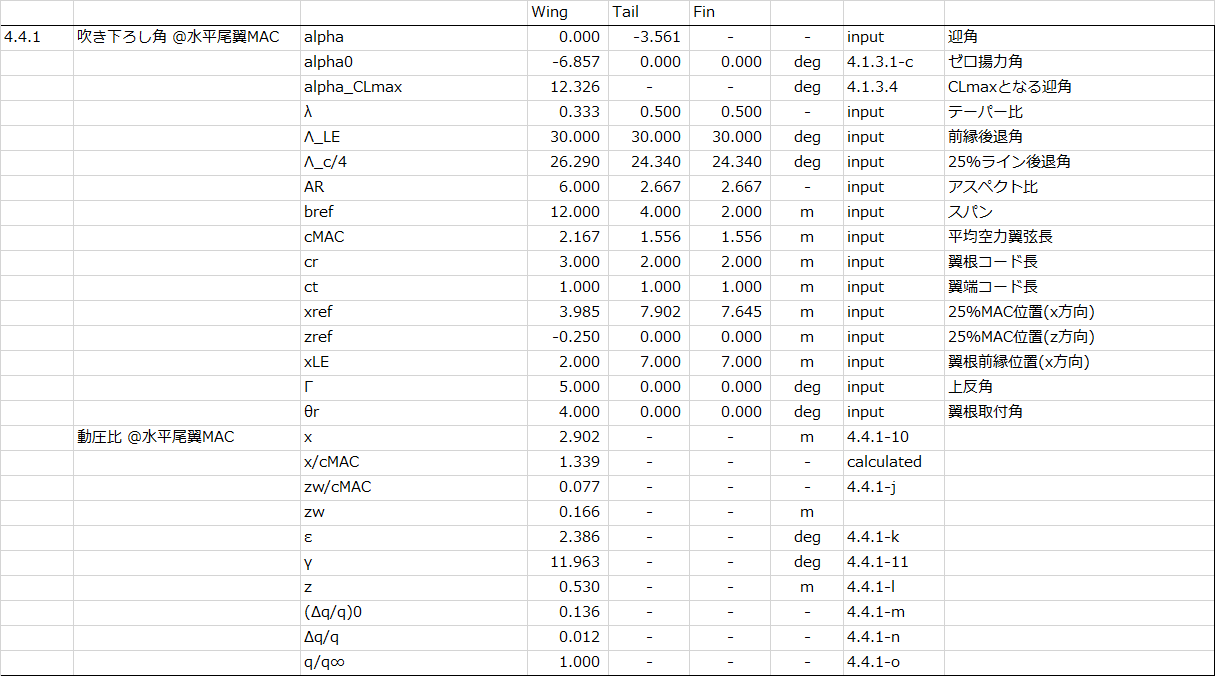
DATCOM 4.4.1 に基づいて、水平尾翼における動圧比を計算する。
はじめに
DATCOM 4.4.1 に基づいて、水平尾翼における動圧比を計算する。
PDFのページは1203ページ
Method
水平尾翼における動圧比は以下の手順で計算する。
- 翼根後端から水平尾翼MACの25%位置までの水平距離\(x\)における対称面内の後流渦の半幅\(z_{w}\)を計算する。
- 対称面内の後流渦における吹き下ろし角\(\epsilon\)を計算する。
- 後流渦から水平尾翼MACの25%位置までの垂直距離\(z\)を計算する。
- 後流渦の中心線上の位置\(x\)における動圧損失\(\left(\Delta q/q \right)_{o}\)を計算する。
- 水平尾翼MACの25%位置における動圧損失\(\Delta q/q\)を計算する。
- 水平尾翼MACの25%位置における動圧比\(q/q_{\infty}\)を計算する
(Sketch(d)改)
STEP 1
翼根後端から水平尾翼MACの25%位置までの水平距離\(x\)における対称面内の後流渦の半幅\(z_{w}\)を次の式で計算する。
\begin{align}
\frac{z_{w}}{\overline{c}}=0.68\sqrt{C_{D_{0}}\left(\frac{x}{c}+0.15\right)}
\tag{4.1.1-j}
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(x\) | m | 翼根後端から水平尾翼MACの25%位置までの水平距離。 後流渦の中心線に沿って測る。 |
| \(z_{w}\) | m | 水平尾翼MACの25%位置における対称面内の後流渦の半幅。 |
| \(C_{D_{0}}\) | - | 主翼のゼロ揚力抗力係数。 DATCOM 4.1.5.1で計算する。 |
| \(\overline{c}\) | m | 主翼の平均空力翼弦長。 DATCOM 2.2.2で計算する。 |
STEP 2
対称面内の後流渦における吹き下ろし角\(\epsilon\)を次の式で計算する。
\begin{align}
\epsilon&=\frac{1.62C_{L}}{\pi A} \tag{4.4.1-k} \\\\
C_{L}&=C_{L_{\alpha}}\left(\alpha-\alpha_{0}\right)\frac{\pi}{180}
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(\epsilon\) | deg | 対称面内の後流渦における吹き下ろし角。 |
| \(C_{L}\) | m | 主翼の揚力係数。 |
| \(C_{L_{\alpha}}\) | 1/rad | 主翼の3次元揚力傾斜。 DATCOM 4.1.3.2で計算する。 |
| \(\alpha_{0}\) | deg | ゼロ揚力角。 DATCOM 4.1.3.1で計算する。 |
| \(A\) | - | 主翼のアスペクト比。 DATCOM 2.2.2で計算する。 |
STEP 3
後流渦から水平尾翼MACの25%位置までの垂直距離\(z\)を次の式で計算する。
\begin{align}
z=x\tan{\left(\gamma+\epsilon-\alpha\right)} \tag{4.4.1-l}
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(z\) | m | 後流渦から水平尾翼MACの25%位置までの垂直距離。 |
| \(x\) | m | 翼根後端から水平尾翼MACの25%位置までの水平距離。 後流渦の中心線に沿って測る。 |
また、\(\gamma\)、\(\epsilon\)、\(\alpha\)の定義は以下の通り。
(Sketch(d))
迎角\(\alpha\)は主翼のコードラインを基準にしている点に注意する。
STEP 4
後流渦の中心線上の位置\(x\)における動圧損失\(\left(\Delta q/q \right)_{o}\)を次の式で計算する。
\begin{align}
\left(\frac{\Delta q}{q}\right)_{o}=\frac{2.42\sqrt{C_{D_{0}}}}{\frac{x}{\overline{c}}+0.30} \tag{4.4.1-m}
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(\left(\frac{\Delta q}{q}\right)_{o}\) | - | 後流渦の中心線上の位置\(x\)における動圧損失 |
| \(C_{D_{0}}\) | - | 主翼のゼロ揚力抗力係数。 DATCOM 4.1.5.1で計算する。 |
| \(x\) | m | 翼根後端から水平尾翼MACの25%位置までの水平距離。 後流渦の中心線に沿って測る。 |
| \(\overline{c}\) | m | 主翼の平均空力翼弦長。 DATCOM 2.2.2で計算する。 |
STEP 5
水平尾翼MACの25%位置における動圧損失\(\Delta q/q\)を次の式で計算する。
\begin{align}
\frac{\Delta q}{q}=\left(\frac{\Delta q}{q}\right)_{o}\cos^2{\left(\frac{\pi}{2}\frac{z}{z_{w}}\right)} \tag{4.4.1-n}
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(\frac{\Delta q}{q}\) | - | 水平尾翼MACの25%位置における動圧損失。 |
| \(\left(\frac{\Delta q}{q} \right)_{o}\) | - | 後流渦の中心線上の位置\(x\)における動圧損失 |
| \(z\) | m | 後流渦から水平尾翼MACの25%位置までの垂直距離。 |
| \(z_{w}\) | m | 水平尾翼MACの25%位置における対称面内の後流渦の半幅。 |
STEP 6
水平尾翼MACの25%位置における動圧比\(q/q_{\infty}\)を次の式で計算する。
\begin{align}
\frac{q}{q_{\infty}}=1-\frac{\Delta q}{q} \tag{4.4.1-o}
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(\frac{q}{q_{\infty}}\) | - | 水平尾翼MACの25%位置における動圧比。 |
| \(\frac{\Delta q}{q}\) | - | 水平尾翼MACの25%位置における動圧損失。 |
reference
-
制限
この手法における注意点は以下の通り
- 遷音速域であること。
- 揚力傾斜の線形の範囲内であること。
- 得られるのは対称面内の動圧比であること。
Sample
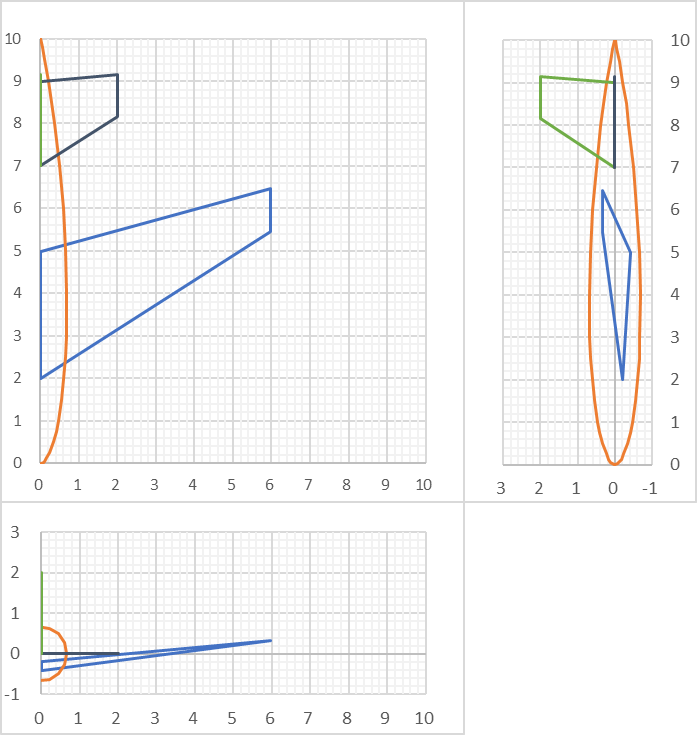
OpenVSPのExample FileにあるPod Planeについて、実際に計算してみる
↓計算に使用したエクセルファイル(マクロ付き)
↓計算結果
以上
おわりに
DATCOM 4.4.1 に基づいて、尾翼における吹き下ろし角の大きさを計算した。
↓次





コメント