安定軸で計算した動安定微係数を機体軸に変換する方法を説明する
はじめに
飛行力学でよく用いられる座標系として機体軸と安定軸がある
機体軸は機体に固定された座標系で、フライトシミュレーターなどで用いられる
一方、対称面内に投影した速度ベクトルとX軸が一致するように機体軸をY軸回りに\(\alpha\)だけ回転させた座標系が安定軸である(下図の赤矢印)
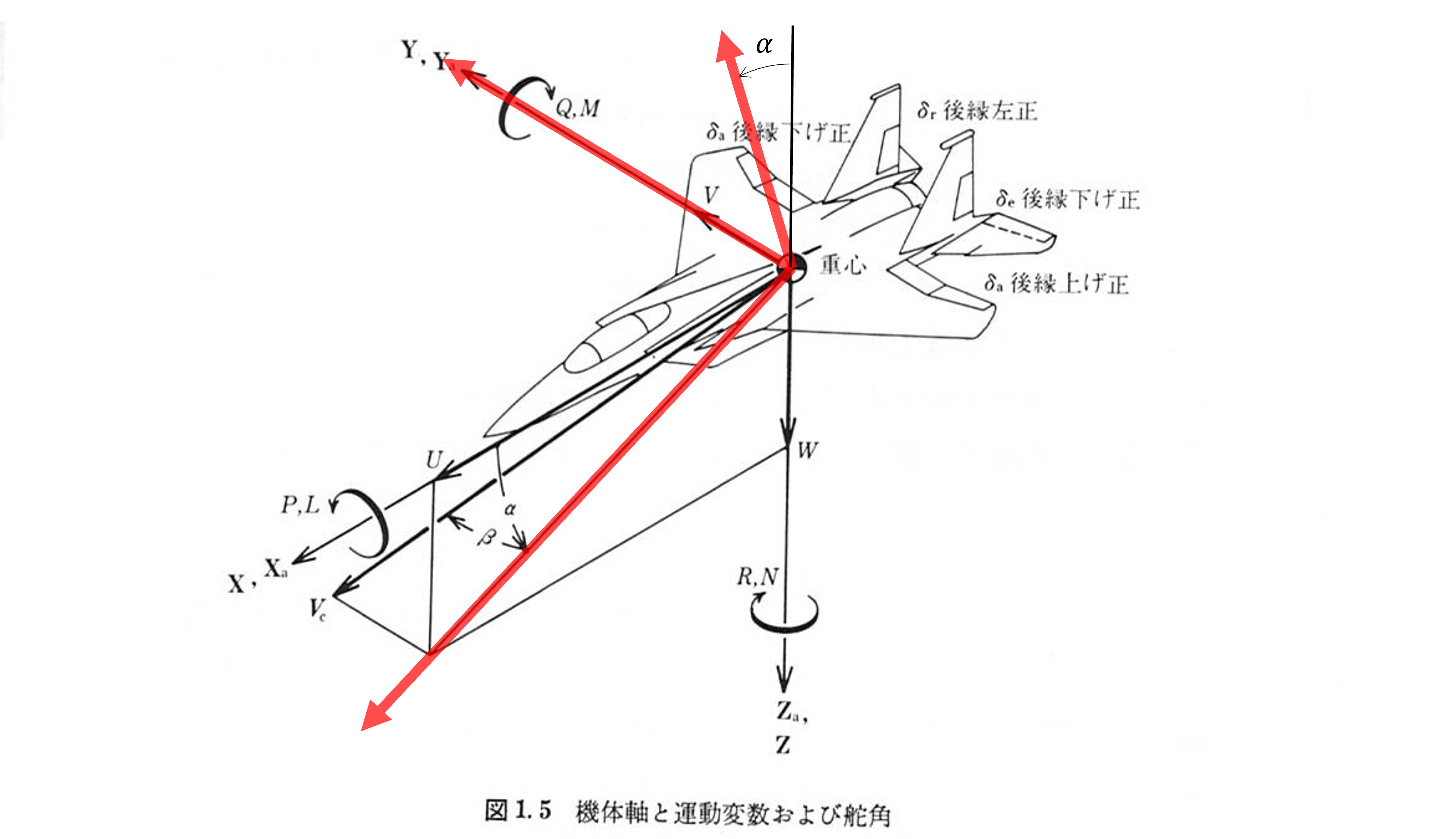
安定軸は安定微係数などを計算するときによく用いられる(揚力と抗力がそれぞれ常にZ軸とX軸に平行になるので、数式が簡単になる)
実際、白本やDATCOMの安定微係数は安定軸に対して計算されている
巡航状態(\(\alpha=0^\circ\))のみを考えるなら、機体軸と安定軸は一致するため、安定軸で計算された安定微係数をそのまま機体軸で計算されるフライトシミュレーターに組み込むことができるが、それなりの迎角範囲に対してシミュレーションをするときは、安定軸で計算された安定微係数を機体軸に変換してから組み込む必要がある
安定軸から機体軸への変換方法
安定軸から機体軸への変換には以下の式を使用する
縦
\begin{align}
\left[\begin{array}{c}
C_{x_{q'}} \\ C_{z_{q'}}
\end{array}\right] &=
\left[\begin{array} {cc}
-\cos{\alpha} & \sin{\alpha}\\
-\sin{\alpha} & -\cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c}
C_{D_{q}} \\ C_{L_{q}}
\end{array}\right] \\\\
C_{m_{q'}}&=C_{m_{q}}
\end{align}
横・方向(無印が安定軸、プライム付きが機体軸)
\begin{align}
\left[\begin{array}{c}
C_{y_{p'}} \\ C'_{y_{r'}}
\end{array}\right] &=
\left[\begin{array} {cc}
\cos{\alpha} & -\sin{\alpha} \\
\sin{\alpha} & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c}
C_{y_{p}} \\ C_{y_{r}}
\end{array}\right] \\\\
\left[\begin{array}{c}
C_{l_{p'}} \\ C_{n_{p'}} \\ C_{l_{r'}} \\ C_{n_{r'}}
\end{array}\right] &=
\left[\begin{array} {cccc}
\cos{\alpha}^2 & -\sin{\alpha}\cos{\alpha} & -\sin{\alpha}\cos{\alpha} & \sin{\alpha} ^2 \\
\sin{\alpha}\cos{\alpha} & \cos{\alpha}^2 & -\sin{\alpha} ^2 & -\sin{\alpha}\cos{\alpha} \\
\sin{\alpha}\cos{\alpha} & -\sin{\alpha} ^2 & \cos{\alpha}^2 & -\sin{\alpha}\cos{\alpha} \\
\sin{\alpha}^2 & \sin{\alpha}\cos{\alpha} & \sin{\alpha}\cos{\alpha} & \cos{\alpha} ^2 \\
\end{array}\right]
\left[\begin{array}{c}
C_{l_{p}} \\ C_{n_{p}} \\ C_{l_{r}} \\ C_{n_{r}}
\end{array}\right]
\end{align}
それでは説明していく
力とモーメントと角速度のベクトルの座標変換
安定軸では、機体にはたらく力、モーメント、角速度のベクトルは以下のようにあらわされる
\begin{align}
\mathbf{F}=\left[\begin{array}{c} -C_{D} \\ C_{y} \\ -C_{L} \end{array}\right], \qquad
\mathbf{M}=\left[\begin{array}{c} C_{l} \\ C_{m} \\ C_{n} \end{array}\right], \qquad
\boldsymbol{\omega}=\left[\begin{array}{c} p \\ q \\ r \end{array}\right]
\end{align}
機体軸では、機体にはたらく力、モーメント、角速度のベクトルは以下のようにあらわされる
\begin{align}
\mathbf{F'}=\left[\begin{array}{c} C_{x'} \\ C_{y'} \\ C_{z'} \end{array}\right], \qquad
\mathbf{M'}=\left[\begin{array}{c} C_{l'} \\ C_{m'} \\ C_{n'} \end{array}\right], \qquad
\boldsymbol{\omega'}=\left[\begin{array}{c} p' \\ q' \\ r' \end{array}\right]
\end{align}
安定軸から機体軸への変換は、Y軸回りに\(\alpha\)だけ回転させればよいので、座標変換行列は以下のようになる
\begin{align}
\mathbf{R}=\left[\begin{array}{ccc}
\cos{\alpha} & 0 & -\sin{\alpha} \\
0 & 1 & 0 \\
\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\end{align}
ちなみに、座標変換行列は正規直交行列なので、転置行列と逆行列は一致する
\begin{align}
\mathbf{R}^{T}=\mathbf{R}^{-1}
\end{align}
安定軸から機体軸への力、モーメント、角速度のベクトルの変換は以下のようになる
\begin{align}
& \mathbf{F'}=\mathbf{R}\mathbf{F} \\\\
& \mathbf{M'}=\mathbf{R}\mathbf{M} \\\\
& \boldsymbol{\omega'}=\mathbf{R}\boldsymbol{\omega}
\end{align}
書き下すと
\begin{align}
& \left[\begin{array}{c} C_{x'} \\ C_{y'} \\ C_{z'} \end{array}\right]
=\left[\begin{array}{ccc}
\cos{\alpha} & 0 & -\sin{\alpha} \\
0 & 1 & 0 \\
\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c} -C_{D} \\ C_{y} \\ -C_{L} \end{array}\right] \\\\
& \left[\begin{array}{c} C_{l'} \\ C_{m'} \\ C_{n'} \end{array}\right]
=\left[\begin{array}{ccc}
\cos{\alpha} & 0 & -\sin{\alpha} \\
0 & 1 & 0 \\
\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c} C_{l} \\ C_{m} \\ C_{n} \end{array}\right] \\\\
& \left[\begin{array}{c} p' \\ q' \\ r' \end{array}\right]
=\left[\begin{array}{ccc}
\cos{\alpha} & 0 & -\sin{\alpha} \\
0 & 1 & 0 \\
\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c} p \\ q \\ r \end{array}\right] \\\\
\end{align}
偏微分の座標変換
安定軸回りの角速度による偏微分と機体軸回りの角速度による偏微分は次のように表される
\begin{align}
\nabla=\left[\begin{array}{c} \frac{\partial}{\partial p} \\ \frac{\partial}{\partial q} \\ \frac{\partial}{\partial r} \end{array}\right], \qquad
\nabla'=\left[\begin{array}{c} \frac{\partial}{\partial p'} \\ \frac{\partial}{\partial q'} \\ \frac{\partial}{\partial r'} \end{array}\right]
\end{align}
安定軸回りの角速度による偏微分から機体軸回りの角速度による偏微分への変換は以下のようになる
\begin{align}
\nabla'=\mathbf{R}\nabla
\end{align}
書き下すと
\begin{align}
& \left[\begin{array}{c} \frac{\partial}{\partial p'} \\ \frac{\partial}{\partial q'} \\ \frac{\partial}{\partial r'} \end{array}\right]=\left[\begin{array}{ccc}
\cos{\alpha} & 0 & -\sin{\alpha} \\
0 & 1 & 0 \\
\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c} \frac{\partial}{\partial p} \\ \frac{\partial}{\partial q} \\ \frac{\partial}{\partial r} \end{array}\right]
\end{align}
先に説明した力、モーメント、角速度の変換と同じである
機体軸の角速度は安定軸の角速度の関数として表されるので、全微分の考え方を用いると、機体軸回りの角速度による偏微分は以下のように表される
\begin{align}
& \frac{\partial}{\partial p'}=\frac{\partial p}{\partial p'}\frac{\partial}{\partial p}
+\frac{\partial q}{\partial p'}\frac{\partial}{\partial q}
+\frac{\partial r}{\partial p'}\frac{\partial}{\partial r} \\\\
& \frac{\partial}{\partial q'}=\frac{\partial p}{\partial q'}\frac{\partial}{\partial p}
+\frac{\partial q}{\partial q'}\frac{\partial}{\partial q}
+\frac{\partial r}{\partial q'}\frac{\partial}{\partial r} \\\\
& \frac{\partial}{\partial r'}=\frac{\partial p}{\partial r'}\frac{\partial}{\partial p}
+\frac{\partial q}{\partial r'}\frac{\partial}{\partial q}
+\frac{\partial r}{\partial r'}\frac{\partial}{\partial r} \\\\
\end{align}
行列形式で表すと
\begin{align}
& \left[\begin{array}{c} \frac{\partial}{\partial p'} \\ \frac{\partial}{\partial q'} \\ \frac{\partial}{\partial r'} \end{array}\right]
=\left[\begin{array}{ccc}
\frac{\partial p}{\partial p'} & \frac{\partial q}{\partial p'} & \frac{\partial r}{\partial p'} \\
\frac{\partial p}{\partial q'} & \frac{\partial q}{\partial q'} & \frac{\partial r}{\partial q'} \\
\frac{\partial p}{\partial r'} & \frac{\partial q}{\partial r'} & \frac{\partial r}{\partial r'} \\
\end{array}\right]
\left[\begin{array}{c} \frac{\partial}{\partial p} \\ \frac{\partial}{\partial q} \\ \frac{\partial}{\partial r} \end{array}\right] \\\\
\end{align}
まとめると
\begin{align}
\nabla'=\left(\nabla' \boldsymbol{\omega}^{T} \right) \nabla
\end{align}
ここで、\(\boldsymbol{\omega}=\mathbf{R}^{-1}\boldsymbol{\omega'}=\mathbf{R}^{T}\boldsymbol{\omega'}\) なので
\begin{align}
\nabla'
&=\left(\nabla' \boldsymbol{\omega}^{T} \right) \nabla
=\left\{\nabla' \left(\mathbf{R}^{T}\boldsymbol{\omega'}\right)^{T} \right\} \nabla \\\\
&=\left\{\nabla' \boldsymbol{\omega'}^{T} \mathbf{R} \right\} \nabla \\\\
\end{align}
\(\nabla' \boldsymbol{\omega'}^{T}=\mathbf{I}\) より
\begin{align}
\nabla'
&=\left\{\left(\nabla' \boldsymbol{\omega'}^{T}\right) \mathbf{R} \right\} \nabla
=\mathbf{R} \nabla \\\\
\end{align}
書き下すと
\begin{align}
& \left[\begin{array}{c} \frac{\partial}{\partial p'} \\ \frac{\partial}{\partial q'} \\ \frac{\partial}{\partial r'} \end{array}\right]=\left[\begin{array}{ccc}
\cos{\alpha} & 0 & -\sin{\alpha} \\
0 & 1 & 0 \\
\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c} \frac{\partial}{\partial p} \\ \frac{\partial}{\partial q} \\ \frac{\partial}{\partial r} \end{array}\right]
\end{align}
↓ここで使ったテンソル解析についてはこちら
↓参考

力についての動安定微係数の座標変換
安定軸における力についての動安定微係数は以下のようになる
\begin{align}
\nabla \mathbf{F}^{T}
&=
\left[\begin{array}{c} \frac{\partial}{\partial p} \\ \frac{\partial}{\partial q} \\ \frac{\partial}{\partial r} \end{array}\right]
\left[\begin{array}{ccc} -C_{D} & C_{m} & -C_{L} \end{array}\right]
=
\left[\begin{array}{ccc}
-\frac{\partial C_{D}}{\partial p} & \frac{\partial C_{y}}{\partial p} & -\frac{\partial C_{L}}{\partial p} \\
-\frac{\partial C_{D}}{\partial q} & \frac{\partial C_{y}}{\partial q} & -\frac{\partial C_{L}}{\partial q} \\
-\frac{\partial C_{D}}{\partial r} & \frac{\partial C_{y}}{\partial r} & -\frac{\partial C_{L}}{\partial r}\\
\end{array}\right]
=
\left[\begin{array}{ccc}
-C_{D_{p}} & C_{y_{p}} & -C_{L_{p}} \\
-C_{D_{q}} & C_{y_{q}} & -C_{L_{q}} \\
-C_{D_{r}} & C_{y_{r}} & -C_{L_{r}} \\
\end{array}\right]
\end{align}
機体軸におけるモーメントについての安定微係数は以下のようになる
\begin{align}
\nabla' \mathbf{M'}^{T}
&=
\left[\begin{array}{c} \frac{\partial}{\partial p'} \\ \frac{\partial}{\partial q'} \\ \frac{\partial}{\partial r'} \end{array}\right]
\left[\begin{array}{ccc} C_{x'} & C_{y'} & C_{z'} \end{array}\right]
=
\left[\begin{array}{ccc}
\frac{\partial C_{x'}}{\partial p'} & \frac{\partial C_{y'}}{\partial p'} & \frac{\partial C_{z'}}{\partial p'} \\
\frac{\partial C_{x'}}{\partial q'} & \frac{\partial C_{y'}}{\partial q'} & \frac{\partial C_{z'}}{\partial q'} \\
\frac{\partial C_{x'}}{\partial r'} & \frac{\partial C_{y'}}{\partial r'} & \frac{\partial C_{z'}}{\partial r'}\\
\end{array}\right]
=
\left[\begin{array}{ccc}
C_{x_{p'}} & C_{y_{p'}} & C_{z_{p'}} \\
C_{x_{q'}} & C_{y_{q'}} & C_{z_{q'}} \\
C_{x_{r'}} & C_{y_{r'}} & C_{z_{r'}} \\
\end{array}\right]
\end{align}
機体軸から安定軸への変換を考えると、以下のようになる
\begin{align}
\nabla' \mathbf{F'}^{T}
=\left(\mathbf{R}\nabla\right) \left(\mathbf{R}\mathbf{F}\right)^{T}
=\mathbf{R}\nabla \mathbf{F}^{T} \mathbf{R}^{T}
=\mathbf{R}\left(\nabla \mathbf{F}^{T}\right) \mathbf{R}^{T}
\end{align}
書き下すと
\begin{align}
\left[\begin{array}{ccc}
C_{x_{p'}} & C_{y_{p'}} & C_{z_{p'}} \\
C_{x_{q'}} & C_{y_{q'}} & C_{z_{q'}} \\
C_{x_{r'}} & C_{y_{r'}} & C_{z_{r'}} \\
\end{array}\right]=
\left[\begin{array}{ccc}
\cos{\alpha} & 0 & -\sin{\alpha} \\
0 & 1 & 0 \\
\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{ccc}
-C_{D_{p}} & C_{y_{p}} & -C_{L_{p}} \\
-C_{D_{q}} & C_{y_{q}} & -C_{L_{q}} \\
-C_{D_{r}} & C_{y_{r}} & -C_{L_{r}} \\
\end{array}\right]
\left[\begin{array}{ccc}
\cos{\alpha} & 0 & \sin{\alpha} \\
0 & 1 & 0 \\
-\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\end{align}
縦と横・方向の運動は分離できるので、\(C_{D_{p}}=C_{D_{r}}=C_{y_{q}}=C_{L_{p}}=C_{L_{r}}=0\)、\(C_{x_{p'}}=C_{x_{r'}}=C_{y_{q'}}=C_{z_{p}}=C_{z_{r}}=0\) として頑張って計算すると、以下のようになる
\begin{align}
&C_{x_{q'}}=-C_{D_{q}}\cos{\alpha}+C_{L_{q}}\sin{\alpha} \\\\
&C_{z_{q'}}=-C_{D_{q}}\sin{\alpha}-C_{L_{q}}\cos{\alpha} \\\\
&C_{y_{p'}}=C_{y_{p}}\cos{\alpha}-C_{y_{r}}\sin{\alpha} \\\\
&C'_{y_{r'}}=C_{y_{p}}\sin{\alpha}+C_{y_{r}}\cos{\alpha} \\\\
\end{align}
行列形式にまとめると
\begin{align}
\left[\begin{array}{c}
C_{x_{q'}} \\ C_{z_{q'}}
\end{array}\right] &=
\left[\begin{array} {cc}
-\cos{\alpha} & \sin{\alpha}\\
-\sin{\alpha} & -\cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c}
C_{D_{q}} \\ C_{L_{q}}
\end{array}\right] \\\\
\left[\begin{array}{c}
C_{y_{p'}} \\ C'_{y_{r'}}
\end{array}\right] &=
\left[\begin{array} {cc}
\cos{\alpha} & -\sin{\alpha} \\
\sin{\alpha} & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c}
C_{y_{p}} \\ C_{y_{r}}
\end{array}\right]
\end{align}
モーメントについての動安定微係数の座標変換
安定軸におけるモーメントについての動安定微係数は以下のようになる
\begin{align}
\nabla \mathbf{M}^{T}
&=
\left[\begin{array}{c} \frac{\partial}{\partial p} \\ \frac{\partial}{\partial q} \\ \frac{\partial}{\partial r} \end{array}\right]
\left[\begin{array}{ccc} C_{l} & C_{m} & C_{n} \end{array}\right]
=
\left[\begin{array}{ccc}
\frac{\partial C_{l}}{\partial p} & \frac{\partial C_{m}}{\partial p} & \frac{\partial C_{n}}{\partial p} \\
\frac{\partial C_{l}}{\partial q} & \frac{\partial C_{m}}{\partial q} & \frac{\partial C_{n}}{\partial q} \\
\frac{\partial C_{l}}{\partial r} & \frac{\partial C_{m}}{\partial r} & \frac{\partial C_{n}}{\partial r}\\
\end{array}\right]
=
\left[\begin{array}{ccc}
C_{l_{p}} & C_{m_{p}} & C_{n_{p}} \\
C_{l_{q}} & C_{m_{q}} & C_{n_{q}} \\
C_{l_{r}} & C_{m_{r}} & C_{n_{r}} \\
\end{array}\right]
\end{align}
機体軸におけるモーメントについての安定微係数は以下のようになる
\begin{align}
\nabla' \mathbf{M'}^{T}
&=
\left[\begin{array}{c} \frac{\partial}{\partial p'} \\ \frac{\partial}{\partial q'} \\ \frac{\partial}{\partial r'} \end{array}\right]
\left[\begin{array}{ccc} C_{l'} & C_{m'} & C_{n'} \end{array}\right]
=
\left[\begin{array}{ccc}
\frac{\partial C_{l'}}{\partial p'} & \frac{\partial C_{m'}}{\partial p'} & \frac{\partial C_{n'}}{\partial p'} \\
\frac{\partial C_{l'}}{\partial q'} & \frac{\partial C_{m'}}{\partial q'} & \frac{\partial C_{n'}}{\partial q'} \\
\frac{\partial C_{l'}}{\partial r'} & \frac{\partial C_{m'}}{\partial r'} & \frac{\partial C_{n'}}{\partial r'}\\
\end{array}\right]
=
\left[\begin{array}{ccc}
C_{l_{p'}} & C_{m_{p'}} & C_{n_{p'}} \\
C_{l_{q'}} & C_{m_{q'}} & C_{n_{q'}} \\
C_{l_{r'}} & C_{m_{r'}} & C_{n_{r'}} \\
\end{array}\right]
\end{align}
機体軸から安定軸への変換を考えると、以下のようになる
\begin{align}
\nabla' \mathbf{M'}^{T}
=\left(\mathbf{R}\nabla\right) \left(\mathbf{R}\mathbf{M}\right)^{T}
=\mathbf{R}\nabla \mathbf{M}^{T} \mathbf{R}^{T}
=\mathbf{R}\left(\nabla \mathbf{M}^{T}\right) \mathbf{R}^{T}
\end{align}
書き下すと
\begin{align}
\left[\begin{array}{ccc}
C_{l_{p'}} & C_{m_{p'}} & C_{n_{p'}} \\
C_{l_{q'}} & C_{m_{q'}} & C_{n_{q'}} \\
C_{l_{r'}} & C_{m_{r'}} & C_{n_{r'}} \\
\end{array}\right]=
\left[\begin{array}{ccc}
\cos{\alpha} & 0 & -\sin{\alpha} \\
0 & 1 & 0 \\
\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{ccc}
C_{l_{p}} & C_{m_{p}} & C_{n_{p}} \\
C_{l_{q}} & C_{m_{q}} & C_{n_{q}} \\
C_{l_{r}} & C_{m_{r}} & C_{n_{r}} \\
\end{array}\right]
\left[\begin{array}{ccc}
\cos{\alpha} & 0 & \sin{\alpha} \\
0 & 1 & 0 \\
-\sin{\alpha} & 0 & \cos{\alpha} \\
\end{array}\right]
\end{align}
縦と横・方向の運動は分離できるので、\(C_{l_{q}}=C_{m_{p}}=C_{m_{r}}=C_{n_{q}}=0\)、\(C_{l_{q'}}=C_{m_{p'}}=C_{m_{r'}}=C_{n_{q'}}=0\) として頑張って計算すると、以下のようになる
\begin{align}
&C_{l_{p'}}=C_{l_{p}}\cos{\alpha}^{2}-\left(C_{l_{r}}+C_{n_{p}}\right)\sin{\alpha}\cos{\alpha}+C_{n_{r}}\sin{\alpha}^{2} \\\\
&C_{n_{p'}}=C_{n_{p}}\cos{\alpha}^{2}-\left(C_{n_{r}}-C_{l_{p}}\right)\sin{\alpha}\cos{\alpha}-C_{l_{r}}\sin{\alpha}^{2} \\\\
&C_{m_{q'}}=C_{m_{q}} \\\\
&C_{l_{r'}}=C_{l_{r}}\cos{\alpha}^{2}+\left(C_{l_{p}}-C_{n_{r}}\right)\sin{\alpha}\cos{\alpha}-C_{n_{p}}\sin{\alpha}^{2} \\\\
&C_{n_{r'}}=C_{n_{r}}\cos{\alpha}^{2}+\left(C_{n_{p}}+C_{l_{r}}\right)\sin{\alpha}\cos{\alpha}+C_{l_{p}}\sin{\alpha}^{2} \\\\
\end{align}
行列形式にまとめると
\begin{align}
C_{m_{q'}} &= C_{m_{q}} \\\\
\left[\begin{array}{c}
C_{l_{p'}} \\ C_{n_{p'}} \\ C_{l_{r'}} \\ C_{n_{r'}}
\end{array}\right] &=
\left[\begin{array} {cccc}
\cos{\alpha}^2 & -\sin{\alpha}\cos{\alpha} & -\sin{\alpha}\cos{\alpha} & \sin{\alpha} ^2 \\
\sin{\alpha}\cos{\alpha} & \cos{\alpha}^2 & -\sin{\alpha} ^2 & -\sin{\alpha}\cos{\alpha} \\
\sin{\alpha}\cos{\alpha} & -\sin{\alpha} ^2 & \cos{\alpha}^2 & -\sin{\alpha}\cos{\alpha} \\
\sin{\alpha}^2 & \sin{\alpha}\cos{\alpha} & \sin{\alpha}\cos{\alpha} & \cos{\alpha} ^2 \\
\end{array}\right]
\left[\begin{array}{c}
C_{l_{p}} \\ C_{n_{p}} \\ C_{l_{r}} \\ C_{n_{r}}
\end{array}\right]
\end{align}
おわりに
安定軸で計算した動安定微係数を機体軸に変換する方法を説明した
↓関連
↓権威






コメント