XFLR5の三次元解析結果から安定微係数を計算するExcelファイルについて説明する
使用するXFLR5のバージョンはv6.48
はじめに
今回は,XFLR5の三次元解析の出力から航空機の安定微係数を計算するExcelファイルについて説明する
今回作成したExcelファイルのダウンロードはこちら
最終的には,鳥人間コンテストの滑空機部門を想定したフライトシミュレーター「BRSimulator for Glider」の機体実装に必要なデータをそろえることを目的としている
機体実装に必要な機体諸元はこれ
| 変数名 | 型 | 説明 | 単位 |
| Rigidbody.mass | float | 全備重量 | kg |
| Rigidbody.centerOfMass | Vector3 | 重心位置 | m |
| Rigidbody.inertiaTensor | Vector3 | 重心まわりの主慣性モーメント | kg m^2 |
| Rigidbody.inertiaTensorRotation | Quaternion | 慣性主軸への回転を表すクォータニオン | - |
| Airspeed0 | float | 設計速度 | m/s |
| alpha0 | float | 設計迎角 | deg |
| CDp0 | float | 全機有害抗力係数の最小値 | - |
| Cmw0 | float | 主翼空力中心回りの主翼ピッチングモーメント係数 | - |
| CLMAX | float | 主翼および尾翼の最大揚力係数(共通) | - |
| Sw | float | 主翼翼面積 | m^2 |
| bw | float | 主翼翼幅 | m |
| cMAC | float | 主翼平均空力翼弦長 | m |
| aw | float | 主翼三次元揚力傾斜 | 1/deg |
| hw | float | 主翼空力中心と全機重心の距離(cMACで無次元化) | - |
| ew | float | 主翼翼効率(楕円翼を1としたときの誘導抗力の大きさ) | - |
| Downwash | bool | 吹きおろしの計算を行うかどうか(通常配置: true,T字尾翼: false) | - |
| St | float | 水平尾翼面積 | m^2 |
| at | float | 水平尾翼三次元揚力傾斜 | 1/deg |
| lt | float | 水平尾翼空力中心と全機重心の距離 | m |
| deMAX | float | エレベーターの最大舵角 | deg |
| tau | float | 舵面の効きを表す係数(白本:p.83) | - |
| drMAX | float | ラダーの最大舵角 | deg |
| CGEMIN | float | 地面効果係数の最小値(0<CGEMIN<1) | - |
| Cyb,Clb,Cnb | float | 横滑りに関する安定微係数 | 1/deg |
| Cyp, Clp, Cnp | float | ロール角速度に関する安定微係数 | 1/rad |
| Cyr,Clr,Cnr | float | ヨー角速度に関する安定微係数 | 1/rad |
| Cydr,Cldr,Cndr | float | ラダー舵角に関する安定微係数 | 1/deg |
↓XFLR5を使った3次元解析の方法はこちら
今回はQX-20を使って説明していく
それではいってみよう
準備するもの
まず,XFLR5で3次元解析を行い,以下のデータを準備する
- 主翼の3次元解析結果の.txtファイル(設計速度・迎角におけるOnPoint)
- 主翼・水平尾翼・垂直尾翼の.xwimpファイル
1つずつ説明していく
主翼の3次元解析結果の.txtファイル(設計速度・迎角におけるOnPoint)
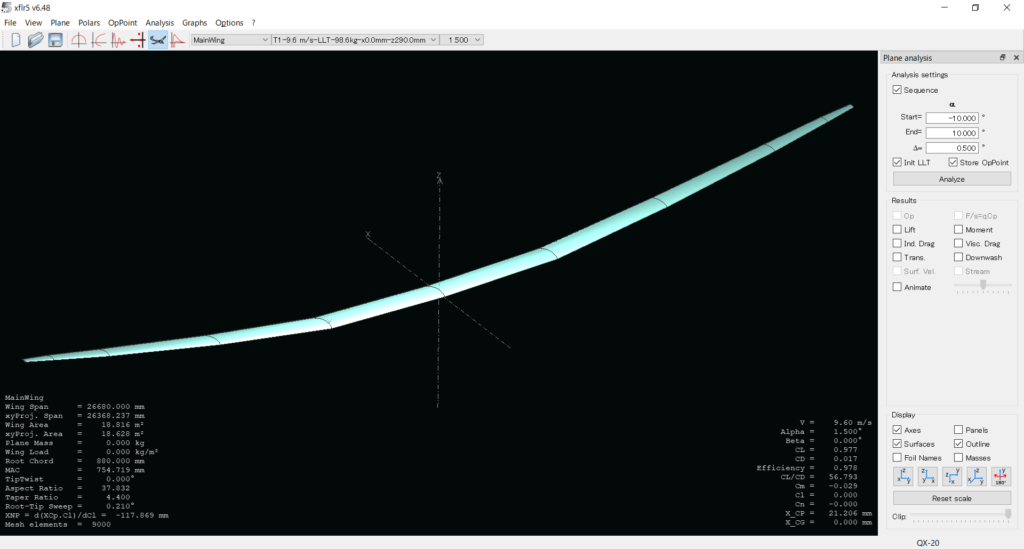
1つ目に関しては,QX-20の主翼をPolar Type1(速度9.6 [m/s],迎角-10~15 [deg]),Analysis MethodをLLT (Wing Only) で計算し,迎角1.5 [deg]のOnPointを出力した
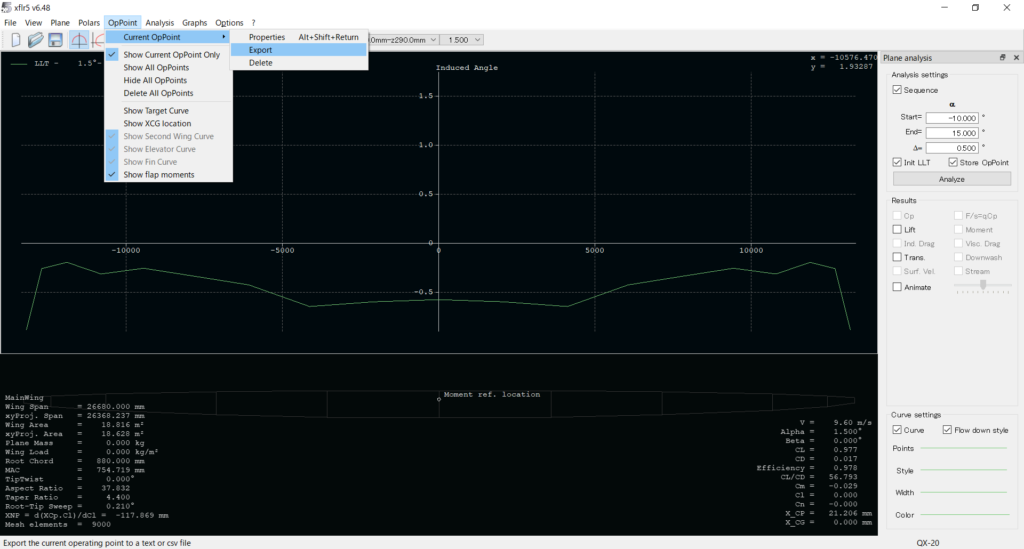
上のメニューから,OnPoint>Current OnPoint>Exportをクリックすると以下のような.txtファイルを出力できる
xflr5 v6.48
MainWing
T1-9.6 m/s-LLT-98.6kg-x0.0mm-z290.0mm
QInf = 9.600000 m/s
Alpha = 1.500000
Beta = 0.000°
Phi = 0.000°
Ctrl = 0.000
CL = 0.976551
Cy = 0.000000
Cd = 0.017195 ICd = 0.008206 PCd = 0.008989
Cl = 1.99858e-17
Cm = -0.0294774
ICn = -0.000000 PCn = -0.000000
XCP = 0.021206 YCP = 0.000000 ZCP = 0.000000
XNP = 0.000000
Bending = 0.000000
Main Wing
y-span Chord Ai Cl PCd ICd CmGeom CmAirf@chord/4 XTrtop XTrBot XCP BM
-13.1758 0.2298 -0.881 0.573215 0.015231 0.008814 -0.043768 -0.103978 0.7459 1.0000 0.4289 0.0000
-12.6871 0.3186 -0.260 0.715365 0.011393 0.003246 -0.052165 -0.100992 0.6786 1.0000 0.3868 1.1272
-11.8860 0.4185 -0.196 0.785593 0.009925 0.002685 -0.046940 -0.099165 0.6241 1.0000 0.3710 9.2897
-10.7923 0.5303 -0.315 0.834768 0.009227 0.004589 -0.036098 -0.097748 0.5758 1.0000 0.3612 38.7087
-9.4328 0.6168 -0.257 0.884883 0.009121 0.003964 -0.030136 -0.096338 0.5333 1.0000 0.3524 114.8674
-7.8411 0.7136 -0.336 0.926053 0.009061 0.005432 -0.022351 -0.095230 0.4955 1.0000 0.3458 272.8015
-6.0562 0.7937 -0.427 0.983423 0.008958 0.007327 -0.022548 -0.101626 0.5016 1.0000 0.3456 556.6917
-4.1223 0.8616 -0.647 1.040795 0.008615 0.011745 -0.030506 -0.113733 0.5457 1.0000 0.3515 1014.8514
-2.0868 0.8800 -0.599 1.076113 0.008623 0.011243 -0.031815 -0.116839 0.5526 1.0000 0.3506 1691.3656
-0.0000 0.8800 -0.576 1.090200 0.008699 0.010962 -0.031874 -0.116768 0.5491 1.0000 0.3489 2603.4337
2.0868 0.8800 -0.599 1.076113 0.008623 0.011243 -0.031815 -0.116839 0.5526 1.0000 0.3506 1691.3656
4.1223 0.8616 -0.647 1.040795 0.008615 0.011745 -0.030506 -0.113733 0.5457 1.0000 0.3515 1014.8514
6.0562 0.7937 -0.427 0.983423 0.008958 0.007327 -0.022548 -0.101626 0.5016 1.0000 0.3456 556.6917
7.8411 0.7136 -0.336 0.926053 0.009061 0.005432 -0.022351 -0.095230 0.4955 1.0000 0.3458 272.8015
9.4328 0.6168 -0.257 0.884883 0.009121 0.003964 -0.030136 -0.096338 0.5333 1.0000 0.3524 114.8674
10.7923 0.5303 -0.315 0.834768 0.009227 0.004589 -0.036098 -0.097748 0.5758 1.0000 0.3612 38.7087
11.8860 0.4185 -0.196 0.785593 0.009925 0.002685 -0.046940 -0.099165 0.6241 1.0000 0.3710 9.2897
12.6871 0.3186 -0.260 0.715365 0.011393 0.003246 -0.052165 -0.100992 0.6786 1.0000 0.3868 1.1272
13.1758 0.2298 -0.881 0.573215 0.015231 0.008814 -0.043768 -0.103978 0.7459 1.0000 0.4289 0.0000主翼・水平尾翼・垂直尾翼の.xwimpファイル
2つ目に関しては,上のメニューのPlane>Current Plane>Edit ○○で主翼,水平尾翼,垂直尾翼それぞれのウィンドウを開き,右下のOther>Export Wing (deprecated, use XML)をクリックすると出力できる
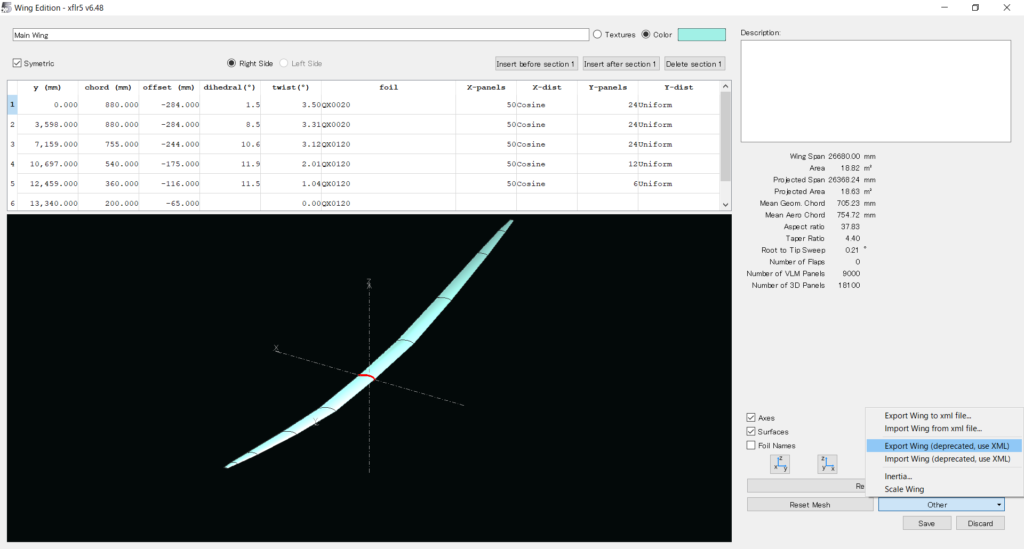
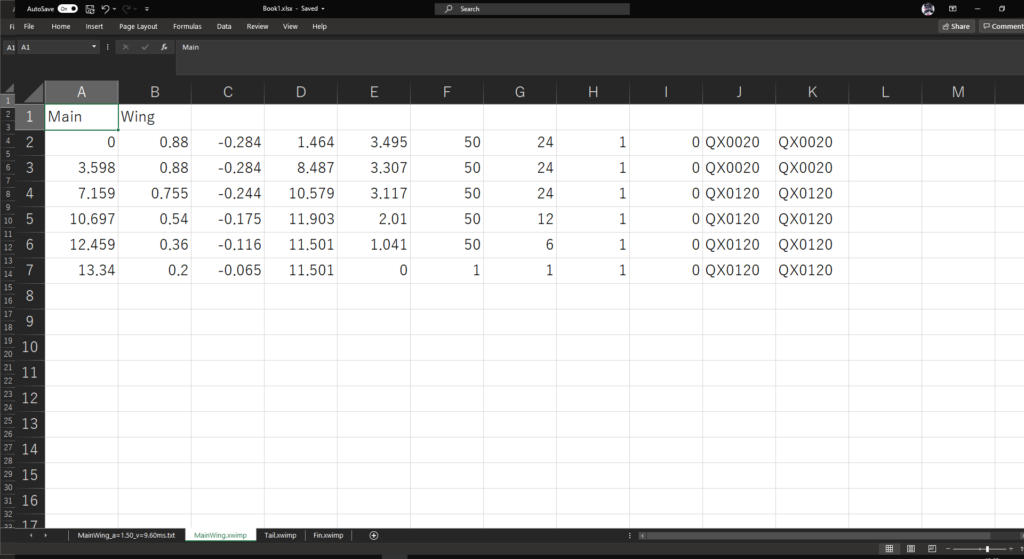
QX-20では以下のようなファイルになった
Main Wing
0 0.88 -0.284 1.464 3.495 50 24 1 0 QX0020 QX0020
3.598 0.88 -0.284 8.487 3.307 50 24 1 0 QX0020 QX0020
7.159 0.755 -0.244 10.579 3.117 50 24 1 0 QX0120 QX0120
10.697 0.54 -0.175 11.903 2.01 50 12 1 0 QX0120 QX0120
12.459 0.36 -0.116 11.501 1.041 50 6 1 0 QX0120 QX0120
13.34 0.2 -0.065 11.501 0 1 1 1 0 QX0120 QX0120
Elevator
0 0.53 -0.15 0 -3.7 1 9 1 0 NACA0012 NACA0012
1.44 0.53 -0.15 0 -3.7 1 1 1 0 NACA0012 NACA0012Fin
0 0.885 -0.309 0.013 0 1 8 1 0 NACA0009 NACA0009
0.8 0.698 -0.279 0.013 0 64 6 1 0 NACA0009 NACA0009Excel作成手順の概要
上で準備したデータをExcelに貼り付けて,エクセルシートをいじることで安定微係数を計算していく
手順は以下のとおり
- 新規のエクセルシートにテキストデータを貼り付ける
- 主翼の翼素面積cdyおよびccdyを計算する
- 主翼の翼面積・スパン・平均空力翼弦長を計算する
- 主翼のピッチングモーメントを計算する
- 主翼の上反角を計算する
- 主翼の横・方向の安定微係数を計算する
- 水平・垂直尾翼の面積・スパンを計算する
- 三次元揚力傾斜を計算する
- 垂直尾翼の横・方向の安定微係数を計算する
一つずつ説明していく
新規のエクセルシートにテキストデータを貼り付ける
新規のエクセルシートとOnPointの.txtファイルを開き,.txtファイルを全選択(Ctrl+A)してコピー(Ctrl+C)する
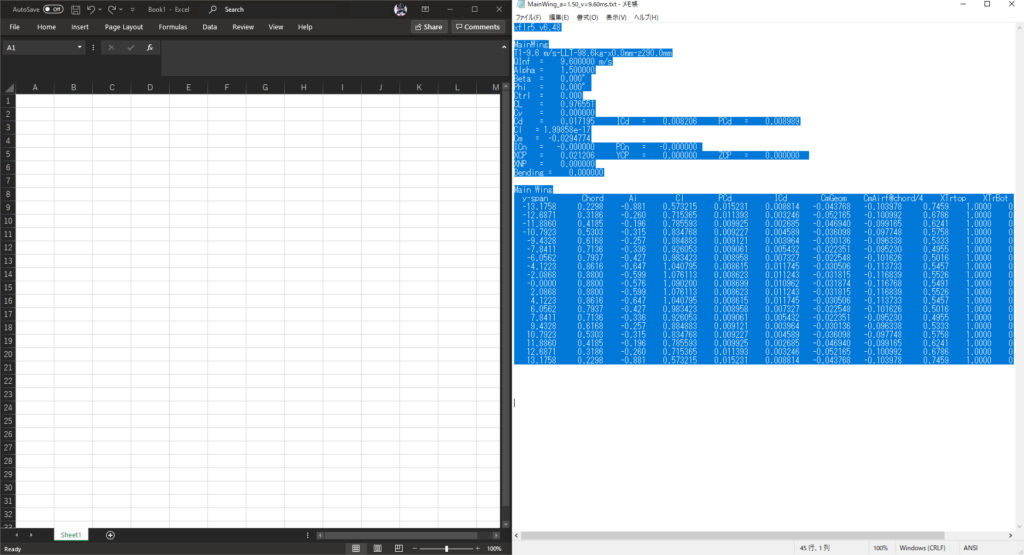
セルA1を選択した状態でHome>Paste>Use Text Import Wizard(Alt+H+V+U)をクリックする
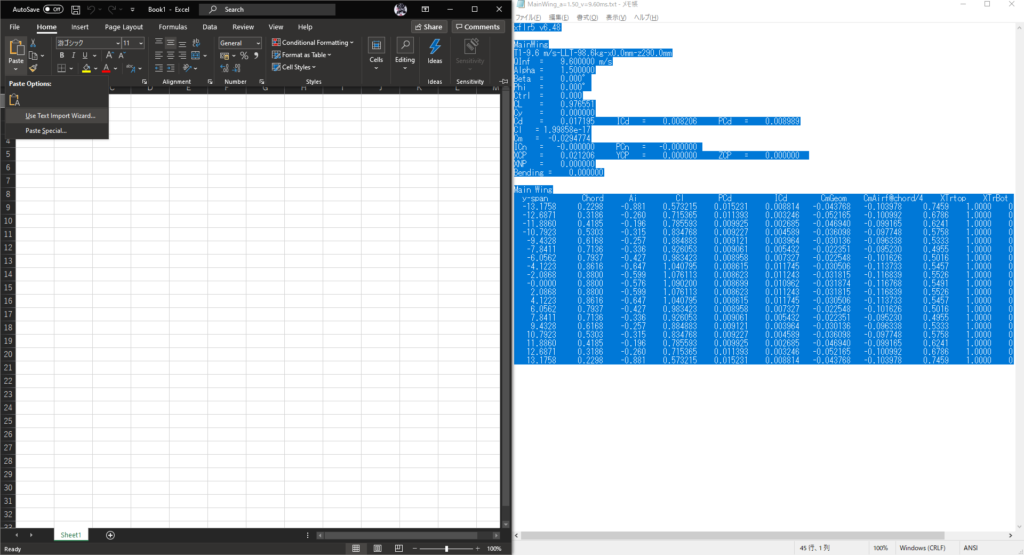
Text Import Wizardが開くので,Delimitedにチェックを入れてNextをクリック
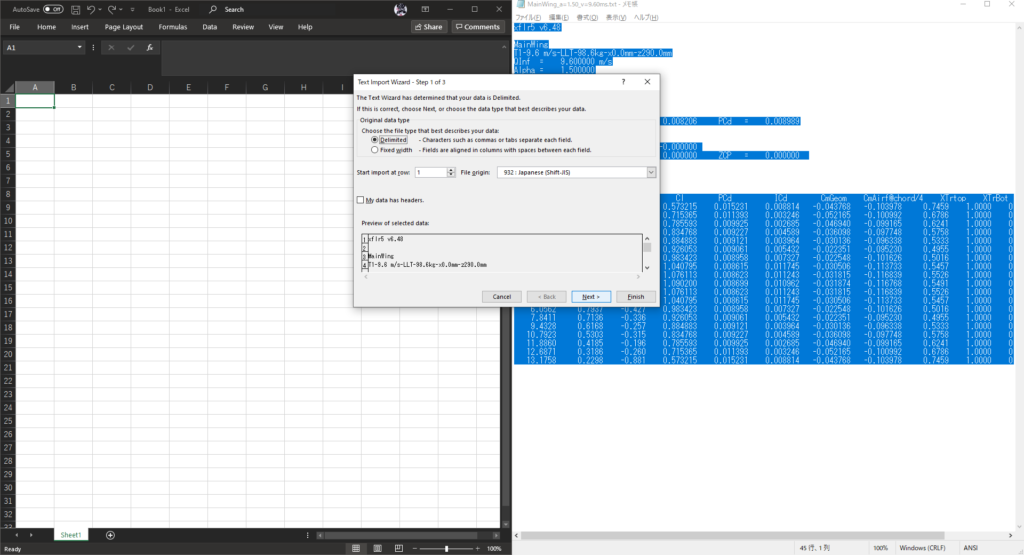
Delimitersにすべてチェックを入れ,Finishをクリックする
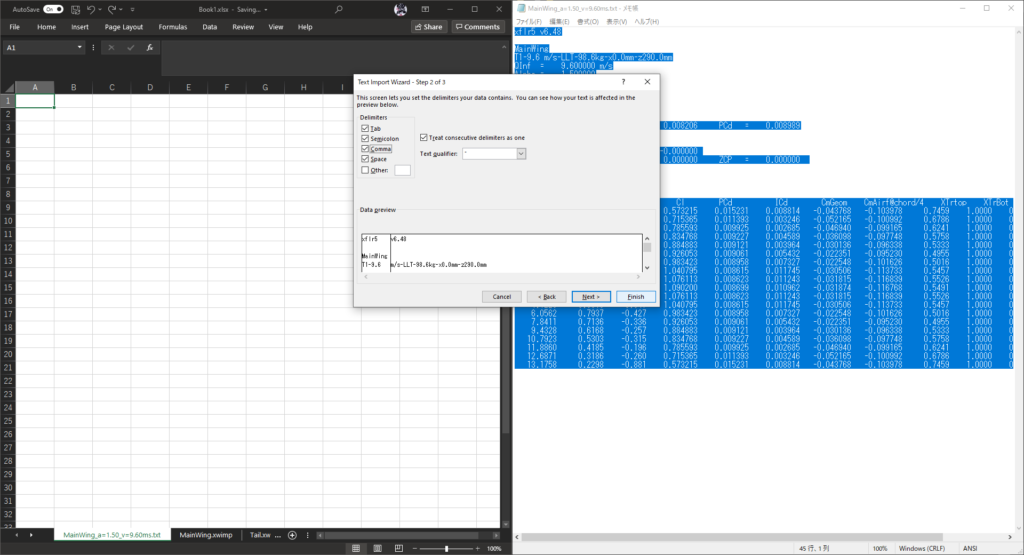
.txtのデータを貼り付けることができたので,シート名をダブルクリックして適当にファイル名などに変更しておく(MainWing_a=1.50_v=9.60ms.txt)
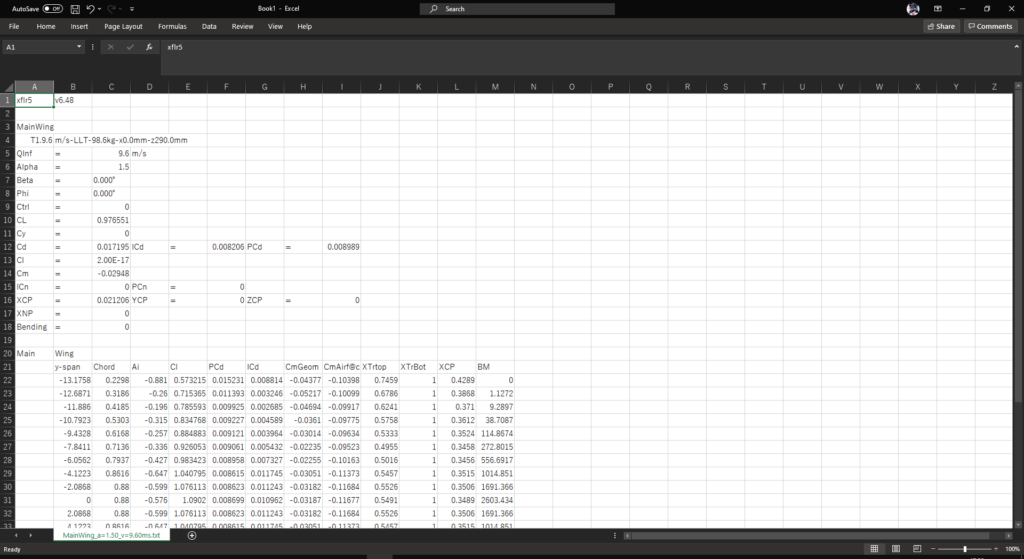
主翼,水平尾翼,垂直尾翼の.xwimpファイルも同様に読み込む(MainWing.xwimp,Elevator.xwimp,Fin.xwimp)
主翼の翼素面積cdyおよびccdyを計算する
MainWing_a=1.50_v=9.60ms.txtのシートに書き込んでいく
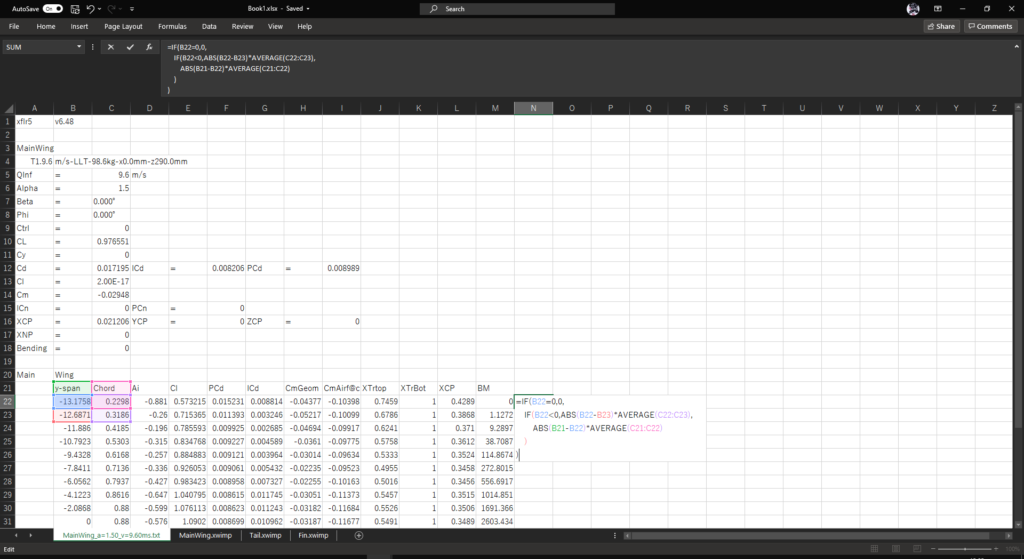
セルN22(BMの1列右)に以下の数式を入力して,翼素面積cdyを計算する
=IF(B22=0,0,
IF(B22<0,ABS(B22-B23)*AVERAGE(C22:C23),
ABS(B21-B22)*AVERAGE(C21:C22)
)
)
セルN22の右下をダブルクリックしてオートフィルを行い,セルN21に「cdy」と入力する
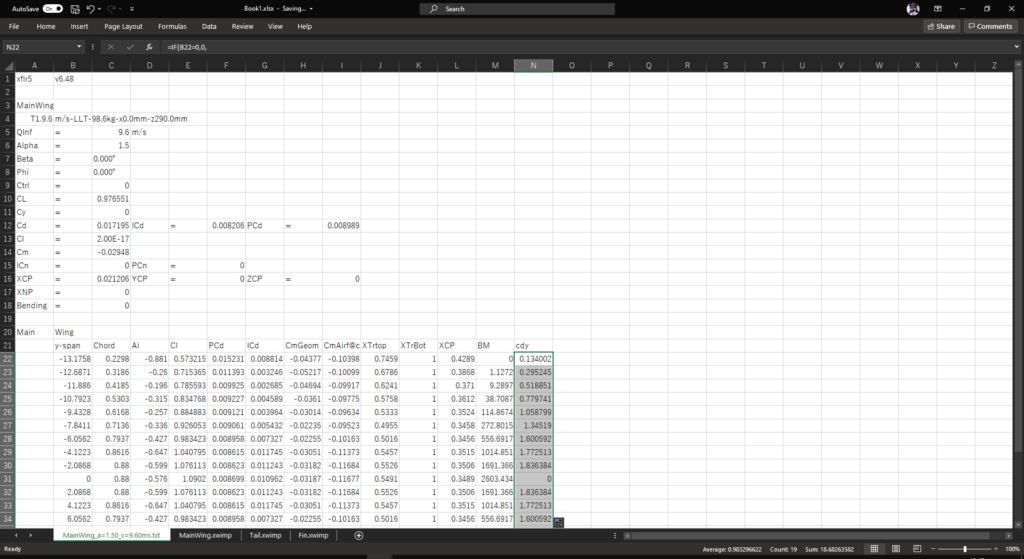
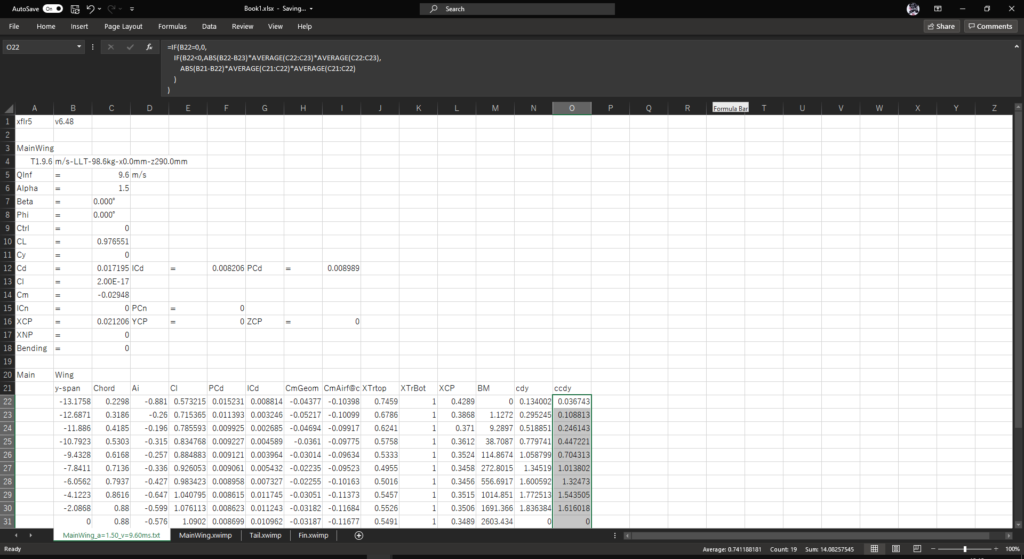
同様に,セルO22に以下の数式を入力し,オートフィルを行ってセルO21に「ccdy」と入力する
=IF(B22=0,0,
IF(B22<0,ABS(B22-B23)*AVERAGE(C22:C23)*AVERAGE(C22:C23),
ABS(B21-B22)*AVERAGE(C21:C22)*AVERAGE(C21:C22)
)
)
主翼の翼面積・スパン・平均空力翼弦長を計算する
セルN20でSUM関数を使って翼素面積の合計(=翼面積)を計算する
≫SUM 関数 - Office サポート - Microsoft Support
=SUM(N22:N40)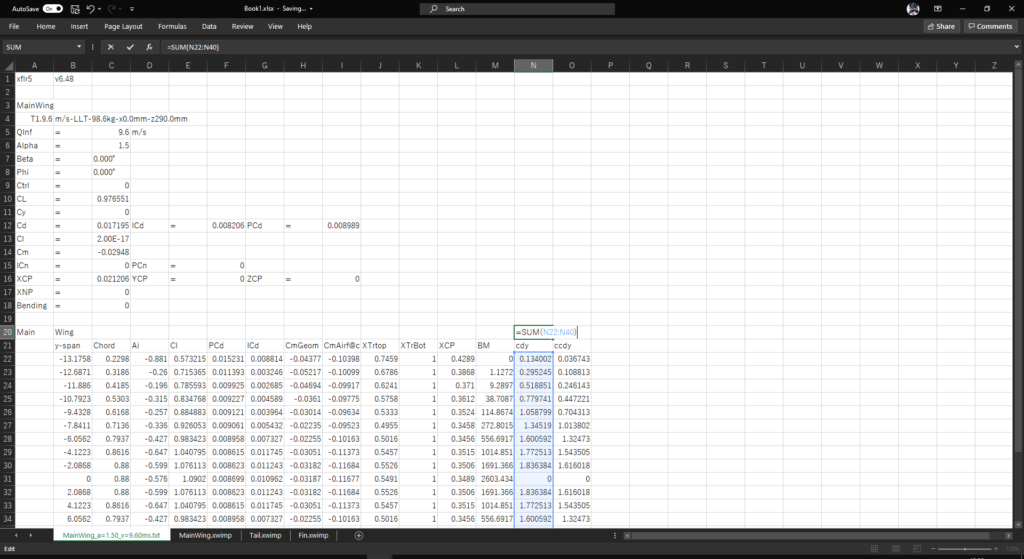
セルB20に以下の数式を入力してスパンを計算する
=ABS(MIN(B22:B40))+MAX(B22:B40)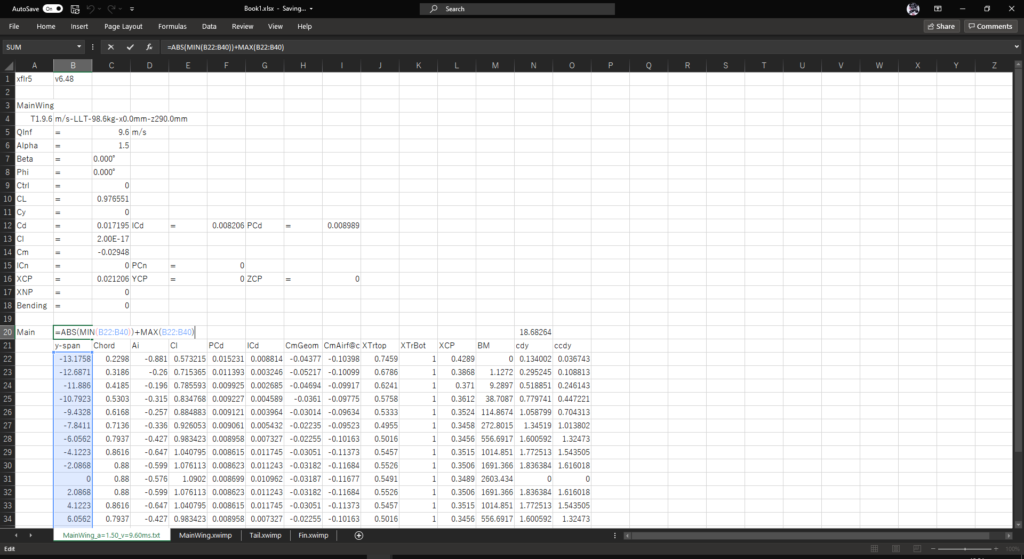
平均空力翼弦長は近似的に以下の式で計算できる(白本:p.44)
\begin{eqnarray}
{\overline c}=\frac{1}{S}\int_{b/2}^{b/2}c^{2}dy
\end{eqnarray}
よって,セルC20に以下の式を入力する
=(1/N20)*SUM(O22:O40)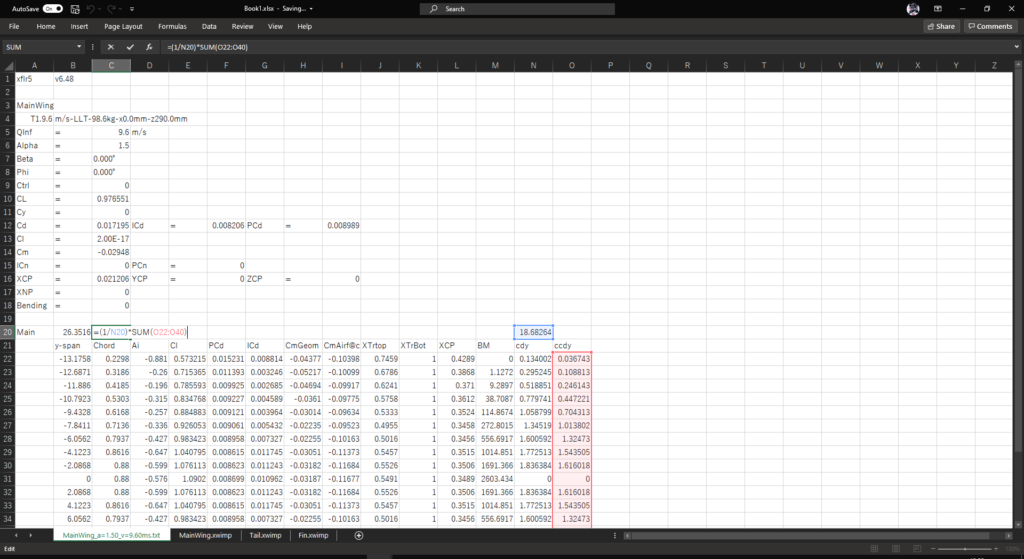
主翼のピッチングモーメントを計算する
翼素ごとの1/4弦点まわりのピッチングモーメント係数から主翼全体のピッチングモーメント係数を計算する
i番目の翼素を\((~)_{i}\)で表すと,主翼全体における1/4弦点まわりのピッチングモーメント係数\(C_{m_{1/4chord}}\)は次の式で計算できる
\begin{eqnarray}
C_{m_{1/4}}&=&\frac{\int_{-b/2}^{b/2} \frac{1}{2}\rho V^{2}(c_{i}\mathrm{dy}) c_{i}C_{m_{1/4_{i}}}}{\frac{1}{2}\rho V^{2}S {\overline c}}\\
&=&\frac{1}{S {\overline c}}\int_{-b/2}^{b/2} c_{i}^{2} C_{m_{1/4_{i}}} \mathrm{dy}\\
\end{eqnarray}
よって,セルI20に以下の式を入力する
=SUMPRODUCT(O22:O40,I22:I40)/(N20*C20)≫SUMPRODUCT 関数 - Office サポート - Microsoft Support
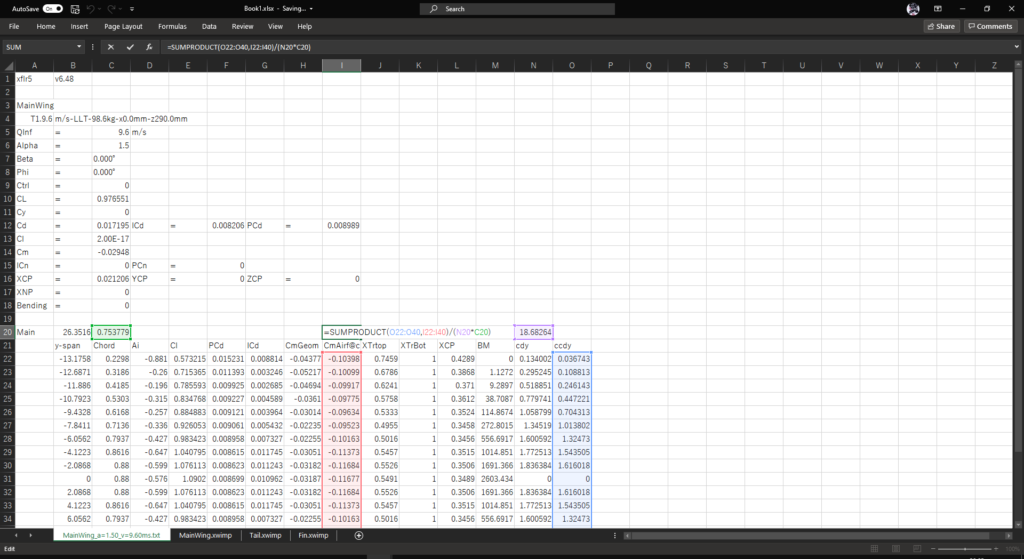
主翼の上反角を計算する
XFLR5に3次元翼を入力するときは,いくつかのブロックに分ける必要がある
上反角はそのブロックの両端で定義されており,ブロックの内部では線形補完が行われている
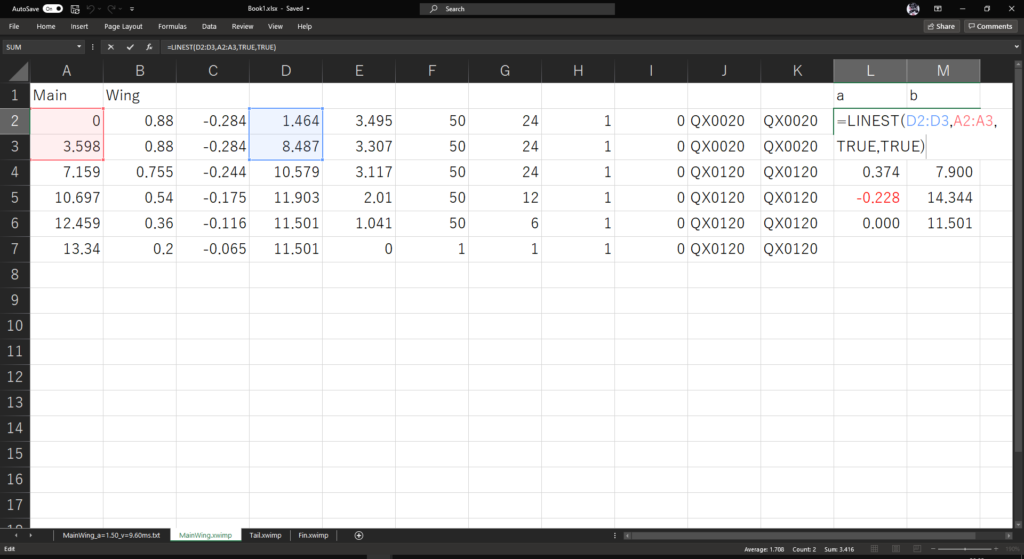
MainWing.xwimpのシートのセルL2:M2を選択した状態で以下の式を入力することで,上反角を線形補完した際の直線の傾きと接線を計算することができる
=LINEST(D2:D3,A2:A3,TRUE,TRUE)数式を入力し終えた時は,「Ctrl+Shift+Enter」を押す必要がある
≫LINEST 関数 - Office サポート - Microsoft Support
2行目に入力した後は,主翼の分割数に応じてオートフィルを行う(今回は6分割なのでセルL6:M6まで)
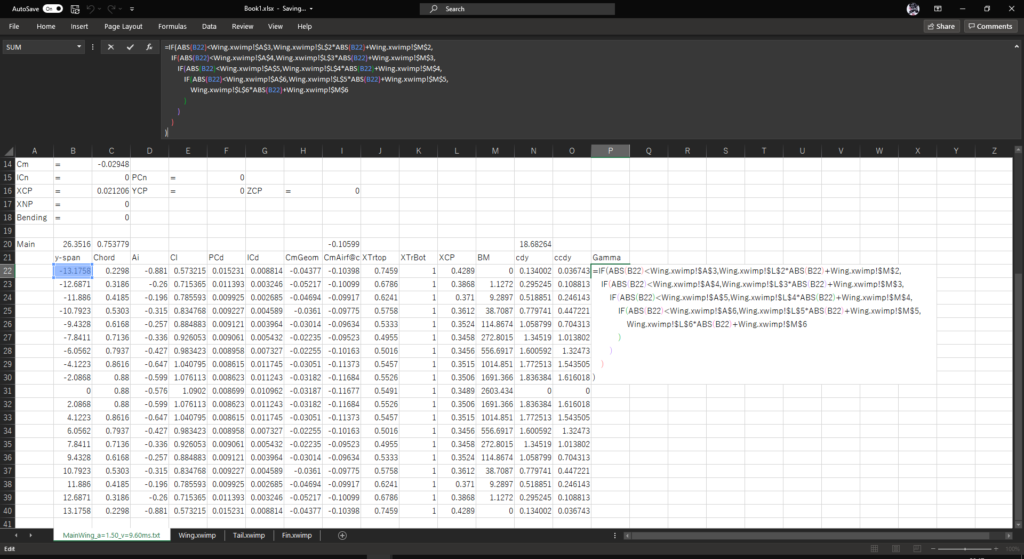
MainWing_a=1.50_v=9.60ms.txtのシートに戻り,セルP21に「Gamma」と入力し,セルP22に以下の数式を入力する
=IF(ABS(B22)<MainWing.xwimp!$A$3,MainWing.xwimp!$L$2*ABS(B22)+MainWing.xwimp!$M$2,
IF(ABS(B22)<MainWing.xwimp!$A$4,MainWing.xwimp!$L$3*ABS(B22)+MainWing.xwimp!$M$3,
IF(ABS(B22)<MainWing.xwimp!$A$5,MainWing.xwimp!$L$4*ABS(B22)+MainWing.xwimp!$M$4,
IF(ABS(B22)<MainWing.xwimp!$A$6,MainWing.xwimp!$L$5*ABS(B22)+MainWing.xwimp!$M$5,
MainWing.xwimp!$L$6*ABS(B22)+MainWing.xwimp!$M$6
)
)
)
)IF関数の回数は翼の分割数に応じて変更する
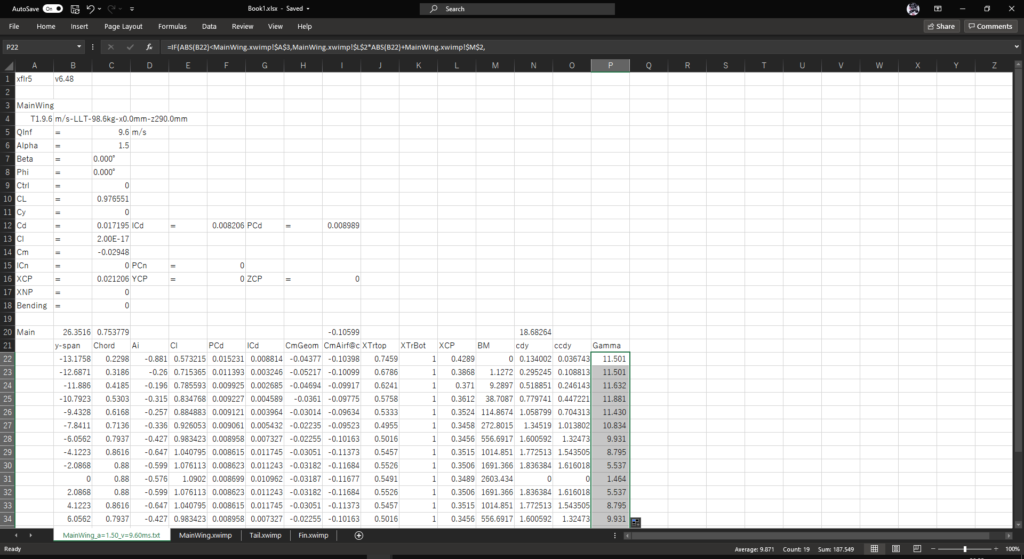
セルP22にオートフィルを実行する
主翼の横・方向の安定微係数を計算する
まず,断面揚力傾斜\(a_{1} \mathrm{[1/deg]}\)を計算する(今回は断面揚力傾斜はスパン方向に\(a_{1}=2\pi\)で一定とする)
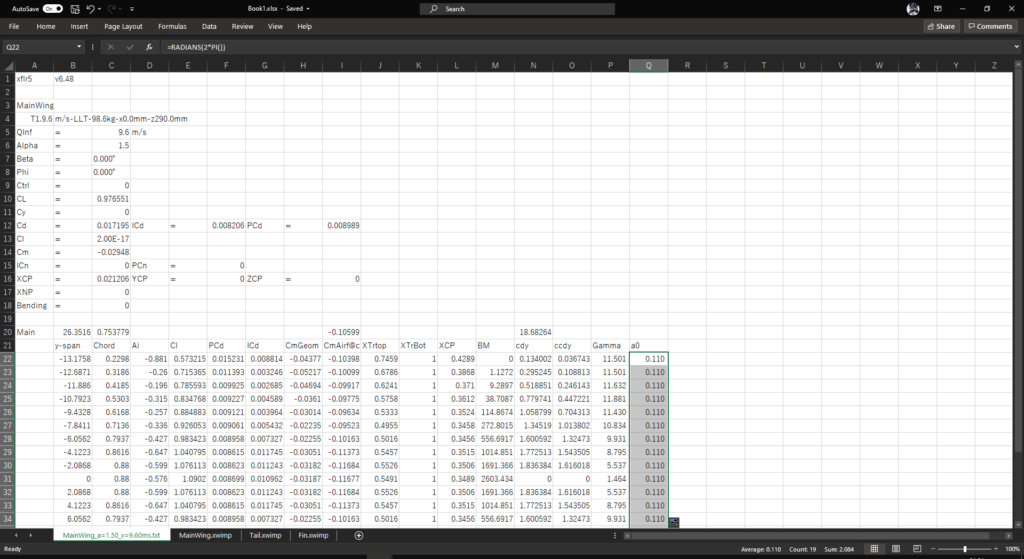
セルQ21に「a1」と入力し,セルQ22:Q40に以下の数式を入力する
=RADIANS(2*PI())RADIANS関数は[deg]を[rad]へ変換する関数で,RADIANS(A1)はA1*(PI()/180)と等価である
ここでは,RADIANS関数を使うことによって,断面揚力傾斜\(a_{1}=2\pi \mathrm{[1/rad]}\)を\(a_{1}=2\pi\frac{\pi}{180}=0.110\mathrm{[1/deg]}\)に変換している
横・方向の安定微係数の計算についてはこちらを参照
ただし,上の記事では右翼の値を計算して2倍しているのに対して,今回のExcelファイルでは両翼を計算していることに注意する(両翼を積分した後にに0.5倍する必要がある)
以下,順番に計算していく
\((C_{y_{\beta}})_{wing}~\mathrm{[1/deg]}\)
\begin{eqnarray}
(C_{y_{\beta}})_{wing} &=& -\frac{2}{S} \int_{0}^{b/2} a_{1} \sin{\Gamma}^2 c \mathrm{dy}\\
\end{eqnarray}
セルR21に「Cyb」と入力し,セルQ22に以下の数式を入力してオートフィルを実行する
=-(2/$N$20)*Q22*SIN(RADIANS(P22))*SIN(RADIANS(P22))*N22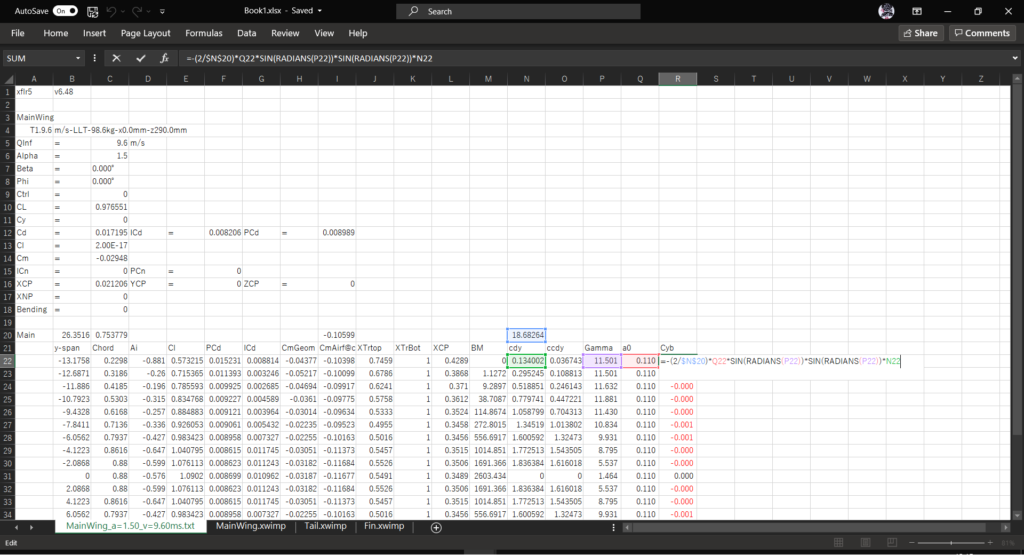
\((C_{y_{p}})_{wing}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{y_{p}})_{wing} &=& -\frac{4}{S_{w}b_{w}} \int_{0}^{b/2} a_{1} y\sin{\Gamma}\cos{\Gamma} c \mathrm{dy}\\
\end{eqnarray}
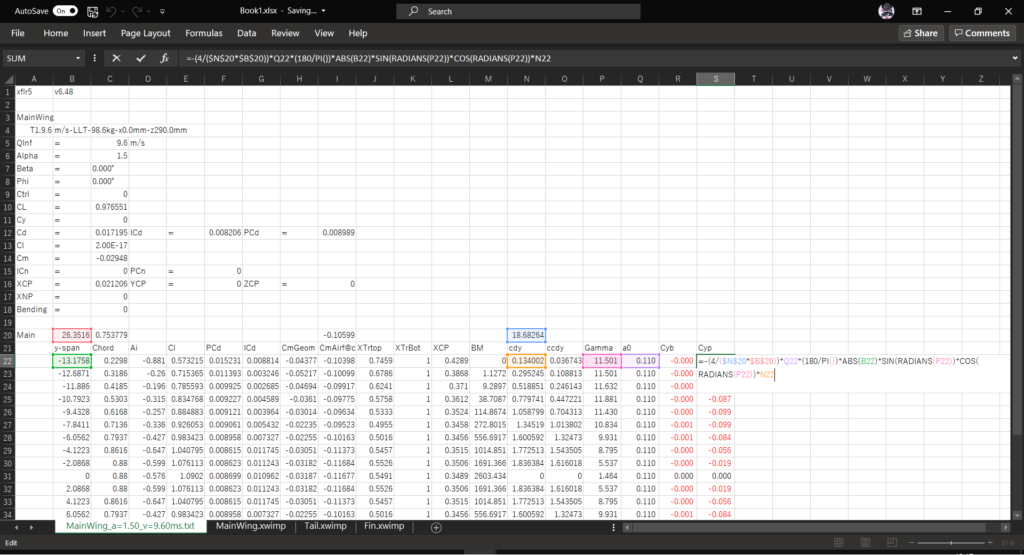
セルS21に「Cyp」と入力し,セルS22に以下の数式を入力してオートフィルを実行する
=-(4/($N$20*$B$20))*Q22*(180/PI())*ABS(B22)*SIN(RADIANS(P22))*COS(RADIANS(P22))*N22安定微係数の単位を[1/rad]にするために,断面揚力傾斜(セルQ22)に\((180/\pi)\)を乗じている
\((C_{y_{r}})_{wing}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{y_{r}})_{wing} &=& \frac{8}{S_{w}b_{w}} \int_{0}^{b/2} C_{L} y\sin{\Gamma} c\mathrm{dy}\\
\end{eqnarray}
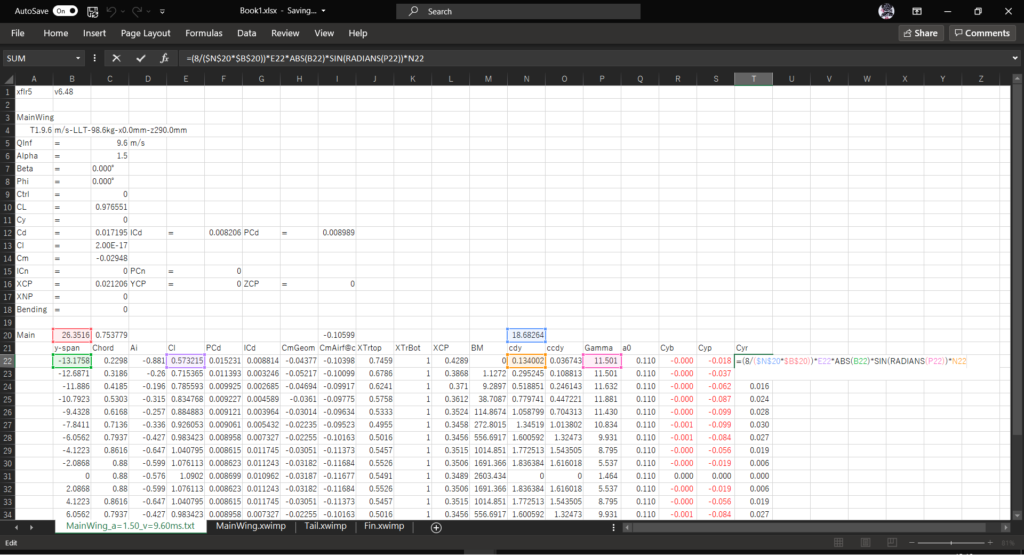
セルT21に「Cyr」と入力し,セルT22に以下の数式を入力してオートフィルを実行する
=(8/($N$20*$B$20))*E22*ABS(B22)*SIN(RADIANS(P22))*N22左翼(y<0)の値も右翼と同様に計算するため,ABS関数を使ってy(セルB22)の絶対値をとっている
≫ABS 関数 - Office サポート - Microsoft Support
\((C_{l_{\beta}})_{wing}~\mathrm{[1/deg]}\)
\begin{eqnarray}
(C_{l_{\beta}})_{wing} &=& -\frac{2}{S_{w}b_{w}} \int_{0}^{b/2} a_{1} \sin{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy}\\
\end{eqnarray}
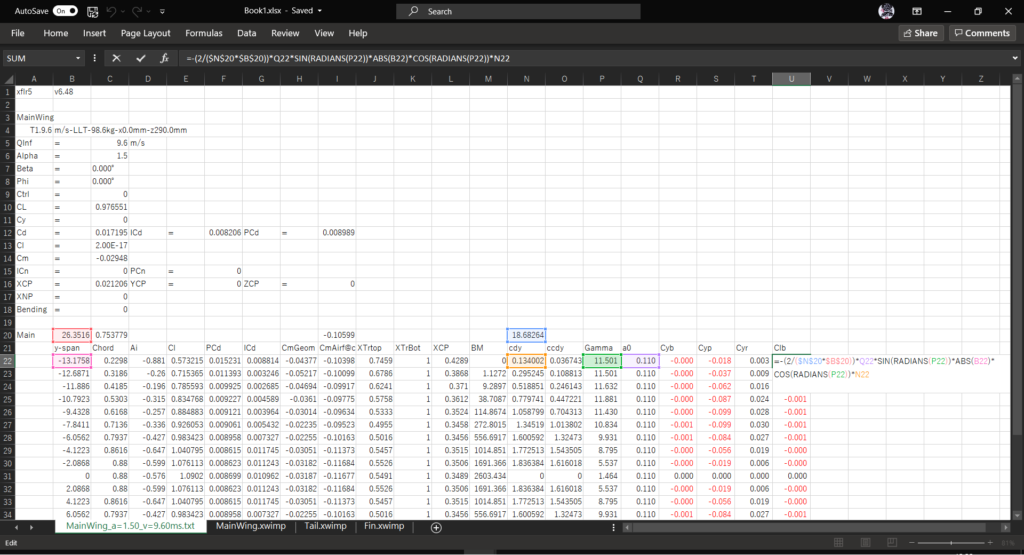
セルU21に「Clb」と入力し,セルU22に以下の数式を入力してオートフィルを実行する
=-(2/($N$20*$B$20))*Q22*SIN(RADIANS(P22))*ABS(B22)*COS(RADIANS(P22))*N22zの影響は小さいうえに計算するのが面倒なので無視している
\((C_{l_{p}})_{wing}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{l_{p}})_{wing} &=& -\frac{4}{S_{w}b_{w}^{2}} \int_{0}^{b/2} a_{1} y \cos{\Gamma} \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
\end{eqnarray}
セルV21に「Clp」と入力し,セルV22に以下の数式を入力してオートフィルを実行する
=-(4/($N$20*$B$20*$B$20))*Q22*(180/PI())*B22*COS(RADIANS(P22))*B22*COS(RADIANS(P22))*N22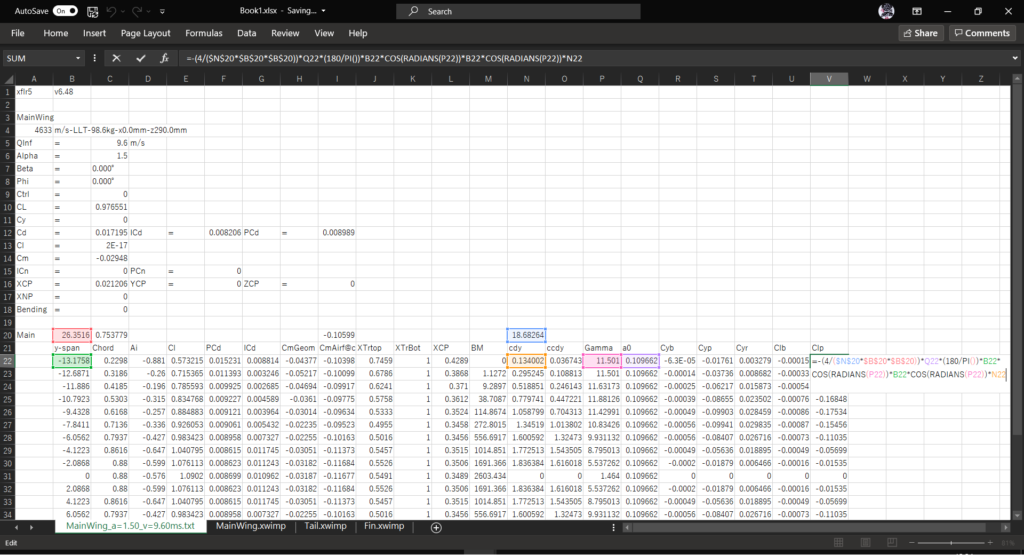
\((C_{l_{r}})_{wing}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{l_{r}})_{wing} &=& \frac{8}{S_{w}b_{w}^{2}} \int_{0}^{b/2} C_{L} y \left( y\cos{\Gamma}+z\sin{\Gamma} \right) c\mathrm{dy} \\
\end{eqnarray}
セルW21に「Clr」と入力し,セルW22に以下の数式を入力してオートフィルを実行する
=(8/($N$20*$B$20*$B$20))*E22*B22*B22*COS(RADIANS(P22))*N22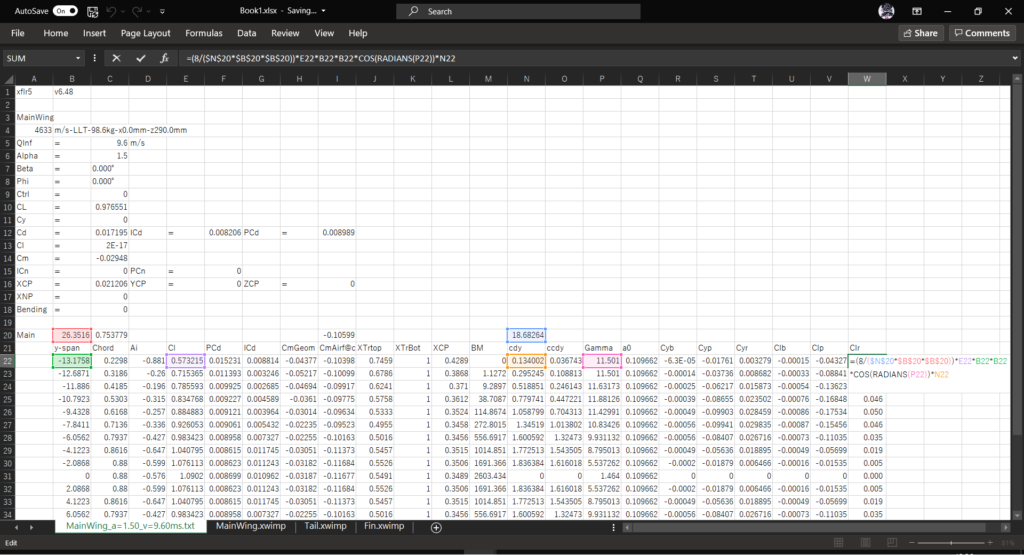
\((C_{n_{\beta}})_{wing}~\mathrm{[1/deg]}\)
\begin{eqnarray}
(C_{n_{\beta}})_{wing} &=& -\frac{2}{S_{w}b_{w}} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \sin{\Gamma} y c\mathrm{dy}\\
\end{eqnarray}
セルX21に「Cnb」と入力し,セルX22に以下の数式を入力してオートフィルを実行する
=-(2/($N$20*$B$20))*(Q22*(180/PI())*SIN(RADIANS($C$6))+E22*COS(RADIANS($C$6))+F22*SIN(RADIANS($C$6)))*(PI()/180)*SIN(RADIANS(P22))*ABS(B22)*N22Q22*(180/PI())*SIN(RADIANS($C$6))+E22*COS(RADIANS($C$6))+F22*SIN(RADIANS($C$6))の単位は[1/rad]である
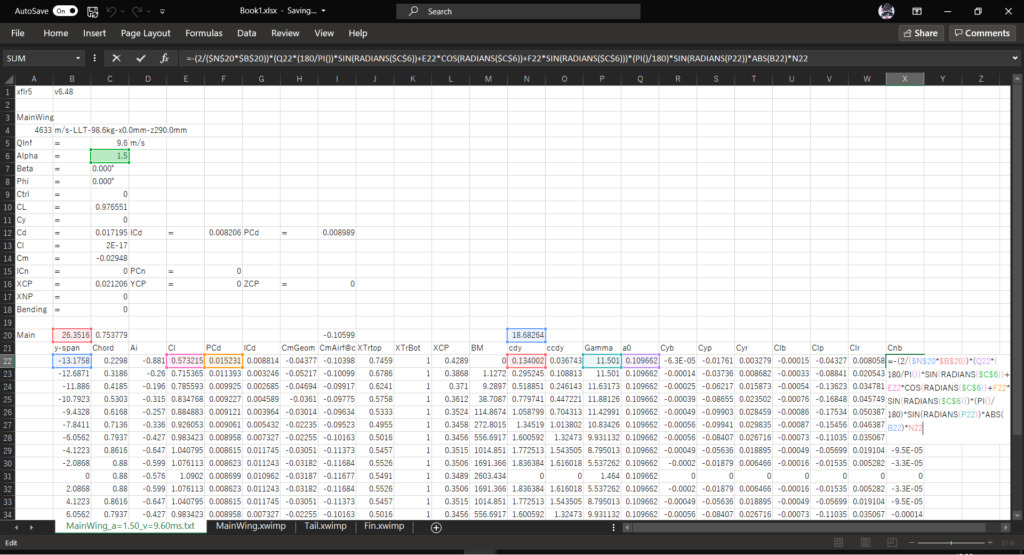
\((C_{n_{p}})_{wing}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{n_{p}})_{wing} &=& -\frac{4}{S_{w}b_{w}^{2}} \int_{0}^{b/2} \left(a_{1}\sin{\alpha}+C_{L}\cos{\alpha}+C_{D}\sin{\alpha}\right) \cos{\Gamma} y^{2} c\mathrm{dy} \\
\end{eqnarray}
セルY21に「Cnp」と入力し,セルY22に以下の数式を入力してオートフィルを実行する
=-(4/($N$20*$B$20*$B$20))*(Q22*(180/PI())*SIN(RADIANS($C$6))+E22*COS(RADIANS($C$6))+F22*SIN(RADIANS($C$6)))*COS(RADIANS(P22))*ABS(B22)*ABS(B22)*N22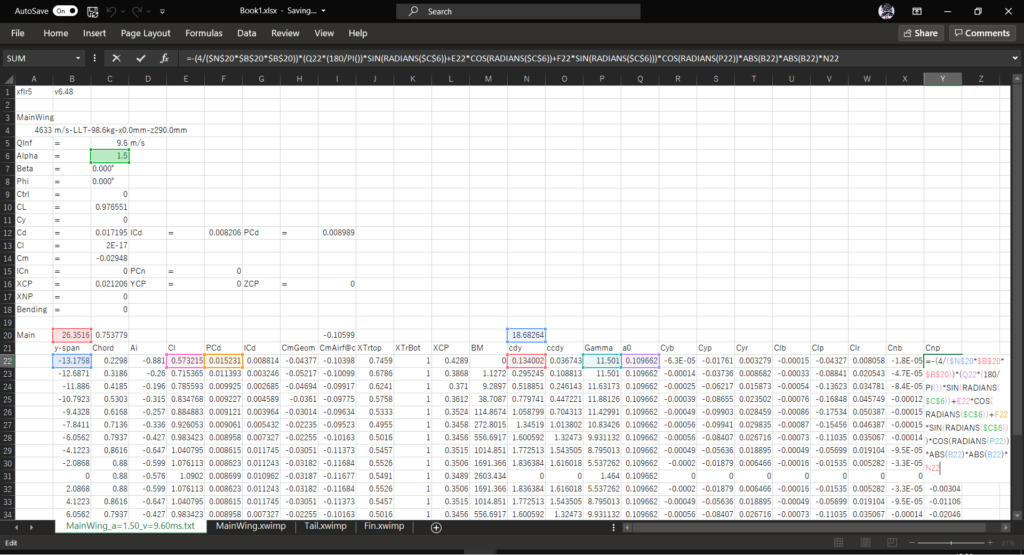
\((C_{n_{r}})_{wing}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{n_{r}})_{wing} &=& \frac{8}{S_{w}b_{w}^{2}} \int_{0}^{b/2} (C_{L}\sin{\alpha}-C_{D}\cos{\alpha}) y^{2} c\mathrm{dy} \\
\end{eqnarray}
セルZ21に「Cnr」と入力し,セルZ22に以下の数式を入力してオートフィルを実行する
=(8/($N$20*$B$20*$B$20))*(E22*SIN(RADIANS($C$6))-F22*COS(RADIANS($C$6)))*B22*B22*N22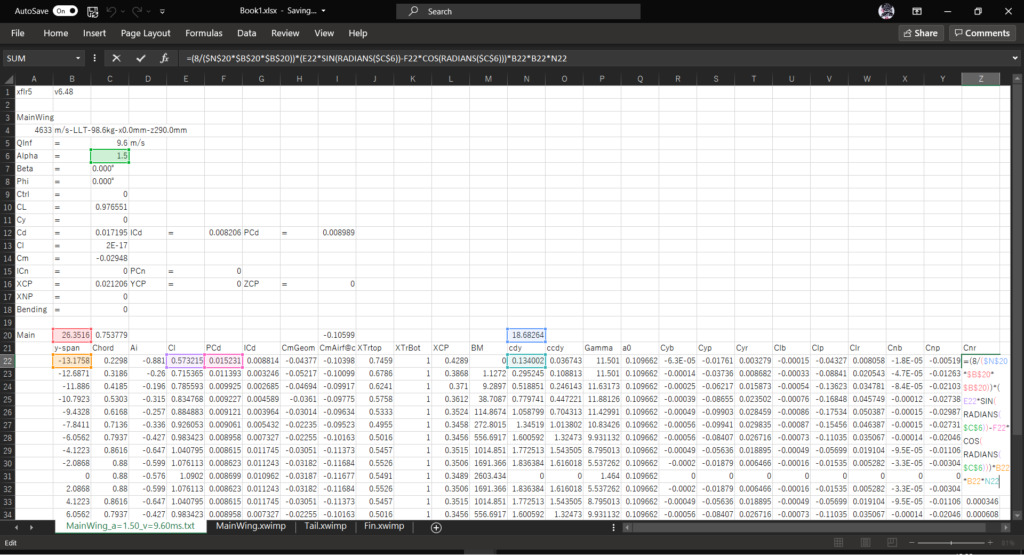
積分
上で計算してきた値を全幅にわたって積分する
セルR20に以下の数式を入力し,セルZ20までオートフィルを実行する
=SUM(R22:R40)*(1/2)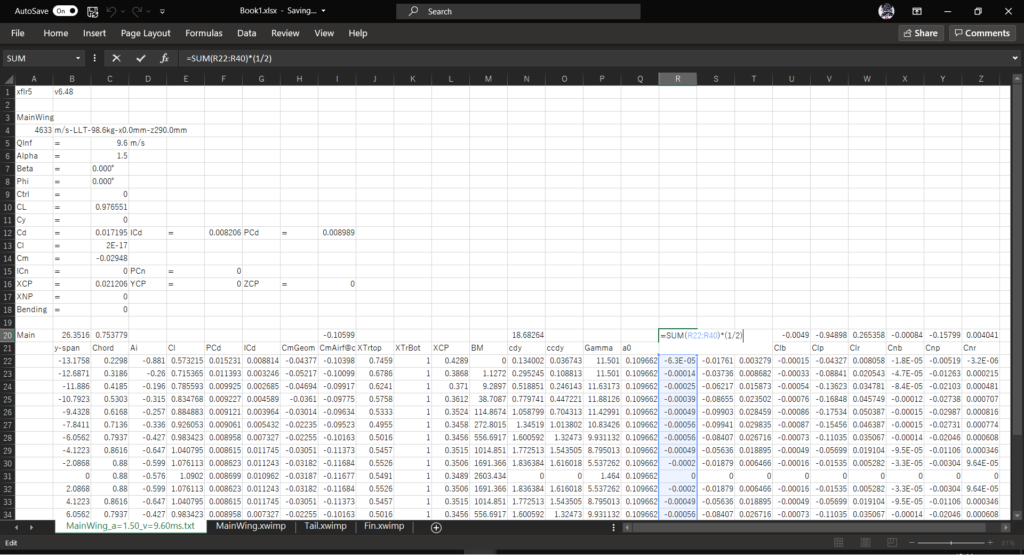
これで横・方向の安定微係数に対する主翼の寄与が計算できた
水平・垂直尾翼の面積・スパンを計算する
水平尾翼
Elevator.xwimpのシートで水平尾翼の面積とスパンを計算する
といっても主翼で計算した方法と同じなのでさっくりと説明する
セルL2に以下の式を入力し,オートフィルを実行して翼素面積を計算する
=IF(A2=0,0,IF(A2<0,ABS(A2-A3)*AVERAGE(B2:B3),ABS(A1-A2)*AVERAGE(B1:B2)))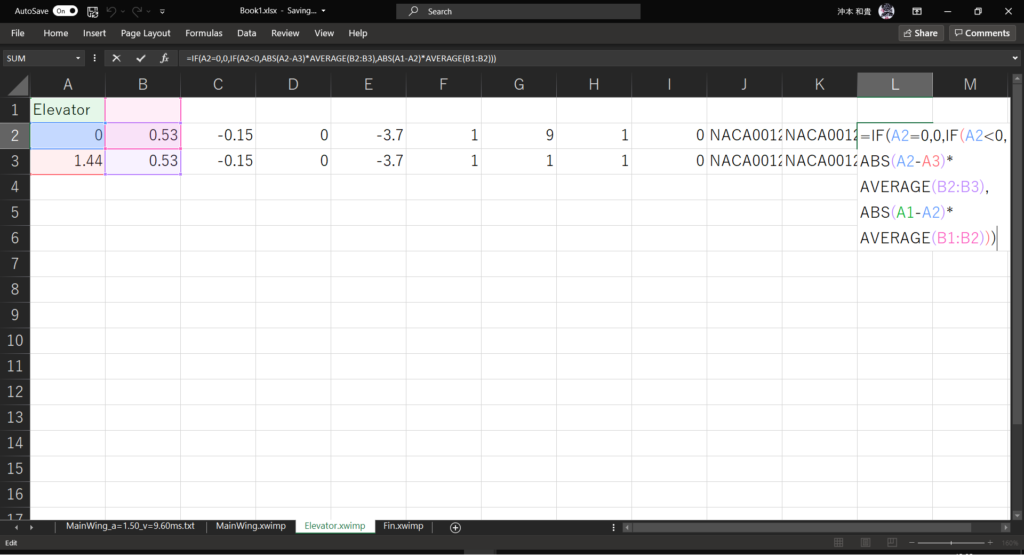
セルL1に以下の式を入力して翼素面積を合計し,翼面積を計算する
=SUM(L2:L3)*2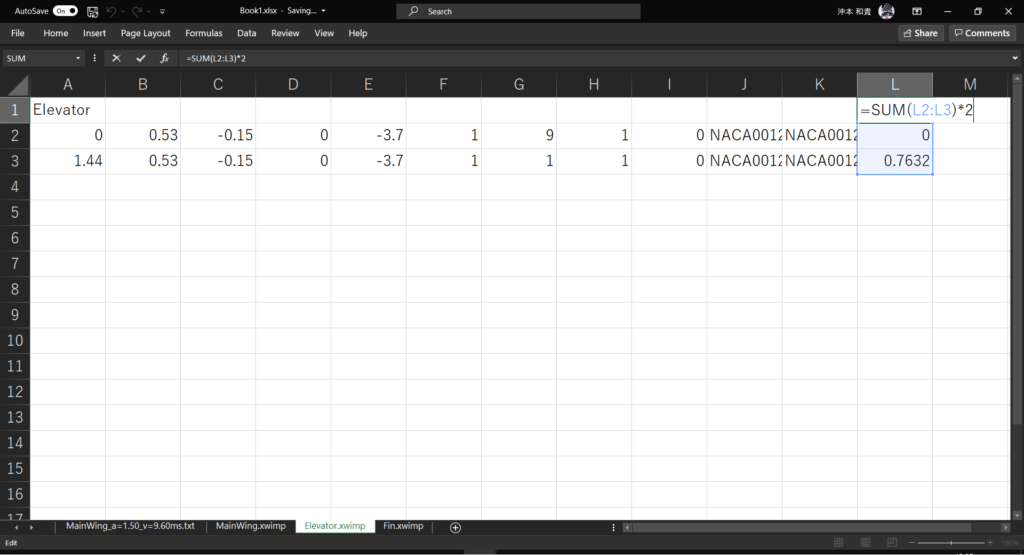
セルM1に以下の式を入力して水平尾翼のスパンを計算する
=(ABS(MIN(A2:A3))+MAX(A2:A3))*2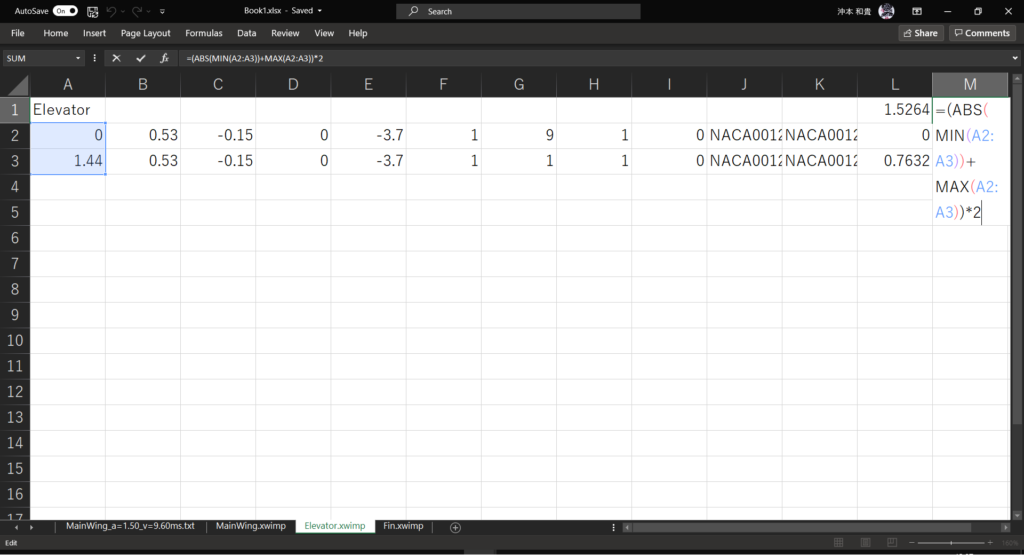
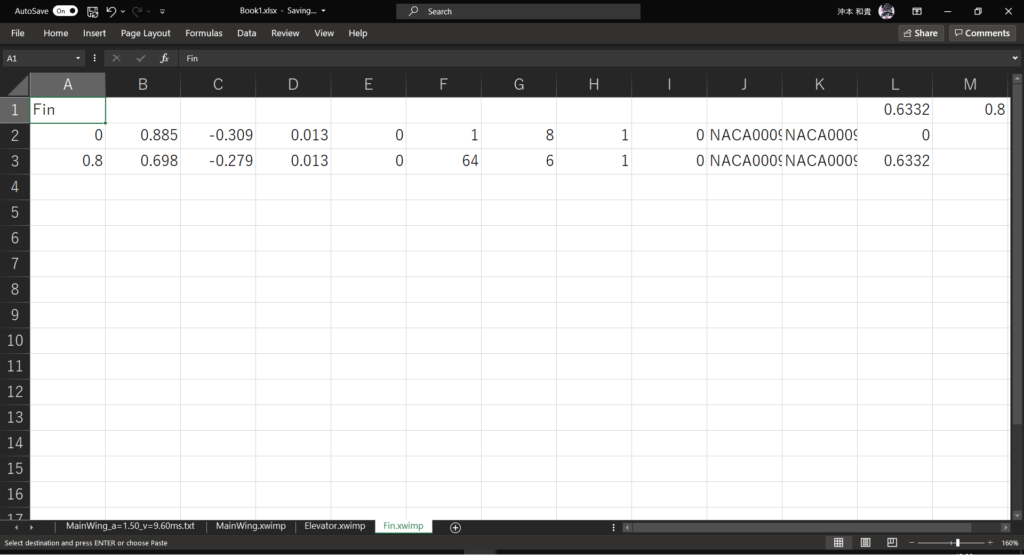
垂直尾翼
垂直尾翼に関しては水平尾翼とほぼ同じなので説明は省略する
面積とスパンを計算する際の*2は必要ないので注意すること
三次元揚力傾斜を計算する
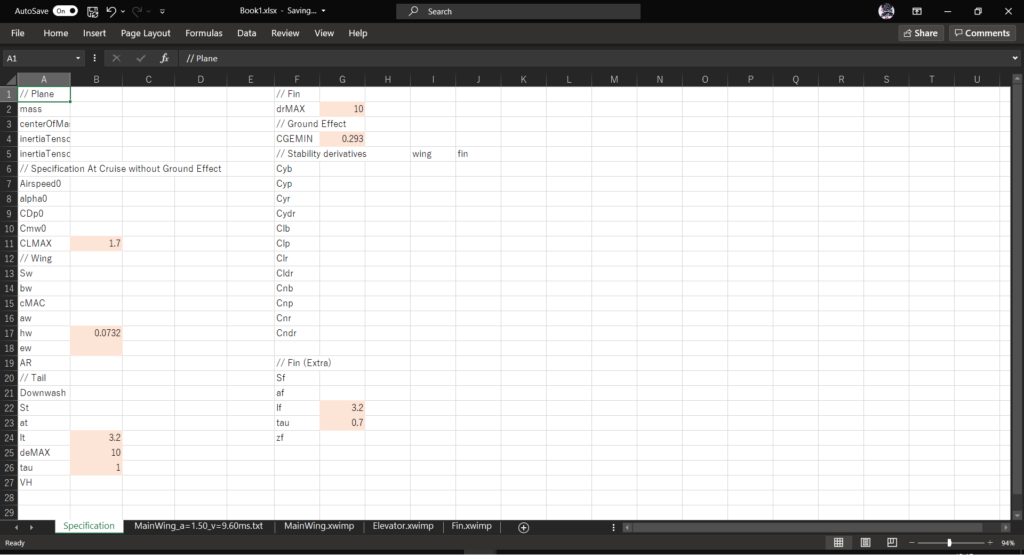
まず,今回必要な諸元をまとめた以下のシート(Specification)を追加する
自分で入力が必要なセルはオレンジ色にして区別してある
以下の値を各シートから引っ張ってくる
| 変数名 | 参照するシート | 参照するセル |
| Airspeed0 | MainWing_a=1.50_v=9.60ms.txt | C5 |
| alpha0 | MainWing_a=1.50_v=9.60ms.txt | C6 |
| CDp0 | MainWing_a=1.50_v=9.60ms.txt | I12 |
| Cmw0 | MainWing_a=1.50_v=9.60ms.txt | I20 |
| Sw | MainWing_a=1.50_v=9.60ms.txt | N20 |
| bw | MainWing_a=1.50_v=9.60ms.txt | B20 |
| cMAC | MainWing_a=1.50_v=9.60ms.txt | C20 |
| AR | - | =(B14*B14)/B13 |
| St | Elevator.xwimp | L1 |
| VH | - | =(B22*B24)/(B13*B15) |
| (Cyb)_wing : (Cnr)_wing | MainWing_a=1.50_v=9.60ms.txt | R20 : Z20 |
| bt | Elevator.xwimp | M1 |
| Sf | Fin.xwimp | L1 |
| bf | Fin.xwimp | M1 |
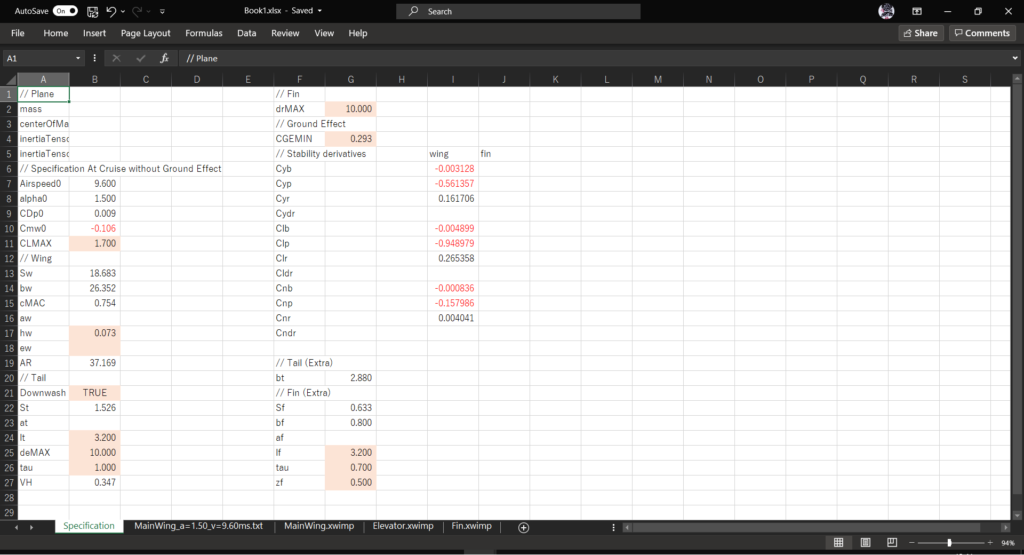
三次元揚力傾斜は以下の式で計算する(白本:p.)
\begin{eqnarray}
a=\frac{a_{1}}{1+\frac{a_{1}}{\pi AR}}
\end{eqnarray}
ただし,上の式の揚力傾斜の単位は三次元・断面ともに[1/rad]であることに注意する
よって,主翼・水平尾翼・垂直尾翼の三次元揚力傾斜[1/deg]を計算するには,セルB16,セルB23,セルG24にそれぞれ次のように入力する
=RADIANS(2*PI()/(1+(2*PI()/(PI()*B19))))=RADIANS(2*PI()/(1+(2*PI())/(PI()*((G20*G20)/B22))))=RADIANS(2*PI()/(1+(2*PI())/(PI()*((G23*G23)/G22))))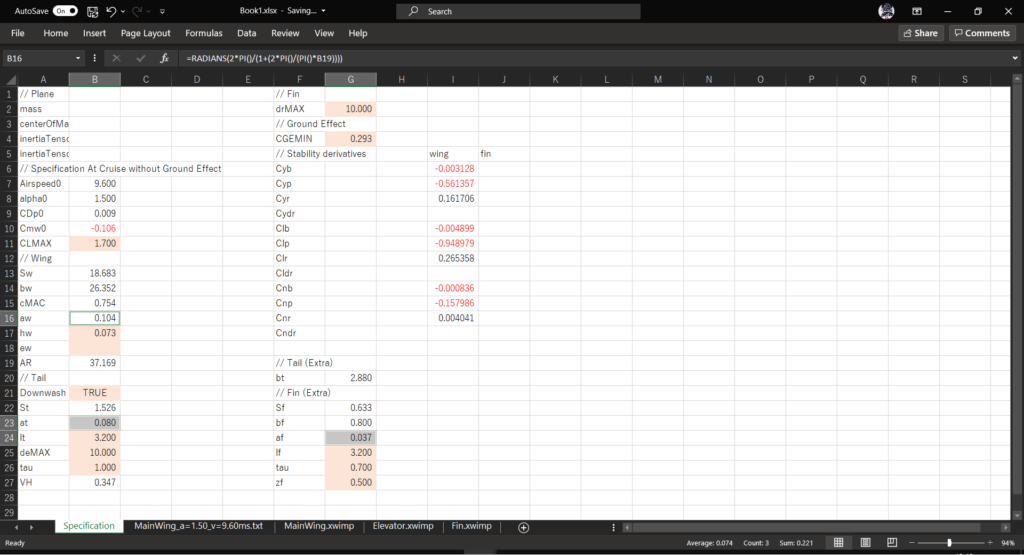
垂直尾翼の横・方向の安定微係数を計算する
横・方向の安定微係数の計算についてはこちらを参照
以下,順番に計算していく
\((C_{y_{\beta}})_{fin}~\mathrm{[1/deg]}\)
\begin{eqnarray}
(C_{y_{\beta}})_{f}
=-\frac{S_{f}}{S_{w}}a_{f}
\end{eqnarray}
セルJ6に以下の数式を入力する
=-(G22/B13)*G24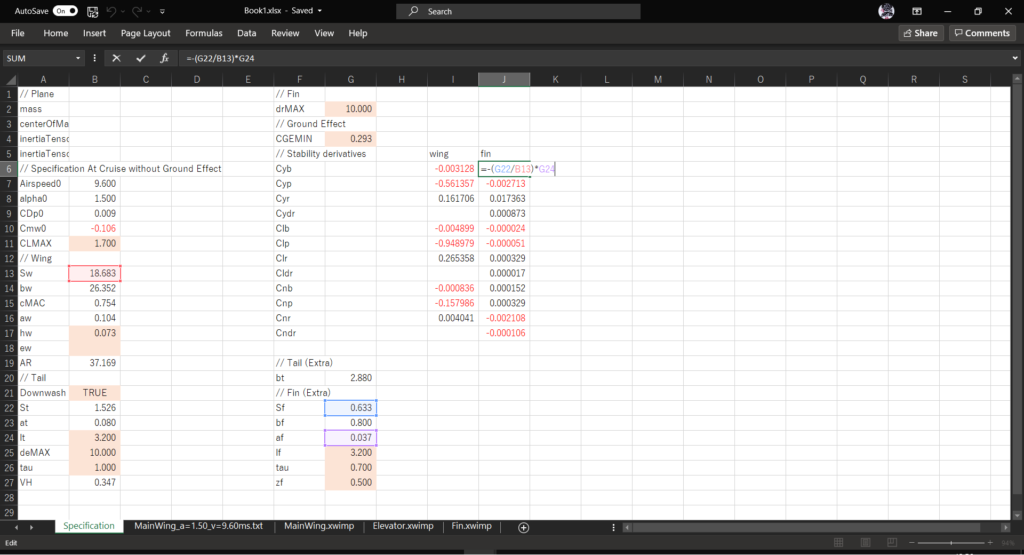
\((C_{y_{p}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{y_{p}})_{fin}
= -\frac{S_{f}}{S_{w}}a_{f}\frac{2z_{f}}{b}
\end{eqnarray}
セルJ7に以下の数式を入力する
=-(G22/B13)*DEGREES(G24)*(2*G27/B14)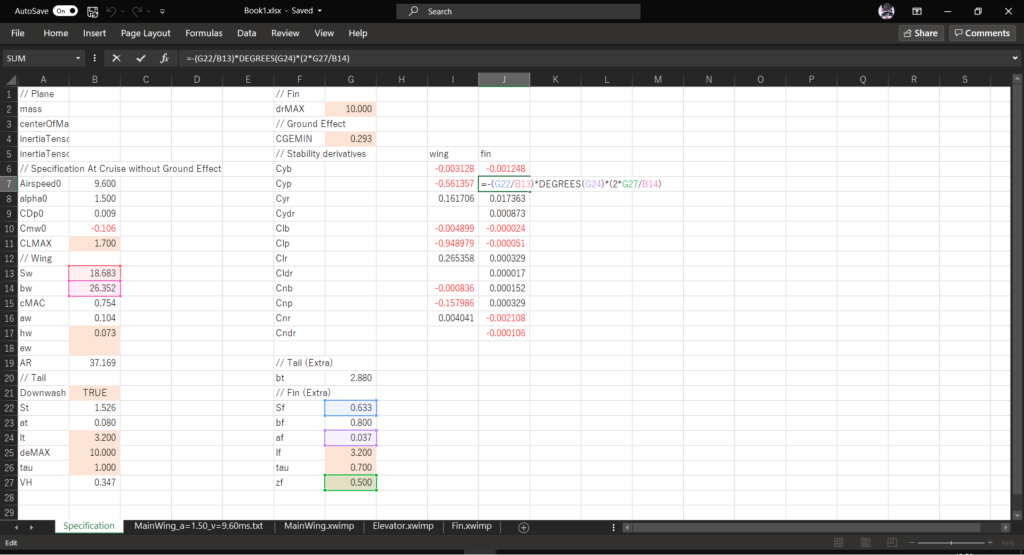
\((C_{y_{r}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{y_{r}})_{fin}= \frac{S_{f}}{S_{w}}a_{f}\frac{2l_{f}}{b}
\end{eqnarray}
セルJ8に以下の数式を入力する
=(G22/B13)*DEGREES(G24)*(2*G25/B14)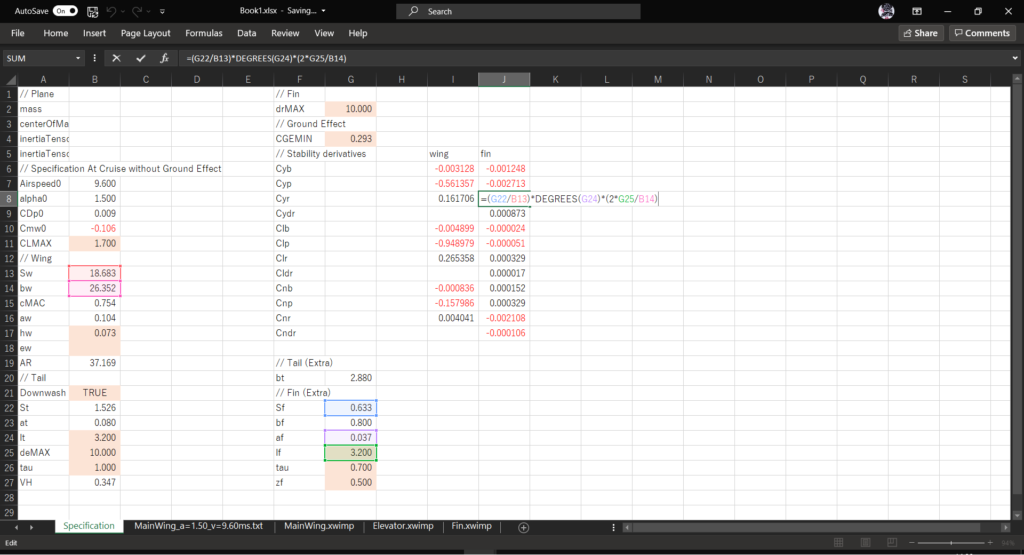
\((C_{y_{delta_{r}}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
C_{y_{\delta_{r}}} = \frac{S_{f}}{S_{w}}a_{f}\tau
\end{eqnarray}
セルJ9に以下の数式を入力する
=(G22/B13)*G24*G26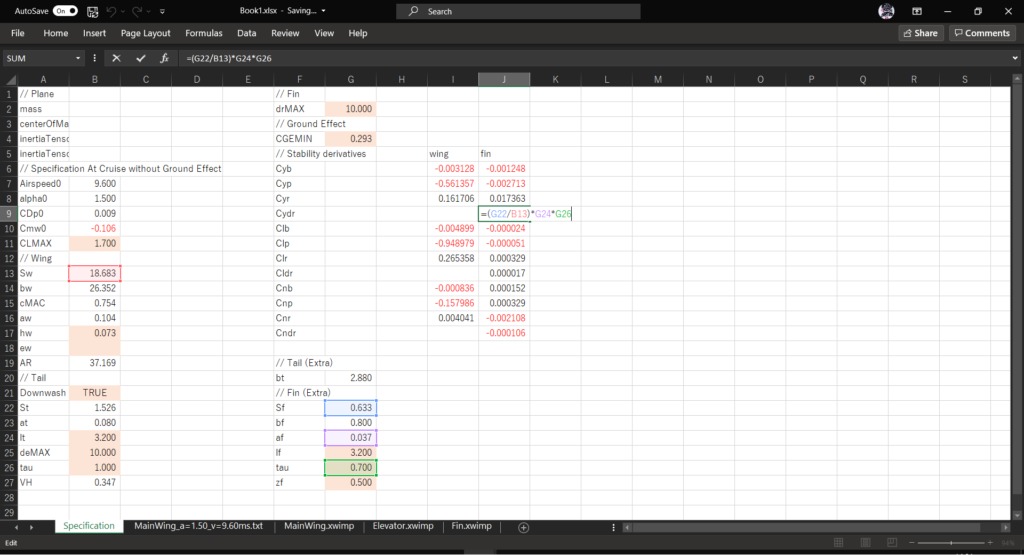
\((C_{l_{\beta}})_{fin}~\mathrm{[1/deg]}\)
\begin{eqnarray}
(C_{l_{\beta}})_{fin}=-\frac{S_{f}}{S_{w}}a_{f}\frac{l_{f}}{b_{w}}
\end{eqnarray}
セルJ10に以下の数式を入力する
=-(G22/B13)*G24*(G27/B14)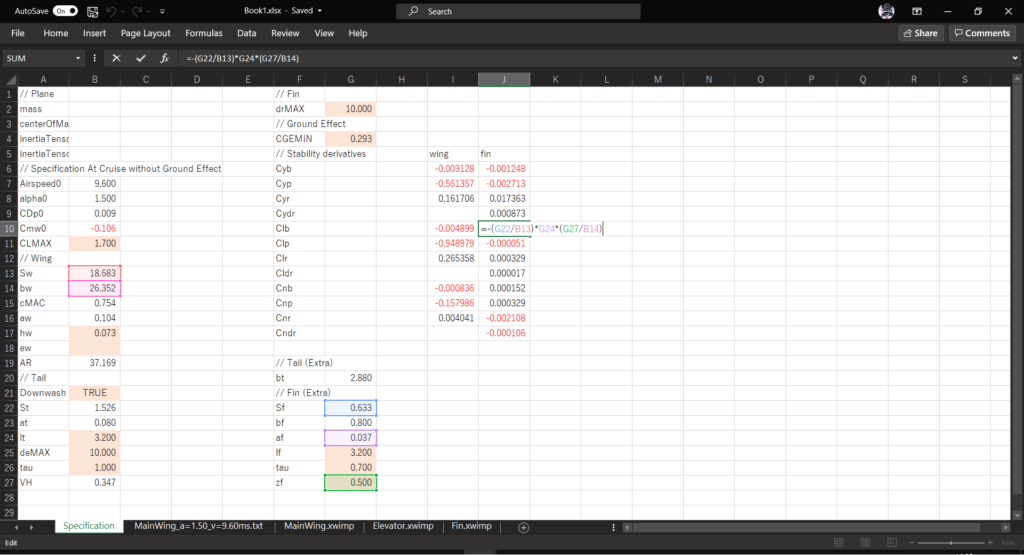
\((C_{l_{p}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{l_{p}})_{fin}=-\frac{S_{f}}{S_{w}}a_{f}\frac{2z_{f}}{b}\frac{z_{f}}{b_{w}}
\end{eqnarray}
セルJ11に以下の数式を入力する
=-(G22/B13)*DEGREES(G24)*(2*G27/B14)*(G27/B14)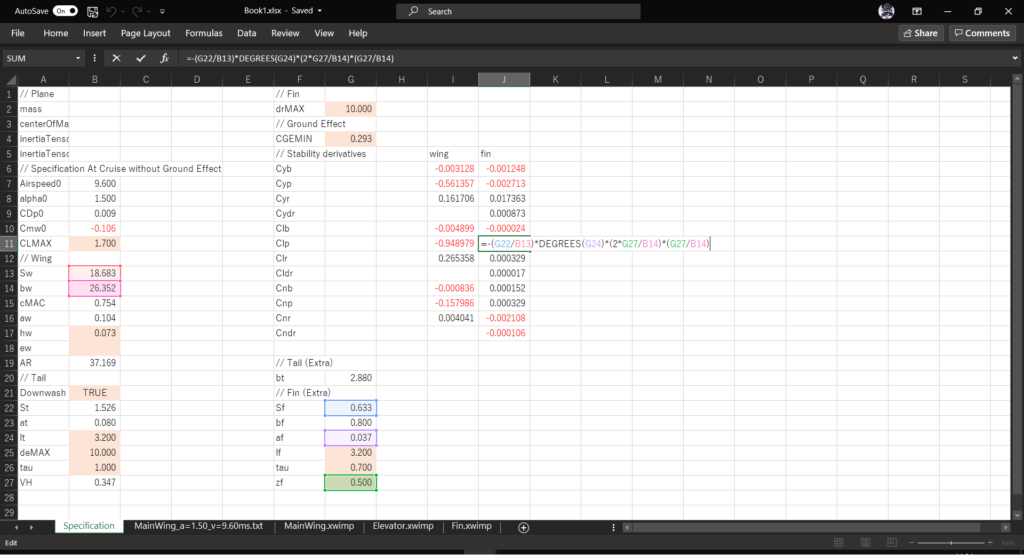
\((C_{l_{r}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{l_{r}})_{fin}=\frac{S_{f}}{S_{w}}a_{f}\frac{2l_{f}}{b}\frac{z_{f}}{b_{w}}
\end{eqnarray}
セルJ12に以下の数式を入力する
=(G22/B13)*DEGREES(G24)*(2*G25/B14)*(G27/B14)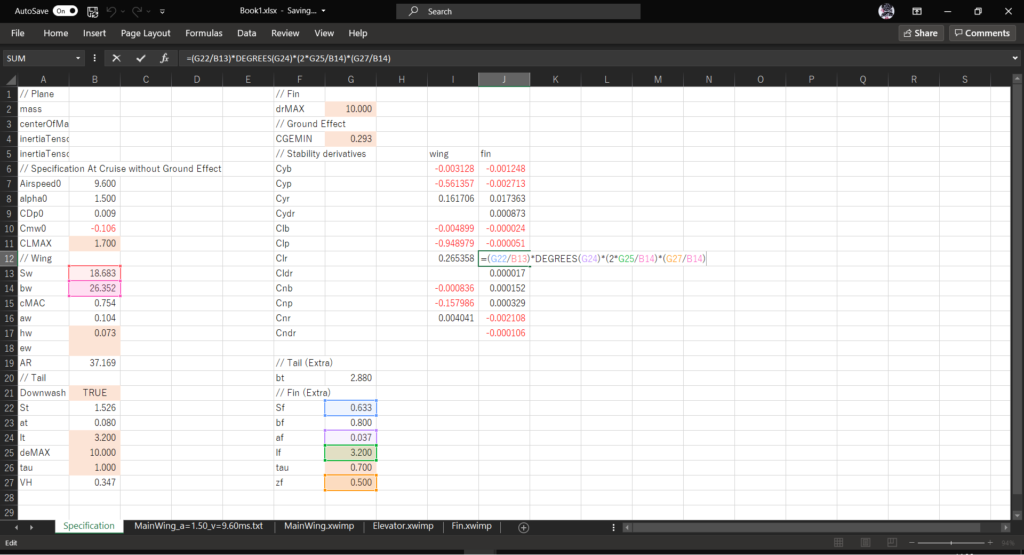
\((C_{l_{delta_{r}}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
C_{l_{\delta_{r}}} = C_{y_{\delta_{r}}}\frac{z_{f}}{b_{w}}
= \frac{S_{f}}{S_{w}}a_{f}\tau\frac{z_{f}}{b_{w}} \\
\end{eqnarray}
セルJ13に以下の数式を入力する
=J9*(G27/B14)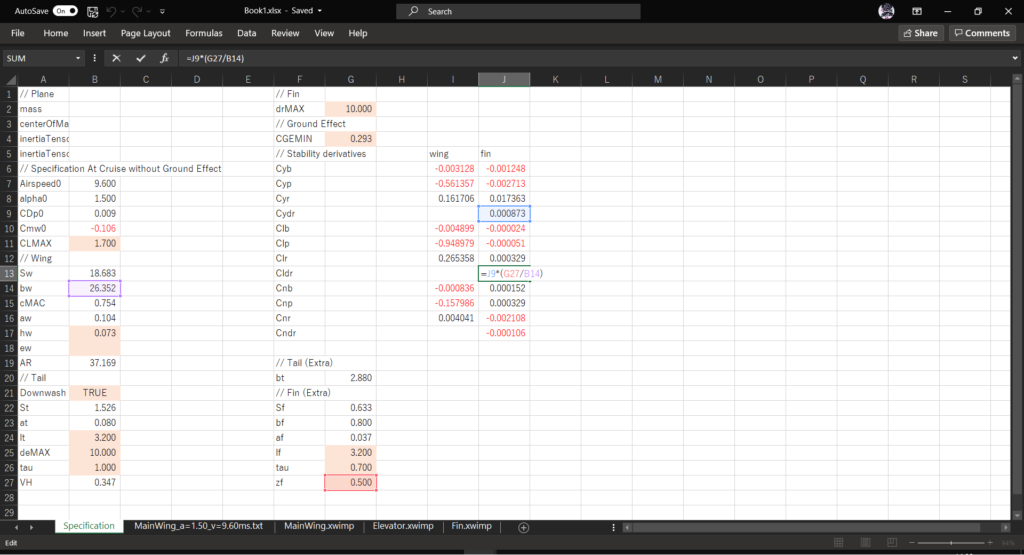
\((C_{n_{\beta}})_{fin}~\mathrm{[1/deg]}\)
\begin{eqnarray}
(C_{n_{\beta}})_{fin}=\frac{S_{f}}{S_{w}}a_{f}\frac{l_{f}}{b_{w}}
\end{eqnarray}
セルJ14に以下の数式を入力する
=(G22/B13)*G24*(G25/B14)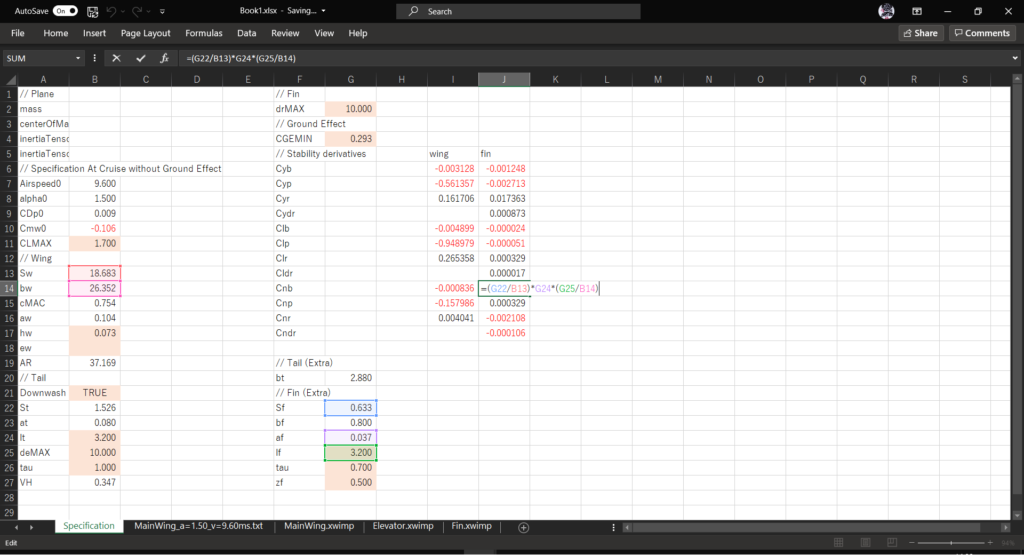
\((C_{n_{p}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{n_{p}})_{fin}=\frac{S_{f}}{S_{w}}a_{f}\frac{2z_{f}}{b}\frac{l_{f}}{b_{w}}
\end{eqnarray}
セルJ15に以下の数式を入力する
=(G22/B13)*DEGREES(G24)*(2*G27/B14)*(G25/B14)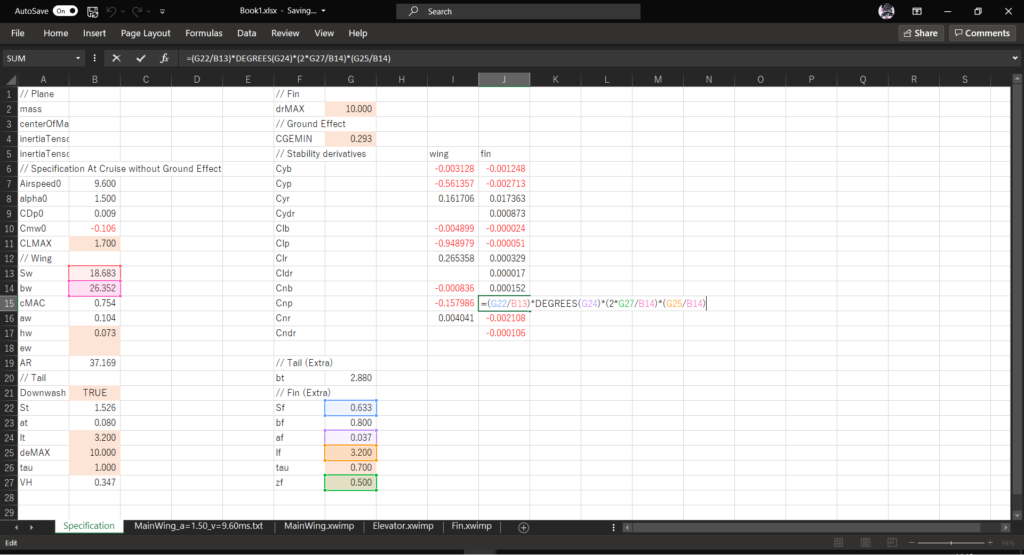
\((C_{n_{r}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
(C_{n_{r}})_{fin}=-\frac{S_{f}}{S_{w}}a_{f}\frac{2l_{f}}{b}\frac{l_{f}}{b_{w}}
\end{eqnarray}
セルJ16に以下の数式を入力する
=-(G22/B13)*DEGREES(G24)*(2*G25/B14)*(G25/B14)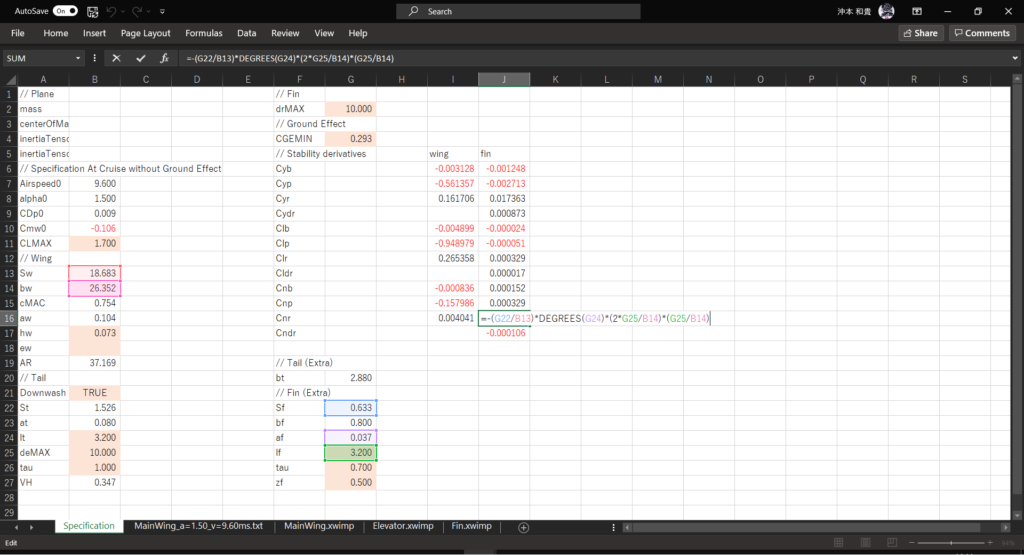
\((C_{n_{delta_{r}}})_{fin}~\mathrm{[1/rad]}\)
\begin{eqnarray}
C_{n_{\delta_{r}}} = -\frac{S_{f}}{S_{w}}a_{f}\tau\frac{l_{f}}{b_{w}} \\
\end{eqnarray}
セルJ16に以下の数式を入力する
=-J9*(G25/B14)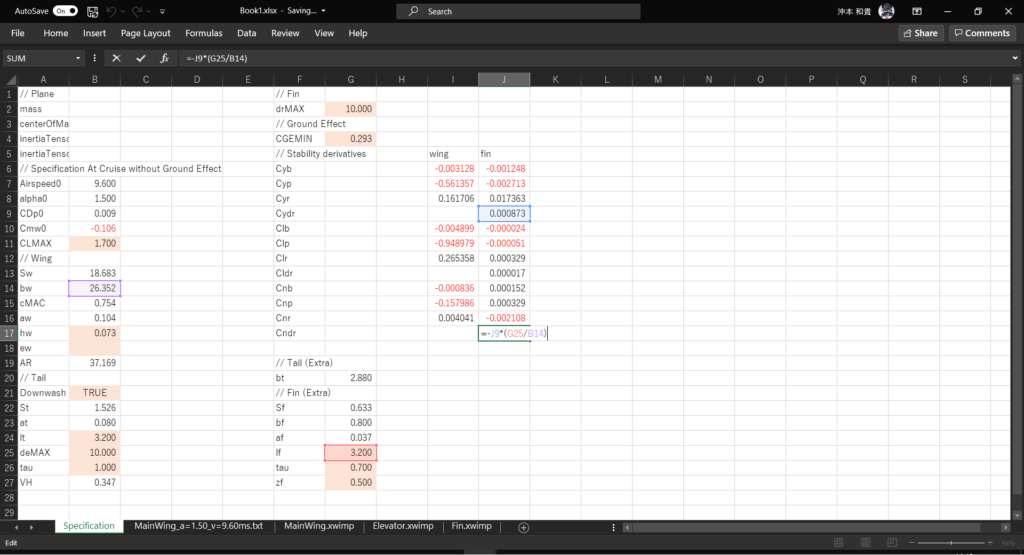
全機の安定微係数を計算する
横・方向の安定微係数における主翼の寄与と垂直尾翼の寄与を合計する
セルG6に以下の数式を入力し,セルG17までオートフィルを実行する
=SUM(I6:J6)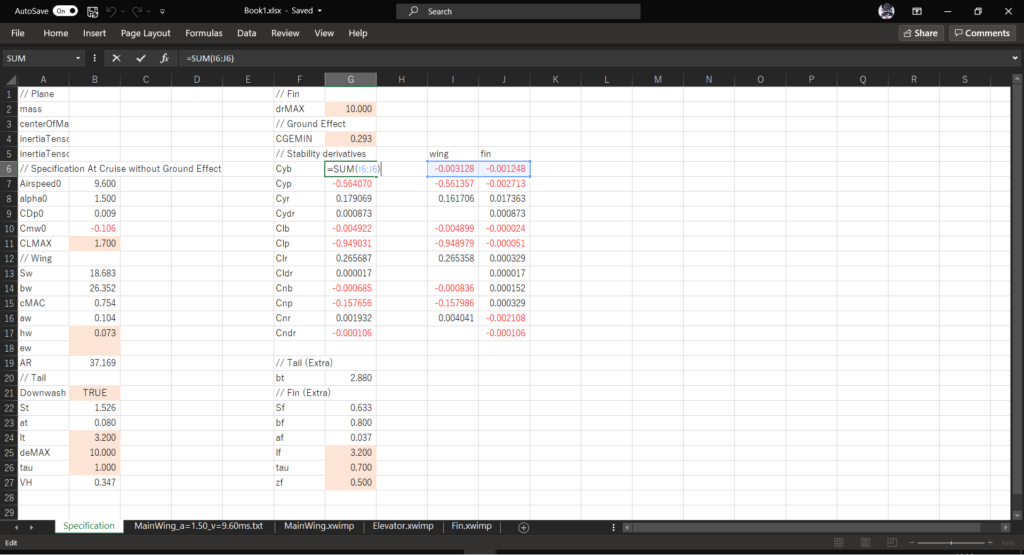
これで全機の横・方向の安定微係数が計算できた
以下の記事にある設計シートで計算した値と比較しても,それっぽい値が計算できていることがわかる
実際にシミュレーターに入力されている値はこれ
void InputSpecifications()
{
if(MyGameManeger.instance.PlaneName == "QX-18"){
// Plane
PlaneRigidbody.mass = 93.875f; // [kg]
PlaneRigidbody.centerOfMass = new Vector3(0f,0.221f,0f); // [m]
PlaneRigidbody.inertiaTensor = new Vector3(876f,947f,76f);
PlaneRigidbody.inertiaTensorRotation = Quaternion.AngleAxis(-4.833f, Vector3.forward);
// Specification At Cruise without Ground Effect
Airspeed0 = 9.700f; // Magnitude of ground speed [m/s]
alpha0 = 1.682f; // Angle of attack [deg]
CDp0 = 0.018f; // Parasitic drag [-]
Cmw0 = -0.164f; // Pitching momentum [-]
CLMAX = 1.700f;
// Wing
Sw = 18.042f; // Wing area of wing [m^2]
bw = 25.133f; // Wing span [m]
cMAC = 0.757f; // Mean aerodynamic chord [m]
aw = 0.108f; // Wing Lift Slope [1/deg]
hw = (0.323f-0.250f); // Length between Wing a.c. and c.g.
ew = 0.949f; // Wing efficiency
AR = (bw*bw)/Sw; // Aspect Ratio
// Tail
Downwash = true; // Conventional Tail: True, T-Tail: False
St = 1.375f; // Wing area of tail
at = 0.076f; // Tail Lift Slope [1/deg]
lt = 4.200f; // Length between Tail a.c. and c.g.
deMAX = 10.000f; // Maximum elevator angle
tau = 1.000f; // Control surface angle of attack effectiveness [-]
VH = (St*lt)/(Sw*cMAC); // Tail Volume
// Fin
drMAX = 10.000f; // Maximum rudder angle
// Ground Effect
CGEMIN = 0.215f; // Minimum Ground Effect Coefficient [-]
// Stability derivatives
Cyb = -0.002410f; // [1/deg]
Cyp = -0.228437f; // [1/rad]
Cyr = 0.090542f; // [1/rad]
Cydr = 0.001908f; // [1/deg]
Clb = -0.002002f; // [1/deg]
Clp = -0.877559f; // [1/rad]
Clr = 0.237651f; // [1/rad]
Cldr = 0.000052f; // [1/deg]
Cnb = -0.000059f; // [1/deg]
Cnp = -0.142441f; // [1/rad]
Cnr = -0.000491f; // [1/rad]
Cndr = -0.000262f; // [1/deg]
}else if(MyGameManeger.instance.PlaneName == "QX-19"){
// Plane
PlaneRigidbody.mass = 96.631f;
PlaneRigidbody.centerOfMass = new Vector3(0f,0.294f,0f);
PlaneRigidbody.inertiaTensor = new Vector3(991f,1032f,60f);
PlaneRigidbody.inertiaTensorRotation = Quaternion.AngleAxis(-9.134f, Vector3.forward);
// Specification At Cruise without Ground Effect
Airspeed0 = 8.800f; // Magnitude of ground speed [m/s]
alpha0 = 1.554f; // Angle of attack [deg]
CDp0 = 0.019f; // Parasitic drag [-]
Cmw0 = -0.170f; // Pitching momentum [-]
CLMAX = 1.700f;
// Wing
Sw = 18.275f; // Wing area of wing [m^2]
bw = 26.418f; // Wing span [m]
cMAC = 0.736f; // Mean aerodynamic chord [m]
aw = 0.105f; // Wing Lift Slope [1/deg]
hw = (0.323f-0.250f); // Length between Wing a.c. and c.g.
ew = 1.010f; // Wing efficiency
AR = (bw*bw)/Sw; // Aspect Ratio
// Tail
Downwash = true; // Conventional Tail: True, T-Tail: False
St = 1.548f; // Wing area of tail
at = 0.082f; // Tail Lift Slope [1/deg]
lt = 3.200f; // Length between Tail a.c. and c.g.
deMAX = 10.000f; // Maximum elevator angle
tau = 1.000f; // Control surface angle of attack effectiveness [-]
VH = (St*lt)/(Sw*cMAC); // Tail Volume
// Fin
drMAX = 10.000f; // Maximum rudder angle
// Ground Effect
CGEMIN = 0.361f; // Minimum Ground Effect Coefficient [-]
// Stability derivatives
Cyb = -0.005300f; // [1/deg]
Cyp = -0.567798f; // [1/rad]
Cyr = 0.225280f; // [1/rad]
Cydr = 0.001721f; // [1/deg]
Clb = -0.005118f; // [1/deg]
Clp = -0.827488f; // [1/rad]
Clr = 0.296796f; // [1/rad]
Cldr = 0.000050f; // [1/deg]
Cnb = -0.000808f; // [1/deg]
Cnp = -0.165533f; // [1/rad]
Cnr = 0.001675f; // [1/rad]
Cndr = -0.000208f; // [1/deg]
}else if(MyGameManeger.instance.PlaneName == "QX-20"){
// Plane
PlaneRigidbody.mass = 98.797f;
PlaneRigidbody.centerOfMass = new Vector3(0f,0.29f,0f);
PlaneRigidbody.inertiaTensor = new Vector3(1003f,1045f,58f);
PlaneRigidbody.inertiaTensorRotation = Quaternion.AngleAxis(-9.112f, Vector3.forward);
// Specification At Cruise without Ground Effect
Airspeed0 = 9.600f; // Magnitude of ground speed [m/s]
alpha0 = 1.459f; // Angle of attack [deg]
CDp0 = 0.016f; // Parasitic drag [-]
Cmw0 =-0.114f; // Pitching momentum [-]
CLMAX = 1.700f;
// Wing
Sw = 18.816f; // Wing area of wing [m^2]
bw = 26.679f; // Wing span [m]
cMAC = 0.755f; // Mean aerodynamic chord [m]
aw = 0.108f; // Wing Lift Slope [1/deg]
hw = (0.323f-0.250f); // Length between Wing a.c. and c.g.
ew = 0.986f; // Wing efficiency
AR = (bw*bw)/Sw; // Aspect Ratio
// Tail
Downwash = false; // Conventional Tail: True, T-Tail: False
St = 1.526f; // Wing area of tail
at = 0.088f; // Tail Lift Slope [1/deg]
lt = 3.200f; // Length between Tail a.c. and c.g.
deMAX = 10.000f; // Maximum elevator angle
tau = 1.000f; // Control surface angle of attack effectiveness [-]
VH = (St*lt)/(Sw*cMAC); // Tail Volume
// Fin
drMAX = 10.000f; // Maximum rudder angle
// Ground Effect
CGEMIN = 0.293f; // Minimum Ground Effect Coefficient [-]
// Stability derivatives
Cyb = -0.003555f; // [1/deg]
Cyp = -0.455493f; // [1/rad]
Cyr = 0.143466f; // [1/rad]
Cydr = 0.000888f; // [1/deg]
Clb = -0.004049f; // [1/deg]
Clp = -0.829690f; // [1/rad]
Clr = 0.227736f; // [1/rad]
Cldr = 0.000016f; // [1/deg]
Cnb = -0.000500f; // [1/deg]
Cnp = -0.132307f; // [1/rad]
Cnr = 0.000942f; // [1/rad]
Cndr = -0.000106f; // [1/deg]
}
}おわりに
XFLR5の三次元解析結果をもとに横・方向の安定微係数の値を計算した
この記事で作成したExcelファイルの情報と機体の3Dモデル(.objファイル)があれば,BRSimulator for Gliderに機体を実装することができる
↓関連記事



コメント
OnPointから数値を出力する時に、XFLR5も勝手に閉じて、データもtxt形式で保存したはずなのに0kbと表示され、中身も空っぽになってしまいます。対処法ありますか?
コメントありがとうございます!
そのような症状には遭遇したことがないですね…
A.Yさんが使用されているOSやXFLR5のバージョンが分からないので何とも言えないのですが,もしまだでしたら,PCの再起動とXFLR5の再インストールを試してみてはいかがでしょうか
お力になれずすみません…
ファイル名にバックスラッシュ等が入っている場合,類似の出力エラーが起きることがあるので
機体名や翼型名のRenameで改善するかもです.
恐らく、主翼だけでなく、ElevatorやRudderの情報も設定しているのではないでしょうか?
僕も同じ症状が出ていて困っていたのですが、Plane EditorでElevatorとFinのチェックを外すと動作するようになりました。
(Clb)finのlfやzfというのは具体的にどのような値でしょうか.主翼と尾翼の空力中心との距離でしょうか.
コメントいただきありがとうございます!
lfは重心から垂直尾翼の空力中心までの水平方向の距離、zfは重心から垂直尾翼の空力中心前の高さ方向の距離になります(要するにモーメントアームです)