数値流体力学(CFD)でよく使うテンソル演算についてまとめる
keywords: テンソル演算,テンソル積,内積,二重内積,外積,クロス積,勾配,発散,回転,偏差テンソル,静水圧テンソル,対称テンソル,非対称テンソル
はじめに
アインシュタインの総和規約についてはこちら
参考資料はこちら(※PDFダウンロード)
≫OpenFOAM® Documentation - Programmer’s Guide
テンソル(Tensor)
スカラー(scalar)=0階のテンソル
\begin{equation}
s
\end{equation}
ベクトル(vector)=1階のテンソル
\begin{equation}
\mathbf{a}=a_{i}
=\begin{bmatrix} a_{1} \\ a_{2} \\ a_{3} \end{bmatrix}
\end{equation}
テンソル(tensor)
\begin{equation}
\mathbf{T}=T_{ij}=
\begin{bmatrix}
T_{11} & T_{12} & T_{13} \\
T_{21} & T_{22} & T_{23} \\
T_{31} & T_{32} & T_{33} \\
\end{bmatrix}
\end{equation}
内積(Inner product)
ベクトルとベクトル
\begin{equation}
s=\mathbf{a}\cdot\mathbf{b}=a_{i}b_{i}= a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}
\end{equation}
ベクトルとテンソル(\(\mathbf{b}=\mathbf{T}\cdot\mathbf{a}\))
\begin{equation}
b_{i}=T_{ij}a_{j}= \begin{bmatrix}
T_{11}a_{1} + T_{12}a_{2} + T_{13}b_{3} \\
T_{21}a_{1} + T_{22}a_{2} + T_{23}b_{3} \\
T_{31}a_{1} + T_{32}a_{2} + T_{33}b_{3} \end{bmatrix}
\end{equation}
ベクトルとテンソル(\(\mathbf{b}=\mathbf{a}\cdot\mathbf{T}=\mathbf{T}^{\mathrm{T}}\cdot\mathbf{a}\))
\begin{equation}
b_{i}=T_{ji}a_{j}= \begin{bmatrix}
T_{11}a_{1} + T_{21}a_{2} + T_{31}b_{3} \\
T_{12}a_{1} + T_{22}a_{2} + T_{32}b_{3} \\
T_{13}a_{1} + T_{23}a_{2} + T_{33}b_{3} \end{bmatrix}
\end{equation}
テンソルとテンソル(\(\mathbf{P}=\mathbf{T}\cdot\mathbf{S}\))
\begin{equation}
P_{ij}=T_{ik}S_{kj}
\end{equation}
二重内積(Double inner product)
テンソルとテンソル
\begin{align}
s = \mathbf{T}\colon\mathbf{S} = T_{ij}S_{ij} =
& T_{11}S_{11} + T_{12}S_{12} + T_{13}S_{13} + \\
& T_{21}S_{21} + T_{22}S_{22} + T_{23}S_{23} + \\
& T_{31}S_{31} + T_{32}S_{32} + T_{33}S_{33}
\end{align}
外積(Outer product)
2つのベクトルに対するテンソル積のことで,外積(outer product)といったり直積(direct product)といったりする(\(\mathbf{T}=\mathbf{a}\otimes\mathbf{b}\))
テンソル積記号\(\otimes\)は省略されることが多い(\(\mathbf{T}=\mathbf{a}\mathbf{b}\))
\begin{equation}
T_{ij}=a_{i}b_{j}=\begin{bmatrix}
a_{1}b_{1} & a_{1}b_{2} & a_{1}b_{3} \\
a_{2}b_{1} & a_{2}b_{2} & a_{2}b_{3} \\
a_{3}b_{1} & a_{3}b_{2} & a_{3}b_{3} \end{bmatrix}
\end{equation}
線型代数学における直積(ちょくせき、英: direct product[1])あるいは外積(がいせき、英: outer product)は典型的には二つのベクトルのテンソル積を言う。座標ベクトル(英語版)の外積をとった結果は行列になる。外積の名称は内積に対照するもので、内積はベクトルの対をスカラーにする。外積は、クロス積の意味で使われることもあるため、どちらの意味で使われているか注意が必要である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
ベクトルとベクトルの外積 \(\mathbf{a}\otimes\mathbf{b}\) は,ベクトル\(\mathbf{a}\)と転置ベクトル\(\mathbf{b}^{\mathrm{T}}\)の積で表現できる
\begin{equation}
\mathbf{a}\otimes\mathbf{b}
=\mathbf{a}\mathbf{b}^{\mathrm{T}}
=\begin{bmatrix}
a_{1} \\
a_{2} \\
a_{3}
\end{bmatrix}
\begin{bmatrix} b_{1} & b_{2} & b_{3} \end{bmatrix}
=\begin{bmatrix}
a_{1}b_{1} & a_{1}b_{2} & a_{1}b_{3} \\
a_{2}b_{1} & a_{2}b_{2} & a_{2}b_{3} \\
a_{3}b_{1} & a_{3}b_{2} & a_{3}b_{3} \end{bmatrix}
\end{equation}
クロス積(Cross product)
ベクトルとベクトル
\begin{equation}
\mathbf{c}=\mathbf{a}\times\mathbf{b}
=\begin{bmatrix}
a_{2}b_{3}-a_{3}b_{2} \\
a_{3}b_{1}-a_{1}b_{3} \\
a_{1}b_{2}-a_{2}b_{1} \end{bmatrix}
\end{equation}
ベクトル積(英語: vector product)とは、ベクトル解析において、3次元の向き付けられた内積空間において定義される、2つのベクトルから新たなベクトルを与える二項演算である。2つのベクトル a, b (以下、ベクトルは太字で表記)のベクトル積は a×b や [a,b] で表される。演算の記号からクロス積(cross product)と呼ばれることもある。2つのベクトルからスカラーを与える二項演算である内積に対して外積(がいせき)とも呼ばれるが、英語でouter productは直積を意味するので注意を要する。ベクトル積を拡張した外積代数があり、ベクトル積はその3次元における特殊な場合である。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
微分演算(Differential operators)
ナブラ演算子(the nabla vector operator)
\begin{equation}
\nabla=\frac{\partial}{\partial x_{i}}
=\begin{bmatrix}
\frac{\partial}{\partial x_{1}} \\
\frac{\partial}{\partial x_{2}} \\
\frac{\partial}{\partial x_{3}}
\end{bmatrix}
\end{equation}
勾配(Gradient)
スカラー
\begin{equation}
\nabla s = \frac{\partial s}{\partial x_{i}}
=\begin{bmatrix} \frac{\partial s}{\partial x_{1}} \\ \frac{\partial s}{\partial x_{2}} \\ \frac{\partial s}{\partial x_{3}} \end{bmatrix}
\end{equation}
ベクトル
\begin{equation}
\nabla \mathbf{a}
=\frac{\partial a_{j}}{\partial x_{i}}
=\begin{bmatrix}
\frac{\partial a_{1}}{\partial x_{1}} & \frac{\partial a_{2}}{\partial x_{1}} & \frac{\partial a_{3}}{\partial x_{1}} \\
\frac{\partial a_{1}}{\partial x_{2}} & \frac{\partial a_{2}}{\partial x_{2}} & \frac{\partial a_{3}}{\partial x_{2}} \\
\frac{\partial a_{1}}{\partial x_{3}} & \frac{\partial a_{2}}{\partial x_{3}} & \frac{\partial a_{3}}{\partial x_{3}} \\
\end{bmatrix}
\end{equation}
勾配はテンソルのランクを1つ上げる作用を持つ操作である
すなわち,スカラー(0階のテンソル)の勾配はベクトル(1階のテンソル)に,ベクトル(1階のテンソル)の勾配は行列(2階のテンソル)になる
\begin{equation}
\nabla \mathbf{a}
=\nabla\otimes\mathbf{a}
=\frac{\partial}{\partial x_{i}}a_{j}
=\begin{bmatrix}
\frac{\partial a_{1}}{\partial x_{1}} & \frac{\partial a_{2}}{\partial x_{1}} & \frac{\partial a_{3}}{\partial x_{1}} \\
\frac{\partial a_{1}}{\partial x_{2}} & \frac{\partial a_{2}}{\partial x_{2}} & \frac{\partial a_{3}}{\partial x_{2}} \\
\frac{\partial a_{1}}{\partial x_{3}} & \frac{\partial a_{2}}{\partial x_{3}} & \frac{\partial a_{3}}{\partial x_{3}} \\
\end{bmatrix}
\end{equation}
発散(Divergence)
ベクトル
\begin{equation}
\nabla\cdot\mathbf{a}=\frac{\partial a_{i}}{\partial x_{i}}
=\frac{\partial a_{1}}{\partial x_{1}} + \frac{\partial a_{2}}{\partial x_{2}} + \frac{\partial a_{3}}{\partial x_{3}}
\end{equation}
テンソル
\begin{equation}
\nabla\cdot\mathbf{T}=\frac{\partial T_{ji}}{\partial x_{j}}
=\begin{bmatrix} \frac{\partial T_{j1}}{\partial x_{j}} \\ \frac{\partial T_{j2}}{\partial x_{j}} \\ \frac{\partial T_{j3}}{\partial x_{j}} \end{bmatrix}
=\begin{bmatrix}
\frac{\partial T_{11}}{\partial x_{1}}+\frac{\partial T_{21}}{\partial x_{2}}+\frac{\partial T_{31}}{\partial x_{3}} \\ \frac{\partial T_{12}}{\partial x_{1}}+\frac{\partial T_{22}}{\partial x_{2}}+\frac{\partial T_{32}}{\partial x_{3}} \\ \frac{\partial T_{13}}{\partial x_{1}}+\frac{\partial T_{23}}{\partial x_{2}}+\frac{\partial T_{33}}{\partial x_{3}}
\end{bmatrix}
\end{equation}
発散は,勾配とは逆に,テンソルのランクを1つ下げるよう作用する操作である
\begin{equation}
\nabla\cdot\mathbf{T}=\mathbf{T}^{\mathrm{T}}\nabla=T_{ji}\frac{\partial}{\partial x_{j}}
=\begin{bmatrix}
\frac{\partial T_{11}}{\partial x_{1}}+\frac{\partial T_{21}}{\partial x_{2}}+\frac{\partial T_{31}}{\partial x_{3}} \\ \frac{\partial T_{12}}{\partial x_{1}}+\frac{\partial T_{22}}{\partial x_{2}}+\frac{\partial T_{32}}{\partial x_{3}} \\ \frac{\partial T_{13}}{\partial x_{1}}+\frac{\partial T_{23}}{\partial x_{2}}+\frac{\partial T_{33}}{\partial x_{3}}
\end{bmatrix}
\end{equation}
回転(Curl)
ベクトル
\begin{equation}
\nabla\times\mathbf{a}=2 \left(^{*}\mathrm{skew}~\nabla\mathbf{a}\right)
=\begin{bmatrix}
\frac{\partial a_{3}}{\partial x_{2}}- \frac{\partial a_{2}}{\partial x_{3}} \\
\frac{\partial a_{1}}{\partial x_{3}}- \frac{\partial a_{3}}{\partial x_{1}} \\
\frac{\partial a_{2}}{\partial x_{1}}- \frac{\partial a_{1}}{\partial x_{2}}
\end{bmatrix}
\end{equation}
テンソル\(\mathbf{T}\)のホッジ双対\(^{*}\mathbf{T}\)は以下で定義される
\begin{equation}
^{*}\mathbf{T}=\begin{bmatrix} T_{23} \\ -T_{13} \\ T_{12} \end{bmatrix}
\end{equation}
ラプラシアン(Laplacian)
ラプラシアン演算子
\begin{align}
\Delta
=\nabla^{2}=\nabla\cdot\nabla
=\frac{\partial^{2}}{\partial x_{1}^{2}} + \frac{\partial^{2}}{\partial x_{2}^{2}} + \frac{\partial^{2}}{\partial x_{3}^{2}}
\end{align}
スカラー
\begin{align}
\Delta s
=\nabla^{2} s
=\frac{\partial^{2} s}{\partial x_{1}^{2}} + \frac{\partial^{2} s}{\partial x_{2}^{2}} + \frac{\partial^{2} s}{\partial x_{3}^{2}}
\end{align}
ベクトル
\begin{align}
\Delta \mathbf{a}
=\nabla^{2} \mathbf{a}
=\begin{bmatrix}
\frac{\partial^{2} a_{1}}{\partial x_{1}^{2}} + \frac{\partial^{2} a_{1} }{\partial x_{2}^{2}} + \frac{\partial^{2} a_{1} }{\partial x_{3}^{2}} \\
\frac{\partial^{2} a_{2}}{\partial x_{1}^{2}} + \frac{\partial^{2} a_{2} }{\partial x_{2}^{2}} + \frac{\partial^{2} a_{2} }{\partial x_{3}^{2}} \\
\frac{\partial^{2} a_{3}}{\partial x_{1}^{2}} + \frac{\partial^{2} a_{3} }{\partial x_{2}^{2}} + \frac{\partial^{2} a_{3} }{\partial x_{3}^{2}} \\
\end{bmatrix}
\end{align}
その他のテンソル演算
単位テンソル(identity tensor)
クロネッカーのデルタ(Kronecker delta)\(\delta_{ij}\)を使う
\begin{equation}
\mathbf{I}=\delta_{ij}
=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
\end{equation}
大きさ(Magnitude)
ベクトル
\begin{equation}
|\mathbf{a}|=\sqrt{\mathbf{a}\cdot\mathbf{a}}=\sqrt{a_{i}a_{i}}=\sqrt{a_{1}a_{1}+a_{2}a_{2}+a_{3}a_{3}}
\end{equation}
テンソル
\begin{equation}
|\mathbf{T}|=\sqrt{\mathbf{T}\colon\mathbf{T}}=\sqrt{T_{ij}T_{ij}}
\end{equation}
転置(Transpose)
テンソル\(\mathbf{T}=T_{ij}\)
\begin{equation}
\mathbf{T}^{\mathrm{T}}=T_{ji}
\end{equation}
対称テンソルと非対称テンソル(Symmetric and Skew tensors)
対称テンソルは\(T_{ij}=T_{ji}\),非対称テンソルは\(T_{ij}\neq T_{ji}\)
\begin{equation}
\mathbf{T}
=\frac{1}{2}\left(\mathbf{T}+\mathbf{T}^{\mathrm{T}}\right)
+\frac{1}{2}\left(\mathbf{T}-\mathbf{T}^{\mathrm{T}}\right)
=\mathrm{symm}~\mathbf{T}+\mathrm{skew}~\mathbf{T}
\end{equation}
\begin{equation}
\mathrm{symm}~\mathbf{T}
=\frac{1}{2}\left(\mathbf{T}+\mathbf{T}^{\mathrm{T}}\right)
=\frac{1}{2}\left(T_{ij}+T_{ji}\right)
\end{equation}
\begin{equation}
\mathrm{skew}~\mathbf{T}
=\frac{1}{2}\left(\mathbf{T}-\mathbf{T}^{\mathrm{T}}\right)
=\frac{1}{2}\left(T_{ij}-T_{ji}\right)
\end{equation}
\begin{equation}
\mathrm{symm}\mathbf{T}
=\begin{bmatrix}
T_{11} & \frac{1}{2}\left(T_{12}+T_{21}\right) & \frac{1}{2}\left(T_{13}+T_{31}\right) \\
\frac{1}{2}\left(T_{21}+T_{12}\right) & T_{22} & \frac{1}{2}\left(T_{23}+T_{32}\right) \\
\frac{1}{2}\left(T_{31}+T_{13}\right) & \frac{1}{2}\left(T_{32}+T_{23}\right) & T_{33} \end{bmatrix}
\end{equation}
\begin{equation}
\mathrm{skew}\mathbf{T}
=\begin{bmatrix}
0 & \frac{1}{2}\left(T_{12}-T_{21}\right) & \frac{1}{2}\left(T_{13}-T_{31}\right) \\
\frac{1}{2}\left(T_{21}-T_{12}\right) & 0 & \frac{1}{2}\left(T_{23}-T_{32}\right) \\
\frac{1}{2}\left(T_{31}-T_{13}\right) & \frac{1}{2}\left(T_{32}-T_{23}\right) & 0 \end{bmatrix}
\end{equation}
トレース(Trace)
対角成分の和
\begin{equation}
\mathrm{tr}~\mathbf{T}=T_{ii}=T_{11}+T_{22}+T_{33}
\end{equation}
Diagonal
2階のテンソルの対角成分を要素に持つベクトル
\begin{equation}
\mathrm{diag}~\mathbf{T}=\begin{bmatrix} T_{11} \\ T_{22} \\ T_{33} \end{bmatrix}
\end{equation}
偏差テンソルと静水圧テンソル(Deviatoric and Hydrostatic tensors)
\begin{equation}
\mathbf{T}=\mathbf{T}-\frac{1}{3}\left(\mathrm{tr}~\mathbf{T}\right)\mathbf{I}+\frac{1}{3}\left(\mathrm{tr}~\mathbf{T}\right)\mathbf{I}
=\mathrm{dev}~\mathbf{T}+\mathrm{hyd}~\mathbf{T}
\end{equation}
\begin{equation}
\mathrm{dev}~\mathbf{T}
=\mathbf{T}-\frac{1}{3}\left(\mathrm{tr}~\mathbf{T}\right)\mathbf{I}
=T_{ij}-\frac{1}{3}T_{kk}\delta_{ij}
\end{equation}
\begin{equation}
\mathrm{hyd}~\mathbf{T}
=\frac{1}{3}\left(\mathrm{tr}~\mathbf{T}\right)\mathbf{I}
=\frac{1}{3}T_{kk}\delta_{ij}
\end{equation}
\begin{equation}
\mathrm{dev}\mathbf{T}
=\begin{bmatrix}
T_{11}-\frac{T_{11}+T_{22}+T_{33}}{3} & T_{12} & T_{13} \\
T_{21} & T_{22}-\frac{T_{11}+T_{22}+T_{33}}{3} & T_{23} \\
T_{31} & T_{32} & T_{33}-\frac{T_{33}+T_{22}+T_{33}}{3}
\end{bmatrix}
\end{equation}
\begin{equation}
\mathrm{hyd}\mathbf{T}
=\begin{bmatrix}
\frac{T_{11}+T_{22}+T_{33}}{3} & 0 & 0 \\
0 & \frac{T_{11}+T_{22}+T_{33}}{3} & 0 \\
0 & 0 & \frac{T_{33}+T_{22}+T_{33}}{3}
\end{bmatrix}
\end{equation}
数値流体力学におけるテンソル演算
流れは非圧縮とする
連続の式
\begin{equation}
\nabla\cdot\mathbf{U}=0
\end{equation}
\begin{equation}
\frac{\partial U_{i}}{\partial x_{i}}=0
\end{equation}
Navier-Stokes方程式
\begin{equation}
\frac{\partial \mathbf{u}}{\partial t}
+\nabla\cdot\left(\mathbf{uu}\right)
= -\nabla p
+\nabla\cdot\left[\nu\left\{\nabla\mathbf{u}+\left(\nabla\mathbf{u}\right)^{\mathrm{T}}\right\}\right]
\end{equation}
\begin{equation}
\frac{\partial u_{i}}{\partial t}+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}} = -\frac{\partial p}{\partial x_{i}}+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
左辺第2項(対流項)については,\(\frac{\partial \left(u_{i}u_{j}\right)}{x_{j}}\),\(u_{j}\frac{\partial u_{i}}{x_{j}}\),\(\nabla\cdot\left(\mathbf{uu}\right)\),\(\mathbf{u}\cdot\nabla\mathbf{u}\),\(\left(\mathbf{u}\cdot\nabla\right)\mathbf{u}\)などの表記があるが,すべて同じ式を表している
\(\frac{\partial \left(u_{i}u_{j}\right)}{x_{j}}\)について,積の微分と連続の式(\( \frac{\partial u_{j}}{\partial x_{j}}=0 \))より
\begin{equation}
\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}
=\frac{\partial u_{i}}{\partial x_{j}}u_{j}+u_{i}\frac{\partial u_{j}}{\partial x_{j}}
=u_{j}\frac{\partial u_{i}}{\partial x_{j}}
\end{equation}
\begin{equation}
\nabla\cdot\left(\mathbf{uu}\right)
=\frac{\partial}{\partial x_{j}}\left(u_{i}u_{j}\right)
=\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}
=u_{j}\frac{\partial u_{i}}{\partial x_{j}}
\end{equation}
\begin{equation}
\mathbf{u}\cdot\left(\nabla\mathbf{u}\right)
=\left(\nabla\mathbf{u}\right)^{\mathrm{T}}\mathbf{u}
=\frac{\partial u_{i}}{\partial x_{j}}u_{j}
=u_{j}\frac{\partial u_{i}}{\partial x_{j}}
\end{equation}
\begin{equation}
\left(\mathbf{u}\cdot\nabla\right)\mathbf{u}
=\left(u_{j}\frac{\partial}{\partial x_{j}}\right)u_{i}
=u_{j}\frac{\partial u_{i}}{\partial x_{j}}
\end{equation}
右辺第2項(粘性項)については,テンソルの発散(\(\nabla\cdot\mathbf{T}=\mathbf{T}^{\mathrm{T}}\nabla=\frac{\partial}{\partial x_{j}}T_{ji}\))より
\begin{equation}
\nabla\cdot\nabla\mathbf{u}
=\left(\nabla\mathbf{u}\right)^{\mathrm{T}}\nabla
=\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}\right)
=\frac{\partial^{2} u_{i}}{\partial x_{1}^{2}}
+\frac{\partial^{2} u_{i}}{\partial x_{2}^{2}}
+\frac{\partial^{2} u_{i}}{\partial x_{3}^{2}}
\end{equation}
\begin{equation}
\nabla\cdot\left(\nabla\mathbf{u}\right)^{\mathrm{T}}
=\left(\nabla\mathbf{u}\right)\nabla
=\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{j}}{\partial x_{i}}\right)
=\frac{\partial}{\partial x_{i}}\left(\frac{\partial u_{j}}{\partial x_{j}}\right)=0
\end{equation}
速度勾配テンソル(Velocity gradient tensor)
\begin{equation}
\nabla\mathbf{u}=\frac{\partial u_{j}}{\partial x_{i}}
=\begin{bmatrix}
\frac{\partial u_{1}}{\partial x_{1}} & \frac{\partial u_{2}}{\partial x_{1}} & \frac{\partial u_{3}}{\partial x_{1}} \\
\frac{\partial u_{1}}{\partial x_{2}} & \frac{\partial u_{2}}{\partial x_{2}} & \frac{\partial u_{3}}{\partial x_{2}} \\
\frac{\partial u_{1}}{\partial x_{3}} & \frac{\partial u_{2}}{\partial x_{3}} & \frac{\partial u_{3}}{\partial x_{3}} \end{bmatrix}
\end{equation}
慣習的に,\(u_{i}\)に対する\(x_{j}\)の偏微分を\(u_{i,j}\)と表記することがある(\(~_{,j}\)が\(x_{j}\)による偏微分を表す)
その場合,速度勾配テンソルの\(ij\)成分が\(u_{j,i}\)となってしまい非常にややこしい
ひずみ速度テンソルと渦度テンソル(Strain rate and Vorticity tensor)
速度勾配テンソルの対称テンソルがひずみ速度テンソル(変形速度テンソル)で,非対称テンソルが渦度テンソル(スピンテンソル)である
\begin{equation}
\mathbf{\nabla\mathbf{u}}
=\frac{1}{2}\left\{\nabla\mathbf{u}+\left(\nabla\mathbf{u}\right)^{\mathrm{T}}\right\}
+\frac{1}{2}\left\{\nabla\mathbf{u}-\left(\nabla\mathbf{u}\right)^{\mathrm{T}}\right\}
=\mathbf{S}+\mathbf{W}
\end{equation}
\begin{equation}
\mathbf{S}=S_{ij}
=\frac{1}{2}\left\{\nabla\mathbf{u}+\left(\nabla\mathbf{u}\right)^{\mathrm{T}}\right\}
=\frac{1}{2}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)
\end{equation}
\begin{equation}
\mathbf{W}=W_{ij}
=-\frac{1}{2}\left\{\nabla\mathbf{u}-\left(\nabla\mathbf{u}\right)^{\mathrm{T}}\right\}
=\frac{1}{2}\left(\frac{\partial u_{i}}{\partial x_{j}}-\frac{\partial u_{j}}{\partial x_{i}}\right)
\end{equation}
渦度テンソルの定義式(\(\mathbf{W}=-\mathrm{skew}~\nabla\mathbf{u}\))に表されるマイナス符号に注意
Filtered Navier-Stokes方程式
\begin{equation}
\frac{\partial \mathbf{\overline{u}}}{\partial t}
+\nabla\cdot\left(\mathbf{\overline{u}\overline{u}}\right)
= -\nabla \overline{p}
+\nabla\cdot\left[\nu\left\{\nabla\mathbf{\overline{u}}+\left(\nabla\mathbf{\overline{u}}\right)^{\mathrm{T}}\right\}-\overline{\mathbf{u'u'}}\right]
\end{equation}
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}} = -\frac{\partial \overline{p}}{\partial x_{i}}+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\overline{u'_{i}u'_{j}}\right\}
\end{equation}
ただし,\(\mathbf{u'}\)は以下の式で定義される変動量である
\begin{equation}
\mathbf{u'}=u'_{i}=\mathbf{u}-\overline{\mathbf{u}}
=u_{i}-\overline{u}_{i}
\end{equation}
レイノルズ応力(SGS応力)
\begin{equation}
\boldsymbol{\tau}=\tau_{ij}=\overline{\mathbf{u'u'}}
=\overline{u'_{i}u'_{j}}
\end{equation}
乱流エネルギーと乱流散逸率(Turbulence kinetic energy and Turbulence dissipation rate)
乱流エネルギー
\begin{equation}
k=\frac{1}{2}\mathrm{tr}~\boldsymbol{\tau}
=\frac{1}{2}\mathrm{tr}~\overline{\mathbf{u'u'}}
=\frac{1}{2}\overline{u'_{i}u'_{i}}
\end{equation}
乱流散逸率
\begin{equation}
\varepsilon=\nu\overline{\nabla\mathbf{u'}\colon\nabla\mathbf{u'}}=\nu\overline{\frac{\partial u'_{i}}{\partial x_{j}}\frac{\partial u'_{i}}{\partial x_{j}}}
\end{equation}
渦粘性モデル(Eddy viscosity model)
\begin{equation}
\mathbf{\tau}=\tau_{ij}
=\frac{2}{3}k\mathbf{I}-2\nu\mathbf{S}
=\frac{2}{3}k\delta_{ij}-2\nu S_{ij}
\end{equation}
\begin{equation}
\mathrm{dev}~\mathbf{\tau}
=\mathbf{\tau}-\frac{1}{3}\left(\mathrm{tr}~\mathbf{ \tau}\right)\mathbf{I}
=\mathbf{\tau}-\frac{2}{3}k\mathbf{I}
=2\nu\mathbf{S}
\end{equation}
おわりに
数値流体力学でよく使うテンソル演算についてまとめた
個人的に速度勾配テンソルまわりの演算がややこしくて苦手
↓おすすめ記事
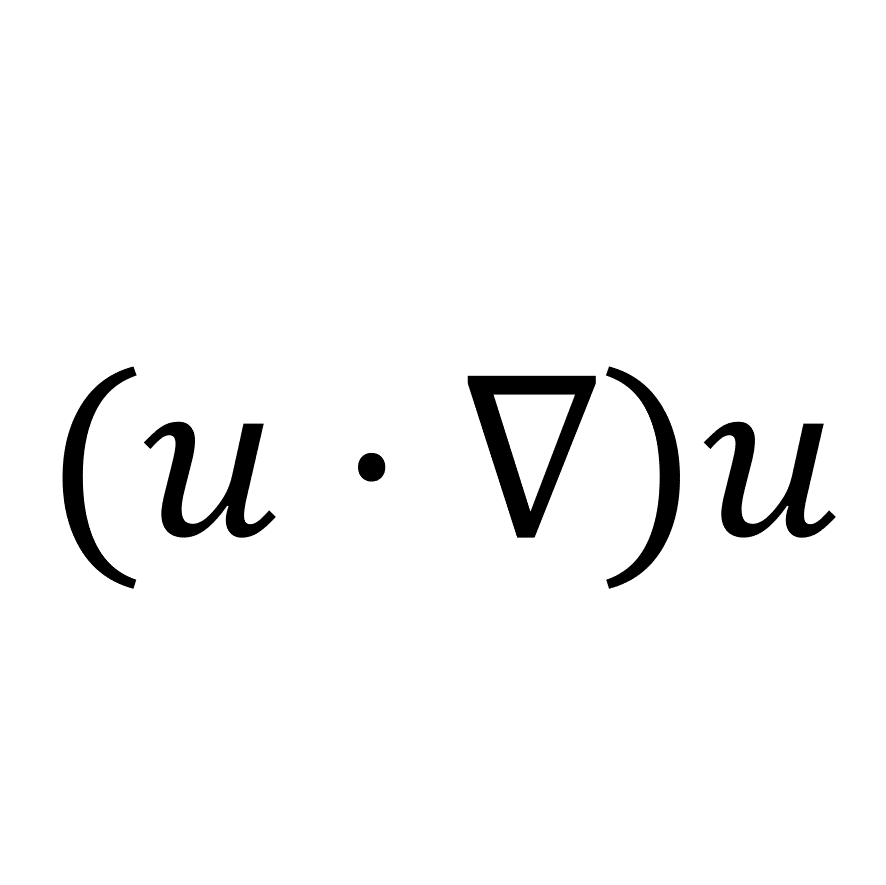
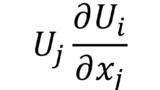


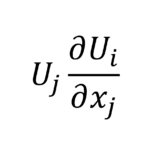

コメント