飛行力学で操縦性/安定性を考えるときに導入される機体座標系について説明する
はじめに
飛行力学では,トリムや操縦性/安定性について考えるために機体に固定された座標軸(機体軸)を定義する
機体軸という相対座標系の導入により,航空機の運動は次の2つに分けられるようになる
- 絶対座標系から見た機体座標系の運動
- 機体座標系から見た機体の運動
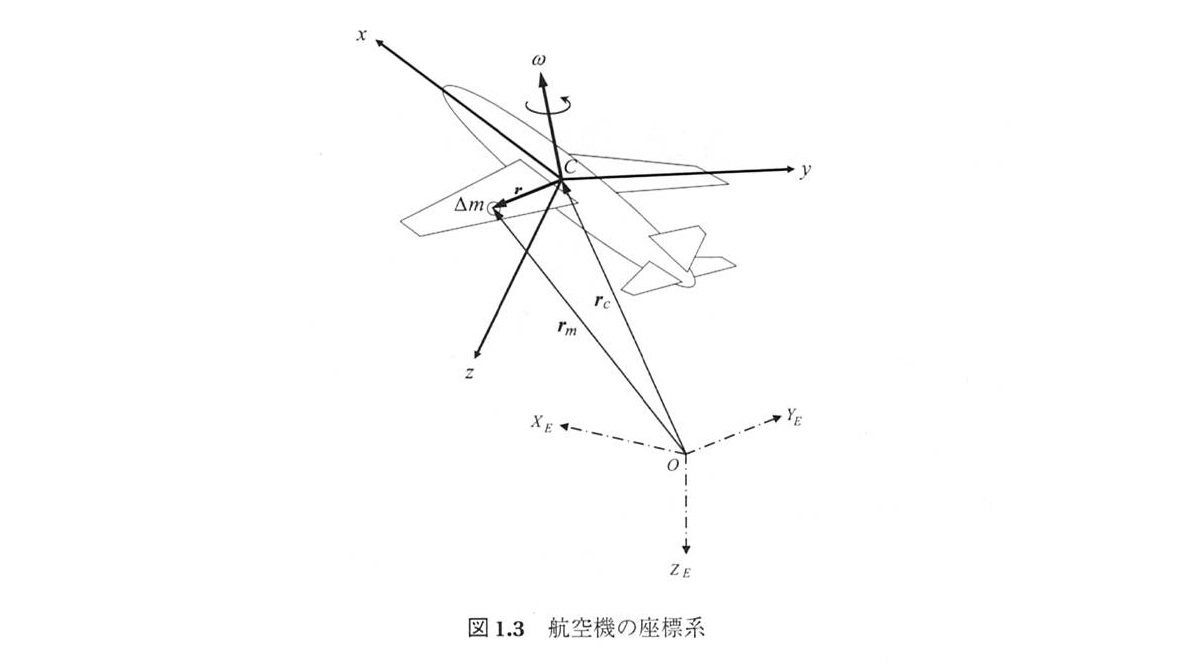
航空機の運動は基本的に航空機に固定した座標系(パイロット目線)で力やモーメントを考えて,最後の仕上げとして絶対座標系(地上にいる人目線)に変換する
ヘリコプターの座標軸の取り方は固定翼機と同じなので,固定翼機の空力制御の参考書をもとに説明していく
≫航空機力学入門(白本)
≫航空機の飛行力学と制御(青本)
機体座標の定義は航空機の操縦性/安定性の説明の大前提なのでどうしても最初に説明せざるをえないが,いかんせん分かりにくいし面白くもない
睡眠導入剤として抜群の威力を誇るため,眠くなるくらいなら読み飛ばしてしまっても構わないと思う(経験談)
ここでは,絶対座標系を\(X_{E}Y_{E}Z_{E}\)座標系,機体座標系を\(xyz\)座標系とする
機体軸の定義
以下のように定義する
- 機体重心に原点を固定する
- 機体前方にx軸,右翼側にy軸,機体下方にz軸を固定する
- 座標軸は機体と一緒に移動/回転する
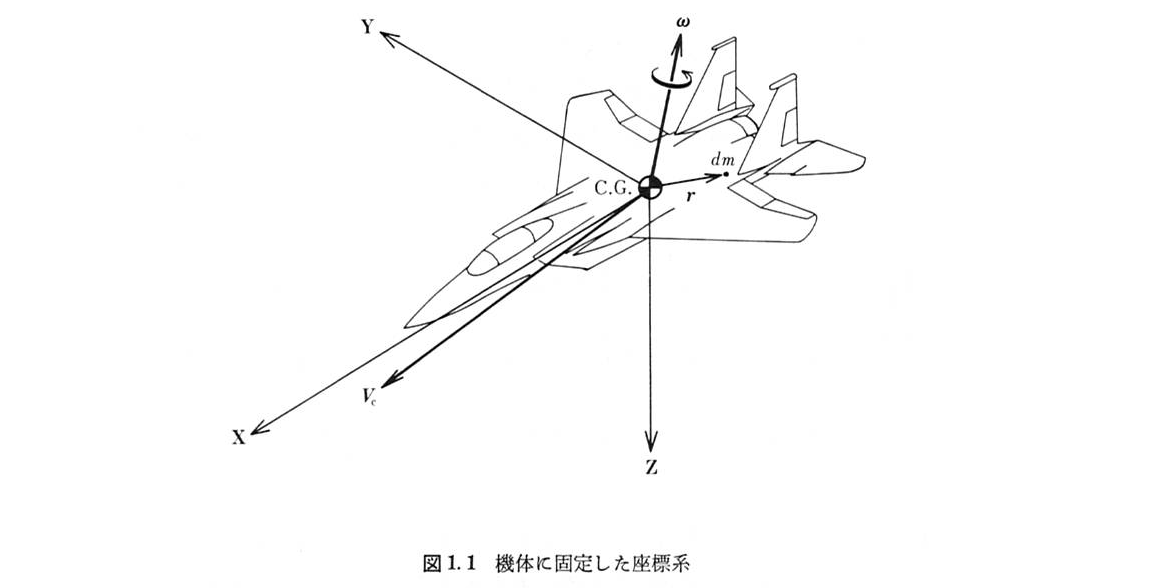
最初は違和感があるかもしれないが,慣れればどうってことはない
z軸が下向きに取ってあるので揚力の符号が負になることに注意する
似たような座標系として「安定軸」だの「風軸」だの「慣性主軸」だのがあるが,使い分けるメリットよりも混乱を招くデメリットの方が多いので今回の記事では使わない
それでは,機体座標を用いた位置/速度/加速度について説明していく
位置/姿勢角
「位置」については,機体座標系の原点が航空機の重心位置に固定されているので (航空機の位置)=(絶対座標系に対する機体座標系の原点の位置) である
「姿勢角」についても,機体座標系のxyz軸が航空機に固定されて一緒に回転するので (航空機の姿勢角)=(絶対座標系に対する機体座標系の回転角)である
航空機の姿勢角(機体座標系の回転角)は次の3つのオイラー角で定義される
- z軸回りの回転角 \(\psi\)(ヨーイング)
- y軸回りの回転角 \(\theta\)(ピッチング)
- x軸回りの回転角 \(\phi\)(ローリング)
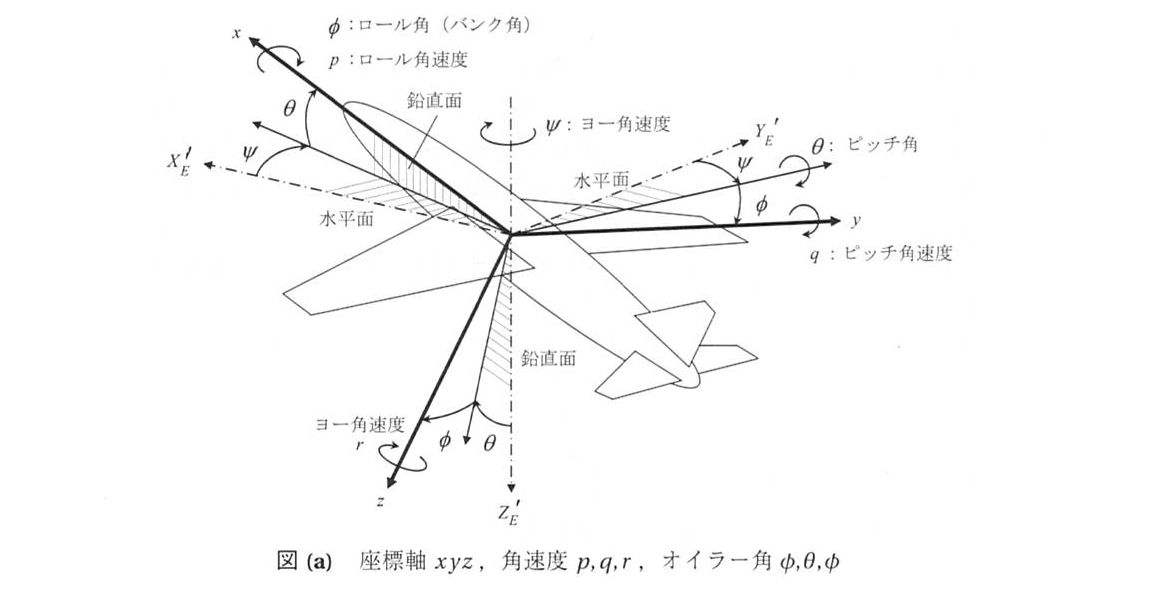
3つの角度を回転させる順番は決まっており,絶対座標系から機体座標系へ変換するときは ヨー→ピッチ→ロール(\(\psi\)→\(\theta\)→\(\phi\))の順番で回転させる
※回転させる順番を間違えると全く違う姿勢になってしまうので注意
絶対座標系から機体座標系への座標変換は以下のようになる
\begin{eqnarray}
\left[\begin{array}{c} x\\ y\\ z \end{array}\right]
=
\left[\begin{array}{lll}
\cos{\theta}\cos{\psi}&
\cos{\theta}\sin{\psi}&
-\sin{\theta}\\
\sin{\phi}\sin{\theta}\cos{\psi}-\cos{\phi}\sin{\psi}&
\sin{\phi}\sin{\theta}\sin{\psi}+\cos{\phi}\cos{\psi}&
\sin{\phi}\cos{\theta} \\
\cos{\phi}\sin{\theta}\cos{\psi}+\sin{\phi}\sin{\psi}&
\cos{\phi}\sin{\theta}\sin{\psi}-\sin{\phi}\cos{\psi}&
\cos{\phi}cos{\theta}
\end{array}\right]
\left[\begin{array}{c} X_{E}\\ Y_{E}\\ Z_{E} \end{array}\right]
\tag{青本 1.5-6}
\end{eqnarray}
逆に,機体座標系から絶対座標系への座標変換は以下のようになる
\begin{eqnarray}
\left[\begin{array}{c} X_{E}\\ Y_{E}\\ Z_{E} \end{array}\right]
=
\left[\begin{array}{lll}
\cos{\theta}\cos{\psi}&\sin{\phi}\sin{\theta}\cos{\psi}-\cos{\phi}\sin{\psi}&\cos{\phi}\sin{\theta}\cos{\psi}+\sin{\phi}\sin{\psi}\\
\cos{\theta}\sin{\psi}&\sin{\phi}\sin{\theta}\sin{\psi}+\cos{\phi}\cos{\psi}&\cos{\phi}\sin{\theta}\sin{\psi}-\sin{\phi}\cos{\psi}\\
-\sin{\theta}&\sin{\phi}\cos{\theta}&\cos{\phi}cos{\theta}
\end{array}\right]
\left[\begin{array}{c} x\\ y\\ z \end{array}\right]
\tag{青本 1.5-7}
\end{eqnarray}
x軸回り(\(\phi\)),y軸回り(\(\theta\)),z軸回り(\(\psi\))の回転行列は以下のようにあらわされる
\begin{eqnarray}
R_{\phi}= \left[\begin{array}{ccc}
1&0&0\\ 0&\cos{\phi}&\sin{\phi}\\ 0&-\sin{\phi}&\cos{\phi}
\end{array}\right] \tag{青本 1.5-4}
\end{eqnarray}
\begin{eqnarray}
R_{\theta}= \left[\begin{array}{ccc}
\cos{\theta}&0&-\sin{\theta}\\ 0&1&0\\ \sin{\theta}&0&\cos{\theta}
\end{array}\right] \tag{青本 1.5-3}
\end{eqnarray}
\begin{eqnarray}
R_{\psi}= \left[\begin{array}{ccc}
\cos{\psi}&\sin{\psi}&0\\ -\sin{\psi}&\cos{\psi}&0\\ 0&0&1
\end{array}\right] \tag{青本 1.5-2}
\end{eqnarray}
絶対座標系から機体座標系への変換は\(\psi\),\(\theta\),\(\phi\)の3つの姿勢角による回転に分けられるので,以下の4つの座標系を定義して1ステップごとに考えてみる
- 絶対座標系\(X_{E}Y_{E}Z_{E}\)
- \(X_{E}Y_{E}Z_{E}\)座標系を\(Z_{E}\)軸回りに\(\psi\)回転させた座標系\(x_{1}y_{1}z_{1}\)
- \(x_{1}y_{1}z_{1}\)座標系を\(y_{1}\)軸回りに\(\theta\)回転させた座標系\(x_{2}y_{2}z_{2}\)
- \(x_{2}y_{2}z_{2}\)座標系を\(x_{2}\)軸回りに\(\phi\)回転させた機体座標系\(xyz\)
すなわち,
\begin{align}
\left[\begin{array}{c} x_{1}\\ y_{1}\\ z_{1} \end{array}\right]
&= \left[\begin{array}{ccc}
\cos{\psi}&\sin{\psi}&0\\ -\sin{\psi}&\cos{\psi}&0\\ 0&0&1
\end{array}\right]
\left[\begin{array}{c} X_{E}\\ Y_{E}\\ Z_{E} \end{array}\right] \\ \\
\left[\begin{array}{c} x_{2}\\ y_{2}\\ z_{2} \end{array}\right]
&= \left[\begin{array}{ccc}
\cos{\theta}&0&-\sin{\theta}\\ 0&1&0\\ \sin{\theta}&0&\cos{\theta}
\end{array}\right]
\left[\begin{array}{c} x_{1}\\ y_{1}\\ z_{1} \end{array}\right] \\ \\
\left[\begin{array}{c} x\\ y\\ z \end{array}\right]
&= \left[\begin{array}{ccc}
1&0&0\\ 0&\cos{\phi}&\sin{\phi}\\ 0&-\sin{\phi}&\cos{\phi}
\end{array}\right]
\left[\begin{array}{c} x_{2}\\ y_{2}\\ z_{2} \end{array}\right] \\ \\
\end{align}
上記3式をまとめると,絶対座標系から機体座標系への座標変換の式を導出できる
逆に,機体座標系から絶対座標系への座標変換は,座標変換行列の転置を取ればいい
ヨーイングは機首を左右に振る運動(右ヨー/左ヨー),ピッチングは機首を上下に振る運動(頭上げ/頭下げ,ピッチアップ/ピッチダウン),ローリングは機体を左右に傾ける運動(右ロール/左ロール)である
ロールのことをバンクと言ったりもするが,違いはあまり分かっていない
速度/角速度
機体座標系における速度\([u, v, w]\)と角速度\([p, q, r]\)は,それぞれの機体軸に対して以下のように定義される
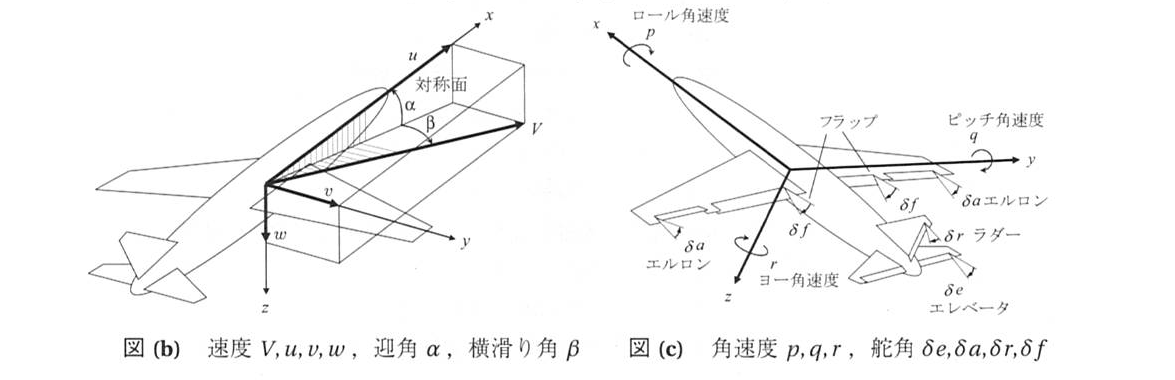
速度の正の方向は以下の通り
- x方向速度 u:前進が正(=機体に正面から風が当たるのが正)
- y方向速度 v:右側に進むのが正(=機体に右から風が当たるのが正)
- z方向速度 w:降下するのが正(=機体に下から風が当たるのが正)
時と場合によって「飛行機がどちらに進むか」と「機体から見てどちらから風が当たるのか」を使い分けて考えるとわかりやすい
角速度の正の方向は以下の通り
- ロール角速度 p:右ロールが正(機体が右に傾くとき正)
- ピッチ角速度 q:頭上げが正
- ヨー角速度 r:右ヨーが正(機首を右に向くとき正)
こちらは単純に,機体座標系の向きを頭に浮かべて「右ねじの向き」で考えればいい
速度を機体座標系から絶対座標系へ変換するには,上で紹介した回転行列を次のように用いる
\begin{eqnarray}
\left[\begin{array}{c} \dot{X_{E}}\\ \dot{Y_{E}}\\ \dot{Z_{E}} \end{array}\right]
=
\left[\begin{array}{lll}
\cos{\theta}\cos{\psi}&\sin{\phi}\sin{\theta}\cos{\psi}-\cos{\phi}\sin{\psi}&\cos{\phi}\sin{\theta}\cos{\psi}+\sin{\phi}\sin{\psi}\\
\cos{\theta}\sin{\psi}&\sin{\phi}\sin{\theta}\sin{\psi}+\cos{\phi}\cos{\psi}&\cos{\phi}\sin{\theta}\sin{\psi}-\sin{\phi}\cos{\psi}\\
-\sin{\theta}&\sin{\phi}\cos{\theta}&\cos{\phi}cos{\theta}
\end{array}\right]
\left[\begin{array}{c} u\\ v\\ w \end{array}\right]
\tag{青本 1.5-9 mod.}
\end{eqnarray}
角速度を機体座標系から絶対座標系へ変換するには少し複雑で,次の式を用いて行う
\begin{eqnarray}
\dot{\phi}&=&p+(r\cos{\phi}+q\sin{\phi})\tan{\theta}\\
\dot{\theta}&=&q\cos{\phi}-r\sin{\phi}\\
\dot{\psi}&=&\frac{r\cos{\phi}+q\sin{\phi}}{\cos{\theta}}
\tag{青本 1.6-9}
\end{eqnarray}
逆に,絶対座標系から機体座標系への変換は以下の式で行う
速度
\begin{eqnarray}
\left[\begin{array}{c} u\\ v\\ w \end{array}\right]
=
\left[\begin{array}{lll}
\cos{\theta}\cos{\psi}&
\cos{\theta}\sin{\psi}&
-\sin{\theta}\\
\sin{\phi}\sin{\theta}\cos{\psi}-\cos{\phi}\sin{\psi}&
\sin{\phi}\sin{\theta}\sin{\psi}+\cos{\phi}\cos{\psi}&
\sin{\phi}\cos{\theta} \\
\cos{\phi}\sin{\theta}\cos{\psi}+\sin{\phi}\sin{\psi}&
\cos{\phi}\sin{\theta}\sin{\psi}-\sin{\phi}\cos{\psi}&
\cos{\phi}cos{\theta}
\end{array}\right]
\left[\begin{array}{c} \dot{X_{E}}\\ \dot{Y_{E}}\\ \dot{Z_{E}} \end{array}\right]
\tag{青本 1.5-6 mod.}
\end{eqnarray}
角速度
\begin{eqnarray}
p&=&\dot{\phi}-\dot{\psi}\sin{\theta} \\
q&=&\dot{\theta}\cos{\phi}+\dot{\psi}\sin{\phi}\cos{\theta} \\
r&=&\dot{\psi}\cos{\phi}\cos{\theta}-\dot{\theta}\sin{\phi}
\tag{青本 1.6-8}
\end{eqnarray}
力/モーメント/舵角
機体座標系における力\([X, Y, Z]\)とモーメント\([L, M, N]\)は,それぞれの機体軸に対して以下のように定義される
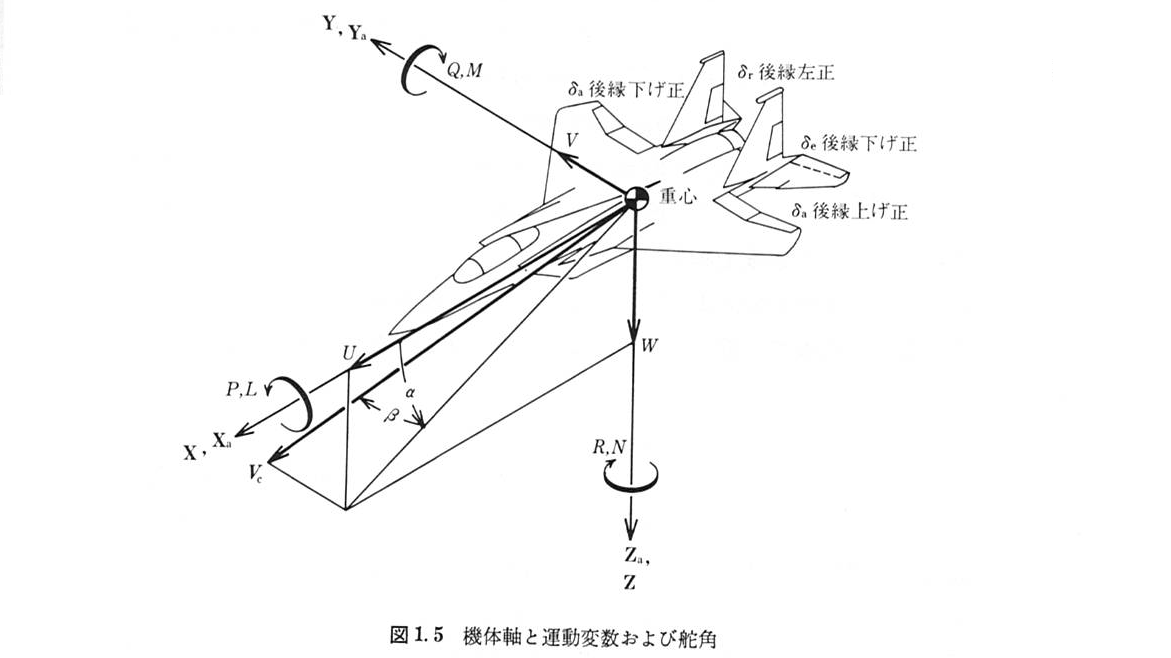
力およびモーメントの正の向きは速度および角速度の正の向きと同じである
- X:前進させる力が正
- Y:右側に進ませる力が正
- Z:降下させる力が正
- L:右ロールが正(ローリングモーメント)
- M:頭上げが正(ピッチングモーメント)
- N:右ヨーが正(ヨーイングモーメント)
また,エルロン/エレベーター/ラダーなどの舵角は機体周りに負のモーメントを発生させる向きを正とする
- エルロン舵角 \(\delta_{a}\):右翼後縁上げ/左翼後縁下げが正(左ロールさせる向き)
- エレベータ舵角 \(\delta_{e}\):後縁下げが正(ピッチダウンさせる向き)
- ラダー舵角 \(\delta_{r}\):後縁左が正(左ヨーさせる向き)
舵角の向きについては「操舵は機体の傾きを修正するためのもの」という考え方のもと,機体の傾きとは反対側に正の向きがとられたんじゃないかと思う
おわりに
飛行力学で操縦性/安定性を考えるときに導入される機体座標系について説明した
- 航空機の運動は機体に固定された機体座標系と地上に固定された絶対座標系に分けて記述される
- 機体座標系は重心位置に原点,機体前方にx軸,右翼側にy軸,機体下方にz軸をとり,機体に固定されている(一緒に運動/回転する)
- 航空機の姿勢はロール角\(\phi\),ピッチ角\(\theta\),ヨー角\(\psi\)の3つのオイラー角で表される
- 航空機の速度/角速度は機体座標系で定義される
- 姿勢角を用いた回転行列で機体座標系と絶対座標系は相互に変換することができる
- 航空機の回転の向きは,頭上げ,右ロール,右ヨーが正である
- 航空機の舵角は機体に負のモーメントを発生させる向きが正である
座標系がらみの話は退屈すぎて勉強するのが大変だが,実際にフライトシミュレーターなどを作成する際には非常に重要になってくる
最初はさらっと学んで概要だけ理解して,あとあと必要になってから振り返って学びなおせばいいんじゃないかと思う
↓関連記事






コメント