クォータニオンを使って航空機のフィードバック制御を行うエクセルシートを作成する
キーワード:quaternion,フィードバック制御
はじめに
参考にしたのはこちら
≫クオータニオンとオイラー角によるキネマティックス表現の比較について - NAL TM-636・・・文献1
≫MATLAB によるクォータニオン数値計算.pdf - 技術レポート(MSS技報)・・・文献2
≫クォータニオン計算便利ノート.pdf - 技術レポート(MSS技報)・・・文献3
この記事では文献1の式番号を(),文献2の式番号を[ ],文献3の式番号を< >で表すことにする
ちなみにオイラー角を使った航空機の制御はこちら
クォータニオンとは
クォータニオンは座標変換行列の親戚みたいなもので,物体を回転させたり姿勢角を表したりできる
四元数(しげんすう、英: quaternion(クォターニオン))は純粋数学のみならず応用数学、特に3Dグラフィクスやコンピュータビジョンにおいて三次元での回転の計算(英語版)でも用いられる。これはオイラー角や回転行列あるいはそれらに代わる道具などとともに、必要に応じて利用される。
四元数 - Wikipedia
航空機では機体の姿勢角を表すのにロール・ピッチ・ヨーのオイラー角を使うことが多いが,垂直上昇や背面飛行を行った際には特異点にはまってしまう可能性がある.
一方,クォータニオンではその心配がない
また,ある姿勢角から別の姿勢角に移るときに,ヨー・ピッチ・ロールに沿って3回回転させるのがオイラー角で,1回の回転ですむような回転軸を見つけてその軸まわりに回転させるのがクォータニオンである
クォータニオンは4つの成分を持ち,次のように表される
\begin{eqnarray}
\tilde{q}&=&q_{4}+q_{1}{\bf i}+q_{2}{\bf j}+q_{3}{\bf k}\\
&=&q_{4}+{\bf q}
\end{eqnarray}
ここで,\({\bf q}=[q_{1}, q_{2}, q_{3}]^{T}\)である
理論的説明
以下,ざっくり説明していく
慣性座標系を\(i\),機体座標系を\(b\)とすると,慣性座標系の座標\({\bf x_{i}}\)から機体座標系の座標\({\bf x_{b}}\)への座標変換は次の式(3.3), [1]で表される
\begin{eqnarray}
{\bf x_{b}}={\bf C}{\bf x_{i}}
\end{eqnarray}
ここで,座標変換行列は次の式(3,14), [2]で表される
\begin{eqnarray}
{\bf C}=
\left[\begin{array}{lll}
\cos{\theta}\cos{\psi} &\cos{\theta}\sin{\psi} &-\sin{\theta}\\
\sin{\phi}\sin{\theta}\cos{\psi}-\cos{\phi}\sin{\psi} &\sin{\phi}\sin{\theta}\sin{\psi}+\cos{\phi}\cos{\psi} &\sin{\phi}\cos{\theta}\\
\cos{\phi}\sin{\theta}\cos{\psi}+\sin{\phi}\sin{\psi} &\cos{\phi}\sin{\theta}\sin{\psi}-\sin{\phi}\cos{\psi} &\cos{\phi}cos{\theta}
\end{array}\right]
\end{eqnarray}
座標変換行列\({\bf C}\)を使うと姿勢角は次の表(2)または式[3a~c]のように求めることができる
\begin{eqnarray}
\phi&=&\arctan{\frac{C_{23}}{C_{33}}}\\
\theta&=&\arctan{\frac{-C_{13}}{\sqrt{C_{23}^2+C_{33}^2}}}\\
\psi&=&\arctan{\frac{C_{12}}{C_{11}}}\\
\end{eqnarray}
クォータニオンで回転させるときの回転軸方向の単位ベクトル\({\bf \lambda}\)および回転角\(\theta_{\lambda}\)は次の式(3.18~19)で求めることができる
\begin{eqnarray}
\theta_{\lambda}&=&\arccos{\frac{1}{2}\{1-(C_{11}+C_{22}+C_{33})\}}\\
\lambda_{1}&=&\frac{1}{2\sin{\theta_{\lambda}}}(C_{23}-C_{32})\\
\lambda_{2}&=&\frac{1}{2\sin{\theta_{\lambda}}}(C_{31}-C_{13})\\
\lambda_{3}&=&\frac{1}{2\sin{\theta_{\lambda}}}(C_{12}-C_{21})
\end{eqnarray}
また,クォータニオンは次の式(4.8), (4.11), [8a~d]で求めることができる
\begin{eqnarray}
q_{4}&=&\frac{1}{2}(1+C_{11}+C_{22}+C_{33})\\
q_{1}&=&\frac{1}{4q_{4}}(C_{23}-C_{32})\\
q_{2}&=&\frac{1}{4q_{4}}(C_{31}-C_{13})\\
q_{3}&=&\frac{1}{4q_{4}}(C_{12}-C_{21})
\end{eqnarray}
逆に,クォータニオンから座標変換行列は次の式(4.7), [7]で求めることができる
\begin{eqnarray}
{\bf C}=
\left[\begin{array}{lll}
q_{1}^2-q_{2}^2-q_{3}^2+q_{4}^2 &2(q_{1}q_{2}+q_{3}q_{4}) &2(q_{1}q_{3}-q_{2}q_{4})\\
2(q_{1}q_{2}-q_{3}q_{4}) &-q_{1}^2+q_{2}^2-q_{3}^2+q_{4}^2 &2(q_{2}q_{3}+q_{1}q_{4})\\
2(q_{1}q_{3}+q_{2}q_{4}) &2(q_{2}q_{3}-q_{1}q_{4}) &-q_{1}^2-q_{2}^2+q_{3}^2+q_{4}^2
\end{array}\right]
\end{eqnarray}
最後に,クォータニオンを用いた剛体の回転運動の方程式は次の式(5.35~36), (6.18)で表される
\begin{eqnarray}
{\bf \dot{\omega}}&=&{\bf I^{-1}}({\bf u}-{\bf \omega\times I\omega})\\
{\bf \dot{q}}&=&\frac{1}{2}(q_{4}{\bf \omega}+{\bf q\times\omega})\\
\dot{q_{4}}&=&-\frac{1}{2}{\bf \omega}\cdot{\bf q}
\end{eqnarray}
ここで,\({\bf I}\)は機体の慣性モーメント,\({\bf \omega}=[p, q, r]^{T}\)は機体座標系における角速度ベクトル,\({\bf u}\)は外力項である
フィードバック制御
今回は外力項\({\bf u}[N\cdot m]\)として下の式を用いる
\begin{eqnarray}
{\bf u}&=&\alpha{\bf q_{err}}+\beta({\bf 0}-{\bf \omega})\\
&=&\alpha{\bf q_{err}}-\beta{\bf \omega}
\end{eqnarray}
ここで,\(\alpha\),\(\beta\)は制御パラメータ―で,\({\bf 0}\)は目標とする角速度\({\bf \omega_{tgt}}={\bf 0}\)である
\({\bf q_{err}}\)は誤差クォータニオンで,現在の姿勢から目標姿勢までに必要な回転を表すクォータニオンである
現在の姿勢を\(\tilde{q}\),目標姿勢を\(\tilde{q}_{tgt}\)とすると,誤差クォータニオン\(\tilde{q}_{err}\)は次のように求められる
\begin{eqnarray}
\tilde{q}_{tgt}&=&\tilde{q}_{err}\tilde{q}\\
\tilde{q}_{err}&=&\tilde{q}_{tgt}\tilde{q}^{-1}=\tilde{q}_{tgt}\tilde{q}^{*}
\end{eqnarray}
ここで,\(\tilde{q}^{-1}\)は逆クォータニオン,\(\tilde{q}^{*}\)は共役クォータニオンで次の式<4>,<8>で表される
\begin{eqnarray}
\tilde{q}^{*}&=&q_{4}-{\bf q}=q_{4}-q_{1}{\bf i}-q_{2}{\bf j}-q_{3}{\bf k}\\
\tilde{q}^{-1}&=&\frac{\tilde{q}^{*}}{||\tilde{q}||}
\end{eqnarray}
単位クォータニオンでは逆クォータニオンと共役クォータニオンは等しくなる
また,2つのクォータニオン\(\tilde{q}\)と\(\tilde{p}\)の積は次の式<5>で定義されている
\begin{eqnarray}
\tilde{q}\tilde{p}&=&(q_{4}+{\bf q})(p_{4}+{\bf p})\\
&=&(q_{4}p_{4}-q_{1}p_{1}-q_{2}p_{2}-q_{3}p_{3})\\
&+&(q_{1}p_{4}+q_{4}p_{1}-q_{3}p_{2}+q_{2}p_{3}){\bf i}\\
&+&(q_{2}p_{4}+q_{3}p_{1}+q_{4}p_{2}-q_{1}p_{3}){\bf j}\\
&+&(q_{3}p_{4}-q_{2}p_{1}+q_{1}p_{2}+q_{4}p_{3}){\bf k}
\end{eqnarray}
これで航空機のフィードバック制御に必要な数式はそろった
全体の流れ
わかりやすい計算の流れのフローチャートを以下に示す
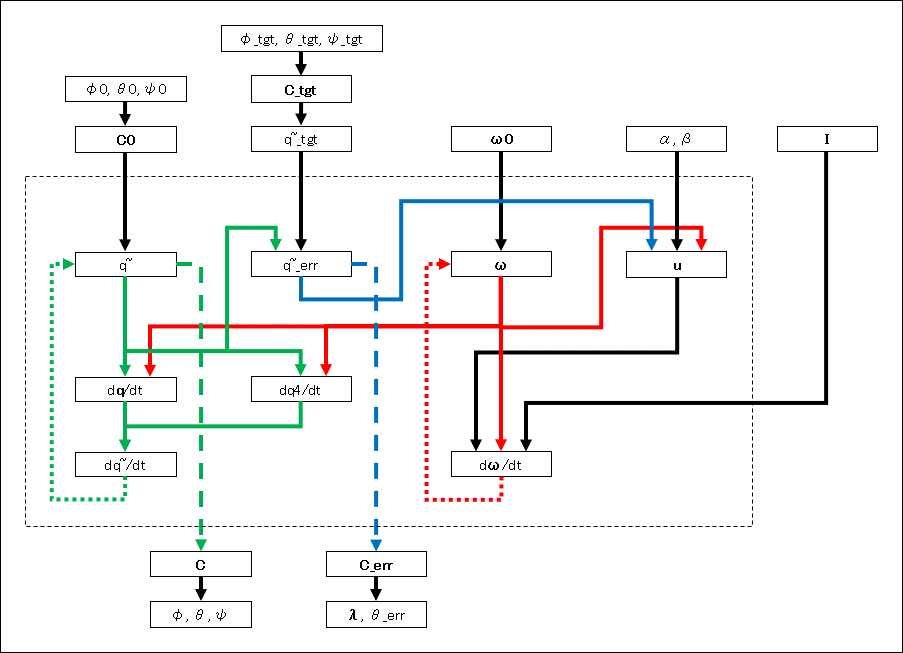
要するにこんな感じである
- 制御パラメータ\(\alpha\),\(\beta\)を入力
- 目標姿勢\(\phi_{tgt}\),\(\theta_{tgt}\),\(\psi_{tgt}\)を入力
- 機体パラメータ\(I_{xx}\), \(I_{yy}\), \(I_{zz}\), \(I_{xy}\), \(I_{yz}\), \(I_{zx}\)を入力
- 初期条件\(\phi_{0}\), \(\theta_{0}\), \(\psi_{0}\), \(\omega_{0}=[p_{0}, q_{0}, r_{0}]^{T}\)を入力
- \(\phi_{0}\), \(\theta_{0}\), \(\psi_{0}\)から\(C_{tgt}\)を計算,\(C_{tgt}\)から\(\tilde{q}_{tgt}\)を計算
- \(\phi_{0}\), \(\theta_{0}\), \(\psi_{0}\)から\(C_{0}\)を計算,\(C_{0}\)から\(\tilde{q}_{0}\)を計算
---7~12を繰り返し--- - \(\tilde{q}_{i}\),\(\tilde{q}_{tgt}\)から\({\tilde{q}_{err}}_{i}\)を計算
- \(\tilde{q}_{i}\)から\(C_{i}\)を計算,\(C_{i}\)から\(\phi_{i}\), \(\theta_{i}\), \(\psi_{i}\)を計算
- \({\tilde{q}_{err}}_{i}\)から\({\bf C_{err}}_{i}\)を計算,\({\bf C_{err}}_{i}\)から\({\bf \lambda_{i}}\), \({\theta_{err}}_{i}\)を計算
- \(\tilde{q}_{tgt}\)と\({\bf \omega_{i}}\)から\({\bf u_{i}}\)を計算
- 運動方程式を解いて\((\frac{d\tilde{q}}{dt})_{i}\),\((\frac{d\tilde{{\bf \omega}}}{dt})_{i}\)を計算
- \((\frac{d\tilde{q}}{dt})_{i}\),\((\frac{d\tilde{{\bf \omega}}}{dt})_{i}\)を使って\(\tilde{q}_{i+1}\),\({\bf \omega}_{i+1}\)を更新
これをエクセルシートに起こしたものがこちら
結果
さっそくシミュレーションを行ってみる
せっかくなので慣性モーメントには人力飛行機っぽい値を入れてみた
≫重量推算②
| dt | 0.100 | ||
| alpha | 1.0E+01 | ||
| beta | 5.0E+01 | ||
| phi_0_deg | 30.000 | ||
| theta_0_deg | 10.000 | ||
| psi_0_deg | -20.000 | ||
| phi_tgt_deg | -5.000 | ||
| theta_tgt_deg | 5.000 | ||
| psi_tgt_deg | 10.000 | ||
| I | 1000 | 0 | 0 |
| 0 | 60 | 0 | |
| -7 | 0 | 1000 |
結果はこんな感じ
誤差クォータニオンが減って値が安定しているのがわかる
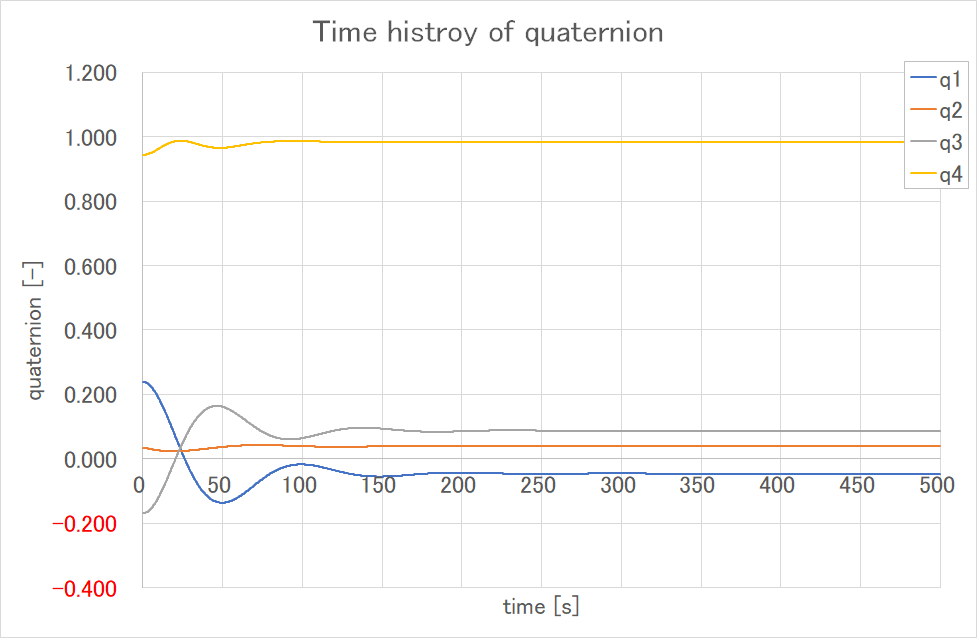
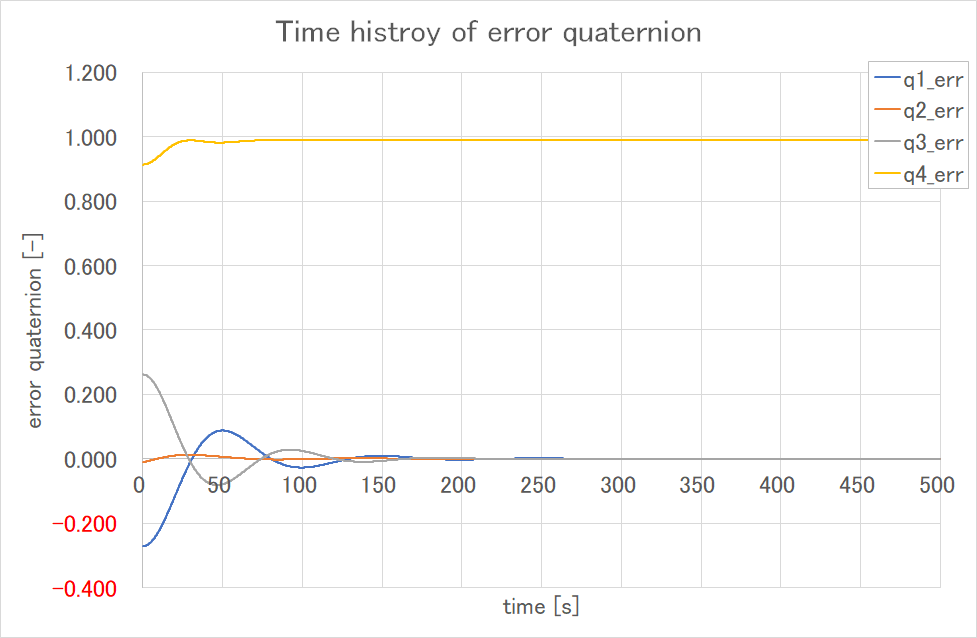
クォータニオンで言われてもわからん!という人はこちら
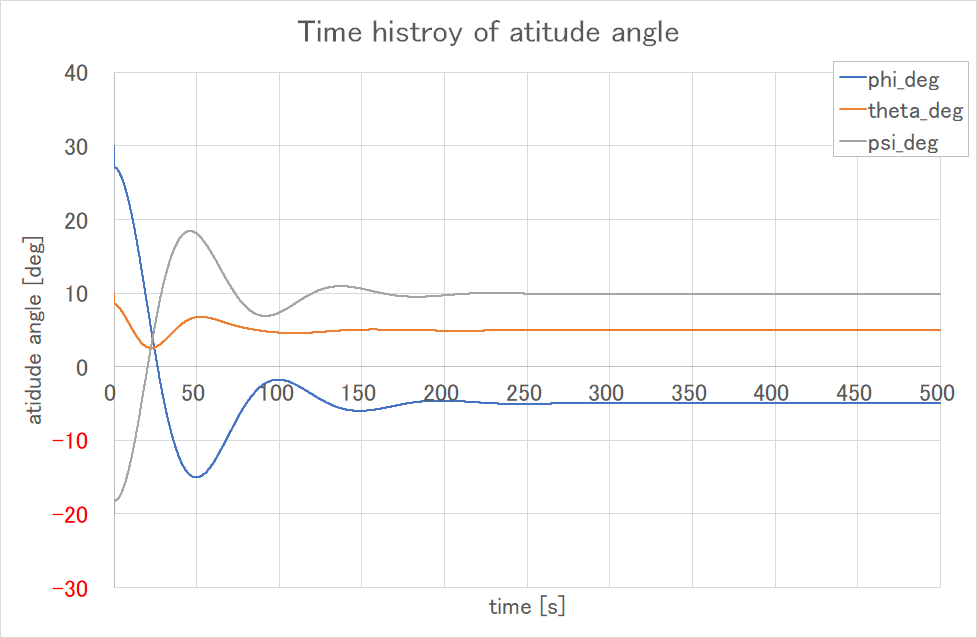
ロール・ピッチ・ヨーで見ても目標の姿勢角に制御できていることがわかる
ちなみに縦の慣性モーメントが横・方向に比べて小さいので,収束も早くなっている
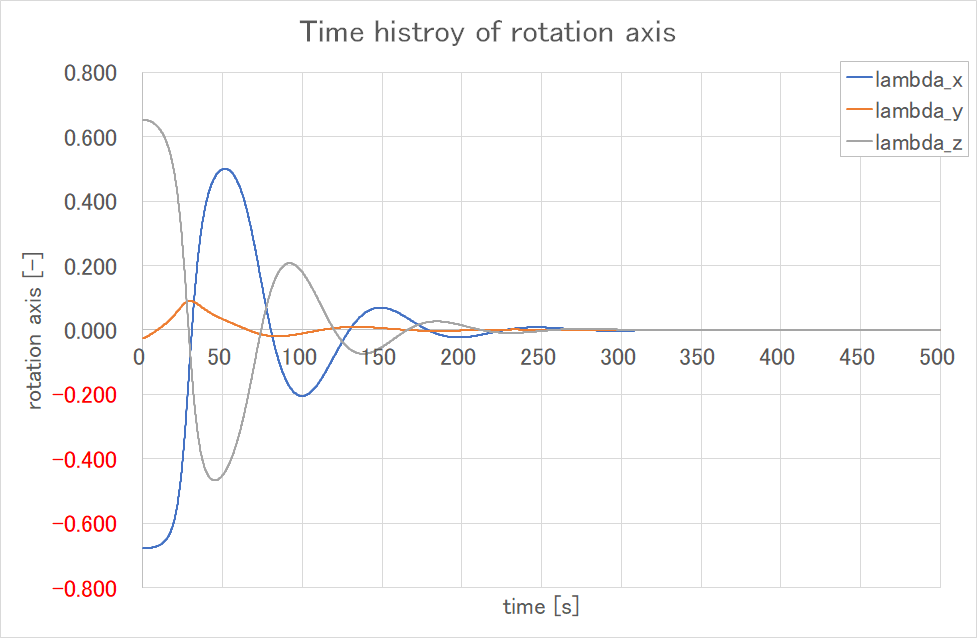
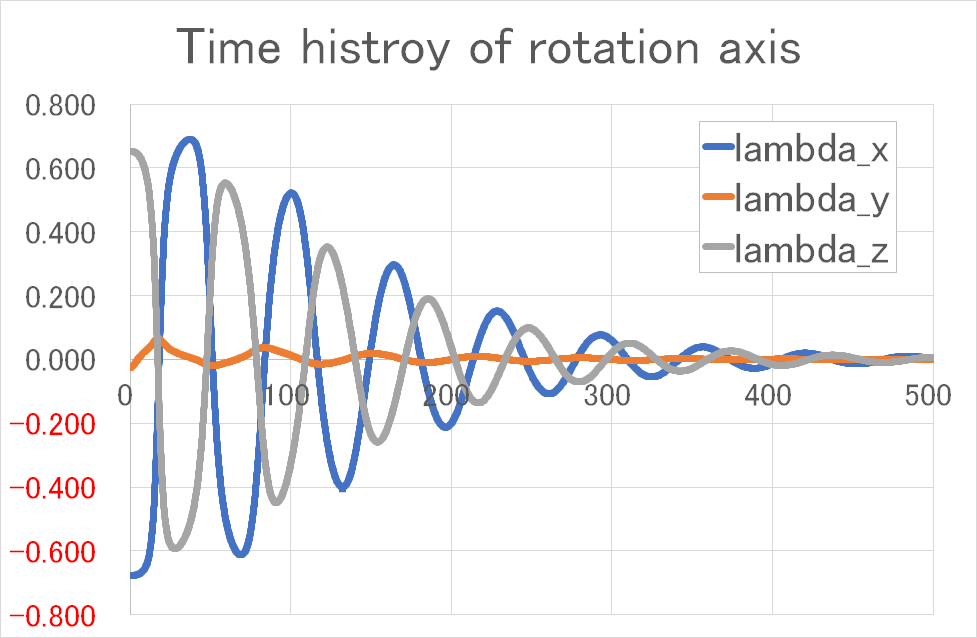
クォータニオンの回転軸の変化がこれ
ほぼx-z平面内で揺れながら0に近づいているのがわかる
まとめ
クォータニオンを使って航空機の姿勢角のフィードバック制御を行った
姿勢角の変化の小さい旅客機などでは使われないが,激しいマニューバを行う戦闘機や宇宙機などでは使うことがあるかもしれない
↓関連記事



コメント