Unityにおいて,左手系のクォータニオンから右手系のZ-Y-X系オイラー角(ロール・ピッチ・ヨー)を求める方法について説明する
実際に作成したフライトシミュレーターはこれ
その他の解説記事はこちら
keywords: Unity,物理演算,フライトシミュレーター,人力飛行機,クォータニオン,左手系,オイラー角,ロール,ピッチ,ヨー,Z-Y-X,Y-Z-X
はじめに
Unityにおいて,左手系のクォータニオンから右手系のZ-Y-X系オイラー角(ロール・ピッチ・ヨー)を求める方法について説明する
Unityのバージョンは2020.3.8f1
航空機の運動についての参考書はこちら
(通称:白本)
(通称:青本)
クォータニオンについてはこちら
≫【Excel】クォータニオンを使った航空機のフィードバック制御
≫回転ベクトル・回転行列・クォータニオン・オイラー角についてまとめてみた - かみのメモ
それではいってみよう
航空機におけるオイラー角
航空機の運動を考えるときは,機体前方にx軸,右翼側にy軸,機体下向きにz軸をとった右手座標系\(xyz\)を用いる(白本:p.2,青本:p.4)
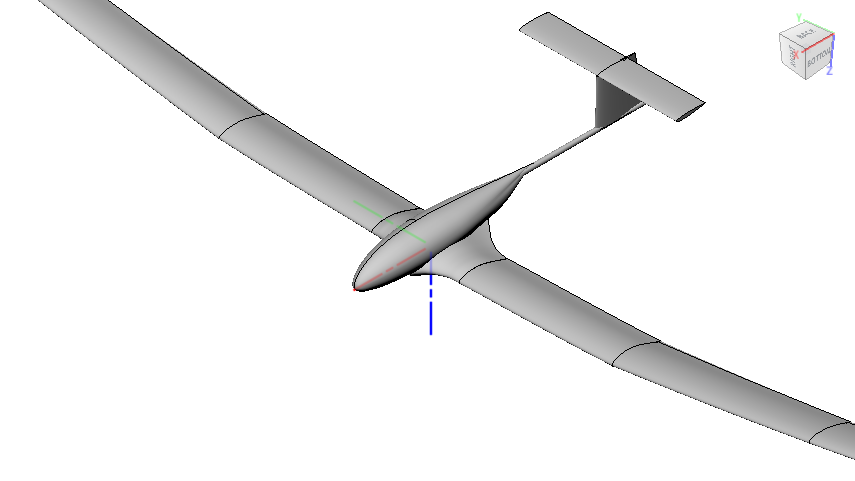
このとき,機体の姿勢は,x軸まわりの回転(ロール)角\(\phi\),y軸まわりの回転(ピッチ)角\(\theta\),z軸まわりの回転(ヨー)角\(\psi\)という3つのオイラー角によって表現される
≫オイラー角 - Wikipedia
≫4. オイラー角 - かみのメモ
それぞれ右ねじの向きを正とするので,ロール角は右ロールが正,ピッチ角は頭上げが正,ヨー角は機首を右に向ける回転が正である
オイラー角は回転させる軸の種類と順番の違いによって12種類存在するが,航空機で用いられるオイラー角はz軸→y軸→x軸(\(\psi\)→\(\theta\)→\(\phi\))の順番で回転させるZ-Y-X系のオイラー角である(白本:p.9,青本:p.17)
Unityにおけるクォータニオンとオイラー角
Unityなどのゲームエンジンにおいては,キャラクター視点で考えた時に,画面右向きにx軸,上向きにy軸をとったとき,進行方向にz軸をとるほうがわかりやすいという理由で左手座標系を使用していることが多い
左手系の時点でお察しだが,とりあえず進行方向にx軸,上向きにy軸をとるのが一番しっくり来たので,今回のフライトシミュレーターでは機体前方にx軸,機体上向きにy軸,左翼側にz軸をとった左手座標系\(x^{\prime\prime}y^{\prime\prime}z^{\prime\prime}\)を使うことにした

さらに,Unityなどのゲームエンジンでは回転を表現するのにオイラー角ではなくクォータニオンを用いることが多い
≫UnityEngine.Quaternion - Unity スクリプトリファレンス
ここで問題になるのが,Unity内でロール・ピッチ・ヨーを求めるにはどうすればいいのか,ということである
いちおうUnityにはクォータニオンからオイラー角を求める関数(Quaternion.eulerAngles)が用意されているが,Z-X-Y系のオイラー角なので全く役に立たない
≫Quaternion-eulerAngles - Unity スクリプトリファレンス
というわけで,「機体前方にx軸,機体上向きにy軸,左翼側にz軸をとった左手座標系で表現されたクォータニオン」から「機体前方にx軸,右翼側にy軸,機体下向きにz軸をとった右手座標系で表現されたZ-Y-X系のオイラー角」を計算する方法について説明する
左手系のクォータニオンから右手系のZ-Y-X系オイラー角への変換
ここからは説明のため以下の記号を用いる
- \(()^{\prime\prime}\):機体前方にx軸,機体上向きにy軸,左翼側にz軸をとった左手座標系で表現された値
- \(()^{\prime}\):機体後方にx軸,機体上向きにy軸,左翼側にz軸をとった右手座標系(上の\(x^{\prime\prime}y^{\prime\prime}z^{\prime\prime}\)座標系のx軸を反転した座標系)で表現された値
- \(()\):機体前方にx軸,右翼側にy軸,機体下向きにz軸をとった右手座標系で表現された値
また,回転角\([\phi, \theta, \psi]\)は,それぞれの座標系におけるx軸まわり,y軸まわり,z軸まわりの回転とする
以上を踏まえて,左手系\(x^{\prime\prime}y^{\prime\prime}z^{\prime\prime}\)のクォータニオンから右手系\(xyz\)のZ-Y-X系オイラー角への変換は,以下の手順で行う
- 左手系のクォータニオン\(q^{\prime\prime}\)を右手系のクォータニオン\(q^{\prime}\)に変換する
- 右手系のクォータニオン\(q^{\prime}\)から右手系の回転行列\(C^{\prime}\)を求める
- 右手系の回転行列\(C^{\prime}\)から右手系の回転角\([\phi^{\prime}, \theta^{\prime},\psi^{\prime}]\)を求める
- 右手系の回転角\([\phi^{\prime}, \theta^{\prime},\psi^{\prime}]\)を右手系のZ-Y-X系オイラー角\([\phi, \theta,\psi]\)に変換する
それではいってみよう
左手系のクォータニオンを右手系のクォータニオンに変換する
そもそもクォータニオン\(q\)は,回転軸方向の単位ベクトル\({\bf n}=[n_{x}, n_{y}, n_{z}]\)とその軸まわりの回転角\(\theta\)によって以下のように定義される
\begin{eqnarray}
q&=&\cos{\frac{\theta}{2}}+{\bf n}\sin{\frac{\theta}{2}}\\
&=&\cos{\frac{\theta}{2}}+{\bf i}~n_{x}\sin{\frac{\theta}{2}}+{\bf j}~n_{y}\sin{\frac{\theta}{2}}+{\bf k}~n_{z}\sin{\frac{\theta}{2}}\\
\end{eqnarray}
ここで,x軸を反転することによる左手系から右手系(右手系から左手系)への変換を考えると,x軸の反転によって\(n_{x}\rightarrow -n_{x}\)であり,回転の正の向きが右ねじから左ねじ(左ねじから右ねじ)に変わることによって\(\theta\rightarrow -\theta\)であるので,変換されたクォータニオン\(q^{\prime}\)は以下のようになる
\begin{eqnarray}
q^{\prime}&=&\cos{(-\frac{\theta}{2})}+{\bf i}(-n_{x})\sin{(-\frac{\theta}{2})}+{\bf j}~n_{y}\sin{(-\frac{\theta}{2})}+{\bf k}~n_{x}\sin{\left(-\frac{\theta}{2}\right)}\\
&=&\cos{\frac{\theta}{2}}+{\bf i}~n_{x}\sin{\frac{\theta}{2}}-{\bf j}~n_{y}\sin{\frac{\theta}{2}}-{\bf k}~n_{z}\sin{\frac{\theta}{2}}\\
&=&q_{w}+q_{x}-q_{y}-q_{z}\\
\end{eqnarray}
要するに,反転させた軸以外の2軸の成分の符号を変えるだけでいい
この関係式を使えば,左手系のクォータニオン\(q^{\prime\prime}\)を右手系のクォータニオン\(q^{\prime}\)に変換することができる
クォータニオンから回転行列を求める
クォータニオン\(q\)と回転行列\({\bf C}\)の関係は以下のようになる
\begin{eqnarray}
{\bf C}=
\left[\begin{array}{ccc}
q_{1}^2-q_{2}^2-q_{3}^2+q_{4}^2 &2(q_{1}q_{2}+q_{3}q_{4}) &2(q_{1}q_{3}-q_{2}q_{4})\\
2(q_{1}q_{2}-q_{3}q_{4}) &-q_{1}^2+q_{2}^2-q_{3}^2+q_{4}^2 &2(q_{2}q_{3}+q_{1}q_{4})\\
2(q_{1}q_{3}+q_{2}q_{4}) &2(q_{2}q_{3}-q_{1}q_{4}) &-q_{1}^2-q_{2}^2+q_{3}^2+q_{4}^2
\end{array}\right]
\end{eqnarray}
この関係式を使えば,右手系のクォータニオン\(q^{\prime}\)から右手系の回転行列\(C^{\prime}\)を求めることができる
回転行列から回転角を求める
機体後方にx軸,機体上向きにy軸,左翼側にz軸をとった\(x^{\prime}y^{\prime}z^{\prime}\)座標系において,\(xyz\)座標系のZ-Y-X系オイラー角と等価なオイラー角はY'-Z'-X'系オイラー角である(ただし回転方向はすべて負)
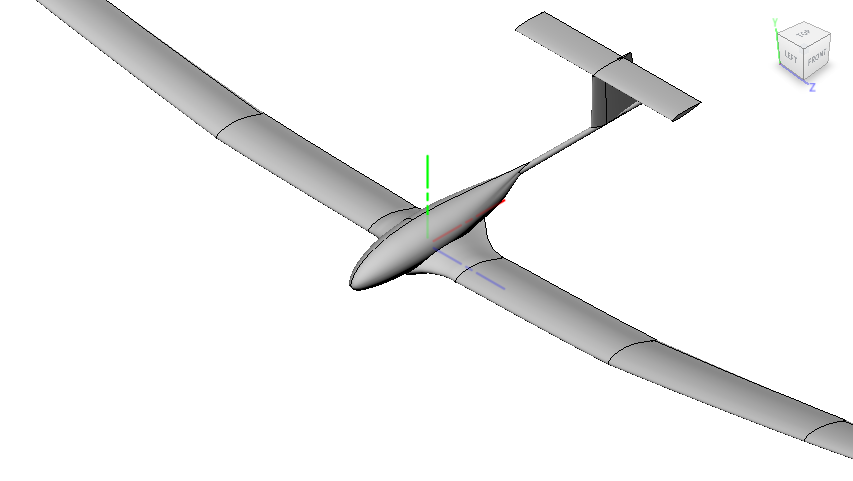
Y-Z-X系オイラー角における回転行列\({\bf C}\)を頑張って計算すると以下のようになる(白本:p.11,青本:p.18)
\begin{eqnarray}
{\bf C}
&=& {\bf C_{x}}{\bf C_{z}}{\bf C_{y}}\\
&=&
\left[\begin{array}{ccc}
1&0&0\\
0&\cos{\phi}&\sin{\phi}\\
0&-\sin{\phi}&\cos{\phi}\\
\end{array}\right]
\left[\begin{array}{ccc}
\cos{\psi}&\sin{\psi}&0\\
-\sin{\psi}&\cos{\psi}&0\\
0&0&1\\
\end{array}\right]
\left[\begin{array}{ccc}
\cos{\theta}&0&-\sin{\theta}\\
0&1&0\\
\sin{\theta}&0&\cos{\theta}\\
\end{array}\right]\\
&=&
\left[\begin{array}{ccc}
\cos{\theta}\cos{\psi}&
\sin{\psi}
&-\sin{\theta}\cos{\psi}\\
\sin{\phi}\sin{\theta}-\cos{\phi}\cos{\theta}\sin{\psi}&
\cos{\phi}\cos{\psi}&
\cos{\phi}\sin{\theta}\sin{\psi}+\sin{\phi}\cos{\theta}\\
\sin{\phi}\cos{\theta}\sin{\psi}+\cos{\phi}\sin{\theta}&
-\sin{\phi}\cos{\psi}&
\cos{\phi}\cos{\theta}-\sin{\phi}\sin{\theta}\sin{\psi}\\
\end{array}\right]
\end{eqnarray}
上の回転行列からオイラー角\([\phi, \theta, \psi]\)を求めると以下のようになる
\begin{eqnarray}
\phi&=& \arctan{(\frac{-C_{32}}{C_{22}})} \\
\theta&=& \arctan{(\frac{-C_{13}}{C_{11}})}\\
\psi&=& \arcsin{(C_{12})}\\
\end{eqnarray}
この関係式を使えば,右手系の回転行列\(C^{\prime}\)から右手系の回転角\([\phi^{\prime}, \theta^{\prime},\psi^{\prime}]\)を求めることができる
右手系の回転角をZ-Y-X系オイラー角に変換する
\(x^{\prime}y^{\prime}z^{\prime}\)座標系の回転角と\(xyz\)座標系の回転角の関係は以下のようになる
\begin{eqnarray}
\phi &=& -\phi^{\prime} \\
\theta &=& -\psi^{\prime}\\
\psi &=& -\theta^{\prime}\\
\end{eqnarray}
これにより,右手系の回転角\([\phi^{\prime}, \theta^{\prime},\psi^{\prime}]\)を右手系のZ-Y-X系オイラー角\([\phi, \theta,\psi]\)に変換することができる
スクリプトの実装
≫
実装すると以下のようになる
float q1 = MyGameManeger.instance.Plane.transform.rotation.x;
float q2 = -MyGameManeger.instance.Plane.transform.rotation.y;
float q3 = -MyGameManeger.instance.Plane.transform.rotation.z;
float q4 = MyGameManeger.instance.Plane.transform.rotation.w;
float C11 = q1*q1-q2*q2-q3*q3+q4*q4;
float C22 = -q1*q1+q2*q2-q3*q3+q4*q4;
float C12 = 2f*(q1*q2+q3*q4);
float C13 = 2f*(q1*q3-q2*q4);
float C32 = 2f*(q2*q3-q1*q4);
float phi = -Mathf.Atan(-C32/C22)*Mathf.Rad2Deg;
float theta = -Mathf.Asin(C12)*Mathf.Rad2Deg;
float psi = -Mathf.Atan(-C13/C11)*Mathf.Rad2Deg;行数にすると少ないが,今回のフライトシミュレーター製作で一番大変だったかもしれない
おわりに
左手系のクォータニオンからZ-Y-X系オイラー角を求めることができた
大学院の講義でクォータニオンを勉強してそれをブログにまとめたが,まさか数か月後にフライトシミュレーターづくりに活かせることになるとは思ってなかった



コメント