DATCOM 4.3.1.2 に基づいて、翼胴の揚力傾斜を計算する。
はじめに
DATCOM 4.3.1.2 に基づいて、翼胴の揚力傾斜を計算する。
PDFのページは1036ページ
Method 1
翼胴の3次元揚力傾斜は以下の2通りの式で計算する。
①胴体に対する翼の取付角が固定されていて、翼と胴体がひとまとめで迎角が変化する場合
\begin{align}
\left(C_{L_{\alpha}}\right)_{_{WB}}&=\left[K_{_N}+K_{_{W(B)}}+K_{_{B(W)}}\right]\left(C_{L_{\alpha}}\right)_{e}\frac{S_{e}}{S_{_W}} \\\\
K_{_N}&=\frac{\left(C_{L_{\alpha}}\right)_{_N}S_{_{N_{ref}}}}{\left(C_{L_{\alpha}}\right)_{e}S_{_{W}}}
\end{align}
②胴体に対する迎角は固定されたままで、胴体に対する翼の取付角のみが変化する場合(オールフライングの水平尾翼など)
\begin{align}
\left(C_{L_{\alpha}}\right)_{_{WB}}=\left[k_{_{W(B)}}+k_{_{B(W)}}\right]\left(C_{L_{\alpha}}\right)_{e}\frac{S_{e}}{S_{_W}}
\end{align}
ここで
| 文字 | 単位 | 説明 |
| \(S_{_{W}}\) | ㎡ | トータルの翼の投影面積。 |
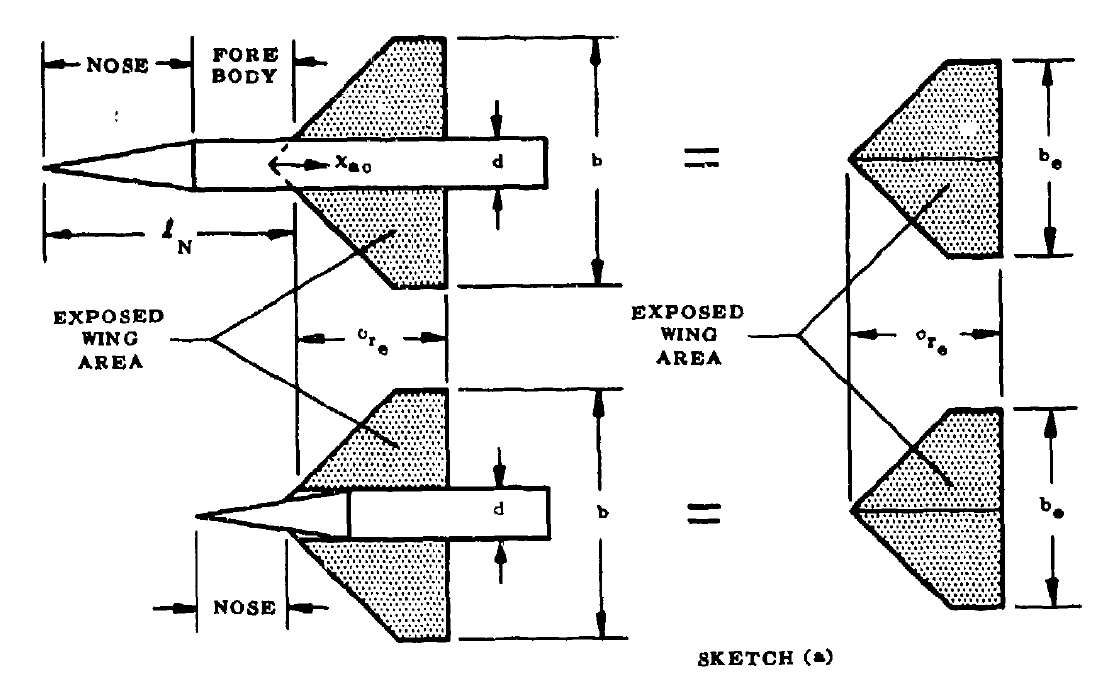
| \(S_{e}\) | ㎡ | Exposed Wingの翼面積。Sketch(d)を参照。 |
| \(\left(C_{L_{\alpha}}\right)_{e}\) | 1/rad | Exposed Wingの3次元揚力傾斜。 Exposed Wingの翼面積とアスペクト比を用いてDATCOM 4.1.3.2で計算する。 |
| \(\left(C_{L_{\alpha}}\right)_{_N}\) | 1/rad | 胴体のノーズ部分の揚力傾斜。 ほとんどのケースでは2 [1/rad]を使用して良い。 より正確にはDATCOM 4.2.1.1で計算する。 |
| \(S_{_{N_{ref}}}\) | ㎡ | 胴体のノーズ部分の揚力傾斜の基準面積。 通常は\(\pi r^2\)。 |
| \(K_{_N}\) | - | 翼の揚力傾斜に対するノーズ部分の揚力傾斜を表す係数。 |
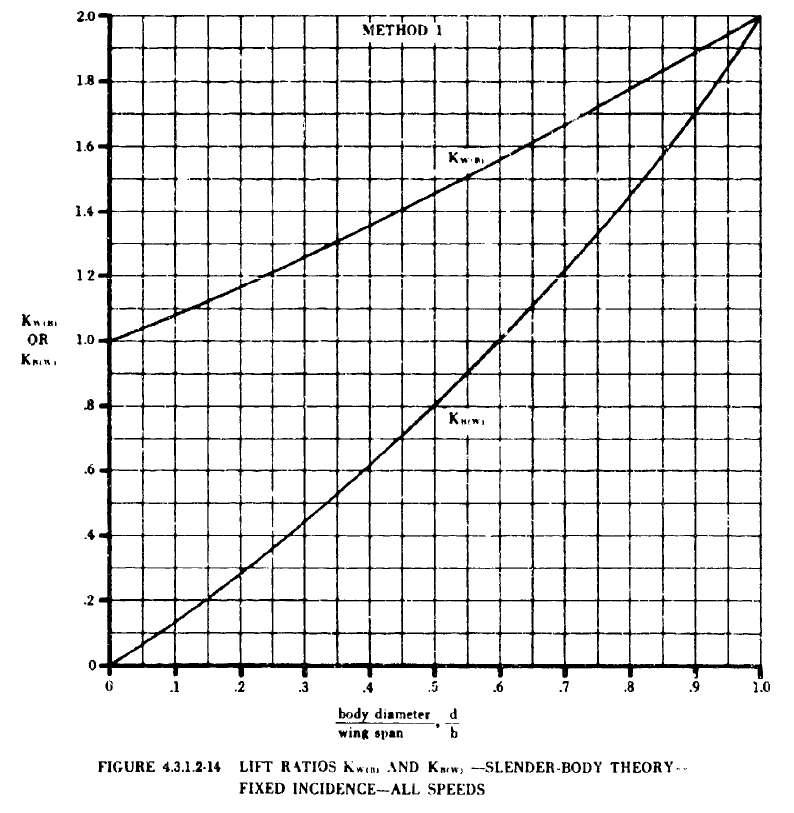
| \(K_{_{W(B)}}\) | - | 胴体があることによる翼の揚力傾斜への影響を表す係数。 FIGURE 4.3.1.2-10から求める。 |
| \(K_{_{B(W)}}\) | - | 翼の揚力傾斜に対する胴体の揚力傾斜を表す係数。 FIGURE 4.3.1.2-10から求める。 |
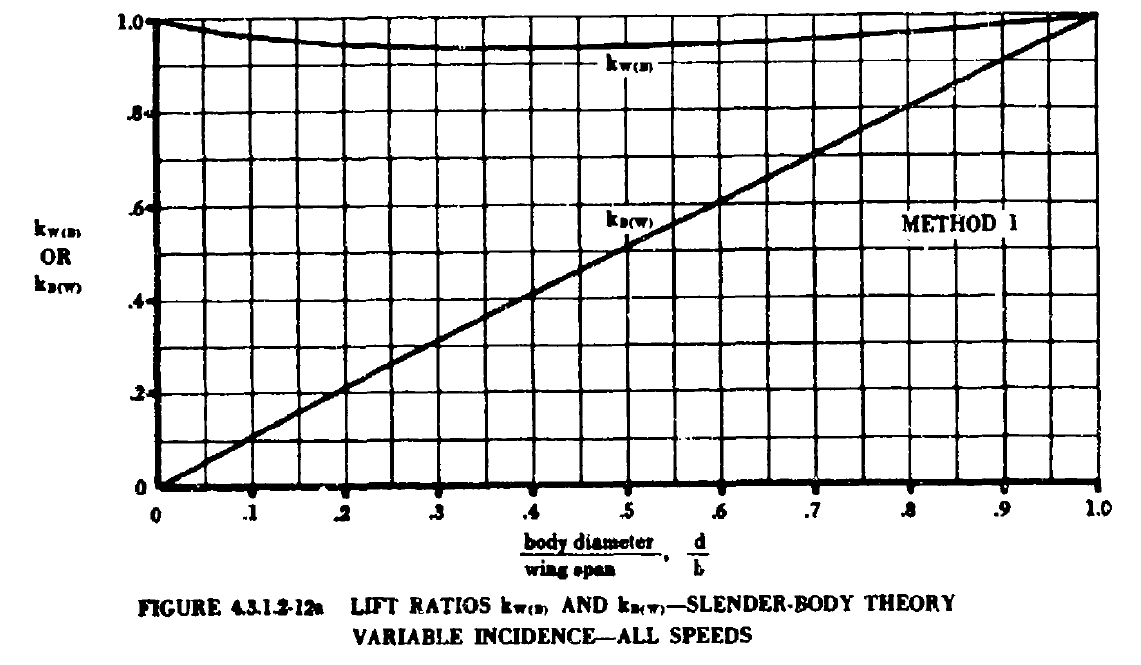
| \(k_{_{W(B)}}\) | - | \(K_{_{W(B)}}\)に同じ。 FIGURE 4.3.1.2-12aから求める。 |
| \(k_{_{B(W)}}\) | - | \(K_{_{B(W)}}\)に同じ。 FIGURE 4.3.1.2-12aから求める。 |
reference
-
制限
この手法における注意点は以下の通り。
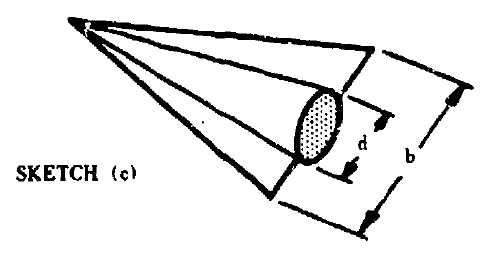
- Sketch(d)のような機体であること。(Sketch(c)のような機体は別の手法で計算する。)
- 胴体の半径がセミスパンの80%を超えないこと。
- 遷音速域であること。
Sample
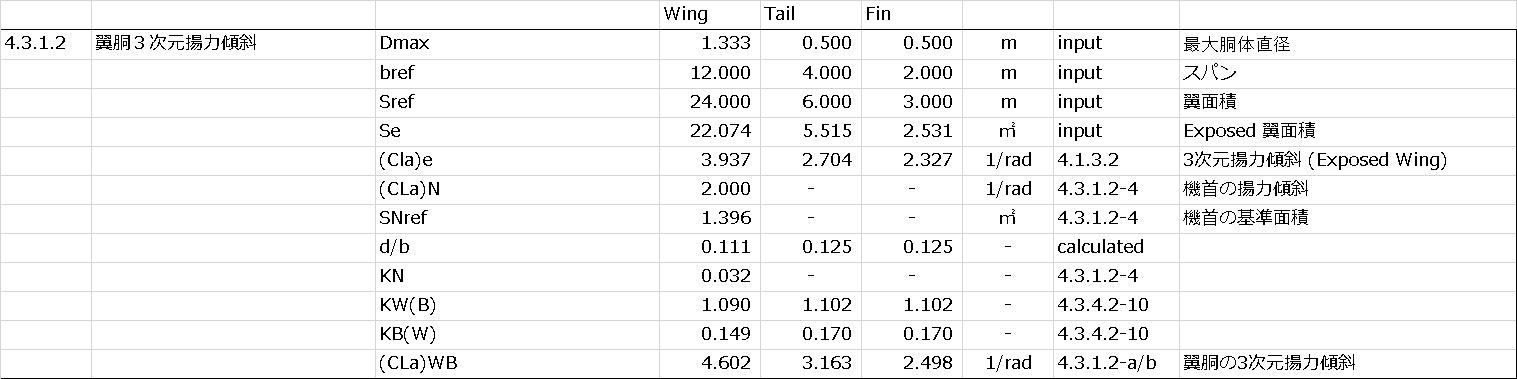
OpenVSPのExample FileにあるPod Planeについて、実際に計算してみる
↓計算に使用したエクセルファイル(マクロ付き)
↓計算結果
おわりに
DATCOM 4.3.1.2 に基づいて、翼胴の揚力傾斜を計算した。
↓次
4.5.1.1





コメント