Scipyのsolve_ivpを使って航空機の6自由度の微分方程式を解いて運動解析を行う
はじめに
Scipyのsolve_ivpを使って航空機の6自由度の微分方程式を解いて運動解析を行う
↓公式のドキュメント
↓これまでの道のり
それではいってみよう
ソースコードの解説
ソースコードはこれ
import time # 時間管理のためのライブラリ
import math # 数学関数のためのライブラリ
import numpy as np # 数値計算のためのライブラリ
from scipy.integrate import solve_ivp # 常微分方程式の数値解法
from scipy.spatial.transform import Rotation # 座標変換のためのライブラリ
import matplotlib.pyplot as plt # グラフ描画のためのライブラリ
from mpl_toolkits.mplot3d import Axes3D # 3Dプロットのためのライブラリ
# 飛行機クラスの定義
class Plane:
def __init__(self, uvw_gE=np.array([0, 0, 0]), X=np.zeros(13)):
# 機体の基本的なパラメータ
self.mass = 100 # 期待質量 [kg]
self.airspeed0 = 10 # 釣り合い対気速度 [m/s]
self.alpha0 = 1.45 # 釣り合い迎え角 [度]
self.CDp0 = 0.015 # 抗力係数
self.Cmw0 = -0.115 # モーメント係数
self.CLMAX = 1.700 # 最大揚力係数
self.Sw = 18 # 翼面積 [m^2]
self.bw = 25 # 翼幅 [m]
self.cMAC = 0.75 # 平均翼弦長 [m]
self.aw = 0.105 # 揚力傾斜
self.hw = (0.333-0.250) # 重心位置
self.ew = 0.985 # 飛行機効率
self.AR = (self.bw*self.bw)/self.Sw # アスペクト比
self.Downwash = False # ダウンウォッシュ効果
self.St = 1.500 # 垂直尾翼面積 [m^2]
self.at = 0.080 # 垂直尾翼揚力傾斜
self.lt = 3.200 # 垂直尾翼のアーム長 [m]
self.dh_max = 0.5 # 最大重心移動量 [-]
self.el_max = 10 # 最大エレベータ舵角 [deg]
self.tau = 1.000 # エレベータ舵角効率
self.VH = (self.St*self.lt)/(self.Sw*self.cMAC) # 垂直尾翼容積比
self.rd_max = 15 # 最大ラダー舵角 [deg]
self.CGEMIN = 0.25 # 最小地面効果係数
self.Cyb = -0.0036
self.Cyp = -0.4500
self.Cyr = 0.1420
self.Cydr = 0.0018
self.Clb = -0.0040
self.Clp = -0.8200
self.Clr = 0.2200
self.Cldr = 0.0000
self.Cnb = -0.0005
self.Cnp = -0.1300
self.Cnr = -0.0025
self.Cndr = -0.0003
self.Ixx = 1000 # 慣性モーメント [kg*m^2]
self.Iyy = 70 # 慣性モーメント [kg*m^2]
self.Izz = 1000 # 慣性モーメント [kg*m^2]
self.Izx = -8 # 慣性モーメント [kg*m^2]
self.Ixz = 8 # 慣性モーメント [kg*m^2]
self.epsilon0 = 0 # 釣り合い吹き下ろし角
self.gravity = 9.81 # 重力加速度 [m/s^2]
self.rho = 1.225 # 空気密度 [kg/m^3]
self.uvw_gE = uvw_gE # 地表風ベクトル
self.PID_Lon = np.zeros(3) # 縦方向PID制御の係数
self.PID_lat = np.zeros(3) # 横方向PID制御の係数
self.t_old = 0 # 前回の時間ステップ
self.dh = 0 # 重心移動量
self.gamma = None
self.phi = None
self.gamma_dive = X[0] # ダイブ角
self.gamma_cruise = X[1] # 巡航角
self.phi_turn = X[2] # 旋回角
self.time_pullup = X[3] # 引き起こし時刻 [s]
self.time_flare = X[4] # フレア時刻 [s]
self.time_entry = X[5] # 旋回開始時刻 [s]
self.time_break = X[6] # 旋回終了時刻 [s]
self.PID_param_lon = X[7:10] # 縦方向PIDパラメータ
self.PID_param_lat = X[10:13] # 横方向PIDパラメータ
# 飛行機の運動方程式
def motion_equations(self, t, state):
# 状態変数の展開
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r , el, rd= state
uvw = np.array([u, v, w], dtype=float)
hE = max([10+ZE, 0.001]) # 地表高度の計算
euler = np.array([phi, theta, psi], dtype=float)
self.phi = phi
# 機体座標系から地表座標系への変換
rot = Rotation.from_euler('ZYX', np.flip(euler), degrees=True)
uE, vE, wE = rot.apply(uvw)
# 地表座標系から機体座標系への変換
rot = Rotation.from_euler('XYZ', -euler, degrees=True)
ug, vg, wg = rot.apply(self.uvw_gE*((hE/10)**(1/7))) # 風速勾配 1/7乗則
# 対気速度の計算
Airspeed = np.sqrt((u+ug)**2+(v+vg)**2+(w+wg)**2)
# 迎え角と経路角の計算
if abs((w+wg)/(u+ug)) < 1:
alpha = math.degrees(math.asin((w+wg)/(u+ug)))
else:
alpha = np.sign((w+wg)/(u+ug))*90
self.gamma = theta-alpha
# 横滑り角の計算
beta = math.degrees(math.asin((v+vg)/Airspeed))
# 揚力係数の計算
CGE = (self.CGEMIN+33*(hE/self.bw)**1.5)/(1+33*(hE/self.bw)**1.5)
CL0 = (self.mass*self.gravity)/(0.5*self.rho*self.airspeed0**2*self.Sw)
CLt0 = (self.Cmw0+CL0*self.hw)/(self.VH+(self.St/self.Sw)*self.hw)
CLw0 = CL0-(self.St/self.Sw)*CLt0
if self.Downwash:
self.epsilon0 = (CL0/(math.pi*self.ew*self.AR))*math.degrees(1)
CLw = CLw0+self.aw*(alpha-self.alpha0)
CLt = (CLt0+self.at*((alpha-self.alpha0)+(1-CGE*(CLw/CLw0))*self.epsilon0+el*self.tau+((self.lt-self.dh*self.cMAC)/Airspeed)*q))
# 最大揚力係数の制限
if abs(CLw) > self.CLMAX:
CLw = (CLw/abs(CLw))*self.CLMAX # Stall
if abs(CLt) > self.CLMAX:
CLt = (CLt/abs(CLt))*self.CLMAX # Stall
CL = CLw+(self.St/self.Sw)*CLt # CL
# 抗力係数の計算
CD = (self.CDp0*(1+(4*2.5)/(math.pi*0.6)*(1/0.04)*math.tan(math.radians(alpha-self.alpha0))**2)+((CL*CL)/(math.pi*self.ew*self.AR))*CGE) # CD
# 動微係数を安定軸から機体軸へ変換
cosA = math.cos(math.radians(alpha))
sinA = math.sin(math.radians(alpha))
Cyp = self.Cyp*cosA-self.Cyr*sinA
Cyr = -self.Cyp*sinA+self.Cyr*cosA
Clp = self.Clp*cosA*cosA-self.Cnp*sinA*cosA-self.Clr*sinA*cosA+self.Cnr*sinA*sinA
Cnp = self.Clp*sinA*cosA+self.Cnp*cosA*cosA-self.Clr*sinA*sinA-self.Cnr*sinA*cosA
Clr = self.Clp*sinA*cosA-self.Cnp*sinA*sinA+self.Clr*cosA*cosA-self.Cnr*sinA*cosA
Cnr = self.Clp*sinA*sinA+self.Cnp*sinA*cosA+self.Clr*sinA*cosA+self.Cnr*cosA*cosA
# 機体軸の空力係数の計算
Cx = CL*sinA-CD*cosA
Cy = (self.Cyb*beta+Cyp*(1/math.degrees(1))*((p*self.bw)/(2*Airspeed))+Cyr*(1/math.degrees(1))*((r*self.bw)/(2*Airspeed))+ self.Cydr*rd) # Cy
Cz = -CL*cosA-CD*sinA # Cz
Cl = (self.Clb*beta+Clp*(1/math.degrees(1))*((p*self.bw)/(2*Airspeed))+Clr*(1/math.degrees(1))*((r*self.bw)/(2*Airspeed))+ self.Cldr*rd) # CL
Cm = self.Cmw0+CLw*self.hw-self.VH*CLt+CL*self.dh # Cm
Cn = (self.Cnb*beta+ Cnp*(1/math.degrees(1))*((p*self.bw)/(2*Airspeed))+Cnr*(1/math.degrees(1))*((r*self.bw)/(2*Airspeed))+ self.Cndr*rd) # Cn
# 機体にはたらく力とモーメントの計算
X = 0.5*self.rho*Airspeed**2*self.Sw*Cx
Y = 0.5*self.rho*Airspeed**2*self.Sw*Cy
Z = 0.5*self.rho*Airspeed**2*self.Sw*Cz
L = ((self.Iyy-self.Izz)*math.radians(q*r)+self.Ixz*math.radians(p*q)+math.degrees(0.5*self.rho*Airspeed**2*self.Sw*self.bw*Cl))
M = ((self.Izz-self.Ixx)*math.radians(r*p)+self.Ixz*math.radians(r**2-p**2)+math.degrees(0.5*self.rho*Airspeed**2*self.Sw*self.cMAC*Cm))
N = ((self.Ixx-self.Iyy)*math.radians(p*q)-self.Ixz*math.radians(q*r)+math.degrees(0.5*self.rho*Airspeed**2*self.Sw*self.bw*Cn))
# 絶対座標系の速度、機体座標系の加速度、姿勢角速度、角加速度の計算
rad_phi = math.radians(phi)
rad_theta = math.radians(theta)
dphi = (p+(r*math.cos(rad_phi)+q*math.sin(rad_phi))*math.tan(rad_theta))
dtheta = (q*math.cos(rad_phi)-r*math.sin(rad_phi))
dpsi = ((r*math.cos(rad_phi)+q*math.sin(rad_phi))/math.cos(rad_theta))
du = (-math.radians(q)*w+math.radians(r)*v-self.gravity*math.sin(rad_theta)+(X/self.mass))
dv = (-math.radians(r)*u+math.radians(p)*w+self.gravity*math.cos(rad_theta)*math.sin(rad_phi)+(Y/self.mass))
dw = (-math.radians(p)*v+math.radians(q)*u+self.gravity*math.cos(rad_theta)*math.cos(rad_phi)+(Z/self.mass))
dp = ((L/self.Ixx)+(self.Ixz/self.Ixx)*(N/self.Izz))/(1-(self.Ixz**2)/(self.Izz*self.Ixx))
dq = M/self.Iyy
dr = ((N/self.Izz)+(self.Ixz/self.Izz)*(L/self.Ixx))/(1-(self.Ixz**2)/(self.Ixx*self.Izz))
# 入力の計算
d_el, d_rd = self._calculate_inputs(t, state)
# 最大舵角の制限
if np.abs(el) > self.el_max:
d_el = 0
if np.abs(rd) > self.rd_max:
d_rd = 0
# 時間の更新
self.t_old = t
return [uE, vE, wE, du, dv, dw, dphi, dtheta, dpsi, dp, dq, dr, d_el, d_rd]
def _calculate_inputs(self, t, state):
# 操舵量の計算する
if t-self.t_old <= 0:
return 0, 0
else:
dt = t-self.t_old
# 縦方向の制御
pullup_flag = True
flare_flag = True
if t < self.time_pullup: # 引き起こし
gamma_target = self.gamma_dive
elif t < self.time_flare: # 定常滑空
if pullup_flag:
self.PID_Lon[1] = 0 # Iをリセット
pullup_flag = False
gamma_target = self.gamma_cruise
else: # フレア
if flare_flag:
self.PID_Lon[1] = 0 # Iをリセット
flare_flag = False
gamma_target = 0
self.PID_Lon[2] = ((self.gamma-gamma_target)-self.PID_Lon[0])/dt
self.PID_Lon[0] = self.gamma-gamma_target
self.PID_Lon[1] += self.PID_Lon[0]*dt
# 横方向の制御
turn_flag = True
if t < self.time_entry: # 操縦しない
phi_target = self.phi
elif t < self.time_break: # 旋回中
phi_target = self.phi_turn
else: # 水平飛行
if turn_flag:
self.PID_lat[1] = 0 # Iをリセット
turn_flag = False
phi_target = 0
self.PID_lat[2] = ((self.phi-phi_target)-self.PID_lat[0])/dt
self.PID_lat[0] = (self.phi-phi_target)
self.PID_lat[1] += self.PID_lat[0]*dt
# 操舵変化量の計算
if t < self.time_pullup:
d_el = np.dot(self.PID_param_lon, self.PID_Lon)*self.el_max
elif t < self.time_flare:
d_el = np.dot(self.PID_param_lon, self.PID_Lon)*self.el_max
else:
d_el = np.dot(self.PID_param_lon, self.PID_Lon)*self.el_max
if t < self.time_entry or t > self.time_break:
d_rd = np.dot(self.PID_param_lat, self.PID_lat)*self.rd_max
else:
d_rd = np.dot(self.PID_param_lat, self.PID_lat)*self.rd_max
# 操舵変化量の制限
d_el = min(max(d_el,-self.el_max/1.0), self.el_max/1.0)
d_rd = min(max(d_rd,-self.rd_max/1.0), self.rd_max/1.0)
return d_el, d_rd
def simulate(self, initial_state, t_start = 0, t_end = 100, first_step = 1/30):
# 解析時間
t_span = [t_start, t_end]
# 終了条件
landing = Landing()
stall = Stall()
reverse = Reverse()
overbank = OverBank()
landing.terminal = True
stall.terminal = True
reverse.terminal = True
overbank.terminal = True
# 運動方程式を解く
solution = solve_ivp(self.motion_equations , t_span, initial_state , events = [landing, stall, reverse, overbank] , first_step = first_step)
return solution
class Landing: # 着水
def __init__(self):
pass
def __call__(self, t, state):
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd = state
return 10-ZE
class Stall: # 失速
def _init__(self):
pass
def __call__(self, t, state):
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd = state
return w/u-math.sin(math.radians(30))
class Reverse: # 逆走
def __init__(self):
pass
def __call__(self, t, state):
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd = state
uvw = np.array([u, v, w], dtype=float)
euler = np.array([phi, theta, psi], dtype=float)
# 機体座標系から地表座標系への変換
rot = Rotation.from_euler('ZYX', np.flip(euler), degrees=True)
uE, vE, wE = rot.apply(uvw)
return uE
class OverBank: #過度のバンク
def __init__(self):
pass
def __call__(self, t, state):
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd = state
return abs(phi)-45
if __name__ == "__main__":
# シミュレーションの開始時刻を記録
start_time = time.time()
# Planeクラスのインスタンスを作成し、外部風速をゼロに設定
plane = Plane(uvw_gE=np.array([0, 0, 0]))
# シミュレーションを実行し、初期状態を設定
# 初期状態: [XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd]
# XE, YE, ZE: 位置座標, u, v, w: 機体軸速度成分, phi, theta, psi: 姿勢オイラー角, p, q, r: 角速度成分, el, rd: エレベータ舵角、ラダー舵角
solution = plane.simulate(initial_state=[0, 0, 0, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])
# シミュレーション結果の最終時刻における位置座標を出力
print(solution.y[0, -1], solution.y[1, -1], 10-solution.y[2, -1])
# シミュレーションの終了時刻を記録し、実行時間を計算
end_time = time.time()
print(f"Run time: {end_time-start_time} s")
# 結果をプロットするための図を設定
fig = plt.figure(figsize=(16/2, 9/2))
ax = fig.add_subplot(111, projection='3d')
# シミュレーション結果の3D散布図を作成
ax.scatter(solution.y[0], solution.y[1], 10-solution.y[2], color='gray')
# 軸ラベルを設定
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# x軸とy軸の表示範囲を設定
xmax = max(np.max(solution.y[0]), np.max(np.abs(solution.y[1])))
ymin = min(-np.max(solution.y[0])/2, np.min(solution.y[1]))
ymax = ymin+xmax
ax.set_xlim(0, max(np.max(solution.y[0]), np.max(np.abs(solution.y[1]))))
ax.set_ylim(ymin, ymax)
ax.set_zlim(0, 20)
# y軸を反転して表示
ax.invert_yaxis()
# 3Dプロットの視点を設定
ax.view_init(elev=60, azim=-180)
# プロットを表示
plt.show()6自由度の運動解析を行うAirplaneクラスを定義してある
状態変数は以下の13個
| 状態変数 | 型 | 説明 | 単位 | 初期値 |
| XE | float | 地表座標系のx座標 | m | 0 |
| YE | float | 地表座標系のy座標 | m | 0 |
| ZE | float | 地表座標系のz座標 | m | 0 |
| u | float | 機体座標系のx方向速度 | m/s | u0 |
| v | float | 機体座標系のy方向速度 | m/s | 0 |
| w | float | 機体座標系の2方向速度 | m/s | w0 |
| phi | float | ロール角 | deg | 0 |
| theta | float | ピッチ角 | deg | theta0 |
| psi | float | ヨー角 | deg | 0 |
| p | float | ローリング角速度 | deg/s | 0 |
| q | float | ピッチング角速度 | deg/s | 0 |
| r | float | ヨーイング角速度 | deg/s | 0 |
| el | float | エレベータ舵角 | deg | 0 |
| rd | float | ラダー舵角 | deg | 0 |
厳密にはエレベータ舵角とラダー舵角は状態変数ではないが、
- 舵角の制御を舵角の操舵速度[deg/s] で行っているので、舵角を状態変数にしてしまえば舵角の計算(積分)が楽
- 解析終了後に舵角も戻り値として欲しい。
という理由から舵角を状態量にすることにした。
制御パラメータXは以下の13個 (PIDパラメータが縦と横・方向で3個ずつ)
| 状態変数 | 型 | 説明 | 単位 | ndarray |
| gamma_dive | float | ダイブ角 | deg | X[0] |
| gamma_cruise | float | 定常滑空角 | deg | X[1] |
| phi_turn | float | 旋回角 | deg | X[2] |
| time_pullup | float | 引き起こし時刻 | s | X[3] |
| time_flare | float | フレア時刻 | s | X[4] |
| time_entry | float | 旋回開始時刻 | s | X[5] |
| time_break | float | 旋回終了時刻 | s | X[6] |
| PID_param_lon | ndarray | 縦方向PIDパラメータ | - | X[7:10] |
| PID_param_lat | ndarray | 横方向PIDパラメータ | - | X[10:13] |
↓基本的には以下の記事で最適化されたパラメータを用いる
Airplane クラス
クラス内のメソッドは以下の通り
- __init__
- simulate
- motion_equations
- calculate_inputs
__init__(self, uvw_gE, X)
パラメータの初期化を行うコンストラクタメソッド
| 引数 | 型 | 説明 | 単位 | デフォルト |
| uvw_gE | ndarray | 地表風ベクトル | m/s | np.array([0,0,0]) |
| X | ndarray | 制御パラメータ | - | np.zeros(13) |
山ほどあるインスタンス変数はソースコードを参照(BRSimulatorと同じ)
コンストラクタ以外のメソッドはこれから解説していく
微分方程式を解く(simulateメソッド)
def simulate(self, initial_state, t_start = 0, t_end = 100, first_step = 1/30):
# 解析時間
t_span = [t_start, t_end]
# 終了条件
landing = Landing()
stall = Stall()
reverse = Reverse()
overbank = OverBank()
landing.terminal = True
stall.terminal = True
reverse.terminal = True
overbank.terminal = True
# 運動方程式を解く
solution = solve_ivp(self.motion_equations , t_span, initial_state , events = [landing, stall, reverse, overbank] , first_step = first_step)
return solutionScipy.solve_ivpはAirplaneクラスのsimulateメソッドで定義してある
| 引数 | 型 | 説明 | 単位 | デフォルト |
| initial_state | ndarray | 初期状態の配列 | - | - |
| t_start | float | シミュレーションの開始時刻 | s | 0 |
| t_end | float | シミュレーションの終了時刻 | s | 100 |
| first_step | float | 最初のステップの時間幅 | s | 1/30 |
| 戻り値 | 型 | 説明 | 単位 |
| solution | Bunch | シミュレーション結果の解析結果 | - |
Scipy.solve_ivp
微分方程式を解くメソッド
特徵:
微分方程式の安定性と計算の効率をバランスしていい感じに最適な時間ステップを決めてくれる
→最大ステップ数は決められないのでどのくらい実行時間がかかるか読みにくい
おもな引数:
fun: callableオブジェクト
時刻tとその時刻における状態量yを引数として、微分方程式の右辺の値を返す関数。自分で設定する。
t_span: list
開始時刻と終了時刻を定義するリスト。 積分はt=t_span[0] から始まり、t=t_span[1] まで行われる
y0: ndarray
初期状態を示す配列
method: str
微分方程式を解くときの積分方法を指定する文字列。 デフォルトは'RK45'
'RK45':
各ステップにおいて、直近の時間ステップを用いて2つの異なる近似値(5次の近似値と4次の近似値)を計算し、それらの差と許容誤差を比較して次の時間ステップを評価する。
2つの近似値が許容誤差に十分に近い場合は直近の時間ステップがそのまま使用され、 2つの近似値の差が許容誤差より大きい場合は時間ステップが小さく、 逆に、2つの近似値の差が許容誤差に対して必要以上に小さい場合は時間ステップが大きくなるよう修正される。 すごい。
t_eval: ndarray
特定の時間点で解を計算してほしいときに与える配列。なくてもいい。
events: callableオブジェクト
時刻tとその時刻における状態量yを引数とした関数
返値がゼロになる瞬間を検出し、以下の属性に応じたアクションがとられる
terminal: この属性をTrueに設定するとイベントが発生した時点 (返値がゼロになったとき) で積分が終了する。 デフォルトはFalse。direction:関数の返値の正負が変わる瞬間(クロッシング)を記録する。この属性を+1に設定すると正から負の方向のみ、-1に設定すると負から正の方向のみ、0に設定すると両方向のクロッシングを記録する。 デフォルトは0。
first_step: float
methodがいい感じの時間ステップを決めるときの初期値。 最適な時間ステップが既知の場合にそれをfirst_stepとして与えると計算の効率が上がることがある
返値: Bunchオブジェクト。おもに次の数値解を保持している
t:
積分された時間点。 t_evalが指定されている場合はt_evalに指定された時間点を含む。
y: ndarray
各時間点での解の値を含む2次元配列。 大きさは (時間点数, 状態変数の数)
他にもいくつかあるが今回は使わなかったので省略
解析終了を判定するeventsはそれぞれクラスで定義されており、属性はtemination=Trueとしている
class Landing: # 着水
def __init__(self):
pass
def __call__(self, t, state):
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd = state
return 10-ZE
class Stall: # 失速
def _init__(self):
pass
def __call__(self, t, state):
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd = state
return w/u-math.sin(math.radians(30))
class Reverse: # 逆走
def __init__(self):
pass
def __call__(self, t, state):
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd = state
uvw = np.array([u, v, w], dtype=float)
euler = np.array([phi, theta, psi], dtype=float)
# 機体座標系から地表座標系への変換
rot = Rotation.from_euler('ZYX', np.flip(euler), degrees=True)
uE, vE, wE = rot.apply(uvw)
return uE
class OverBank: #過度のバンク
def __init__(self):
pass
def __call__(self, t, state):
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd = state
return abs(phi)-45 解析の終了条件(events)は以下の4つ
- 着水 (Landingクラス): ZEが10以上になったら解析終了
- 失速 (Stallクラス): 迎角が30度以上になったら解析終了
- 逆走 (Reverseクラス): uE が負になったら解析終了
- 過度のバンク (OverBankクラス): バンク角が45度以上になったら解析終了
※ 失速判定では迎角に風の影響も考慮すべきだが、わざわざ他クラスに地表風の値を持ってくるのが面倒だったので省略した
引数 funの中身は次の項で説明する
運動方程式の定義 (motion_equationメソッド)
Scipy.solve_ivpに引数として与えるfunは、 Airplaneクラスのmotion_equationメソッドで定義してある
| 引数 | 型 | 説明 | 単位 | デフォルト |
| t | float | 時間 | s | - |
| state | ndarray | 状態変数の配列 | - | - |
| 戻り値 | 型 | 説明 | 単位 |
| ※ | list | 状態変数の時間変化 | - |
ここで、12個の状態変数に対する微分方程式は次の式で表される
対地速度
\begin{eqnarray}
\left[\begin{array}{c}
\dot{X_{E}}\\
\dot{Y_{E}}\\
\dot{h_{E}}
\end{array}\right]=
\left[\begin{array}{lll}
\cos{\theta}\cos{\psi}&\sin{\phi}\sin{\theta}\cos{\psi}-\cos{\phi}\sin{\psi}&\cos{\phi}\sin{\theta}\cos{\psi}+\sin{\phi}\sin{\psi}\\
\cos{\theta}\sin{\psi}&\sin{\phi}\sin{\theta}\sin{\psi}+\cos{\phi}\cos{\psi}&\cos{\phi}\sin{\theta}\sin{\psi}-\sin{\phi}\cos{\psi}\\
\sin{\theta}&-\sin{\phi}\cos{\theta}&-\cos{\phi}cos{\theta}
\end{array}\right]
\left[\begin{array}{c}
u\\
v\\
w
\end{array}\right]
\end{eqnarray}
機体軸加速度
\begin{eqnarray}
\dot{u}&=&-\frac{q}{(180/\pi)}w&+\frac{r}{(180/\pi)}v&-g\sin{\theta}&+\frac{\rho V^2 S}{2m}C_{x}\\
\dot{v}&=&-\frac{r}{(180/\pi)}u&+\frac{p}{(180/\pi)}w&-g\cos{\theta}\sin{\phi}&+\frac{\rho V^2 S}{2m}C_{y}\\
\dot{w}&=&-\frac{p}{(180/\pi)}v&+\frac{q}{(180/\pi)}u&-g\cos{\theta}\cos{\phi}&+\frac{\rho V^2 S}{2m}C_{z}\
\end{eqnarray}
姿勢角速度
\begin{eqnarray}
\dot{\phi}&=&p+(r\cos{\phi}+q\sin{\phi})\tan{\theta}\\
\dot{\theta}&=&q\cos{\phi}-r\sin{\phi}\\
\dot{\psi}&=&\frac{r\cos{\phi}+q\sin{\phi}}{\cos{\theta}}
\end{eqnarray}
角加速度
\begin{eqnarray}
\dot{p}&=&\frac{\frac{L}{I_{x}}+\frac{I_{xz}}{I_{x}}\frac{N}{I_{z}}}{1-\frac{I_{xz}^2}{I_{x}I_{z}}}\\
\dot{q}&=&\frac{M}{I_{y}}\\
\dot{r}&=&\frac{\frac{N}{I_{z}}+\frac{I_{xz}}{I_{z}}\frac{L}{I_{x}}}{1-\frac{I_{xz}^2}{I_{x}I_{z}}}
\end{eqnarray}
これを頑張って計算していく
状態変数の展開
# 状態変数の展開
XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r , el, rd= state
uvw = np.array([u, v, w], dtype=float)
hE = max([10+ZE, 0.001]) # 地表高度の計算
euler = np.array([phi, theta, psi], dtype=float)
self.phi = phistateから状態変数を受け取り、 機体軸の速度、オイラー角、高度、制御に渡すためのバンク角を設定する
機体軸と慣性軸 (地面固定座標系) の変換 (& 風速勾配)
# 機体座標系から地表座標系への変換
rot = Rotation.from_euler('ZYX', np.flip(euler), degrees=True)
uE, vE, wE = rot.apply(uvw)
# 地表座標系から機体座標系への変換
rot = Rotation.from_euler('XYZ', -euler, degrees=True)
ug, vg, wg = rot.apply(self.uvw_gE*((hE/10)**(1/7))) # 風速勾配 1/7乗則座標変換を用いて以下の2つを行う
- 機体軸の速度を対地速度へ変換する
- 地表風に風速勾配を加え、機体軸へ変換する
\begin{eqnarray}
\left[\begin{array}{c}
\dot{X_{E}}\\
\dot{Y_{E}}\\
\dot{h_{E}}
\end{array}\right]=
\left[\begin{array}{lll}
\cos{\theta}\cos{\psi}&\sin{\phi}\sin{\theta}\cos{\psi}-\cos{\phi}\sin{\psi}&\cos{\phi}\sin{\theta}\cos{\psi}+\sin{\phi}\sin{\psi}\\
\cos{\theta}\sin{\psi}&\sin{\phi}\sin{\theta}\sin{\psi}+\cos{\phi}\cos{\psi}&\cos{\phi}\sin{\theta}\sin{\psi}-\sin{\phi}\cos{\psi}\\
\sin{\theta}&-\sin{\phi}\cos{\theta}&-\cos{\phi}cos{\theta}
\end{array}\right]
\left[\begin{array}{c}
u\\
v\\
w
\end{array}\right]
\tag{1.5-9}
\end{eqnarray}
座標変換については、 Scipy. Rotationを用いる ( すごい便利)
今回使用するScipy.Rotationのメソッドは以下の2つ
- Rotation.from_euler
- Rotation.apply
Rotation.from_euler
オイラー角を用いてベクトルを回転させるRotationインスタンスを作成するメソッド
引数:
seq: str
回転の軸の順番を指定する文字列。intrinsic rotationsの場合は {'X', 'Y', 'Z'}から、extrinsic rotationsの場合は {'x','y', 'z'}のから最大3文字を選ぶ。
angles: float or ndarray
オイラー角を指定する数値または配列。 デフォルトでは角度はラジアン。
degrees: boolean
角度を度数法で指定する場合はTrueにする。 デフォルトは False。
- intrinsic rotations: 最初の回転が適用された後、次の回転は新しい回転された座標系に対して行われる。 航空機のオイラー角はこっち。
- extrinsic rotations: すべての回転は最初の座標系の軸に沿って行われる。
戻り値: Rotationインスタンス
Rotation.apply
作成したRotationインスタンスを使ってベクトルを回転させるメソッド
引数:
vectors: ndarray
回転させたいベクトル。 単一のベクトルの形状は(3,)、複数のベクトルの形状は (N, 3)
inverse: boolean
Trueに設定すると回転の逆がベクトルに適用される。 デフォルトは False。
戻り値: 回転後のベクトルのndarray
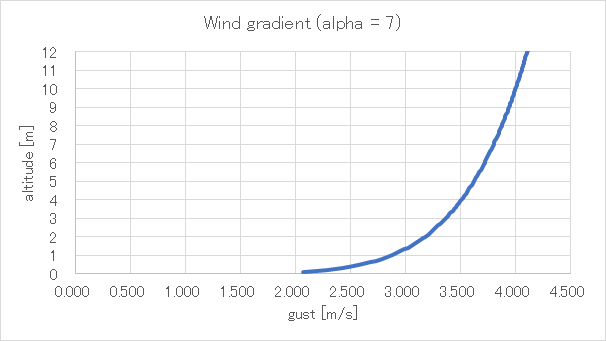
風速勾配(Wind Gradient)
突風成分を\([u_{g}, v_{g}, w_{g}]\)とし,それぞれ各軸の正方向から吹いてくる場合を正とする
つまり,\(u_{g}\)は正対風が正,\(v_{g}\)は右から吹いてきたら正,\(w_{g}\)は上昇風が正である
また,今回の物理演算では風速勾配として1/7乗則を採用する
≫Wind Gradient
\begin{eqnarray}
V_{g}(h)=V_{0}\left(\frac{h}{h_{0}}\right)^{\frac{1}{7}}
\end{eqnarray}
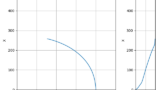
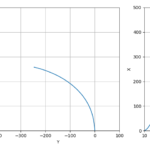
プラホの高さ(\(h_{0}=10.5\)[m])で\(V_{0}=4 \)[m/s]の風が吹いているときの風速\(V_{g}\)の分布は次のようになる
速度、迎角、 横滑り角
# 対気速度の計算
Airspeed = np.sqrt((u+ug)**2+(v+vg)**2+(w+wg)**2)
# 迎え角と経路角の計算
if abs((w+wg)/(u+ug)) < 1:
alpha = math.degrees(math.asin((w+wg)/(u+ug)))
else:
alpha = np.sign((w+wg)/(u+ug))*90
self.gamma = theta-alpha
# 横滑り角の計算
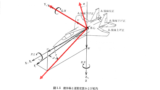
beta = math.degrees(math.asin((v+vg)/Airspeed))機体の対地速度を\([u, v, w]\),突風成分を\([u_{g}, v_{g}, w_{g}]\)とすると,機体の迎角\(\alpha\)と横滑り角\(\beta\)はそれぞれ次の式で表される(青本:式1.7-2)
\begin{eqnarray}
V&=&\sqrt{(u+u_{g})^{2}+(v+v_{g})^{2}+(w+w_{g})^{2}}\\
\alpha&=&\left( \frac{180}{\pi} \right) \arctan{\frac{w+w_{g}}{u+u_{g}}}\\
\beta&=&\left( \frac{180}{\pi} \right) \arcsin{\frac{v+v_{g}}{V}}
\tag{1.7-2}
\end{eqnarray}
経路角\(\gamma\)はピッチ角\(\theta\)と迎角\(\alpha\)を用いて次のように表される
\begin{eqnarray}
\gamma=\theta-\alpha
\tag{1.8-6}
\end{eqnarray}
地面効果
CGE = (self.CGEMIN+33*(hE/self.bw)**1.5)/(1+33*(hE/self.bw)**1.5)地面効果の影響については,以下の論文にあるHoerner and Borstの式を参考にする
\begin{eqnarray}
\frac{(C_{D_{i}}/C_{L}^{2})_{h}}{(C_{D_{i}}/C_{L}^{2})_{\infty}}
=\frac{33(h/b)^{1.5}}{1+33(h/b)^{1.5}}
\end{eqnarray}
Hoerner and Borstの式は高度5m以上の範囲ではよく一致するが,5m以下では誘導抗力が小さくなりすぎ,高度0mで誘導抗力が0になってしまう
今回の物理演算では水面付近の精度を優先し,以下の式を用いる
\begin{eqnarray}
C_{L}(h) &\simeq& C_{L_{\infty}} \\
C_{D_{i}}(h)&=&C_{GE}(h)C_{D_{i_{\infty}}}\\
\end{eqnarray}
\begin{eqnarray}
C_{GE}(h) = \frac{C_{GE_{min}}+33(h/b)^{1.5}}{1+33(h/b)^{1.5}}\\
\end{eqnarray}
ここで,\(C_{GE_{min}}\)は\(\frac{(C_{D_{i}}/C_{L}^{2})_{h}}{(C_{D_{i}}/C_{L}^{2})_{\infty}}\)の最小値であり,QX-20では\(C_{GE_{min}}=0.283\)である
比較してみるとこんな感じになる
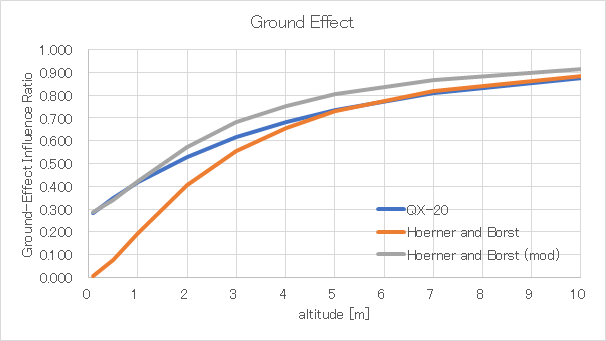
計算の負荷を下げるための近似なのである程度の誤差はしょうがない
鳥コン滑空機の地面効果について厳密に計算する方法についてはこちら
揚力係数、抗力係数、ピッチング モーメント係数
# 揚力係数の計算
CL0 = (self.mass*self.gravity)/(0.5*self.rho*self.airspeed0**2*self.Sw)
CLt0 = (self.Cmw0+CL0*self.hw)/(self.VH+(self.St/self.Sw)*self.hw)
CLw0 = CL0-(self.St/self.Sw)*CLt0
if self.Downwash:
self.epsilon0 = (CL0/(math.pi*self.ew*self.AR))*math.degrees(1)
CLw = CLw0+self.aw*(alpha-self.alpha0)
CLt = (CLt0+self.at*((alpha-self.alpha0)+(1-CGE*(CLw/CLw0))*self.epsilon0+el*self.tau+((self.lt-self.dh*self.cMAC)/Airspeed)*q))
# 最大揚力係数の制限
if abs(CLw) > self.CLMAX:
CLw = (CLw/abs(CLw))*self.CLMAX # Stall
if abs(CLt) > self.CLMAX:
CLt = (CLt/abs(CLt))*self.CLMAX # Stall
CL = CLw+(self.St/self.Sw)*CLt # CL
# 抗力係数の計算
CD = (self.CDp0*(1+(4*2.5)/(math.pi*0.6)*(1/0.04)*math.tan(math.radians(alpha-self.alpha0))**2)+((CL*CL)/(math.pi*self.ew*self.AR))*CGE) # CD
Cm = self.Cmw0+CLw*self.hw-self.VH*CLt+CL*self.dh # Cm 巡航状態では,力とモーメントは次のように釣り合っている
\begin{eqnarray}
C_{L_{0}}&=&C_{L_{w_{0}}}+\frac{S_{t}}{S_{w}}C_{L_{t_{0}}}\\
0&=&C_{m_{w_{0}}}+C_{L_{w_{0}}}h_{w}-V_{H}C_{L_{t_{0}}}\\
\end{eqnarray}
これより,巡航時の\(C_{L_{w_{0}}}\)と\(C_{L_{t_{0}}}\)は次のように求まる
\begin{eqnarray}
C_{L_{w_{0}}}&=&C_{L_{0}}-\frac{S_{t}}{S_{w}}C_{L_{t_{0}}}\\
C_{L_{t_{0}}}&=&\frac{C_{m_{w_{0}}}+C_{L_{0}}h_{w}}{V_{H}+\frac{S_{t}}{S_{w}}h_{w}}\\
\end{eqnarray}
縦の空気力とモーメントはこのつり合いをもとに計算していく
まず,揚力係数\(C_{L}\)は次のように計算する
\begin{eqnarray}
C_{L}&=&C_{L_{w}}+\frac{S_{t}}{S_{w}}C_{L_{t}}\\
\\
C_{L_{w}}&=&C_{L_{w_{0}}}+a_{w}(\alpha-\alpha_{0})\\
C_{L_{t}}&=&C_{L_{t_{0}}}+a_{t}\left\{(\alpha-\alpha_{0})+(1-C_{GE}\frac{C_{L_{w}}}{C_{L_{w_{0}}}})\varepsilon_{0}+\delta_{e}\tau+\frac{l_{t}}{V}q\right\}\\
\end{eqnarray}
ここで,\((1-C_{GE}\frac{C_{L_{w}}}{C_{L_{w_{0}}}})\varepsilon_{0}\)の項は主翼の吹きおろしの変化を表し,次のように求められる
\begin{eqnarray}
\Delta \varepsilon&=&\varepsilon-\varepsilon_{0}
&=&C_{GE}\frac{C_{L_{w}}}{\pi e (AR)}-\frac{C_{L_{w_{0}}}}{\pi e (AR)}
&=&-(1-C_{GE}\frac{C_{L_{w}}}{C_{L_{w_{0}}}})\varepsilon_{0}
\end{eqnarray}
ただし,失速を表現するため\(|C_{L_{w}}|<C_{L_{max}}\),\(|C_{L_{t}}|<C_{L_{max}}\)の制約を加える
次に,抗力係数\(C_{D}\)は次のように計算する
\begin{eqnarray}
C_{D}&=&C_{D_{p}}+C_{D_{i}}\\
\\
C_{D_{p}}&=&C_{D_{p_{0}}}\left\{1+\left(\frac{|\alpha|}{9}\right)^{3}\right\}\\
C_{D_{i}}&=&\frac{C_{L}^{2}}{\pi e (AR)}C_{GE}\\
\end{eqnarray}
重心まわりのピッチングモーメント\(M\)は次のように表される
\begin{eqnarray}
M_{cg}&=&\frac{1}{2}\rho V^{2}S_{w}{\overline c}C_{m}\\
\\
C_{m}&=&C_{m_{w}}+C_{L_{w}}h_{w}-V_{H}C_{L_{t}}\\
\end{eqnarray}
ただし,主翼によるピッチングモーメント係数は一定(\(C_{m_{w}}=C_{m_{w_{0}}}=const.\))とする
動微係数の安定軸から機体軸への変換
# 動微係数を安定軸から機体軸へ変換
cosA = math.cos(math.radians(alpha))
sinA = math.sin(math.radians(alpha))
Cyp = self.Cyp*cosA-self.Cyr*sinA
Cyr = -self.Cyp*sinA+self.Cyr*cosA
Clp = self.Clp*cosA*cosA-self.Cnp*sinA*cosA-self.Clr*sinA*cosA+self.Cnr*sinA*sinA
Cnp = self.Clp*sinA*cosA+self.Cnp*cosA*cosA-self.Clr*sinA*sinA-self.Cnr*sinA*cosA
Clr = self.Clp*sinA*cosA-self.Cnp*sinA*sinA+self.Clr*cosA*cosA-self.Cnr*sinA*cosA
Cnr = self.Clp*sinA*sinA+self.Cnp*sinA*cosA+self.Clr*sinA*cosA+self.Cnr*cosA*cosA動微係数の安定軸から機体軸への変換には以下の式を使用する
縦
\begin{align}
\left[\begin{array}{c}
C_{x_{q'}} \\ C_{z_{q'}}
\end{array}\right] &=
\left[\begin{array} {cc}
-\cos{\alpha} & \sin{\alpha}\\
-\sin{\alpha} & -\cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c}
C_{D_{q}} \\ C_{L_{q}}
\end{array}\right] \\\\
C_{m_{q'}}&=C_{m_{q}}
\end{align}
横・方向(無印が安定軸、プライム付きが機体軸)
\begin{align}
\left[\begin{array}{c}
C_{y_{p'}} \\ C'_{y_{r'}}
\end{array}\right] &=
\left[\begin{array} {cc}
\cos{\alpha} & -\sin{\alpha} \\
-\sin{\alpha} & \cos{\alpha} \\
\end{array}\right]
\left[\begin{array}{c}
C_{y_{p}} \\ C_{y_{r}}
\end{array}\right] \\\\
\left[\begin{array}{c}
C_{l_{p'}} \\ C_{n_{p'}} \\ C_{l_{r'}} \\ C_{n_{r'}}
\end{array}\right] &=
\left[\begin{array} {cccc}
\cos{\alpha}^2 & -\sin{\alpha}\cos{\alpha} & -\sin{\alpha}\cos{\alpha} & \sin{\alpha} ^2 \\
\sin{\alpha}\cos{\alpha} & \cos{\alpha}^2 & -\sin{\alpha} ^2 & -\sin{\alpha}\cos{\alpha} \\
\sin{\alpha}\cos{\alpha} & -\sin{\alpha} ^2 & \cos{\alpha}^2 & -\sin{\alpha}\cos{\alpha} \\
\sin{\alpha}^2 & \sin{\alpha}\cos{\alpha} & \sin{\alpha}\cos{\alpha} & \cos{\alpha} ^2 \\
\end{array}\right]
\left[\begin{array}{c}
C_{l_{p}} \\ C_{n_{p}} \\ C_{l_{r}} \\ C_{n_{r}}
\end{array}\right]
\end{align}
機体軸の空力係数、 力とモーメント
# 機体軸の空力係数の計算
Cx = CL*sinA-CD*cosA
Cy = (self.Cyb*beta+Cyp*(1/math.degrees(1))*((p*self.bw)/(2*Airspeed))+Cyr*(1/math.degrees(1))*((r*self.bw)/(2*Airspeed))+ self.Cydr*rd) # Cy
Cz = -CL*cosA-CD*sinA # Cz
Cl = (self.Clb*beta+Clp*(1/math.degrees(1))*((p*self.bw)/(2*Airspeed))+Clr*(1/math.degrees(1))*((r*self.bw)/(2*Airspeed))+ self.Cldr*rd) # CL
Cm = self.Cmw0+CLw*self.hw-self.VH*CLt+CL*self.dh # Cm
Cn = (self.Cnb*beta+ Cnp*(1/math.degrees(1))*((p*self.bw)/(2*Airspeed))+Cnr*(1/math.degrees(1))*((r*self.bw)/(2*Airspeed))+ self.Cndr*rd) # Cn
# 機体にはたらく力とモーメントの計算
X = 0.5*self.rho*Airspeed**2*self.Sw*Cx
Y = 0.5*self.rho*Airspeed**2*self.Sw*Cy
Z = 0.5*self.rho*Airspeed**2*self.Sw*Cz
L = ((self.Iyy-self.Izz)*math.radians(q*r)+self.Ixz*math.radians(p*q)+math.degrees(0.5*self.rho*Airspeed**2*self.Sw*self.bw*Cl))
M = ((self.Izz-self.Ixx)*math.radians(r*p)+self.Ixz*math.radians(r**2-p**2)+math.degrees(0.5*self.rho*Airspeed**2*self.Sw*self.cMAC*Cm))
N = ((self.Ixx-self.Iyy)*math.radians(p*q)-self.Ixz*math.radians(q*r)+math.degrees(0.5*self.rho*Airspeed**2*self.Sw*self.bw*Cn)) 機体軸の空力係数は以下の式で計算できる
\begin{eqnarray}
C_{x}&=&-C_{D}\cos{\alpha}+C_{L}\sin{\alpha}\\
C_{y}&=&C_{y_{\beta}}\beta+C_{y_{p}}\frac{1}{180/\pi}\frac{pb}{2V}+C_{y_{r}}\frac{1}{180/\pi}\frac{rb}{2V}+C_{y_{\delta_{r}}}\delta_{r}\\
C_{z}&=&-C_{L}\cos{\alpha}-C_{D}\sin{\alpha}\\
C_{l}&=&C_{l_{\beta}}\beta+C_{l_{p}}\frac{1}{180/\pi}\frac{pb}{2V}+C_{l_{r}}\frac{1}{180/\pi}\frac{rb}{2V}+C_{l_{\delta_{r}}}\delta_{r}\\
C_{m}&=&C_{m_{w}}+C_{L_{w}}h_{w}-V_{H}C_{L_{t}}\\
C_{n}&=&C_{n_{\beta}}\beta+C_{n_{p}}\frac{1}{180/\pi}\frac{pb}{2V}+C_{n_{r}}\frac{1}{180/\pi}\frac{rb}{2V}+C_{n_{\delta_{r}}}\delta_{r}\\
\end{eqnarray}
機体にはたらく力とモーメントは以下の式で計算できる
\begin{eqnarray}
X&=&\frac{1}{2}\rho V^{2} S_{w} C_{x}\\
Y&=&\frac{1}{2}\rho V^{2}S_{w}C_{y}\\
Z&=&\frac{1}{2}\rho V^{2} S_{w} C_{z}\\
L&=&(I_{y}-I_{z})\frac{qr}{(180/\pi)}+I_{xz}\frac{pq}{(180/\pi)}+\frac{\rho V^2 S b}{2}(\frac{180}{\pi})C_{l}\\
M&=&(I_{z}-I_{x})\frac{rp}{(180/\pi)}+I_{xz}\frac{r^{2}-p^{2}}{(180/\pi)}+\frac{\rho V^2 S \overline{c}}{2}(\frac{180}{\pi})C_{m}\\
N&=&(I_{x}-I_{y})\frac{pq}{(180/\pi)}+I_{xz}\frac{qr}{(180/\pi)}+\frac{\rho V^2 S b}{2}(\frac{180}{\pi})C_{n} \\
\end{eqnarray}
状態変数の時間変化
# 絶対座標系の速度、機体座標系の加速度、姿勢角速度、角加速度の計算
rad_phi = math.radians(phi)
rad_theta = math.radians(theta)
dphi = (p+(r*math.cos(rad_phi)+q*math.sin(rad_phi))*math.tan(rad_theta))
dtheta = (q*math.cos(rad_phi)-r*math.sin(rad_phi))
dpsi = ((r*math.cos(rad_phi)+q*math.sin(rad_phi))/math.cos(rad_theta))
du = (-math.radians(q)*w+math.radians(r)*v-self.gravity*math.sin(rad_theta)+(X/self.mass))
dv = (-math.radians(r)*u+math.radians(p)*w+self.gravity*math.cos(rad_theta)*math.sin(rad_phi)+(Y/self.mass))
dw = (-math.radians(p)*v+math.radians(q)*u+self.gravity*math.cos(rad_theta)*math.cos(rad_phi)+(Z/self.mass))
dp = ((L/self.Ixx)+(self.Ixz/self.Ixx)*(N/self.Izz))/(1-(self.Ixz**2)/(self.Izz*self.Ixx))
dq = M/self.Iyy
dr = ((N/self.Izz)+(self.Ixz/self.Izz)*(L/self.Ixx))/(1-(self.Ixz**2)/(self.Ixx*self.Izz)) 対地速度は座標変換ですでに計算している
機体軸加速度
\begin{eqnarray}
\dot{u}&=&-\frac{q}{(180/\pi)}w&+\frac{r}{(180/\pi)}v&-g\sin{\theta}&+\frac{\rho V^2 S}{2m}C_{x}\\
\dot{v}&=&-\frac{r}{(180/\pi)}u&+\frac{p}{(180/\pi)}w&-g\cos{\theta}\sin{\phi}&+\frac{\rho V^2 S}{2m}C_{y}\\
\dot{w}&=&-\frac{p}{(180/\pi)}v&+\frac{q}{(180/\pi)}u&-g\cos{\theta}\cos{\phi}&+\frac{\rho V^2 S}{2m}C_{z}\
\tag{1.4-1}
\end{eqnarray}
姿勢角速度
\begin{eqnarray}
\dot{\phi}&=&p+(r\cos{\phi}+q\sin{\phi})\tan{\theta}\\
\dot{\theta}&=&q\cos{\phi}-r\sin{\phi}\\
\dot{\psi}&=&\frac{r\cos{\phi}+q\sin{\phi}}{\cos{\theta}}
\tag{1.6-9}
\end{eqnarray}
角加速度
\begin{eqnarray}
\dot{p}&=&\frac{\frac{L}{I_{x}}+\frac{I_{xz}}{I_{x}}\frac{N}{I_{z}}}{1-\frac{I_{xz}^2}{I_{x}I_{z}}}\\
\dot{q}&=&\frac{M}{I_{y}}\\
\dot{r}&=&\frac{\frac{N}{I_{z}}+\frac{I_{xz}}{I_{z}}\frac{L}{I_{x}}}{1-\frac{I_{xz}^2}{I_{x}I_{z}}}
\tag{1.4-4}
\end{eqnarray}
舵角の更新
# 入力の計算
d_el, d_rd = self._calculate_inputs(t, state)
# 最大舵角の制限
if np.abs(el) > self.el_max:
d_el = 0
if np.abs(rd) > self.rd_max:
d_rd = 0後述する_calculate_inputメソッドで計算した舵角の操舵速度を受け取り、最大舵角の制限を加える
戻り値
return [uE, vE, wE, du, dv, dw, dphi, dtheta, dpsi, dp, dq, dr, d_el, d_rd]計算した状態変数の変動量をリストにして返す
制御 (_calculate_inputメソッド)
def _calculate_inputs(self, t, state):
# 操舵量の計算する
if t-self.t_old <= 0:
return 0, 0
else:
dt = t-self.t_old
# 縦方向の制御
pullup_flag = True
flare_flag = True
if t < self.time_pullup: # 引き起こし
gamma_target = self.gamma_dive
elif t < self.time_flare: # 定常滑空
if pullup_flag:
self.PID_Lon[1] = 0 # Iをリセット
pullup_flag = False
gamma_target = self.gamma_cruise
else: # フレア
if flare_flag:
self.PID_Lon[1] = 0 # Iをリセット
flare_flag = False
gamma_target = 0
self.PID_Lon[2] = ((self.gamma-gamma_target)-self.PID_Lon[0])/dt
self.PID_Lon[0] = self.gamma-gamma_target
self.PID_Lon[1] += self.PID_Lon[0]*dt
# 横方向の制御
turn_flag = True
if t < self.time_entry: # 操縦しない
phi_target = self.phi
elif t < self.time_break: # 旋回中
phi_target = self.phi_turn
else: # 水平飛行
if turn_flag:
self.PID_lat[1] = 0 # Iをリセット
turn_flag = False
phi_target = 0
self.PID_lat[2] = ((self.phi-phi_target)-self.PID_lat[0])/dt
self.PID_lat[0] = (self.phi-phi_target)
self.PID_lat[1] += self.PID_lat[0]*dt
# 操舵変化量の計算
if t < self.time_pullup:
d_el = np.dot(self.PID_param_lon, self.PID_Lon)*self.el_max
elif t < self.time_flare:
d_el = np.dot(self.PID_param_lon, self.PID_Lon)*self.el_max
else:
d_el = np.dot(self.PID_param_lon, self.PID_Lon)*self.el_max
if t < self.time_entry or t > self.time_break:
d_rd = np.dot(self.PID_param_lat, self.PID_lat)*self.rd_max
else:
d_rd = np.dot(self.PID_param_lat, self.PID_lat)*self.rd_max
# 操舵変化量の制限
d_el = min(max(d_el,-self.el_max/1.0), self.el_max/1.0)
d_rd = min(max(d_rd,-self.rd_max/1.0), self.rd_max/1.0)
return d_el, d_rdAirplane.motion_equationメソッド内で用いるエレベータ舵角およびラダー舵角の操舵速度[deg/s]は、 Airplane.calculate_inputメソッドで計算する
| 引数 | 型 | 説明 | 単位 | デフォルト |
| t | float | 時間 | s | - |
| state | ndarray | 状態変数の配列 | - | - |
| 戻り値 | 型 | 説明 | 単位 |
| d_el | float | エレベータ舵角の操舵速度 | deg/s |
| d_rd | float | ラダー舵角の操舵速度 | deg/s |
PID制御
NLFS6 ver2.0.0では、縦の操縦はエレベーター、 横方向の操縦はラダーを用いて行う
舵角の操舵速度は、 縦は経路角\(\gamma\)、横方向はバンク角\(\phi\)に応じて以下の式でを計算する
\begin{align}
d\_el &= P_{lon}\left(\gamma_{target}-\gamma\right)
+I_{lon}\int_{0}^{t}{\left(\gamma_{target}-\gamma\right)}dt
+D_{lon}\frac{\partial \left(\gamma_{target}-\gamma\right)}{\partial t} \\\\
d\_rd &= P_{lat}\left(\phi_{target}-\phi\right)
+I_{lat}\int_{0}^{t}{\left(\phi_{target}-\phi\right)}dt
+D_{lat}\frac{\partial \left(\phi_{target}-\phi\right)}{\partial_t}
\end{align}
PIDのパラメータのうち、
\(\int_{0}^{t}{\left(\gamma_{target}-\gamma\right)}dt\) と \(\int_{0}^{t}{\left(\phi_{target}-\phi\right)}dt\) については後述するフェーズの切り替わりで値をゼロにリセットする
フライトのフェーズ
Airplane._calculate_inputメソッドでは、縦および横・方向それぞれでフライトを3つのフェーズに分ける
縦
| フェーズ | 目標値 | 目標値の範囲 | 時刻 | 備考 |
| 引き起こし | ダイブ角 | -30°~ 0° | テイクオフ ~ 引き起こし | 引き起こしは20 [s]までに行う |
| 定常滑空 | 定常滑空角 | -5°~0° | 引き起こし ~ フレア開始 | 着水までにはフレアを行う |
| フレア | 高度維持 | 0° | フレア開始 ~ 着水 | 失速するまでひたすら高度を維持する |
横・方向
| フェーズ | 目標値 | 目標値の範囲 | 時刻 | 備考 |
| なにもしない | なし | (現在のバンク角) | テイクオフ ~ 旋回開始 | 離陸直後は見に回る |
| 旋回 | 定常バンク角 | -10°~0° | 旋回開始 ~ 旋回終了 | 対称性を考慮して左旋回のみに限定する |
| ウィングレベル | 翼を水平に | 0° | 旋回終了 ~ 着水 | 翼を水平にして翼端から着水しないようにする |
※ 旋回開始時刻≒旋回終了時刻≒着水時刻だと旋回操作をしないフライトになる
使い方
__init__にある性能諸元を任意に設定する
__main__関数内でuvw_gEとinitial_stateを任意に設定する
# Planeクラスのインスタンスを作成し、外部風速をゼロに設定
plane = Plane(uvw_gE=np.array([0, 0, 0]))
# シミュレーションを実行し、初期状態を設定
# 初期状態: [XE, YE, ZE, u, v, w, phi, theta, psi, p, q, r, el, rd]
# XE, YE, ZE: 位置座標, u, v, w: 機体軸速度成分, phi, theta, psi: 姿勢オイラー角, p, q, r: 角速度成分, el, rd: エレベータ舵角、ラダー舵角
solution = plane.simulate(initial_state=[0, 0, 0, 10, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])ターミナルで以下のコマンドを実行する
py NLFS.py実行後は、解析終了時の位置座標が標準出力され、 matplotlib の3次元プロットが表示される
↓飛行経路の最適化に用いる場合はこっち
以上
おわりに
Scipyのsolve_ivpを使って航空機の6自由度の微分方程式を解いて運動解析を行った
やはりFORTRANよりも実装が簡単で、しかも時間ステップも積分の誤差がいい感じになるように最適に選んでくれるので、至れり尽くせりである
↓参考文献




コメント