PR

多目的遺伝的アルゴリズムを用いた鳥コン滑空機の飛行経路最適化 v2.0.0

pymooの多目的遺伝的アルゴリズムであるNSGA-IIと、 Scipy.solve_ivpを用いた航空機の6自由度の運動解析を用いて、久しぶりに鳥コン滑空機の飛行経路の最適化を行った（NSGA_NLFS6）

mtkbirdman.com/GA_NLFS/py at master · mtkbirdman/mtkbirdman.com
mtk_birdman's blog ＠mtk_birdman. Contribute to mtkbirdman/mtkbirdman.com development by creating an account on GitHub.
github.com
スポンサーリンク

はじめに

pymooの多目的遺伝的アルゴリズムであるNSGA-IIと、 Scipy.solve_ivpを用いた航空機の6自由度の運動解析を用いて、久しぶりに鳥コン滑空機の飛行経路の最適化を行った

↓Scipy.solve_ivpについて

Scipyのsolve_ivpで航空機の6自由度の運動方程式を解く
Scipyのsolve_ivpを使って航空機の６自由度の微分方程式を解いて運動解析を行う
mtkbirdman.com
2024.06.09

以前にもFORTRANを用いて鳥コン滑空機の飛行経路最適化を行ったことがあるので、今回のNSGA_NLFS6はv2.0.0である

↓前回の挑戦(GA_NLFS6)

遺伝的アルゴリズムを用いた鳥コン滑空機の飛行経路最適化
遺伝的アルゴリズム(GA: Genetic Algorithm)を用いて，鳥コン滑空機の飛行経路最適化を試みた
mtkbirdman.com
2020.06.26
前回からの改善点
  • (主にChatGPTが) FORTANで書かれた前回のプログラムをpythonで書き直した
  • (主にChatGPTが) C++で書かれたBRSimulatorの運動モデルをPythonで書き直し、必要な機体情報を共通化した
  • 舵角の制御を舵角そのものではなく舵角の操舵速度 [deg/s]にした
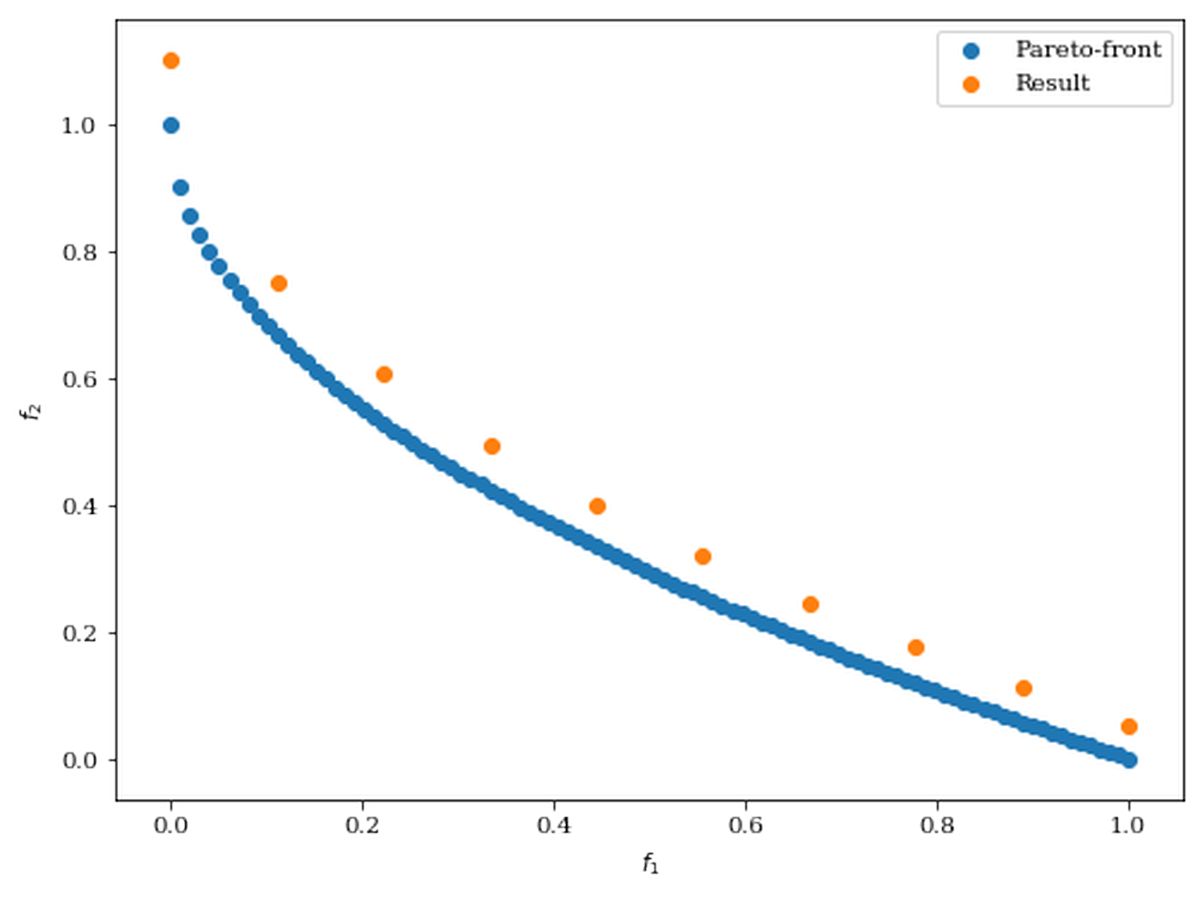
  • pymooのNSGA2を用いることで、飛行距離だけでなく縦、横方向の目標値とのずれ量も対象にした多目的最適化にした
  • 積分にScipy.solve_ivpを用いることで時間ステップの最適化ができた

最終的にはこんな感じになる

それではいってみよう

最適化問題の設定

今回作成したNSGA_NLFS6は、多目的遺伝的アルゴリズムNAGA-IIを用いてNLFS6_v2.0.0の制御パラメータを最適化することで、鳥コン滑空機における最適な飛行経路を求めるプログラムである

多目的最適化の概要は以下の通り

設計変数(遺伝子)

NLFS6 v2.0.0の制御パラメータ13個+テイクオフ時の初期ピッチ角の計14個

設計変数型説明単位最小値最大値ndarray
gamma_divefloatダイブ角deg-300X[0]
gamma_cruisefloat巡航角deg-50X[1]
phi_turnfloat旋回角deg-100X[2]
time_pullupfloat引き起こし時刻s020X[3]
time_flarefloatフレア時刻s060X[4]
time_entryfloat旋回開始時刻s060X[5]
time_breakfloat旋回終了時刻s060X[6]
PID_param_lonndarray縦方向PIDバラメータ--11X[7:10]
PID_param_latndarray横方向PIDパラメータ--11X[10:13]
theta0float初期ピッチ角deg-55X[13]

目的関数

目的関数説明
f1目標経路角と実際の経路角とのずれ量の絶対値の時間平均値
f2目標バンク角と実際のパンク角とのずれ量の絶対値の時間平均値
f3飛行距離の逆符号
※ f2はフェーズ1の操縦していない時間は除く

pymooのNSGA-IIでは目的関数の「最小化」を行うため、飛行距離の逆符号を目的関数にしている

制約条件

制約条件説明
g1引き起こし時刻<フレア開始時刻
g2旋回開始時刻<旋回終了時刻
g3フレア開始時刻<フライト終了時刻
g4旋回終了時刻<フライト終了時刻

g1とg2は当たり前の制約で、g3は明示しなくても勝手に着水前にフレアをするよう最適化される

g4が案外重要で、これがないと、f2との兼ね合いで、操縦しないフライト(ずっとフェーズ1 → f2=0で理論的な最適解) に収束してしまう

個体数、世代数、交差、突然変異、など

個体数は100、世代数は100、 交差と突然変異はよくわからないのでコピペ元のコードのまま

多目的最適化に特化したPythonライブラリpymooの使い方まとめ
ライブラリのバージョンアップ(0.6.0)で使用方法がガラッと変わってしまったので、近々修正予定です（22/12/03）⇒修正完了しました（22/12/17）pymoo は多目的最適化に特化した Python ライブラリです。最適化分野で有
yuyumoyuyu.com

ソースコードの解説

MyProblemクラス

Problemクラスを継承したMyProblemクラスを定義し、最適化問題を定義している

メソッドは以下の通り

  • __init__
  • evaluate
__init__(self, u0=5.5.gamma0-3.5, uvw_gE=np.array({0.0.0]))
    def __init__(self, u0=5.5, gamma0=3.5, uvw_gE=np.array([0, 0, 0])):
        self.u0 = u0  # 初期速度
        self.w0 = u0 * math.tan(math.radians(gamma0))  # 初期速度
        self.uvw_gE = uvw_gE  # 対地風速
        # 最適化変数の下限と上限
        xl = np.array([-30, -2, -10,  0,  0,  0,  0, -1, -1, -1, -1, -1, -1, -5])
        xu = np.array([ -2, -1,   0, 10, 60, 60, 60, +1, +1, +1, +1, +1, +1, +5])
        super().__init__(n_var=14, n_obj=3, n_constr=4, xl=xl, xu=xu)  # 問題の初期化

初期化メソッド

引数:

変数名型説明単位デフォルト値
u0float初期速度m/s5.5
gamma0float初期経路角deg-3.5
uvw_gEndarray対地風速m/s(0,0,0)

以下のインスタンス変数を初期化する

変数名型説明単位デフォルト値
u0float機体軸x方向の初期速度m/s5.5
w0float機体軸z方向の初期速度m/s-5.5*tan(theta0)
uvw_gEndarray対地風速m/s(0,0,0)
xlndarray最適化変数の下限-np.array([-30, -2, -10, 0, 0, 0, 0, -1, -1, -1, -1, -1, -1, -5])
xundarray最適化変数の上限-np.array([ -2, -1, 0, 10, 60, 60, 60, +1, +1, +1, +1, +1, +1, +5])

継承元のProblemクラスの初期化メソッドに以下を引数として与える

引数型説明単位デフォルト
n_varint設計変数の数-14
n_objint目的関数の数-3
n_constint制約条件の数-4
xl, xundarray設計変数の上限値と下限値--
_evaluate (self, X, out, *args, **kwargs)
    def _evaluate(self, X, out, *args, **kwargs):
        # Xを丸める
        X = np.round(X,5)
        # 目的関数のリスト
        f1_list = []
        f2_list = []
        f3_list = []
        g3_list = []
        g4_list = []
        for i in range(X.shape[0]):
            theta0 = X[i, 13]  # 初期ピッチ角
            initial_state = [0, 0, 0, self.u0, 0, self.w0, 0, theta0, 0, 0, 0, 0, 0, 0]  # 初期状態
            airplane = Plane(uvw_gE=self.uvw_gE, X=X[i, :13])  # Planeクラスのインスタンス作成
            solution = airplane.simulate(initial_state=initial_state)  # シミュレーション実行
            XE, YE, ZE = solution.y[:3]  # 結果の取得
            Distance = np.sqrt(XE[-1]**2 + YE[-1]**2)  # 飛行距離

            # 時間差分と速度成分の計算
            dt = np.diff(solution.t)
            uE = np.diff(XE) / dt
            wE = np.diff(ZE) / dt
            gamma = np.degrees(np.arctan(wE / uE))  # 経路角の計算

            # 目的関数1の計算
            target = np.where(solution.t <= X[i, 3], X[i, 0], np.where(solution.t >= X[i, 4], 0, X[i, 1]))
            diff1 = np.sum(np.abs(gamma - target[1:])) / solution.t[-1]

            # 目的関数2の計算
            phi = solution.y[6]
            target = np.where(solution.t <= X[i, 5], phi, np.where(solution.t >= X[i, 6], 0, X[i, 2]))
            diff2 = np.sum(np.abs(phi - target))/ np.abs(solution.t[-1]-X[i,5])

            # 目的関数リストに追加
            f1_list.append(diff1)
            f2_list.append(diff2)
            f3_list.append(-Distance)
            g3_list.append(X[i,4]-solution.t[-1]) # time_flare < flight time
            g4_list.append(X[i,6]-solution.t[-1]) # time_break < flight time

        # 目的関数の結果をnumpy配列に変換
        f1 = np.array(f1_list)
        f2 = np.array(f2_list)
        f3 = np.array(f3_list)

        # 制約条件の計算
        g1 = X[:, 3] - X[:, 4]
        g2 = X[:, 5] - X[:, 6]
        g3 = np.array(g3_list)
        g4 = np.array(g4_list)

        # 出力として目的関数と制約条件を設定
        out["F"] = np.column_stack([f1, f2, f3])
        out["G"] = np.column_stack([g1, g2, g3, g4])

最適化アルゴリズムによって呼び出されるメソッド

目的関数と制約条件の計算を行い、結果をoutに設定する

なお、制御パラメータの丸め誤差を回避するため、 Xを小数点以下5桁で四捨五入している

引数型説明単位デフォルト
Xndarray設計変数-xlとxuから生成される
戻り値型説明単位
outdictionary目的関数と制約条件の計算結果を格納する辞書-

↓Airplaneクラスの使い方についてはこちらを参照

Scipyのsolve_ivpで航空機の6自由度の運動方程式を解く
Scipyのsolve_ivpを使って航空機の６自由度の微分方程式を解いて運動解析を行う
mtkbirdman.com
2024.06.09

MyOutputクラス

class MyOutput(Output):
    def __init__(self):
        super().__init__()
        self.Dist_max = Column("Dist_max", width=13)
        self.Dist_ave = Column("Dist_ave", width=13)
        self.diff1 = Column("diff1", width=13)
        self.diff2 = Column("diff2", width=13)
        self.RunTime = Column("RunTime", width=13)
        self.columns += [self.Dist_max, self.Dist_ave, self.diff1, self.diff2, self.RunTime]
        self.start_time = time.time()  # 開始時刻を記録

    def update(self, algorithm):
        super().update(algorithm)
        self.diff1.set(np.min(algorithm.pop.get("F"), axis=0)[0])
        self.diff2.set(np.min(algorithm.pop.get("F"), axis=0)[1])
        self.Dist_max.set(-np.min(algorithm.pop.get("F"), axis=0)[2])
        self.Dist_ave.set(-np.average(algorithm.pop.get("F"), axis=0)[2])
        self.RunTime.set(time.time()-self.start_time)

Outputクラスを継承したMyOutputクラスを定義し、最適化実行中のプログラムの標準出力をアレンジする

NSGA_NLFS6では以下の値を出力する

表示説明単位
n_genこれまでの世代数-
n_evalこれまでの関数評価の数-
Dist_max見つかった最適解の最大飛距離m
Dist_ave見つかった最適解の平均飛距離m
diff1見つかった最適解の目的関数1の最小値-
diff2見つかった最適解の目的関数2の最小値-
RunTimeこれまでの実行時間s

Columnクラスのsetメソッドに値を渡すときに、指数標記にならないようひと工夫している

__main__関数

if __name__ == '__main__':
    start_time = time.time()  # 開始時刻を記録

    （処理）

    # 終了時刻を記録し、実行時間を計算
    end_time = time.time()
    print(f"Run time: {end_time - start_time} s")

実行部分はここ

処理:

テイクオフ時の初速と経路角および地表風を引数として与えてMyProblemクラスのインスタンスを作成する

    # 最適化問題の設定
    problem = MyProblem(
        u0=5.5,
        gamma0=3.5,
        uvw_gE=np.array([0, 2*math.sqrt(2), 0]),
    )

NSGA-IIのパラメータを設定する

    # NSGA-IIアルゴリズムの設定
    algorithm = NSGA2(
        pop_size=100,
        sampling=LHS(),
        crossover=SBX(prob=0.9, eta=15),
        mutation=PolynomialMutation(eta=20),
        eliminate_duplicates=True,
    )

最適化を実行する(100個体100世代の最適化で半日かかる。 寝る前/出かける前の実行を推奨)

    # 最適化の実行
    res = minimize(
        problem,
        algorithm,
        ("n_gen", 100),
        seed=1,
        save_history=False,
        verbose=True,
        output=MyOutput(),
    )

飛行距離が大きい順に結果をソートしてからCSVファイルに保存する

    res_X = pd.DataFrame(np.round(res.X,5), columns=[f'X{i}' for i in range(14)])
    res_F = pd.DataFrame(res.F, columns=['diff1', 'diff2', 'Distance'])
    res_G = pd.DataFrame(res.G, columns=['Time_Cruise', 'Time_Turn'])

    # 結果をCSVファイルに保存
    res = pd.concat([res_X, res_F, res_G], axis=1)  # 変数データと目的関数データを結合
    res = res.sort_values('Distance')  # 距離でソート
    res[[f'X{i}' for i in range(14)]].to_csv('./res_X.csv', index=False)
    res[['Distance','diff1', 'diff2']].to_csv('./res_F.csv', index=False)
    res[['Time_Cruise', 'Time_Turn', 'Time_Flare', 'Time_NoBank']].to_csv('./res_G.csv', index=False)

使い方

NLFS.pyのinitにある性能諸元を任意に設定する

NSGA2.pyとcheck.pyの_main関数にあるu0, gamma0, uvw_gEの値を任意に設定する

NSGA2.py___main_関数にあるn_genとpop_sizeを任意に設定する

ターミナルで以下のコマンドを実行する

py NSGA2.py

実行中は、MyOutputクラスで定義した値が出力されるので、気長に放置する

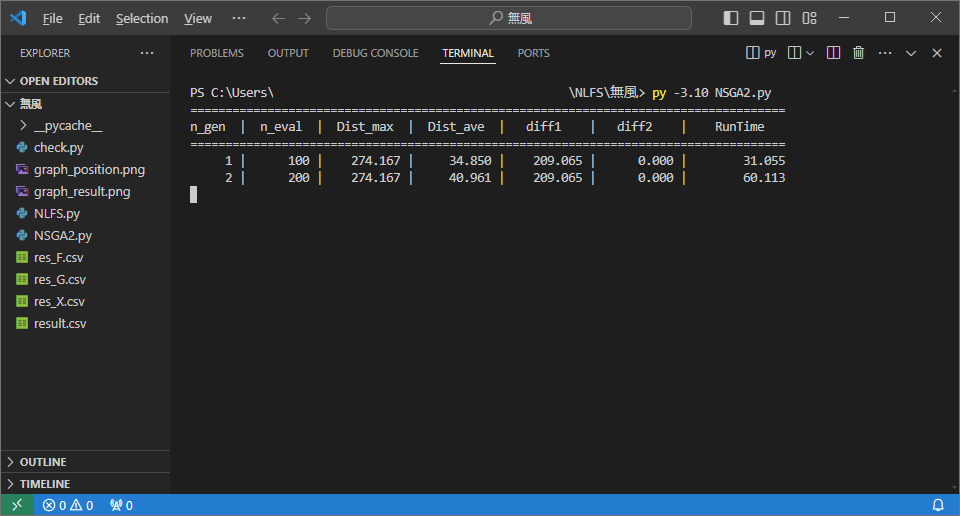
プログラムが終了したら、 結果を確認するためにターミナルで以下のコマンドを実行する 

py check.py

結果を示すグラフが続けて2枚表示され、主要な状態変数などがresult.csvに書き出される

考察

せっかくなので、いくつかのケースの最適化を行ってみた

Caseu0gamma0uvw_gEtheta0gamma
dive		time
dive		gamma
cruise		time
flare		time
entry		phi
turn		time
break		flight_timeDistance
(単位)m/sdegm/sdegdegsdegssdegssm
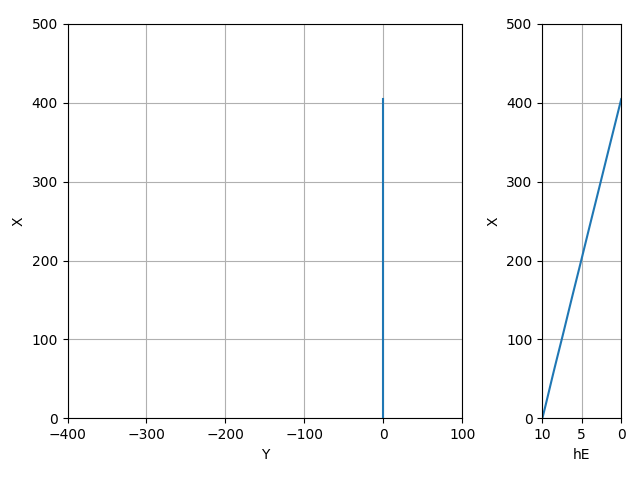
基本性能10-1.45(0,0,0)--------40.514404.830
無風5.5-3.5(0,0,0)0.928-21.8551.263-1.16129.7389.279-0.1699.41736.245332.470
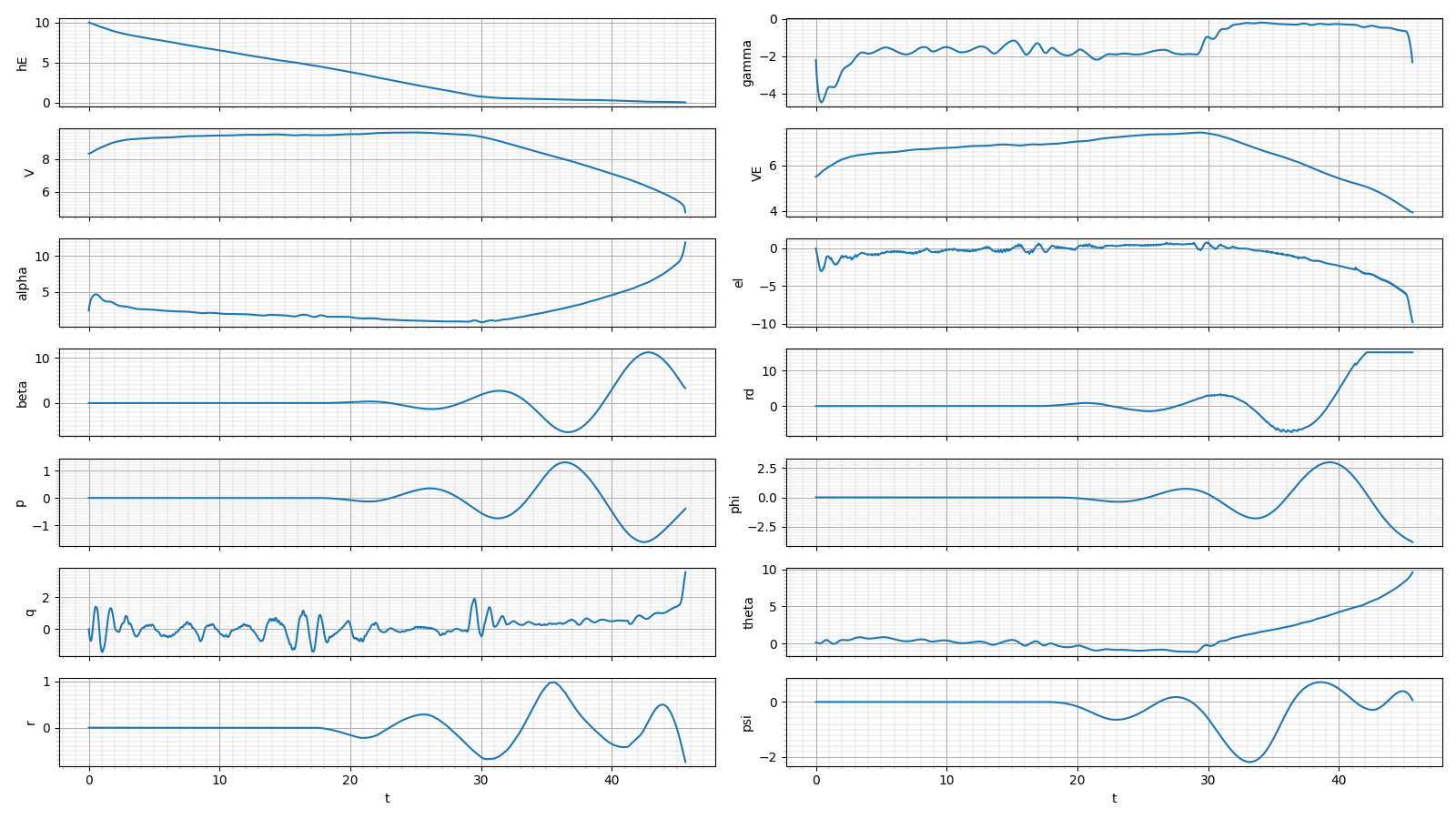
正対風5.5-3.5(2√2,0,0)0.160-4.3530.792-1.72228.93317.199-0.06122.21045.631297.986
斜め風5.5-3.5(2,2,0)-0.932-4.0124.390-1.23132.8753.615-2.19130.92043.806356.284
横風5.5-3.5(0,2√2,0)-0.345-3.0860.615-1.59422.90218.084-1.19430.13838.790357.617
背風5.5-3.5(-2,0,0)3.324-3.4351.278-1.09116.1312.961-1.2154.55826.999311.890

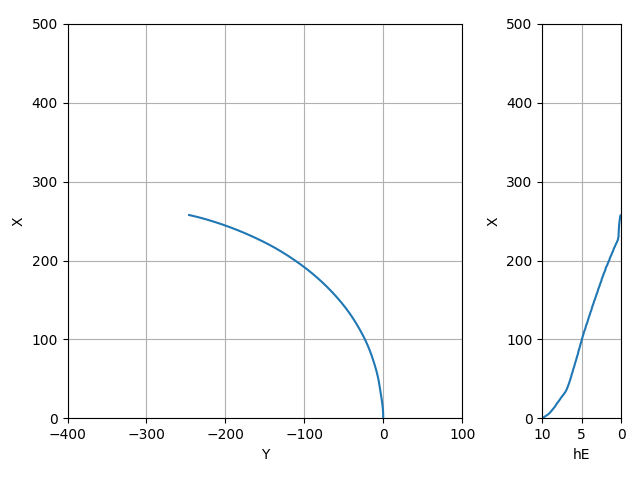
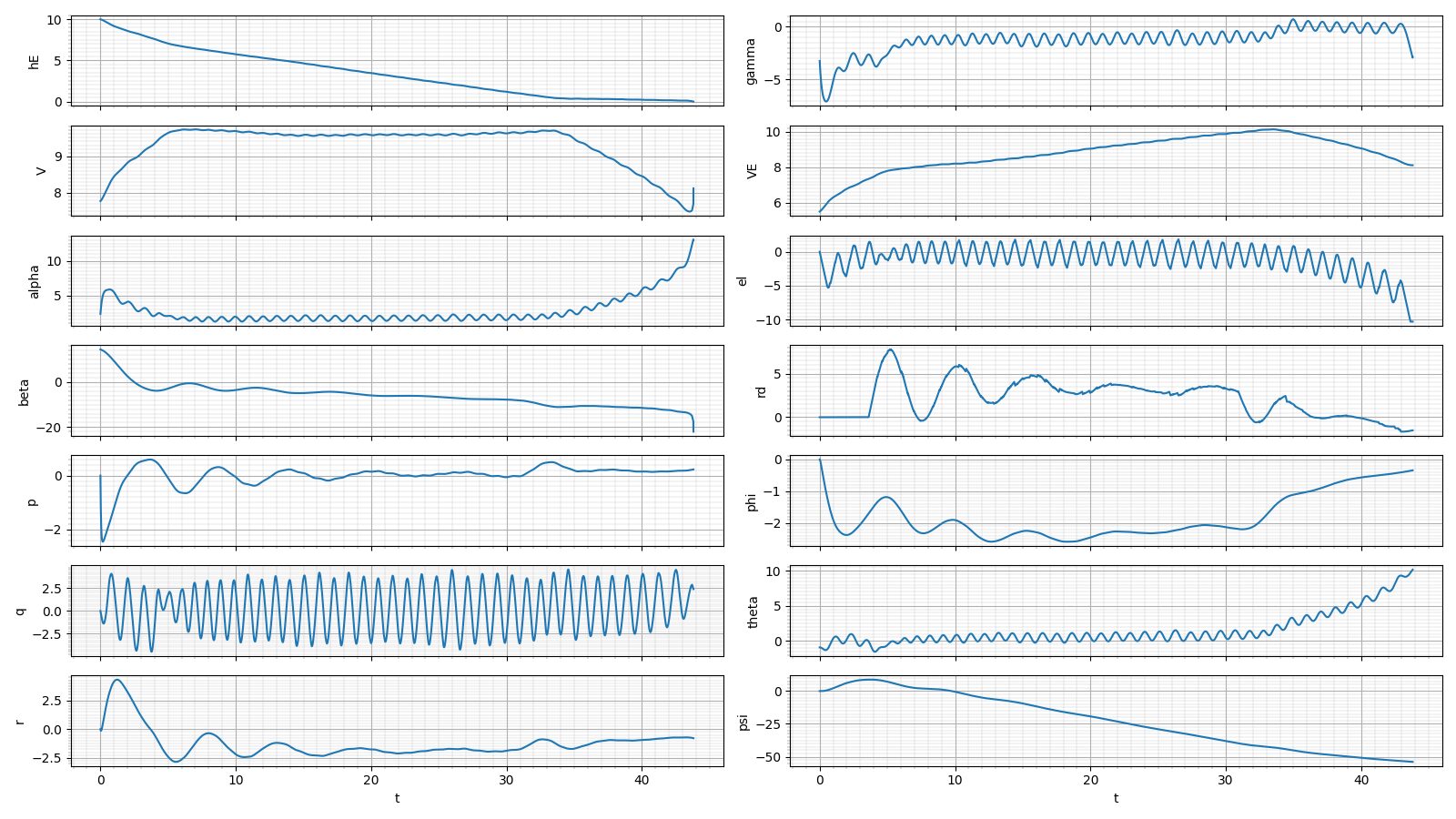
だいたい全機L/Dが40くらいの機体だと、 初速5.5[m/s]で飛距離が298m～358mまでぶれている

当日の風とそれに合わせたフライトプランの重要性がわかる

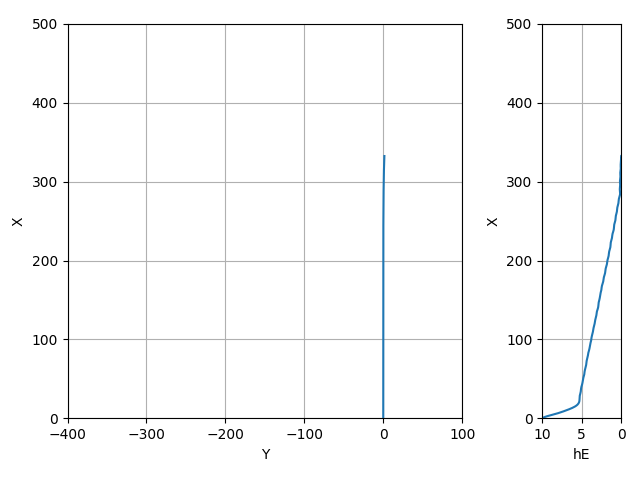
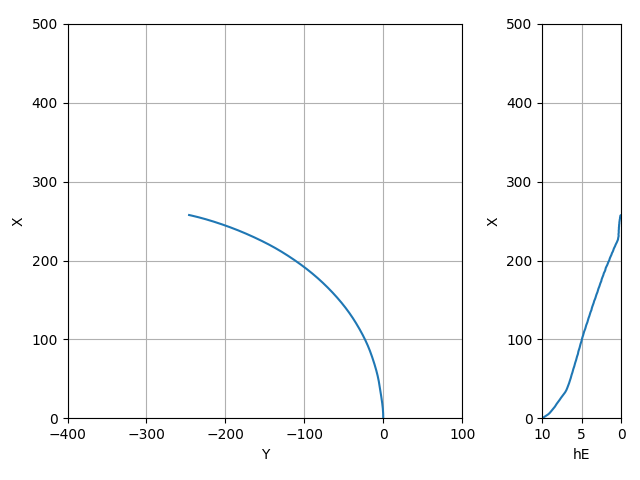
すごくきれいなダイブ→引き起こし→フレア

当然旋回は全くしていない

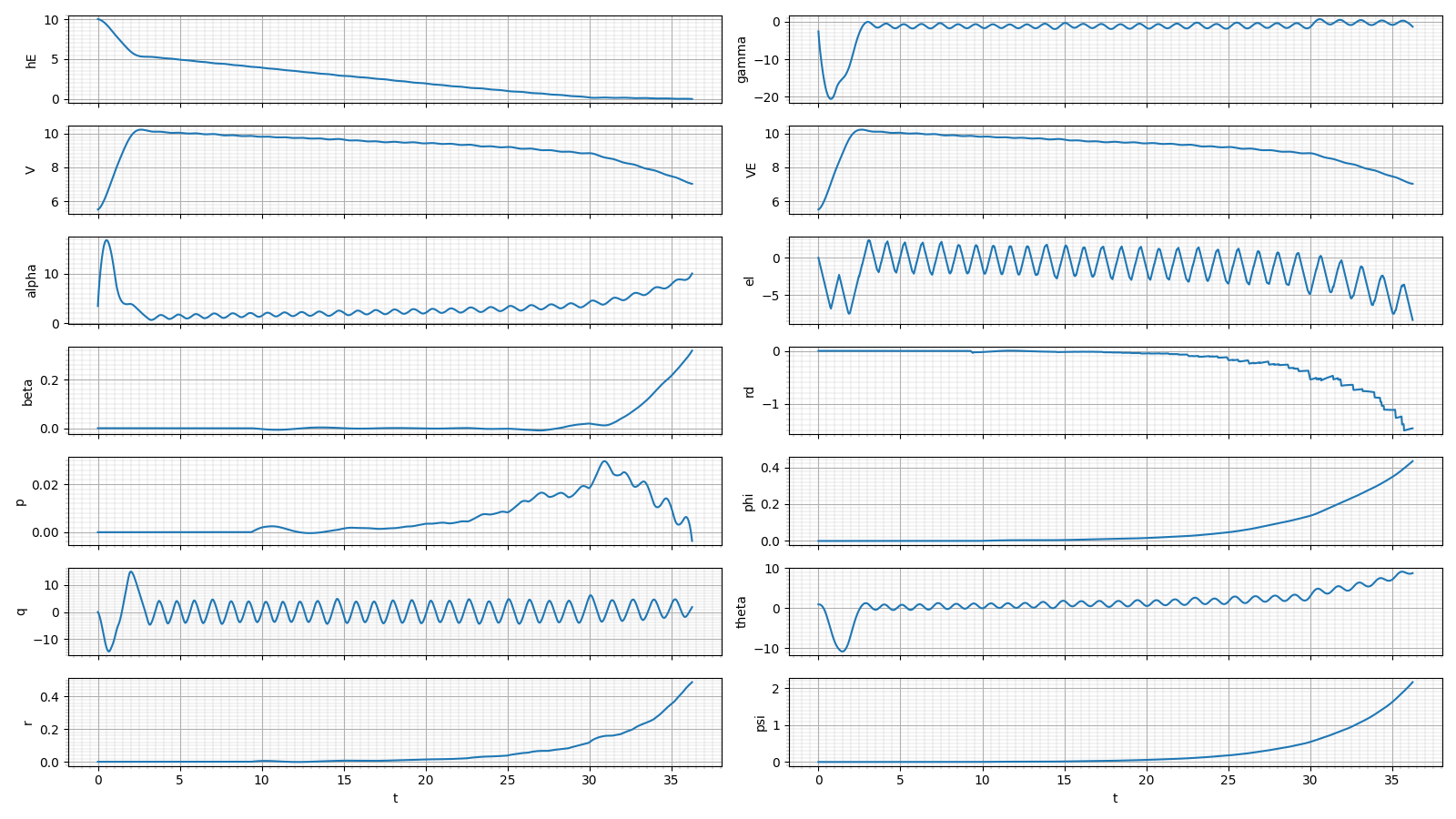
失速速度は7.5m/s程度、その時の迎角は10度程度

着水時のピッチ角も10度程度なので、尻摺り角とか胴体の角度を設計するときの参考になるかも

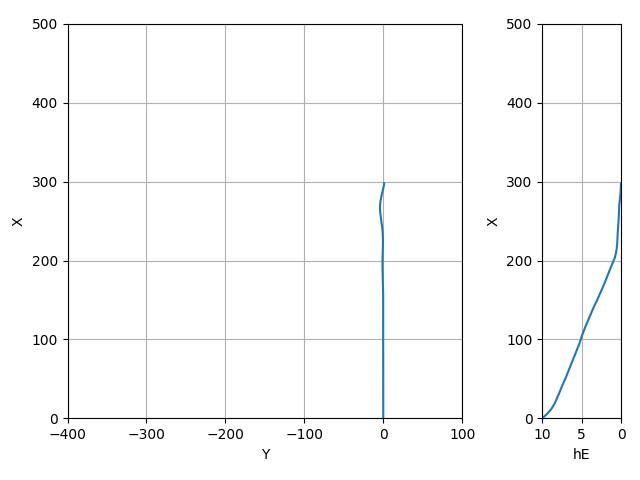
最後に謎のバンクが入ってしまっているのでもう少し最適化の余地はありそう

無風の時よりもダイブが短く、定常滑空角がやや深い

ポーラーカーブに従ってきちんと飛行速度を増しているのが良い

フレアを打つ際にエレベータの最大舵角-10まで切っている

俗にいうベストコンディション

きちんと緩やかに旋回しながら背風を背負うフライトに移行している

対気速度は10m/s 弱でほぼ一定のまま、対地速度が6m/s → 10m/s 強へと増加している

ラダーの最大舵角は8度程度

真横からの風なのでそこまで旋回する必要はなく、最初は流されるままにフライトしている

フレアが謎に長かったり、ラダーをぶんぶん振り回したりしているのでもう少し最適化の余地は残っていそう

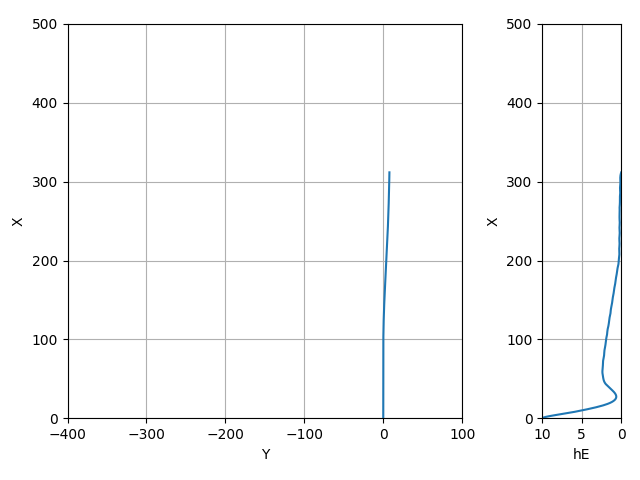
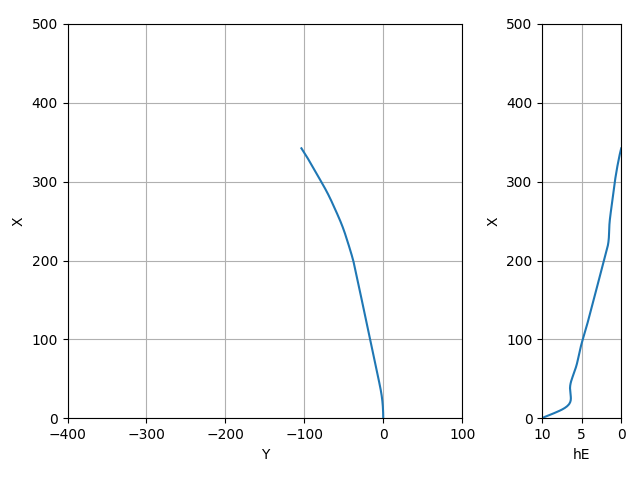
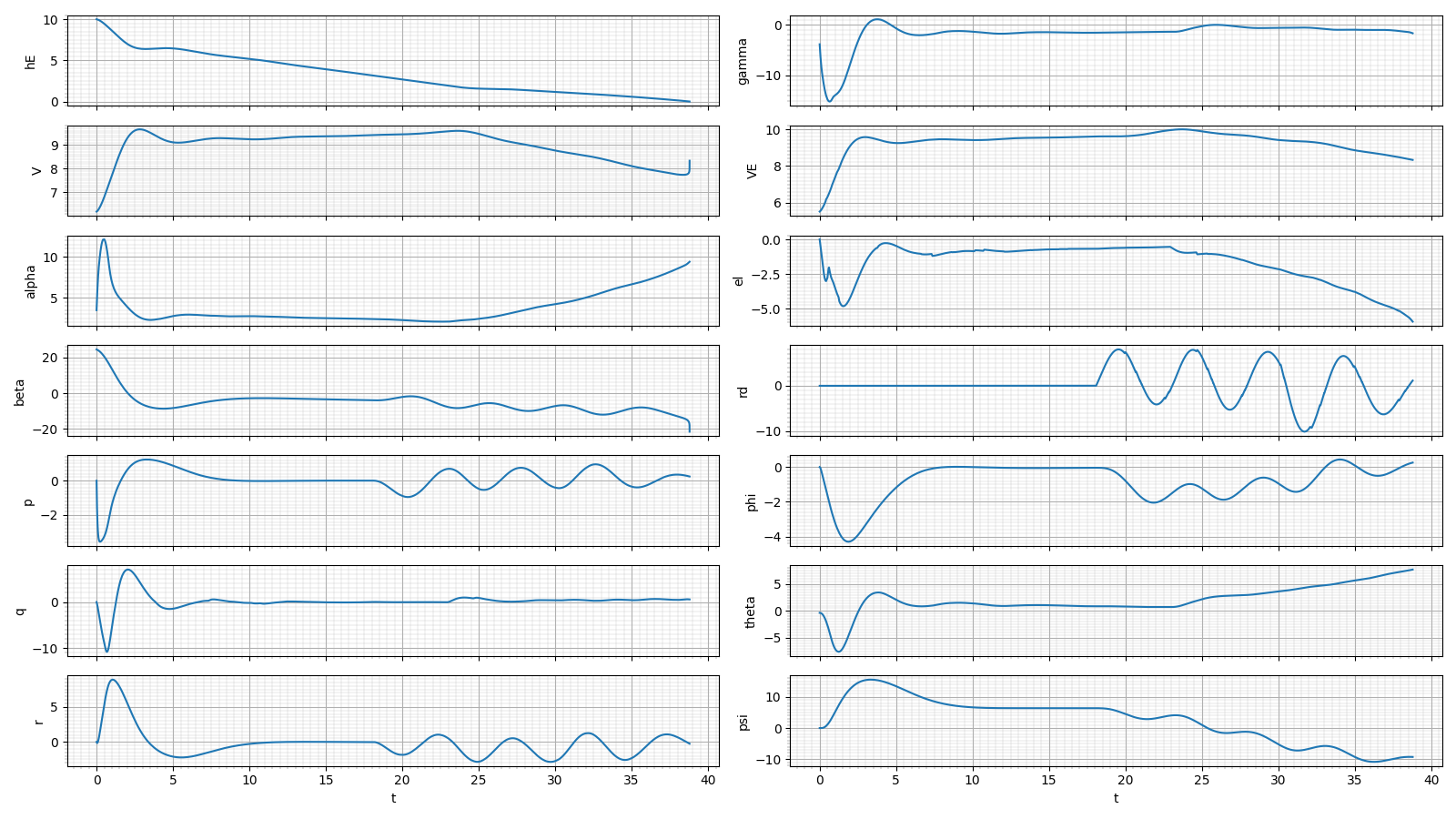
狂気のコンディション

水面スレッスレで最大舵角のアップを打って引き起こしている

このコンディションだけきちんと初期ピッチ角を3degほどのして少しでも揚力を稼ごうとしているのが良い

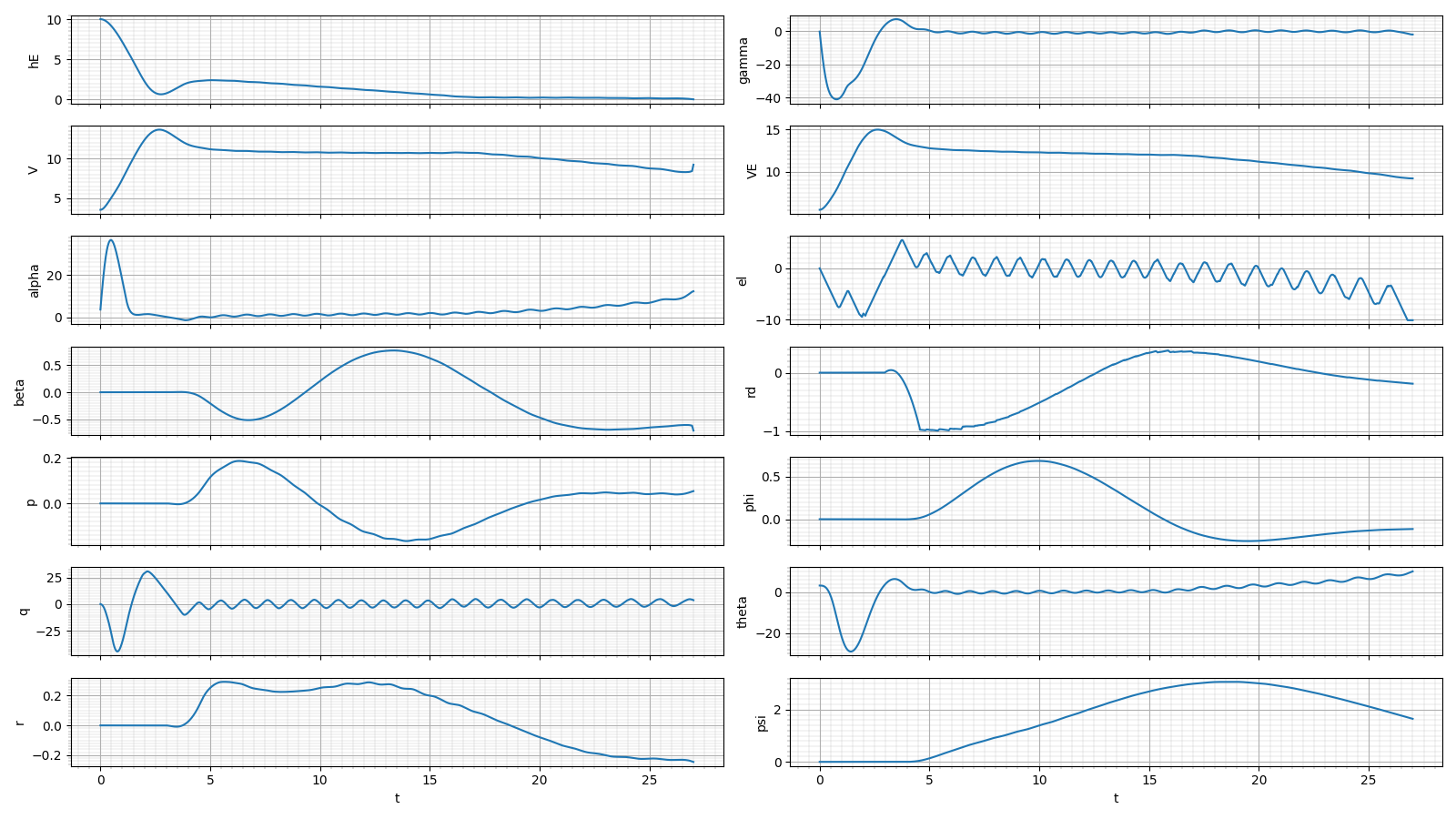
対地速度が13m/sほど出ている

着水の瞬間にエレベーター舵角が最大舵角に到達しているが、その時の対気速度は8m/s強あるので、フレアが打ち切れていない可能性がある

引き起こしのことも考えると、エレベーター舵角のマイナス側（頭上げ側）の最大舵角はもう少し余裕を持たせた方がいいかもしれない

以上

おわりに

pymooの多目的遺伝的アルゴリズムであるNSGA-IIと、 Scipy.solve_ivpを用いた航空機の6自由度の運動解析を用いて、久しぶりに鳥コン滑空機の飛行経路の最適化を行った（NSGA_NLFS6）

個人的には、多目的最適化にしたことによって飛行経路がぬるぬる滑らかになったのが良かった

スポンサーリンク

コメント