大学院生のための数値流体力学入門⑥：計算格子と境界条件の設定

CFDにおける計算格子と境界条件について，大学院生の研究活動に役立つような説明を行う

keyword: 格子生成，流入条件，流出条件，滑りなし条件，初期条件

はじめに
流れの数値シミュレーションの概要
計算格子
境界条件
流入条件
流出条件
周期境界条件
滑りなし条件
初期条件
まとめ

はじめに

この記事の内容は以下の前提に基づいている

非圧縮性流体の乱流流れ
密度\(\rho\)，粘性係数\(\mu\)は一定
熱移動はなし
CFDを研究で使う大学院生に必要な知識に重点を置く（ググって得られる知識と専門書の中間くらい）

参考文献はこちら

数値流体力学で必須のテンソル解析についての知識はこちら

流れの数値シミュレーションの概要

流れの数値シミュレーションは大きく以下の手順で行う

再現しようとしている流れのモデル化
計算格子の作成および偏微分方程式の離散化
計算の実行
結果の可視化

今回の記事では(2)と(3)に関連して，計算格子と境界条件について説明する

↓前回までの記事はこちらから

計算格子

数値流体力学の支配方程式を解くためには，解析対象に適した計算領域を設定し，計算領域内に作成した計算格子上で偏微分方程式を離散化する必要がある

計算格子の作成はCFDにおいて非常に重要な技術であり，最も複雑な技術でもある

「数値流体力学ハンドブック」の格子形成法の章では次のように述べられている

本章では，これまで実装されてきた様々な格子形成法の基本的な考え方を紹介する．実用的な格子形成プログラムでは，通常さらに膨大なノウハウが組み込まれている．これら詳細な技術はプログラムを作成し使って改善される段階で付け加えられるものであり，数式なり言葉での記述が困難である．
数値流体力学ハンドブック p.509

数値流体力学の参考書の多くが，これまで説明してきた乱流モデルや離散化した偏微分方程式の解法については詳しく説明しているのに対して，品質の良い格子生成法についてほとんど言及していないのはこういう理由がある

格子の自動生成法は存在するものの，格子生成は熟練した技術者による職人芸が必要なのである

とはいえ，高品質なメッシュを作成するために気を付けるべき普遍的な注意点は存在する

外部流れでは計算領域内の結果に影響を与えないよう十分に大きな計算領域を確保する
流れの変化が急激に起こる場所では計算格子を密に配置する
計算格子は歪みなどがなく滑らかになるようにする
壁面近傍では構造格子のメッシュを使用し，第一格子点の位置は乱流モデルに応じて適切に設定する
表面形状が重要なモデルに対しては表面形状の再現性をできる限り高め，必要であればモデルの形状を簡単なものにする

実際にどのような計算格子が高品質なのかはやってみなければわからないので，高品質な計算格子を作成できるようになるためには，熟練者の指導を受けながら「プログラムを作成し使って改善する」しかない

この「プログラムを作成し使って改善する」プロセスは非常に時間がかかるので，特に大学院に入って初めてCFDに触れるような人は，最初の1年間はひたすら格子生成を続ける覚悟を持っておいた方がいい（格子生成ソフトの使い方の勉強，格子の生成でエラー，計算を回してエラー，計算は回ったけど値がおかしい，...）

高品質な計算格子を作成するためには膨大なノウハウが必要である

「プログラムを作成し使って改善する」という試行錯誤を通して高品質な計算格子を作成する

参考
≫メッシュとは - Mesh Wiki
≫誤差との上手なつき合い方(3) メッシュによる誤差について

境界条件

境界条件には大きく分けて値指定境界条件（ディリクレ境界条件）と勾配指定境界条件（ノイマン境界条件）がある

主な境界面には流入面，流出面，壁面の3つの種類があり，それぞれの面における速度，圧力，スカラー量（\(k\)や\(\varepsilon\)）に対して，値指定境界条件か勾配指定境界条件が設定される

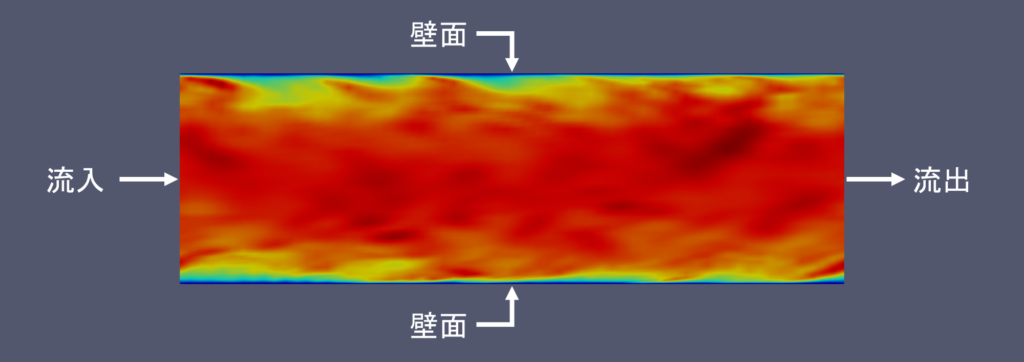
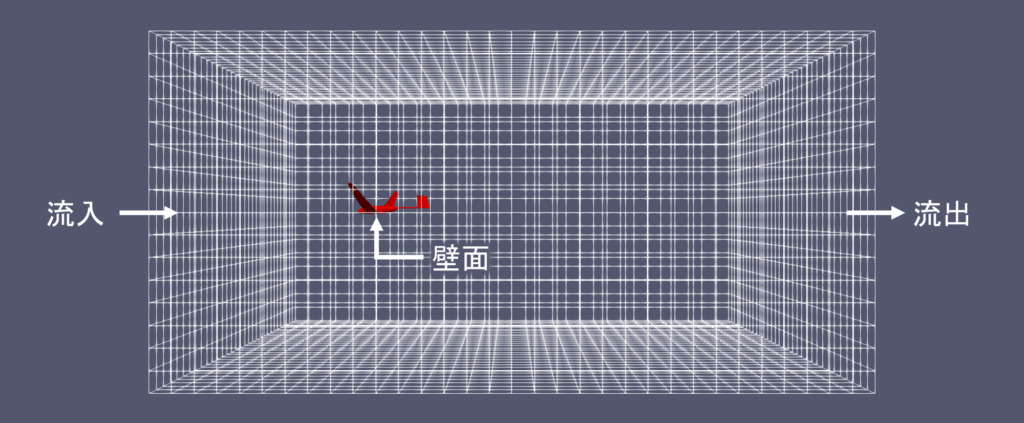
流入条件

流入条件は，流入面に適用する境界条件である

それぞれの物理量に適用する条件は次の通り

速度 \(U_{i}\)	圧力 \(p\)	渦粘性係数 \(\nu_{t}\)	乱流エネルギー \(k\)	乱流散逸率 \(\varepsilon\)
値指定	ゼロ勾配指定	値指定	値指定	値指定

値指定でどのような値を指定するかは乱流モデルによって異なる

RANS

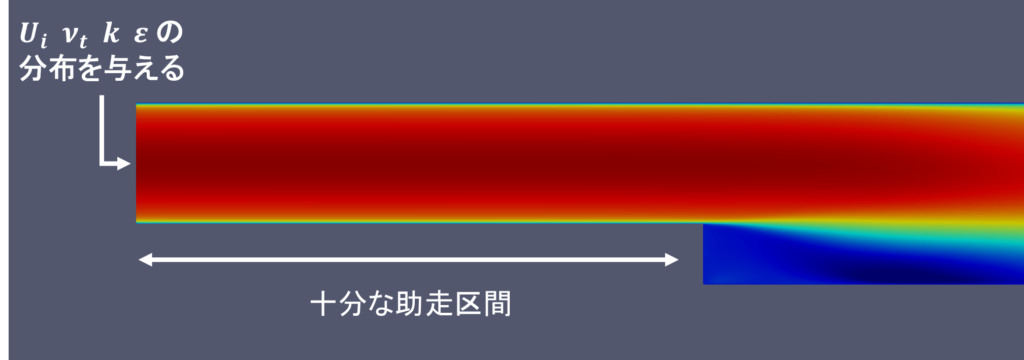
RANSの場合はほとんどが定常流なので，内部流れなら何かしらの解析結果や実験結果から得られた\(U_{i}\)，\(\nu_{t}\)，\(k\)，\(\varepsilon\)の値の分布を直接与え，外部流れなら一様流の値を指定すればいい

流入面の直後では多少不自然なふるまいをすることがあるので，解析対象に影響を与える前に十分な助走区間を設ける必要がある

LES

LESの場合は非定常流れなので，流入面でも非定常に変化する値を与える必要がある

だが，そもそも非定常に乱れる流れの値がわからないからCFDで計算しているのであって，流入面で非定常な流れの値を指定できるようならCFDの計算を行う必要はない

よって，LESでは次のように流入面における値を設定する

RANSなどで計算した平均分布に乱数を加えて疑似的な乱れを与える
さらに上流に流れを乱すような障害物を置いて，流入面の位置で発達した乱流になるようにする
上流にドライバ部として周期境界条件を用いた乱流流れを計算し，ドライバ部のある断面における値を流入面の値をして使用する

(1)や(2)の方法は乱れが発達するまでに長い助走区間が必要であり，数値計算が不安定になりやすい

(3)の方法はドライバ部の分だけ計算の負荷が増加してしまう

↓ドライバ部を用いた計算についての詳細はこちら

流出条件

流出条件は，流出面に適用する境界条件である

それぞれの物理量に適用する条件は次の通り

速度 \(U_{i}\)	圧力 \(p\)	渦粘性係数 \(\nu_{t}\)	乱流エネルギー \(k\)	乱流散逸率 \(\varepsilon\)
ゼロ勾配指定	値指定	ゼロ勾配指定	ゼロ勾配指定	ゼロ勾配指定

ゼロ勾配指定は十分に発達した流れを想定しているため，流出面は解析対象から十分に離した位置に設定する必要がある

圧力については数値流体力学の支配方程式で勾配\(\nabla p\)しか関与していないため，相対的な値しか計算には必要ない

圧力の具体的な値の計算を行うにはどこかに圧力の基準値を設定する必要があり，流出面がある場合は流出面で基準値 \(p=0\) が指定される

周期境界条件

周期境界条件は，周期的に繰り返すような形状に対する解析に用いる境界条件で，流入面と流出面に適用する境界条件である

例えば，次に示すような周期的に繰り返される形状に対して流入面と流出面に周期境界条件を設定すれば，流出面から出て言った流れ場が流入面から入ってくるような計算を行うことができる

参考
≫User Guide: Periodic hill - OpenFOAM

それぞれの物理量に適用する条件は次の通り

速度 \(U_{i}\)	圧力 \(p\)	渦粘性係数 \(\nu_{t}\)	乱流エネルギー \(k\)	乱流散逸率 \(\varepsilon\)
周期境界	周期境界	周期境界	周期境界	周期境界

流入面から入ってきた流れは流出面に至るまでに減速され，減速した流れが再び流入面から入ってきてしまうと流れはさらに減速されてしまう

周期境界条件において流れが減速され続けてしまうことを防ぐために，周期境界条件を適用する際は次の手法をとることで断面平均流速を維持する必要がある

圧力勾配を加える
運動量をソース項として加える

滑りなし条件

滑りなし条件は，壁面に適用する境界条件である

それぞれの物理量に適用する条件は次の通り

速度 \(U_{i}\)	圧力 \(p\)	渦粘性係数 \(\nu_{t}\)	乱流エネルギー \(k\)	乱流散逸率 \(\varepsilon\)
値指定	ゼロ勾配指定	値指定	値指定	値指定

速度の値指定は \(u_{i}=0\)とし，\(\nu_{t}\)，\(k\)，\(\varepsilon\)の値指定でどのような値を指定するかは乱流モデルによって異なる

RANS

一般的なRANSモデルでは，壁面近傍の第1格子点を対数流域に設定し，\(\nu_{t}\)，\(k\)，\(\varepsilon\)の壁面の境界条件として壁関数を用いる

↓壁関数についてはこちら

低レイノルズ数型RANS

低レイノルズ数型RANSモデルでは，壁面近傍の第1格子点を粘性低層に設定し，壁面の境界条件として \(\nu_{t}=0\)，\(k=0\)，\(\varepsilon=\frac{2\nu k}{y^2}\) を用いる

↓導出についてはこちら

LES

LESでは，壁面近傍の第1格子点を粘性低層に設定し，壁面の境界条件として \(\nu_{t}=0\)，\(k=0\) を用いる（LESでは\(\varepsilon\)の輸送方程式を解かないので境界条件は必要ない）

初期条件

初期条件の設定方法について，「乱流の数値シミュレーション」では次のように述べられている

残念ながら初期条件の与え方には特別のルールはない．例えば静止状態を初期値として，いきなり外力を加えたり，境界を移動させたりしても，十分に慎重に時間進行すれば何とか目的とする状態までたどり着くことができるだろう．
あまりにも（質量や運動量のバランスの悪い）不自然な初期値を与えると，発達した流れに到達する前に計算が破綻しやすい．（中略）このような過渡状態を効率的に乗り切るには経験を積むしかないだろう．
乱流の数値シミュレーション p.118

基本的には初期条件として一様流やポテンシャル流れの計算結果などを与えればよいが，計算が発散することもあるので注意する必要がある（何をどうやって注意するかはノウハウである）

筆者が1つノウハウを共有するとすれば，「発達した乱流を周期境界条件で非定常計算する際は初期条件に発達した乱流を与える必要がある」ということである（初期条件に一様流を与えるといつまでたっても層流が計算され続ける）

境界面には流入面，流出面，壁面の3種類があり，それぞれの境界面上において速度，圧力，スカラー量に値指定条件もしくは勾配指定条件が与えられる

初期条件の与え方に特別なルールはなく，それなりに自然な値を与えれば計算を行うことはできる

まとめ

流れの数値シミュレーションは大きく以下の手順で行う

再現しようとしている流れのモデル化
計算格子の作成および偏微分方程式の離散化
計算の実行
結果の可視化

今回の記事では(2)と(3)に関連して，計算格子と境界条件について説明した

計算格子の作成や適切な境界条件の設定は，CFDにおいて非常に重要であると同時に非常に複雑な手順である

適切な取り扱いを習得するためには試行錯誤を繰り返して経験とノウハウを積む必要がある

↓まとめ記事

全6回にわたった「大学院生のための数値流体力学」シリーズもこれにて完結である

大学院で勉強した数値流体力学についての引継ぎ資料でも書くか～と軽い気持ちでブログを書き始めたが，期間にして1か月半，作業時間だと200時間近くを費やした大作になってしまった

この記事が，大学院でCFDを扱うことになったどこかの誰かの参考になれば幸いである