標準k-εモデルの定数と壁関数の導出

RANSのモデルの中で最も広く利用されている標準k－εモデルについて，定数の決定方法や壁関数について説明する

keyword: 2方程式モデル，標準k－εモデル，乱流境界層，粘性低層，壁関数

渦粘性モデル

RANSにおける渦粘性モデルの基礎方程式は次の式で表される

\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}

\begin{equation}
\nu_{e}=\nu+\nu_{t}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}

\(\overline{u}_{i}\)，\(\overline{p}\)以外の変数は渦粘性係数\(\nu_{t}\)ただ1つであり，この\(\nu_{t}\)をどのように求めるかが渦粘性モデルの唯一にして最も重要な点である

渦粘性モデルは，\(\nu_{t}\)を求めるために追加する方程式の数で，0方程式モデル，1方程式モデル，2方程式モデルに分類される

この記事では，2方程式モデルの1つである 標準k－εモデル について説明する

標準k-εモデル

k-εモデルの中でも最も基本となる「標準k-εモデル」とよばれるモデルは，乱流エネルギー\(k\)と乱流散逸率\(\varepsilon\)を用いて次のように渦粘性係数を計算している

\begin{equation}
\nu_{t}=C_{\mu}\frac{k^{2}}{\varepsilon}
\end{equation}

乱流エネルギー\(k\)と乱流散逸率\(\varepsilon\)はそれぞれの輸送方程式を解くことで求められる

\begin{equation}
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=P_{k}-\varepsilon
+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{equation}

\begin{equation}
\frac{\partial \varepsilon}{\partial t}+\overline{u}_{j}\frac{\partial \varepsilon}{\partial x_{j}}
=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \varepsilon}{\partial x_{j}}\right\}
\end{equation}

ここで，モデル定数は次の通り

\begin{equation}
C_{\mu}=0.09, \quad \sigma_{k}=1.0, \quad \sigma_{\varepsilon}=1.3, \quad
C_{\varepsilon_{1}}=1.44, \quad C_{\varepsilon_{2}}=1.92
\end{equation}

標準k-εモデルの定数群の決定方法

標準k-εモデルの定数は，以下のことを仮定して決定されている

• 定常2次元せん断乱流の乱流境界層の対数領域である
• 一様等方乱流（乱れの移流，生成，拡散がない）である

上記の仮定を大きく逸脱するような複雑な流れに対しては，標準k-εモデルの精度は低下してしまう

標準k-εモデルの定数の決定方法について，1つずつ説明していく

定常2次元せん断流

平行平板間乱流などのように，平均速度勾配テンソルの\(\frac{\partial \overline{u}}{\partial y}\)以外の成分がすべて0である流れ場のことである

壁面近くの平均速度分布は次のようになる

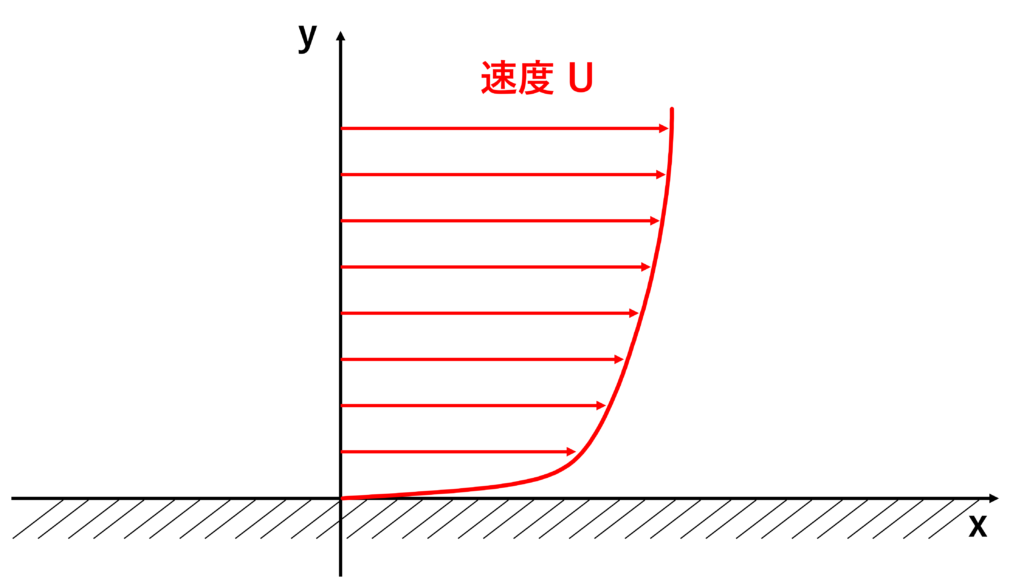
定常2次元せん断流では，せん断応力\(\tau\)は次の式で表される

\begin{equation}
\tau=\left(\mu+\mu_{t}\right)\frac{\partial u}{\partial y}
\end{equation}

壁面上では \(\nu_{t}=\mu_{t}/\rho=0\)なので，壁面せん断応力\(\tau_{w}\)は次のようになる

\begin{equation}
\tau_{w}=\mu\frac{\partial u}{\partial y}
\end{equation}

壁面せん断応力から摩擦速度\(u_{\tau}\)が定義され，主流速度\(\overline{u}\)および壁面からの距離\(y\)はそれぞれ次のように無次元化される

\begin{equation}
u_{\tau}=\sqrt{\frac{\tau_{w}}{\rho}}=\sqrt{\nu\frac{\partial u}{\partial y}}
\end{equation}

\begin{equation}
u^{+}=\frac{\overline{u}}{u_{\tau}}, \qquad y^{+}=\frac{u_{\tau}y}{\nu}
\end{equation}

乱流境界層の速度分布

一般に，乱流境界層は壁面近くで壁からの影響を受ける内層と自由流近くの外層に分けられ，さらに内層は壁面ごく近くの分子粘性の影響が大きい領域である粘性低層，渦粘性の影響が大きい対数領域，それらの中間にある緩和層に分けられる

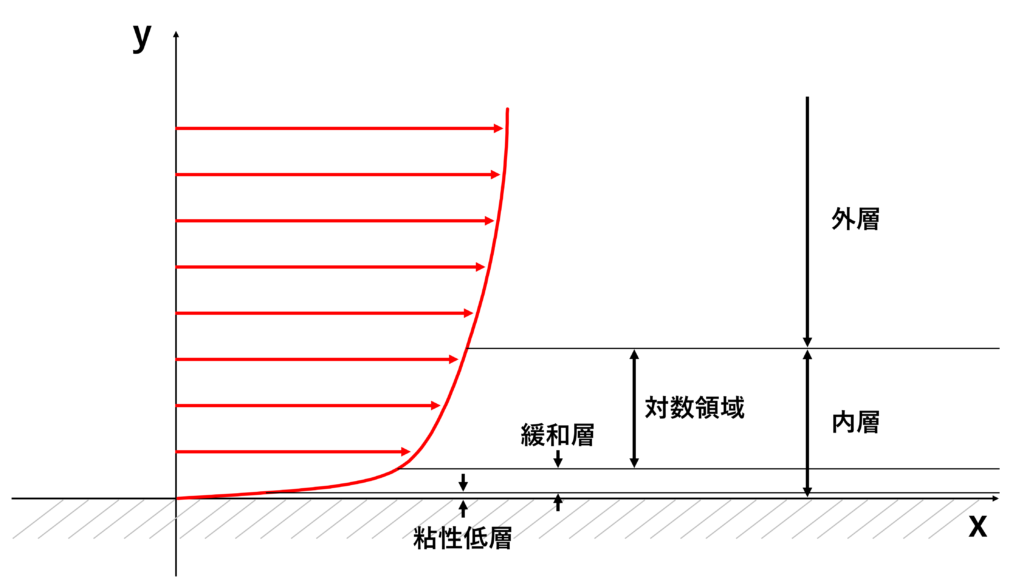
縦軸に無次元速度\(u^{+}\)，横軸に無次元距離\(y^{+}\)の対数をプロットした片対数グラフは次のようになる

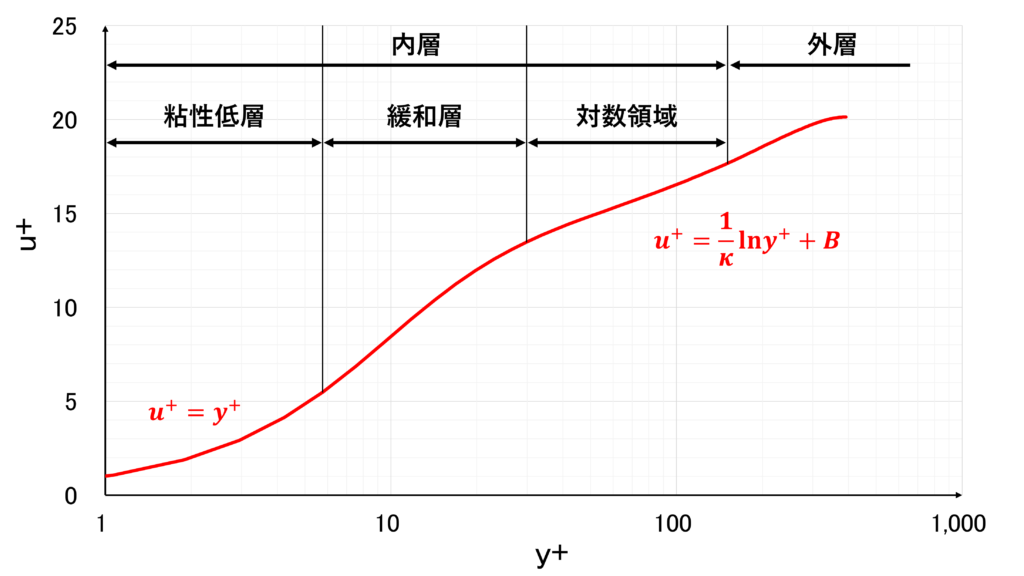
（粘性低層）

\(0 \leq y^{+} \leq 5\) であり，壁面の極近傍の領域である

壁面近くで乱れが減衰し，分子粘性が支配的になる（\(\nu \gg \nu_{t}\)）

粘性低層では次のような層流の速度分布になる

\begin{equation}
u^{+}=y^{+}
\end{equation}

（緩和層）

\(5 \leq y^{+} \leq 30\) であり，粘性低層と対数領域の中間にある領域である

（対数領域）

\(30 \leq y^{+} \leq \delta_{t}^{+}\) であり，内層の一番外側にある領域である（\(\delta_{t}^{+}\)はレイノルズ数とともに大きくなる）

対数領域ではレイノルズ数が十分大きく分子粘性が無視できる（\(\nu \ll \nu_{t}\)）ほか，乱れの生成と散逸の局所平衡が成立する

\begin{equation}
P_{k}=\varepsilon \qquad \left(P_{k}=-\overline{uv}\frac{\partial u}{\partial y}\right)
\end{equation}

速度分布は次のような対数速度分布になる

\begin{equation}
u^{+}=\frac{1}{\kappa}\ln{y^{+}}+B
\end{equation}

定数\(\kappa\)はカルマン定数とよばれ，乱流境界層では実験的に\(\kappa \simeq 0.4\)，\(B \simeq 5\)とされている

また，対数領域では実験的に次の関係式が成り立つことがわかっている

\begin{equation}
\frac{|\overline{uv}|}{k}=0.3 \quad (=\sqrt{C_{\mu}})
\end{equation}

一様等方乱流

乱れの移流，生成，拡散がなく，ただ減衰していくだけの乱流を考えると，乱流エネルギー\(k\)および乱流散逸率\(\varepsilon\)の輸送方程式はそれぞれ次のようになる

\begin{equation}
\frac{\partial k}{\partial t}=-\varepsilon
\end{equation}

\begin{equation}
\frac{\partial \varepsilon}{\partial t}=-C_{\varepsilon_{2}}\varepsilon\frac{\varepsilon}{k}
\end{equation}

また，このような乱流の減衰初期には実験的に次の関係が確認されている

\begin{equation}
k \propto t^{-1}
\end{equation}

定数の決定

以上の仮定を用いて，標準k-εモデルの定数を決定していく

\(C_{\mu}\)

対数領域では \(\nu \ll \nu_{t}\)なので，せん断応力はレイノルズ応力に等しく，

\begin{equation}
\overline{uv}=-\nu_{t}\frac{\partial u}{\partial y}
\qquad\rightarrow\qquad
\nu_{t}=-\frac{\overline{uv}}{\frac{\partial u}{\partial y}}
\tag{i}
\end{equation}

対数領域では局所平衡 \(P_{k}=\varepsilon\) が成り立つので，

\begin{equation}
-\overline{uv}\frac{\partial u}{\partial y}=\varepsilon
\qquad\rightarrow\qquad
\frac{\partial u}{\partial y}=-\frac{\varepsilon}{\overline{uv}}
\tag{ii}
\end{equation}

(i)に(ii)を代入して，実験的に得られた式 \(|\overline{uv}|/k=0.3\)を代入すると

\begin{equation}
\nu_{t}=\frac{\left(\overline{uv}\right)^{2}}{\varepsilon}=0.09\frac{k^{2}}{\varepsilon}
\qquad\rightarrow\qquad
C_{\mu}=0.09 \qquad \left(\sqrt{C_{\mu}}=0.3\right)
\end{equation}

\(C_{\varepsilon_{2}}\)

一様等方乱流における乱流エネルギー\(k\)の輸送方程式および乱流散逸率\(\varepsilon\)の輸送方程式より，

\begin{equation}
\left\{\begin{array}{rl}
&\frac{\partial \varepsilon}{\partial t}=-C_{\varepsilon_{2}}\frac{1}{k}\varepsilon^{2} \\
&\varepsilon=-\frac{\partial k}{\partial t} \\
\end{array}\right.
\qquad\rightarrow\qquad
\frac{\partial^{2} k}{\partial t^{2}}=C_{\varepsilon_{2}}\frac{1}{k}\left(\frac{\partial k}{\partial t}\right)^{2}
\tag{iii}
\end{equation}

(iii)に，実験から得られた式 \(k=at^{-1}\)（\(a\)は任意定数）を代入すると

\begin{equation}
2at^{-3}=C_{\varepsilon_{2}}\frac{1}{at}\left(-at^{-1}\right)^{2}
\qquad\rightarrow\qquad
C_{\varepsilon_{2}}=2
\end{equation}

\(\sigma_{k}\)，\(\sigma_{\varepsilon}\)

\(\sigma_{k}\)および\(\sigma_{\varepsilon}\)は，勾配拡散近似の係数であり，実験的に1.0に近い数値だと考えられる

\(C_{\varepsilon_{1}}\)

圧力勾配のない定常な2次元せん断乱流の対数領域では，\(\varepsilon\)の実質微分が0になり（\(\frac{\partial \varepsilon}{\partial t}+\overline{u}_{j}\frac{\partial \varepsilon}{\partial x_{j}}=0\)），分子粘性が無視でき（\(\nu \ll \nu_{t}\)），局所平衡 \(P_{k}=\varepsilon\)が成り立つので，\(\varepsilon\)の輸送方程式は次のようになる

\begin{equation}
0
=\left(C_{\varepsilon_{1}}-C_{\varepsilon_{2}}\right)\frac{\varepsilon^{2}}{k}+\frac{\partial}{\partial y}\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}\frac{\partial \varepsilon}{\partial y}\right)
\tag{iv}
\end{equation}

ここで，上記の式から\(\varepsilon\)と\(\nu_{t}\)を消去するために，対数速度分布を用いて\(\varepsilon\)を\(k\)で表すことを考える

対数速度分布の式 \(u^{+}=\frac{1}{\kappa}\ln{y^{+}}+B\)の両辺を\(y\)で微分して

\begin{equation}
\frac{\partial}{\partial y}\left(\frac{\overline{u}}{u_{\tau}}\right)
=\frac{\partial}{\partial y}\left(\frac{1}{\kappa}\ln{\frac{u_{\tau}y}{\nu}}+B\right)\qquad\rightarrow\qquad
\frac{\partial u}{\partial y}
=\frac{u_{\tau}}{\kappa y}
\end{equation}

局所平衡の式 \(\varepsilon=P_{k}\)に，対数速度分布における速度勾配を代入して，

\begin{equation}
\varepsilon=P_{k}=-\overline{uv}\frac{\partial u}{\partial y}
=-\overline{uv}\frac{u_{\tau}}{\kappa y}
\end{equation}

さらに，乱流境界層内でレイノルズ応力が一定（\(-\rho\overline{uv} \simeq \tau_{w} = \rho u_{\tau}^{2}\)）という仮定を追加し，実験から得られた式 \(|\overline{uv}|=u_{\tau}^{2}=\sqrt{C_{\mu}}k\) を代入すると，次の式が得られる

\begin{equation}
\varepsilon=\frac{u_{\tau}^{3}}{\kappa y}
=\frac{C_{\mu}^{\frac{3}{4}}k^{\frac{3}{2}}}{\kappa y}
\tag{v}
\end{equation}

(v)より，\(\nu_{t}\)は次のようになる

\begin{equation}
\nu_{t}=C_{\mu}\frac{k^2}{\varepsilon}
=C_{\mu}\frac{k^{2}}{\frac{C_{\mu}^{3/4}k^{3/2}}{\kappa y}}
=C_{\mu}^{\frac{1}{4}}k^{\frac{1}{2}}\kappa y
\tag{vi}
\end{equation}

(iv)に(v)と(vi)を代入し，\(k\)が\(y\)によらず一定だと仮定すると，

\begin{align}
&0=
\left(C_{\varepsilon_{1}}-C_{\varepsilon_{2}}\right)
\frac{\left(\frac{C_{\mu}^{3/4}k^{3/2}}{\kappa y}\right)^{2}}{k}
+\frac{\partial}{\partial y}\left(\frac{C_{\mu}^{\frac{1}{4}}k^{\frac{1}{2}}\kappa y}{\sigma_{\varepsilon}}\frac{\partial}{\partial y}\left(\frac{C_{\mu}^{\frac{3}{4}}k^{\frac{3}{2}}}{\kappa y}\right)\right) \\

\rightarrow\qquad
&0=
\left(C_{\varepsilon_{1}}-C_{\varepsilon_{2}}\right)\frac{C_{\mu}^{3/2}k^{2}}{\kappa^{2} y^{2}}
+\frac{\partial}{\partial y}\left(-\frac{1}{\sigma_{\varepsilon}}\frac{C_{\mu}k^{2}}{y}\right) \\

\rightarrow\qquad
&0=\left(C_{\varepsilon_{1}}-C_{\varepsilon_{2}}\right)\frac{C_{\mu}^{3/2}k^{2}}{\kappa^{2} y^{2}}
+\frac{1}{\sigma_{\varepsilon}}\frac{C_{\mu}k^{2}}{y^{2}}
\end{align}

結局，以下の関係式が得られる

\begin{equation}
C_{\varepsilon_{2}}-C_{\varepsilon_{1}}
=\frac{\kappa^{2}}{\sigma_{\varepsilon}C_{\mu}^{1/2}}
\end{equation}

\(C_{\varepsilon_{1}}\)，\(C_{\varepsilon_{2}}\)，\(\sigma_{\varepsilon}\)は上記の関係式を満たすように決定する必要があり，すでにわかっている値として\(\kappa=0.4\)，\(\sigma_{\varepsilon}=1.0\)，\(C_{\varepsilon_{2}}=2.0\)，\(C_{\mu}=0.09\)を代入すると，\(C_{\varepsilon_{1}}=1.5\)が得られる

標準k-εモデルの定数群はこれらの定数を各種計算によってさらに最適化したものである

壁関数（Wall function）

標準k-εモデルはレイノルズ数が高く局所平衡が成り立つ対数領域をもとに定数を決定しているので，このままではより壁面に近い低レイノルズ数効果の大きい領域（粘性低層）を扱うことができない

CFDの計算を行うためには壁面の境界条件を必ず設定する必要があるので，標準k－εモデルの計算の際は壁面の境界条件として壁関数とよばれる関数を設定することで，粘性低層の計算を省略している

壁面境界条件として壁関数を使う際は，第1格子点を対数領域（\(30 \leq y^{+} \leq 200\)）に配置する

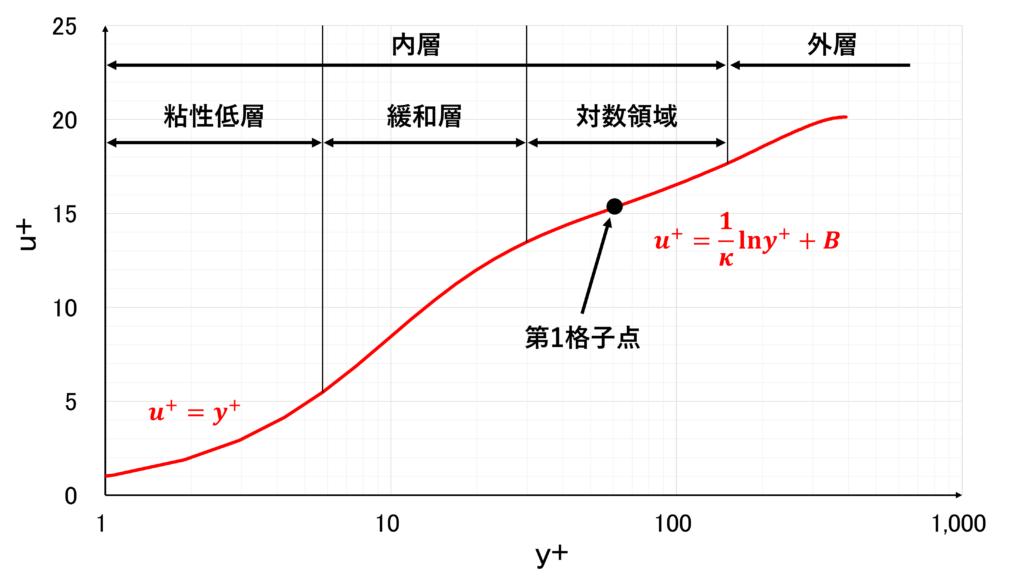
良かれと思って壁面近くの格子を細かくしすぎると，壁関数を使っているのに第1格子点が緩和層や粘性低層に入ってしまい逆に精度が悪くなるので注意が必要である

メリットとデメリットは以下の通り

具体的な壁面境界条件としては，速度については \(u_{i}=0\)，圧力については \(\frac{\partial p}{\partial n}=0\) を設定し，乱流エネルギー，乱流散逸率，渦粘性係数に関してはそれぞれに応じた壁関数を設定する

対数速度分布から\(u\)を計算することもできるが，CFDでは \(u_{i}=0\) と与えても問題ない

壁面上の\(\nu_{t}\)の値は\(k\)と\(\varepsilon\)の壁関数を与えた時点で計算できるが，CFDでは数値計算の都合上\(\nu_{t}\)にも壁関数を適用する

代表的な壁関数

代表的な壁関数について説明する（第1格子点を表す添え字を\(_{P}\)とする）

摩擦速度\(u_{\tau}\)

対数速度分布の式 \(u^{+}=\frac{1}{\kappa}\mathrm{ln}y^{+}+B\)より，関数\(F(u_{\tau})\)を定義すれば，ニュートン法などの反復計算によって\(u_{\tau}\)が計算できる

\begin{equation}
F(u_{\tau})=\frac{u_{P}}{u_{\tau}}-\frac{1}{\kappa}\mathrm{ln}\frac{u_{\tau}y_{P}}{\nu}-B=0, \quad\rightarrow\quad
u_{\tau}^{n+1}=u_{\tau}^{n}-\frac{F(u_{\tau}^{n})}{F'(u_{\tau}^{n})}
\end{equation}

もしくは，対数領域において実験的に \(|uv|=\sqrt{C_{\mu}}k\) が成立し，粘性低層と対数領域でせん断応力が一定 \(|uv|=\tau_{w}/\rho=u_{\tau}^{2}\) であると仮定すれば次のようにも計算できる

\begin{equation}
u_{\tau}=\sqrt{|uv|}=C_{\mu}^{\frac{1}{4}}k^{\frac{1}{2}}
\end{equation}

乱流エネルギー\(k\)

同様の仮定において\(k_{P}\)は次のように計算できる

\begin{equation}
k_{P}=\frac{u_{\tau}^{2}}{\sqrt{C_{\mu}}}=const.
\quad\rightarrow\quad
\frac{\partial k_{P}}{\partial y_{P}}=0
\end{equation}

乱流散逸率\(\varepsilon\)

上記の仮定にさらに局所平衡 \(\varepsilon=P_{k}\)を加えると，\(\varepsilon_{P}\)は次のように計算できる（ 標準k-εモデルの定数群の決定方法 を参照）

\begin{equation}
\varepsilon_{P}=\frac{u_{\tau}^{3}}{\kappa y_{P}}
=\frac{C_{\mu}^{\frac{3}{4}}k_{P}^{\frac{3}{2}}}{\kappa y_{P}}
\end{equation}

渦粘性係数\(\nu_{t}\)

対数速度分布は次のように書き換えることができる

\begin{equation}
u^{+}=\frac{1}{\kappa}\mathrm{ln}\left(Ey^{+}\right) \qquad \left(E=9.8\right)
\end{equation}

上記の対数速度分布から\(u_{\tau}\)を計算する

\begin{equation}
\frac{u}{u_{\tau}}=\frac{1}{\kappa}\mathrm{ln}\left(Ey^{+}\right)
\quad\rightarrow\quad
u_{\tau}=\frac{\kappa u}{\mathrm{ln}\left(Ey^{+}\right)}
\tag{i}
\end{equation}

壁面せん断応力 \(\tau_{w}=\rho u_{\tau}^{2}\)の式に(i)を代入し，第1格子点における速度勾配 \(\left(\frac{\partial u}{\partial y}\right)_{P}=\frac{u_{P}-0}{y_{P}-0}=\frac{u_{P}}{y_{P}}\) をくくりだす

\begin{equation}
\tau_{w}=\rho u_{\tau}^{2}
=\rho u_{\tau}\frac{\kappa u_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}
=\frac{\rho\kappa u_{\tau} y_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}\frac{u_{P}}{y_{P}}
=\frac{\mu \kappa y^{+}_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}\frac{u_{P}}{y_{P}}
\end{equation}

上記の式と壁面せん断応力の別表式 \(\tau_{w}=\left(\mu+\mu_{t_{P}}\right)\frac{u_{P}}{y_{P}}\) を比較して両辺を\(\rho\)で割ることで，渦粘性係数の壁関数を求めることができる

\begin{equation}
\mu+\mu_{t_{P}}=\frac{\mu \kappa y^{+}_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}
\quad\rightarrow\quad
\nu_{t_{P}}=\nu\left(\frac{\kappa y^{+}_{P}}{\mathrm{ln}\left(Ey^{+}_{P}\right)}-1\right)
\end{equation}

まとめ

RANSのモデルの中で最も広く利用されている標準k－εモデルについて，定数の決定方法や壁関数について説明した

メリットとデメリットは次の通り

工学・工業の分野で最も広く利用されているモデルであり，k-εモデルをベースとしたモデルも多数開発されていることから，RANSを代表するようなモデルであるといえる

↓おすすめ記事

数値流体力学のおすすめ参考書

大学院の研究でCFDを使うことになったときに参考にした書籍を紹介する

mtkbirdman.com

2021.11.04

【まとめ】大学院生のための数値流体力学シリーズ

研究でCFDを使うことになった大学院生の役に立つような説明を行う記事のまとめ

mtkbirdman.com

2021.12.15

参考

OpenFOAMの壁関数 from Fumiya Nozaki