航空分野で用いられているSpalart-Allmarasモデルについて説明する
keyword: 1方程式モデル
渦粘性モデル
RANSにおける渦粘性モデルの基礎方程式は次の式で表される
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{t}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}
\(\overline{u}_{i}\),\(\overline{p}\)以外の変数は渦粘性係数\(\nu_{t}\)ただ1つであり,この\(\nu_{t}\)をどのように求めるかが渦粘性モデルの唯一にして最も重要な点である
渦粘性モデルは,\(\nu_{t}\)を求めるために追加する方程式の数で,0方程式モデル,1方程式モデル,2方程式モデルに分類される
この記事では,1方程式モデルの1つである Spalart-Allmarasモデル について説明する
Spalart-Allmarasモデル
Spalart-Allmarasモデルは,渦粘性係数の輸送方程式を解くことによって渦粘性係数を計算する1方程式モデルである
経験的な仮定を含んでいるため普遍的なモデルではないが,そのぶん航空分野において高度にチューニングされており,正しい運用をすることで計算コストの低さと高い精度の両立が可能である
このモデルにおいて,渦粘性係数は次の式で与えられる
\begin{equation}
\nu_{t}=\tilde{\nu}\frac{\left(\tilde{\nu}/\nu\right)^{3}}{\left(\tilde{\nu}/\nu\right)^{3}+C_{V}^{3}}
\end{equation}
\(\tilde{\nu}\)は次の輸送方程式によって求められる
\begin{equation}
\frac{\partial \tilde{\nu}}{\partial t}
+\overline{u}_{i}\frac{\partial \tilde{\nu}}{\partial x_{i}}
=
C_{p}\tilde{\nu}\tilde{S}
-C_{\varepsilon_{1}}f_{\varepsilon}\left(\frac{\tilde{\nu}}{d}\right)^{2}
+\frac{1}{\sigma}\left\{\frac{\partial}{\partial x_{j}}
\left(\tilde{\nu}+\nu\right)\frac{\partial \tilde{\nu}}{\partial x_{j}}
+C_{D}\frac{\partial \tilde{\nu}}{\partial x_{j}}\frac{\partial \tilde{\nu}}{\partial x_{j}}\right\}
\end{equation}
\(d\)は壁面からの距離であり,\(\tilde{S}\)および\(f_{\varepsilon}\)は次の式で与えられる
\begin{equation}
\tilde{S}=\frac{1}{\sqrt{2}}\left|\overline{\mathbf{\Omega}}\right|
+\frac{\nu}{\left(\kappa d\right)^{2}}f_{p}, \qquad
f_{\varepsilon}=g\left(\frac{1+C_{\varepsilon_{2}}^{6}}{g^{6}+C_{\varepsilon_{2}}^{6}}\right)^{1/6}
\end{equation}
ここで
\begin{equation}
f_{p}=\frac{\left(\tilde{\nu}/ u\right)^{3}-C_{V}^{3}\left(\tilde{\nu}/ \nu\right)+C_{V}^{3}}{\left(\tilde{\nu}/ \nu\right)^{4}+\left(\tilde{\nu}/ \nu\right)^{3}+C_{V}^{3}}
\end{equation}
\begin{equation}
g=r+C_{\varepsilon_{3}}\left(r^{6}-r\right), \qquad
r=\frac{\tilde{\nu}}{\tilde{S}\left(\kappa d\right)^{2}}
\end{equation}
モデル定数は次の通り
\begin{align}
&\sigma=2/3, \quad
C_{V}=7.1, \quad
\kappa=0.41, \quad
C_{p}=0.13, \quad
C_{D}=0.62, \quad \\
&C_{\varepsilon_{1}}=\frac{C_{p}}{\kappa^{2}}+\frac{1+C_{D}}{\sigma}, \quad
C_{\varepsilon_{2}}=2, \quad
C_{\varepsilon_{3}}=0.3, \quad
\end{align}
曲率および回転に対する補正
翼周りの流れのように主流が曲面に沿うような流れでは,主流方向で乱れの特性が変化し,モデルの精度が大きく低下してしまう
また,系全体が回転するような流れ場で発生するコリオリ力もモデルの精度に悪影響を与える
その補正として,\(\tilde{\nu}\)の輸送方程式の生成項を次のように変更する
\begin{equation}
C_{p}\rightarrow C_{p}F_{CR}
\end{equation}
補正関数\(F_{CR}\)は次の式で定義される
\begin{equation}
F_{CR}=
\left(1+C_{CR_{1}}\right)
\frac{C_{CR_{0}}\tilde{r}_{1}}{1+\tilde{r}_{1}}
\left\{1-C_{CR_{3}}\arctan{\left(C_{CR_{2}}\tilde{r}_{2}\right)}\right\}
-C_{CR_{1}}
\end{equation}
\begin{equation}
\tilde{r}_{1}=\frac{\left|\overline{\mathbf{S}}\right|}{\left|\overline{\mathbf{\Omega}}\right|}
\end{equation}
\begin{equation}
\tilde{r}_{2}=\frac{1}{4}\frac{\overline{\Omega}_{ik}\overline{S}_{kj}}{D^{4}}
\left(\frac{\partial \overline{S}_{ij}}{\partial t}+\overline{u}_{j}\frac{\partial \overline{S}_{ij}}{\partial x_{j}}+\varepsilon_{imn}\omega_{F_{m}}\overline{S_{jn}}+\varepsilon_{jmn}\omega_{F_{m}}\overline{S}_{in}\right)
\end{equation}
\begin{equation}
D=\frac{1}{2}\sqrt{\overline{S}_{ij}\overline{S}_{ij}+\overline{\tilde{\Omega}}_{ij}\overline{\tilde{\Omega}}_{ij}}
\end{equation}
ここで,\(\omega_{F}\)は系の回転角速度であり,この系の渦度テンソル\(\Omega_{ij}\)は次のように変換される
\begin{equation}
\Omega_{ij}\rightarrow \tilde{\Omega}_{ij}=\Omega_{ij}+2\varepsilon_{ikj}\omega_{F_{k}}
\end{equation}
定数は次の通り
\begin{equation}
C_{CR_{0}}=2, \quad
C_{CR_{1}}=1.0, \quad
C_{CR_{2}}=12, \quad
C_{CR_{3}}=1
\end{equation}
レイノルズ応力の非線形性に対する補正
レイノルズ応力を渦粘性係数と速度勾配で線形近似する線形渦粘性モデルでは,矩形ダクト内の第二次第二種流れに代表されるような「主流に垂直な断面内に発生する速度成分が重要な流れ場」を適切に記述できない
航空機の解析では翼と胴体の結合部付近でこのような流れが生じるため,Spalart-Allmarasモデルではそれに対する補正も行っている
レイノルズ応力の線形渦粘性近似からのずれ\(N_{ij}\)は次の式で計算される
\begin{equation}
N_{ij}=\nu_{t}C_{S_{\omega}}\frac{\overline{S}_{ik}\overline{\Omega}_{kj}+\overline{\Omega}_{ik}\overline{S}_{kj}}{\sqrt{\overline{S}_{mn}\overline{S}_{mn}+\overline{\Omega}_{mn}\overline{\Omega}_{mn}}}, \qquad
C_{S_{\omega}}=0.6
\end{equation}
この非線形項\(N_{ij}\)を追加して,レイノルズ応力は次のように補正される
\begin{equation}
\tau_{ij}=\frac{2}{3}k\delta_{ij}-2\nu S_{ij}+N_{ij}
\end{equation}
非線形渦粘性モデルをCFDで実装する際は,追加の非線形項\(N_{ij}\)は外力項としてNavier-Stokes方程式に組み込まれる
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
+\frac{\partial}{\partial x_{j}}N_{ij}
\end{equation}
追加の非線形項を外力項として組み込むことで,プログラムをいじることなく線形渦粘性モデルを非線形モデルに拡張することができる
まとめ
航空分野で用いられているSpalart-Allmarasモデルについて説明した
Spalart-Allmarasモデルは,輸送方程式を解くことで渦粘性を直接計算するモデルである
定数群や関係式は経験的な仮定を多く含んでいるため汎用的なモデルにはなりえないものの,航空分野のモデルとしては高度にチューニングされており,適切に運用すれば低い計算コストで高い予測性能が期待できる
参考
≫宇宙航空研究開発機構研究開発報告 - 航空工学におけるレイノルズ平均乱流モデルの概観と 時間スケールによる物理的意味の考察
↓おすすめ記事
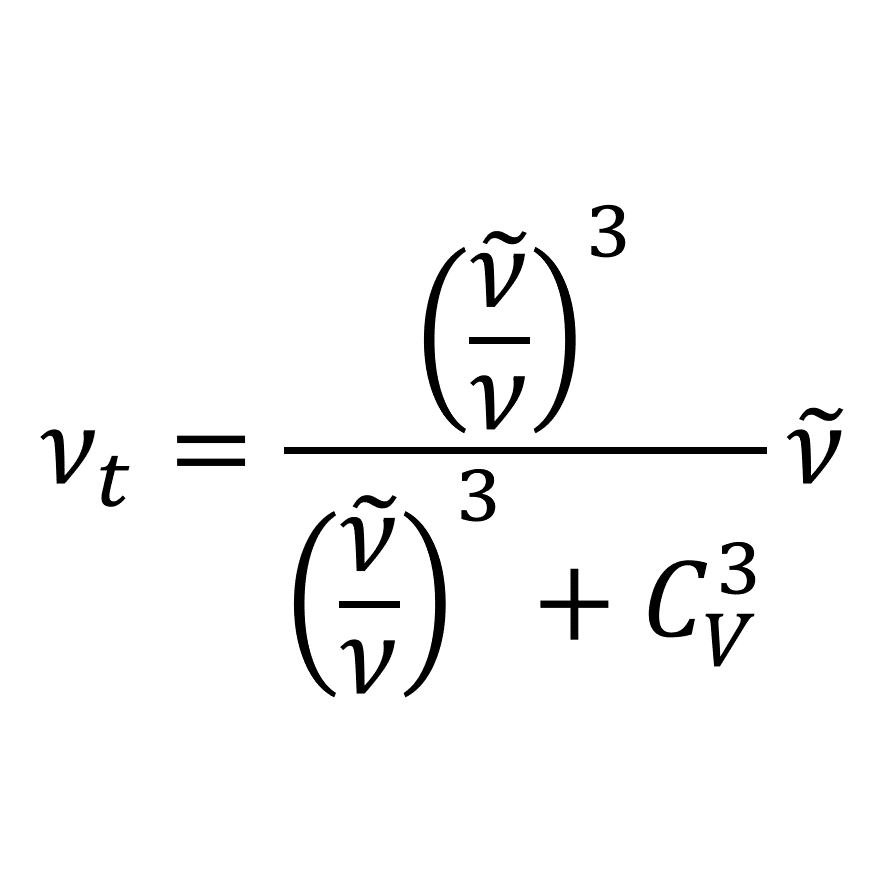


コメント