航空分野で用いられてきたBaldwin-Lomaxモデルについて説明する
keyword: 0方程式モデル
渦粘性モデル
RANSにおける渦粘性モデルの基礎方程式は次の式で表される
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{t}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}
\(\overline{u}_{i}\),\(\overline{p}\)以外の変数は渦粘性係数\(\nu_{t}\)ただ1つであり,この\(\nu_{t}\)をどのように求めるかが渦粘性モデルの唯一にして最も重要な点である
渦粘性モデルは,\(\nu_{t}\)を求めるために追加する方程式の数で,0方程式モデル,1方程式モデル,2方程式モデルに分類される
この記事では,0方程式モデルの1つである Baldwin-Lomaxモデル について説明する
Baldwin-Lomaxモデル
aldwin-Lomaxモデルは,航空分野における翼周りの流れに対して有効なモデルとして,これまで広く使用されてきた
Baldwin-Lomaxモデルでは,流れ場の領域を内層(添え字\(_{I}\))と外層(添え字\(_{O}\))に分割し,渦粘性係数を次の式で与える
\begin{equation}
\nu_{t}=\left\{\begin{array}{ll}
\nu_{t_{I}} & \left(\nu_{t_{I}}<\nu_{t_{O}}\right) \\
\nu_{t_{O}} & \left(\nu_{t_{I}}>\nu_{t_{O}}\right)
\end{array}\right.
\end{equation}
内層の渦粘性係数\(\nu_{t_{I}}\)は,特性長さ\(l_{I}\)と平均渦度テンソルの大きさ\(\left|\boldsymbol{\overline{\Omega}}\right|\)を用いていて次の式で表される
\begin{equation}
\nu_{t_{I}}=\frac{1}{\sqrt{2}}l_{I}^{2}\left|\boldsymbol{\overline{\Omega}}\right|
\end{equation}
ここで,平均渦度テンソル\(\overline{\mathbf{\Omega}}\)は
\begin{equation}
\overline{\mathbf{\Omega}}=\overline{\Omega}_{ij}
=\frac{1}{2}\left(\frac{\partial u_{i}}{\partial x_{j}}-\frac{\partial u_{j}}{\partial x_{i}}\right), \qquad
\left|\boldsymbol{\overline{\Omega}}\right|
=\sqrt{\overline{\Omega}_{ij}\overline{\Omega}_{ij}}
\end{equation}
混合長\(l_{I}\)は,壁面からの距離\(d\),摩擦速度\(u_{\tau}=\sqrt{\nu_{e}|\frac{\partial u}{\partial y}|}\),壁面での動粘性係数\(\nu_{w}\)を用いて次の式で表される
\begin{equation}
l_{i}=\kappa y\left\{1-\exp{\left(-\frac{y^{+}}{A_{VD}}\right)}\right\}, \qquad
y^{+}=\frac{u_{\tau}d}{\nu_{w}}
\end{equation}
\begin{equation}
\kappa=0.41, \qquad A_{VD}=26
\end{equation}
外層では,
\begin{align}
F
=\frac{1}{\sqrt{2}}\frac{l_{I}}{\kappa}\left|\boldsymbol{\overline{\Omega}}\right|
=\frac{1}{2}y\left(1-\exp{\left\{-\frac{y^{+}}{A_{VD}}\right)}\right\}\left|\boldsymbol{\overline{\Omega}}\right|
\simeq \frac{1}{2}y\left|\boldsymbol{\overline{\Omega}}\right|
\end{align}
を用いて,\(F_{max}\)と\(y_{max}\)を次のように定義する
\begin{equation}
F_{max}=\mathrm{max}(F), \qquad F(y_{max})=F_{max}
\end{equation}
ここから,\(\overline{u}_{Diff}=\overline{u}_{max}-\overline{u}_{min}\)を用いて
\begin{equation}
F_{O_{1}}=y_{max}F_{max}\mathrm{min}\left(1,C_{O_{1}}\left(\frac{\overline{u}_{Diff}}{F_{max}}\right)^{2}\right)
\end{equation}
\begin{equation}
F_{O_{2}}=\left\{1+C_{O_{21}}\left(C_{O_{22}}\frac{y}{y_max}\right)^{6}\right\}^{-1}
\end{equation}
を導入し,外層の渦粘性係数\(\nu_{t_{O}}\)を次の式で計算する
\begin{equation}
\nu_{t_{O}}=\alpha C_{O_{3}}F_{O_{1}}F_{O_{2}}
\end{equation}
ここで,定数群は以下で与えられる
\begin{align}
\alpha=0.0168, \quad C_{O_{1}}=0.25, \quad C_{O_{21}}=5.5, \quad C_{O_{22}}=0.3, \quad C_{O_{3}}=1.6
\end{align}
翼周りの流れ場は,翼付近の乱れが非常に大きい領域と翼から離れた乱れが非常に小さい領域という性質の大きく異なる2つの領域をもった外部流れである
そのような流れ場に対しては,内層と外層で流れ場を分割してそれぞれの渦粘性係数を設定するというBaldwin-Lomaxモデルの考え方が有効になる
まとめ
航空分野で用いられてきたBaldwin-Lomaxモデルについて説明した
0方程式モデルはシンプルなモデルで汎用なモデルにはなりえないが,今回のように特定の分野の特定の流れ場に対して特化すれば,計算コストが低く精度の高い有効なモデルになりうる
参考
≫宇宙航空研究開発機構研究開発報告 - 航空工学におけるレイノルズ平均乱流モデルの概観と 時間スケールによる物理的意味の考察
↓おすすめ記事
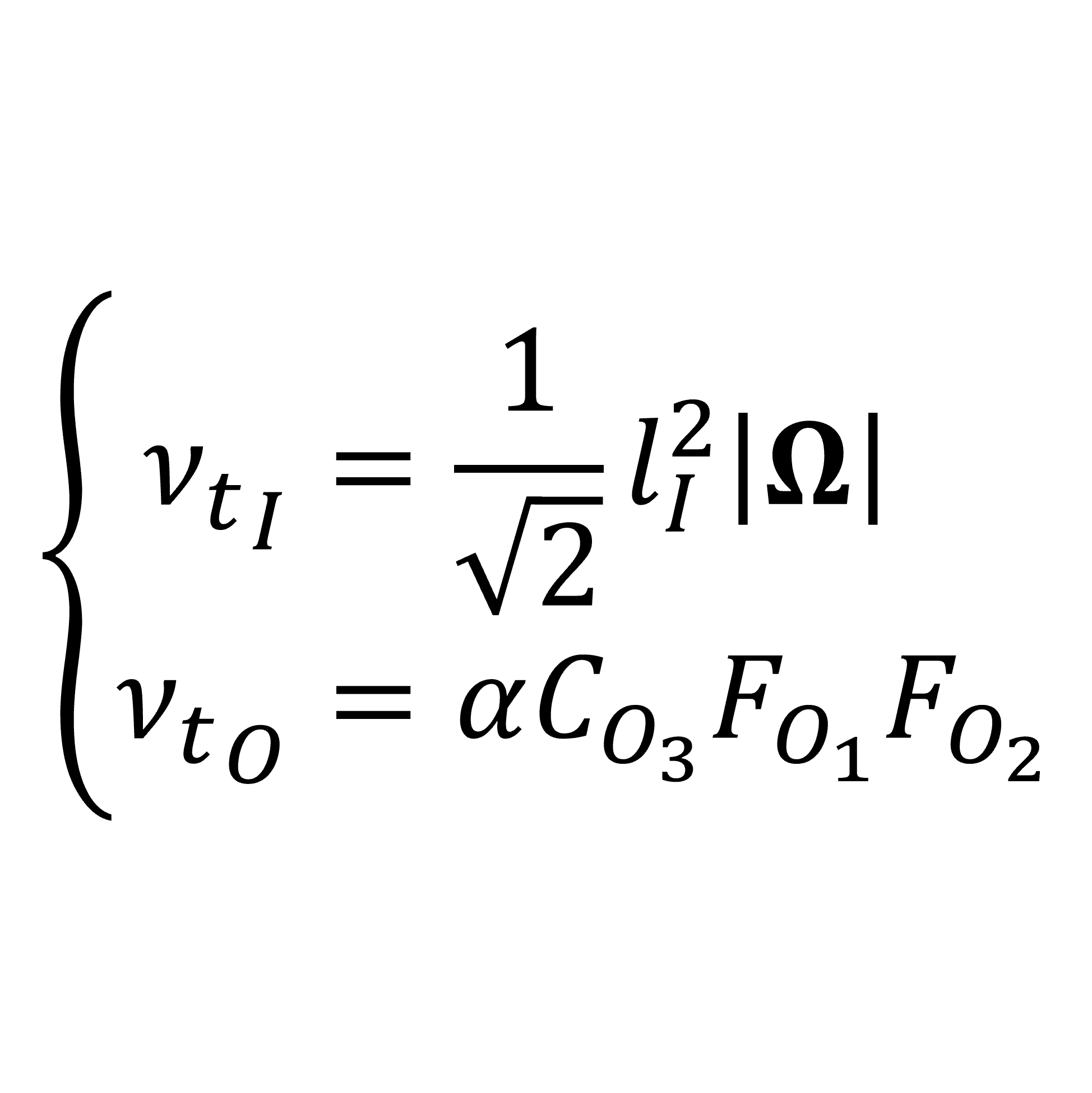

コメント