レイノルズ応力方程式の導出と各項の説明を行う
keyword: 応力方程式モデル,レイノルズ応力方程式
はじめに
レイノルズ応力方程式を省略せずに書くと次の式になる
\begin{align}
\frac{\partial \tau_{ij}}{\partial t}
+\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
&=
-\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
+\overline{\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)}
-2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}} \\
&\quad+\frac{\partial }{\partial x_{k}}\left\{
-\overline{u'_{i}u'_{j}u'_{k}}
-\frac{1}{\rho}\left(\overline{p'u'_{j}\delta_{ik}}+\overline{p'u'_{i}\delta_{jk}}\right)
+\nu\frac{\partial \tau_{ij}}{\partial x_{k}}
\right\}
\end{align}
複雑な式で面倒だが,頑張って導出してみる
導出
レイノルズ応力の輸送方程式は,まず変動速度\(u'_{i}\)についての連続の式とNavier-Stoke方程式を求め,\(\frac{\partial \tau_{ij}}{\partial t}\)を計算することで求めることができる
連続の式とNavier-Stokes方程式は次の式で表される
(連続の式)
\begin{equation}
\frac{\partial u_{k}}{\partial x_{k}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial u_{i}}{\partial t}
+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\end{equation}
これに\(u_{i}=\overline{u}_{i}+u'_{i}\)を代入する
(連続の式)
\begin{equation}
\frac{\partial}{\partial x_{k}}\left(\overline{u}_{k}+u'_{k}\right)=0
\end{equation}
(Navier-Stokes方程式)
\begin{align}
&\frac{\partial}{\partial t}\left(\overline{u}_{i}+u'_{i}\right)
+\frac{\partial}{\partial x_{j}}\left(\overline{u}_{i}\overline{u}_{j}+u'_{i}\overline{u}_{j}+\overline{u}_{i}u'_{j}+u'_{i}u'_{j}\right)
= \\
&-\frac{1}{\rho}\frac{\partial}{\partial x_{i}}\left(\overline{p}+p'\right)
+\frac{\partial}{\partial x_{j}}\left[\nu\left\{\frac{\partial}{\partial x_{j}}\left(\overline{u}_{i}+u'_{i}\right)+\frac{\partial}{\partial x_{i}} \left(\overline{u}_{j}+u'_{j}\right) \right\}\right]
\tag{i}
\end{align}
また,レイノルズ平均を施した連続の式とNavier-Stokes方程式は次の式になる
(連続の式)
\begin{equation}
\frac{\partial \overline{u}_{k}}{\partial x_{k}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\tag{ii}
\end{equation}
2つの式の差(i)-(ii)をとることによって,変動速度\(u'_{i}\)に対する連続の式とNavier-Stokes方程式が求まる
(連続の式)
\begin{equation}
\frac{\partial u'_{k}}{\partial x_{k}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{align}
\frac{\partial u'_{i}}{\partial t}
+\frac{\partial}{\partial x_{j}}
\left(u'_{i}\overline{u}_{j}+\overline{u}_{i}u'_{j}+u'_{i}u'_{j}\right)
=
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial u'_{i}}{\partial x_{j}}+\frac{\partial u'_{j}}{\partial x_{i}}\right)+\tau_{ij}\right\}
\end{align}
整理して
\begin{align}
&\frac{\partial u'_{i}}{\partial t}
+\frac{\partial \left(u'_{i}\overline{u}_{j}\right)}{\partial x_{j}}
= \\
&-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{-u'_{i}u'_{j}-\overline{u}_{i}u'_{j}+\nu\left(\frac{\partial u'_{i}}{\partial x_{j}}+\frac{\partial u'_{j}}{\partial x_{i}}\right)+\tau_{ij}\right\} \\
\tag{iii}
\end{align}
(iii)を用いて,レイノルズ応力\(\tau_{ij}\)の輸送方程式を求めていく
ただし,次のことを常に意識しておく
- 積の微分 \((fg)'=f'g+fg'\)
- アンサンブル平均の性質 \(\overline{\overline{f}g'}=\overline{f}\:\overline{g'}\),\(\overline{f'\overline{g}}=\overline{f'}\:\overline{g}\)
- 変動速度の連続の式 \(\frac{\partial u_{k}}{\partial x_{k}}=0\)
\(\tau_{ij}\)の時間微分は次の式で表される
\begin{equation}
\frac{\partial \tau_{ij}}{\partial t}=\frac{\partial \overline{u'_{i}u'_{j}}}{\partial t}
=\overline{\frac{\partial u'_{i}}{\partial t}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial t}} \\
\tag{iv}
\end{equation}
\(\frac{\partial u'_{i}}{\partial t}\)は(iii)において\(j \rightarrow k\)とし,\(\frac{\partial u'_{j}}{\partial t}\)は(iii)において\(i \rightarrow j\),\(j \rightarrow k\)とすることで次のようになる
\begin{align}
\frac{\partial u'_{i}}{\partial t}
&=
-\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}} \\
&\quad+\frac{\partial}{\partial x_{k}}\left\{-u'_{i}u'_{k}-\overline{u}_{i}u'_{k}+\nu\left(\frac{\partial u'_{i}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{i}}\right)+\tau_{ik}\right\} \\
\frac{\partial u'_{j}}{\partial t}
&=
-\frac{\partial u'_{j}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{j}} \\
&\quad+\frac{\partial}{\partial x_{k}}\left\{-u'_{j}u'_{k}-\overline{u}_{j}u'_{k}+\nu\left(\frac{\partial u'_{j}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{j}}\right)+\tau_{jk}\right\}
\tag{v}
\end{align}
(iv)の最右辺の\(\frac{\partial u'_{i}}{\partial t}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial t}\)に(v)を代入する
\begin{align}
&\frac{\partial u'_{i}}{\partial t}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial t}\\
&=u'_{j}\left[-\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}
+\frac{\partial}{\partial x_{k}}\left\{-u'_{i}u'_{k}-\overline{u}_{i}u'_{k}+\nu\left(\frac{\partial u'_{i}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{i}}\right)+\tau_{ik}\right\}\right] \\
&\quad+u'_{i}\left[-\frac{\partial u'_{j}\overline{u}_{k}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial p'}{\partial x_{j}}
+\frac{\partial}{\partial x_{k}}\left\{-u'_{j}u'_{k}-\overline{u}_{j}u'_{k}+\nu\left(\frac{\partial u'_{j}}{\partial x_{k}}+\frac{\partial u'_{k}}{\partial x_{j}}\right)+\tau_{jk}\right\}\right] \\
&=\left(-u'_{j}\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}-u'_{i}\frac{\partial u'_{j}\overline{u}_{k}}{\partial x_{k}} \right)
+\left(-u'_{j}\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}-u'_{i}\frac{1}{\rho}\frac{\partial p'}{\partial x_{j}}\right) \\
&\quad+\left(-u'_{j}\frac{\partial u'_{i}u'_{k}}{\partial x_{k}}-u'_{i}\frac{\partial u'_{j}u'_{k}}{\partial x_{k}}\right)
+\left(-u'_{j}\frac{\partial \overline{u}_{i}u'_{k}}{\partial x_{k}}-u'_{i}\frac{\partial \overline{u}_{j}u'_{k}}{\partial x_{k}}\right) \\
&\quad+\left(u'_{j}\frac{\partial \tau_{ik}}{\partial x_{k}}+u'_{i}\frac{\partial \tau_{jk}}{\partial x_{k}}\right) \\
&\quad+\left(\nu u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}+\nu u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}\right)
+\left(\nu u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{k}}{\partial x_{i}}+\nu u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{k}}{\partial x_{j}}\right)
\tag{vi}
\end{align}
(vi)の右辺の各項をそれぞれ計算し,レイノルズ平均を行う
(右辺第1項)
\begin{align}
&-u'_{j}\frac{\partial u'_{i}\overline{u}_{k}}{\partial x_{k}}-u'_{i}\frac{\partial u'_{j}\overline{u}_{k}}{\partial x_{k}} \\
&=-u'_{j}\left(\frac{\partial u'_{i}}{\partial x_{k}}\overline{u}_{k}+u'_{i}\frac{\partial \overline{u}_{k}}{\partial x_{k}}\right)-u'_{i}\left(\frac{\partial u'_{j}}{\partial x_{k}}\overline{u}_{k}+u'_{j}\frac{\partial \overline{u}_{k}}{\partial x_{k}}\right)
=-\overline{u}_{k}\left(\frac{\partial u'_{i}}{\partial x_{k}}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial x_{k}}\right) \\
&=-\overline{u}_{k}\frac{\partial u'_{i}u'_{j}}{\partial x_{k}} \\
&\longrightarrow \overline{-\overline{u}_{k}\frac{\partial u'_{i}u'_{j}}{\partial x_{k}}}
=-\overline{u}_{k}\frac{\partial \overline{u'_{i}u'_{j}}}{\partial x_{k}}
=-\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
\end{align}
(右辺第2項)
\begin{align}
&-u'_{j}\frac{1}{\rho}\frac{\partial p'}{\partial x_{i}}-u'_{i}\frac{1}{\rho}\frac{\partial p'}{\partial x_{j}} \\
&=-\frac{1}{\rho}\left\{\left(u'_{j}\frac{\partial p'}{\partial x_{i}}+\frac{\partial u_{j}}{\partial x_{i}}p'\right)-\frac{\partial u_{j}}{\partial x_{i}}p'\right\}
-\frac{1}{\rho}\left\{\left(u'_{i}\frac{\partial p'}{\partial x_{j}}+\frac{\partial u_{i}}{\partial x_{j}}p'\right)-\frac{\partial u_{i}}{\partial x_{j}}p'\right\} \\
&=-\frac{1}{\rho}\left(\frac{\partial p'u'_{j}}{\partial x_{i}}-\frac{\partial u_{j}}{\partial x_{i}}p'\right)-\frac{1}{\rho}\left(\frac{\partial p'u'_{i}}{\partial x_{j}}-\frac{\partial u_{i}}{\partial x_{j}}p'\right) \\
&=-\frac{1}{\rho}\left(\frac{\partial p'u'_{j}}{\partial x_{i}}+\frac{\partial p'u'_{i}}{\partial x_{j}}\right)
+\frac{p'}{\rho}\left(\frac{\partial u_{j}}{\partial x_{i}}+\frac{\partial u_{i}}{\partial x_{j}}\right) \\
&=-\frac{1}{\rho}\frac{\partial }{\partial x_{k}}\left(p'u'_{j}\delta_{ik}+p'u'_{i}\delta_{jk}\right)
+\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right) \\
&\longrightarrow \overline{-\frac{1}{\rho}\frac{\partial }{\partial x_{k}}\left(p'u'_{j}\delta_{ik}+p'u'_{i}\delta_{jk}\right)
+\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)} \\
&\qquad=-\frac{1}{\rho}\frac{\partial }{\partial x_{k}}\left(\overline{p'u'_{j}\delta_{ik}}+\overline{p'u'_{i}\delta_{jk}}\right)
+\overline{\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)}
\end{align}
ただし,クロネッカーのデルタを使った超絶技巧を用いている
\begin{equation}
\frac{\partial}{\partial x_{k}}\delta_{ik}
=\left\{\begin{array}{cl}
\frac{\partial}{\partial x_{i}} & (i=k) \\
0 & (i \neq k) \end{array}\right.
\end{equation}
(右辺第3項)
\begin{align}
&-u'_{j}\frac{\partial u'_{i}u'_{k}}{\partial x_{k}}-u'_{i}\frac{\partial u'_{j}u'_{k}}{\partial x_{k}} \\
&=-u'_{j}\frac{\partial u'_{i}u'_{k}}{\partial x_{k}}-u'_{i}\left(\frac{\partial u'_{j}}{\partial x_{k}}u'_{k}+u'_{j}\frac{\partial u'_{k}}{\partial x_{k}}\right)
=-\left(u'_{j}\frac{\partial u'_{i}u'_{k}}{\partial x_{k}}+\frac{\partial u'_{j}}{\partial x_{k}}u'_{i}u'_{k}\right)
=-\frac{\partial u'_{i}u'_{j}u'_{k}}{\partial x_{k}} \\
&\longrightarrow -\overline{\frac{\partial u'_{i}u'_{j}u'_{k}}{\partial x_{k}}}
=-\frac{\partial \overline{u'_{i}u'_{j}u'_{k}}}{\partial x_{k}}
\end{align}
(右辺第4項)
\begin{align}
&-u'_{j}\frac{\partial \overline{u}_{i}u'_{k}}{\partial x_{k}}-u'_{i}\frac{\partial \overline{u}_{j}u'_{k}}{\partial x_{k}} \\
&=-u'_{j}\left(\frac{\partial \overline{u}_{i}}{\partial x_{k}}u'_{k}+\overline{u}_{i}\frac{\partial u'_{k}}{\partial x_{k}}\right)
-u'_{i}\left(\frac{\partial \overline{u}_{j}}{\partial x_{k}}u'_{k}+\overline{u}_{j}\frac{\partial u'_{k}}{\partial x_{k}}\right)
=-u'_{j}u'_{k}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-u'_{i}u'_{k}\frac{\partial \overline{u}_{j}}{\partial x_{k}} \\
&\longrightarrow \overline{-u'_{j}u'_{k}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-u'_{i}u'_{k}\frac{\partial \overline{u}_{j}}{\partial x_{k}}}
=-\overline{u'_{j}u'_{k}}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\overline{u'_{i}u'_{k}}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
=-\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
\end{align}
(右辺第5項)
\begin{align}
&u'_{j}\frac{\partial \tau_{ik}}{\partial x_{k}}+u'_{i}\frac{\partial \tau_{jk}}{\partial x_{k}} \\
&=u'_{j}\frac{\partial \overline{u'_{i}u'_{k}}}{\partial x_{k}}+u'_{i}\frac{\partial \overline{u'_{j}u'_{k}}}{\partial x_{k}} \\
&\longrightarrow \overline{u'_{j}\frac{\partial \overline{u'_{i}u'_{k}}}{\partial x_{k}}+u'_{i}\frac{\partial \overline{u'_{j}u'_{k}}}{\partial x_{k}}}
=\overline{u'}_{j}\frac{\partial \overline{u'_{i}u'_{k}}}{\partial x_{k}}+\overline{u'}_{i}\frac{\partial \overline{u'_{j}u'_{k}}}{\partial x_{k}}
=0
\end{align}
(右辺第6項)
\begin{align}
&\nu u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}+\nu u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}} \\
&=\nu \left\{\left(\frac{\partial u'_{j}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}+u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}\right)-\frac{\partial u'_{j}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}\right\} \\
&\quad+\nu \left\{\left(\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}+u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}\right)-\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}\right\} \\
&=\nu\left\{\frac{\partial}{\partial x_{k}}\left(u'_{j}\frac{\partial u'_{i}}{\partial x_{k}}\right)-\frac{\partial u'_{j}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}\right\}
+\nu\left\{\frac{\partial}{\partial x_{k}}\left(u'_{i}\frac{\partial u'_{j}}{\partial x_{k}}\right)-\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}\right\} \\
&=\nu\frac{\partial}{\partial x_{k}}\left(\frac{\partial u'_{i}}{\partial x_{k}}u'_{j}+u'_{i}\frac{\partial u'_{j}}{\partial x_{k}}\right)
-2\nu\frac{\partial u'_{j}}{\partial x_{k}}\frac{\partial u'_{i}}{\partial x_{k}}
=\nu\frac{\partial}{\partial x_{k}}\left(\frac{\partial u'_{i}u'_{j}}{\partial x_{k}}\right)
-2\nu\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}} \\
&\longrightarrow \overline{\nu\frac{\partial}{\partial x_{k}}\left(\frac{\partial u'_{i}u'_{j}}{\partial x_{k}}\right)
-2\nu\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
=\frac{\partial}{\partial x_{k}}\left(\nu\frac{\partial \tau_{ij}}{\partial x_{k}}\right)
-2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
\end{align}
(右辺第7項)
\begin{align}
\nu u'_{j}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{k}}{\partial x_{i}}+\nu u'_{i}\frac{\partial}{\partial x_{k}}\frac{\partial u'_{k}}{\partial x_{j}}
=\nu u'_{j}\frac{\partial}{\partial x_{i}}\frac{\partial u'_{k}}{\partial x_{k}}+\nu u'_{i}\frac{\partial}{\partial x_{j}}\frac{\partial u'_{k}}{\partial x_{k}}
=0
\end{align}
よって,\(\tau_{ij}\)の時間微分\(\frac{\partial \tau_{ij}}{\partial t}\)は次のようになる
\begin{align}
\frac{\partial \tau_{ij}}{\partial t}
&=-\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
-\frac{1}{\rho}\frac{\partial }{\partial x_{k}}\left(\overline{p'u'_{j}\delta_{ik}}+\overline{p'u'_{i}\delta_{jk}}\right)
+\overline{\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)}
-\frac{\partial \overline{u'_{i}u'_{j}u'_{k}}}{\partial x_{k}} \\
&\quad -\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
+\frac{\partial}{\partial x_{k}}\left(\nu\frac{\partial \tau_{ij}}{\partial x_{k}}\right)
-2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
\end{align}
両辺整理すると,レイノルズ応力方程式が得られる
\begin{align}
\frac{\partial \tau_{ij}}{\partial t}
+\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
&=
-\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}
+\overline{\frac{p'}{\rho}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)}
-2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}} \\
&\quad+\frac{\partial }{\partial x_{k}}\left\{
-\overline{u'_{i}u'_{j}u'_{k}}
-\frac{1}{\rho}\left(\overline{p'u'_{j}\delta_{ik}}+\overline{p'u'_{i}\delta_{jk}}\right)
+\nu\frac{\partial \tau_{ij}}{\partial x_{k}}
\right\}
\end{align}
レイノルズ応力方程式の各項の説明
レイノルズ応力方程式の各項の名称と簡単な説明を行う
実質微分項
\begin{equation}
\frac{\partial \tau_{ij}}{\partial t}+\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
\end{equation}
第1項\(\frac{\partial \tau_{ij}}{\partial t}\)が時間項,第2項 \(\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}\)が移流項であり,左辺全体でレイノルズ応力\(\tau_{ij}\)の実質微分を表している
生成項
\begin{equation}
P_{ij}=-\tau_{ik}\frac{\partial \overline{u}_{j}}{\partial x_{k}}-\tau_{jk}\frac{\partial \overline{u}_{i}}{\partial x_{k}}
\end{equation}
平均速度勾配による\(\tau_{ij}\)の生成項である
この項をモデル化せずに扱えるのが応力方程式モデルの最大のメリットである
圧力-ひずみ相間項
\begin{equation}
\Pi_{ij}=\overline{\frac{p'}{\rho}\left(\frac{\partial u'_{i}}{\partial x_{j}}+\frac{\partial u'_{j}}{\partial x_{i}}\right)}
\end{equation}
レイノルズ応力間の再配分を行う役割を持つ項で,この項のモデル化が応力方程式モデルで最も重要となる
散逸項
\begin{equation}
\varepsilon_{ij}=2\nu\overline{\frac{\partial u'_{i}}{\partial x_{k}}\frac{\partial u'_{j}}{\partial x_{k}}}
\end{equation}
散逸については,\(\varepsilon_{ij}=\frac{2}{3}\delta_{ij}\varepsilon\)として,\(\varepsilon\)の輸送方程式を解くことによって求められる
拡散項
\begin{equation}
J_{ijk}=J_{(T)ijk}+J_{(P)ijk}+J_{(V)ijk}
\end{equation}
\begin{align}
J_{(T)ijk}&=-\overline{u'_{i}u'_{j}u'_{k}} \\
J_{(P)ijk}&=-\frac{1}{\rho}\left(\overline{p'u'_{i}}\delta_{jk}+\overline{p'u'_{j}}\delta_{ik}\right) \\
J_{(V)ijk}&=\nu\frac{\partial \tau_{ij}}{\partial x_{k}}
\end{align}
\(J_{(T)ijk}\),\(J_{(P)ijk}\),\(J_{(V)ijk}\)はそれぞれ速度変動,圧力変動,粘性による拡散流束を表している
まとめ
最終的に,レイノルズ応力方程式は次の形で表される
\begin{equation}
\frac{\partial \tau_{ij}}{\partial t}
+\overline{u}_{k}\frac{\partial \tau_{ij}}{\partial x_{k}}
=P_{ij}+\Pi_{ij}-\varepsilon_{ij}+\frac{\partial J_{ijk}}{\partial x_{k}}
\end{equation}
この方程式をレイノルズ応力の輸送方程式として使うのが応力方程式モデルであり,その際 \(\Pi_{ij}\),\(\varepsilon_{ij}\),\(J_{ijk}\)は\(\overline{u}_{i}\),\(\overline{p}\),\(\tau_{ij}\)を使って表すことができない項なので,それぞれモデル化を行う必要がある
レイノルズ応力は対称テンソルなので独立な成分は6つであり,\(\varepsilon_{ij}\)については輸送方程式を解いて求める必要があるので,合計で7つの方程式を解くことで\(\tau_{ij}\)を求めることができる
↓おすすめ記事
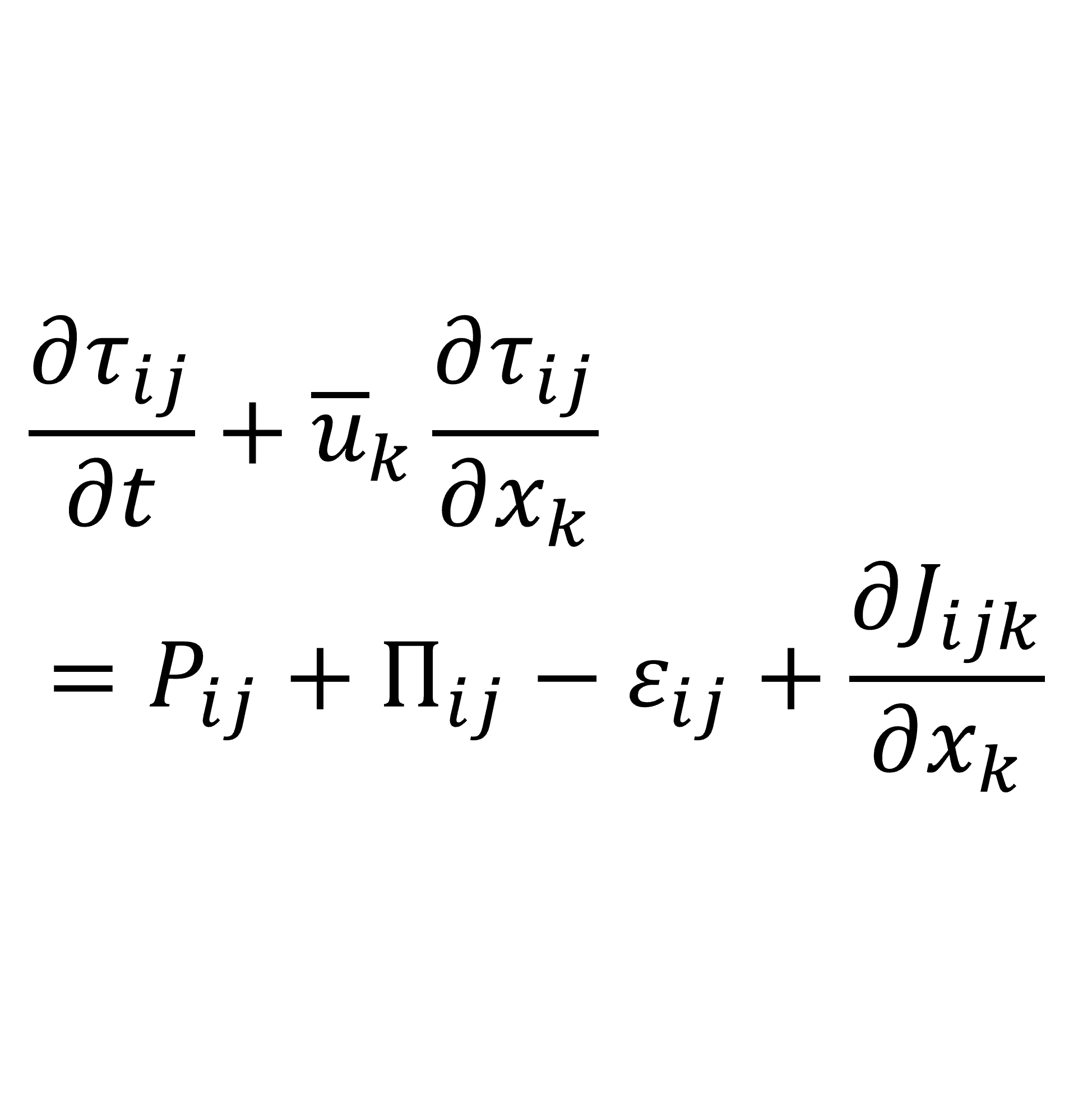

コメント