RANSの基礎方程式を導出するのフィルター操作におけるアンサンブル平均と時間平均の関係について説明する
keyword: レイノルズ平均,アンサンブル平均,時間平均,非定常RANS,URANS
はじめに
RANSでは,流れ場を粗視化して計算コストを下げるためにレイノルズ平均という平均操作を施したNavier-Stokes方程式を計算する
一方,CFDの説明で「RANSは時間平均したNavier-Stokes方程式を解いて定常計算を行う」とされることがあるが,この説明は厳密には間違っており,RANSでも非定常計算は不可能ではない
このことを理解するために,アンサンブル平均(レイノルズ平均)と時間平均の定義を確認してみる
アンサンブル平均と時間平均
アンサンブル平均とは,N個のサンプルの平均であり,次の式で定義される
\begin{equation}
\overline{u}=\frac{1}{N}\sum_{N} u
\end{equation}
時間平均とは,ある時間Tにおける平均であり,次の式で定義される
\begin{equation}
\overline{u}=\frac{1}{T}\int_{t}^{t+T}u\:dt
\end{equation}
2つの平均は一見違うものに見えるかもしれないが,時間平均は「ある時間Tの中から抜き出した異なるNt個の時刻に対するアンサンブル平均」と言い換えることができる
\begin{equation}
\overline{u}=\frac{1}{N_{t}}\sum_{N_{t}} u(t)
\end{equation}
つまり,時間平均はアンサンブル平均の一種であり,アンサンブル平均はより一般的な平均の概念ということである
RANSにおける定常計算
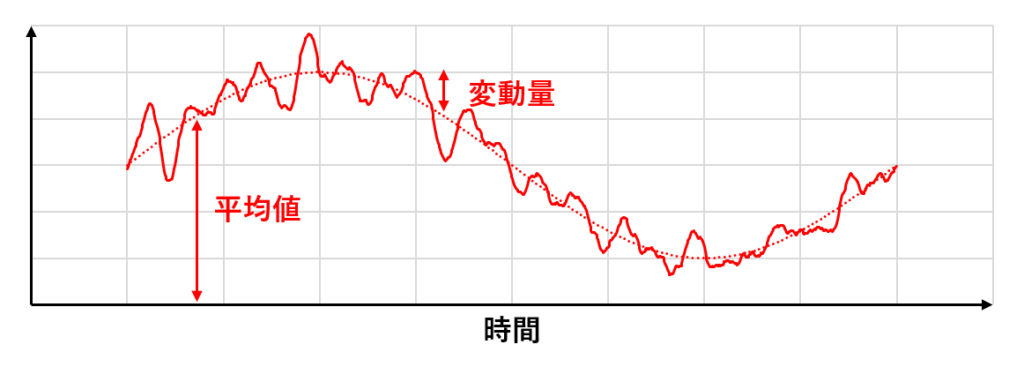
定常的な乱流は下の図のようになる(縦軸は速度や圧力などの物理量)
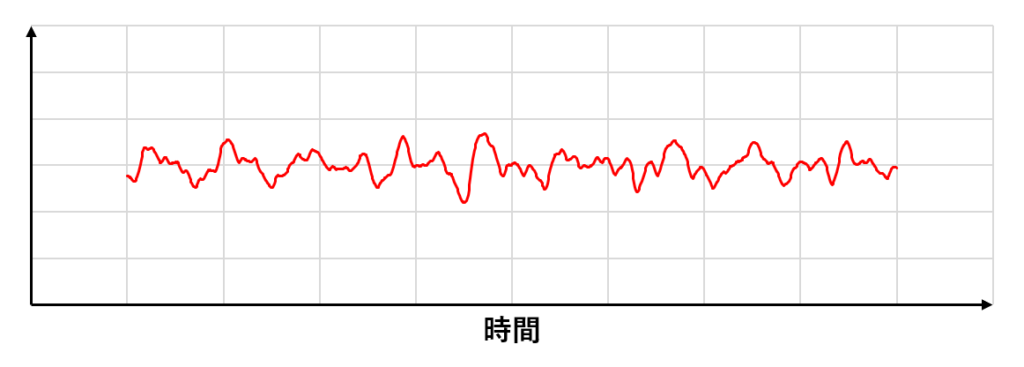
時間平均をとると図の点線の定常流になり,レイノルズ分解によって平均値と変動量に分けられる
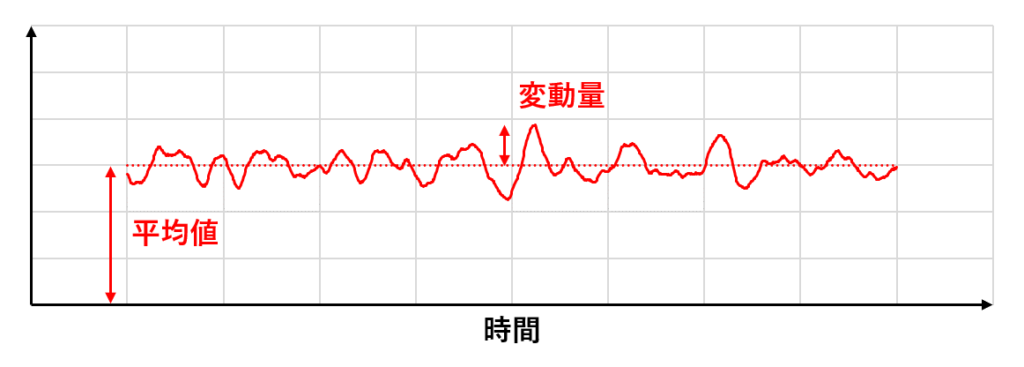
時間平均よりも一般的な概念であるアンサンブル平均の考え方をするならば,下の図のようになる
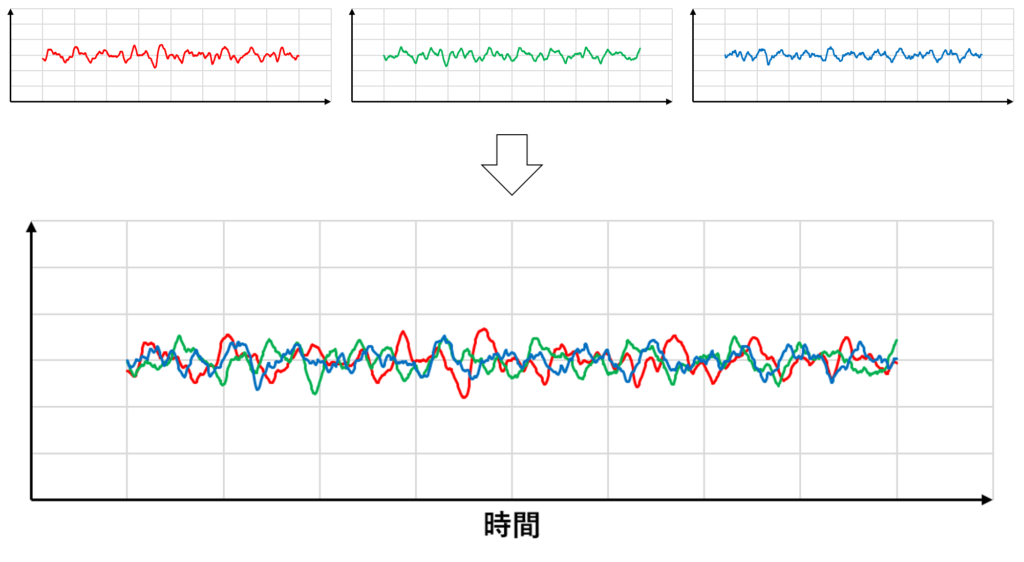
サンプル数を十分に大きくすればアンサンブル平均は時間平均の直線に限りなく近づいていくはずなので,定常流ではアンサンブル平均と時間平均は同じものであるということがわかる
RANSにおける非定常計算
非定常的な乱流は下の図のようになる(おおきなsinカーブが流れ場の非定常性で小さな乱れが乱流によるもの)
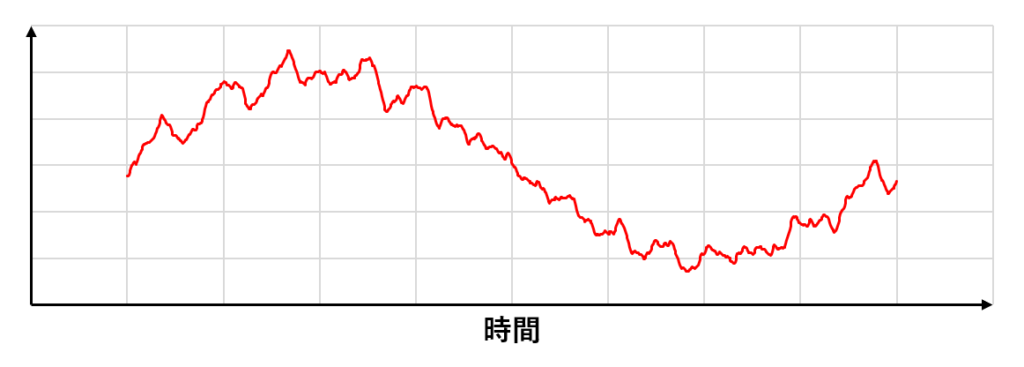
時間平均の考え方だとこのような非定常流れは計算できないように感じるが,より一般的な概念であるアンサンブル平均を用いると次のように考えることができる
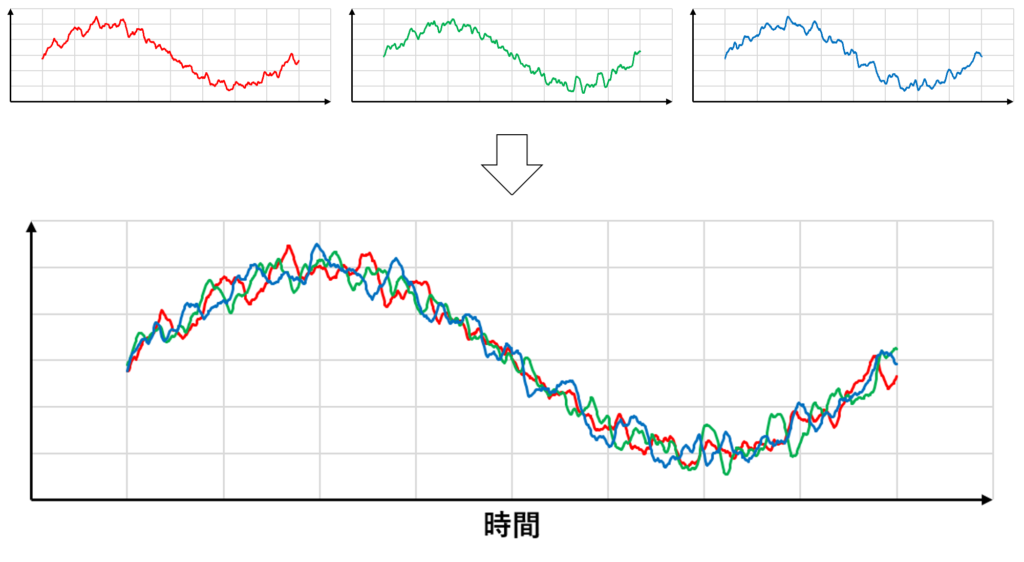
このように,アンサンブル平均を使えば非定常流れでも平均値と変動量を考えることができるため,RANSでも非定常計算が不可能ではないことが理解できる
実際,Re数が低い円柱まわりの流れをRANSで計算すると,円柱の背後に非定常的な渦(カルマン渦)が現れることが確認されている
≫パッと知りたい! 人と差がつく乱流と乱流モデル講座 第13回 13.1 円柱周り流れ解析、13.2 LESの計算結果、13.3 RANSとの比較
非定常RANSの注意点
ただし,非定常RANSを計算するためには流れ場の非定常性と乱れのスケールがしっかりと分離している必要がある
下の図のように,流れ場の非定常性と乱れのスケールが近い場合はアンサンブル平均をとったとしても流れ場の非定常性をうまく把握することができない
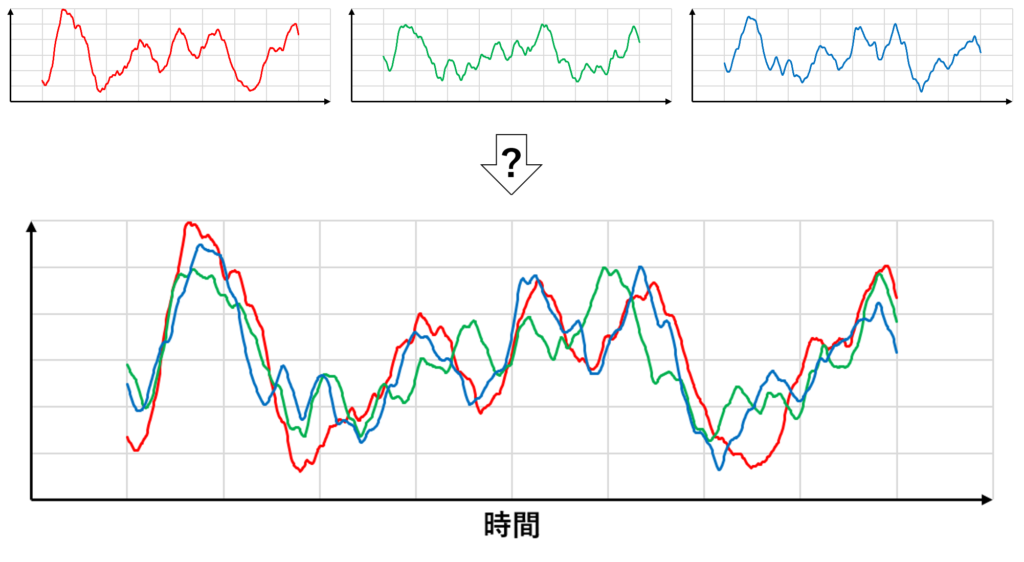
まとめ
RANSの基礎方程式を導出するのフィルター操作におけるアンサンブル平均と時間平均の関係について説明した
アンサンブル平均とは,N個のサンプルの平均である
時間平均は,N個のサンプルを「異なる時刻における流れ場」としたアンサンブル平均である
定常な流れ場ではアンサンブル平均と時間平均は一致する
RANSでも非定常計算を行うことはできなくはないが,乱れのタイムスケールと非定常性のタイムスケールが分離されている必要がある
ここまで長々と説明してきたが,実際非定常計算をRANSでやることはあまりないと思うので,RANS=時間平均という理解でもあまり問題はない
ただ,論文や学会発表などで「RANSは時間平均をとって定常計算を行う手法です」と言ってしまうと思わぬところから横やりが来るかもしれないので注意が必要である
↓おすすめ記事



コメント