低レイノルズ数型k-εモデルと壁面漸近挙動について説明を行う
keyword: 2方程式モデル,低Re数型RANSモデル,壁面漸近挙動,near wall limiting behavior
渦粘性モデル
RANSにおける渦粘性モデルの基礎方程式は次の式で表される
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{t}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}
\(\overline{u}_{i}\),\(\overline{p}\)以外の変数は渦粘性係数\(\nu_{t}\)ただ1つであり,この\(\nu_{t}\)をどのように求めるかが渦粘性モデルの唯一にして最も重要な点である
渦粘性モデルは,\(\nu_{t}\)を求めるために追加する方程式の数で,0方程式モデル,1方程式モデル,2方程式モデルに分類される
この記事では,2方程式モデルの1つであるk-εモデルの拡張版である低レイノルズ数型k-εモデルについて説明する
標準k-εモデル
k-εモデルの中でも最も基本となる「標準k-εモデル」とよばれるモデルは,乱流エネルギー\(k\)と乱流散逸率\(\varepsilon\)を用いて次のように渦粘性係数を計算している
\begin{equation}
\nu_{t}=C_{\mu}\frac{k^{2}}{\varepsilon}
\end{equation}
乱流エネルギー\(k\)と乱流散逸率\(\varepsilon\)はそれぞれの輸送方程式を解くことで求められる
\begin{equation}
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=P_{k}-\varepsilon
+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{equation}
\begin{equation}
\frac{\partial \varepsilon}{\partial t}+\overline{u}_{j}\frac{\partial \varepsilon}{\partial x_{j}}
=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \varepsilon}{\partial x_{j}}\right\}
\end{equation}
ここで,モデル定数は次の通り
\begin{equation}
C_{\mu}=0.09, \quad \sigma_{k}=1.0, \quad \sigma_{\varepsilon}=1.3, \quad
C_{\varepsilon_{1}}=1.44, \quad C_{\varepsilon_{2}}=1.92
\end{equation}
標準k-εモデルの欠陥
標準k-εモデルはレイノルズ数が高く局所平衡が成り立つ対数領域をもとに定数を決定しているので,より壁面に近い低レイノルズ数効果の大きい領域(粘性低層)を扱うことができない
標準k-εモデルでは壁関数という壁面境界条件を使うことで粘性低層の計算を省略しているが,伝熱を伴う温度境界層のように壁面近傍の乱れの諸量が特別に重要な場合については,壁面上で滑りなし条件の計算を行う必要がある
上記の問題を解決するために開発されたのが低レイノルズ数型k-εモデルである
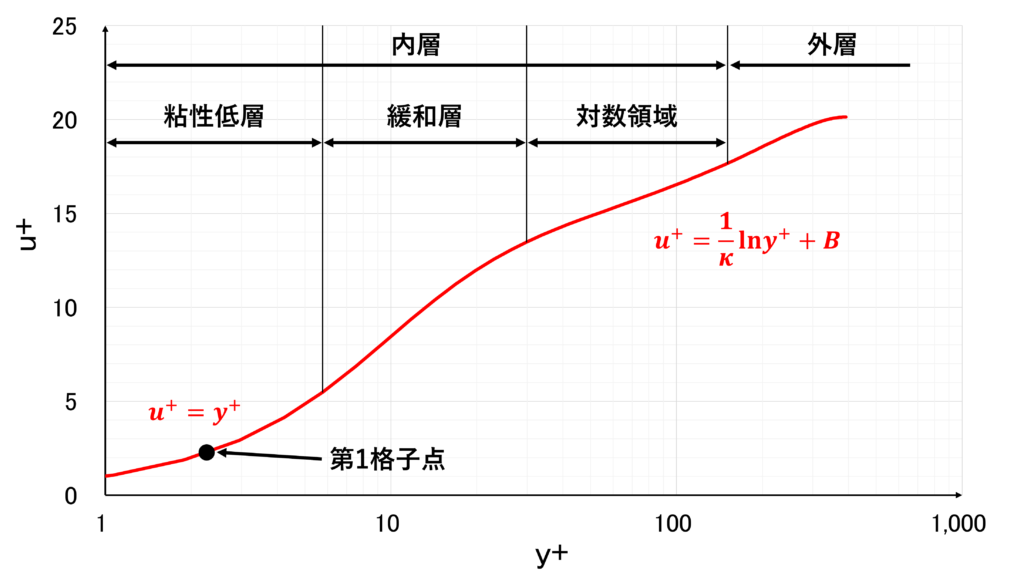
一般に,乱流境界層は壁面近くで壁からの影響を受ける内層と自由流近くの外層に分けられ,さらに内層は壁面ごく近くの分子粘性の影響が大きい領域である粘性低層,渦粘性の影響が大きい対数領域,それらの中間にある緩和層に分けられる

縦軸に無次元速度\(u^{+}\),横軸に無次元距離\(y^{+}\)の対数をプロットした片対数グラフは次のようになる

(粘性低層)
\(0 \leq y^{+} \leq 5\) であり,壁面の極近傍の領域である
壁面近くで乱れが減衰し,分子粘性が支配的になる(\(\nu \gg \nu_{t}\))
粘性低層では次のような層流の速度分布になる
\begin{equation}
u^{+}=y^{+}
\end{equation}
(緩和層)
\(5 \leq y^{+} \leq 30\) であり,粘性低層と対数領域の中間にある領域である
(対数領域)
\(30 \leq y^{+} \leq \delta_{t}^{+}\) であり,内層の一番外側にある領域である(\(\delta_{t}^{+}\)はレイノルズ数とともに大きくなる)
対数領域ではレイノルズ数が十分大きく分子粘性が無視できる(\(\nu \ll \nu_{t}\))ほか,乱れの生成と散逸の局所平衡が成立する
\begin{equation}
P_{k}=\varepsilon \qquad \left(P_{k}=-\overline{uv}\frac{\partial u}{\partial y}\right)
\end{equation}
速度分布は次のような対数速度分布になる
\begin{equation}
u^{+}=\frac{1}{\kappa}\ln{y^{+}}+B
\end{equation}
定数\(\kappa\)はカルマン定数とよばれ,乱流境界層では実験的に\(\kappa \simeq 0.4\),\(B \simeq 5\)とされている
また,対数領域では実験的に次の関係式が成り立つことがわかっている
\begin{equation}
\frac{|\overline{uv}|}{k}=0.3 \quad (=\sqrt{C_{\mu}})
\end{equation}
低レイノルズ数型k-εモデル
低Re数型モデルを使うときは,第1格子点を粘性低層(\(y^{+} \leq 2 \sim 4\))に配置して, 粘性低層の低レイノルズ数効果を取り扱えるように修正を加えた低レイノルズ数型モデルによって滑りなしの壁面境界条件を計算する
基本形
一般的な低レイノルズ数型モデルは次のように表される
\begin{equation}
\nu_{t}=C_{\mu}f_{\mu}\frac{k^{2}}{\varepsilon}
\end{equation}
\begin{equation}
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=P_{k}-\left(\tilde{\varepsilon}+D\right)
+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{equation}
\begin{equation}
\frac{\partial \tilde{\varepsilon}}{\partial t}+\overline{u}_{j}\frac{\partial \tilde{\varepsilon}}{\partial x_{j}}
=\left(C_{\varepsilon_{1}}f_{1}P_{k}-C_{\varepsilon_{2}}f_{2}\tilde{\varepsilon}\right)\frac{\tilde{\varepsilon}}{k}+E+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \tilde{\varepsilon}}{\partial x_{j}}\right\}
\end{equation}
\(f_{\mu}\)は\(\nu_{t}\)に対する減衰関数,\(f_{1}\)および\(f_{2}\)は\(\varepsilon\)の生産項および消滅項における補正関数,\(D\)および\(E\)は壁面補正項である
\(P_{k}\)は乱流エネルギー\(k\)の生成項で次の式で表される(\(S_{ij}=\frac{1}{2}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\))
\begin{equation}
P_{k}=-\tau_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}=2\nu_{t}S_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
\end{equation}
粘性散逸率の真の値は壁面補正項\(D\)を用いて \(\varepsilon=\tilde{\varepsilon}+D\) として計算される
壁面漸近挙動
壁面の極近傍に乱れの挙動を壁面漸近挙動といい,低レイノルズ数型モデルの補正項はこの壁面漸近挙動を満たすように決める必要がある
変動速度の各方向成分\([u', v', w']\)を壁面からの垂直距離\(y\)についてテイラー展開すると次のようになる
\begin{equation}
\left\{\begin{array}{rcl}
u'(y)&=&a_{0}+a_{1}y+a_{2}y^{2}+a_{3}y^{3}+\cdots \\
v'(y)&=&b_{0}+b_{1}y+b_{2}y^{2}+b_{3}y^{3}+\cdots \\
w'(y)&=&c_{0}+c_{1}y+c_{2}y^{2}+c_{3}y^{3}+\cdots \\
\end{array}\right.
\end{equation}
壁面上での滑りなし条件 \(u'(0)=v'(0)=w'(0)=0\)および壁面上での連続の式\(\frac{\partial u'}{\partial x}(0)=\frac{\partial v'}{\partial y}(0)=\frac{\partial w'}{\partial z}(0)=0\)より,変動速度の各方向成分の壁面漸近挙動が得られる
\begin{equation}
\left\{\begin{array}{rcccl}
u'(y)&=&a_{1}y&+&a_{2}y^{2}+a_{3}y^{3}+\cdots \\
v'(y)&=& & &b_{2}y^{2}+b_{3}y^{3}+\cdots \\
w'(y)&=&c_{1}y&+&c_{2}y^{2}+c_{3}y^{3}+\cdots \\
\end{array}\right.
\tag{i}
\end{equation}
(i)を用いると,壁面における各乱流諸量の\(y\)についてのテイラー展開は次のようになる
(乱流エネルギー)
\begin{align}
k=\frac{1}{2}\left(\overline{u'u'}+\overline{v'v'}+\overline{w'w'}\right)
\quad\rightarrow\quad k(y)=\frac{1}{2}\left(a_{1}^{2}+c_{1}^{2}\right)y^{2}+\cdots
\end{align}
(乱流散逸率)
\begin{align}
&\varepsilon=\nu\left(\overline{\frac{\partial u'}{\partial y}\frac{\partial u'}{\partial y}}+\overline{\frac{\partial v'}{\partial y}\frac{\partial v'}{\partial y}}+\overline{\frac{\partial w'}{\partial y}\frac{\partial w'}{\partial y}}\right)
\quad\rightarrow\quad \varepsilon(y)=\nu\left(a_{1}^{2}+c_{1}^{2}\right)+\cdots
\end{align}
(レイノルズ応力のuv成分)
\begin{align}
-\overline{u'v'}(y)=a_{1}b_{2}y^{3}+\cdots
\end{align}
(渦粘性係数)
\begin{align}
&\nu_{t}=\frac{-\overline{uv}}{\partial u/\partial y}
\quad\rightarrow\quad \nu_{t}(y)=\frac{a_{1}b_{2}y^{3}+\cdots}{a_{1}+\cdots}
\end{align}
よって,それぞれの壁面漸近挙動は,\(k \propto y^{2}\),\(\varepsilon \propto y^{0}\),\(\overline{u'v'} \propto y^{3}\),\(\nu_{t} \propto y^{3}\)である
壁面境界条件
前節で求めた壁面上での乱流諸量のテイラー展開に \(y=0\) 代入することで,低レイノルズ数型k-εモデルにおける壁面境界条件(添え字\(_{w}\))を求めることができる
(乱流エネルギー)
\begin{equation}
k_{w}=0
\end{equation}
(乱流散逸率)
\begin{equation}
\varepsilon_{w}=\nu\left(a_{1}^{2}+c_{1}^{2}\right)
=\left\{\begin{array}{l}
\nu\frac{\partial^{2} k(y)}{\partial y^{2}} \\
\nu\left(\frac{\partial \sqrt{k(y)}}{\partial y}\right)^{2} \\
2\nu\frac{k(y)}{y^{2}} \\
\end{array}\right.
\end{equation}
(渦粘性係数)
\begin{equation}
\nu_{t_{w}}=0
\end{equation}
\(\varepsilon\)の壁面境界条件の与え方は3通りあるが,CFDでは境界端での微分の精度が確保できないことから,微分の必要がない \(\varepsilon_{P}=\frac{2\nu k_{P}}{y_{P}^{2}}\) の境界条件が使われる
ただし,Launder-Sharmaモデルのように低レイノルズ数型モデルの補正項として\(D\)項を用いている場合は \(\varepsilon_{w}=\tilde{\varepsilon}_{w}+D=\frac{2\nu k}{y^{2}}\)なので,\(\tilde{\varepsilon}\)の壁面境界条件として \(\tilde{\varepsilon}_{w}=0\) を設定する必要がある
速度と圧力については,それぞれ滑りなし条件 \(u_{i}=0\),\(\frac{\partial p}{\partial n}=0\) を設定する
まとめ
低レイノルズ数型k-εモデルと壁面漸近挙動について説明を行った
低レイノルズ数型k-εモデルは,壁面近傍の低レイノルズ数効果の大きい領域(粘性低層)を扱えるよう修正を加えられたk-εモデルである
第1格子点を粘性低層(\(y^{+}<2 \sim 4\))に置くことで壁面境界条件として滑りなし条件を設定できるので,伝熱がかかわる問題などに利用される
OpenFOAMに実装されている代表的な低レイノルズ数型モデルはこちら
↓おすすめ記事
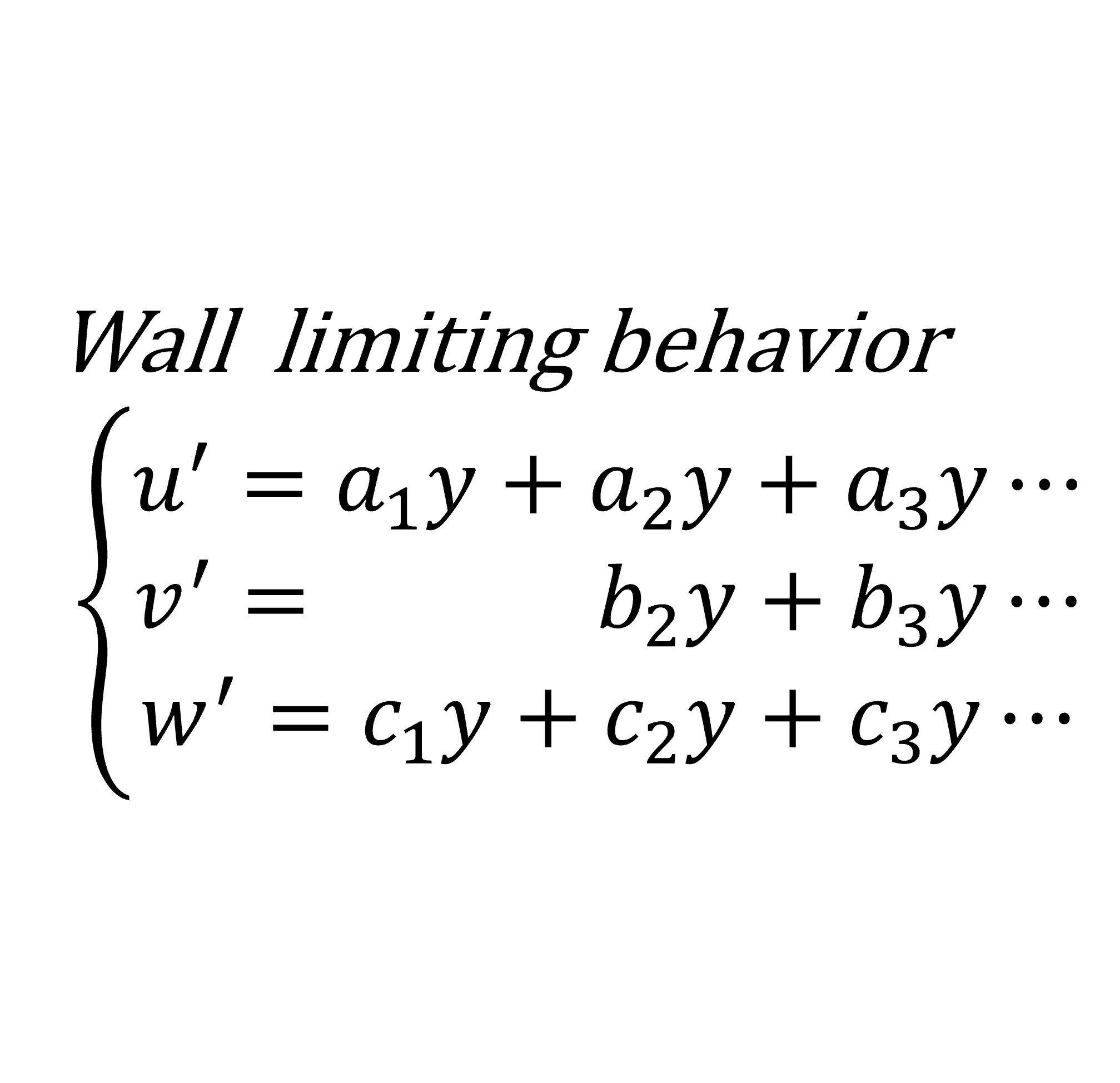






コメント