OpenFOAMで実装されている低Re数型k-εモデルであるLienLeschzinerについて説明する
keywords: OpenFOAM,乱流モデル,LienLeschziner
低レイノルズ数型k-εモデル
RANSにおける渦粘性モデルの基礎方程式は次の式で表される
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{t}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}
\(\overline{u}_{i}\),\(\overline{p}\)以外の変数は渦粘性係数\(\nu_{t}\)ただ1つであり,この\(\nu_{t}\)をどのように求めるかが渦粘性モデルの唯一にして最も重要な点である
一般的な低レイノルズ数型モデルは次のように表される
(渦粘性係数)
\begin{equation}
\nu_{t}=C_{\mu}f_{\mu}\frac{k^{2}}{\varepsilon}
\end{equation}
(\(k\)の輸送方程式)
\begin{equation}
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
=P_{k}-\left(\tilde{\varepsilon}+D\right)
+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{equation}
(\(\varepsilon\)の輸送方程式)
\begin{equation}
\frac{\partial \tilde{\varepsilon}}{\partial t}+\overline{u}_{j}\frac{\partial \tilde{\varepsilon}}{\partial x_{j}}
=\left(C_{\varepsilon_{1}}f_{1}P_{k}-C_{\varepsilon_{2}}f_{2}\tilde{\varepsilon}\right)\frac{\tilde{\varepsilon}}{k}+E+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \tilde{\varepsilon}}{\partial x_{j}}\right\}
\end{equation}
\(P_{k}\)は乱流エネルギー\(k\)の生成項で次の式で表される(\(S_{ij}=\frac{1}{2}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\))
\begin{equation}
P_{k}=2\nu_{t}S_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
\end{equation}
\(f_{\mu}\)は\(\nu_{t}\)に対する減衰関数,\(f_{1}\)および\(f_{2}\)は\(\varepsilon\)の生産項および消滅項における補正関数,\(D\)および\(E\)は壁面補正項である
粘性散逸率の真の値は壁面補正項\(D\)を用いて \(\varepsilon=\tilde{\varepsilon}+D\) として計算される
LienLeschziner
OpenFOAMで実装されているLienLeschzinerは次のようなモデルである
\begin{equation}
f_{\mu}=\frac{1-\exp{\left(-A_{\nu}y^{*}\right)}}{1-\exp{\left(-A_{\varepsilon}y^{*}\right)}}, \qquad
f_{1}=1, \qquad
f_{2}=1-0.3\exp{\left(-R_{t}^{2}\right)}
\end{equation}
\begin{equation}
D=0, \qquad
E=C_{\varepsilon_{2}}C_{\mu}^{\frac{3}{4}}f_{2}\sqrt{k}\frac{\varepsilon}{l_{e}}\exp{\left(-A_{E}{y^{*}}^{2}\right)}
\end{equation}
\begin{equation}
R_{t}=\frac{k^2}{\nu\varepsilon}, \qquad
y^{*}=\frac{\sqrt{k}y}{\nu}, \qquad
l_{e}=\kappa y\left\{1-\exp{\left(-A_{\varepsilon}y^{*}\right)}\right\}
\end{equation}
\begin{align}
&C_{\mu}=0.09, \quad
C_{\varepsilon_{1}}=1.44, \quad
C_{\varepsilon_{2}}=1.92, \quad
\sigma_{k}=1.0, \quad
\sigma_{\varepsilon}=1.3 \\
&\kappa=0.41, \quad
A_{\nu}=0.016, \quad
A_{\varepsilon}=0.263, \quad
A_{E}=0.00222 \\
\end{align}
OpenFOAMにおける実装
LienLeschzinerの実装を確認する
参考
≫LienLeschziner Class Reference
≫LienLeschziner.C
≫LienLeschziner.H
実際に計算が行われるときは,simpleFOAMやpisoFOAMなどのソルバーで turbulence->correct() が呼び出されているので,乱流モデルのプログラムは correct() → correctNut() → correctNonlinearStress() の順番で実行されている
while (simple.loop())
{
Info<< "Time = " << runTime.timeName() << nl << endl;
// --- Pressure-velocity SIMPLE corrector
{
#include "UEqn.H"
#include "pEqn.H"
}
laminarTransport.correct();
turbulence->correct();
runTime.write();
runTime.printExecutionTime(Info);
}≫applications/solvers/incompressible/simpleFoam/simpleFoam.C
渦粘性係数
\begin{equation}
\nu_{t}=C_{\mu}f_{\mu}\frac{k^{2}}{\varepsilon}
\end{equation}
void LienLeschziner::correctNut()
{
nut_ = Cmu_*fMu()*sqr(k_)/epsilon_;
nut_.correctBoundaryConditions();
}輸送方程式
\begin{equation}
P_{k}=2\nu_{t}S_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}
\end{equation}
tmp<volTensorField> tgradU = fvc::grad(U_);
volScalarField G
(
GName(),
nut_*(tgradU() && twoSymm(tgradU()))
);
tgradU.clear();\begin{align}
\frac{\partial \tilde{\varepsilon}}{\partial t}+\overline{u}_{j}\frac{\partial \tilde{\varepsilon}}{\partial x_{j}}
&=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}f_{2}\tilde{\varepsilon}\right)\frac{\tilde{\varepsilon}}{k}+E+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{\varepsilon}}+\nu\right)\frac{\partial \tilde{\varepsilon}}{\partial x_{j}}\right\} \\
&\\
\frac{\partial k}{\partial t}+\overline{u}_{j}\frac{\partial k}{\partial x_{j}}
&=P_{k}-\left(\tilde{\varepsilon}+D\right)
+\frac{\partial}{\partial x_{j}}\left\{\left(\frac{\nu_{t}}{\sigma_{k}}+\nu\right)\frac{\partial k}{\partial x_{j}}\right\}
\end{align}
// Update epsilon and G at the wall
epsilon_.boundaryFieldRef().updateCoeffs();
const volScalarField f2(this->f2());
// Dissipation equation
tmp<fvScalarMatrix> epsEqn
(
fvm::ddt(epsilon_)
+ fvm::div(phi_, epsilon_)
- fvm::laplacian(DepsilonEff(), epsilon_)
==
Ceps1_*G*epsilon_/k_
- fvm::Sp(Ceps2_*f2*epsilon_/k_, epsilon_)
+ E(f2)
);
epsEqn.ref().relax();
epsEqn.ref().boundaryManipulate(epsilon_.boundaryFieldRef());
solve(epsEqn);
bound(epsilon_, epsilonMin_);
// Turbulent kinetic energy equation
tmp<fvScalarMatrix> kEqn
(
fvm::ddt(k_)
+ fvm::div(phi_, k_)
- fvm::laplacian(DkEff(), k_)
==
G
- fvm::Sp(epsilon_/k_, k_)
);
kEqn.ref().relax();
solve(kEqn);
bound(k_, kMin_); //- Return the effective diffusivity for k
tmp<volScalarField> DkEff() const
{
return tmp<volScalarField>
(
new volScalarField("DkEff", nut_/sigmak_ + nu())
);
}
//- Return the effective diffusivity for epsilon
tmp<volScalarField> DepsilonEff() const
{
return tmp<volScalarField>
(
new volScalarField("DepsilonEff", nut_/sigmaEps_ + nu())
);
}補正項
\begin{equation}
f_{\mu}=\frac{1-\exp{\left(-A_{\nu}R_{y}\right)}}{1-\exp{\left(-0A_{\varepsilon}R_{y}\right)}}, \qquad
y^{*}=\frac{\sqrt{k}y}{\nu}
\end{equation}
tmp<volScalarField> LienLeschziner::fMu() const
{
const volScalarField yStar(sqrt(k_)*y_/nu());
return
(scalar(1) - exp(-Anu_*yStar))
/((scalar(1) + SMALL) - exp(-Aeps_*yStar));
}\begin{equation}
f_{2}=1-0.3\exp{\left(-R_{t}^{2}\right)}, \qquad
R_{t}=\frac{k^2}{\nu\varepsilon}
\end{equation}
tmp<volScalarField> LienLeschziner::f2() const
{
tmp<volScalarField> Rt = sqr(k_)/(nu()*epsilon_);
return scalar(1) - 0.3*exp(-sqr(Rt));
}\begin{align}
E=C_{\varepsilon_{2}}C_{\mu}^{\frac{3}{4}}f_{2}\sqrt{k}\frac{\varepsilon}{l_{e}}\exp{\left(-A_{E}{y^{*}}^{2}\right)}, \qquad
l_{e}=\kappa y\left\{1-\exp{\left(-A_{\varepsilon}y^{*}\right)}\right\}
\end{align}
tmp<volScalarField> LienLeschziner::E(const volScalarField& f2) const
{
const volScalarField yStar(sqrt(k_)*y_/nu());
const volScalarField le
(
kappa_*y_*((scalar(1) + SMALL) - exp(-Aeps_*yStar))
);
return
(Ceps2_*pow(Cmu_, 0.75))
*(f2*sqrt(k_)*epsilon_/le)*exp(-AE_*sqr(yStar));
}定数群
\begin{align}
&C_{\mu}=0.09, \quad
C_{\varepsilon_{1}}=1.44, \quad
C_{\varepsilon_{2}}=1.92, \quad
\sigma_{k}=1.0, \quad
\sigma_{\varepsilon}=1.3 \\
&\kappa=0.41, \quad
A_{\nu}=0.016, \quad
A_{\varepsilon}=0.263, \quad
A_{E}=0.00222 \\
\end{align}
Ceps1_
(
dimensioned<scalar>::getOrAddToDict
(
"Ceps1",
coeffDict_,
1.44
)
),
Ceps2_
(
dimensioned<scalar>::getOrAddToDict
(
"Ceps2",
coeffDict_,
1.92
)
),
sigmak_
(
dimensioned<scalar>::getOrAddToDict
(
"sigmak",
coeffDict_,
1.0
)
),
sigmaEps_
(
dimensioned<scalar>::getOrAddToDict
(
"sigmaEps",
coeffDict_,
1.3
)
),
Cmu_
(
dimensioned<scalar>::getOrAddToDict
(
"Cmu",
coeffDict_,
0.09
)
),
kappa_
(
dimensioned<scalar>::getOrAddToDict
(
"kappa",
coeffDict_,
0.41
)
),
Anu_
(
dimensioned<scalar>::getOrAddToDict
(
"Anu",
coeffDict_,
0.016
)
),
Aeps_
(
dimensioned<scalar>::getOrAddToDict
(
"Aeps",
coeffDict_,
0.263
)
),
AE_
(
dimensioned<scalar>::getOrAddToDict
(
"AE",
coeffDict_,
0.00222
)
),壁面境界条件
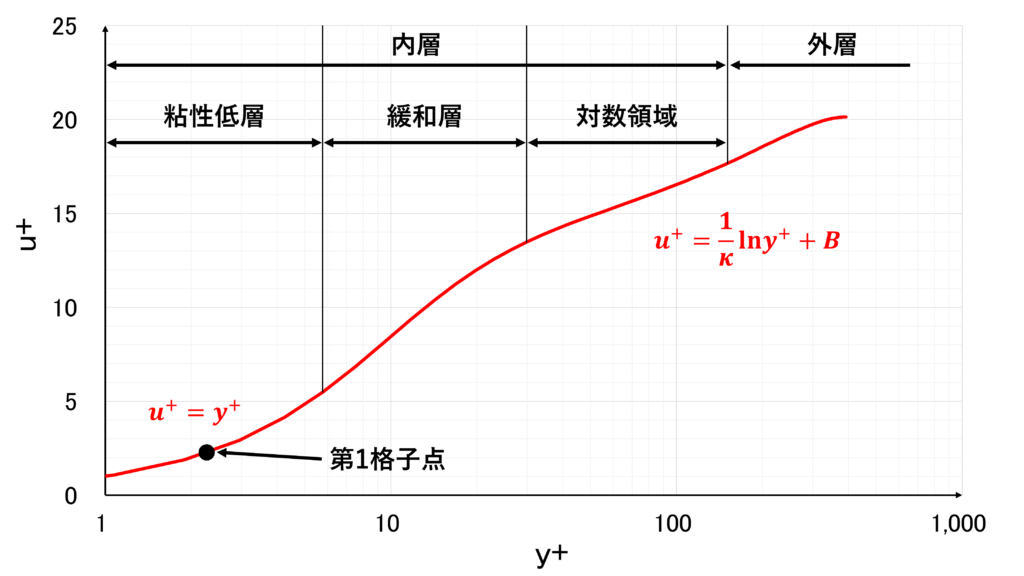
低Re数型モデルを使うときは,第1格子点を粘性低層(\(y^{+} \leq 2 \sim 4\))に配置して, 滑りなしの壁面境界条件を計算する
(速度)
\begin{equation}
u_{i}=0
\end{equation}
(圧力)
\begin{equation}
\frac{\partial p}{\partial n}=0
\end{equation}
(乱流エネルギー)
\begin{equation}
k_{w}=0
\end{equation}
(乱流散逸率)
\begin{equation}
\tilde{\varepsilon}_{w}=\frac{2\nu k}{y^{2}}
\end{equation}
(渦粘性係数)
\begin{equation}
\nu_{t_{w}}=0
\end{equation}
まとめ
OpenFOAMで実装されている低Re数型k-εモデルであるLienLeschzinerについて説明した
そのほかの乱流モデルについてはこちら




コメント