CFDにおける離散化スキームについて,大学院生の研究活動に役立つような説明を行う
keyword: 有限体積法,数値粘性,中心差分,風上差分,QUICK
はじめに
この記事の内容は以下の前提に基づいている
- 非圧縮性流体の乱流流れ
- 密度\(\rho\),粘性係数\(\mu\)は一定
- 熱移動はなし
- CFDを研究で使う大学院生に必要な知識に重点を置く(ググって得られる知識と専門書の中間くらい)
参考文献はこちら
数値流体力学で必須のテンソル解析についての知識はこちら
流れの数値シミュレーションの概要
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(2)に関連して,偏微分方程式を離散化する際の離散化スキームについて説明する
↓前回までの記事はこちらから
CFDの基礎方程式
密度\(\rho\),粘性係数\(\mu\)が一定な非圧縮性流体の基礎方程式は,連続の式(質量保存式)およびNavier-Stokes方程式(運動量保存式)である
(連続の式)
\begin{equation}
\frac{\partial u_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial u_{i}}{\partial t}+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial P}{\partial x_{i}}+\nu_{e}\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)
+f_{i}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{t}, \qquad {P}={p}+\frac{2}{3}\rho k
\end{equation}
※モデル化のためのフィルター操作を表すオーバーライン(\(\overline{u}_{i}\),\(\overline{p}\))は省略している
密度\(\rho\)と動粘性係数\(\nu\)は水や空気などの物性値であり,渦粘性係数\(\nu_{t}\)は乱流の影響による拡散を表している
未知数は速度\(\mathbf{u}\)の3つの成分\(u_{i}\),圧力\(p\),渦粘性係数\(\nu_{t}\)の5つであり,渦粘性係数を乱流モデルによって与えれば,連続の式とNavier-Stokes方程式を解くことですべての物理量を求めることができる
また,これ以降は簡単のため \(P \rightarrow p\) と表記することとする
基礎方程式の離散化
コンピュータでCFDの基礎方程式であるNavier-Stokes方程式を解くためには,計算格子上に偏微分方程式を離散化する必要がある
SIMPLE系の解法で用いられる有限体積法によってNavier-Stokes方程式を離散化すると次の式になる
\begin{equation}
\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}
=-\nabla p+\mathbf{s}_{_{P}}
\end{equation}
\(\mathbf{A}\)はセル中心の速度\(\mathbf{u}\)が他のセルに及ぼす影響を表し,\(\mathbf{s}\)は圧力項以外のソース項である
添え字\(_{{P}}\)は注目しているセル\(P\)を表し,添え字\(_{nb}\)はセル\(P\)に影響を及ぼす全ての隣接セル(neighbours)を表している
\(\mathbf{A}\)の具体的な値を決定するのは偏微分方程式の離散化に用いられた離散化スキームであり,離散化スキームの精度や性質によって計算の安定性や結果の精度は大きく変化する
↓離散化した方程式の解き方についてはこちら
CFDの基礎方程式は連続の式とNavier-Stokes方程式であり,これらの方程式を計算格子上で離散化することによってコンピューター上で解を求めている
離散化方程式の係数行列の値は離散化に用いられる離散化スキームによって決まる
離散化の種類と精度
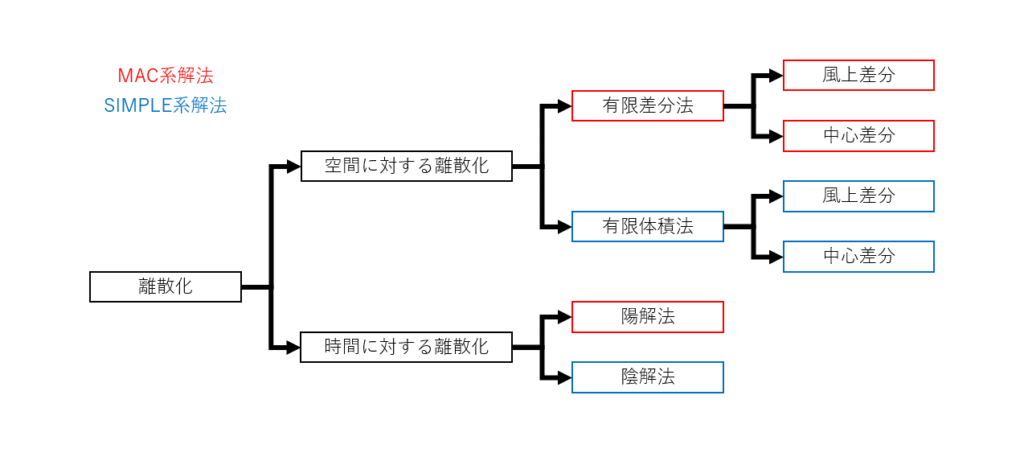
離散化の種類
偏微分方程式の離散化は,「空間に対する離散化」と「時間に対する離散化」の2つに分けられる
空間に対する離散化の手法には有限差分法や有限体積法などがあり,それぞれにおいて中心差分と風上差分が存在する
時間に対する離散化の手法には陽解法と陰解法があり,陽解法は有限差分法を用いるMAC系の解法に,陰解法は有限体積法を用いるSIMPLE系の解法に用いられる
離散化の精度
次のような格子幅\(\Delta x\)の1次元の計算格子を考える
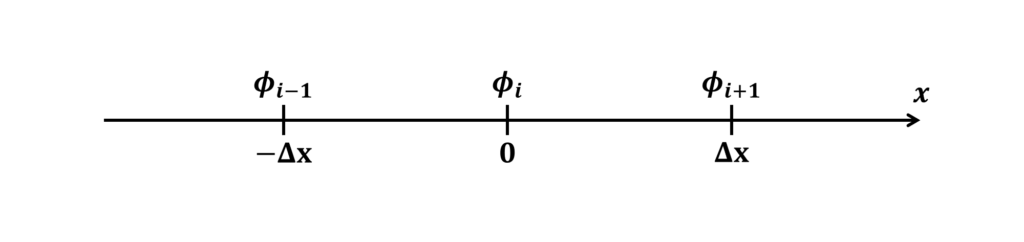
ここで,\(\phi_{i}\)に対する風上差分による補間\(\phi_{i_{_{UD}}}\)と中心差分による補間\(\phi_{i_{_{CD}}}\)はテイラー展開によって次の式で表される
\begin{align}
&\phi_{i_{_{UD}}}=\phi_{i-1}+\frac{\partial \phi_{i}}{\partial x}\Delta x+\cdots \\ \\
&\phi_{i_{_{CD}}}=\frac{\phi_{i-1}+\phi_{i+1}}{2}-\frac{1}{2}\frac{\partial^{2} \phi_{i}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\end{align}
上記の式で,\(\Delta x\)を含む項は離散化に伴う誤差であり,計算格子を極限まで細かくしていけば \(\Delta x=0\)となり,誤差も0になる
離散化式のテイラー展開で出てくる項が計算格子幅(もしくは時間ステップ)のn乗に比例しているとき,その離散化スキームは「n次精度」であるという
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{i}=\phi(0)\),\(\phi_{i-1}=\phi(-\Delta x)\),\(\phi_{i+1}=\phi(\Delta x)\) なので
\begin{align}
\phi_{i-1}=\phi_{i}-\frac{\partial \phi_{i}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{i}}{\partial x^{2}}{\Delta x}^{2}-\cdots
\tag{i} \\ \\
\phi_{i+1}=\phi_{i}+\frac{\partial \phi_{i}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{i}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\tag{ii} \\ \\
\end{align}
風上差分は上流の値をそのまま用いる差分 \(\phi_{i}=\phi_{i-1}\) なので,(1)より
\begin{align}
\phi_{i}=\phi_{i-1}+\frac{\partial \phi_{i}}{\partial x}\Delta x
-\frac{1}{2}\frac{\partial^{2} \phi_{i}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\end{align}
中心差分は両側の平均を用いる差分 \(\phi_{i}=\frac{\phi_{i-1}+\phi_{i+1}}{2}\) なので,(1)+(2)より
\begin{align}
\phi_{i}=\frac{\phi_{i-1}+\phi_{i+1}}{2}-\frac{1}{2}\frac{\partial^{2} \phi_{i}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\end{align}
離散化には空間に対する離散化と時間に対する離散化がある
空間に対する離散化手法には有限差分法と有限体積法があり,時間に対する離散化手法には陽解法と陰解法がある
離散化に伴う誤差が計算格子幅や時間ステップ幅のn乗に比例するとき,n次精度の離散化スキームであるという
今回の記事では,有限体積法の離散化として中心差分,風上差分,線形風上差分,QUICKを説明し,時間発展の陰解法としてオイラー法と後退差分について説明する
有限体積法を用いた離散化
有限体積法は次のような特徴を持つ離散化手法である
- 積分型の流れの方程式を基礎とする
- 速度や圧力などの物理量は検査体積(セル)の代表値を求める
- 質量や運動量などの保存則はセルの境界からの流入/流出およびセル内部での発生/消滅によって表す
- 非構造格子を用いる
セルが不規則に配置されている非構造格子では,離散化に使える値は注目セル\(P\)の代表値\(\phi_{_{P}}\)と隣接セル\(N\)の代表値\(\phi_{_{N}}\)の2つのみである
2つのセルの間にある境界面\(f\)の代表値\(\phi_{f}\)は\(\phi_{_{P}}\)と\(\phi_{_{N}}\)を用いた補間によって求められる
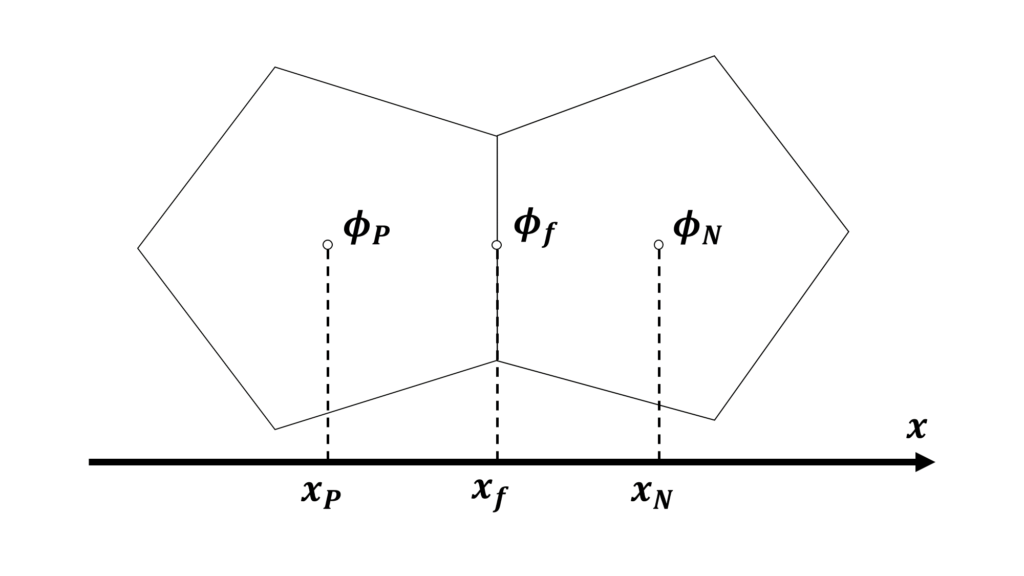
一般的な輸送方程式に対する離散化
一般に,物理量\(\phi\)の輸送方程式は時間項,対流項,粘性項,ソース項(生成項+散逸項)から構成され,次のようにあらわされる
\begin{equation}
\frac{\partial}{\partial t}(\rho\phi)
+\nabla\cdot(\rho\mathbf{u}\phi)
=s
+\nabla\cdot\left(\Gamma\nabla \phi\right)
\end{equation}
ここで,
- \(\phi=\mathbf{u}\),\(\Gamma=\mu+\mu_{t}\),\(s=-\frac{\partial p}{\partial x}\)とすればNavier-Stokes方程式
- \(\phi=k\),\(\Gamma=\mu+\frac{\mu_{t}}{\sigma_{k}}\),\(s=P_{k}-\varepsilon\)とすれば標準k-εモデルの\(k\)の輸送方程式,
- \(\phi=\varepsilon\),\(\Gamma=\mu+\frac{\mu_{t}}{\sigma_{\varepsilon}}\),\(s=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}\)とすれば標準k-εモデルの\(\varepsilon\)の輸送方程式
である
上記の輸送方程式をセル体積で積分し,離散化すると次のようになる
\begin{equation}
\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
+\sum_{f}{F\phi_{f}}
=s_{_{P}}V_{_{P}}
+\sum_{f}{\Gamma_{f}\left|S_{f}\right|\frac{\phi_{_{N}}-\phi_{_{P}}}{|\mathbf{x}_{_{N}}-\mathbf{x}_{_{P}}|}}
\end{equation}
また,\(\phi\)の発散と勾配を有限体積法で離散化すると次のようになる
\begin{align}
\nabla\cdot\phi \quad &\rightarrow \quad \sum_{f}\mathbf{S}_{f}\cdot\phi_{f} \\ \\
\nabla\phi \quad &\rightarrow \quad \sum_{f}\mathbf{S}_{f}\phi_{f} \\
\end{align}
ここで,\(V_{_{P}}\)はセル体積,\(|S_{f}|\)は注目セルと隣接セルの境界面の面積,\(\mathbf{S}_{f}\)は境界面に垂直で境界面の面積\(|S_{f}|\)を大きさに持つ法線ベクトルであり,\(\sum_{f}\)はセルがもつすべての面に対する総和を表す
上記3つの離散化を見てみると未知数は\(\phi_{f}\)のみであり,有限体積法の離散化は「境界面上の代表値\(\phi_{f}\)をどのように補間するか」という点に集約されていることがわかる
有限差分法の離散化は微分を「差分」で表し,有限体積法の離散化は微分を「補間」で表すことが両者の大きな違いの1つである
有限体積法は速度や圧力などの物理量を検査体積(セル)の代表値として求めるので,\(\phi\)についての輸送方程式をセル\(P\)について体積積分する
\begin{equation}
\int_{V}{\frac{\partial}{\partial t}(\rho\phi)}dV
+\int_{V}{\nabla\cdot(\rho\mathbf{u}\phi)}dV
=
\int_{V}{s}dV
+\int_{V}{\nabla\cdot\left(\Gamma\nabla \phi\right)}dV
\end{equation}
上式の各項の積分について離散化を行う
ちなみに,ここからの式変形ではガウスの発散定理を多用する
\begin{equation}
\int_{V}{\nabla\cdot\phi}dV=\int_{S}{d\mathbf{S}\cdot\phi}
\end{equation}
参考
≫ガウスの発散定理・ストークスの定理の証明 _ 高校数学の美しい物語
対流項(convection term)
ガウスの発散定理より,対流項は次のように離散化される
\begin{equation}
\int_{V}{\nabla\cdot(\rho\mathbf{u}\phi)}dV
=\int_{S}{d\mathbf{S}\cdot(\rho\mathbf{u}\phi)}
=\sum_{f}{\mathbf{S}_{f}\cdot(\rho\mathbf{u})_{f}\phi_{f}}
=\sum_{f}{F\phi_{f}}
\end{equation}
ここで,\(F=\mathbf{S}_{f}\cdot(\rho\mathbf{u})_{f}\)は質量流束である
対流項は\(\mathbf{u}\)と\(\phi\)という2つの変数の積で表される非線形項であり,離散化に対して最も慎重になる必要がある項である
拡散項
ガウスの発散定理より,対流項は次のように離散化される
\begin{equation}
\int_{V}{\nabla\cdot\left(\Gamma\nabla \phi\right)}dV
=\int_{S}{d\mathbf{S}\cdot(\Gamma\nabla\phi)}
=\sum_{f}{\Gamma_{f}\mathbf{S}_{f}\cdot(\nabla\phi)_{f}}
\end{equation}
ここで,\(\mathbf{S}_{f}\cdot(\nabla\phi)_{f}\)は中心差分を用いて次のように計算される
\begin{equation}
\mathbf{S}_{f}\cdot(\nabla\phi)_{f}
=|S_{f}|\frac{\phi_{_{N}}-\phi_{_{P}}}{|\mathbf{x}_{_{N}}-\mathbf{x}_{_{N}}|}
\end{equation}
ソース項(Source terms)
ソース項は次の3つの条件に応じて計算の仕方が異なる
- ソース項が既知の変数を用いて陽的に計算できる
- ソース項の中に変数\(\phi\)が入っており,係数\(\rho\)が正である
- ソース項の中に変数\(\phi\)が入っており,係数\(\rho\)が負である
(1)の場合は,注目セルにおける代表値を用いて直接計算できる
\begin{equation}
\int_{V}{s}dV
=s_{_{P}}V_{_{P}}
\end{equation}
(2)と(3)の場合は,係数行列\(\mathbf{A}_{p}\)の対角優位性を保って計算の安定性を高めるために,係数\(\rho\)の符号によって計算方法を切り替える(係数行列の対角成分が大きくなると計算が安定する)
(2)の場合は,ソース項を陰的に計算して係数行列の対角成分を大きくする
\begin{align}
&\int_{V}{\rho\phi}dV=\rho_{_{P}}V_{_{P}}\phi_{_{P}} \\
\\ \rightarrow \quad
& \mathbf{A}_{_{P}}\phi_{_{P}}
+\mathrm{max}\left(\rho_{_{P}},0\right)V_{_{P}}\phi_{_{P}}
=\left\{\mathbf{A}_{_{P}}+\mathrm{max}\left(\rho_{_{P}},0\right)V_{_{P}}\right\}
\phi_{_{P}}
\end{align}
(3)の場合は,ソース項を陽的に計算する
\begin{align}
\int_{V}{\rho\phi}dV=\rho_{_{P}}V_{_{P}}\phi_{_{P}}
=\mathrm{min}\left(\rho_{_{P}},0\right)V_{_{P}}\phi_{_{P}}
\end{align}
参考
≫ヤコビ法,ガウス・ザイデル法の 収束条件と対角優位性(PDF)
3.4.9 Source terms
Source terms can be specified in 3 ways
Explicit Every explicit term is a volField. Hence, an explicit source term can be incorporated into an equation simply as a field of values. For example if we wished to solve Poisson’s equation \(\nabla^{2}\phi=f\), we would define phi and f as volScalarField and then do\begin{equation}
\mathrm{solve(fvm::laplacian(phi) == f)}
\end{equation}Implicit An implicit source term is integrated over a control volume and linearised by
\begin{equation}
\int_{V}{\rho\phi}dV=\rho_{_{P}}V_{_{P}}\phi_{_{P}}
\end{equation}Implicit/Explicit The implicit source term changes the coefficient of the diagonal of the matrix. Depending on the sign of the coefficient and matrix terms, this will either increase or decrease diagonal dominance of the matrix. Decreasing the diagonal dominance could cause instability during iterative solution of the matrix equation. Therefore OpenFOAM provides a mixed source discretisation procedure that is implicit when the coefficients that are greater than zero, and explicit for the coefficients less than zero. In mathematical terms the matrix coefficient for node P is \(V_{_{P}}\mathrm{max}\left(\rho_{_{P}}, 0\right)\) and the source term is \(V_{_{P}}\phi_{_{P}}\mathrm{min}\left(\rho_{_{P}}, 0\right)\).
OpenFOAM Programmar's Guide p.43
発散(Divergence)
ガウスの発散定理より,発散は次のように離散化される
\begin{equation}
\int_{V}{\nabla\cdot\phi}dV
=\int_{S}{d\mathbf{S}\cdot\phi}
=\sum_{f}{\mathbf{S}_{f}\cdot\phi_{f}}
\end{equation}
輸送方程式の一般形には含まれていないが,
- \(\phi=\nu_{e}\left(\nabla\mathbf{u}\right)^{T}\)とすれば Navier-Stokes方程式の粘性項の片割れ
- \(\phi=\mathbf{N}=\tau_{ij}^{a}-(-2\nu_{t}S_{ij})\)とすれば外力項として実装される乱流応力の非線形項
である
勾配(Gradient)
ガウスの発散定理より,勾配は次のように離散化される
\begin{equation}
\int_{V}{\nabla\phi}dV
=\int_{S}{d\mathbf{S}\phi}
=\sum_{f}{\mathbf{S}_{f}\phi_{f}}
\end{equation}
輸送方程式の一般形には含まれていないが,\(\phi=-\frac{1}{\rho}p\)とすれば Navier-Stokes方程式の圧力項である
時間項
時間項は次のように計算できる
\begin{equation}
\int_{V}{\frac{\partial}{\partial t}(\rho\phi)}dV
=\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
\end{equation}
時間微分\(\frac{\partial}{\partial t}\)に対する離散化は後述する
非構造格子で離散化に使える値は,注目セル\(P\)の代表値\(\phi_{_{P}}\)と隣接セル\(N\)の代表値\(\phi_{_{N}}\)の2つのみである
有限体積法による離散化は「境界面上の代表値\(\phi_{f}\)をどのように補間するか」という点に集約されている
それでは,具体的な離散化スキームについて説明していく
中心差分
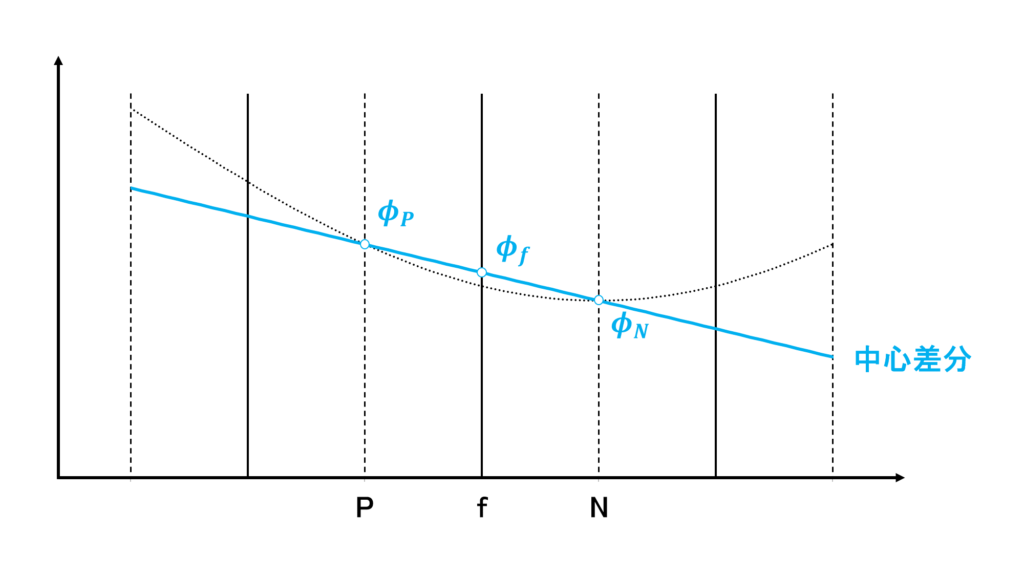
中心差分(central difference:CD)では,\(\phi_{f}\)を次のように補完する
\begin{equation}
\phi_{f}=w\phi_{_{P}}+\left(1-w\right)\phi_{_{N}}, \qquad
w=\frac{\left|\mathbf{x}_{f}-\mathbf{x}_{_{N}}\right|}{\left|\mathbf{x}_{_{P}}-\mathbf{x}_{_{N}}\right|}
\end{equation}
中心差分は2次精度であり,対流項,発散,勾配,すべてに使用できる有限体積法で最もポピュラーな離散化スキームである
離散化スキームについてよくわからないならとりあえずこれを設定しておけばいい
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{f}\)に原点をとり,\(\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|=\left|\mathbf{x}_{f}-\mathbf{x}_{_{_N}}\right|=\Delta x\) とすると,\(\phi_{f}=\phi(0)\),\(\phi_{_{P}}=\phi(-\Delta x)\),\(\phi_{_N}=\phi(\Delta x)\) なので
\begin{align}
\phi_{_{P}}=\phi_{f}-\frac{\partial \phi_{f}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}-\cdots
\tag{i} \\ \\
\phi_{_N}=\phi_{f}+\frac{\partial \phi_{f}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\tag{ii} \\ \\
\end{align}
(i)+(ii)より,中心差分は2次精度である
\begin{align}
\phi_{f}=\frac{\phi_{_P}+\phi_{_N}}{2}-\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}-\cdots
\end{align}
風上差分
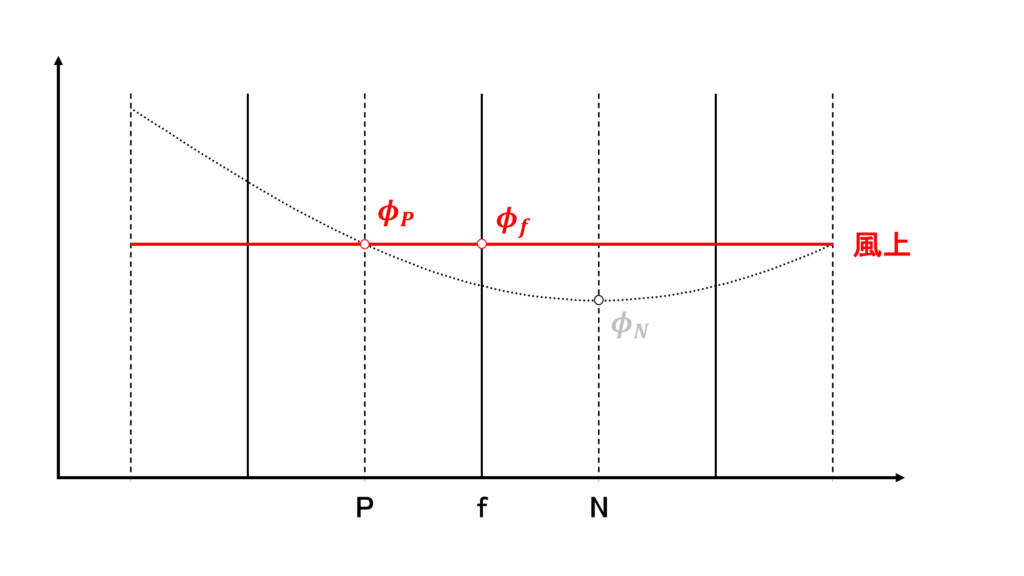
風上差分(upwind difference:UD)では,上流側の値をそのまま持ってくることによって\(\phi_{f}\)を次のように補完する
\begin{equation}
\phi_{f}=\left\{\begin{array}{ll}
\phi_{_{P}} & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\right) \\
\phi_{_{N}} & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}<0\right) \\
\end{array}\right.
\end{equation}
質量流束\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}\) の符号で上流側を判断している
風上差分は1次精度であり,後述する数値粘性が非常に大きく,計算の安定性は大きく向上するが計算結果の精度は非常に悪い
計算が難しい複雑な流れ場をRANSで計算するときに,速度の対流項に二次精度以上の風上差分を設定したうえで,\(k\)や\(\varepsilon\)の対流項に風上差分を設定するのはまだ許される
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{f}\)に原点をとり,\(\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|=\Delta x\) とすると,\(\phi_{f}=\phi(0)\),\(\phi_{_{P}}=\phi(-\Delta x)\) なので
\begin{align}
\phi_{_{P}}=\phi_{f}-\frac{\partial \phi_{f}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}-\cdots
\tag{i}
\end{align}
\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\) とすると,(i)より風上差分は1次精度である
\begin{align}
\phi_{f}=\phi_{_{P}}+\frac{\partial \phi_{f}}{\partial x}\Delta x
-\frac{1}{2}\frac{\partial^{2} \phi_{f}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\end{align}
線形風上差分
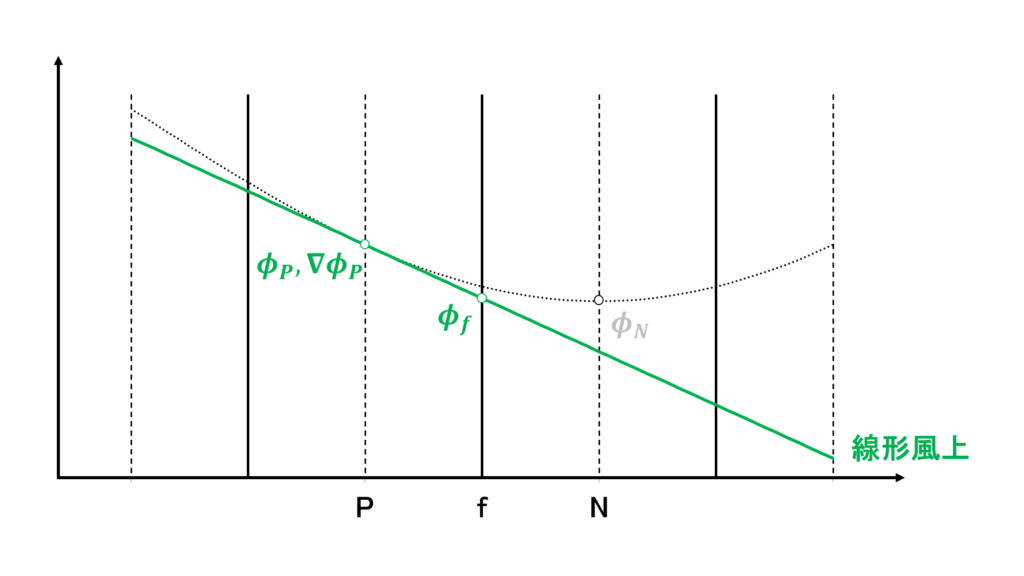
線形風上差分(linear upwind difference:LUD)では,上流側の値とその点における勾配を使って,\(\phi_{f}\)を次のように線形補完する
\begin{equation}
\phi_{f}=\left\{\begin{array}{ll}
\phi_{_{P}}+\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{P}\right) & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\right) \\
\phi_{_{N}}+\left(\nabla\phi\right)_{N}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{N}\right) & \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}<0\right) \\
\end{array}\right.
\end{equation}
質量流束\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}\) の符号で上流側を判断している
線形風上差分は2次精度であり,1次風上差分よりは数値粘性が大きくないので,計算が難しい複雑な流れ場をRANSで計算するときに,速度の対流項などに設定する
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{P}\)に原点をとり,\(\Delta x=\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|\) とすると,\(\phi_{P}=\phi(0)\),\(\phi_{f}=\phi(\Delta x)\) なので
\begin{align}
\phi_{f}=\phi_{P}+\frac{\partial \phi_{P}}{\partial x}\Delta x
+\frac{1}{2}\frac{\partial^{2} \phi_{P}}{\partial x^{2}}{\Delta x}^{2}+\cdots
\tag{i}
\end{align}
(i)で二次以上の誤差を無視しすると,\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\) のときの線形風上差分の式が得られる
\begin{align}
\phi_{f}=\phi_{P}
+\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right)
\end{align}
QUICK
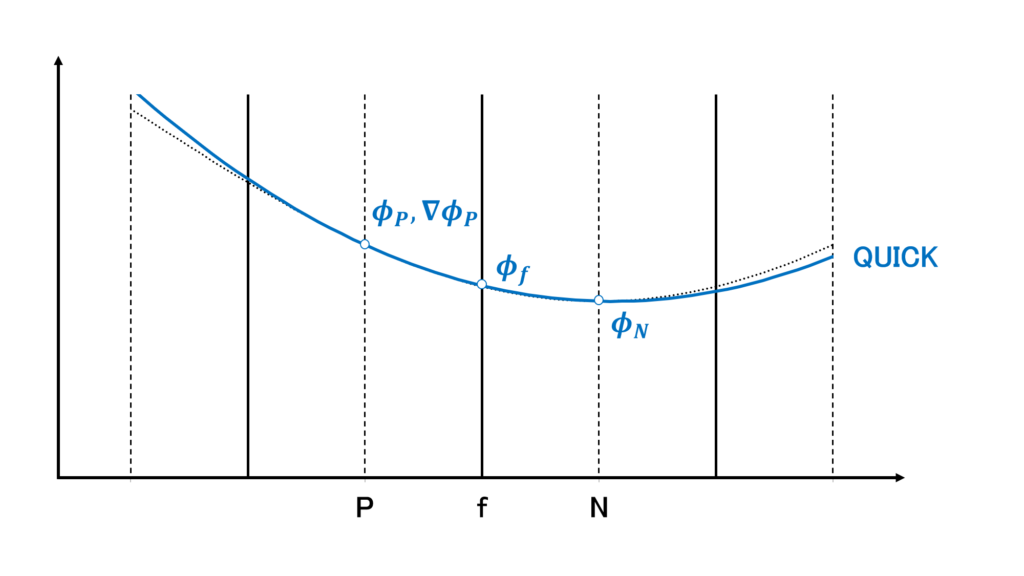
QUICK(Quadratic Upstream Interpolation for Convective Kinematics)では,上流側の値,上流側の点における勾配,下流側の値の3つを使って,\(\phi_{f}\)を次のように補完する
\begin{equation}
\phi_{f}=\left\{\begin{array}{ll}
\frac{3}{4}\phi_{_{P}}+\frac{1}{4}\phi_{_{N}}
+\frac{1}{4}\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{N}-\mathbf{x}_{P}\right)
& \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\right) \\
\frac{1}{4}\phi_{_{P}}+\frac{3}{4}\phi_{_{N}}
+\frac{1}{4}\left(\nabla\phi\right)_{N}\cdot\left(\mathbf{x}_{P}-\mathbf{x}_{N}\right)
& \left(\mathbf{u}_{f}\cdot\mathbf{S}_{f}<0\right) \\
\end{array}\right.
\end{equation}
質量流束\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}\) の符号で上流側を判断している
QUICKは補間としては3次精度であり,少しだけ数値粘性の力を借りたいときの速度の対流項としてよく設定される
\(\phi(x)\)についてテイラー展開を行うと次のようになる
\begin{equation}
\phi(x)=\phi(0)+\frac{\partial \phi(0)}{\partial x} x
+\frac{1}{2}\frac{\partial^{2} \phi(0)}{\partial x^{2}}{x}^{2}+\cdots
\end{equation}
\(\phi_{f}\)に原点をとり,上式の3次以上の誤差を無視して次のような2次式として考える
\begin{align}
&\phi(x)=a_{0}+a_{1} x+a_{2}x^{2} \\ \\
&\phi'(x)=a_{1}+2a_{2}x
\end{align}
簡単のため \(\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|=\left|\mathbf{x}_{f}-\mathbf{x}_{_{N}}\right|=\Delta x\) であると仮定し,\(\phi(-\Delta x)=\phi_{_{P}}\),\(\phi(\Delta x)=\phi_{_{N}}\),\(\phi'(-\Delta x)=\phi'_{_{P}}\) という3つの関係式を考えることで \(\phi_{f}=\phi(0)=a_{0}\) を求める
\begin{align}
&\phi_{_P}=a_{0}-a_{1} \Delta x+a_{2}{\Delta x}^{2} \tag{i} \\
&\phi_{_N}=a_{0}+a_{1} \Delta x+a_{2}{\Delta x}^{2} \tag{ii} \\
&\phi'_{_P}=a_{1}-2a_{2}{\Delta x} \tag{iii} \\
\end{align}
(i)+(ii),(ii)-(i),(iii)より
\begin{align}
&a_{0}+a_{2}{\Delta x}^{2}=\frac{\phi_{_P}+\phi_{_N}}{2} \\
&2\Delta xa_{1}=\phi_{_N}-\phi_{_P} \\
&a_{1}-2a_{2}{\Delta x}=\phi'_{_P} \\
\end{align}
よって,
\begin{align}
&a_{0}=\frac{\phi_{_P}+\phi_{_N}}{2}+\frac{\phi'_{_P}}{2}\Delta x-\frac{\phi_{_N}-\phi_{_P}}{4} \\
&a_{1}=\frac{\phi_{_N}-\phi_{_P}}{2\Delta x} \\
&a_{2}=-\frac{\phi'_{_P}}{2\Delta x}+\frac{\phi_{_N}-\phi_{_P}}{(2\Delta x)^2} \\
\end{align}
\(\Delta x=\frac{\mathbf{x}_{_N}-\mathbf{x}_{_P}}{2}\)とすると,\(\mathbf{u}_{f}\cdot\mathbf{S}_{f}>0\) のときのQUICKの式が得られる
\begin{align}
&\phi_{f}=a_{0}=\frac{\phi_{_P}+\phi_{_N}}{2}+\frac{\phi'_{_P}}{2}\frac{\mathbf{x}_{_N}-\mathbf{x}_{_P}}{2}-\frac{\phi_{_N}-\phi_{_P}}{4} \\
\\ \rightarrow \quad
&\phi_{f}=\frac{3}{4}\phi_{_{P}}+\frac{1}{4}\phi_{_{N}}
+\frac{1}{4}\left(\nabla\phi\right)_{P}\cdot\left(\mathbf{x}_{N}-\mathbf{x}_{P}\right)
\end{align}
参考
≫非構造型格子における離散化スキーム (PDFダウンロード)
数値粘性
CFDの計算を行う際はユーザーがどの離散化スキームを使うかを設定する必要があるが,選択の基準として精度次数とならんで重要となるのが数値粘性である
数値粘性とは,対流項の離散化に風上差分を用いた際に生じる非物理的な拡散の増大であり,低次の風上差分のほうが数値粘性は大きい
数値粘性が大きくなることによって解はより鈍るようになるため,計算が難しい複雑な形状などでも安定に計算ができるようになる
一方で,数値粘性を大きくしすぎると,実際の物理現象以上に粘性の影響を過大評価してしまい,最悪の場合まったくのでたらめな解を導き出してしまう
中心差分(CD)による対流項の離散化と風上差分(UD)による対流項の離散化の差をとって比較し,数値粘性について考えてみる
簡単のため \(\left|\mathbf{x}_{f}-\mathbf{x}_{_{P}}\right|=\left|\mathbf{x}_{f}-\mathbf{x}_{_{_N}}\right|\) とすると,風上差分による補間\(\phi_{f_{_{UD}}}\)と中心差分による補間\(\phi_{f_{_{CD}}}\)の関係は次のようになる
\begin{align}
&\phi_{f_{_{CD}}}-\phi_{f_{_{UD}}}
=\frac{\phi_{_{P}}+\phi_{_{N}}}{2}-\phi_{_{P}}
=\frac{\phi_{_{N}}-\phi_{_{P}}}{2} \\
\\ \rightarrow \quad
&\phi_{f_{_{UD}}}
=\phi_{f_{_{CD}}}-\frac{\phi_{_{N}}-\phi_{_{P}}}{2} \\
\end{align}
\(\left|\mathbf{x}_{_N}-\mathbf{x}_{_{P}}\right|=\Delta\)として,移流拡散方程式(ソース項を除いた一般的な輸送方程式)の対流項を風上差分で離散化すると
\begin{align}
&\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
+\sum_{f}{F\phi_{f_{_{UD}}}}
=
\sum_{f}{\Gamma_{f}\left|S_{f}\right|\frac{\phi_{_{N}}-\phi_{_{P}}}{\Delta}}\\
\\ \rightarrow \quad
&\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
+\sum_{f}{F\left(\phi_{f_{_{CD}}}-\frac{\phi_{_{N}}-\phi_{_{P}}}{2}\right)}
=
\sum_{f}{\Gamma_{f}\left|S_{f}\right|\frac{\phi_{_{N}}-\phi_{_{P}}}{\Delta}} \\
\\ \rightarrow \quad
&\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
+\sum_{f}{F\phi_{f_{_{CD}}}}
=
\sum_{f}{\Gamma_{f}\left|S_{f}\right|\frac{\phi_{_{N}}-\phi_{_{P}}}{\Delta}}
+\sum_{f}{F\frac{\phi_{_{N}}-\phi_{_{P}}}{2}} \\
\end{align}
ここで,境界面に対する速度の垂直成分を\(u_{f}>0\)として,質量流束を\(F=\left(\rho\mathbf{u}\right)_{f}\cdot\mathbf{S}_{f}=\rho u_{f}|S_{f}|\)と表すと
\begin{align}
&\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
+\sum_{f}{F\phi_{f_{_{CD}}}}
=
\sum_{f}{\Gamma_{f}\left|S_{f}\right|\frac{\phi_{_{N}}-\phi_{_{P}}}{\Delta}}
+\sum_{f}{\rho u_{f}|S_{f}|\frac{\phi_{_{N}}-\phi_{_{P}}}{2}}\\
\\ \rightarrow \quad
&\frac{\partial}{\partial t}(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
+\sum_{f}{F\phi_{f_{_{CD}}}}
=
\sum_{f}{\left(\Gamma_{f}+\frac{\rho u_{f} \Delta}{2}\right)\left|S_{f}\right|\frac{\phi_{_{N}}-\phi_{_{P}}}{\Delta}} \\
\end{align}
以上より,対流項の離散化に風上差分を用いると,実質的に拡散係数を\(\Gamma_{f}\rightarrow\Gamma_{f}+\frac{\rho u_{f} \Delta}{2}\)と過大評価して計算してしまっていることがわかる
ここで,\(\frac{\rho u_{f} \Delta}{2}\)の項が風上差分の離散化誤差による数値粘性であり,数値粘性の大きさは格子幅\(\Delta\)に比例することがわかる
数値粘性の検証
数値粘性は格子幅に比例して大きくなるので,異なる格子幅の計算格子を用いた計算結果を比較することで,数値粘性の影響が結果に悪影響を与えているかどうかが確認できる
① \(\Gamma_{f}\gg\frac{\rho u_{f} \Delta}{2}\) の場合
物理的な粘性に比較して数値粘性が十分に小さい理想的な状態
計算格子の幅を変えても計算結果が変わらない
② \(\Gamma_{f}\approx\frac{\rho u_{f} \Delta}{2}\) の場合
物理的な粘性に比較して数値粘性が同じくらいある状態
計算格子の幅を変えて数値粘性の大きさを変えると計算結果が変わる
③ \(\Gamma_{f}\ll\frac{\rho u_{f} \Delta}{2}\) の場合
物理的な粘性に比較して数値粘性が大きすぎる状態
計算格子の幅を変えると計算結果が変わるのはもちろん,数値粘性が流れ場を支配しているのでレイノルズ数をいくつにしても結果が変わらない
離散化スキームの選び方
乱流モデルと流れ場に対応したざっくりとした離散化スキームの選び方は以下の通り
- LES:基本的に中心差分しか使えない
- 簡単な流れ場に対するRANS:中心差分を使いたい
- 複雑な流れ場に対するRANS:速度の対流項に2次精度以上の風上差分,乱流諸量(\(k\),\(\varepsilon\))の対流項には1次精度の風上差分を使う
LESでは非定常に乱れた流れ場を取り扱うので,解がなまってしまう風上差分は基本的に使えない
簡単な流れ場とは乱流モデルの検証に使われるようなチャネル流れ,バックステップ流れ,hill flowなどの流れ場であり,自動車や航空機の解析は複雑な流れ場に該当する
数値粘性で特に重要なのが速度の対流項の離散化スキームである
1次精度の風上差分では精度が悪すぎて話にならず,なんとしてでも2次精度以上の風上差分を使う必要がある
計算の安定性に関しては離散化スキームよりも偏微分方程式の不足緩和のほうが影響が大きので,計算が安定しない場合はまず不足緩和係数の見直しを行ったほうがいい
鳥人間コンテストに出場する人力飛行機の解析を行った際に,数値粘性が結果に悪影響を与えた実例を見てみる
上記の解析では,解析領域は以下のように機体後方まで大きく確保した
にもかかわらず,最初に作成した計算格子を用いた解析結果を見てみると翼端から出た渦が機体直後でぶつ切りのように途切れてしまっていた

この解析では,速度の対流項に線形風上差分,乱流諸量の対流項に風上差分を設定しており,機体周辺の格子は次のように作成していた

上の画像を見てみると,機体後方で格子が粗くなるのと同じ位置で翼端渦が途切れてしまっていることがわかる
つまり,このような不自然な解析結果は次のような理由で引き起こされたと考えられる
- 対流項に風上差分を使っている
- 風上差分は数値粘性を伴う
- 数値粘性の大きさは格子幅に比例する
- 機体後方で格子が粗くなって数値粘性が大きくなった
- 粘性の影響で翼端渦が散逸した
その後,機体後方まで十分に計算格子を細かくすると,機体後方まで伸びる翼端渦を計算できるようになった

数値粘性とは対流項に風上差分を用いた際に生じる非物理的な拡散の増大であり,低次の風上差分ほど大きく,格子幅に比例して大きくなる
数値粘性は計算の安定性を向上させるが,過剰な数値粘性は計算精度を悪化させる
数値粘性はできる限り使わないことが好ましいので,不足緩和の大きさを見直したり,格子の解像度を変えた結果を比較したりして数値粘性の影響を抑える必要がある
陰解法
時間項の離散化手法には次のようなスキームがある
オイラー陰解法(Euler implicit)
\begin{equation}
\int_{V}{\frac{\partial}{\partial t}(\rho\phi)}dV
=\frac{(\rho_{_{P}}\phi_{_{P}}V_{_{P}})-(\rho_{_{P}}\phi_{_{P}}V_{_{P}})^{(n-1)}}{\Delta t}
\end{equation}
後退差分(Backward differencing)
\begin{equation}
\int_{V}{\frac{\partial}{\partial t}(\rho\phi)}dV
=\frac{3(\rho_{_{P}}\phi_{_{P}}V_{_{P}})
-4(\rho_{_{P}}\phi_{_{P}}V_{_{P}})^{(n-1)}
+(\rho_{_{P}}\phi_{_{P}}V_{_{P}})^{(n-2)}}{2\Delta t}
\end{equation}
ここで,添え字\(^{(n-1)}\)は1つ前の時間ステップ,\(^{(n-2)}\)は2つ前の時間ステップにおける値を表し,\(\Delta t\)は時間刻み幅である
オイラー陰解法は1次精度,後退差分は2次精度である
陰解法では理論的にどんな大きさの時間刻みでも安定して計算できるが,時間刻みの大きさはクーラン数が1以下になるように設定するのが好ましい
参考
≫クーラン数と流体解析:初心者のための流体解析入門(7)- MONOist
時刻\(t=t_{n}\)において,\(\phi(t_{n})=\phi\) についてテイラー展開を行うと次のようになる
\begin{equation}
\phi^{(n-1)}=\phi(t_{n}-\Delta t)=\phi-\frac{\partial \phi}{\partial t} \Delta t
+\frac{1}{2}\frac{\partial^{2} \phi}{\partial t^{2}}{\Delta t}^{2}
-\frac{1}{6}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{3}+\cdots
\tag{i}
\end{equation}
\begin{equation}
\phi^{(n-2)}=\phi(t_{n}-2\Delta t)=\phi-2\frac{\partial \phi}{\partial t} \Delta t
+2\frac{\partial^{2} \phi}{\partial t^{2}}{\Delta t}^{2}
-\frac{4}{3}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{3}+\cdots
\tag{ii}
\end{equation}
(i)より,オイラー陰解法は次の式で表される
\begin{equation}
\frac{\partial \phi}{\partial t}=\frac{\phi-\phi^{(n-1)}}{\Delta t}
+\frac{1}{2}\frac{\partial^{2} \phi}{\partial t^{2}}{\Delta t}
-\frac{1}{6}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{3}+\cdots
\end{equation}
(i)×4-(ii)より,後退差分は次の式で表される
\begin{align}
&4\phi^{(n-1)}-\phi^{(n-2)}=3\phi-2\frac{\partial \phi}{\partial t} \Delta t
-\frac{2}{3}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{3}+\cdots \\
\\ \rightarrow \quad
&\frac{\partial \phi}{\partial t}=\frac{3\phi-4\phi^{(n-1)}+\phi^{(n-2)}}{2 \Delta t}
-\frac{1}{3}\frac{\partial^{3} \phi}{\partial t^{3}}{\Delta t}^{2}+\cdots \\
\end{align}
まとめ
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(2)に関連して,偏微分方程式を離散化する際の離散化スキームについて説明した
輸送方程式においては,対流項の離散化に細心の注意を払う必要がある
n次精度の離散化スキームの離散化誤差は離散化の刻み幅のn乗に比例する
空間に対する離散化スキームには中心差分と風上差分があり,対流項の離散化に風上差分を用いると数値粘性が発生する
数値粘性は計算の安定性を向上させるが,結果の精度を損なう恐れがある
陰解法はどんな時間刻みに対しても安定ではあるが,クーラン数が1以下になるように時間刻みを設定する
次回は計算格子と境界条件について説明する
↓まとめ記事
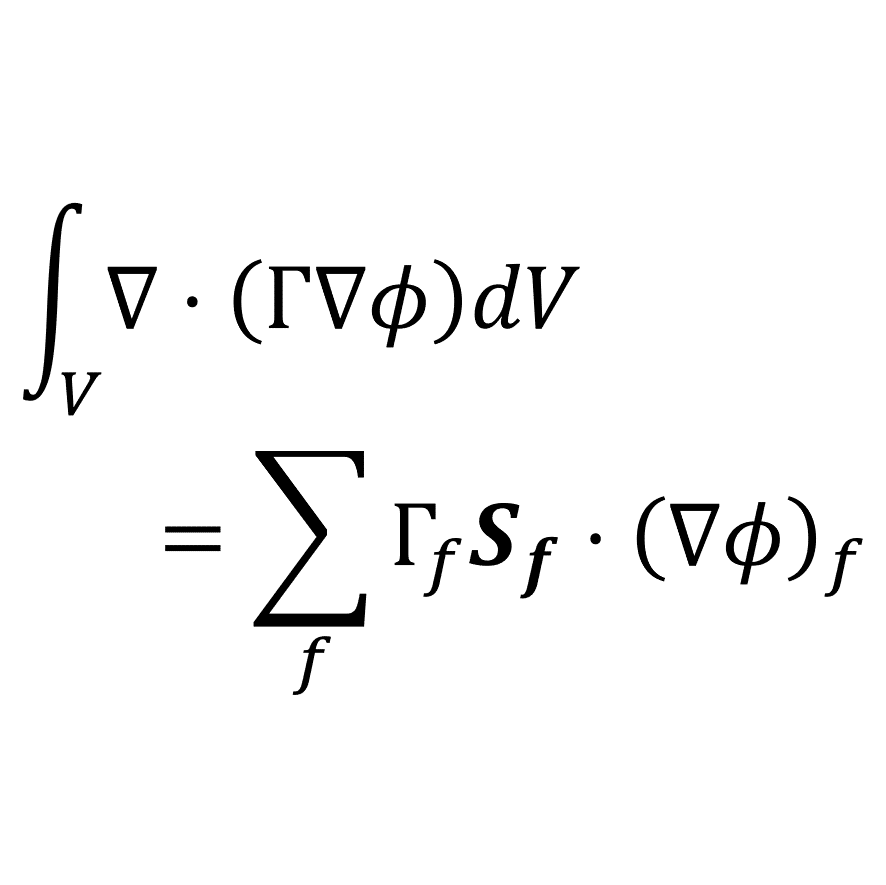

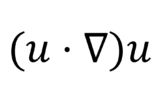

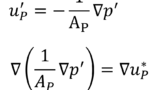


コメント