離散化された速度と圧力の連成解法であるSIMPLE法とPISO法について,研究でCFDを使うことになった大学院生の役に立つような説明を行う
keyword: SIMPLE法,PISO法
はじめに
この記事の内容は以下の前提に基づいている
- 非圧縮性流体の乱流流れ
- 密度\(\rho\),粘性係数\(\mu\)は一定
- 熱移動はなし
- CFDを研究で使う大学院生に必要な知識に重点を置く(ググって得られる知識と専門書の中間くらい)
参考文献はこちら
数値流体力学で必須のテンソル解析についての知識はこちら
流れの数値シミュレーションの概要
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(2)に関連して,離散化された連続の式とNavier-Stokes方程式の主な解法である次の2つの手法を取り上げる
- SIMPLE法:定常計算に使用される.SIMPLE系解法の原点.
- PISO法:SIMPLE法を非定常計算用に派生させたもの
↓前回までの記事はこちらから
↓離散化された支配方程式の代表的な解法であるMAC系解法とSIMPLE系解法についてはこちら
CFDの基礎方程式
密度\(\rho\),粘性係数\(\mu\)が一定な非圧縮性流体の基礎方程式は,連続の式(質量保存式)およびNavier-Stokes方程式(運動量保存式)である
(連続の式)
\begin{equation}
\frac{\partial u_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial u_{i}}{\partial t}+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial P}{\partial x_{i}}+\nu_{_{E}}\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)
+f_{i}
\end{equation}
\begin{equation}
\nu_{_{E}}=\nu+\nu_{t}, \qquad {P}={p}+\frac{2}{3}\rho k
\end{equation}
※モデル化のためのフィルター操作を表すオーバーライン(\(\overline{u}_{i}\),\(\overline{p}\))は省略している
密度\(\rho\)と動粘性係数\(\nu\)は水や空気などの物性値であり,渦粘性係数\(\nu_{t}\)は乱流の影響による拡散を表している
未知数は速度\(\mathbf{u}\)の3つの成分\(u_{i}\),圧力\(p\),渦粘性係数\(\nu_{t}\)の5つであり,渦粘性係数を乱流モデルによって与えれば,連続の式とNavier-Stokes方程式を解くことですべての物理量を求めることができる
また,これ以降は簡単のため \(P \rightarrow p\) と表記することとする
圧力-速度連成
連続の式とNavier-Stokes方程式には次のような問題がある
- 連続の式には時間微分項が含まれておらず,速度場に対して強い制約(発散なし:divergence free)を課しているだけである
- 変数である圧力\(p\)に対する時間微分項\(\frac{\partial p}{\partial t}\)が明示的に示されていない
流れ場の速度と圧力を計算するためには,基礎方程式で明示的に示されていない圧力\(p\)を計算しつつ,連続の式による強い制約を満たすような速度\(u_{i}\)を計算する,というような手法を考える必要がある
ポアソン方程式
そこで,連続の式とNavier-Stokes方程式を用いて圧力\(p\)についての方程式(ポアソン方程式)を導出する
\begin{equation}
\frac{1}{\rho}\nabla^{2}p
=
-\nabla\cdot\nabla\cdot\left(\mathbf{uu}\right)
+\nabla\cdot\mathbf{f}
\end{equation}
Navier-Stokes方程式の両辺に\(\nabla\)を内積する
\begin{align}
&\frac{\partial \mathbf{u}}{\partial t}+\nabla\cdot\left(\mathbf{uu}\right)
=-\frac{\nabla p}{\rho}
+\nu_{_{E}}\Delta\mathbf{u}
+\mathbf{f} \\
\\ \rightarrow \quad
&\frac{\partial \left(\nabla\cdot\mathbf{u}\right)}{\partial t}
+\nabla\cdot\nabla\cdot\left(\mathbf{uu}\right)
=-\frac{\nabla\cdot\nabla p}{\rho}+\nu_{_{E}}\Delta\left(\nabla\cdot\mathbf{u}\right)
+\nabla\cdot\mathbf{f} \\
\end{align}
連続の式 \(\nabla\cdot\mathbf{u}=0\) より
\begin{align}
&\nabla\cdot\nabla\cdot\left(\mathbf{uu}\right)
=-\frac{\nabla^{2} p}{\rho}
+\nabla\cdot\mathbf{f} \\
\\ \rightarrow \quad
&\frac{\nabla^{2} p}{\rho}
=-\nabla\cdot\nabla\cdot\left(\mathbf{uu}\right)
+\nabla\cdot\mathbf{f} \\
\end{align}
ポアソン方程式が連続の式を用いて導出されたということは,ポアソン方程式を解くことによって「連続の式を満たすように計算された圧力\(p\)」を求めることができるということである
そして,「連続の式を満たすように計算された圧力\(p\)」を用いてNavier-Stokes方程式を解けば,必然的に「連続の式を満たす速度\(u_{i}\)」を計算することができる
ポアソン方程式を使うことで,圧力\(p\)の具体的な値を求めつつ,圧力\(p\)を介して連続の式の制約をNaver-Stokesに組み込むことができる
一般に,CFDソルバーで用いられている圧力-速度連成解法はこの考え方に基づいており,
- ポアソン方程式を解いて連続の式を満たす圧力\(p\)を求める
- 1.の圧力\(p\)を用いて速度\(u_{i}\)を求める
という流れで計算を行っている
CFDの基礎方程式は連続の式とNavier-Stokes方程式である
CFDソルバーではポアソン方程式とNavier-Stokes方程式の2つの方程式を解くことで速度と圧力を計算している
離散化された偏微分方程式
コンピュータでCFDの基礎方程式であるNavier-Stokes方程式を解くためには,計算格子上に偏微分方程式を離散化する必要がある
SIMPLE系の解法で用いられる有限体積法によってNavier-Stokes方程式を離散化すると次の式になる
\begin{equation}
\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}
=-\nabla p+\mathbf{s}_{_{P}}
\tag{4.1}
\end{equation}
\(\mathbf{A}\)はセル中心の速度\(\mathbf{u}\)が他のセルに及ぼす影響を表し,\(\mathbf{s}\)は圧力項以外のソース項である
添え字\(_{{P}}\)は注目しているセル\(P\)を表し,添え字\(_{nb}\)はセル\(P\)に影響を及ぼす全ての隣接セル(neighbours)を表している
(4.1)より,\(\mathbf{u}_{_{P}}\)は次のようになる
\begin{equation}
\mathbf{u}_{_{P}}
=
\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}}{\bf{A}_{_{P}}}
-\frac{1}{\bf{A}_{_{P}}}\nabla p
\tag{4.2}
\end{equation}
これを連続の式 \(\nabla\cdot\mathbf{u}_{_{P}}=0\) に代入すると,離散化されたポアソン方程式が得られる
\begin{equation}
\nabla\cdot\left(\frac{1}{\bf{A}_{_{P}}}\nabla p\right)
=
\nabla\cdot\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}}{\bf{A}_{_{P}}}\right)
\tag{4.3}
\end{equation}
離散化されたNavier-Stokes方程式とポアソン方程式を解くことで,セル中心で定義された速度場と圧力場を求めることができる
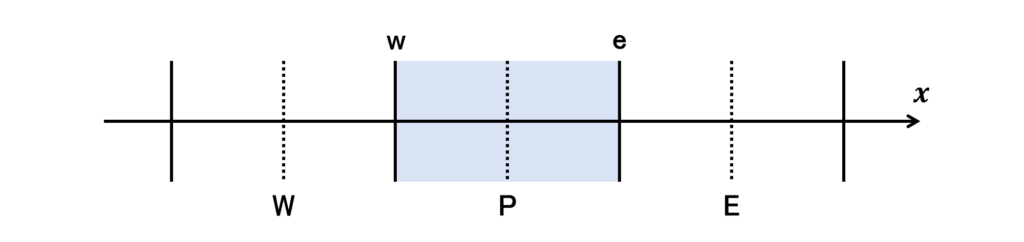
簡単のため,次の図のような1次元流れの有限体積法による離散化を考える
\(P\)が注目セル,\(W\)と\(E\)は隣接セル(West,East),\(w\)と\(e\)は注目セルと隣接セルの境界面である
一般に,物理量\(\phi\)の輸送方程式は時間項,対流項,粘性項,ソース項(生成項+散逸項)から構成され,次のようにあらわされる
\begin{equation}
\frac{\partial}{\partial t}(\rho\phi)
+\frac{\partial}{\partial x}(\rho u\phi)
-\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)
=
S
\tag{i}
\end{equation}
ここで,
- \(\phi=u\),\(\Gamma=\mu+\mu_{t}\),\(S=-\frac{\partial p}{\partial x}\)とすればNavier-Stokes方程式
- \(\phi=k\),\(\Gamma=\mu+\frac{\mu_{t}}{\sigma_{k}}\),\(S=P_{k}-\varepsilon\)とすれば標準k-εモデルの\(k\)の輸送方程式,
- \(\phi=\varepsilon\),\(\Gamma=\mu+\frac{\mu_{t}}{\sigma_{\varepsilon}}\),\(S=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}\)とすれば標準k-εモデルの\(\varepsilon\)の輸送方程式
である
有限体積法は保存則をセルの境界からの流入/流出およびセル内部での発生/消滅によって表すので,(i)をセル\(P\)について積分する
\begin{equation}
\int{\frac{\partial}{\partial t}(\rho\phi)}dx
+\int{\frac{\partial}{\partial x}(\rho u\phi)}dx
-\int{\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)}dx
=
\int{S}dx
\tag{ii}
\end{equation}
(ii)の各項について離散化を行う
時間項
陰解法である後退オイラー法を用いて次のように離散化する
\begin{align}
\int{\frac{\partial}{\partial t}(\rho\phi)}dx
&\simeq \frac{(\rho\phi)_{P}-(\rho\phi)_{P}^{(n-1)}}{\Delta t}\Delta x \\
&=\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}-\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)}
\end{align}
ただし,上付き添え字\(^{(n-1)}\)は1つ前の時間ステップを表している
対流項
2次精度中心差分と2次精度中心補間を用いて次のように離散化する
\begin{align}
\int{\frac{\partial}{\partial x}(\rho u\phi)}dx &\simeq \frac{(\rho u \phi)_{e}-(\rho u \phi)_{w}}{\Delta x}\Delta x =(\rho u)_{e} \phi_{e}-(\rho u)_{w} \phi_{w} \\
&=c_{e}\phi_{e}-c_{w}\phi_{w} =c_{e}\frac{\phi_{_{E}}+\phi_{{_P}}}{2}-c_{w}\frac{\phi_{{_P}}+\phi_{_{W}}}{2} \\ \\
\rightarrow \quad \int{\frac{\partial}{\partial x}(\rho u\phi)}dx &=\left(\frac{1}{2}c_{e}-\frac{1}{2}c_{w}\right)\phi_{_{P}}-\frac{1}{2}c_{w}\phi_{_{W}}+\frac{1}{2}c_{e}\phi_{_{E}}
\end{align}
\begin{align}
c_{e}=(\rho u)_{e}=\rho\frac{u_{_{E}}+u_{_{P}}}{2}, \quad
c_{w}=(\rho u)_{w}=\rho\frac{u_{_{P}}+u_{_{W}}}{2}
\end{align}
拡散項
2次精度中心差分を用いて次のように離散化する
\begin{align}
\int{\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)}dx
&\simeq \frac{\left(\Gamma\frac{\partial \phi}{\partial x}\right)_{e}-\left(\Gamma\frac{\partial \phi}{\partial x}\right)_{w}}{\Delta x}\Delta x
=\left(\Gamma\frac{\partial \phi}{\partial x}\right)_{e}-\left(\Gamma\frac{\partial \phi}{\partial x}\right)_{w} \\
&=\frac{\Gamma\left(\phi_{_{E}}-\phi_{_{P}}\right)}{\Delta x}-\frac{\Gamma\left(\phi_{_{P}}-\phi_{_{W}}\right)}{\Delta x} \\
&=\left(\frac{\Gamma}{\Delta x}\right)_{e}\left(\phi_{_{E}}-\phi_{_{P}}\right)
-\left(\frac{\Gamma}{\Delta x}\right)_{w}\left(\phi_{_{P}}-\phi_{_{W}}\right)\\ \\
&=d_{e}\left(\phi_{_{E}}-\phi_{_{P}}\right)-d_{w}\left(\phi_{_{P}}-\phi_{_{W}}\right)\\ \\
\rightarrow \quad
\int{\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)}dx
&=\left(-d_{e}-d_{w}\right)\phi_{_{P}}+d_{w}\phi_{_{W}}+d_{e}\phi_{_{E}}
\end{align}
\begin{align}
d_{e}=\left(\frac{\Gamma}{\Delta x}\right)_{e}, \quad
d_{w}=\left(\frac{\Gamma}{\Delta x}\right)_{w}
\end{align}
ソース項
\begin{align}
\int{S}dx
&\simeq S\Delta x
\end{align}
すべての項を(ii)に代入すると
\begin{align}
&\int{\frac{\partial}{\partial t}(\rho\phi)}dx
+\int{\frac{\partial}{\partial x}(\rho u\phi)}dx
-\int{\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)}dx
=
\int{S}dx \\ \\
\rightarrow \quad
&\left\{\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}-\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)}\right\}
+\left\{\left(\frac{1}{2}c_{e}-\frac{1}{2}c_{w}\right)\phi_{_{P}}-\frac{1}{2}c_{w}\phi_{_{W}}+\frac{1}{2}c_{e}\phi_{_{E}}\right\} \\ \\
&\quad -\left\{\left(-d_{e}-d_{w}\right)\phi_{_{P}}+d_{w}\phi_{_{W}}+d_{e}\phi_{_{E}}\right\}
=
S\Delta x \\ \\
\rightarrow \quad
& \left(\frac{\rho\Delta x}{\Delta t}+\frac{1}{2}c_{e}-\frac{1}{2}c_{w}+d_{e}+d_{w}\right)\phi_{_{P}}
+\left(-\frac{1}{2}c_{w}-d_{w}\right)\phi_{_{W}}
+\left(\frac{1}{2}c_{e}-d_{e}\right)\phi_{_{E}} \\ \\
&\quad =
S\Delta x
+\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)}
\end{align}
まとめると次のようになる
\begin{align}
&a_{_{P}}\phi_{_{P}}+a_{_{W}}\phi_{_{W}}+a_{_{E}}\phi_{_{E}} = b \\
\\ \rightarrow \quad
&a_{_{P}}\phi_{_{P}}+\sum{a_{nb}\phi_{nb}} = b
\end{align}
ただし,それぞれの係数は以下の通り
\begin{align}
&a_{_{P}}=-a_{_{W}}-a_{_{E}}+c_{e}-c_{w}+\frac{\rho\Delta x}{\Delta t} \qquad&
&c_{e}=(\rho u)_{e}=\rho\frac{u_{_{E}}+u_{_{P}}}{2} \\
&a_{_{W}}=-\frac{1}{2}c_{w}-d_{w} &
&c_{w}=(\rho u)_{w}=\rho\frac{u_{_{P}}+u_{_{W}}}{2}\\
&a_{_{E}}=\frac{1}{2}c_{e}-d_{e} &
&d_{e}=\left(\frac{\Gamma}{\Delta x}\right)_{e} \\
&b=S\Delta x+\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)} &
&d_{w}=\left(\frac{\Gamma}{\Delta x}\right)_{w}\\
\end{align}
最初に述べたように,\(\phi=u\),\(\Gamma=\mu+\mu_{t}\),\(S=-\frac{\partial p}{\partial x}\),\(s_{_{P}}=\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)}\)とすれば,離散化されたNavier-Stokes方程式が得られる
\begin{equation}
a_{_{P}}u_{_{P}}+\sum{a_{nb}u_{nb}}
=-\frac{\partial p}{\partial x}+s_{_{P}}
\end{equation}
今回はオイラー後退法と2次精度中心差分を用いたが,それ以外の離散化スキームを用いても同様の式を導出できる
SIMPLE法
SIMPLE(Semi-Implicit Method for Pressure-Liked Equation)法は時間発展に陰解法を使っているので,反復計算を行いながら速度と圧力を少しずつ真の解に近づけていく必要がある
そこで,ある時刻\(t_{n}\)における速度 \(\mathbf{u}^{(n)}\) と圧力 \(p^{(n)}\) を,それぞれの推定値(\(\mathbf{u}^{*}\),\(p^{*}\))と修正量(\(\mathbf{u'}\),\(p'\))に分解する
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{u}^{*}+\mathbf{u'} \\
&p^{(n)}=p^{*}+p'
\tag{5.1}
\end{align}
「対象の流れ場が定常流れである」と仮定すれば,十分に時間進行を行うとやがて修正量は0になり(\(\mathbf{u}'=p'=0\)),推定値は真の解に収束すると考えられる(\(\mathbf{u}=\mathbf{u}^{*}\),\(p=p^{*}\))
基本形
速度の推定値 \(\mathbf{u}^{*}\) は次の式であらわされる
\begin{equation}
\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{*}
+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}^{*}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}+\frac{1-\alpha_{u}}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{(n-1)}
\tag{5.2}
\end{equation}
圧力の修正量\(p'\)および速度の修正量\(u'\)は次の式で表される
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}_{_{P}}^{*}
\tag{5.3} \\ \\
&\mathbf{u'}=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
\tag{5.4}
\end{align}
時刻\(t_{n}\)における速度と圧力は次の式で表される
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{u}^{*}+\mathbf{u'} \\
&p^{(n)}=p^{(n-1)}+\alpha_{p}p'
\tag{5.5}
\end{align}
\(\alpha_{u}\)と\(\alpha_{p}\)は不足緩和係数であり,計算を安定させて収束を早めるはたらきをしている
以上の式を用いて,SIMPLE法では次に示す①~⑥の手順を収束するまで繰り返すことによって真の速度場と圧力を計算する
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める (5.2)
③ 速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から圧力の修正量\(p'\)を求める (5.3)
④ 圧力の修正量\(p'\)から速度の修正量\(u'\)を求める (5.4)
⑤ 時刻\(t_{n}\)における速度 \(\mathbf{u}^{(n)}\) と圧力 \(p^{(n)}\) を計算する (5.5)
⑥ 時刻を\(t_{n+1}\)に進めて,①に戻る
不足緩和係数は,通常 \(\alpha_{u}=0.3 \sim 0.8\),\(\alpha_{p}=0.3 \sim 0.8\) の値をとり,試行錯誤的に決定される
係数を小さくすると計算は安定するが収束が遅くなるので,まずは小さい値から初めて,計算が安定するぎりぎりまで大きくしていくとよい
ちなみに,定常流れでは時間刻みの大きさは特に考慮しなくていいので,便宜的に\(\Delta t = 1\)とする
(5.3)について十分に時間進行を行って解が収束すれば,\(p'=0\) かつ \(\mathbf{u}^{*}_{_{P}}=\mathbf{u}_{_{P}}\) なので
\begin{equation}
\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}_{_{P}}^{*}
\quad\rightarrow\quad
\nabla\cdot\mathbf{u}_{_{P}}=0
\end{equation}
となり,\(\mathbf{u}_{_{P}}\) は連続の式を満たすようになる
離散化されたNavier-Stokes方程式と連続の式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\) と \(p=p^{*}+p'\)を代入することで,SIMPLE法に必要な式を導出する
(連続の式)
\begin{equation}
\nabla\cdot\mathbf{u}_{_{P}}=0
\end{equation}
(離散化されたNavier-Stokes方程式)
\begin{equation}
\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}
=-\nabla p+\mathbf{s}_{_{P}}
\end{equation}
基本式
まず,離散化されたNavier-Stokes方程式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\) と \(p=p^{*}+p'\)を代入すると次のようになる
\begin{align}
&\mathbf{A}_{_{P}}\left(\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\right)
+\sum{\mathbf{A}_{nb}\left(\mathbf{u}^{*}_{nb}+\mathbf{u'}_{nb}\right)}
=-\nabla \left(p^{*}+p'\right)+\mathbf{s}_{_{P}} \\
\\ \rightarrow \quad
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{*}+\mathbf{s}_{_{P}}
-\left(\mathbf{A}_{_{P}}\mathbf{u'}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}
+\nabla p'
\right)
\tag{i}
\end{align}
十分に時間進行を行うと,(i)の右辺第3項は0になるので
\begin{align}
&\mathbf{A}_{_{P}}\mathbf{u'}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}
+\nabla p' =0 \\
\\ \rightarrow \quad
&\mathbf{u'}_{_{P}}
=
-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
\tag{ii}
\end{align}
よって,(i)は次のようになる
\begin{equation}
\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{*}+\mathbf{s}_{_{P}}
\tag{iii}
\end{equation}
次に,連続の式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\) を代入する
\begin{align}
\nabla\cdot\mathbf{u}^{*}_{_{P}}+\nabla\cdot\mathbf{u'}_{_{P}}=0
\end{align}
(ii)を代入すると
\begin{align}
&\nabla\cdot\mathbf{u}^{*}_{_{P}}+\nabla\cdot\left(-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)=0 \\
\\ \rightarrow \quad
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
-\nabla\cdot\left(\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}\right)
\tag{iv}
\end{align}
(ii)と(iv)より,速度と圧力の修正量に関する連立方程式が得られた
\begin{align}
&\mathbf{u'}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}} \\ \\
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
-\nabla\cdot\left(\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}\right)
\end{align}
上式は\(\mathbf{u'}\)と\(p'\)についての完全陰解法であり,\(\mathbf{u'}\)と\(p'\)を求めるには大規模な連立一次方程式を解く必要があるため,多大な計算コストがかかってしまう
そこで,「\(\mathbf{u'}\)と\(p'\)は解が収束したらどうせ0になるのだから,それまでの過程で多少不正確な値であっても解の信頼性には関係ない」という考え方に基づき,\(\mathbf{u'}_{nb}\)に関する項を無視することにする
\begin{align}
&\mathbf{u'}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
\tag{5.4}\\ \\
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
\tag{5.3}
\end{align}
さらに,(iii)における\(p^{*}\)については1つ前のステップにおける圧力\(p^{(n-1)}\)を用いることにすれば
\begin{align}
&p^{(n)}=p^{(n-1)}+p'
\tag{5.5'} \\ \\
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}
\tag{5.2'}
\end{align}
これにより,\(\mathbf{u}^{*}_{_{P}}\) → \(p'\) → \(\mathbf{u'}_{_{P}}\) → \(p^{(n)}(=p^{*})\) → \(\mathbf{u}^{(n)}_{_{P}}\) という順番で求めれば,すべての変数を計算することができるようになった
本来は完全陰解法で求めるはずの\(\mathbf{u'}_{_{P}}\)と\(p'\)を,\(\mathbf{u'}_{nb}\)に関する項を無視することで陽的に求めるという手法が,SIMPLE法が Semi-Implict Method(半陰解法)と呼ばれる所以である
不足緩和
SIMPLE法では,速度と圧力の修正量として\(\mathbf{u'}_{nb}\)に関する項を無視した不正確な値を使用していることが原因で,時間進行の序盤(修正量が大きいとき)に計算が発散しやすくなってしまう
上記の計算の発散を抑制するため,速度と圧力の更新の際に次のような緩和係数を導入する(これを不足緩和という)
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{u}^{n-1}_{_{P}}+\alpha_{u}\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}}{\mathbf{A}_{_{P}}}-\mathbf{u}^{(n-1)}_{_{P}}\right)
\tag{v} \\ \\
&p^{(n)}=p^{(n-1)}+\alpha_{p}p'
\tag{5.5} \\ \\
\end{align}
圧力に対する不足緩和は修正量\(p'\)を小さくするように陽的に行われているが,速度に対する不足緩和は推定値\(\mathbf{u}^{*}_{_{P}}\)の変化を小さくする形で陰的に導入されている
(v)を整理すると,(5.2)が得られる
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{u}^{n-1}_{_{P}}+\alpha_{u}\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}}{\mathbf{A}_{_{P}}}-\mathbf{u}^{(n-1)}_{_{P}}\right) \\
\\ \rightarrow \quad
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
=\mathbf{A}_{_{P}}\mathbf{u}^{n-1}_{_{P}}
+\alpha_{u}\left(\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}-\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}}\right) \\
\\ \rightarrow \quad
&\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
=\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{n-1}_{_{P}}
+\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}
-\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}} \\
\\ \rightarrow \quad
&\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{(n-1)}
+\mathbf{s}_{_{P}}
+\frac{1-\alpha_{u}}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}}
\tag{5.2}
\end{align}
参考
≫非圧縮性流体計算の圧力-速度連成手法 (PDF)
修正量を用いないSIMPLE法
SIMPLE法は,修正量(\(\mathbf{u}'\),\(p'\))を用いない形に書き直すことができる
時刻 \(t_{n}\) における速度の推定値は,先ほどと同様に次の式で求められる
\begin{equation}
\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{*}
+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}^{*}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}+\frac{1-\alpha_{u}}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{(n-1)}
\tag{6.1}
\end{equation}
ここで,\(\mathbf{\tilde{u}}^{*}_{_{P}}\)を次のように定義する
\begin{equation}
\mathbf{\tilde{u}}^{*}_{_{P}}
=\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}^{*}}}{\mathbf{A}_{_{P}}}
\tag{6.2}
\end{equation}
時刻\(t_{n}\)における圧力\(p^{(n)}\)と速度\(\mathbf{u}^{(n)}\)は次のように求められる
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}\right)
=\nabla\cdot\mathbf{\tilde{u}}^{*}_{_{P}}
\tag{6.3} \\ \\
&\mathbf{u}^{(n)}_{_{P}}=\mathbf{\tilde{u}}^{*}_{_{P}}-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}
\tag{6.4}
\end{align}
以上の式を用いて,修正量を用いないSIMPLE法では次に示す①~⑥の手順を収束するまで繰り返すことによって真の速度場と圧力を計算する
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める (6.1)
③ 速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から\(\mathbf{\tilde{u}}^{*}_{_{P}}\)を求める (6.2)
④ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)から時刻\(t_{n}\)における圧力\(p^{(n)}\)を求める (6.3)
⑤ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)と圧力\(p^{(n)}\)から時刻\(t_{n}\)における速度\(\mathbf{u}^{(n)}\)を求める (6.4)
⑥ 時刻を\(t_{n+1}\)に進めて,①に戻る
ちなみに,(6.3)と(6.4)より
\begin{equation}
\nabla\cdot\left(\mathbf{\tilde{u}}^{*}_{_{P}}-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}\right)
=\nabla\cdot\mathbf{u}^{(n)}_{_{P}}=0
\end{equation}
となり,\(\mathbf{u}^{(n)}_{_{P}}\) は連続の式を満たしている
先述したSIMPLE法の導出より,次の関係がわかっている
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{u}^{*}+\mathbf{u'} \tag{i} \\
&p^{(n)}=p^{(n-1)}+p' \tag{ii} \\ \\
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}
\tag{iii} \\ \\
&\mathbf{u'}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
\tag{iv} \\
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
\tag{v}
\end{align}
これらの式を用いて,修正量(\(\mathbf{u'}\),\(p'\))を用いないSIMPLE法を導出する
基本形
(iii)を次のように変形する
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n-1)}
\tag{vi} \\ \\
&\mathbf{\tilde{u}}^{*}_{_{P}}
=\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}}{\mathbf{A}_{_{P}}}
\tag{6.2} \\ \\
\end{align}
(v)に(vi)を代入し,\(p^{(n)}=p^{(n-1)}+p'\) を適用する
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\left(\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n-1)}\right)\\
\\ \rightarrow \quad
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n-1)}+\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{\tilde{u}}^{*}_{_{P}} \\
\\ \rightarrow \quad
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}\right)
=\nabla\cdot\mathbf{\tilde{u}}^{*}_{_{P}}
\tag{6.3} \\
\end{align}
同様に,\(\mathbf{u}^{(n)}=\mathbf{u}^{*}+\mathbf{u'}\) に(vi)と(iv)を代入し,\(p^{(n)}=p^{(n-1)}+p'\) を適用する
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n-1)}
+\left(-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)\\
\\ \rightarrow \quad
&\mathbf{u}^{(n)}=\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\left(\nabla p^{(n-1)}
+\nabla p'\right)\\
\\ \rightarrow \quad
&\mathbf{u}^{(n)}=\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}
\tag{6.4} \\
\end{align}
これにより,\(\mathbf{u}^{*}_{_{P}}\) → \(\mathbf{\tilde{u}}^{*}_{_{P}}\) → \(p^{(n)}\) → \(\mathbf{u}^{(n)}_{_{P}}\)という順番で求めれば,すべての変数を計算することができるようになった
不足緩和
修正量を用いないSIMPLE法では,速度と圧力の不足緩和を次のように行う
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{u}^{n-1}_{_{P}}+\alpha_{u}\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}}{\mathbf{A}_{_{P}}}-\mathbf{u}^{(n-1)}_{_{P}}\right)
\tag{v} \\ \\
&p^{(n)}=p^{(n-1)}+\alpha_{p}\left(p^{(n)}-p^{(n-1)}\right)
\tag{5.5} \\ \\
\end{align}
圧力に対する不足緩和の方法が若干変更されている
参考
≫非圧縮性流体計算の圧力-速度連成手法 (PDF)
SIMPLE法は,「対象の流れ場が定常流れであること」を仮定し,速度と圧力をそれぞれ推定値と修正量に分けて計算を行う
定常流れの計算なので,便宜的に\(\Delta t=1\) として時間発展を計算する
不足緩和の係数を設定することで,計算の安定性と収束の速さを調整する
PISO法
PISO(Pressure Implicit with Splitting Operators)法は,非定常計算が行えるようにSIMPLE法を拡張した手法である
SIMPLE法の導出において,速度と圧力の修正量を求める際に\(\mathbf{u'}_{nb}\)の項を無視したが,それが原因でSIMPLE法では収束までの時々刻々における速度と圧力の値は不正確なものになっている
上記の問題を解決するために,PISO法では速度と圧力の推定値と修正量の計算を複数回(通常は2回)行うことで,時々刻々における速度と圧力の精度を確保して非定常流れの計算を可能にしている
基本形
PISO法では次に示す①~⑦の手順を繰り返すことによって非定常な速度場と圧力場を計算している
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める (6.1)
③ 速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から\(\mathbf{\tilde{u}}^{*}_{_{P}}\)を求める (6.2)
④ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)から時刻\(t_{n}\)における圧力\(p^{(n)}\)を求める (6.3)
⑤ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)と圧力\(p^{(n)}\)から時刻\(t_{n}\)における速度\(\mathbf{u}^{(n)}\)を求める (6.4)
⑥ ⑤で得られた\(\mathbf{u}^{(n)}_{_{P}}\)を\(\mathbf{u}^{*}_{_{P}}\)として,③に戻る
⑦ ③~⑥を複数回(通常は2回)繰り返したら,時刻を\(t_{n+1}\)に進めて,①に戻る
SIMPLE法と同様に,(6.3)と(6.4)より\(\mathbf{u}^{(n)}_{_{P}}\) は連続の式を満たしていることがわかる
\(\alpha_{u}\)は計算を安定させて収束を早めるはたらきを持つ不足緩和係数であり,通常は \(\alpha_{u}=0.3 \sim 0.8\) の値で試行錯誤的に決定される
PISO法では圧力に対する不足緩和は必要ないとされている
ある時刻\(t_{n}\)における速度 \(\mathbf{u}^{(n)}\) と圧力 \(p^{(n)}\) の精度を高めるために,速度と圧力の修正を1次修正量(\(\mathbf{u'}\),\(p'\))と2次修正量(\(\mathbf{u^{\prime\prime}}\),\(p^{\prime\prime}\))の2回にわけて行い,1次推定値と1次修正量の和を2次推定値(\(\mathbf{u}^{**}\),\(p^{**}\))として定義する
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{u}^{*}+\left(\mathbf{u'}+\mathbf{u^{\prime\prime}}\right), \qquad &
&p^{(n)}=p^{*}+\left(p'+p^{\prime\prime}\right) \\
&\mathbf{u}^{**}=\mathbf{u}^{*}+\mathbf{u'}, \qquad &
&p^{**}=p^{*}+p' \tag{i}\\
\\ \rightarrow \quad
&\mathbf{u}^{(n)}=\mathbf{u}^{**}+\mathbf{u^{\prime\prime}}, \qquad &
&p^{(n)}=p^{**}+p^{\prime\prime} \tag{ii}\\
\end{align}
これら2つの修正量を用いて各時刻の速度と圧力を計算する手法がPISO法である
基本形
まず,離散化されたNavier-Stokes方程式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}+\mathbf{u'}+\mathbf{u^{\prime\prime}}\) と \(p=p^{*}+p'+p^{\prime\prime}\)を代入すると次のようになる
\begin{align}
\mathbf{A}_{_{P}}\left(\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}+\mathbf{u^{\prime\prime}}_{_{P}}\right)
+\sum{\mathbf{A}_{nb}\left(\mathbf{u}^{*}_{nb}+\mathbf{u'}_{nb}+\mathbf{u^{\prime\prime}}_{nb}\right)}
=-\nabla \left(p^{*}+p'+p^{\prime\prime}\right)+\mathbf{s}_{_{P}}
\end{align}
これを次の2つの段階に分けて考える
\begin{align}
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{*}+\mathbf{s}_{_{P}}
-\left(\mathbf{A}_{_{P}}\mathbf{u'}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}
+\nabla p'
\right) \\ \\
&\mathbf{A}_{_{P}}\mathbf{u}^{**}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{**}_{nb}}
=-\nabla p^{**}+\mathbf{s}_{_{P}}
-\left(\mathbf{A}_{_{P}}\mathbf{u^{\prime\prime}}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u^{\prime\prime}}_{nb}}
+\nabla p^{\prime\prime}
\right) \\ \\
\end{align}
各時刻において真の解と推定値が一致するためには,上式の右辺第3項は0にならなければならないので
\begin{align}
&\mathbf{u'}_{_{P}}
=-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p' \tag{A} \\ \\
&\mathbf{u^{\prime\prime}}_{_{P}}
= -\frac{\sum{\mathbf{A}_{nb}\mathbf{u^{\prime\prime}}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime} \\ \\
\end{align}
\begin{align}
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{*}+\mathbf{s}_{_{P}} \tag{iii} \\ \\
&\mathbf{A}_{_{P}}\mathbf{u}^{**}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{**}_{nb}}
=-\nabla p^{**}+\mathbf{s}_{_{P}}
\end{align}
次に,連続の式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\) と \(\mathbf{u}_{_{P}}=\mathbf{u}^{**}_{_{P}}+\mathbf{u^{\prime\prime}}_{_{P}}\) をそれぞれ代入し,SIMPLE法と同様に\(\mathbf{u}_{nb}\)に関する項を無視すると次のようになる
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}} \tag{iv} \\
&\mathbf{u'}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p' \tag{v} \\ \\
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime}\right)
=\nabla\cdot\mathbf{u}^{**}_{_{P}} \tag{vi} \\
&\mathbf{u^{\prime\prime}}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime} \tag{vii} \\ \\
\end{align}
上記の考えに基づいて,PISO法では次に示す①~⑨の手順を繰り返すことによって非定常な速度場と圧力場を計算している
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② (iii)より,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の1次推定値 \(\mathbf{u}^{*}\) を求める
③ (iv)より,速度の1次推定値\(\mathbf{u}_{_{P}}^{*}\)から圧力の1次修正量\(p'\)を求める
④ (v)より,圧力の1次修正量\(p'\)から速度の1次修正量\(u'\)を求める
⑤ (i)より,速度の2次推定値\(\mathbf{u}^{**}\) と圧力の2次推定値 \(p^{**}\) を計算する
⑥ (vi)より,速度の2次推定値\(\mathbf{u}_{_{P}}^{**}\)から圧力の2次修正量\(p^{\prime\prime}\)を求める
⑦ (vii)より,圧力の2次修正量\(p^{\prime\prime}\)から速度の2次修正量\(u^{\prime\prime}\)を求める
⑧ (ii)より,時刻\(t_{n}\)における速度\(\mathbf{u}\) と圧力 \(p\) を計算する
⑨ 時刻を\(t_{n+1}\)に進めて,①に戻る
2回の修正は何を意味しているのか
速度の1次推定値\(\mathbf{u}_{_{P}}^{*}\)は離散化された偏微分方程式を解くことで求めているが,速度の2次推定値は1次推定値と1次修正量の和 \(\mathbf{u}_{_{P}}^{**}=\mathbf{u}_{_{P}}^{*}+\mathbf{u'}_{_{P}}\) で求めている
手順⑥の(vi)に \(\mathbf{u}_{_{P}}^{**}=\mathbf{u}_{_{P}}^{*}+\mathbf{u'}_{_{P}}\)を代入すると
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime}\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}+\nabla\cdot\mathbf{u'}_{_{P}}
\end{align}
(A)より\(\mathbf{u'}_{_{P}}\)を代入すると次のようになる
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime}\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
+\nabla\cdot\left(-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)\\
\\ \rightarrow \quad
&\nabla\cdot\left\{\frac{1}{\mathbf{A}_{_{P}}}\nabla \left(p'+p^{\prime\prime}\right)\right\}
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
-\nabla\cdot\left(\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}\right) \\
\end{align}
同様に,\(\mathbf{u'}+\mathbf{u^{\prime\prime}}\)に(A)と(vii)を代入すると次のようになる
\begin{align}
&\mathbf{u'}+\mathbf{u^{\prime\prime}}
=-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime} \\
\\ \rightarrow \quad
&\mathbf{u'}+\mathbf{u^{\prime\prime}}
=-\frac{1}{\mathbf{A}_{_{P}}}\left(\nabla p'+\nabla p^{\prime\prime}\right)
-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}} \\
\end{align}
上式から,PISO法では速度と圧力の修正を行う2回行うことで,速度と圧力の合計修正量に速度の1次修正量\(\mathbf{u'}_{nb}\)の項を考慮していることが分かる
依然として速度の2次修正量による\(\mathbf{u^{\prime\prime}}_{nb}\)の項は無視しているが,速度の修正量による項を完全に無視していたSIMPLE法と比べると,時々刻々における速度と圧力の精度は向上している
PISO法の簡略化
基本形の手順をよく見てみると,③~⑤と⑥~⑧は変数の見た目が違うだけで,全く同じ計算をしていることがわかる
全く同じ計算をしているならプログラムにおいてメモリを使いまわすことができるし,メモリを使いまわすことができるなら修正回数を2回に限定する必要はない
よって,上記に示したPISO法の計算手順は次のように簡略化できる
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② (iii)より,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める
③ (iv)より,速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から圧力の修正量\(p'\)を求める
④ (v)より,圧力の修正量\(p'\)から速度の修正量\(u'\)を求める
⑤ (i)より,速度\(\mathbf{u}^{(n)}\) と圧力 \(p^{(n)}\) を計算し,\(\mathbf{u}^{*}=\mathbf{u}^{(n)}\)として③に戻る
⑦ ③~⑥を複数回(通常は2回)繰り返したら,時刻を\(t_{n+1}\)に進めて,①に戻る
修正量を用いないPISO法
PISO法もSIMPLE法と同様に修正量を用いない形に書き換えることができ,修正量を用いない簡略化したPISO法が1番最初に示した手順である
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める (6.1)
③ 速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から\(\mathbf{\tilde{u}}^{*}_{_{P}}\)を求める (6.2)
④ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)から時刻\(t_{n}\)における圧力\(p^{(n)}\)を求める (6.3)
⑤ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)と圧力\(p^{(n)}\)から時刻\(t_{n}\)における速度\(\mathbf{u}^{(n)}\)を求める (6.4)
⑥ ⑤で得られた\(\mathbf{u}^{(n)}_{_{P}}\)を\(\mathbf{u}^{*}_{_{P}}\)として,③に戻る
⑦ ③~⑥を複数回(通常は2回)繰り返したら,時刻を\(t_{n+1}\)に進めて,①に戻る
不足緩和
PISO法では,速度に対する不足緩和はSIMPLE法と同様に行うが,圧力に対する不足緩和は必要ないとされている
参考
≫非圧縮性流体計算の圧力-速度連成手法 (PDF)
PISO法は,SIMPLE法において速度と圧力の修正を2回行うことで非定常計算を扱えるよう改良した手法である
非定常流れの計算なので,クーラン数に応じて時間刻みを設定する
圧力の不足緩和は必要ないとされている
まとめ
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(2)に関連して,離散化された連続の式とNavier-Stokes方程式の主な解法としてSIMPLE法とPISO法を取り上げた
次回は偏微分方程式を離散化するために必要な離散化スキームについて説明する
↓まとめ記事
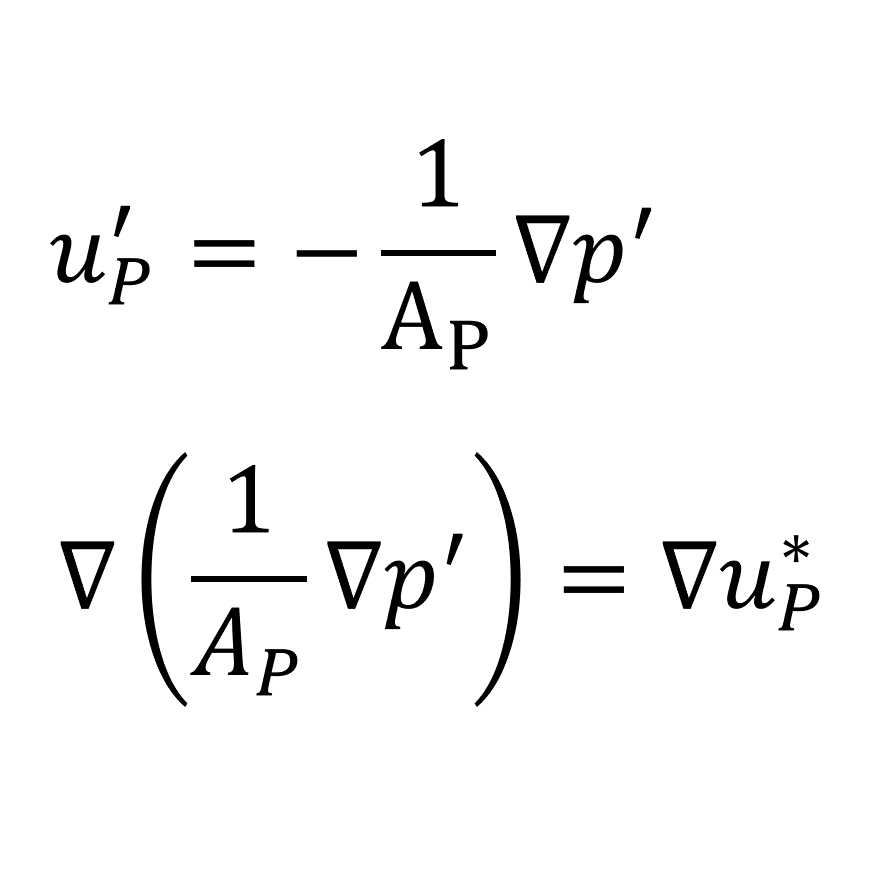


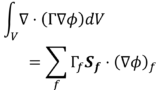
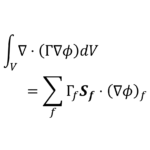
コメント