MAC法とSIMPLE法の違いについて

離散化された速度と圧力の連成解法として代表的なMAC系解法とSIMPLE系解法についての違いを説明する

keyword: SIMPLE法，MAC法，陽解法，陰解法，有限差分法，有限体積法，構造格子，非構造格子，スタガード格子，コロケート格子

MAC系とSIMPLE系
陽解法と陰解法
有限差分法と有限体積法
構造格子と非構造格子
スタガード格子とコロケート格子
まとめ

MAC系とSIMPLE系

CFDに実装されている圧力-速度連成ソルバーは，MAC系とSIMPLE系の2つの系統の解法に分けられる

それぞれの特徴は以下の通り

	MAC系	SIMPLE系
時間発展法	陽解法	陰解法
離散化手法	有限差分法	有限体積法
格子の種類	構造格子	非構造格子
変数の配置	スタガード格子コロケート格子	コロケート格子

商用ソルバーでは複雑な形状に対応できるよう非構造格子を用いることが多いので，SIMPLE系の解法を採用している

陽解法と陰解法

運動方程式の時間項を離散化する際に，未知の時刻\(t^{n+1}\)における速度場\(u^{n+1}\)が既知の時刻（\(t^{n},\,t^{n-1},\,\cdots\)）の情報のみで与えられる解法を陽解法（explicit method），未知の時刻\(t^{n+1}\)の情報も使う解法を陰解法（implicit method）という

陽解法はシンプルで計算時間が短縮できる一方で，計算を安定に進めるためには時間刻み\(\delta t\)を十分に小さくする必要がある

陰解法は時間と空間を連立した大規模な連立方程式を解く必要があるため計算時間が多くかかるが，時間刻み\(\delta t\)を大きくとっても計算を安定に進めることができる

代表的な手法は以下の通り

陽解法

オイラー陽解法（1次精度）

\begin{equation}
\frac{u^{n+1}-u^{n}}{\delta t}=f^{n}
\end{equation}

Adams-Bashforth法（2次精度）

\begin{equation}
\frac{u^{n+1}-u^{n}}{\delta t}=\frac{3}{2}f^{n}-\frac{1}{2}f^{n-1}
\end{equation}

陰解法

オイラー陰解法（1次精度）

\begin{equation}
\frac{u^{n+1}-u^{n}}{\delta t}=f^{n+1}
\end{equation}

Crank-Nicolson法（2次精度）

\begin{equation}
\frac{u^{n+1}-u^{n}}{\delta t}=\frac{1}{2}f^{n+1}+\frac{1}{2}f^{n}
\end{equation}

有限差分法と有限体積法

基礎方程式を流れ場で記述するためには，空間に格子を配置し，偏微分方程式を離散化する必要がある

離散化手法にはいくつかの種類があるが，その中でも有限差分法と有限体積法について説明する

それぞれの特徴は以下の通り

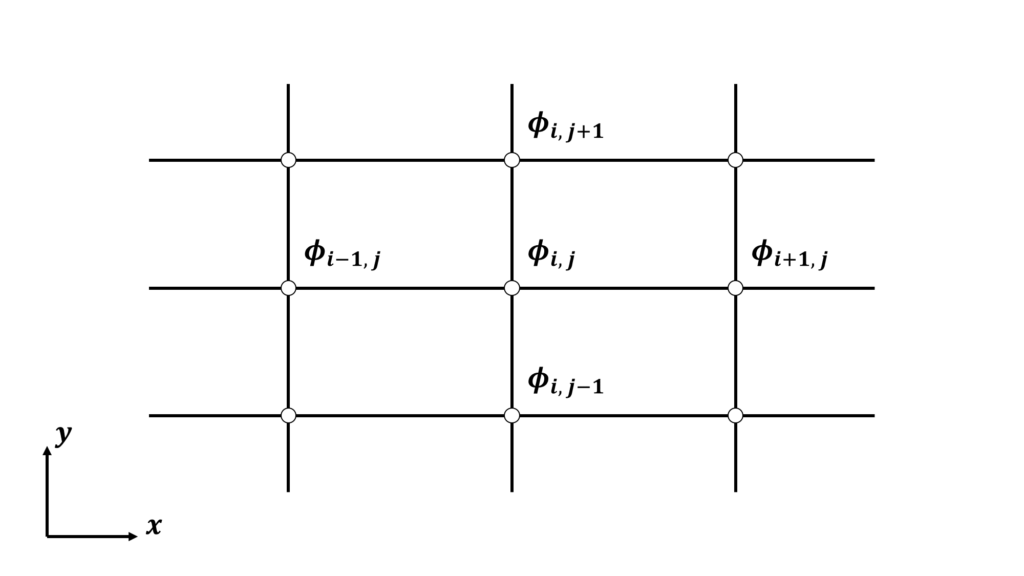
有限差分法（Finiete Difference Method：FDM）

微分型の流れの方程式を基礎とする
格子点上での解を求める（点と点との間は考えない）
基礎方程式の中の微係数（速度勾配や圧力勾配）は差分近似によって表される
構造格子を使用する

有限体積法（Finite Volume Method：FVM）

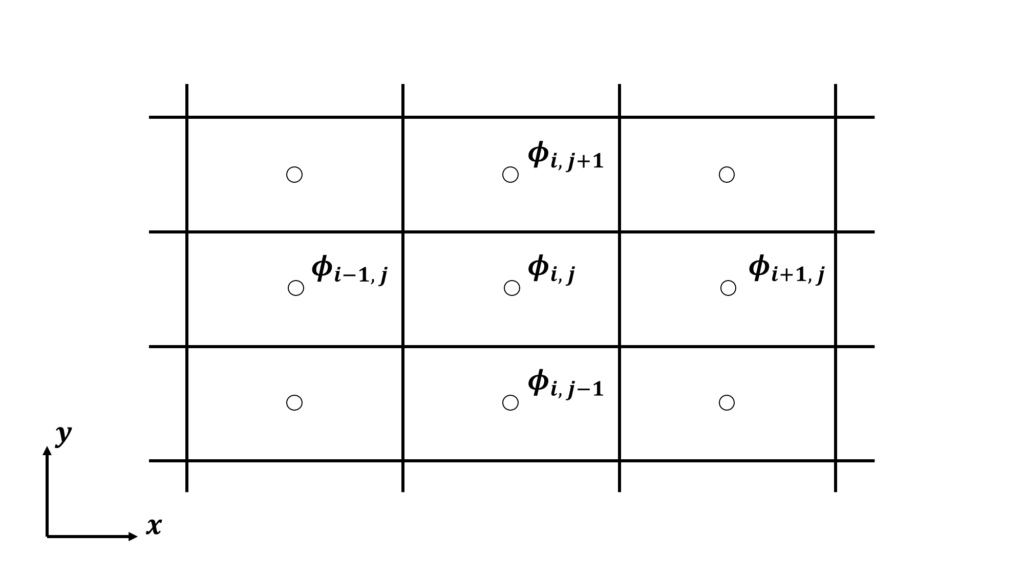
積分型の流れの方程式を基礎とする
検査体積（セル）の代表値を求める
保存則はセルの境界からの流入/流出およびセル内部での発生/消滅によって表される
構造格子でも非構造格子でも使用できる

構造格子に適している有限差分法は高い精度と計算効率が必要で単純な形状を扱うことが多い基礎研究などで利用される

非構造格子にも対応している有限体積法は複雑な形状を扱う必要のある実務の現場などで用いられる

構造格子と非構造格子

空間上に配置する格子の種類は，構造格子と非構造格子の2種類に大別される

それぞれの特徴は以下の通り

構造格子

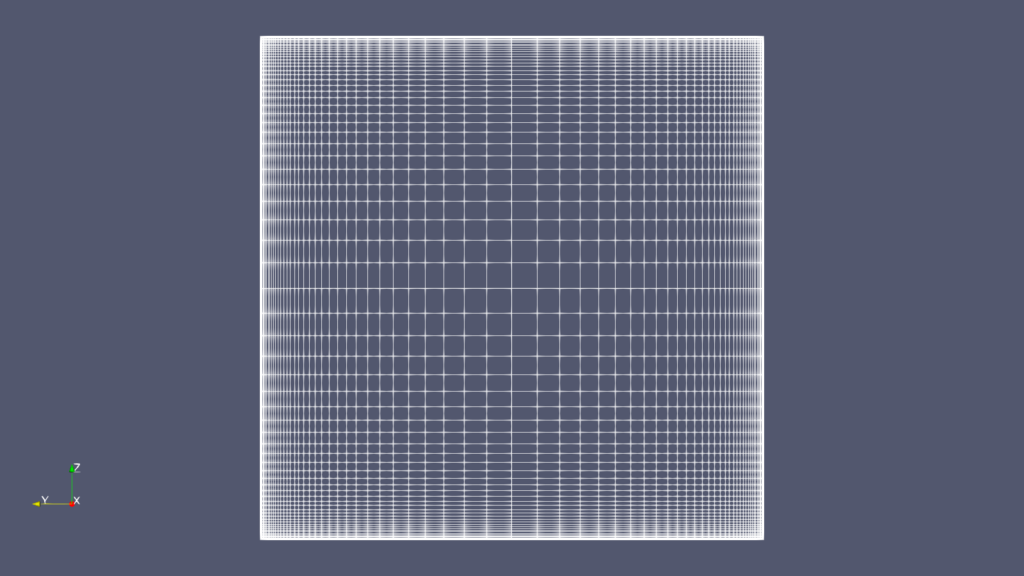
格子は直交性がよく滑らかになるよう整然と配置する
セルの形状は直方体のみ（曲線に対しては座標変換を施して一般座標で計算）
簡単な形状しか扱えない
メモリ効率がよく，高速で計算できる
高次精度の離散化スキームを利用可能
壁面近傍の流れの計算に向いている

非構造格子

格子は物体形状に合わせて不規則に配置
セルの形状は4面体，5面体，6面体などの任意多面体に対応可能
任意の複雑な形状を扱える
任意の場所の格子解像度を変更できる
基本的に2次精度までの離散化スキームしか扱えない

上記の特徴から，構造格子は高い精度と計算効率が必要で単純な形状を扱うことが多い基礎研究などで用いられ，非構造格子は複雑な形状を扱う必要のある実務の現場などで用いられる

また，非構造格子を用いるときでも，壁面近傍は構造格子で計算し，それ以外の領域を非構造格子で計算するハイブリッド格子にすることがある

スタガード格子とコロケート格子

変数の配置には，レギュラー格子，スタガード格子，コロケート格子の3種類がある

レギュラー格子

速度と圧力を同じ点に配置する
チェス盤状に圧力が分布してしまうチェッカーボード不安定とよばれる圧力振動が発生する
数値的に不安定なので使用されることはない

スタガード格子

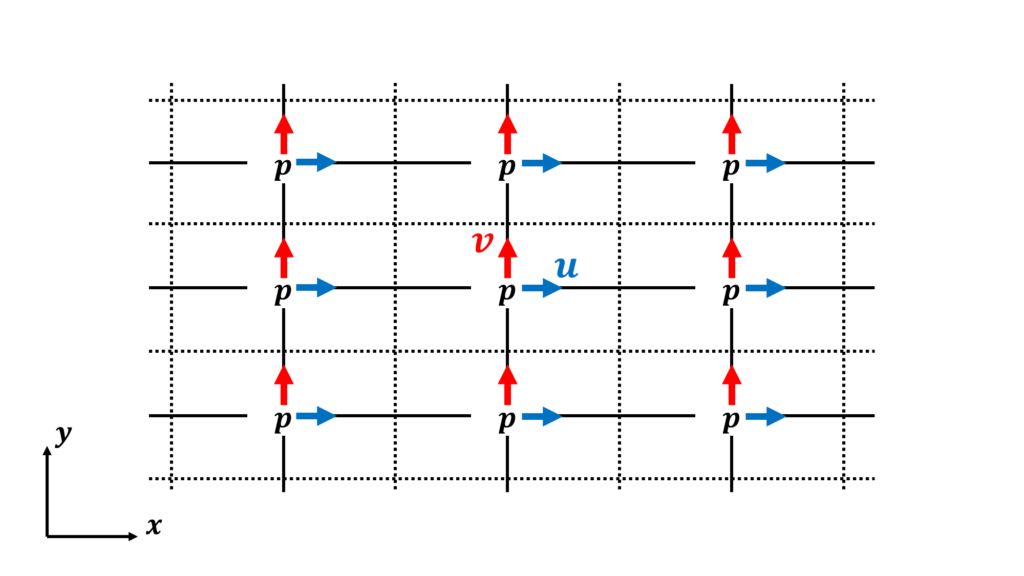
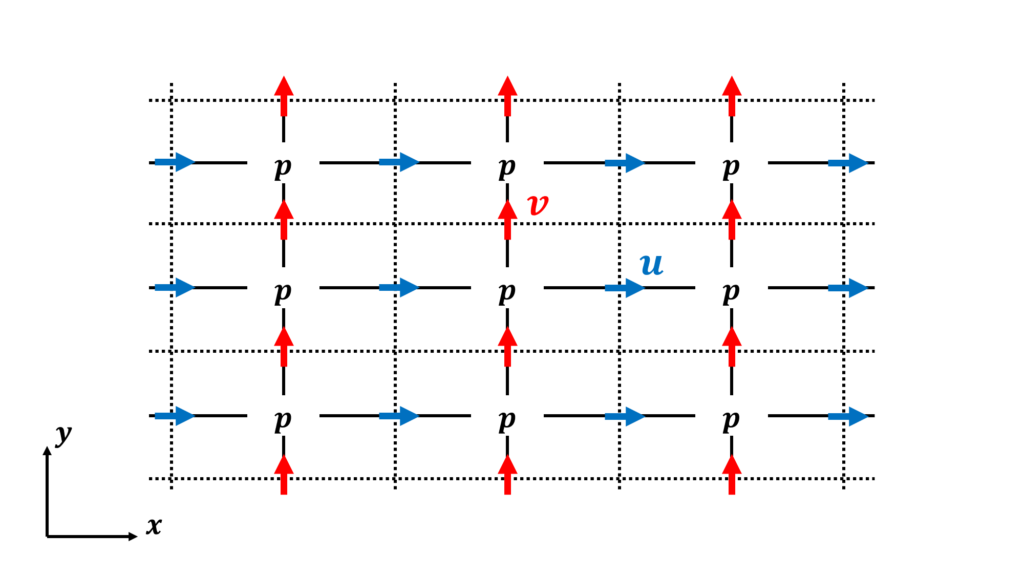
速度と圧力をずらして配置する
チェス盤状に圧力が分布しても圧力差によって速度がきちんと変化し，チェッカーボード不安定に陥ることはない
ずらして配置した速度成分のインデックスや形状の記憶，値の補間をする必要があるというプログラム上の煩雑さがある
計算格子が各速度成分と同じ方向に与えられている一部の構造格子にしか利用できない

コロケート格子

速度と圧力を同じ点に配置し，Rhie-Chow補間を用いてチェッカーボード不安定を抑制する
非構造格子を使う多くの商用ソルバーに用いられている

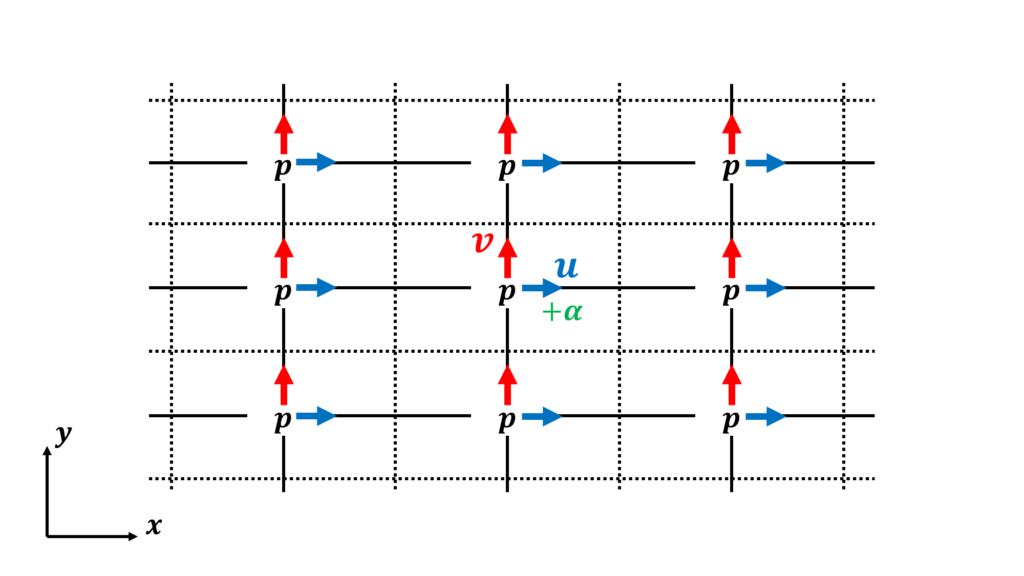
基本的に構造格子でも非構造格子でもコロケート格子を用いるが，計算格子が各速度成分と同じ方向に与えられている構造格子ではスタガード格子も利用できる

まとめ

CFDに実装されている圧力-速度連成ソルバーとして代表的なMAC系とSIMPLE系の2つの系統の解法の違いについて説明した

	MAC系	SIMPLE系
時間発展法	陽解法	陰解法
離散化手法	有限差分法	有限体積法
格子の種類	構造格子	非構造格子
変数の配置	スタガード格子コロケート格子	コロケート格子