流れの基礎方程式である連続の式とNavier-Stokes方程式を有限体積法によって離散化する方法について説明する
keyword: 偏微分方程式の離散化,有限体積法,移流拡散方程式
CFDの基礎方程式
密度\(\rho\),粘性係数\(\mu\)が一定な非圧縮性流体の基礎方程式は,連続の式(質量保存式)およびNavier-Stokes方程式(運動量保存式)である
(連続の式)
\begin{equation}
\frac{\partial u_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial u_{i}}{\partial t}+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial P}{\partial x_{i}}+\nu_{_{E}}\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)
+f_{i}
\end{equation}
\begin{equation}
\nu_{_{E}}=\nu+\nu_{t}, \qquad {P}={p}+\frac{2}{3}\rho k
\end{equation}
※モデル化のためのフィルター操作を表すオーバーライン(\(\overline{u}_{i}\),\(\overline{p}\))は省略している
密度\(\rho\)と動粘性係数\(\nu\)は水や空気などの物性値であり,渦粘性係数\(\nu_{t}\)は乱流の影響による拡散を表している
未知数は速度\(\mathbf{u}\)の3つの成分\(u_{i}\),圧力\(p\),渦粘性係数\(\nu_{t}\)の5つであり,渦粘性係数を乱流モデルによって与えれば,連続の式とNavier-Stokes方程式を解くことですべての物理量を求めることができる
また,これ以降は簡単のため \(P \rightarrow p\) と表記することとする
格子の種類と離散化手法
基礎方程式を流れ場で記述するためには,空間に格子を配置し,偏微分方程式を離散化する必要がある
構造格子と非構造格子
空間上に配置する格子の種類は,構造格子と非構造格子の2種類に大別される
それぞれの特徴は以下の通り
- 格子は直交性がよく滑らかになるよう整然と配置する
- セルの形状は直方体のみ(曲線に対しては座標変換を施して一般座標で計算)
- 簡単な形状しか扱えない
- メモリ効率がよく,高速で計算できる
- 高次精度の離散化スキームを利用可能
- 壁面近傍の流れの計算に向いている
- 格子は物体形状に合わせて不規則に配置
- セルの形状は4面体,5面体,6面体などの任意多面体に対応可能
- 任意の複雑な形状を扱える
- 任意の場所の格子解像度を変更できる
- 基本的に2次精度までの離散化スキームしか扱えない

上記の特徴から,構造格子は高い精度と計算効率が必要で単純な形状を扱うことが多い基礎研究などで用いられ,非構造格子は複雑な形状を扱う必要のある実務の現場などで用いられる
また,非構造格子を用いるときでも,壁面近傍は構造格子で計算し,それ以外の領域を非構造格子で計算するハイブリッド格子にすることがある
有限体積法
離散化手法にはいくつかの種類があるが,そのうちの1つである有限体積法は次のような特徴を持つ
- 積分型の流れの方程式を基礎とする
- 検査体積(セル)の代表値を求める
- 保存則はセルの境界からの流入/流出およびセル内部での発生/消滅によって表される
- 構造格子でも非構造格子でも使用できる
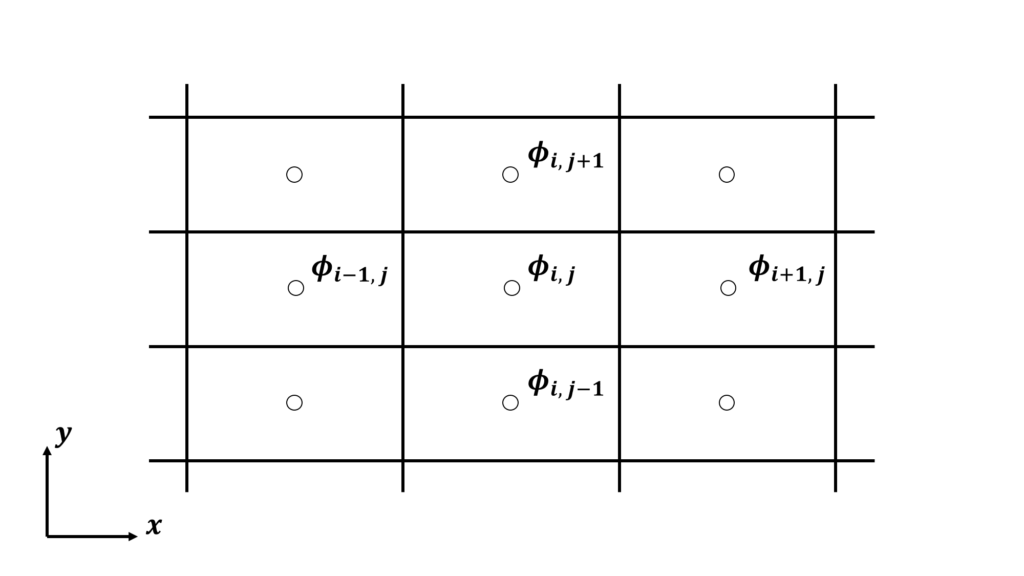
非構造格子にも対応している有限体積法は複雑な形状を扱う必要のある実務の現場などで用いられる
離散化された偏微分方程式
有限体積法によってNavier-Stokes方程式を離散化すると次の式になる
\begin{equation}
\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}
=-\nabla p+\mathbf{s}_{_{P}}
\tag{4.1}
\end{equation}
\(\mathbf{A}\)はセル中心の速度\(\mathbf{u}\)が他のセルに及ぼす影響を表し,\(\mathbf{s}\)は圧力項以外のソース項である
添え字\(_{{P}}\)は注目しているセル\(P\)を表し,添え字\(_{nb}\)はセル\(P\)に影響を及ぼす全ての隣接セル(neighbours)を表している
(4.1)より,\(\mathbf{u}_{_{P}}\)は次のようになる
\begin{equation}
\mathbf{u}_{_{P}}
=
\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}}{\bf{A}_{_{P}}}
-\frac{1}{\bf{A}_{_{P}}}\nabla p
\tag{4.2}
\end{equation}
これを連続の式 \(\nabla\cdot\mathbf{u}_{_{P}}=0\) に代入すると,離散化されたポアソン方程式が得られる
\begin{equation}
\nabla\cdot\left(\frac{1}{\bf{A}_{_{P}}}\nabla p\right)
=
\nabla\cdot\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}}{\bf{A}_{_{P}}}\right)
\tag{4.3}
\end{equation}
離散化されたNavier-Stokes方程式とポアソン方程式を解くことで,セル中心で定義された速度場と圧力場を求めることができる
導出
簡単のため,次の図のような1次元流れの有限体積法による離散化を考える
\(P\)が注目セル,\(W\)と\(E\)は隣接セル(West,East),\(w\)と\(e\)は注目セルと隣接セルの境界面である
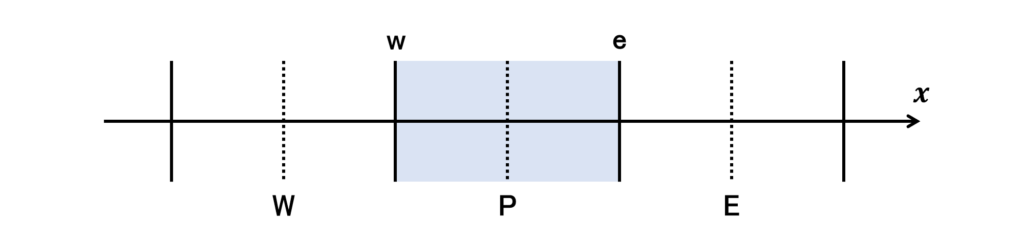
一般に,物理量\(\phi\)の輸送方程式は時間項,対流項,粘性項,ソース項(生成項+散逸項)から構成され,次のようにあらわされる
\begin{equation}
\frac{\partial}{\partial t}(\rho\phi)
+\frac{\partial}{\partial x}(\rho u\phi)
-\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)
=
S
\tag{i}
\end{equation}
ここで,
- \(\phi=u\),\(\Gamma=\mu+\mu_{t}\),\(S=-\frac{\partial p}{\partial x}\)とすればNavier-Stokes方程式
- \(\phi=k\),\(\Gamma=\mu+\frac{\mu_{t}}{\sigma_{k}}\),\(S=P_{k}-\varepsilon\)とすれば標準k-εモデルの\(k\)の輸送方程式,
- \(\phi=\varepsilon\),\(\Gamma=\mu+\frac{\mu_{t}}{\sigma_{\varepsilon}}\),\(S=\left(C_{\varepsilon_{1}}P_{k}-C_{\varepsilon_{2}}\varepsilon\right)\frac{\varepsilon}{k}\)とすれば標準k-εモデルの\(\varepsilon\)の輸送方程式
である
有限体積法は保存則をセルの境界からの流入/流出およびセル内部での発生/消滅によって表すので,(i)をセル\(P\)について積分する
\begin{equation}
\int{\frac{\partial}{\partial t}(\rho\phi)}dx
+\int{\frac{\partial}{\partial x}(\rho u\phi)}dx
-\int{\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)}dx
=
\int{S}dx
\tag{ii}
\end{equation}
(ii)の各項について離散化を行う
時間項
陰解法である後退オイラー法を用いて次のように離散化する
\begin{align}
\int{\frac{\partial}{\partial t}(\rho\phi)}dx
&\simeq \frac{(\rho\phi)_{P}-(\rho\phi)_{P}^{(n-1)}}{\Delta t}\Delta x \\
&=\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}-\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)}
\end{align}
ただし,上付き添え字\(^{(n-1)}\)は1つ前の時間ステップを表している
対流項
2次精度中心差分と2次精度中心補間を用いて次のように離散化する
\begin{align}
\int{\frac{\partial}{\partial x}(\rho u\phi)}dx &\simeq \frac{(\rho u \phi)_{e}-(\rho u \phi)_{w}}{\Delta x}\Delta x =(\rho u)_{e} \phi_{e}-(\rho u)_{w} \phi_{w} \\
&=c_{e}\phi_{e}-c_{w}\phi_{w} =c_{e}\frac{\phi_{_{E}}+\phi_{{_P}}}{2}-c_{w}\frac{\phi_{{_P}}+\phi_{_{W}}}{2} \\ \\
\rightarrow \quad \int{\frac{\partial}{\partial x}(\rho u\phi)}dx &=\left(\frac{1}{2}c_{e}-\frac{1}{2}c_{w}\right)\phi_{_{P}}-\frac{1}{2}c_{w}\phi_{_{W}}+\frac{1}{2}c_{e}\phi_{_{E}}
\end{align}
\begin{align}
c_{e}=(\rho u)_{e}=\rho\frac{u_{_{E}}+u_{_{P}}}{2}, \quad
c_{w}=(\rho u)_{w}=\rho\frac{u_{_{P}}+u_{_{W}}}{2}
\end{align}
拡散項
2次精度中心差分を用いて次のように離散化する
\begin{align}
\int{\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)}dx
&\simeq \frac{\left(\Gamma\frac{\partial \phi}{\partial x}\right)_{e}-\left(\Gamma\frac{\partial \phi}{\partial x}\right)_{w}}{\Delta x}\Delta x
=\left(\Gamma\frac{\partial \phi}{\partial x}\right)_{e}-\left(\Gamma\frac{\partial \phi}{\partial x}\right)_{w} \\
&=\frac{\Gamma\left(\phi_{_{E}}-\phi_{_{P}}\right)}{\Delta x}-\frac{\Gamma\left(\phi_{_{P}}-\phi_{_{W}}\right)}{\Delta x} \\
&=\left(\frac{\Gamma}{\Delta x}\right)_{e}\left(\phi_{_{E}}-\phi_{_{P}}\right)
-\left(\frac{\Gamma}{\Delta x}\right)_{w}\left(\phi_{_{P}}-\phi_{_{W}}\right)\\ \\
&=d_{e}\left(\phi_{_{E}}-\phi_{_{P}}\right)-d_{w}\left(\phi_{_{P}}-\phi_{_{W}}\right)\\ \\
\rightarrow \quad
\int{\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)}dx
&=\left(-d_{e}-d_{w}\right)\phi_{_{P}}+d_{w}\phi_{_{W}}+d_{e}\phi_{_{E}}
\end{align}
\begin{align}
d_{e}=\left(\frac{\Gamma}{\Delta x}\right)_{e}, \quad
d_{w}=\left(\frac{\Gamma}{\Delta x}\right)_{w}
\end{align}
ソース項
\begin{align}
\int{S}dx
&\simeq S\Delta x
\end{align}
すべての項を(ii)に代入すると
\begin{align}
&\int{\frac{\partial}{\partial t}(\rho\phi)}dx
+\int{\frac{\partial}{\partial x}(\rho u\phi)}dx
-\int{\frac{\partial}{\partial x}\left(\Gamma\frac{\partial \phi}{\partial x}\right)}dx
=
\int{S}dx \\ \\
\rightarrow \quad
&\left\{\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}-\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)}\right\}
+\left\{\left(\frac{1}{2}c_{e}-\frac{1}{2}c_{w}\right)\phi_{_{P}}-\frac{1}{2}c_{w}\phi_{_{W}}+\frac{1}{2}c_{e}\phi_{_{E}}\right\} \\ \\
&\quad -\left\{\left(-d_{e}-d_{w}\right)\phi_{_{P}}+d_{w}\phi_{_{W}}+d_{e}\phi_{_{E}}\right\}
=
S\Delta x \\ \\
\rightarrow \quad
& \left(\frac{\rho\Delta x}{\Delta t}+\frac{1}{2}c_{e}-\frac{1}{2}c_{w}+d_{e}+d_{w}\right)\phi_{_{P}}
+\left(-\frac{1}{2}c_{w}-d_{w}\right)\phi_{_{W}}
+\left(\frac{1}{2}c_{e}-d_{e}\right)\phi_{_{E}} \\ \\
&\quad =
S\Delta x
+\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)}
\end{align}
まとめると次のようになる
\begin{align}
&a_{_{P}}\phi_{_{P}}+a_{W}\phi_{_{W}}+a_{_{E}}\phi_{_{E}} = b \\
\\ \rightarrow \quad
&a_{_{P}}\phi_{_{P}}+\sum{a_{nb}\phi_{nb}} = b
\end{align}
ただし,それぞれの係数は以下の通り
\begin{align}
&a_{_{P}}=-a_{_{W}}-a_{_{E}}+c_{e}-c_{w}+\frac{\rho\Delta x}{\Delta t} \qquad&
&c_{e}=(\rho u)_{e}=\rho\frac{u_{_{E}}+u_{_{P}}}{2} \\
&a_{_{W}}=-\frac{1}{2}c_{w}-d_{w} &
&c_{w}=(\rho u)_{w}=\rho\frac{u_{_{P}}+u_{_{W}}}{2}\\
&a_{_{E}}=\frac{1}{2}c_{e}-d_{e} &
&d_{e}=\left(\frac{\Gamma}{\Delta x}\right)_{e} \\
&b=S\Delta x+\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)} &
&d_{w}=\left(\frac{\Gamma}{\Delta x}\right)_{w}\\
\end{align}
最初に述べたように,\(\phi=u\),\(\Gamma=\mu+\mu_{t}\),\(S=-\frac{\partial p}{\partial x}\),\(s_{_{P}}=\frac{\rho\Delta x}{\Delta t}\phi_{_{P}}^{(n-1)}\)とすれば,離散化されたNavier-Stokes方程式が得られる
\begin{equation}
a_{_{P}}u_{_{P}}+\sum{a_{nb}u_{nb}}
=-\frac{\partial p}{\partial x}+s_{_{P}}
\end{equation}
まとめ
流れの基礎方程式である連続の式とNavier-Stokes方程式を有限体積法によって離散化する方法について説明した
今回はオイラー後退法と2次精度中心差分を用いたが,それ以外の離散化スキームを用いても同様の式を導出できる
↓より一般的な説明はこちら
↓おすすめ記事
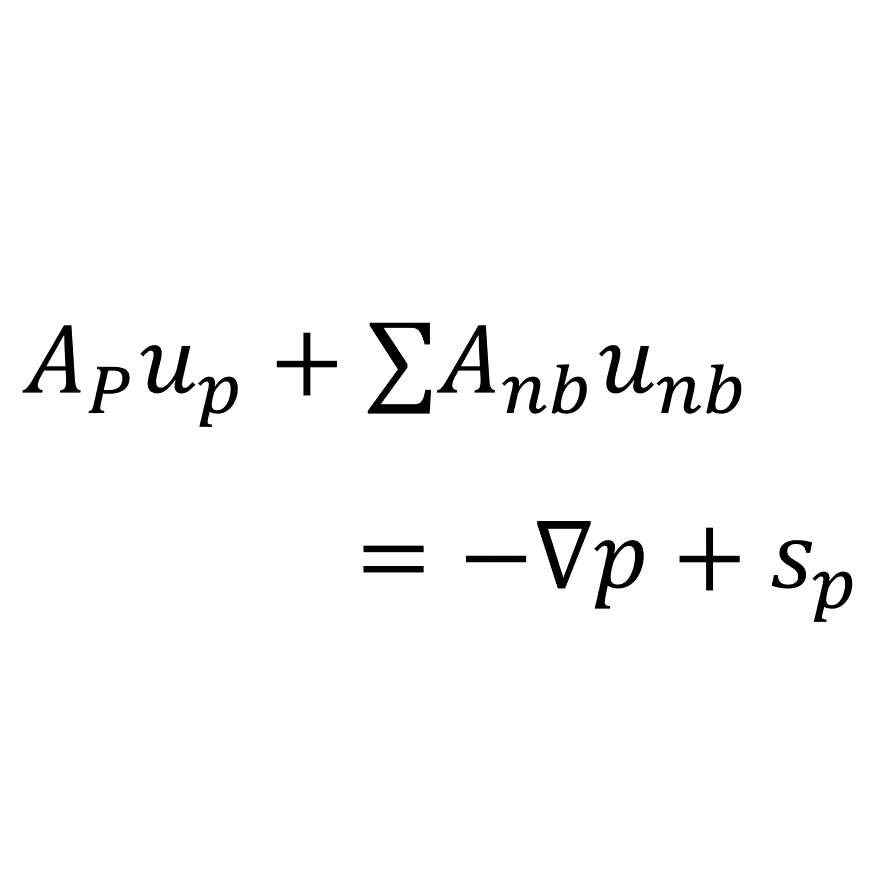



コメント