離散化された速度と圧力の連成解法であるSIMPLE法について説明する
keyword: SIMPLE法
CFDの基礎方程式
密度\(\rho\),粘性係数\(\mu\)が一定な非圧縮性流体の基礎方程式は,連続の式(質量保存式)およびNavier-Stokes方程式(運動量保存式)である
(連続の式)
\begin{equation}
\frac{\partial u_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial u_{i}}{\partial t}+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial P}{\partial x_{i}}+\nu_{_{E}}\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)
+f_{i}
\end{equation}
\begin{equation}
\nu_{_{E}}=\nu+\nu_{t}, \qquad {P}={p}+\frac{2}{3}\rho k
\end{equation}
※モデル化のためのフィルター操作を表すオーバーライン(\(\overline{u}_{i}\),\(\overline{p}\))は省略している
密度\(\rho\)と動粘性係数\(\nu\)は水や空気などの物性値であり,渦粘性係数\(\nu_{t}\)は乱流の影響による拡散を表している
未知数は速度\(\mathbf{u}\)の3つの成分\(u_{i}\),圧力\(p\),渦粘性係数\(\nu_{t}\)の5つであり,渦粘性係数を乱流モデルによって与えれば,連続の式とNavier-Stokes方程式を解くことですべての物理量を求めることができる
また,これ以降は簡単のため \(P \rightarrow p\) と表記することとする
連続の式およびNavier-Stokes方程式の離散化についてはこちら
圧力-速度連成
連続の式とNavier-Stokes方程式には次のような問題がある
- 連続の式には時間微分項が含まれておらず,速度場に対して強い制約(発散なし:divergence free)を課しているだけである
- 変数である圧力\(p\)に対する時間微分項\(\frac{\partial p}{\partial t}\)が明示的に示されていない
流れ場の速度と圧力を計算するためには,基礎方程式で明示的に示されていない圧力\(p\)を計算しつつ,連続の式による強い制約を満たすような速度\(u_{i}\)を計算する,というような手法を考える必要がある
SIMPLE法の概要
SIMPLE(Semi-Implicit Method for Pressure-Liked Equation)法は時間発展に陰解法を使っているので,反復計算を行いながら速度と圧力を少しずつ真の解に近づけていく必要がある
そこで,ある時刻\(t_{n}\)における速度 \(\mathbf{u}^{(n)}\) と圧力 \(p^{(n)}\) を,それぞれの推定値(\(\mathbf{u}^{*}\),\(p^{*}\))と修正量(\(\mathbf{u'}\),\(p'\))に分解する
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{u}^{*}+\mathbf{u'} \\
&p^{(n)}=p^{*}+p'
\tag{1.1}
\end{align}
「対象の流れ場が定常流れである」と仮定すれば,十分に時間進行を行うとやがて修正量は0になり(\(\mathbf{u}'=p'=0\)),推定値は真の解に収束すると考えられる(\(\mathbf{u}=\mathbf{u}^{*}\),\(p=p^{*}\))
基本形
速度の推定値 \(\mathbf{u}^{*}\) は次の式であらわされる
\begin{equation}
\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{*}
+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}^{*}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}+\frac{1-\alpha_{u}}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{(n-1)}
\tag{1.2}
\end{equation}
圧力の修正量\(p'\)および速度の修正量\(u'\)は次の式で表される
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}_{_{P}}^{*}
\tag{1.3} \\ \\
&\mathbf{u'}=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
\tag{1.4}
\end{align}
時刻\(t_{n}\)における速度と圧力は次の式で表される
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{u}^{*}+\mathbf{u'} \\
&p^{(n)}=p^{(n-1)}+\alpha_{p}p'
\tag{1.5}
\end{align}
\(\alpha_{u}\)と\(\alpha_{p}\)は不足緩和係数であり,計算を安定させて収束を早めるはたらきをしている
以上の式を用いて,SIMPLE法では次に示す①~⑥の手順を収束するまで繰り返すことによって真の速度場と圧力を計算する
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める (1.2)
③ 速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から圧力の修正量\(p'\)を求める (1.3)
④ 圧力の修正量\(p'\)から速度の修正量\(u'\)を求める (1.4)
⑤ 時刻\(t_{n}\)における速度 \(\mathbf{u}^{(n)}\) と圧力 \(p^{(n)}\) を計算する (1.5)
⑥ 時刻を\(t_{n+1}\)に進めて,①に戻る
不足緩和係数は,通常 \(\alpha_{u}=0.3 \sim 0.8\),\(\alpha_{p}=0.3 \sim 0.8\) の値をとり,試行錯誤的に決定される
係数を小さくすると計算は安定するが収束が遅くなるので,まずは小さい値から初めて,計算が安定するぎりぎりまで大きくしていくとよい
ちなみに,定常流れでは時間刻みの大きさは特に考慮しなくていいので,便宜的に\(\Delta t = 1\)とする
(1.3)について十分に時間進行を行って解が収束すれば,\(p'=0\) かつ \(\mathbf{u}^{*}_{_{P}}=\mathbf{u}_{_{P}}\) なので
\begin{equation}
\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}_{_{P}}^{*}
\quad\rightarrow\quad
\nabla\cdot\mathbf{u}_{_{P}}=0
\end{equation}
となり,\(\mathbf{u}_{_{P}}\) は連続の式を満たすようになる
導出
離散化されたNavier-Stokes方程式と連続の式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\) と \(p=p^{*}+p'\)を代入することで,SIMPLE法に必要な式を導出する
(連続の式)
\begin{equation}
\nabla\cdot\mathbf{u}_{_{P}}=0
\end{equation}
(離散化されたNavier-Stokes方程式)
\begin{equation}
\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}}
=-\nabla p+\mathbf{s}_{_{P}}
\end{equation}
まず,離散化されたNavier-Stokes方程式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\) と \(p=p^{*}+p'\)を代入すると次のようになる
\begin{align}
&\mathbf{A}_{_{P}}\left(\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\right)
+\sum{\mathbf{A}_{nb}\left(\mathbf{u}^{*}_{nb}+\mathbf{u'}_{nb}\right)}
=-\nabla \left(p^{*}+p'\right)+\mathbf{s}_{_{P}} \\
\\ \rightarrow \quad
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{*}+\mathbf{s}_{_{P}}
-\left(\mathbf{A}_{_{P}}\mathbf{u'}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}
+\nabla p'
\right)
\tag{i}
\end{align}
十分に時間進行を行うと,(i)の右辺第3項は0になるので
\begin{align}
&\mathbf{A}_{_{P}}\mathbf{u'}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}
+\nabla p' =0 \\
\\ \rightarrow \quad
&\mathbf{u'}_{_{P}}
=
-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
\tag{ii}
\end{align}
よって,(i)は次のようになる
\begin{equation}
\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{*}+\mathbf{s}_{_{P}}
\tag{iii}
\end{equation}
次に,連続の式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\) を代入する
\begin{align}
\nabla\cdot\mathbf{u}^{*}_{_{P}}+\nabla\cdot\mathbf{u'}_{_{P}}=0
\end{align}
(ii)を代入すると
\begin{align}
&\nabla\cdot\mathbf{u}^{*}_{_{P}}+\nabla\cdot\left(-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)=0 \\
\\ \rightarrow \quad
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
-\nabla\cdot\left(\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}\right)
\tag{iv}
\end{align}
(ii)と(iv)より,速度と圧力の修正量に関する連立方程式が得られた
\begin{align}
&\mathbf{u'}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}} \\ \\
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
-\nabla\cdot\left(\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}\right)
\end{align}
上式は\(\mathbf{u'}\)と\(p'\)についての完全陰解法であり,\(\mathbf{u'}\)と\(p'\)を求めるには大規模な連立一次方程式を解く必要があるため,多大な計算コストがかかってしまう
そこで,「\(\mathbf{u'}\)と\(p'\)は解が収束したらどうせ0になるのだから,それまでの過程で多少不正確な値であっても解の信頼性には関係ない」という考え方に基づき,\(\mathbf{u'}_{nb}\)に関する項を無視することにする
\begin{align}
&\mathbf{u'}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
\tag{1.4}\\ \\
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
\tag{1.3}
\end{align}
さらに,(iii)における\(p^{*}\)については1つ前のステップにおける圧力\(p^{(n-1)}\)を用いることにすれば
\begin{align}
&p^{(n)}=p^{(n-1)}+p'
\tag{1.5'} \\ \\
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}
\tag{1.2'}
\end{align}
これにより,\(\mathbf{u}^{*}_{_{P}}\) → \(p'\) → \(\mathbf{u'}_{_{P}}\) → \(p^{(n)}(=p^{*})\) → \(\mathbf{u}^{(n)}_{_{P}}\) という順番で求めれば,すべての変数を計算することができるようになった
本来は完全陰解法で求めるはずの\(u'_{_{P}}\)と\(p'\)を,\(\mathbf{u'}_{nb}\)に関する項を無視することで陽的に求めるという手法が,SIMPLE法が Semi-Implict Method(半陰解法)と呼ばれる所以である
不足緩和
SIMPLE法では,速度と圧力の修正量として\(\mathbf{u'}_{nb}\)に関する項を無視した不正確な値を使用していることが原因で,時間進行の序盤(修正量が大きいとき)に計算が発散しやすくなってしまう
上記の計算の発散を抑制するため,速度と圧力の更新の際に次のような緩和係数を導入する(これを不足緩和という)
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{u}^{n-1}_{_{P}}+\alpha_{u}\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}}{\mathbf{A}_{_{P}}}-\mathbf{u}^{(n-1)}_{_{P}}\right)
\tag{v} \\ \\
&p^{(n)}=p^{(n-1)}+\alpha_{p}p'
\tag{1.5} \\ \\
\end{align}
圧力に対する不足緩和は修正量\(p'\)を小さくするように陽的に行われているが,速度に対する不足緩和は推定値\(\mathbf{u}^{*}_{_{P}}\)の変化を小さくする形で陰的に導入されている
(v)を整理すると,(1.2)が得られる
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{u}^{n-1}_{_{P}}+\alpha_{u}\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}}{\mathbf{A}_{_{P}}}-\mathbf{u}^{(n-1)}_{_{P}}\right) \\
\\ \rightarrow \quad
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
=\mathbf{A}_{_{P}}\mathbf{u}^{n-1}_{_{P}}
+\alpha_{u}\left(\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}-\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}}\right) \\
\\ \rightarrow \quad
&\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
=\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{n-1}_{_{P}}
+\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}
-\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}} \\
\\ \rightarrow \quad
&\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{(n-1)}
+\mathbf{s}_{_{P}}
+\frac{1-\alpha_{u}}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}}
\tag{1.2}
\end{align}
修正量を用いないSIMPLE法
SIMPLE法は,修正量(\(\mathbf{u}'\),\(p'\))を用いない形に書き直すことができる
時刻 \(t_{n}\) における速度の推定値は,先ほどと同様に次の式で求められる
\begin{equation}
\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{*}
+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}^{*}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}+\frac{1-\alpha_{u}}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{(n-1)}
\tag{2.1}
\end{equation}
ここで,\(\mathbf{\tilde{u}}^{*}_{_{P}}\)を次のように定義する
\begin{equation}
\mathbf{\tilde{u}}^{*}_{_{P}}
=\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}^{*}}}{\mathbf{A}_{_{P}}}
\tag{2.2}
\end{equation}
時刻\(t_{n}\)における圧力\(p^{(n)}\)と速度\(\mathbf{u}^{(n)}\)は次のように求められる
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}\right)
=\nabla\cdot\mathbf{\tilde{u}}^{*}_{_{P}}
\tag{2.3} \\ \\
&\mathbf{u}^{(n)}_{_{P}}=\mathbf{\tilde{u}}^{*}_{_{P}}-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}
\tag{2.4}
\end{align}
以上の式を用いて,修正量を用いないSIMPLE法では次に示す①~⑥の手順を収束するまで繰り返すことによって真の速度場と圧力を計算する
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める (2.1)
③ 速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から\(\mathbf{\tilde{u}}^{*}_{_{P}}\)を求める (2.2)
④ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)から時刻\(t_{n}\)における圧力\(p^{(n)}\)を求める (2.3)
⑤ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)と圧力\(p^{(n)}\)から時刻\(t_{n}\)における速度\(\mathbf{u}^{(n)}\)を求める (2.4)
⑥ 時刻を\(t_{n+1}\)に進めて,①に戻る
ちなみに,(2.3)と(2.4)より
\begin{equation}
\nabla\cdot\left(\mathbf{\tilde{u}}^{*}_{_{P}}-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}\right)
=\nabla\cdot\mathbf{u}^{(n)}_{_{P}}=0
\end{equation}
となり,\(\mathbf{u}^{(n)}_{_{P}}\) は連続の式を満たしている
導出
先述したSIMPLE法の導出より,次の関係がわかっている
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{u}^{*}+\mathbf{u'} \tag{vi} \\
&p^{(n)}=p^{(n-1)}+p' \tag{vii} \\ \\
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}
\tag{viii} \\ \\
&\mathbf{u'}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
\tag{ix} \\
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
\tag{x}
\end{align}
これらの式を用いて,修正量(\(\mathbf{u'}\),\(p'\))を用いないSIMPLE法を導出する
(viii)を次のように変形する
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n-1)}
\tag{xi} \\ \\
&\mathbf{\tilde{u}}^{*}_{_{P}}
=\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}}{\mathbf{A}_{_{P}}}
\tag{2.2} \\ \\
\end{align}
(x)に(xi)を代入し,\(p^{(n)}=p^{(n-1)}+p'\) を適用する
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\left(\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n-1)}\right)\\
\\ \rightarrow \quad
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n-1)}+\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{\tilde{u}}^{*}_{_{P}} \\
\\ \rightarrow \quad
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}\right)
=\nabla\cdot\mathbf{\tilde{u}}^{*}_{_{P}}
\tag{2.3} \\
\end{align}
同様に,\(\mathbf{u}^{(n)}=\mathbf{u}^{*}+\mathbf{u'}\) に(xi)と(ix)を代入し,\(p^{(n)}=p^{(n-1)}+p'\) を適用する
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n-1)}
+\left(-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)\\
\\ \rightarrow \quad
&\mathbf{u}^{(n)}=\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\left(\nabla p^{(n-1)}
+\nabla p'\right)\\
\\ \rightarrow \quad
&\mathbf{u}^{(n)}=\mathbf{\tilde{u}}^{*}_{_{P}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}
\tag{2.4} \\
\end{align}
これにより,\(\mathbf{u}^{*}_{_{P}}\) → \(\mathbf{\tilde{u}}^{*}_{_{P}}\) → \(p^{(n)}\) → \(\mathbf{u}^{(n)}_{_{P}}\)という順番で求めれば,すべての変数を計算することができるようになった
不足緩和
修正量を用いないSIMPLE法では,速度と圧力の不足緩和を次のように行う
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{u}^{n-1}_{_{P}}+\alpha_{u}\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}}{\mathbf{A}_{_{P}}}-\mathbf{u}^{(n-1)}_{_{P}}\right) \\ \\
&p^{(n)}=p^{(n-1)}+\alpha_{p}\left(p^{(n)}-p^{(n-1)}\right) \\ \\
\end{align}
圧力に対する不足緩和の方法が若干変更されている
まとめ
離散化された速度と圧力の連成解法であるSIMPLE法について説明した
SIMPLE法は,「対象の流れ場が定常流れであること」を仮定し,速度と圧力をそれぞれ推定値と修正量に分けて計算を行う
定常流れの計算なので,便宜的に\(\Delta t=1\) として時間発展を計算する
不足緩和の係数を設定することで,計算の安定性と収束の速さを調整する
↓非定常計算ができるようSIMPLE法を改良した手法はこちら
↓おすすめ記事
参考
≫非圧縮性流体計算の圧力-速度連成手法 (PDF)
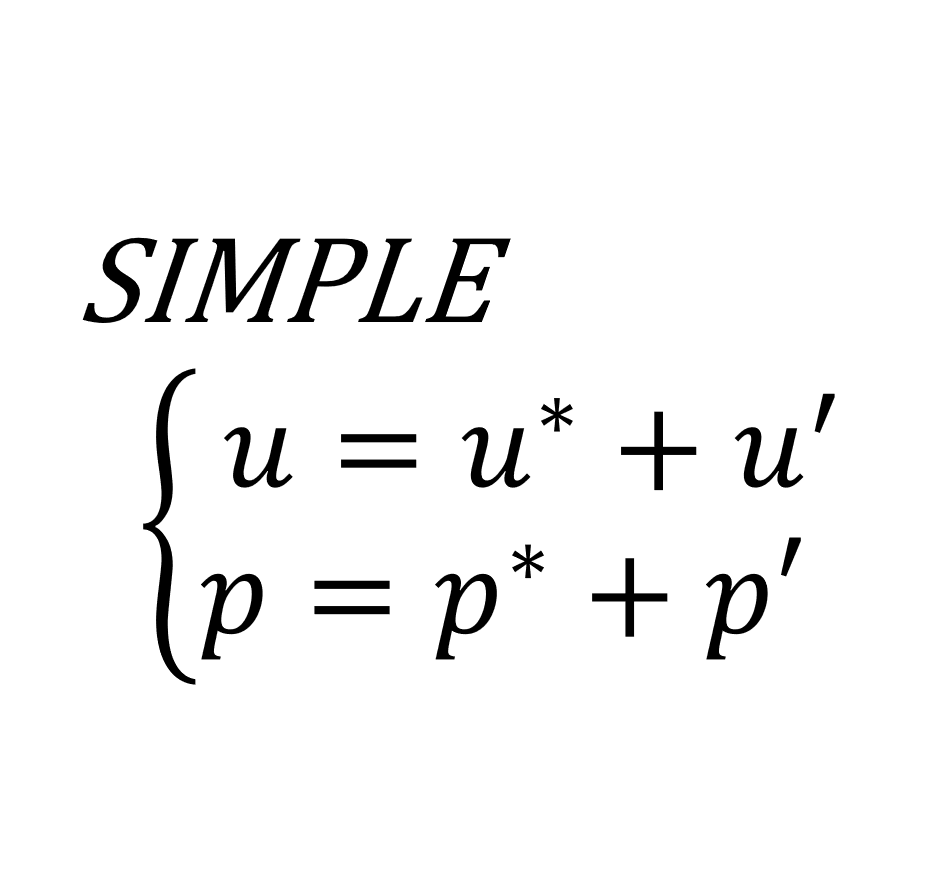
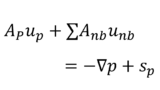
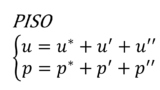

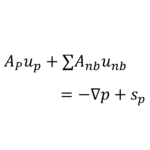
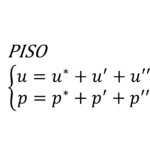
コメント