離散化された速度と圧力の連成解法であるPISO法について説明する
keyword: PISO法
CFDの基礎方程式
密度\(\rho\),粘性係数\(\mu\)が一定な非圧縮性流体の基礎方程式は,連続の式(質量保存式)およびNavier-Stokes方程式(運動量保存式)である
(連続の式)
\begin{equation}
\frac{\partial u_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial u_{i}}{\partial t}+\frac{\partial \left(u_{i}u_{j}\right)}{\partial x_{j}}=-\frac{1}{\rho}\frac{\partial P}{\partial x_{i}}+\nu_{_{E}}\frac{\partial}{\partial x_{j}}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)
+f_{i}
\end{equation}
\begin{equation}
\nu_{_{E}}=\nu+\nu_{t}, \qquad {P}={p}+\frac{2}{3}\rho k
\end{equation}
※モデル化のためのフィルター操作を表すオーバーライン(\(\overline{u}_{i}\),\(\overline{p}\))は省略している
密度\(\rho\)と動粘性係数\(\nu\)は水や空気などの物性値であり,渦粘性係数\(\nu_{t}\)は乱流の影響による拡散を表している
未知数は速度\(\mathbf{u}\)の3つの成分\(u_{i}\),圧力\(p\),渦粘性係数\(\nu_{t}\)の5つであり,渦粘性係数を乱流モデルによって与えれば,連続の式とNavier-Stokes方程式を解くことですべての物理量を求めることができる
また,これ以降は簡単のため \(P \rightarrow p\) と表記することとする
↓連続の式およびNavier-Stokes方程式の離散化についてはこちら
PISO法の概要
PISO(Pressure Implicit with Splitting Operators)法は,非定常計算が行えるようにSIMPLE法を拡張した手法である
SIMPLE法の導出において,速度と圧力の修正量を求める際に\(\mathbf{u'}_{nb}\)の項を無視したが,それが原因でSIMPLE法では収束までの時々刻々における速度と圧力の値は不正確なものになっている
上記の問題を解決するために,PISO法では速度と圧力の推定値と修正量の計算を複数回(通常は2回)行うことで,時々刻々における速度と圧力の精度を確保して非定常流れの計算を可能にしている
↓SIMPLE法についてはこちら
基本形
ある時刻\(t_{n}\)における速度 \(\mathbf{u}^{(n)}\) と圧力 \(p^{(n)}\) の精度を高めるために,速度と圧力の修正を1次修正量(\(\mathbf{u'}\),\(p'\))と2次修正量(\(\mathbf{u^{\prime\prime}}\),\(p^{\prime\prime}\))の2回にわけて行い,1次推定値と1次修正量の和を2次推定値(\(\mathbf{u}^{**}\),\(p^{**}\))として定義する
\begin{align}
&\mathbf{u}^{(n)}=\mathbf{u}^{*}+\left(\mathbf{u'}+\mathbf{u^{\prime\prime}}\right), \qquad &
&p^{(n)}=p^{*}+\left(p'+p^{\prime\prime}\right) \\
&\mathbf{u}^{**}=\mathbf{u}^{*}+\mathbf{u'}, \qquad &
&p^{**}=p^{*}+p' \tag{1.1}\\
\\ \rightarrow \quad
&\mathbf{u}^{(n)}=\mathbf{u}^{**}+\mathbf{u^{\prime\prime}}, \qquad &
&p^{(n)}=p^{**}+p^{\prime\prime} \tag{1.2}\\
\end{align}
これら2つの修正量を用いて各時刻の速度と圧力を計算する手法がPISO法である
まず,離散化されたNavier-Stokes方程式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}+\mathbf{u'}+\mathbf{u^{\prime\prime}}\) と \(p=p^{*}+p'+p^{\prime\prime}\)を代入すると次のようになる
\begin{align}
\mathbf{A}_{_{P}}\left(\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}+\mathbf{u^{\prime\prime}}_{_{P}}\right)
+\sum{\mathbf{A}_{nb}\left(\mathbf{u}^{*}_{nb}+\mathbf{u'}_{nb}+\mathbf{u^{\prime\prime}}_{nb}\right)}
=-\nabla \left(p^{*}+p'+p^{\prime\prime}\right)+\mathbf{s}_{_{P}}
\end{align}
これを次の2つの段階に分けて考える
\begin{align}
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{*}+\mathbf{s}_{_{P}}
-\left(\mathbf{A}_{_{P}}\mathbf{u'}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}
+\nabla p'
\right) \\ \\
&\mathbf{A}_{_{P}}\mathbf{u}^{**}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{**}_{nb}}
=-\nabla p^{**}+\mathbf{s}_{_{P}}
-\left(\mathbf{A}_{_{P}}\mathbf{u^{\prime\prime}}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u^{\prime\prime}}_{nb}}
+\nabla p^{\prime\prime}
\right) \\ \\
\end{align}
各時刻において真の解と推定値が一致するためには,上式の右辺第3項は0にならなければならないので
\begin{align}
&\mathbf{u'}_{_{P}}
=-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p' \tag{A} \\ \\
&\mathbf{u^{\prime\prime}}_{_{P}}
= -\frac{\sum{\mathbf{A}_{nb}\mathbf{u^{\prime\prime}}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime} \\ \\
\end{align}
\begin{align}
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{*}+\mathbf{s}_{_{P}} \tag{1.3} \\ \\
&\mathbf{A}_{_{P}}\mathbf{u}^{**}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{**}_{nb}}
=-\nabla p^{**}+\mathbf{s}_{_{P}}
\end{align}
次に,連続の式に \(\mathbf{u}_{_{P}}=\mathbf{u}^{*}_{_{P}}+\mathbf{u'}_{_{P}}\) と \(\mathbf{u}_{_{P}}=\mathbf{u}^{**}_{_{P}}+\mathbf{u^{\prime\prime}}_{_{P}}\) をそれぞれ代入し,SIMPLE法と同様に\(\mathbf{u}_{nb}\)に関する項を無視すると次のようになる
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}} \tag{1.4} \\
&\mathbf{u'}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p' \tag{1.5} \\ \\
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime}\right)
=\nabla\cdot\mathbf{u}^{**}_{_{P}} \tag{1.6} \\
&\mathbf{u^{\prime\prime}}_{_{P}}
=-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime} \tag{1.7} \\ \\
\end{align}
上記の考えに基づいて,PISO法では次に示す①~⑨の手順を繰り返すことによって非定常な速度場と圧力場を計算している
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の1次推定値 \(\mathbf{u}^{*}\) を求める (1.3)
③ 速度の1次推定値\(\mathbf{u}_{_{P}}^{*}\)から圧力の1次修正量\(p'\)を求める (1.4)
④ 圧力の1次修正量\(p'\)から速度の1次修正量\(u'\)を求める (1.5)
⑤ 速度の2次推定値\(\mathbf{u}^{**}\) と圧力の2次推定値 \(p^{**}\) を計算する (1.1)
⑥ 速度の2次推定値\(\mathbf{u}_{_{P}}^{**}\)から圧力の2次修正量\(p^{\prime\prime}\)を求める (1.6)
⑦ 圧力の2次修正量\(p^{\prime\prime}\)から速度の2次修正量\(u^{\prime\prime}\)を求める (1.7)
⑧ 時刻\(t_{n}\)における速度\(\mathbf{u}\) と圧力 \(p\) を計算する (1.2)
⑨ 時刻を\(t_{n+1}\)に進めて,①に戻る
2回の修正は何を意味しているのか
速度の1次推定値\(\mathbf{u}_{_{P}}^{*}\)は離散化された偏微分方程式を解くことで求めているが,速度の2次推定値は1次推定値と1次修正量の和 \(\mathbf{u}_{_{P}}^{**}=\mathbf{u}_{_{P}}^{*}+\mathbf{u'}_{_{P}}\) で求めている
手順⑥の(1.6)に \(\mathbf{u}_{_{P}}^{**}=\mathbf{u}_{_{P}}^{*}+\mathbf{u'}_{_{P}}\)を代入すると
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime}\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}+\nabla\cdot\mathbf{u'}_{_{P}}
\end{align}
(A)より\(\mathbf{u'}_{_{P}}\)を代入すると次のようになる
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime}\right)
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
+\nabla\cdot\left(-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'\right)\\
\\ \rightarrow \quad
&\nabla\cdot\left\{\frac{1}{\mathbf{A}_{_{P}}}\nabla \left(p'+p^{\prime\prime}\right)\right\}
=\nabla\cdot\mathbf{u}^{*}_{_{P}}
-\nabla\cdot\left(\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}\right) \\
\end{align}
同様に,\(\mathbf{u'}+\mathbf{u^{\prime\prime}}\)に(A)と(1.7)を代入すると次のようになる
\begin{align}
&\mathbf{u'}+\mathbf{u^{\prime\prime}}
=-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}}
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p'
-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{\prime\prime} \\
\\ \rightarrow \quad
&\mathbf{u'}+\mathbf{u^{\prime\prime}}
=-\frac{1}{\mathbf{A}_{_{P}}}\left(\nabla p'+\nabla p^{\prime\prime}\right)
-\frac{\sum{\mathbf{A}_{nb}\mathbf{u'}_{nb}}}{\mathbf{A}_{_{P}}} \\
\end{align}
上式から,PISO法では速度と圧力の修正を行う2回行うことで,速度と圧力の合計修正量に速度の1次修正量\(\mathbf{u'}_{nb}\)の項を考慮していることが分かる
依然として速度の2次修正量による\(\mathbf{u^{\prime\prime}}_{nb}\)の項は無視しているが,速度の修正量による項を完全に無視していたSIMPLE法と比べると,時々刻々における速度と圧力の精度は向上している
PISO法の簡略化
基本形の手順をよく見てみると,③~⑤と⑥~⑧は変数の見た目が違うだけで,全く同じ計算をしていることがわかる
全く同じ計算をしているならプログラムにおいてメモリを使いまわすことができるし,メモリを使いまわすことができるなら修正回数を2回に限定する必要はない
よって,上記に示したPISO法の計算手順は次のように簡略化できる
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める (1.3)
③ 速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から圧力の修正量\(p'\)を求める (1.4)
④ 圧力の修正量\(p'\)から速度の修正量\(u'\)を求める (1.5)
⑤ 速度\(\mathbf{u}^{(n)}\) と圧力 \(p^{(n)}\) を計算し,\(\mathbf{u}^{*}=\mathbf{u}^{(n)}\)として③に戻る (1.1)
⑦ ③~⑥を複数回(通常は2回)繰り返したら,時刻を\(t_{n+1}\)に進めて,①に戻る
修正量を用いないPISO法
PISO法もSIMPLE法と同様に修正量を用いない形に書き換えることができる
時刻 \(t_{n}\) における速度の推定値は,先ほどと同様に次の式で求められる
\begin{equation}
\mathbf{A}_{_{P}}\mathbf{u}_{_{P}}^{*}
+\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}^{*}}
=-\nabla p^{(n-1)}+\mathbf{s}_{_{P}}
\tag{2.1}
\end{equation}
ここで,\(\mathbf{\tilde{u}}^{*}_{_{P}}\)を次のように定義する
\begin{equation}
\mathbf{\tilde{u}}^{*}_{_{P}}
=\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}_{nb}^{*}}}{\mathbf{A}_{_{P}}}
\tag{2.2}
\end{equation}
時刻\(t_{n}\)における圧力\(p^{(n)}\)と速度\(\mathbf{u}^{(n)}\)は次のように求められる
\begin{align}
&\nabla\cdot\left(\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}\right)
=\nabla\cdot\mathbf{\tilde{u}}^{*}_{_{P}}
\tag{2.3} \\ \\
&\mathbf{u}^{(n)}_{_{P}}=\mathbf{\tilde{u}}^{*}_{_{P}}-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}
\tag{2.4}
\end{align}
※導出法はSIMPLE法の記事を参照
修正量を用いないPISO法では次に示す①~⑦の手順を繰り返すことによって非定常な速度場と圧力場を計算している
① 時刻\(t_{n}\)において,\(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から \(\nu_{t}\) を計算し,偏微分方程式を離散化して係数\(\mathbf{A}_{_{P}}\)と\(\mathbf{A}_{nb}\)を求める
② \(\mathbf{u}^{(n-1)}\) と \(p^{(n-1)}\) から時刻 \(t_{n}\) における速度の推定値 \(\mathbf{u}^{*}\) を求める (2.1)
③ 速度の推定値\(\mathbf{u}_{_{P}}^{*}\)から\(\mathbf{\tilde{u}}^{*}_{_{P}}\)を求める (2.2)
④ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)から時刻\(t_{n}\)における圧力\(p^{(n)}\)を求める (2.3)
⑤ \(\mathbf{\tilde{u}}^{*}_{_{P}}\)と圧力\(p^{(n)}\)から時刻\(t_{n}\)における速度\(\mathbf{u}^{(n)}\)を求める (2.4)
⑥ ⑤で得られた\(\mathbf{u}^{(n)}_{_{P}}\)を\(\mathbf{u}^{*}_{_{P}}\)として,③に戻る
⑦ ③~⑥を複数回(通常は2回)繰り返したら,時刻を\(t_{n+1}\)に進めて,①に戻る
ちなみに,(2.3)と(2.4)より
\begin{equation}
\nabla\cdot\left(\mathbf{\tilde{u}}^{*}_{_{P}}-\frac{1}{\mathbf{A}_{_{P}}}\nabla p^{(n)}\right)
=\nabla\cdot\mathbf{u}^{(n)}_{_{P}}=0
\end{equation}
となり,\(\mathbf{u}^{(n)}_{_{P}}\) は連続の式を満たしている
不足緩和
PISO法では,速度に対する不足緩和はSIMPLE法と同様に行うが,圧力に対する不足緩和は必要ないとされている
\begin{equation}
\mathbf{u}^{*}_{_{P}}
=\mathbf{u}^{n-1}_{_{P}}+\alpha_{u}\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}}{\mathbf{A}_{_{P}}}-\mathbf{u}^{(n-1)}_{_{P}}\right) \tag{B}
\end{equation}
速度に対する不足緩和は推定値\(\mathbf{u}^{*}_{_{P}}\)の変化を小さくする形で陰的に導入される
(B)を整理すると,不足緩和を考慮した\(\mathbf{u}^{*}_{_{P}}\)に関する離散化方程式が得られる
\begin{align}
&\mathbf{u}^{*}_{_{P}}
=\mathbf{u}^{n-1}_{_{P}}+\alpha_{u}\left(\frac{\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}}{\mathbf{A}_{_{P}}}-\mathbf{u}^{(n-1)}_{_{P}}\right) \\
\\ \rightarrow \quad
&\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
=\mathbf{A}_{_{P}}\mathbf{u}^{n-1}_{_{P}}
+\alpha_{u}\left(\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}-\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}}\right) \\
\\ \rightarrow \quad
&\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
=\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{n-1}_{_{P}}
+\mathbf{s}_{_{P}}-\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}-\nabla p^{(n-1)}
-\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}} \\
\\ \rightarrow \quad
&\frac{1}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{*}_{_{P}}
+\sum{\mathbf{A}_{nb}\mathbf{u}^{*}_{nb}}
=-\nabla p^{(n-1)}
+\mathbf{s}_{_{P}}
+\frac{1-\alpha_{u}}{\alpha_{u}}\mathbf{A}_{_{P}}\mathbf{u}^{(n-1)}_{_{P}}
\tag{1.3}
\end{align}
不足緩和係数は \(\alpha_{u}=0.3 \sim 0.8\) の値で試行錯誤的に決定される
まとめ
離散化された速度と圧力の連成解法であるPISO法について説明した
PISO法は,SIMPLE法において速度と圧力の修正を2回行うことで非定常計算を扱えるよう改良した手法である
非定常流れの計算なので,クーラン数などに応じて時間刻みを設定する
圧力の不足緩和は必要ないとされている
↓おすすめ記事
参考
≫非圧縮性流体計算の圧力-速度連成手法 (PDF)
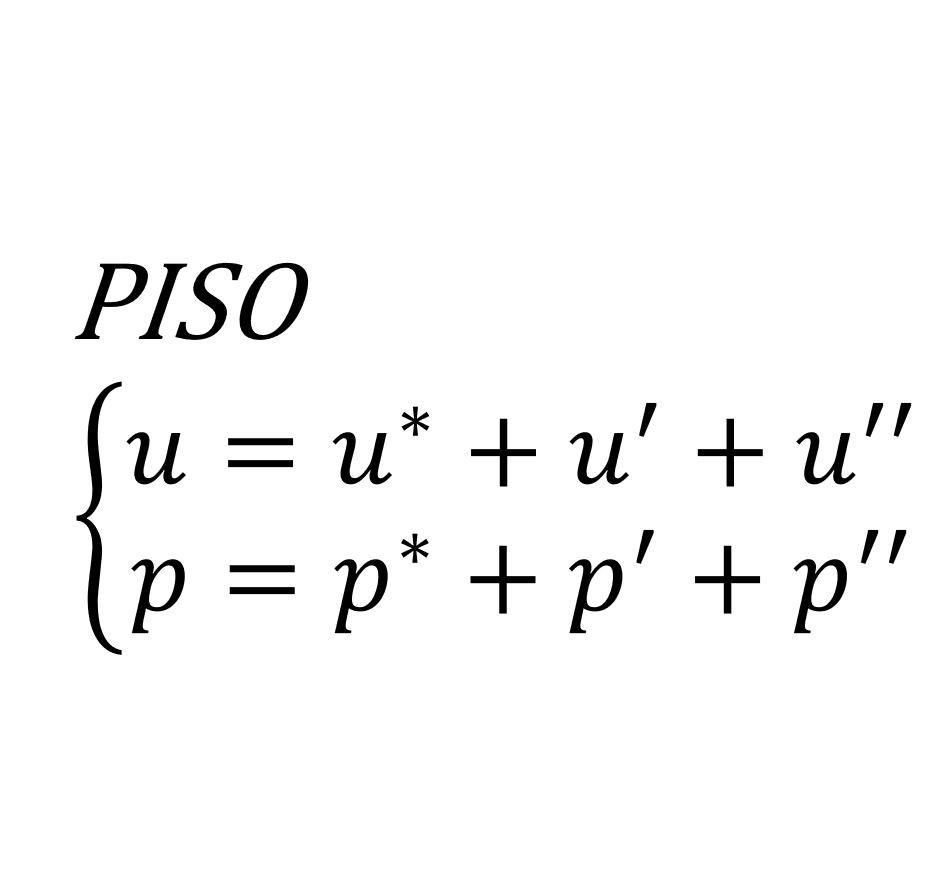
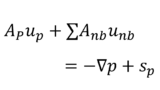
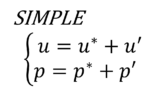

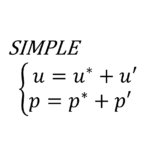

コメント