LESについて,研究でCFDを使うことになった大学院生の役に立つような説明を行う
keyword: Smagorinskyモデル,k Equationモデル,スケール相似則モデル,Dynamicモデル
はじめに
この記事の内容は以下の前提に基づいている
- 非圧縮性流体の乱流流れ
- 密度\(\rho\),粘性係数\(\mu\)は一定
- 熱移動はなし
- CFDを研究で使う大学院生に必要な知識に重点を置く(ググって得られる知識と専門書の中間くらい)
参考文献はこちら
数値流体力学で必須のテンソル解析についての知識はこちら
流れの数値シミュレーションの概要
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(1)に関連して,モデル化の手法の1つであるLESについて説明する
前々回の記事
前回の記事
LESの概要
LESは,流れ場の乱れを格子スケール(Grid Scale:GS)と格子以下のスケール(Sub Grid Scale:SGS)に分解し,SGSの乱れのみをモデル化して非定常計算を行うモデルである
RANSに比べて計算コストは高いが,様々な流れ場においてRANSよりも高い精度の計算を行うことができるので,コンピューターの性能向上に伴って利用が拡大しているモデルである
RANS,LES,DNSの特徴をまとめたものは次のようになる
| RANS | LES | DNS | |
| フィルター | レイノルズ平均 | 空間平均 | なし |
| 計算の次元 | 2次元 or 3次元 | 3次元 | 3次元 |
| 定常/非定常 | 主に定常計算 | 非定常計算 | 非定常計算 |
| \(\tau_{ij}\) | レイノルズ応力 | SGS応力 | なし |
| モデルする乱れ | ほぼすべてのスケール | 格子幅以下のスケール | なし |
| 計算コスト | 低い(1~10) | 高い(100) | 非常に高い(1000~) |
| 実用性 | 産業界で広く普及 | 実用化までもう少し | 基礎研究レべル |
| 特徴 | 簡単な流れ場で高い精度 | 複雑な流れ場に対応可能 | ほぼ正しい |
| 精度 | モデルの種類に依存 | 格子の精度に依存 | 計算手法に依存 |
LESで用いる空間平均フィルター操作は下の図のようなイメージになる
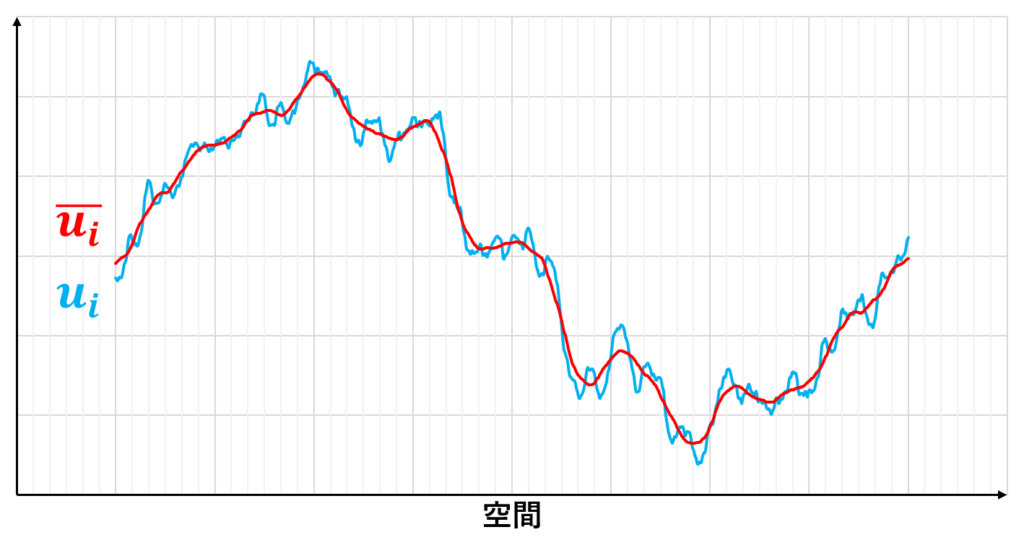
空間平均操作によって速度\(u_{i}\)が粗視化され,GS成分\(\overline{u}_{i}\)とSGS成分に分けられている様子がわかる
RANSは流れ場のほぼすべての乱れをモデル化するため,特定の流れ場に特化した数多くの派生モデルが存在したが,LESは後述するように流れ場に依存しない乱れのみをモデル化するのでモデルの種類はそこまで多くはない
SGS応力のモデル化の基礎となっているエネルギーカスケードという考え方について説明する
エネルギーカスケード
流れ場に存在する乱れ(渦)の生成と消滅の過程は次のようになる
- 流れ場のスケール(壁面の段差や航空機の翼)からエネルギーが与えられて大きな渦が生成される
- 大きな渦が分裂を繰り返して小さな渦になる
- 最終的にこれ以上分裂できない最小スケールになった渦が粘性によって熱となって散逸する
このような,外部から大きい渦へ注入されたエネルギーが小さな渦へと段階的に伝達していく過程のことを エネルギーカスケード(Energy cascade)という
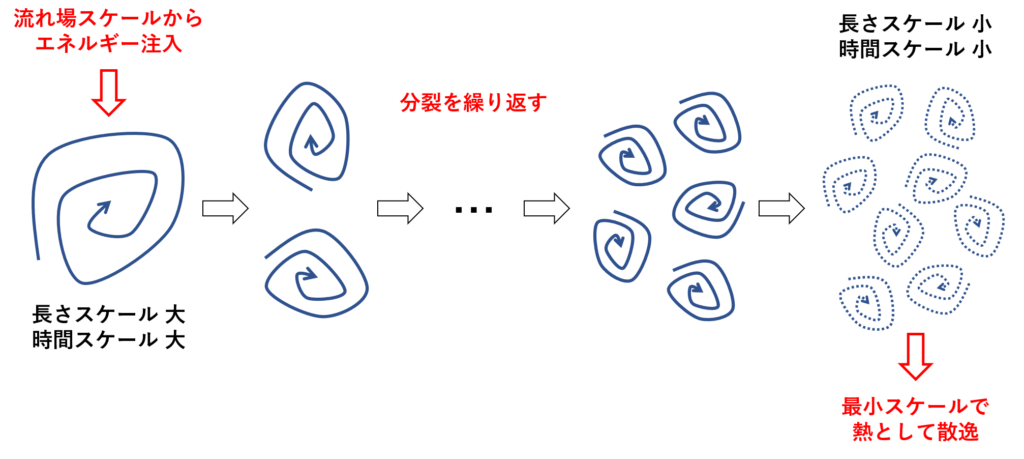
最初に作られた大きな渦は流れ場の影響を受けており,統計的な非等方性が現れる(大きな渦の形状や数は流れ場に依存する)が,渦が分裂するにしたがって最初の渦が持っていた非等方性はなくなっていき,何度も分裂を繰り返したある程度の小さいスケールの渦は流れ場に依存しない等方的な渦になると考えられる
このような考え方を局所等方性(局所=小さいスケールでの)といい,流れ場の影響を受けない小さいスケールの渦はどんな流れ場に対しても普遍的なものであるという仮定を「コルモゴロフの第一相似則」という
局所等方性をもつような小さいスケールの渦は,流れ場によって作られる大きな渦と比べて時間スケール(分裂や合体にかかる時間)が非常に小さく,常に平衡状態にあるとみなせる
よって,局所等方性が成り立ち平衡状態にある普遍的な渦のスケールを「普遍平衡領域」とよぶ
また,流れ場に存在する乱れのエネルギーに注目すると,普遍平衡領域の渦のもつエネルギーはほとんどなく,その大部分は流れ場の形状に依存する大きな渦が担っている
普遍平衡領域に対して,流れ場の形状に依存し,乱れエネルギーの大部分を保有する大きな渦のスケールを「エネルギー保有領域」とよぶ
LESは,普遍平衡領域の乱れをモデル化し,エネルギー保有領域の乱れを直接格子上で計算することで,どんな流れ場にも使える普遍的なモデルとなっている
渦(乱れ)が流れ場のスケールによって生成され,分裂を繰り返し,これ以上分裂できない最小スケールにおいて粘性によって熱として散逸する過程をエネルギーカスケードという
何度も分裂を繰り返した小さなスケールの渦は,流れ場の形状に依存せず,どんな流れ場においても普遍的なものになる(コルモゴロフの第一相似則)
乱れのスケールは,乱れエネルギーの大部分を担っている大きなスケールである「エネルギー保有領域」と,局所等方性をもち平衡状態にある小さなスケールである「普遍平衡領域」に分けられる
LESでは普遍平衡領域の乱れをモデル化する
慣性小領域
渦が粘性によって熱として散逸していく渦のスケールを「散逸領域」といい,普遍平衡領域の中でも最も小さいスケールである
前々回の記事で説明したように,流れ場の代表スケール(エネルギー保有領域のスケール)\(l\)と流れ場に存在する渦の最小スケール(散逸領域のスケール)\(\eta\)には次のような関係がある
\begin{equation}
\frac{l}{\eta}={Re}^{\frac{3}{4}}
\end{equation}
この式は,レイノルズ数が大きくなるとその3/4乗に比例してエネルギー保有領域と散逸領域のスケールが離れていくことを意味している
レイノルズ数が十分に高い流れ場では,エネルギー保有領域と散逸領域には大きな隔たりがあり,大きな渦が分裂を繰り返して普遍平衡領域に入ってからしばらくはひたすら分裂を続けるだけの領域がある
このように,普遍平衡領域の中で粘性による散逸の影響を受けずに分裂だけを繰り返す領域を「慣性小領域」とよぶ
また,このような領域が存在するという仮説を「コルモゴロフの第二相似則」という
レイノルズ数が十分に高い流れ場では,普遍平衡領域は慣性小領域と散逸領域に分けらえる
渦は,慣性小領域ではエネルギーを保持したまま分裂を繰り返し,散逸領域にて粘性によって熱に変換される
エネルギースペクトル
これまでの説明をグラフにしたものがエネルギースペクトルである
グラフの縦軸に乱れの速度をフーリエ変換して得られるエネルギースペクトル\(E(k)\)をとり,横軸に乱れの波数\(k\)をとると,次のようになる
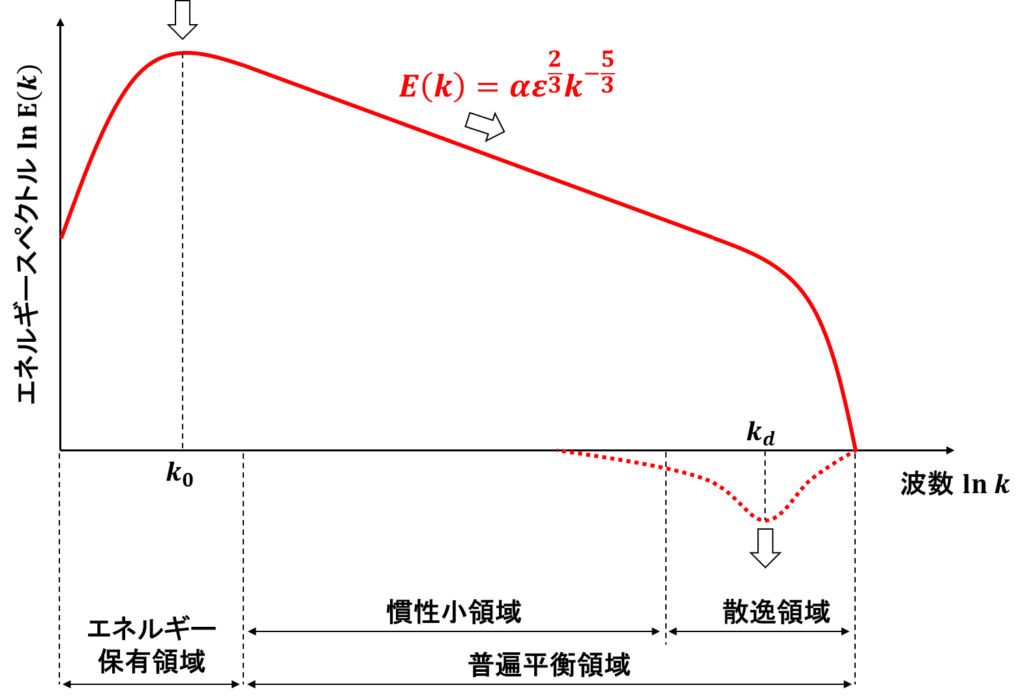
グラフ左側の波数が小さい(波長が大きい)領域がエネルギー保有領域であり,流れ場からエネルギーをもらうとともに流れ場の大部分のエネルギーを保有している
グラフ右側の波数が大きい(波長が小さい)領域が散逸領域であり,粘性による散逸によってエネルギースペクトルが急速に減少している
グラフ中央の領域が慣性小領域であり,慣性小領域におけるエネルギースペクトルは次元解析によって次のように求められる
\begin{equation}
E(k)=\alpha \varepsilon^{2}{3}k^{-\frac{5}{3}}
\end{equation}
慣性小領域における-5/3乗スペクトルは実験でも確認されており,係数\(\alpha\)は実験的に \(\alpha=1.2 \sim 2.0\)であることがわかっている
LESのモデルにおいては,格子サイズを慣性小領域に設定することを前提としており,慣性小領域を境にGS成分とSGS成分が隔てられている
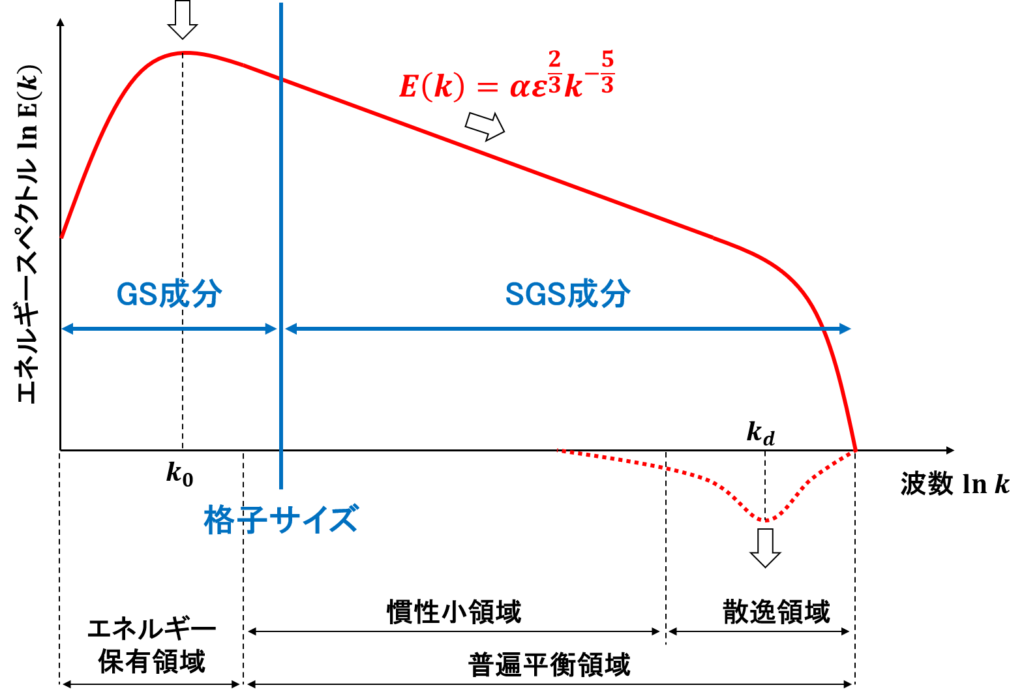
LESでは格子サイズを慣性小領域に設定する
慣性小領域ではエネルギースペクトルについて-3/5乗則がなりたつ
\begin{equation}
E(k)=\alpha \varepsilon^{2}{3}k^{-\frac{5}{3}}
\end{equation}
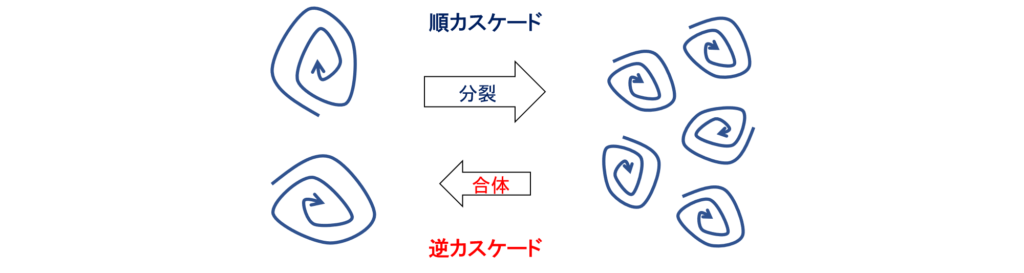
順カスケードと逆カスケード
乱れのエネルギーが渦の分裂によってより小さい渦へと伝達していく過程を「順カスケード」といい,その逆に,小さい渦が合体することによって乱れのエネルギーが大きな渦へと伝達していく過程を「逆カスケード」という
乱れの中では常に順カスケードと逆カスケードが起こっているが,それらは相対的に非常に小さな時間スケールで起こっており平衡状態にある
全体としては順カスケードのほうが多いため,平均的に見ると,渦はより小さい渦へと分裂していく順カスケードにあるとみなせる
LESの基礎方程式
Filtered Navier-Stokes方程式
LESの基礎方程式は,前々回の記事で紹介したFiltered Navier-Stokes方程式である
フィルター操作によって速度\(u_{i}\)と圧力\(p\)はGS成分(平均値)とSGS成分(変動量)に分けられる
\begin{align}
u_{i}&=\overline{u}_{i}+u'_{i} \\
p&=\overline{p}+p'
\end{align}
フィルターをかけた支配方程式は次のように表される
(連続の式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial x_{i}}=0
\end{equation}
(Navier-Stokes方程式)
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{p}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)-\tau_{ij}\right\}
\end{equation}
LESでは,乱流の効果を表す未知数である\(\tau_{ij}\)はSGS応力とよばれ,次の式で表される
\begin{equation}
\tau_{ij}=\overline{u_{i}u_{j}}-\overline{u}_{i}\overline{u}_{j}
\end{equation}
RANSでは上式に対してアンサンブル平均の性質を適用することでさらに簡単な式にすることができたが,LESで用いる空間平均ではそのような操作はできない
変数は速度のGS成分\(\overline{u}_{i}\),圧力のGS成分\(\overline{p}\),SGS応力\(\tau_{ij}\)であり,SGS応力を与えるモデル式を追加することで速度と圧力を求めることができる
SGS応力の式に \(u_{i}=\overline{u}_{i}+u'_{i}\) を代入すると,SGS応力は異なる役割を持つ3つの項に分けられる
\begin{align}
\tau_{ij}
&=\overline{\left(\overline{u}_{i}+u'_{i}\right)\left(\overline{u}_{i}+u'_{i}\right)}-\overline{u}_{i}\overline{u}_{j} \\
&=\overline{\overline{u}_{i}\overline{u}_{j}+\overline{u}_{i}u'_{j}+u'_{i}\overline{u}_{j}+u'_{i}u'_{j}}-\overline{u}_{i}\overline{u}_{j} \\
&=\left(\overline{\overline{u}_{i}\overline{u}_{j}}-\overline{u}_{i}\overline{u}_{j}\right)+\left(\overline{\overline{u}_{i}u'_{j}}+\overline{u'_{i}\overline{u}_{j}}\right)+\overline{u'_{i}u'_{j}} \\
&=L_{ij}+C_{ij}+R_{ij}
\end{align}
(レナード項:Leonard Term)
\begin{equation}
L_{ij}=\overline{\overline{u}_{i}\overline{u}_{j}}-\overline{u}_{i}\overline{u}_{j}
\end{equation}
レナード項は,平均的に見るとGS成分からSGS成分への運動エネルギーの輸送(順カスケード)を担っており,既知の変数\(\overline{u}_{i}\)にフィルターをかけることで直接計算することができる
(クロス項:crossTerm)
\begin{equation}
C_{ij}=\overline{\overline{u}_{i}u'_{j}}+\overline{u'_{i}\overline{u}_{j}}
\end{equation}
クロス項は,平均的に見るとSGS成分からGS成分への運動エネルギーの逆輸送(逆カスケード)を担っている
(SGSレイノルズ応力:SGS Reynolds stress)
\begin{equation}
R_{ij}=\overline{u'_{i}u'_{j}}
\end{equation}
SGSレイノルズ応力は,主にSGSにおける運動エネルギーの散逸を担っている
SGS応力はRANSの渦粘性モデルと同様に渦粘性近似によってモデル化される
\begin{equation}
\tau_{ij}=\frac{2}{3}k\delta_{ij}-2\nu_{_{SGS}}\overline{S}_{ij}
\end{equation}
ここで,\(\nu_{_{SGS}}\)はSGS渦粘性係数であり,\(\overline{S}_{ij}\)はひずみ速度テンソル \(\overline{S}_{ij}=\frac{1}{2}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\) である
これをFiltered Navier-Stokes方程式に代入すると次のようになる
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
\end{equation}
\begin{equation}
\nu_{e}=\nu+\nu_{_{SGS}}, \qquad \overline{P}=\overline{p}+\frac{2}{3}\rho k
\end{equation}
支配方程式の形はLESとRANSで共通であり,乱流モデルの種類にかかわらず共通のソルバーを使うことができる
それでは具体的なLESのモデルについての説明を行っていく
Smagorinskyモデル
Smagorinskyモデルでは,SGS渦粘性係数は次の式で定義される
\begin{equation}
\nu_{_{SGS}}=\left(C_{s}f_{s}\Delta\right)^{2}\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}
\end{equation}
\(\Delta\)は後述するフィルター幅であり,\(C_{s}\)はこのモデルで与える必要のある唯一のモデル定数でSmagorinsky定数とよばれる
\(f_{s}\)は壁面で滑りなし条件 \(\left.\nu_{_{SGS}}\right|_{wall}=0\)を与えるための減衰関数で,Van Driest関数が用いられる
\begin{equation}
f_{s}=1-\exp{\left(-\frac{y^{+}}{A^{+}}\right)}, \qquad A^{+} \simeq 25
\end{equation}
Smagorinsky定数の理論値は \(C_{s}=0.173\) であり,一様等方乱流では実験結果とよく一致することが確認されている
一方で,チャネル乱流などのせん断乱流に対してはより低い値 \(C_{s}=0.10 \sim 0.15\) を設定する必要があることもわかっており,Smagorinsky定数はどんな流れ場でも共通して使える普遍定数ではないことがわかる
Smagorinskyモデルのメリットとデメリットは以下の通り
- SGS渦粘性係数が常に正 \(\nu_{_{SGS}}>0\) であり,数値計算の安定性が高い
- 適当なSmagorinsky定数を設定すれば,エネルギー散逸の総量に対してよいモデルになる
- Smagorinsky定数は普遍定数ではなく,流れ場に応じて適切に設定する必要がある
- SGS渦粘性係数が常に正 \(\nu_{_{SGS}}>0\) なので,SGSからGSへエネルギーが戻る逆カスケードを表現することができない
- 壁面で滑りなし条件 \(\left.\nu_{_{SGS}}\right|_{wall}=0\) を適用するために減衰関数\(f_{s}\)を必要とする
- GS成分に速度勾配があれば必ず \(\nu_{_{SGS}}>0\) となってしまうため,速度勾配はあるが乱流ではない領域がある流れ(層流から乱流への遷移,再層流化がある流れ)に対してはSmagorinskyモデルの使用/不使用を切り替えなければいけない
有名なモデルゆえデメリットが多く列挙されているが,2つのメリット(解くに数値安定性)が大きいので,幅広く利用されているモデルである
流れ場にフィルターをかけると,流れ全体の運動エネルギー \(\overline{k}=\frac{\overline{u_{i}u_{i}}}{2}\)(乱流エネルギーではない)はGS成分 \(k_{_{GS}}=\frac{\overline{u}_{i}\overline{u}_{i}}{2}\)とSGS成分 \(k_{_{SGS}}=\frac{\overline{u_{i}u_{i}}-\overline{u}_{i}\overline{u}_{i}}{2}\) に分けられる
運動エネルギーのそれぞれの成分の輸送方程式は次のように表される
\begin{align}
&\frac{\partial k_{_{GS}}}{\partial t}
+\overline{u}_{j}\frac{\partial k_{_{GS}}}{\partial x_{j}}
=
\tau_{ij}\overline{S}_{ij}-\varepsilon_{_{GS}}
+\frac{\partial}{\partial x_{j}}
\left(-\overline{u}_{i}\tau_{ij}-\frac{\overline{p}\overline{u}_{j}}{\rho}+\nu\frac{\partial k_{_{GS}}}{\partial x_{j}}\right) \\
\\
&\frac{\partial k_{_{SGS}}}{\partial t}
+\overline{u}_{j}\frac{\partial k_{_{SGS}}}{\partial x_{j}}
=
-\tau_{ij}\overline{S}_{ij}-\varepsilon_{_{SGS}} \\
&\qquad +\frac{\partial}{\partial x_{j}}
\left\{\overline{u}_{i}\tau_{ij}-\frac{\overline{u_{i}u_{i}u_{j}}+\overline{u}_{j}\overline{u_{i}u_{i}}}{2}-\frac{\overline{pu_{j}}-\overline{p}\overline{u}_{j}}{\rho}+\nu\frac{\partial k_{_{SGS}}}{\partial x_{j}}\right\}
\end{align}
GS成分の輸送方程式においては\(\tau_{ij}S_{ij}\)の項がSGS運動エネルギーへの輸送率を表し,これを受けてSGS成分の輸送方程式では\(-\tau_{ij}S_{ij}\)の項がSGS運動エネルギーの生成率になる
SGSにおいて運動エネルギーの生成と散逸がつりあっているという局所平衡を仮定すると,SGSにおける運動エネルギーの散逸率\(\varepsilon_{_{SGS}}\)は次のようになる
\begin{equation}
\varepsilon_{_{SGS}}=-\tau_{ij} \overline{S}_{ij}
\tag{i}
\end{equation}
ここで突然SGS応力の渦粘性近似を行う
\begin{equation}
\tau_{ij}=\frac{2}{3}k\delta_{ij}-2\nu_{_{SGS}}\overline{S}_{ij}
\tag{ii}
\end{equation}
(i)に(ii)を代入すると次のようになる
\begin{align}
\varepsilon_{_{SGS}}
=-\left(\frac{2}{3}k\delta_{ij}-2\nu_{_{SGS}}\overline{S}_{ij}\right) \overline{S}_{ij}
=2\nu_{_{SGS}}\overline{S}_{ij}\overline{S}_{ij}-\frac{2}{3}k\delta_{ij}\overline{S}_{ij}
=2\nu_{_{SGS}}\overline{S}_{ij}\overline{S}_{ij}
\end{align}
(\(\delta_{ij}\overline{S}_{ij}=\overline{S}_{kk}=0\))
SGS渦粘性係数\(\nu_{_{SGS}}\)は速度\(q\)と長さ\(l\)の次元 \(\mathrm{[m^2/s]}\) を持つので,次元解析的に次のように表すことができる
\begin{equation}
\nu_{_{SGS}}=C_{\nu}ql
\tag{iii}
\end{equation}
同様に,エネルギー散逸率の次元 \(\mathrm{[m^2/s^3]}\) を考慮すると,\(\varepsilon_{_{SGS}}\)は次元解析的に次のように表せる
\begin{equation}
\varepsilon_{_{SGS}}=2\nu_{_{SGS}}\overline{S}_{ij}\overline{S}_{ij}=C_{\varepsilon}\frac{q^{3}}{l}
\tag{iv}
\end{equation}
(iii)と(iv)より
\begin{equation}
\left\{\begin{array}{rcl}
q&=&\nu_{_{SGS}}/C_{\nu}l \\
q&=&\left(\frac{1}{C_{\varepsilon}}2\nu_{_{SGS}}l \overline{S}_{ij}\overline{S}_{ij}\right)^{\frac{1}{3}}
\end{array}\right.
\end{equation}
\begin{align}
\frac{\nu_{_{SGS}}}{C_{\nu}l}=\left(\frac{1}{C_{\varepsilon}}2\nu_{_{SGS}}l \overline{S}_{ij}\overline{S}_{ij}\right)^{\frac{1}{3}}
\rightarrow \quad
\nu_{_{SGS}}=\left\{\left(\frac{C_{\nu}^{3}}{C_{\varepsilon}}\right)^{\frac{1}{4}}l\right\}^{2}\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}
\end{align}
上式に長さのスケール\(l\)としてフィルター幅\(\Delta\)を用いて,定数をまとめると,Smagorinskyモデルの\(\nu_{_{SGS}}\)を求めることができる
\begin{equation}
\nu_{_{SGS}}=\left(C_{s}\Delta\right)^{2}\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}
\tag{v}
\end{equation}
SmagorinskyモデルのSGS渦粘性係数は
- SGSにおける運動エネルギーの生成と散逸における局所平衡
- 渦粘性係数とエネルギー散逸率の次元解析
によって導出されている
Smagorinsky定数の導出
(v)を(iv)に代入すると,次のようになる
\begin{align}
&\varepsilon_{_{SGS}}=2\left\{\left(C_{s}\Delta\right)^{2}\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}\right\}\overline{S}_{ij}\overline{S}_{ij}
=\left(C_{s}\Delta\right)^{2}\left(2\overline{S}_{ij}\overline{S}_{ij}\right)^{\frac{3}{2}} \\
\\ &\rightarrow\quad
|\mathbf{S}|^{2}=\overline{S}_{ij}\overline{S}_{ij}=\frac{\varepsilon_{_{SGS}}^{2/3}}{2\left(C_{s}\Delta\right)^{4/3}}
\tag{vi}
\end{align}
ここで,フィルター幅\(\Delta\)が慣性小領域にあるように格子分割を定めると,その波数\(k\)付近のエネルギースペクトル\(E(k)\)は-5/3乗則 \(E(k)=\alpha\varepsilon^{\frac{2}{3}}k^{-\frac{5}{3}}\) に従うと考えられる(\(k\)は波数で\(\varepsilon\)は粘性散逸総量)
このとき,\(|\mathbf{S}|^{2}=\overline{S}_{ij}\overline{S}_{ij}\) は渦度スペクトル関数の波数積分から次のように求められる
\begin{align}
|\mathbf{S}|^{2}=\int_{0}^{\pi/4} k^{2}E(k)\:dk
=\frac{3}{4}\alpha|\varepsilon|^{\frac{2}{3}}\left(\frac{\pi}{\Delta}\right)^{\frac{4}{3}}
\tag{vii}
\end{align}
SGSスケールの運動エネルギー散逸率とエネルギースペクトルにおける粘性散逸総量が等しい \(\varepsilon_{_{SGS}}=\varepsilon\) とすると,(vi)と(vii)よりSmagorinsky定数が計算できる
\begin{align}
\frac{\varepsilon_{_{SGS}}^{2/3}}{2\left(C_{s}\Delta\right)^{4/3}}
=\frac{3}{4}\alpha|\varepsilon_{_{SGS}}|^{\frac{2}{3}}\left(\frac{\pi}{\Delta}\right)^{\frac{4}{3}}
\quad \rightarrow \quad
C_{s}=\frac{1}{\pi}\left(\frac{2}{3\alpha}\right)^{\frac{3}{4}}
\end{align}
ここで,実験的に \(\alpha=1.5\) であることが確認されているので,Smagorinsky定数の理論値 \(C_{s}=0.173\) が導かれる
Smagorinsky定数の理論値は,
- SGSにおける運動エネルギーの生成と散逸における局所平衡
- フィルター幅\(\Delta\)が慣性小領域にあるとしたときのエネルギースペクトルの-5/3乗則
- SGSエネルギー散逸率と粘性散逸総量が等しいという仮定
によって導出されている
Dynamic Smagorinsky モデル(DSM)
Dynamic Smagorinskyモデルでは,Smagorinskyモデルの定数\(C_{s}\)を変数と考え,GSの流れ場の情報から動的に\(C_{s}\)を決定する
そのために,グリッドフィルター\(\overline{G}\)(LESの基礎方程式を求めるときに使ったフィルター)とテストフィルター\(\tilde{G}\)(GSの流れ場に対してかけられるフィルター)の2種類のフィルター操作を考える
2つのフィルターは違う種類のフィルターで,グリッドフィルターのフィルター幅\(\overline{\Delta}\)よりもテストフィルターのフィルター幅\(\tilde{\Delta}\)が大きくなるように設定する
\begin{equation}
\gamma=\tilde{\Delta}/\overline{\Delta}>1
\end{equation}
上記2種類のフィルター操作によって,Dynamic Smagorinskyモデルにおける渦粘性係数\(\nu_{_{SGS}}\)と\(C\)は次の式で与えられる
\begin{equation}
\nu_{_{SGS}}=C\Delta^{2}|\overline{S}|, \qquad
C=-\frac{1}{2\overline{\Delta}^{2}}\frac{\left[L_{ij}M_{ij}\right]}{\left[M_{kl}M_{kl}\right]}
\end{equation}
\begin{equation}
L_{ij}=\widetilde{\overline{u}_{i}\overline{u}_{j}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}, \qquad
M_{ij}=\gamma |\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij}-\widetilde{|\overline{S}|\overline{S}_{ij}}
\end{equation}
ここで,\(\overline{S}_{ij}\)はひずみ速度テンソルであり,\(|\overline{S}|\)は次の式で定義されている
\begin{equation}
|\overline{S}|=\sqrt{2\overline{S}_{ij}\overline{S}_{ij}}
\end{equation}
\([\quad]\)は数値計算を安定化させるために用いられる何らかの平均操作(一様乱流では体積平均,平行平板間乱流では面平均,矩形ダクト内乱流では軸方向線上での平均,など)や上限下限の制限を表す
Dynamic Smagorinskyモデルのメリットとデメリットは以下の通り
- フィルター幅の比さえ決めれば,経験的な定数を一切使わずに渦粘性係数を求められる
- グリッドフィルターとテストフィルターの両スケールの間に乱れがなければ \(L_{ij}=0\)となり,渦粘性も\(0\)になることから,層流・乱流遷移の切り替えや壁面近傍の減衰関数が必要ない
- \(C\)の値は \(C<0\) にもなりうるので,エネルギーの逆カスケードを表現することができる
- \(C\)の値は空間的に大きく変動し,数値的に不安定である
- 実際の計算では\(C\)の変動を緩和するために何らかの平均操作を行う必要があり,Dynamicモデルの概念から大幅に後退せざるを得ない
エネルギーカスケードの考え方より,SGSの流れの挙動は,GSの流れの中でもより小さく,SGSに近いスケールの流れによって決定されていると考えられる
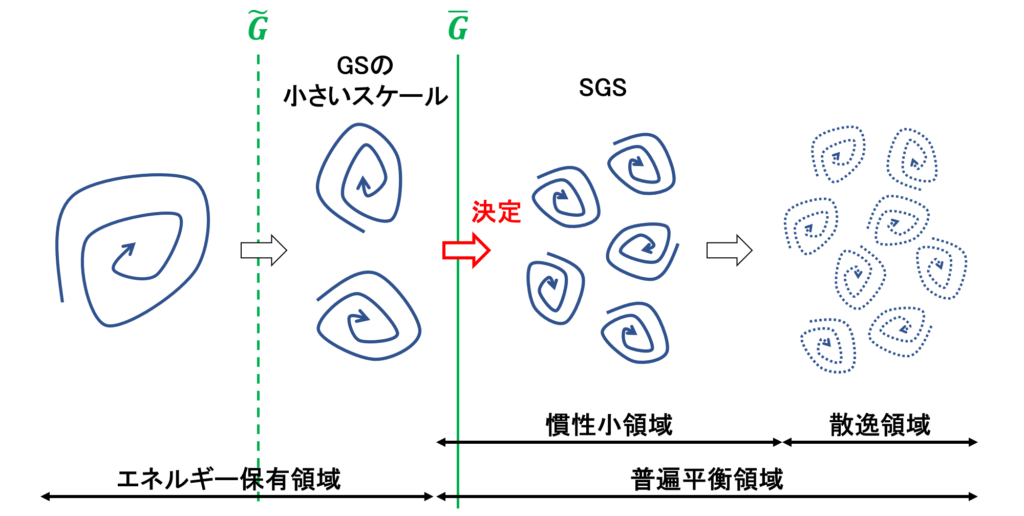
そこで,GSの中からより小さいスケールを取り出すため,Filtered Naver-Stokes方程式にさらにフィルターをかけることを考える
\begin{align}
\frac{\partial \widetilde{\overline{u}}_{i}}{\partial t}
+\frac{\partial \widetilde{\overline{u_{i}u_{j}}}}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \widetilde{\overline{p}}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{2\nu\widetilde{\overline{S}}_{ij}\right\}
\end{align}
両辺から\(\frac{\partial \widetilde{\overline{u_{i}u_{j}}}}{\partial x_{j}}\)を引いて\(\frac{\partial \widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}}{\partial x_{j}}\)を足すと
\begin{align}
\frac{\partial \widetilde{\overline{u}}_{i}}{\partial t}
+\frac{\partial \widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \widetilde{\overline{p}}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{2\nu\widetilde{\overline{S}}_{ij}-T_{ij}\right\}
\end{align}
サブテストフィルタースケール応力\(T_{ij}\)(GSの中の小さいスケールの乱れ)
\begin{equation}
T_{ij}=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}_{i}\overline{u}_{j}}
\end{equation}
が求まる
サブテストフィルタースケール応力がSGSの乱れに与える影響を考えるために,\(T_{ij}\)と\(\tau_{ij}\)の関係式を求める
\(\tau_{ij}\)にテストフィルターをかけると
\begin{align}
\widetilde{\tau}_{ij}=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}_{i}\overline{u}_{j}}
=\widetilde{\overline{u_{i}u_{j}}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}
-\left(\widetilde{\overline{u}_{i}\overline{u}_{j}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}\right)
=T_{ij}-L_{ij}
\end{align}
\(T_{ij}\)と\(\tau_{ij}\)の関係式
\begin{equation}
L_{ij}=\widetilde{\overline{u}_{i}\overline{u}_{j}}-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}=T_{ij}-\widetilde{\tau}_{ij}
\tag{i}
\end{equation}
を求めることができる
\(L_{ij}\)は,サブテストフィルタースケール応力に対するレナード項にあたり,既知の速度成分\(\overline{u}_{i}\)のみで構成されているので直接計算で求めることができる(\(\overline{u_{i}u_{j}}\)は二次の相関項なので計算できない)
\(T_{ij}\)と\(\tau_{ij}\)の関係式からSmagorinsky定数を計算するために,それぞれのスケールの乱流応力にSmagorinskyモデルを適用する
\begin{align}
T_{ij}-\frac{1}{3}T_{kk}\delta_{ij}
&=-2C\tilde{\Delta}^{2}|\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij} \\
\tilde{\tau}_{ij}-\frac{1}{3}\tilde{\tau}_{kk}\delta_{ij}
&=-2C\overline{\Delta}^{2}\widetilde{|\overline{S}|\overline{S}_{ij}}
\tag{ii}
\end{align}
\(\tilde{\Delta}\)はテストフィルターのフィルター幅,\(\overline{\Delta}\)はグリッドフィルターのフィルター幅である
(ii)を(i)に代入すると次のようになる
\begin{equation}
L_{ij}-\frac{1}{3}\left(T_{kk}-\tilde{\tau}_{kk}\right)\delta_{ij}
=T_{ij}-\frac{1}{3}T_{kk}\delta_{ij}-\left(\widetilde{\tau}_{ij}-\frac{1}{3}\widetilde{\tau}_{kk}\delta_{ij}\right) \\
\end{equation}
\begin{equation}
\rightarrow \quad
L_{ij}^{a}
=-2C\tilde{\Delta}^{2}|\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij}-\left(-2C\overline{\Delta}^{2}\widetilde{|\overline{S}|\overline{S}_{ij}}\right)
=-2C\overline{\Delta}^{2}\left(\frac{\tilde{\Delta}^{2}}{\overline{\Delta}^{2}}|\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij}-\widetilde{|\overline{S}|\overline{S}_{ij}}\right)
\end{equation}
\(L_{ij}^{a}=L_{ij}-\frac{1}{3}L_{kk}\delta_{ij}\) は \(L_{ij}\) の非等方テンソル(anisotropic tensor)であり,テストフィルターとグリッドフィルターのフィルター幅の比を \(\gamma=\tilde{\Delta}/{\overline{\Delta}}\)とすれば次のようになる
\begin{equation}
L_{ij}^{a}=-2C\overline{\Delta}^{2}M_{ij}
\tag{iii}
\end{equation}
\begin{equation}
M_{ij}=\gamma^{2}|\widetilde{\overline{S}}|\widetilde{\overline{S}}_{ij}-\widetilde{|\overline{S}|\overline{S}_{ij}}
\end{equation}
ここで,\(L_{ij}^{a}\) と \(-2C\overline{\Delta}^{2}M_{ij}\) は対称テンソルかつトレースレス \(L_{kk}=-2C\overline{\Delta}^{2}M_{kk}=0\) なので,それぞれの独立な成分は5つである
1つのスカラー\(C\)だけを用いて2つのテンソルの独立な5つの成分をすべて一致させることはできないので,2つのテンソルの誤差が最小になるように,最小二乗法を用いて\(C\)を決定する
(iii)の両辺を比較したときの誤差テンソルを \(e_{ij}=L_{ij}^{a}-\left(-2\overline{\Delta}^{2}M_{ij}\right)\) としたとき,最小二乗法より\(e_{ij}\)の二乗を考えると
\begin{align}
&E=e_{ij}e_{ij}=\left(L_{ij}^{a}+2C\overline{\Delta}^{2}M_{ij}\right)^{2}\\
\\
\rightarrow \quad
&\frac{\partial E}{\partial C}
=2\left(L_{ij}^{a}+2C\overline{\Delta}^{2}M_{ij}\right)2\overline{\Delta}^{2}M_{ij}
=4\overline{\Delta}^{2}\left(L_{ij}^{a}M_{ij}+2C\overline{\Delta}^{2}M_{ij}M_{ij}\right)
\end{align}
となり,誤差を最小にするには \(\frac{\partial E}{\partial C}=0\) となればいいので
\begin{align}
&\frac{\partial E}{\partial C}
=4\overline{\Delta}^{2}\left(L_{ij}^{a}M_{ij}+2C\overline{\Delta}^{2}M_{ij}M_{ij}\right)=0 \\
\\ \rightarrow \quad
&L_{ij}^{a}M_{ij}+2C\overline{\Delta}^{2}M_{ij}M_{ij}=0
\end{align}
よって,Dynamic Smagorinskyモデルの係数\(C\)は次のようになる
\begin{equation}
C=-\frac{1}{2\overline{\Delta}^{2}}\frac{L_{ij}^{a}M_{ij}}{M_{ij}M_{ij}}
\end{equation}
実際の計算では\(C\)の値の変動を緩和するため,右辺の分母分子にそれぞれ何らかの平均値を用いる必要がある
\begin{equation}
C=-\frac{1}{2\overline{\Delta}^{2}}\frac{\left[L_{ij}^{a}M_{ij}\right]}{\left[M_{ij}M_{ij}\right]}
\end{equation}
Smagorinskyモデルは,フィルター幅\(\Delta\)とひずみ速度テンソル\(S_{ij}\)によってSGS渦粘性係数を計算する0方程式モデルである
数値的に安定であり,適切な定数\(C_{s}\)を与えればエネルギー散逸に対して精度の高いモデルになることから,幅広く利用されている
Dynamic Smagorinskyモデルを使えば,係数\(C\)を動的に計算することができる
k Equationモデル
k Equationモデルは乱流エネルギー\(k\)を用いた1方程式モデルである
k Equationモデルでは,SGS渦粘性係数\(\nu_{_{SGS}}\)は次の式で定義される
\begin{equation}
\nu_{_{SGS}}=C_{k}\Delta\sqrt{k_{_{SGS}}}
\end{equation}
ここで,\(C_{k}\)はモデル定数,\(k_{_{SGS}}\)はSGS乱流エネルギーであり,\(k_{_{SGS}}\)は以下の輸送方程式を解くことによって求められる
\begin{equation}
\frac{\partial k_{_{SGS}}}{\partial t}
+\overline{u}_{j}\frac{\partial k_{_{SGS}}}{\partial x_{j}}
=
-\tau_{ij}\frac{\partial \overline{u}_{i}}{\partial x_{j}}-\varepsilon_{_{SGS}}
+\frac{\partial}{\partial x_{j}}\left\{\left(\nu+\nu_{_{SGS}}\right)\frac{\partial k_{_{SGS}}}{\partial x_{j}}\right\}
\end{equation}
\begin{equation}
\varepsilon_{_{SGS}}=C_{\varepsilon}\frac{k_{_{SGS}}^{\frac{3}{2}}}{\Delta}
\end{equation}
OpenFOAMに実装されているk Equationモデルでは,モデル定数として \(C_{k}=0.094\),\(C_{\varepsilon}=1.048\)が使われている
≫OpenFOAM User Guide k Equation
Dynamic k Equationモデル
k Equationモデルでも,GSの流れ場から定数を動的に計算するDynamicモデルが提案されている
Dynamic k Equationモデルでは,\(C_{k}\)および\(C_{\varepsilon}\)は次のように与えられる
\begin{equation}
C_{k}=-\frac{1}{2}\frac{L_{ij}^{a}M_{ij}}{M_{kl}M_{kl}}, \qquad
C_{\varepsilon}=\frac{\left(\nu+\nu_{_{SGS}}\right)\widetilde{\Delta}}{k_{_{test}}^{3/2}}
\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right)
\end{equation}
\begin{equation}
L_{ij}^{a}=L_{ij}-\frac{1}{3}L_{kk}\delta_{ij}, \qquad
L_{ij}=\widetilde{\overline{u}_{i}\overline{u}_{j}}
-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}, \qquad
M_{ij}=-\widetilde{\Delta}\sqrt{k_{_{test}}}\widetilde{\overline{S}}_{ij}, \qquad
k_{_{test}}=\frac{L_{ii}}{2}
\end{equation}
Dynamic Smagorinskyモデルと同様に,サブテストフィルタースケール応力のレナード項\(L_{ij}\)は次のようになる
\begin{equation}
L_{ij}
=\widetilde{\overline{u}_{i}\overline{u}_{j}}
-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{j}
\end{equation}
ここで,テストフィルターをかけた流れ場における流体の運動エネルギー\(\widetilde{k}\)とエネルギー散逸率\(\widetilde{\varepsilon}\)を考えると,次のようにテストフィルタースケールとサブテストフィルタースケールに分けることができる
\begin{align}
&\widetilde{k}=\frac{1}{2}\widetilde{\overline{u}_{i}\overline{u}_{i}}
=\frac{1}{2}\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{i}
+\frac{1}{2}\left(\widetilde{\overline{u}_{i}\overline{u}_{i}}
-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{i}\right)
\\ \\
&\widetilde{\varepsilon}=\left(\nu+\nu_{_{SGS}}\right)\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
=\left(\nu+\nu_{_{SGS}}\right)\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}+\left(\nu+\nu_{_{SGS}}\right)\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right)
\end{align}
上式の中で,サブテストフィルタースケール(GSの中の小さいスケール)の運動エネルギー\(k_{_{test}}\)とエネルギー散逸率\(\varepsilon_{_{test}}\)は次の部分である
\begin{align}
&k_{_{test}}=\frac{1}{2}\left(\widetilde{\overline{u}_{i}\overline{u}_{i}}
-\widetilde{\overline{u}}_{i}\widetilde{\overline{u}}_{i}\right)=\frac{L_{ii}}{2}
\\ \\
&\varepsilon_{_{test}}=
\left(\nu+\nu_{_{SGS}}\right)\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right)
\tag{i}
\end{align}
サブテストフィルタースケールは壁面から離れた十分にレイノルズ数の高い領域なので,エネルギーの散逸は分子粘性と渦粘性の両方によって担われている(\(\nu+\nu_{_{SGS}}\))
\(C_{k}\)
サブテストフィルタースケール応力のレナード項\(L_{ij}\)とSGS応力\(\tau_{ij}\)は相似の関係にあることがわかっている
そこで,\(L_{ij}\)に対してk Equationモデルを適用する
\begin{align}
&L_{ij}-\frac{1}{3}L_{kk}\delta_{ij}
=-2C_{k}\widetilde{\Delta}\sqrt{k_{_{test}}}\widetilde{\overline{S}}_{ij} \\
\rightarrow \quad
&L_{ij}^{a}=-2C_{k}M_{ij}, \qquad
M_{ij}=\widetilde{\Delta}\sqrt{k_{_{test}}}\widetilde{\overline{S}}_{ij}
\end{align}
この式に対して,Dynamic Smagorinskyモデルと同様に最小二乗法を用いると
\begin{equation}
e_{ij}=L_{ij}^{a}-\left(-2C_{k}M_{ij}\right), \quad
E=e_{ij}e_{ij}=\left(L_{ij}^{a}+2C_{k}M_{ij}\right)^{2}
\end{equation}
\begin{equation}
\frac{\partial E}{\partial C_{k}}
=2\left(L_{ij}^{a}+2C_{k}M_{ij}\right)2M_{ij}
=4\left(L_{ij}^{a}M_{ij}+2C_{k}M_{ij}M_{ij}\right)=0 \\
\end{equation}
\(C_{k}\)は次のように導かれる
\begin{equation}
C_{k}=-\frac{1}{2}\frac{L_{ij}M_{ij}}{M_{kl}M_{kl}}
\end{equation}
\(C_{\varepsilon}\)
\(\varepsilon_{_{SGS}}\)と同様に,\(\varepsilon_{_{test}}\)は次の式で表される
\begin{equation}
\varepsilon_{_{test}}=C_{\varepsilon}\frac{k_{_{test}}^{\frac{3}{2}}}{\widetilde{\Delta}}
\tag{ii}
\end{equation}
(i)と(ii)より,\(C_{\varepsilon}\)を導くことができる
\begin{align}
C_{\varepsilon}\frac{k_{_{test}}^{\frac{3}{2}}}{\widetilde{\Delta}}
=
\left(\nu+\nu_{_{SGS}}\right)\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right) \\
\\ \rightarrow \quad
C_{\varepsilon}
=
\frac{\left(\nu+\nu_{_{SGS}}\right)\widetilde{\Delta}}{k_{_{test}}^{3/2}}\left(\widetilde{\frac{\partial \overline{u}_{i}}{\partial x_{j}}\frac{\partial \overline{u}_{i}}{\partial x_{j}}}
-\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\frac{\partial \widetilde{\overline{u}}_{i}}{\partial x_{j}}\right) \\
\end{align}
参考
≫OpenFOAM User Guide Dynamic k eqn
≫W-W Kim and S. Menon. A new dynamic one-equation subgrid-scale model for large eddy simulations. In 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 1995.
以下のサイトにあるPDFのpp.184-193が上記の論文
≫A New Approach to Validate Subgrid Models in Complex High Reynolds Number Flows.
k Equationモデルは,フィルター幅\(\Delta\)とSGS乱流エネルギー\(k_{_{SGS}}\)を用いてSGS渦粘性係数を与える1方程式モデルである
Dynamic k Equationモデルを使えば,2つの係数\(C_{k}\),\(C_{\varepsilon}\)を動的に計算することができる
スケール相似則モデル
GS成分のうちの比較的小さなスケールの変動と,SGS成分のうちの比較的大きなスケールの変動が相似であるという考え方をスケール相似則という
スケール相似則を用いると,SGS応力は次のようにモデル化される
\begin{equation}
\tau_{ij}=\overline{\overline{u}_{i}\overline{u}_{j}}-\overline{\overline{u}}_{i}\overline{\overline{u}}_{j}
\end{equation}
スケール相似則モデルのメリットとデメリットは次の通り
DNSのデータから得られたSGS応力テンソルの各成分に対して比較的高い相関がある
スケール相似則モデル単体では十分な散逸を与えることができず,数値的に不安定である
デメリットにある数値的な不安定さゆえ,スケール相似則モデルは単独で用いられることはなく,後述の混合モデルとして用いられる
スケール相似則
SGS成分の定義式 \(u'_{i}=u_{i}-\overline{u}_{i}\) の両辺にさらにフィルターをかけると次のようになる
\begin{equation}
\overline{u'}_{i}=\overline{u}_{i}-\overline{\overline{u}}_{i}
\tag{i}
\end{equation}
左辺の\(\overline{u'}_{i}\)は,フィルターをかけることによって粗視化された変動量であり,\(u'_{i}\)のうちの大きなスケールを意味する
右辺第2項の\(\overline{\overline{u}}_{i}\)はフィルターをかけることによってさらに粗視化されたGS成分であり,\(\overline{u}_{i}\)のうちのより大きなスケールを意味しているので,右辺全体の \(\overline{u}_{i}-\overline{\overline{u}}_{i}\) はGS成分とGS成分のうちのより大きなスケールとの差,すなわちGS成分のうちの小さいスケールを意味している
以上の考察から,(i)の等式は,SGS成分\(u'_{i}\)のうちの大きなスケールとGS成分\(\overline{u}_{i}\)のうちの小さいスケールが相似であることを意味しており,このことをスケール相似則という
Bardinaモデル
上記のスケール相似則の考え方を用いて,BardinaはSGS応力のクロス項とSGSレイノルズ応力項にたいして以下のモデルを提案した
(クロス項:crossTerm)
\begin{equation}
C_{ij}=\overline{\overline{u}_{i}u'_{j}}+\overline{u'_{i}\overline{u}_{j}}
=\overline{\overline{u}}_{i}\left(\overline{u}_{j}-\overline{\overline{u}}_{j}\right)
+\left(\overline{u}_{i}-\overline{\overline{u}}_{i}\right)\overline{\overline{u}}_{j}
\end{equation}
(SGSレイノルズ応力:SGS Reynolds stress)
\begin{equation}
R_{ij}=\overline{u'_{i}u'_{j}}
=C_{B}\left(\overline{u}_{i}-\overline{\overline{u}}_{i}\right)\left(\overline{u}_{j}-\overline{\overline{u}}_{j}\right), \qquad C_{B}=1
\end{equation}
ここで,レナード項
\begin{equation}
L_{ij}=\overline{\overline{u}_{i}\overline{u}_{j}}-\overline{u}_{i}\overline{u}_{j}
\end{equation}
はGS成分の速度にフィルターをかけることで直接計算できるので,Bardinaによるスケール相似則モデルは次のようになる
\begin{align}
\tau_{ij}
&=L_{ij}+C_{ij}+R_{ij} \\
&=\left(\overline{\overline{u}_{i}\overline{u}_{j}}-\overline{u}_{i}\overline{u}_{j}\right)
+\left\{\overline{\overline{u}}_{i}\left(\overline{u}_{j}-\overline{\overline{u}}_{j}\right)+\left(\overline{u}_{i}-\overline{\overline{u}}_{i}\right)\overline{\overline{u}}_{j}\right\}
+\left\{\left(\overline{u}_{i}-\overline{\overline{u}}_{i}\right)\left(\overline{u}_{j}-\overline{\overline{u}}_{j}\right)\right\} \\
&=\overline{\overline{u}_{i}\overline{u}_{j}}-\overline{\overline{u}}_{i}\overline{\overline{u}}_{j}
\end{align}
混合モデル
数値安定性があり,エネルギー散逸の表現にたけているSGS渦粘性モデルと,SGS応力テンソルの各成分に対して高い相関を得ることができるスケール相似則モデルは,それぞれ別の役割を担っているといえる
それら2つのモデルを組み合わせたモデルを混合モデルといい,次の式で表される
\begin{equation}
\tau_{ij}^{a}=-2\nu_{_{SGS}}S_{ij}+\tau'_{ij}
\end{equation}
ここで,\(\tau'_{ij}\)はスケール相似則モデルによるSGS応力テンソルである
RANSにおける非線形渦粘性モデルの非線形項\(N_{ij}\)と同様に,混合モデルにおけるスケール相似則モデルのSGS応力テンソルはFiltered Navier-Stokes方程式において外力項として組み込まれる
\begin{equation}
\frac{\partial \overline{u}_{i}}{\partial t}
+\frac{\partial \left(\overline{u}_{i}\overline{u}_{j}\right)}{\partial x_{j}}
=
-\frac{1}{\rho}\frac{\partial \overline{P}}{\partial x_{i}}
+\frac{\partial}{\partial x_{j}}\left\{\nu_{e}\left(\frac{\partial \overline{u}_{i}}{\partial x_{j}}+\frac{\partial \overline{u}_{j}}{\partial x_{i}}\right)\right\}
+\frac{\partial}{\partial x_{j}}\tau'_{ij}
\end{equation}
スケール相似則モデルは,GSのうちの小さいスケールとSGSのうちの大きいスケールが相似であることを利用したモデルである
SGS応力テンソルの各成分に対して高い相関を与えるモデルだが,単独では数値的に不安定なため,Smagorinskyモデルやk Equationモデルに付加する形で混合モデルとして使われる
フィルター幅の計算
Smagorinskyモデル,Dynamic Smagorinskyモデル,k Equationモデル,Dynamic k Equationモデルでは,フィルター幅\(\Delta\)を計算する必要がある
\(\Delta\)の計算には次のような方法がある
(セルの体積の3乗根)
\begin{equation}
\Delta=\sqrt[3]{\Delta_{x}\Delta_{y}\Delta_{z}}
\end{equation}
(セルの対角線の長さ)
\begin{equation}
\Delta=\sqrt{\Delta_{x}^{2}+\Delta_{y}^{2}+\Delta_{z}^{2}+}
\end{equation}
(セルの最長の辺の長さ)
\begin{equation}
\Delta=\mathrm{max}\left(\Delta_{x},\Delta_{y},\Delta_{z}\right)
\end{equation}
(セルの面の最大面積の平方根)
\begin{equation}
\Delta=\sqrt{\mathrm{max}\left(\Delta_{x}\Delta_{y},\Delta_{y}\Delta_{z},\Delta_{z}\Delta_{x}\right)}
\end{equation}
よく使われるのは上の2つだが,\(\Delta\)の決め方は一意ではないので,そのモデルが推奨している\(\Delta\)があればそれを使う必要がある
まとめ
流れの数値シミュレーションは大きく以下の手順で行う
- 再現しようとしている流れのモデル化
- 計算格子の作成および偏微分方程式の離散化
- 計算の実行
- 結果の可視化
今回の記事では(1)に関連して,モデル化の手法の1つであるLESについて説明した
LESには大きく分けてSmagoriskyモデル,k Equationモデルの2つのモデルがあり,それぞれに対して係数を動的に計算するDynamicモデルと,スケール相似則との混合モデルが存在する
RANSに比べると計算コストが非常に高いが,そのぶん高い精度で計算ができるので,コンピューターの性能向上に伴って普及していくと考えれれる
RANSの記事を書く時と比べると,参考文献でも記述があいまいな箇所が多く,まだまだ未完成なモデルであるように感じた
次回は,いよいよNavier-Stokes方程式の離散化について説明していく
↓まとめ記事
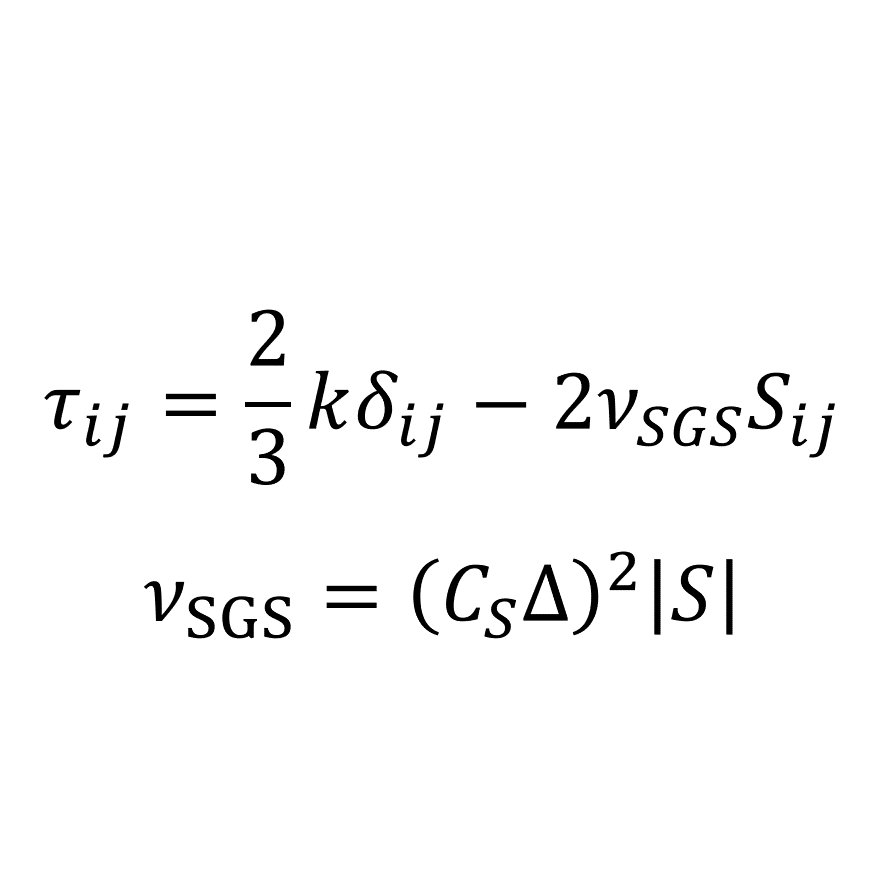


コメント